Unsupervised Analysis of Cyclist Performance for Route Segmentation

and Ranking

Rensso Mora-Colque

1 a

and William Robson Schwartz

2 b

Data Science Department, Universidad de Ingenieria y Tecnologia UTEC, Barranco, Lima, Peru

Department of Computer Science, Universidade Federal de Minas Gerais, Belo Horizonte - MG, Brazil

Keywords:

Cyclist Behavior Analysis, Unsupervised Learning, Temporal Series Autoencoder, Smart Mobility Data.

Abstract:

This paper presents a study on the analysis of cycling tours along a designated route, addressing the limited

attention given to non-professional cyclists in existing research. Unlike previous work focused on elite ath-

letes, this study considers a broader population, including commuters, recreational riders, and ﬁtness-oriented

cyclists. Data was collected using advanced sensors to capture diverse ride characteristics. An unsupervised

learning approach was applied to segment cyclists based on behavioral and performance patterns. Further-

more, a novel ranking method based on genetic algorithms was developed to classify and prioritize cyclist

groups meaningfully. Experiments were conducted on a newly proposed dataset tailored to this objective, en-

abling deeper insights into cycling dynamics across user types. The results validate the effectiveness of both

the segmentation and ranking methods, offering practical implications for route planning and cyclist-focused

infrastructure management.

1 INTRODUCTION

In recent years, the analysis of amateur cycling data

has gained signiﬁcant attention due to the growing

popularity of cycling as both a sport and a means of

transportation (Holmgren et al., 2017). With advance-

ments in wearable technology and sensors devices, a

substantial amount of data is generated by amateur

cyclists (De Brouwer et al., 2018b), providing a rich

source of information for clustering and prediction

tasks (Hilmkil et al., 2018a). For instance, the ap-

plication of clustering algorithms can help in iden-

tifying different cycling behavior patterns and opti-

mizing group training sessions (Dalton-Barron et al.,

2022). Predictive models can further enhance in-

dividual training plans by forecasting performance

outcomes based on historical data (Mirizio et al.,

2021a). Moreover, the ﬁndings can inform city plan-

ners and policymakers to improve cycling infrastruc-

ture, promoting sustainable transportation (Kaiser,

2023). However, most research focuses on profes-

sional cyclists, often neglecting those who cycle for

purposes other than professional competition. This

study aims to address that gap by providing a com-

https://orcid.org/0000-0003-4734-8752

https://orcid.org/0000-0003-1449-8834

prehensive analysis of the general cyclist, considering

the various motivations and contexts in which cycling

occurs beyond the realm of professional sports.

Nowadays, technology has become a part of the

vast majority of people who engage in any sport (Aro-

ganam et al., 2019). The world of cycling is no excep-

tion, and there is a lot of enthusiasm among cyclists

because information about their routes can be visual-

ized on mobile devices, providing technological sup-

port (Kapousizis et al., 2022). The data displayed can

be diverse; however, in many cases, it is merely infor-

mative and does not imply any intelligence that would

allow an analysis of the route taken. Although the

goals for which people cycle can vary greatly (Zhang

et al., 2024), many cyclists use various computational

models to monitor or track their activity.It is impor-

tant to consider that our work ﬁts into an initial con-

text where, while cyclists may not be professionals,

they at least use basic sensors to monitor their devel-

opment as cyclists. In other words, cyclists want to

understand how they perform in their cycling activity.

Although it is relatively straightforward to differ-

entiate an elite athlete who participates in competi-

tions (Martinez-Noguera et al., 2021), it is more chal-

lenging to do the same for other cyclists, as their goals

can vary widely (van Bon and Vroemen, 2019). This

complicates the deﬁnition of what constitutes an ama-

Mora-Colque, R. and Schwartz, W. R.

Unsupervised Analysis of Cyclist Performance for Route Segmentation and Ranking.

DOI: 10.5220/0013722700003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 1, pages 461-468

ISBN: 978-989-758-770-2; ISSN: 2184-2809

461

teur cyclist. For example, people might ride bikes for

various reasons, such as transportation, health, recre-

ation, improvement of ﬁtness, or training (Fraboni

et al., 2021). In addition, professionals can share

these goals. This ambiguity is reﬂected in the lit-

erature, where a large majority of studies focus on

elite athletes (Phillips and Hopkins, 2020), speciﬁ-

cally on prediction models for races or route devel-

opment (Kataoka and Gray, 2019). However, with the

increasing number of cyclists and the use of new tech-

nologies, new models are necessary that include all

types of cyclist (Murillo Burford, 2020).

To delineate between a cyclist with general objec-

tives and a dedicated athlete, we can employ the no-

tion of metrics used to measure their level of train-

ing. Generally, a cyclist oriented towards competi-

tion conducts various tests to calculate values such as

PSP (Power Sustained Peak), FTP (Power Threshold

Function), and VO2 max, among others (Jeukendrup

and Diemen, 1998). These values help predict their

performance based on factors such as power output,

heart rate, caloric expenditure, and lactic acid usage.

Nonetheless, most cyclists do not perform these types

of tests. Therefore, we can establish a division be-

tween cyclists who train based on classical metrics

(whom we will call non-amateur cyclists) and those

who, for various reasons, do not perform these classi-

cal tests. Then, our study focuses on information that

can be obtained from the latter cyclists.

Our proposal aims to provide cyclists with infor-

mation about their performance on a speciﬁc route

through the analysis of cyclists who have completed

that route. Unlike an individual study, our model con-

ducts a collective study by collecting data from all

cyclists who complete the same route. With this in-

formation, the idea is to create clusters and provide

cyclists with insights into cyclist behavior. Also our

model provides a cluster categorization, in such a way

that they generate a growing categorical organization

based on optimization criteria. Therefore, our model

aims to generate meaningful groupings based on opti-

mization criteria, facilitating the categorization of cy-

clists. This enables cyclists seeking to improve their

performance to target climbs within their assigned

category. It is important to note that our model pro-

duces groupings speciﬁc to each route, which is rea-

sonable given that different routes serve distinct ob-

jectives. Consequently, the model can be effectively

applied across various contexts.

One of the main motivations is that there are many

enthusiastic cyclists interested in learning more about

their development with the bicycle (De Brouwer et al.,

2018a). This is important because it introduces the

need for models that provide more specialized infor-

mation to the cyclist. While cycling as a sport has

been studied for a long time by sports professionals, it

is important to highlight that our proposal and the fo-

cus of our study lie in a computational model. There-

fore, the idea is to provide a technological tool for all

types of cyclists. This poses a challenge as the met-

rics used require speciﬁc preparation and protocols,

along with information that a new or amateur cyclist

may not have. In this sense, the analysis conducted is

much broader, based on common information from a

particular route. The main contributions of our pro-

posed approach are: i) A simple model that allows

generating sets of cyclists and performing a classiﬁ-

cation based on that segmentation. ii) A new database

that contains a diversity of types of cyclists, including

non professional individuals. iii) The proposed model

performs an unsupervised analysis of a speciﬁc route,

providing a ranking of the established clusters.

2 RELATED WORK

Collective Analysis and Hierarchy. An important as-

pect in most studies is the number of athletes or cy-

clists observed for the analyses. Usually, they em-

ploy between ﬁve to ﬁfteen cyclists (Hilmkil et al.,

2018b; Thiel and Sarkar, 2014). Despite the fact that

this range of values can be somewhat arbitrary, we

can divide the studies into two groups: those that em-

ploy a few cyclists for their research and those where

the number of cyclists exceeds hundreds (Mart

ınez-

Cevallos et al., 2020; Baron et al., 2023). With the

latter group being the focus of our analysis.

The idea of being able to perform clustering is

precisely to create a kind of hierarchy where the cy-

clist can somehow determine the characteristics of the

group to which they belong (Cejuela et al., 2024).

Some works present hierarchies based on the gen-

eral objective of the paper. We can highlight pro-

posals (Mart

ınez-Cevallos et al., 2020; Gallo et al.,

2021) that are based on data analysis from survey in-

formation, where the process is more statistical and

does not require an advanced learning model (Mirizio

et al., 2021b). Other models (Cesanelli et al., 2024)

use information from cyclists to generate hierarchies

using computational algorithms; however, these anal-

yses are usually not collective in nature, as the focus

of these works is more individual. Our model aims to

propose a hierarchy based on a collective analysis of

the data. This analysis can be conducted with limited

sensor information and in various cycling contexts.

A similar work to ours is proposed in (van der

Zwaard et al., 2019), which aims to categorize cy-

clists using unsupervised analysis through clustering

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

462

algorithms like K-means. However, this study uses

static information regarding the cyclists, whereas our

model introduces temporal data from bicycle sensors,

providing a different perspective on the information.

Clustering Methods. In the realm of clustering

and classiﬁcation, recent research has employed var-

ious algorithms to segment athletes based on phys-

iological and performance data. One study clas-

siﬁed cyclists according to their fatigue outcomes

from ultra-endurance events, using cluster analysis

to identify distinct groups with different fatigue re-

sponses (Lewis et al., 2016). Another study utilized

k-means clustering to group amateur cyclists based

on observational data, which helped in understanding

different training and performance proﬁles (Priego

et al., 2018). However, clustering and classiﬁcation

models also have their drawbacks. One of the main

challenges is the high variability in cyclists’ perfor-

mance data, which can lead to overﬁtting in classiﬁ-

cation models. Moreover, many studies focus on elite

athletes, often neglecting recreational or less compet-

itive cyclists. This gap indicates a need for more in-

clusive research that encompasses a broader spectrum

of the cycling population. Despite these challenges,

the use of clustering and classiﬁcation in cycling re-

search shows promise. For example, cluster analy-

sis has been used effectively to understand the im-

pact of different training regimens on cyclists’ per-

formance and to tailor training programs accordingly

(Ørtenblad et al., 2013). Additionally, classiﬁcation

models have been instrumental in identifying key fac-

tors that inﬂuence performance and recovery in ultra-

endurance events (Mrakic et al., 2015).

3 APPROACH

Route Representation. Given a speciﬁc route, we de-

ﬁne a set R, where each element r ∈ R represents a cy-

clist’s completion of the route. Each observation r is a

sequence of variables p, such as speed, heart rate, and

power output, collected over time. The data construc-

tion process is detailed in Section 4. Importantly, the

number of observations within each r may vary due

to differences in completion times among cyclists. To

generate a compact, unsupervised representation of

the performance of a cyclist on a route, we use a time

series autoencoder, a well-established technique for

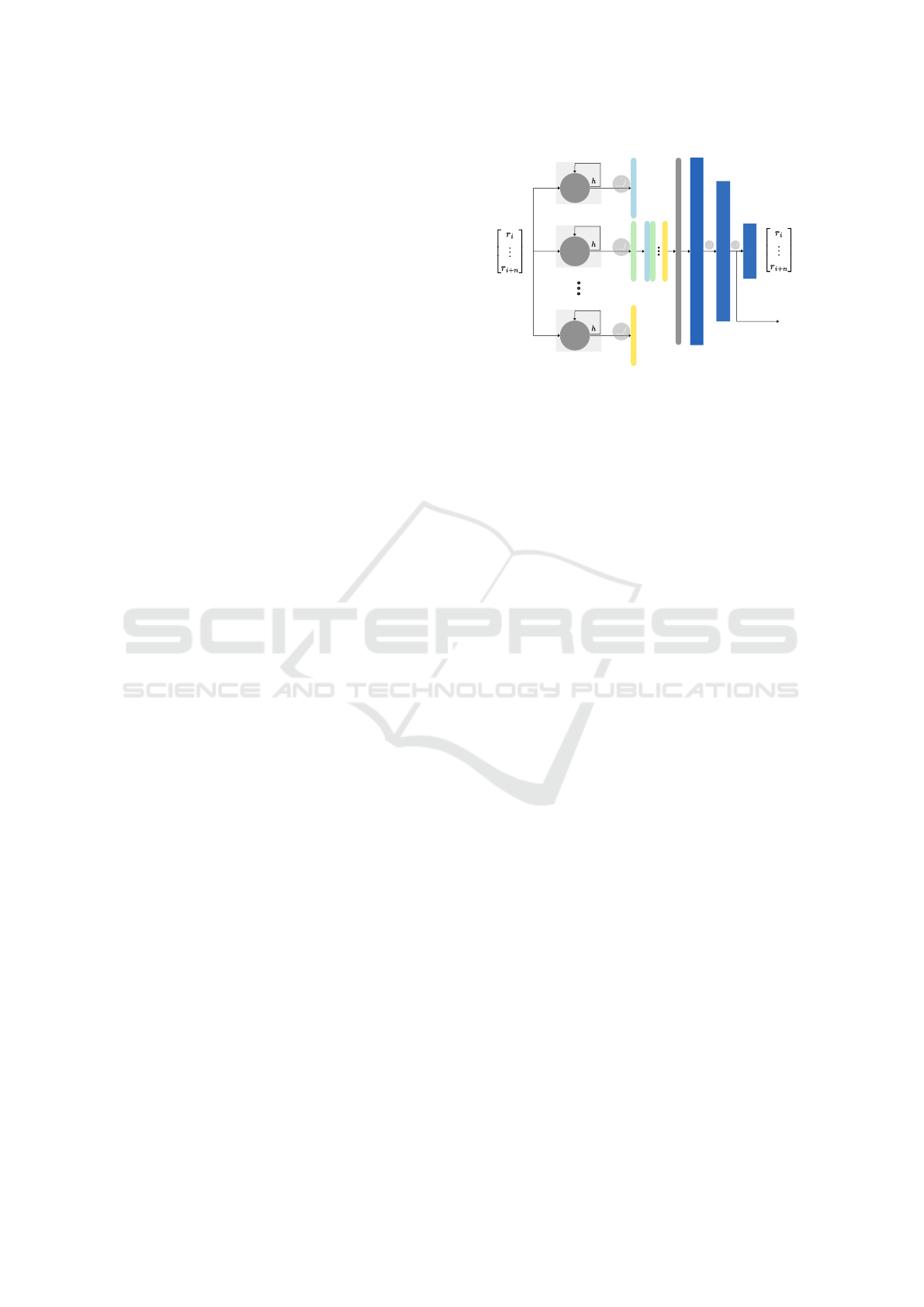
encoding temporal data.The proposed architecture is

shown in Figure 1. The input to the model consists

of sequential segments r[i, i + 1, . . . , i + l] ∈ r at time

step i, where l deﬁnes the temporal window. Each

variable is processed through an LSTM cell, with the

resulting hidden states (h) stacked and ﬂattened. This

Relu

LSTM

Stack

Flat

MLP

Features

LSTM

Relu

LSTM

...

Figure 1: Time series autoencoder architecture. The en-

coder processes sequential segments using LSTM cells,

while the decoder reconstructs the signal through MLP lay-

ers. The latent representation is extracted from the second

MLP layer.

representation is passed through three multilayer per-

ceptron (MLP) layers, introducing a bottleneck at the

second layer. The output of this bottleneck layer de-

ﬁnes the feature vector f

. Subsequently, the model

reconstructs the original sequence, and training is

guided by a Mean Squared Error (MSE) loss function.

The core idea behind this architecture is to leverage

LSTM cells to capture temporal dependencies, while

the MLP layers combine and abstract these dependen-

cies into a concise feature representation, effectively

integrating both sequential patterns and multivariate

relationships.

Dual-Stage Clustering. Although simple, the bag-

of-words model remains widely used in various do-

mains (Bakheet et al., 2023). We adopt this ap-

proach in a two-stage clustering process. First, the K-

means algorithm is applied to the set of segment fea-

ture vectors F

extracted from the autoencoder, pro-

ducing K centroids. Using the same temporal seg-

mentation as in the autoencoder input, each segment

is assigned to its nearest centroid. This assignment

builds a histogram g

representing the distribution

of feature types throughout the route. Next, a sec-

ond clustering step is performed on the set of his-

tograms g

. At this stage, Spectral Clustering (Ng

et al., 2001) is employed to partition the data into

a set of clusters C. The reason for using two dif-

ferent clustering algorithms lies in the nature and

goals of each stage. Initially, K-means efﬁciently

captures diverse patterns across a large set of time-

series segments. Subsequently, Spectral Clustering,

which excels in identifying non-convex and intricate

data structures, organizes the histograms into more

meaningful groups. This dual-stage clustering strat-

egy ensures both ﬁne-grained feature discovery and

high-level pattern grouping, ultimately enhancing the

Unsupervised Analysis of Cyclist Performance for Route Segmentation and Ranking

463

interpretability of the results.

Group Categorization. Based on the centroids C ob-

tained in the previous stage, our model builds a hier-

archical categorization of cyclist behavior. To achieve

this, we apply NSGA-II, a widely used genetic algo-

rithm for multi-objective optimization (Yang, 2014).

In our setting, NSGA-II ranks the clusters by opti-

mizing a set of domain-speciﬁc objectives, reﬂecting

characteristics that we seek to maximize or minimize.

The output is an ordered list of clusters, providing

a categorization criterion grounded in multiple rele-

vant variables. It is crucial to note that the goal of

this categorization is not to summarize cyclists based

on a single variable but to organize them based on

multivariate behavior patterns observed during route

completion. By grouping cyclists with similar multi-

dimensional performance proﬁles, our model offers a

reference framework for cyclists to assess their pro-

gression and identify performance benchmarks rela-

tive to others who completed the same route. This

structured categorization facilitates meaningful com-

parisons and provides deeper insights into training

and competition strategies.

4 EXPERIMENT RESULTS AND

DISCUSSION

To conduct the experiments, we introduced a new

dataset called Lagoa. It contains information from

several cyclists performing a route around the Pam-

pulha Lagoon located in Belo Horizonte, Minas

Gerais, Brazil. The data are: time, heart rate,

smoothed velocity, grade smooth, watts, distance and

other variables that were not considered in our analy-

sis because they appeared only in the records of a few

cyclists. The database contains information on 126

cyclists, for whom |R| = 1014 rides were recorded.

The vast majority of cyclists rode around the lake

multiple times.

Data Preparation. The Lagoa dataset consists of a

list of observations. Each observation represents the

start and end of an entire route taken by the cyclist.

Speciﬁcally, it records the complete lap around the la-

goon, which has a perimeter of 18 km. Each element

is composed of four main data points: observations

per unit of time, cyclist ID, general statistics, and the

date when the route was completed. In our experi-

ments, we only used the observations r for clustering

and data analysis, and the cyclist ID r

for classiﬁca-

tion.

Essentially, r is the time series in the form of a

matrix with n rows and m columns, where each row

represents data collected at a speciﬁc time t. This

information is obtained from sensors installed on the

bicycle or carried by the cyclist. A key feature of

our study is the use of data from popular sensors that

most cyclists can install on their bicycles. In our anal-

ysis, we use information on speed, heart rate, and

watts. Additionally, we employ grade smooth also for

a better analysis. We include the time information in

each row to enable preprocessing since, in the obser-

vations, data recording does not always occur every

second. To minimize the processing time of the au-

toencoder and avoid redundant data, we use intervals

of q = 5 seconds, nonetheless for ﬁnal cyclist repre-

sentation, the interval is q = 1, we can see this in-

terval as the overlapping in a time series. Thus, if a

cyclist records data every second, we take the aver-

age of all information in the q interval. Generally, in

the database, the recording interval does not exceed

this time. Another important aspect of the database is

that while most cyclists complete the full lap, a small

group does not reach 18 km. Therefore, to obtain a

consistent dataset, we ﬁlter using the distance trav-

eled, ensuring that all cyclists covered at least 16 km,

which becomes our endpoint. This allows us to in-

clude the information of all cyclists in the database.

Note that although we use the time and distance data

present in the database observations, these variables

will not be part of the data representation process.

Experiments Methodology. For our experiments, we

used two conﬁgurations that differ primarily by the in-

troduction of an additional variable in the time series.

The ﬁrst conﬁguration A, uses the variables: speed,

heart rate, and watts. In the second conﬁguration B,

we added the variable grade smooth to the existing

conﬁguration A. Our proposal was developed using

a computer with 25 GB of RAM, 40 core processors,

and a 11 GB of memory GeForce GTX 1080 Ti graph-

ics card. The complete framework was deployed in

Python language.

Autoencoder Training and Feature Extraction. For

training the autoencoder, the Adam optimizer was

utilized. The model underwent 20 epochs to opti-

mize the MSE loss function. For this training, each

dataset was divided into 80% for training and 20%

for validation, with elements selected randomly. Be-

fore starting the training of the models, the data was

normalized using Z-normalization. For conﬁguration

A, the loss value was 0.0005 for validation and test-

ing. In the case of conﬁguration B, the loss value were

0.0011 and 0.0019 for validation and testing, respec-

tively. The autoencoder takes time series as input and

output, and the time range l used in our experiments is

10 observations. Note that the model varies according

to the number of variables used. In the case of con-

ﬁguration A, the initial part of the encoder consists of

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

464

three layers containing LSTM cells, whereas in con-

ﬁguration B, there are four LSTM cells. Once the

network was trained, for both conﬁgurations A and

B, features were extracted from all elements associ-

ated with each conﬁguration. To clarify, in conﬁgu-

ration A, the data contains only three variables, while

in conﬁguration B, information from another sensor

is added. Certainly, the data is the same, but with an

additional variable. However, the autoencoder model

changes in the number of LSTM cells.

Clustering. The clustering stage is divided into two

processes: time window clustering and clustering for

the generation of a bag of words. The objective is to

describe small route segments r[i, i + l] and use this

granular information to describe the entire route r.

(a) Conﬁguration A

(b) Conﬁguration B

Figure 2: T-SNE visualization of both conﬁgurations of all

routes R in dataset. These ﬁgures present the c = 8 centroids

generated by Spectral clustering.

Figure 3: Clustering evaluation metrics across different

numbers of clusters The vertical dashed lines at k=64 and

k=128 highlight a candidate value.

The ﬁrst clustering uses features extracted from

the autoencoder. Given a time window of l = 10 with

a stride of s = 5 observations of the time series, this

means that the features extracted from the autoen-

coder correspond to a minimum span of 50 seconds

(in our dataset). These feature vectors are grouped

into k = 64 clusters. The choice of k = 64 emerges as

a suitable balance between cluster compactness, sep-

aration, and model complexity. At this value, the in-

ertia shows diminishing returns (elbow point), the sil-

houette score remains positive, unlike at higher val-

ues where it becomes negative, and both the Davies-

Bouldin and Calinski-Harabasz indices indicate stable

and well-deﬁned clustering. This suggests that k = 64

provides meaningful structure without overfragment-

ing the data. Figure 3 graphically presents this analy-

sis.

Once the k centroids are obtained, the route de-

scriptor is constructed using a bag-of-words strat-

egy (Jurafsky and Martin, 2009). In this case, the

stride within the time series is s = 1, ensuring that

each route segment contributes information to the cre-

ation of the feature vector g

(64 dimensions). Fig-

ure 2 shows the segments generated using the Spectral

Clustering algorithm. For visualization purposes, we

use T-SNE for dimensionality reduction. In our exper-

iments, the number of selected segments or clusters is

8, and the number of components is the same. The

afﬁnity matrix is constructed by calculating the graph

with nearest neighbors, and the number of different

K-means seeds is set to 10. To facilitate interpretation

of Figure 2, Table 1 presents the mean and standard

deviation of the elements belonging to each segment

for both conﬁgurations. The numbers and colors in

Figure 2 correspond to the values in the Class column

of Table 1.

Ranking the Segments. To generate the cluster rank-

ing, NSGA-II (Yang, 2014) genetic algorithm is em-

ployed. The input to this model is a matrix for each

conﬁguration, containing the means of the centroids

(the µ columns of each variable in Table 1). The

data is normalized using Z-scaling before being used

as input. The hyperparameter n speciﬁes the num-

ber of times the generator function is called to cre-

ate an individual, with n=3 indicating that each indi-

vidual is initialized with three genes. An important

hyperparameter in the ﬁnal stage of our framework

is the weight vector of the ﬁtness function. For the

experiments conducted, the vector is [0.3, −0.3, 0.4]

(speed, heart rate, watts), aiming to maximize speed

and watts while minimizing heart rate. This distribu-

tion is inspired by the studies presented by (Garvican

et al., 2015) and is crucial for optimizing cyclist per-

formance metrics.

In Tables 2 and 3, the ranking generated by the

optimization algorithm is shown. The ‘Class’ column

represents the cluster number, colored according to

its assigned color. Cells with the highest (dark gray)

and lowest (light gray) values in each column are also

Unsupervised Analysis of Cyclist Performance for Route Segmentation and Ranking

465

Table 1: Variable centroids for conﬁgurations A and B.

Conﬁguration A Conﬁguration B

Velocity Heartrate Watts Velocity Heartrate Watts

Class µ σ µ σ µ σ µ σ µ σ µ σ

0 9.70 0.35 148.44 4.08 192.26 18.03 9.09 0.37 144.58 3.78 173.61 20.38

1 10.90 0.54 152.84 4.67 232.71 32.94 8.99 0.34 125.67 2.85 163.67 15.86

2 8.52 0.36 133.01 3.41 147.41 20.68 10.19 0.31 112.50 3.18 180.83 20.09

3 8.75 0.33 161.09 4.11 169.20 18.15 7.89 0.25 110.63 3.46 124.17 16.59

4 7.16 0.36 143.40 3.51 142.85 15.67 11.58 0.55 170.44 4.33 252.31 17.35

5 7.86 0.16 105.58 2.34 125.65 13.06 7.01 0.22 143.44 2.93 145.35 9.27

6 12.02 0.30 158.44 1.59 200.62 72.80 10.95 0.52 148.42 4.63 220.39 37.46

7 9.78 0.32 113.31 2.90 174.11 14.48 8.84 0.32 162.86 4.24 175.63 17.63

highlighted. The algorithm creates a hierarchy that

ranks the groups based on a speciﬁc criterion. In our

experiment, the goal is to minimize heart rate while

maximizing both watts and velocity. In the weighting

used, slightly more importance is given to watts, as

velocity is highly correlated with power output.

Table 2: Conﬁguration A (Data ordered by Rnk in descend-

ing order).

Measurements

Class Velocity Heartrate Watts Rnk

1 10.90 152.84 232.71 7

6 12.02 158.44 200.62 6

7 9.78 113.31 174.11 5

0 9.70 148.44 192.26 4

5 7.86 105.58 125.65 3

2 8.52 133.01 147.41 2

3 8.75 161.09 169.20 1

4 7.16 143.40 142.85 0

Table 3: Conﬁguration B (Data ordered by Rnk in descend-

ing order).

Measurements

Class Velocity Heartrate Watts Rnk

4 11.58 170.44 252.31 7

6 10.95 148.42 220.39 6

2 10.19 112.50 180.83 5

1 8.99 125.67 163.67 4

0 9.09 144.58 173.61 3

3 7.89 110.63 124.17 2

7 8.84 162.86 175.63 1

5 7.01 143.44 145.35 0

Discussion. In this section, we will discuss several

key aspects of our research, starting with the proposed

model, examining variables, and analyzing speciﬁc

points from the results.

Although the proposed model, as a feature extrac-

tor, presents a relatively simple architecture, it is ef-

fective for our purposes. It is important to highlight

that the algorithm’s primary objective is to achieve a

representation of the route or tour. From a modular

perspective, our approach requires a model that char-

acterizes the tour. Given the unsupervised nature of

our method, we can assert, based on the visualiza-

tion in Figure 2 and the data from Table 1, that the

autoencoder successfully describes the segments con-

sidering the employed variables. This is signiﬁcant as

our model differs from conventional models that pro-

cess multivariate time series data. In our case, the ﬁrst

MLP layer handles this information processing.

The selection of the number of clusters is another

important aspect to discuss. Given that these values

are somewhat arbitrary, we chose 64 clusters for the

K-means algorithm and 8 clusters for the spectral al-

gorithm. These choices are justiﬁed as follows: In

the case of K-means clustering, determining the num-

ber of segments is difﬁcult without prior knowledge

of the route or a criterion to establish an appropri-

ate number of clusters for a given route. To ensure

robustness across different types of routes, we based

the selection on the number of segments that could

be generated from the route information. Speciﬁcally,

the 64 clusters generate sufﬁcient information for the

histograms that describe the routes to be representa-

tive. Although this choice is somewhat arbitrary and

dependent on the number of observations per tour, we

found it suitable for our experiments, especially after

conducting tests with 128 clusters. For spectral clus-

tering, which uses only 8 clusters, we selected this

number primarily because, in an unsupervised setting,

we can assume the number of groups we want to rep-

resent. Determining the exact number is challenging,

as cyclists undertaking the routes are not necessarily

professionals or trained athletes (Lewis et al., 2016),

thus excluding models that rely on precise metrics like

VO2max or FTP (Pardo Albiach et al., 2021) or an-

thropometric measures (van der Zwaard et al., 2019).

Our experiments aim to demonstrate that it is possible

to generate sets and provide a ranking, with the num-

ber of sets being a hyperparameter for further study.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

466

We believe that the choice of values is not a limita-

tion but rather parameters that can be ﬁne-tuned de-

pending on the speciﬁc characteristics of the routes

our model is applied to. However, we consider it

a good starting point for future research (de Leeuw

et al., 2023) on our proposal and new models that ex-

plore the optimal selection of hyperparameters.

Given the information on speed, power (watts),

and heart rate, a cyclist typically aims to achieve

higher speeds or generate more power while mini-

mizing their heart rate (Mazzoleni et al., 2016). This

goal reﬂects the desire to enhance performance by in-

creasing speed and power output—indicators of im-

proved athletic capability—without corresponding in-

creases in physiological strain (Burke, 2001). By

maintaining a lower heart rate, the cyclist can reduce

fatigue and sustain high performance over longer peri-

ods (Schnohr et al., 2006). Therefore, the objective is

to optimize these metrics to become faster and more

powerful while experiencing less fatigue, ultimately

improving overall efﬁciency and endurance.

5 CONCLUSIONS

This study presents an innovative approach to analyz-

ing and clustering cyclists along a given route, regard-

less of their experience or physical condition. Using

autoencoders, we model the routes and apply unsu-

pervised learning to segment cyclists and rank them

meaningfully, despite challenges such as data vari-

ability, sensor limitations, and the absence of stan-

dardized physical metrics. Our method is designed

to work with basic, low-cost sensors and considers

the diverse motivations behind cycling. The proposed

model enables the positioning of new cyclists within

identiﬁed clusters and offers general yet practical in-

sights applicable to various types of users and routes.

We also highlight opportunities for future work, in-

cluding expanding the dataset and exploring hyperpa-

rameter tuning to reﬁne behavioral analysis and pro-

vide personalized recommendations based on cluster

proﬁles.

ACKNOWLEDGEMENTS

The authors would like to thank the National Coun-

cil for Scientiﬁc and Technological Development –

CNPq (Grant 312565/2023-2).

REFERENCES

Aroganam, G., Manivannan, N., and Harrison, D. (2019).

Review on wearable technology sensors used in con-

sumer sport applications. Sensors, 19(9).

Bakheet, S., Al-Hamadi, A., Soliman, E., and Heshmat,

M. (2023). Hybrid bag-of-visual-words and fea-

turewiz selection for content-based visual information

retrieval. Sensors, 23(3).

Baron, E., Janssens, B., and Bogaert, M. (2023). Bike2vec:

Vector embedding representations of road cycling rid-

ers and races. In Proceedings of the 10th MathSport

International Conference.

Burke, L. (2001). Improving cycling performance: How

should we spend our time and money? Sports

Medicine, 31(7):521–532.

Cejuela, R., Ar

evalo-Chico, H., and Sell

es-P

erez, S. (2024).

Power proﬁle during cycling in world triathlon series

and olympic games. Journal of Sports Science and

Medicine, 23(1):25–33.

Cesanelli, L., Lagoute, T., Ylaite, B., Calleja-Gonz

alez, J.,

Fern

andez-Pe

na, E., Satkunskiene, D., Leite, N., and

Venckunas, T. (2024). Uncovering success patterns

in track cycling: Integrating performance data with

coaches and athletes’ perspectives. Applied Sciences,

14(7).

Dalton-Barron, N., Palczewska, A., Weaving, D., Rennie,

G., Beggs, C., Roe, G., and Jones, B. (2022). Clus-

tering of match running and performance indicators

to assess between- and within-playing position simi-

larity in professional rugby league. Journal of Sports

Sciences, 40(15):1712–1721.

De Brouwer, M., Ongenae, F., Daneels, G., Municio, E.,

Famaey, J., Latr

e, S., and De Turck, F. (2018a). Per-

sonalized real-time monitoring of amateur cyclists on

low-end devices: Proof-of-concept & performance

evaluation. In WWW ’18: The Web Conference 2018,

pages 1833–1840.

De Brouwer, M., Ongenae, F., Daneels, G., Municio, E.,

Famaey, J., Latr

e, S., and De Turck, F. (2018b). Per-

sonalized real-time monitoring of amateur cyclists on

low-end devices: Proof-of-concept and performance

evaluation. In WWW ’18: Companion Proceedings of

the The Web Conference 2018, pages 1833–1840.

de Leeuw, A.-W., Oberkoﬂer, T., Heijboer, M., and Knobbe,

A. (2023). Athlete monitoring in professional road cy-

cling using similarity search on time series data. In

Brefeld, U., Davis, J., Van Haaren, J., and Zimmer-

mann, A., editors, Machine Learning and Data Min-

ing for Sports Analytics, pages 115–126. Springer Na-

ture Switzerland.

Fraboni, F., Prati, G., Casu, G., De Angelis, M., and Pietran-

toni, L. (2021). A cluster analysis of cyclists in eu-

rope: common patterns, behaviours, and attitudes.

Transportation, 49.

Gallo, G., Filipas, L., Tornaghi, M., Garbin, M., Codella,

R., Lovecchio, N., and Zaccaria, D. (2021). Thresh-

olds power proﬁles and performance in youth road cy-

cling. International Journal of Sports Physiology and

Performance.

Unsupervised Analysis of Cyclist Performance for Route Segmentation and Ranking

467

Garvican, L., Clark, B., Martin, D., Schumacher, Y., Mc-

Donald, W., and Stephens, B. (2015). Impact of al-

titude on power output during cycling stage racing.

PLOS ONE, 10(12):e0143028.

Hilmkil, A., Ivarsson, O., Johansson, M., Kuylenstierna,

D., and van Erp, T. (2018a). Towards machine learn-

ing on data from professional cyclists. In Proceedings

of the 12th World Congress on Performance Analysis

of Sports, pages 168–176, Opatija-Croatia. Faculty of

Kinesiology, University of Zagreb.

Hilmkil, A., Ivarsson, O., Johansson, M., Kuylenstierna, D.,

and van Erp, T. (2018b). Towards machine learning

on data from professional cyclists. In Proceedings of

the 12th World Congress on Performance Analysis of

Sports, pages 168–176, Opatija, Croatia. Faculty of

Kinesiology, University of Zagreb.

Holmgren, J., Aspegren, S., and Dahlstr

oma, J. (2017). Pre-

diction of bicycle counter data using regression. Pro-

cedia Computer Science, 113:502–507.

Jeukendrup, A. E. and Diemen, A. V. (1998). Heart rate

monitoring during training and competition in cy-

clists. Journal of sports sciences, 16 Suppl:S91–9.

Jurafsky, D. and Martin, J. H. (2009). Speech and language

processing. Prentice Hall series in artiﬁcial intelli-

gence. Prentice Hall, Pearson Education International,

2. ed., [pearson international edition] edition.

Kaiser, S. K. (2023). Predicting cycling trafﬁc in cities:

Is bike-sharing data representative of the cycling vol-

ume? In ICLR 2023 Workshop on Tackling Climate

Change with Machine Learning.

Kapousizis, G., Ulak, M., Geurs, K., and Havinga, P.

(2022). A review of state-of-the-art bicycle technolo-

gies affecting cycling safety: level of smartness and

technology readiness. Transport Reviews, 43:1–23.

Kataoka, Y. and Gray, P. (2019). Real-time power perfor-

mance prediction in tour de france. In Brefeld, U.,

Davis, J., Van Haaren, J., and Zimmermann, A., edi-

tors, Machine Learning and Data Mining for Sports

Analytics, pages 121–130, Cham. Springer Interna-

tional Publishing.

Lewis, N. A., Towey, C., Bruinvels, G., Howatson, G., and

Pedlar, C. R. (2016). Clustering classiﬁcation of cy-

clists according to the acute fatigue outcomes pro-

duced by an ultra-endurance event. European Journal

of Human Movement.

Martinez-Noguera, F., Alcaraz, P., Ortolano-R

ıos, R., Du-

four, S., and Mar

ın-Pag

an, C. (2021). Differences

between professional and amateur cyclists in endoge-

nous antioxidant system proﬁle. Antioxidants, 10:282.

Mart

ınez-Cevallos, D., Proa

no-Grijalva, A., Alguacil, M.,

Duclos-Bast

ıas, D., and Parra-Camacho, D. (2020).

Segmentation of participants in a sports event using

cluster analysis. Sustainability, 12(14).

Mazzoleni, M., Battaglini, C., Martin, K., et al. (2016).

Modeling and predicting heart rate dynamics across

a broad range of transient exercise intensities during

cycling. Sports Engineering, 19(2):117–127.

Mirizio, G. G., Mu

noz, R., Mu

noz, L., Ahumada, F., and

Del Coso, J. (2021a). Race performance prediction

from the physiological proﬁle in national level youth

cross-country cyclists. International Journal of Envi-

ronmental Research and Public Health, 18:5535.

Mirizio, G. G., Mu

noz, R., Mu

noz, L., Ahumada, F., and

Del Coso, J. (2021b). Race performance prediction

from the physiological proﬁle in national level youth

cross-country cyclists. International Journal of Envi-

ronmental Research and Public Health, 18:5535.

Mrakic, S., Gussoni, M., Moretti, S., Pratali, L., Giardini,

G., Tacchini, P., Dellanoce, C., Tonacci, A., Mastorci,

F., Borghini, A., Montorsi, M., and Vezzoli, A. (2015).

Effects of mountain ultra-marathon running on ros

production and oxidative damage by micro-invasive

analytic techniques. PLoS ONE, 10(11):e0141780.

Murillo Burford, E. (2020). Predicting cycling performance

using machine learning. Master’s thesis, Wake For-

est University Graduate School of Arts and Sciences,

Winston-Salem, North Carolina. A Thesis Submitted

in Partial Fulﬁllment of the Requirements for the De-

gree of Master of Science in Computer Science.

Ng, A., Jordan, M., and Weiss, Y. (2001). On spectral clus-

tering: Analysis and an algorithm. In Dietterich, T.,

Becker, S., and Ghahramani, Z., editors, Advances in

Neural Information Processing Systems, volume 14.

MIT Press.

Ørtenblad, N., Westerblad, H., and Nielsen, J. (2013). Mus-

cle glycogen stores and fatigue. The Journal of Phys-

iology, 591(18):4405–4413.

Pardo Albiach, J., Mir-Jimenez, M., Hueso Moreno, V.,

acher Molt

o, I., and Mart

ınez-Gramage, J. (2021).

The relationship between vo2max, power manage-

ment, and increased running speed: Towards gait pat-

tern recognition through clustering analysis. Sensors,

21(7).

Phillips, K. and Hopkins, W. (2020). Determinants of cy-

cling performance: a review of the dimensions and

features regulating performance in elite cycling com-

petitions. Sports Medicine - Open, 6.

Priego, J. I., Kerr, Z. Y., Bertucci, W. M., and Carpes, F. P.

(2018). The categorization of amateur cyclists as re-

search participants: Findings from an observational

study. Journal of Sports Sciences, 36(17):2018–2024.

Schnohr, P., O’Keefe, J. H., Marott, J. L., Lange, P., Jensen,

G. B., Riegger, G. A., Allard, N. A., and Green, C. A.

(2006). Intensity versus duration of cycling, impact

on all-cause and coronary heart disease mortality: the

copenhagen city heart study. European Journal of

Preventive Cardiology, 9(5):924–930.

Thiel, D. and Sarkar, A. (2014). Swing proﬁles in sport:

An accelerometer analysis. Procedia Engineering,

72:624–629.

van Bon, M. and Vroemen, G. (2019). Power speed proﬁle:

Performance model for road cycling.

van der Zwaard, S., de Ruiter, C. J., Jaspers, R. T., and

de Koning, J. J. (2019). Anthropometric clusters of

competitive cyclists and their sprint and endurance

performance. Frontiers in Physiology, 10.

Yang, X.-S. (2014). Chapter 14 - multi-objective optimiza-

tion. In Yang, X.-S., editor, Nature-Inspired Optimiza-

tion Algorithms, pages 197–211. Elsevier, Oxford.

Zhang, R., Te Br

ommelstroet, M., Nikolaeva, A., and Liu,

G. (2024). Cycling subjective experience: A concep-

tual framework and methods review. Transportation

Research Part F: Trafﬁc Psychology and Behaviour,

101:142–159.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

468