Optimizing Collision Avoidance in Dynamic Multi-Robot Systems:
A Velocity Obstacle and BB-PSO Approach with Priority Consideration
Luis H. Sanchez-Vaca
a
, Gildardo Sanchez-Ante
b
and Hernan Abaunza
∗ c
Tecnologico de Monterrey, Department of Computing, Gral. Ramon Corona 2514, Zapopan, JAL, Mexico
Keywords:
Multi-Robot Systems, Prioritized Navigation, Collision Avoidance, Velocity Obstacles, Particle Swarm
Optimization.
Abstract:
This study proposes integrating Reciprocal Velocity Obstacles (RVO) with Bare Bones Particle Swarm Opti-
mization (BB-PSO) for prioritized motion planning in multi-robot systems. BB-PSO was chosen because it
has fewer parameters to tune, reduced computational complexity, and provides potentially faster convergence
compared to standard PSO. The methodology enables collision avoidance and path planning while allowing
differentiated robot behaviors based on priority levels. Simulations used a two-phase experimental strategy:
first, tuning cost function parameters through grid search, and second, evaluating various priority configu-
rations and random scenarios. Results show that the selected weight configuration (α = 4,β = 2) balances
goal-seeking and obstacle avoidance, enabling high-priority agents to move directly while ensuring overall
group safety. Scenarios with higher average priorities exhibited shorter travel distances and faster completion
times, whereas those with lower or imbalanced priorities led to more conservative behavior and delays. Com-
pared to a greedy baseline, the proposed method significantly reduced collisions, achieving an average of 1.0
collision per scenario versus 6.6 with the greedy approach. Some priority configurations achieved complete
task fulfillment without any collisions, highlighting the potential for optimized multi-robot coordination. The
proposed method offers a promising strategy for prioritized motion planning, balancing efficiency and safety
based on task importance. Future research includes comparing BB-PSO with other optimization methods,
reducing sample requirements, dynamically adjusting priorities, and extending the model to incorporate task
parameterizations and autonomous priority adaptation.
1 INTRODUCTION
Motion planning in robotics involves determining a
sequence of movements that allow a robot to navi-
gate from an initial position to a desired goal while
avoiding obstacles. This essential aspect of robotics
requires computing a collision-free path through the
robot environment, accounting for kinematics, dy-
namics, and environmental constraints (Latombe,
1991). Even in its simplest form, where a rigid object
navigates among static obstacles, the problem is NP-
hard (Canny, 1988) and its complexity increases in the
presence of dynamic obstacles, deformable bodies, or
multiple robots.
This work addresses the Multi-Robot Motion
Planing Problem (MRMP) (Saha and Isto, 2006),
a
https://orcid.org/0009-0003-8875-0315
b
https://orcid.org/0000-0003-3666-0855
c
https://orcid.org/0000-0001-5325-730X
∗
while prioritizing the motion of certain robots over
others, with the goal of enabling efficient, coordi-
nated navigation where some agents are granted pas-
sage preference owing to task urgency, resource con-
straints, or mission-critical roles.
A central challenge in multi-robot systems is co-
ordinating robot motion to prevent collisions and en-
sure efficient operation. Effective coordination en-
ables robots to move simultaneously without unnec-
essary delays, thereby demanding quick decisions
in dynamic settings. The complexity of MRMP
increases exponentially with the number of robots,
owing to the expansion of the joint configuration
space. Researchers have explored various strategies,
including centralized and decentralized approaches,
sampling-based algorithms, and optimization tech-
niques (Sanchez and Latombe, 2002). Among the
recent trends, heuristic and AI-based methods have
demonstrated improved adaptability and efficiency.
Bio-inspired strategies, as reviewed by Banik et
Sanchez-Vaca, L. H., Sanchez-Ante, G. and Abaunza, H.
Optimizing Collision Avoidance in Dynamic Multi-Robot Systems: A Velocity Obstacle and BB-PSO Approach with Priority Consideration.
DOI: 10.5220/0013720000003982
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 309-316
ISBN: 978-989-758-770-2; ISSN: 2184-2809
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.
309

al. (Banik et al., 2025), highlight the growing inter-
est in hybrid approaches that blend heuristics with AI
to enhance performance in dynamic environments.
Chen et al. (Chen et al., 2024) present a veloc-
ity prediction algorithm combining backpropagation
(BP) neural networks with reciprocal velocity obsta-
cles (PRVO). This method predicts velocities to re-
construct the velocity obstacle region and optimizes
robot navigation in dense and dynamic environments.
Likewise, Jathunga and Rajapaksha (Jathunga and
Rajapaksha, 2025) proposed a hybrid Probabilistic
Roadmap (PRM) method enhanced with Genetic Al-
gorithms (GA), termed PRM-GA. Their approach im-
proves the path quality by reducing the path length
and turn count, outperforming traditional PRMs in
dynamic environments.
Task prioritization is also critical in multi-robot
systems, particularly when resources are limited or
mission objectives vary in urgency. For instance, in
search and rescue missions, it is vital to prioritize
robots that locate survivors over those that clear de-
bris (Banik et al., 2025). Dynamic task prioritization
requires the adaptation of priorities based on real-time
performance metrics, which can be computationally
intensive, but is essential for maintaining system ef-
ficiency (Guo et al., 2018). Tian et al. (Tian et al.,
2021) explored real-time path planning using wireless
sensor networks and enhanced AI algorithms, stress-
ing the importance of adaptive prioritization to avoid
delays and ensure continuous operation.
Another challenge lies in learning task priorities
from demonstrations. Extending models to incorpo-
rate task parameterizations and enable autonomous
priority adaptation are essential for enhancing robot
autonomy (Silv
´
erio et al., 2018). Kumar et al. (Ku-
mar et al., 2023) introduced a hybrid controller that
combines artificial bee colony optimization with re-
current neural networks, thereby achieving significant
improvements in navigation performance in unknown
environments.
Prioritized motion planning assigns priority levels
to robots based on criteria, such as task urgency or
energy constraints. Higher-priority robots plan their
paths first, whereas others adjust their trajectories ac-
cordingly. This sequential strategy simplifies compu-
tation compared to centralized methods, but can limit
the solution space for lower-priority robots, poten-
tially leading to suboptimal routes.
The velocity-obstacle (VO) approach is widely
used in mobile robotics for motion planning and col-
lision avoidance. VO defines sets of velocities that
would result in a collision and represents them geo-
metrically in the velocity space. By selecting veloci-
ties outside these regions, robots can navigate safely
in dynamic environments (Fiorini and Shiller, 1998).
This method extends naturally to multi-robot systems
by treating each robot as a moving obstacle, enabling
decentralized coordination.
An important refinement of VO is the Recipro-
cal Velocity Obstacles (RVO) approach, which as-
sumes mutual collision avoidance between robots.
Van den Berg et al. (Van den Berg et al., 2008) in-
troduced RVO to improve navigation efficiency by
considering reciprocal behavior. Further develop-
ments, such as Optimal Reciprocal Collision Avoid-
ance (ORCA) (Alonso-Mora et al., 2013) enhance
RVO by integrating optimization methods, resulting
in smoother and more robust trajectories in dense en-
vironments.
Paikray et al. (Paikray et al., 2021) proposed
an improved version of Particle Swarm Optimiza-
tion (PSO) using sine and cosine algorithms (IPSO-
SCA) to generate optimal deadlock-free paths. Their
method balances exploration and exploitation while
minimizing individual path lengths, underscoring the
robustness of PSO in dynamic and cluttered scenar-
ios.
1.1 Problem Statement
The Velocity Obstacle (VO) approach is an effective
framework for constructing motion plans for multiple
robots. Several VO variants have emerged that focus
on optimal trajectory generation. This study proposes
a novel VO variant guided by Particle Swarm Op-
timization (PSO) to enhance local decision-making
within the VO framework.
PSO is a population-based optimization algorithm
inspired by the collective behavior of swarms such
as bird flocks and fish schools. Each particle rep-
resents a potential solution, and navigates a multi-
dimensional search space by adjusting its position
based on personal and global bests. PSO’s simplic-
ity, adaptability, and efficiency make it suitable for
addressing complex high-dimensional optimization
problems. Besides, PSO has recently being applied
to mobile robots, sometimes in hybrid approaches, as
the one presented in (Najm et al., 2024), where the
authors combine PSO with a Whale Optimization Al-
gorithm (WOA). They found good reductions in path
length with this approach. The versatility of PSO is
such that in (Nasir et al., 2025), the PSO is used to
fine tune the parameters of Fuzzy Logic Controllers.
Its applications span robotics, engineering, and ma-
chine learning, particularly in parameter tuning, path
planning, and feature selection.
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
310

1.2 Specific Goals and Scope of the
Study
A key component of sampling-based MRMP is the
tensor roadmap, which combines individual PRMs
for each robot. Recent work introduces the ”stag-
gered grid” sampling scheme, which significantly re-
duces the number of required samples while maintain-
ing near-optimality (Banik et al., 2025). This method
demonstrates high-quality solutions with fewer sam-
ples in multi-robot scenarios (Jathunga and Rajapak-
sha, 2025) and outperforms uniform random sam-
pling, particularly in low-sample regimes. Distributed
navigation and obstacle avoidance strategies further
enhance performance in complex, dynamic environ-
ments (Yang et al., 2023).
2 METHODOLOGY
2.1 System Model and Assumptions
Let us consider a set of N mobile robots that operate
in a shared two-dimensional environment. Each robot
R
i
, where i = 1,..., N, is modeled as a disc-shaped
holonomic agent with radius r, position x
i
∈ R
2
, and
velocity v
i
∈ R
2
. Robots can select their velocity at
discrete time steps, t
k
= k∆t, where ∆t is fixed. Each
robot’s motion follows simple kinematics: straight-
line motion with constant velocity within each time
step, subject to velocity and acceleration constraints.
All robots are assumed to have the same size and ca-
pabilities.
We assume that all agents have access to the posi-
tions and velocities of other robots at all times. This
capability allows reactive navigation and avoidance
behaviors. However, each robot maintains its own pri-
vate navigation goal g
i
∈ R
2
. This approach resem-
bles a real-world scenario in which agents can have
sensing capabilities to detect other agents while main-
taining a decentralized navigation system.
Each robot R
i
is assigned a priority level P
i
∈ [0, 1].
This scalar value represents the importance of an
agent’s task. Robots with higher priority are expected
to maintain more direct trajectories toward their goals.
Robots with a lower priority are expected to adjust
their paths to avoid interference with higher-priority
agents.
Priority values influence the weights of the cost
functions used during the optimization. This mecha-
nism enables implicit hierarchical coordination with-
out requiring centralized control or explicit negotia-
tion between robots.
2.2 Reciprocal Velocity Obstacle
Formulation
To ensure safe navigation in a shared environment,
each robot must avoid collisions with the other agents.
We adopted the Velocity Obstacle (VO) framework to
identify the velocities that would lead to a future col-
lision if both agents maintain their current velocities.
The Velocity Obstacle is defined as follows. Let
two robots, R
A
and R
B
, with current positions p
A
and
p
B
, velocities v
A
and v
B
, and radii r
A
and r
B
, the VO
for robot R
A
induced by robot R
B
is defined in Eq. 1.
VO
AB
:=
{v
i
∈ R
2
|v
A
− v
B
∈ CC(p
B
− p
A
,r
A
+ r
B
)}
(1)
This equation implies that v
i
lies within a collision
cone (CC) of relative velocities that would result in a
collision with R
B
, assuming that both agents main-
tain a constant velocity. The cone is centered along
the vector p
B
− p
A
, and its angular aperture is defined
as the sum of r
A
+ r
B
. Any velocity v
A
within VO
AB
would eventually bring robot R
A
into contact with R
B
.
However, in VO, avoidance is unilateral; robot R
A
is responsible for avoiding R
B
. When both agents try
to avoid each other independently, this can lead to
overly conservative behavior or oscillations. To ad-
dress this, we adopted the Reciprocal Velocity Obsta-
cles (RVO) formulation.
The key idea in RVO is to share the responsibil-
ity for collision avoidance between agents. Instead
of avoiding the entire VO, each agent avoids only the
portion of the velocity space that would lead to col-
lision, assuming that the relative velocity is equally
adjusted. The RVO for robot R
A
with respect to R
B
is
defined in Eq. 2.
RVO
AB
:= {v
A
∈ R
2
|v
A
−
v
A
+ v
B
2
∈ VO
AB
} (2)
Similarly, R
A
avoids the VO region centered at
the average velocity of both agents rather than at V
B
.
This formulation results in more balanced and natural
agent interactions, reducing unnecessary detours and
avoiding deadlocks in symmetric scenarios.
At each planning step, robot R
A
generates a dis-
crete set of velocity candidates V
A
based on its dy-
namic constraints, known as Reachable Velocities
(RV). We then filter this set by removing all veloci-
ties within the union of the velocity obstacles induced
by neighboring agents, as shown in Eq. 3.
RAV
A
:= {v ∈ V
A
|v /∈ U(V O
AB
)} (3)
The resulting set, the Reachable Avoiding Veloci-
ties (RAV), is the feasible domain for the subsequent
optimization step. The following section describes
how a Particle Optimization (PSO) strategy guides the
velocity selection process.
Optimizing Collision Avoidance in Dynamic Multi-Robot Systems: A Velocity Obstacle and BB-PSO Approach with Priority Consideration
311

2.3 Particle Swarm Optimization
Algorithm
To select the optimal velocity from the set of safe
candidates (RAV), we employ the Bare Bones Parti-
cle Swarm Optimization (BB-PSO) algorithm. This
variant of PSO eliminates the use of velocity vectors
and generates new candidate solutions by sampling a
Gaussian distribution defined by the best-known po-
sitions.
Each robot runs an independent instance of BB-
PSO at every time step to select the next velocity. The
swarm comprises particles, each representing a can-
didate velocity, v ∈ R
2
.
For each particle p, a new position is generated by
sampling from the normal distribution given in Eq. 4.
µ
p
=
1
2
(p
best
+ g
best
)
σ = |p
best
− g
best
|
x
(t+1)
p
∼ N(µ
p
,σ),
(4)
Here, µ
p
is the mean of the distribution, calculated
as the average of the particle’s best-known position
(p
best
) and the global best position among all parti-
cles (g
best
). σ is the standard deviation, defined as the
absolute difference between p
best
and g
best
. The new
position x
(t+1)
p
is sampled from a normal distribution
N(µ
p
,σ).
The new position is considered only if it is a part
of the RAV set. Otherwise, the particle will maintain
the same position. This ensures that only valid ve-
locities are generated for all particles during the op-
timization process. We evaluate each valid candidate
velocity by using the cost function in Eq. 5.
J(v) = α ·
∥
g − (x + v · ∆t)
∥
+ β ·
∑
o∈O

−
1
2
tanh(k · (A − d
safe
)) +
1
2

(5)
where A = ∥x
o
−x
′
∥, x denotes the current position of
the robot, g denotes the goal of the robot, v denotes
the candidate velocity, and ∆t denotes the time step.
The predicted position is given by x
′
= x +v · ∆t, The
set O contains all obstacles, each located at x
o
. Pa-
rameters d
safe
and k control the shape of the penalty
from being close to the obstacle, whereas α and β re-
spectively determine the relative weights of the goal-
seeking and obstacle avoidance terms.
The particle with the lowest cost across all iter-
ations (g
best
) is selected as the robot’s next velocity
command.
The implementation of this algorithm is summa-
rized in the pseudocode shown in Alg. 1.
Algorithm 1: BB-PSO for Velocity Selection.
Initialize particles {v
1
,... , v
n
} ← RAV;
Set pbest
i
← v
i
, and evaluate J(pbest
i
);
Set global best gbest ← argmin
i
J(pbest
i
);
for k = 1 to N do
for each particle i do
Compute µ ← 0.5(pbest
i
+ gbest);
Compute σ ← ||pbest
i
− gbest||;
Sample new position v
′
i
∼ N (µ,σ);
if v
′
i
is valid (within RAV) then
Update particle: v
i
← v
′
i
;
end
Evaluate J(v
i
);
if J(v
i
) < J(pbest
i
) then
Update personal best:
pbest
i
← v
i
;
end
end
Update global best
gbest ← argmin
i
J(pbest
i
);
end
return gbest as the optimal velocity v
∗
2.4 Integration of RVO and PSO
To integrate VO constraints into the BB-PSO frame-
work—and, more importantly, to account for the in-
fluence of robot priorities on the optimization—we
adopted the following procedure. At each planning
step, robot R
A
computes the set of RAV, which is
defined as the subset of dynamically feasible veloc-
ities that do not fall inside any VO generated by other
agents. This set serves as the search domain for the
BB-PSO algorithm. Particles outside the RAV are re-
jected, and their positions will not be updated.
Each robot is assigned a scalar priority value, P
i
,
where a higher value indicates greater importance.
Priorities do not alter the VO constraints directly, but
they modulate the weights in the cost function to en-
courage differentiated behavior.
Specifically, the weights α and β in the cost func-
tion are adjusted using Eqs. 6.
α
i
= max(αP
i
,0.1)
β
i
= max(β(1 − P
i
),1.0)
(6)
A high-priority robot (P
i
→ 1) emphasizes reach-
ing a goal and reduces obstacle avoidance penalties.
A low-priority robot (P
i
→ 0) becomes more con-
servative, placing greater weight on obstacle avoid-
ance.
We ensured that the obstacle avoidance weight
did not fall below the minimum threshold of 1.0.
This helps to prevent agents with the highest pri-
ority from taking too many risks by ignoring other
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
312

agents, possibly causing collisions in clustered envi-
ronments. Simultaneously, we ensured that the goal-
seeking weight was never below 0.1. This ensures that
even if the agent has the lowest priority, it will still try
to reach its goal.
3 IMPLEMENTATION
3.1 Simulation Setup
To evaluate the proposed approach, we developed
a series of simulations in a controlled 2D environ-
ment using custom-built tools and clearly defined
robot configurations. The simulation was developed
in Python and executed using a fixed time-step of
dt = 0.1 s. The environment comprises a bounded
two-dimensional (2D) workspace with multiple holo-
nomic robots. All motion-planning logic, includ-
ing VO construction and BB-PSO, was implemented
from scratch using NumPy for numerical operations
and Matplotlib for visualization.
The simulation loop is synchronous; however, the
system is nondeterministic owing to the stochastic
sampling in BB-PSO. Specifically, new particle posi-
tions are sampled from a normal distribution, making
the outcome of each run sensitive to random initial-
ization and updates.
Each robot is modeled as a circular agent with a
radius r = 0.3 m, capable of holonomic motion. The
robots are constrained by a maximum speed of v
max
=
0.7 m/s and a maximum acceleration of a
max
= 2.0
m/s². These parameters are based on a robot that will
be used for further testing (Hiwonder, 2025).
The robots are initialized with predefined initial
positions and static goal locations, allowing a consis-
tent running configuration. Each robot was assigned
a fixed priority level that was manually specified at
the beginning of each simulation. These values influ-
ence the cost function used in the optimization phase.
Higher-priority robots seek faster and direct paths to
their goals, while lower-priority robots seek safer col-
lision avoidance paths.
3.2 Algorithm Implementation
The algorithm integrates RVO constraints with BB-
PSO optimization to compute collision-free velocities
in a decentralized multi-robot setting. Each robot iter-
atively evaluates its reachable velocity space, filters it
based on dynamic constraints and collision avoidance
conditions, and then applies the BB-PSO to select the
most suitable velocity. This process is repeated at
each time step until all robots converge to their re-
spective goals within a specified tolerance. The steps
in this loop are summarized in the pseudocode shown
in Alg. 2. For simplicity, the pseudocode updates the
velocities and positions of the robots within the same
loop. However, it is important to note that in the ac-
tual simulation, these updates are applied only after
all robots have independently computed their next ve-
locity. This ensures that each robot makes its decision
without access to the updated actions of the others,
preserving simultaneity in decision-making.
Algorithm 2: RVO with BB-PSO Optimization.
while distance to goal > threshold do
for R
i
in Robots do
Compute the reciprocal velocity
obstacle of R
i
Calculate the reachable velocities of
R
i
Filter reachable avoidance velocities
of R
i
Optimize RAV with BB-PSO to get
the best velocity of R
i
(t + 1)
Update the velocity of R
i
Update the position of R
i
end
end
The simulation used an object-oriented approach
centered on a Robot class, encapsulating all relevant
information and methods required for motion plan-
ning. Each robot instance stores its current position,
velocity, goal, radius, dynamic limits, priority, and in-
ternal buffers for storing RVO and RAV. The class
also includes methods for updating positions, com-
puting the VO geometry, and filtering velocities based
on collision constraints.
This modular design allows each robot to op-
erate autonomously in the simulation loop, thereby
enabling straightforward scaling to a larger number
of agents. Although the current implementation is
single-threaded, the independence of the agents al-
lows parallelization in further research.
4 RESULTS
4.1 Experiment Setup
A two-phase experimental strategy was employed
to evaluate the performance of the proposed motion
planning algorithm.
In the first phase, a baseline scenario was defined
Optimizing Collision Avoidance in Dynamic Multi-Robot Systems: A Velocity Obstacle and BB-PSO Approach with Priority Consideration
313

in which four agents were placed at the corners of a
square and tasked with exchanging positions diago-
nally. Two experiments were conducted using this
setup. First, a grid search was performed to identify
the optimal values of the cost function parameters α
and β, assuming equal priorities among agents. Sec-
ond, a set of evaluations was conducted under varying
priority configurations, using the previously selected
parameters that balanced both efficiency and safety.
The same priority scenarios were also tested using a
greedy approach instead of BB-PSO, to enable a fair
performance comparison.
Table 1: Top 5 configurations by mean arrival time.
α β Arrival time [s] Collision Number
5.0 2.0 15.67 ± 1.61 10.6
5.0 1.0 15.73 ± 0.85 6.4
4.0 1.0 16.52 ± 0.63 1.8
4.0 2.0 16.56 ± 0.23 0.0
3.0 2.0 16.63 ± 0.68 2.2
The second phase involved testing the algorithm
in random scenarios, where both initial and goal posi-
tions were sampled randomly to assess the robustness
of the approach under varying conditions.
Each individual experiment was repeated five
times to account for the stochastic nature of the opti-
mization process, as BB-PSO relies on sampling from
Gaussian distributions.
The average performance was evaluated using
three metrics: the total travel time, the total travel dis-
tance, and the number of collisions observed. Colli-
sions were evaluated at every time step to detect over-
laps between robots. As a result, a single collision
event could be counted multiple times if the robots
remained in contact across consecutive time steps.
The results of these experiments are presented in
the next section.
4.2 Parameter Tuning and Weight
Selection
To tune the cost function parameters, 25 experiments
were conducted by performing a grid search over
α,β ∈ {1, 2, 3,4,5}, resulting in 5 × 5 combinations.
Table 1 presents the top five parameter configura-
tions with the lowest mean arrival times.
4.3 Evaluation Under Priority-Driven
Scenarios
After completing the grid search over α and β, con-
figurations α = 4 and β = 2 were selected for further
evaluation under varying priority assignments. Al-
though this combination did not yield the lowest aver-
age arrival time, it consistently demonstrated compet-
itive performance with zero collisions. Therefore, the
selected configuration provided a balanced trade-off
between speed and safety.
Table 2: Priority configuration for each scenario (Robot
0–3).
Robot Sc.0 Sc.1 Sc.2 Sc.3 Sc.4 Sc.5 Sc.6 Sc.7 Sc.8 Sc.9
P
0
1.00 1.00 0.25 1.00 0.50 1.00 0.80 0.20 1.00 0.30
P
1
1.00 0.75 0.50 1.00 0.50 0.00 0.60 0.40 0.30 1.00
P
2
1.00 0.50 0.75 0.50 0.50 1.00 0.40 0.60 0.30 0.30
P
3
1.00 0.25 1.00 0.50 0.50 0.00 0.20 0.80 0.30 0.30
To evaluate the impact of priority levels on multi-
robot behavior, ten custom scenarios were tested us-
ing the selected configurations. In each scenario, the
four robots were assigned different static priority val-
ues ranging from 0.0 to 1.0, as shown in Table 2.
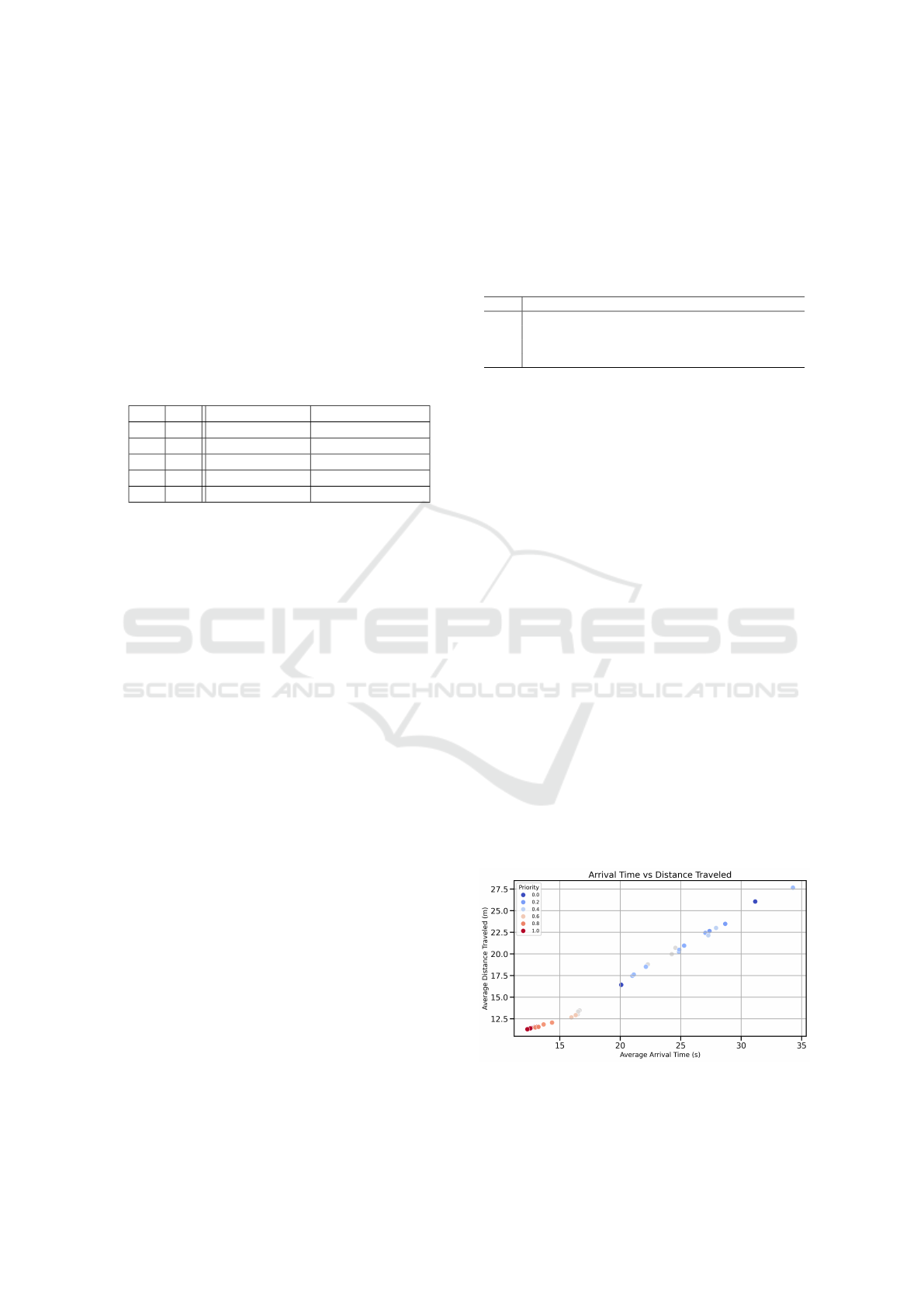
Figure 1 presents the trade-off between the av-
erage arrival time and average distance traveled for
all scenarios. Each point is colored according to
the average priority assigned to all the agents in that
scenario. A general trend was observed: scenarios
with higher average priorities (darker red points) re-
sulted in shorter travel distances and shorter comple-
tion times. In contrast, scenarios with lower average
priorities or greater imbalance tend to show increased
path lengths and delays, often owing to more conser-
vative behavior or yielding to high-priority agents.
Almost half of the scenarios resulted in full task
completion without any collisions. In contrast, the
first scenario—where all robots had maximum prior-
ity—exhibited the highest number of collisions, but
also achieved the fastest arrival times and the short-
est distances traveled. On average, only one collision
occurred per scenario, highlighting the overall feasi-
bility and efficiency of the proposed method.
Table 3 presents a summary of the quantitative re-
sults for the ten evaluated priority scenarios, including
the average arrival time, distance traveled, and num-
Figure 1: Trade-off between average arrival time and dis-
tance traveled for each scenario. Color indicates the aver-
age priority value across all four robots.
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
314

ber of collisions recorded across simulation runs.
On the other hand, Table 4 presents the results
of running the same set of experiments using a
greedy approach instead of BB-PSO for the veloc-
ity optimization phase. Although the greedy method
achieved better average results in terms of arrival time
and distance traveled, it resulted in a significantly
higher number of collisions, with an average of 6.6
per scenario. This suggests that BB-PSO was able to
explore more diverse solutions beyond those initially
included in the RAV set. While the proposed method
prioritized safety, the greedy strategy led to more ag-
gressive decisions in pursuit of goal completion.
Table 3: Average performance metrics for each scenario us-
ing BB-PSO.
Scenario
Arrival
Time (s)
Distance
(m)
Collisions
(avg.)
0 12.82 11.50 3.0
1 18.80 16.07 0.6
2 19.10 16.10 2.6
3 18.02 15.60 1.0
4 16.53 13.21 0.0
5 19.24 16.37 0.6
6 20.99 17.31 0.0
7 21.45 17.68 0.0
8 20.14 16.91 2.2
9 23.15 19.26 0.0
Average 19.02 16.00 1.0
Table 4: Average performance metrics for each scenario us-
ing the greedy approach.
Scenario
Arrival
Time (s)
Distance
(m)
Collisions
(avg.)
0 14.80 12.03 10.0
1 17.03 14.07 19.0
2 19.20 16.19 0.0
3 17.38 14.56 2.0
4 18.40 13.93 4.0
5 20.20 16.66 1.0
6 17.55 14.42 18.0
7 21.65 17.19 4.0
8 21.95 17.73 0.0
9 17.30 13.77 8.0
Average 18.55 15.06 6.6
4.4 Evaluation with Random Initial
Positions and Goals
To evaluate the performance of the proposed method
under varying conditions, five additional experiments
were conducted using randomly assigned initial po-
sitions and goals, with all agents assigned the same
priority value of 0.5.
The positions were generated under two con-
straints: each agent’s path had to be at least 3 meters
long, and both initial and goal positions were placed
to prevent overlaps that could lead to collisions at the
start or upon arrival.
Table 5: Average performance metrics for scenarios with
random positions and goals.
Scenario
Arrival
Time (s)
Distance
(m)
Collisions
(avg.)
0 5.67 4.58 0.0
1 10.66 8.81 2.0
2 7.55 6.28 0.0
3 7.28 5.57 0.0
4 9.31 7.42 0.0
Average 8.09 6.53 0.4
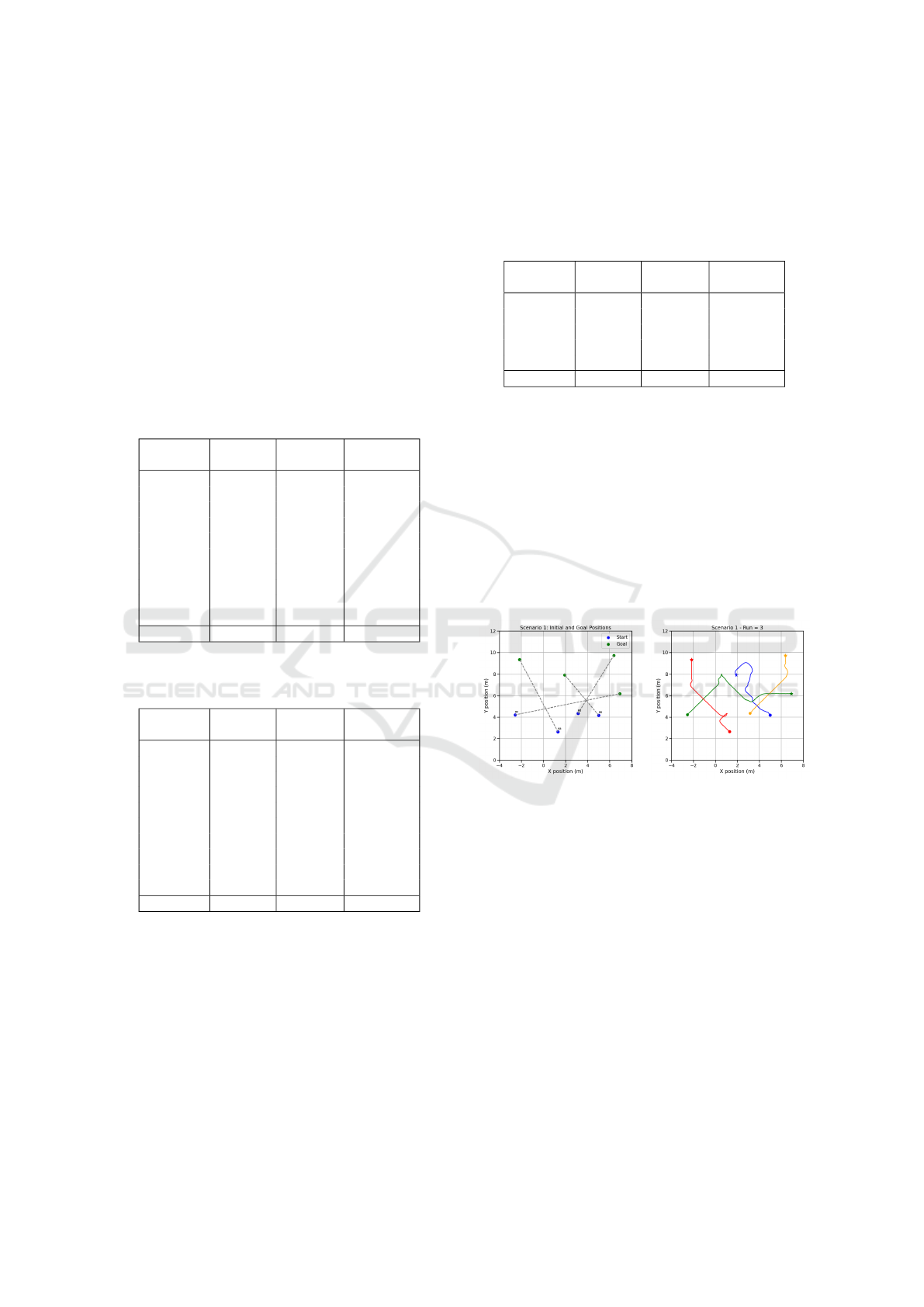
Figure 2 illustrates one of the randomly generated
scenarios, along with the trajectories followed by the
agents to reach their respective goals. Table 5 summa-
rizes the average performance across multiple runs.
Almost all experiments resulted in zero collisions, ex-
cept for Scenario 1—the case shown in the figure.
In this particular instance, several path intersections
likely contributed to the observed collisions. Despite
this, the results demonstrate that the proposed method
is robust across diverse scenarios, consistently main-
taining a low collision rate and successfully generat-
ing feasible solutions under varying configurations.
(a) (b)
Figure 2: Random Scenario 1. (a) shows the initial and goal
positions of the robots, and (b) shows the resulting trajecto-
ries.
5 CONCLUSIONS
The proposed methodology, which integrates Recip-
rocal Velocity Obstacles (RVO) with Bare Bones
Particle Swarm Optimization (BB-PSO), effectively
facilitates collision avoidance and path planning in
multi-robot systems. The incorporation of priority
levels into the cost function significantly influences
the robot’s behavior, enabling differentiated actions
based on the assigned importance. A balance between
goal-seeking and obstacle avoidance was achieved
with the selected weight configuration (α = 4, β = 2),
allowing high-priority agents to move more directly
Optimizing Collision Avoidance in Dynamic Multi-Robot Systems: A Velocity Obstacle and BB-PSO Approach with Priority Consideration
315

while ensuring overall group safety. Scenarios char-
acterized by higher average priorities generally re-
sulted in shorter travel distances and faster comple-
tion times, whereas those with lower or imbalanced
priorities exhibited more conservative behavior and
potential delays. Certain priority configurations (e.g.,
scenarios 4, 6, 7, and 9) achieved complete task fulfill-
ment without any collisions, demonstrating the poten-
tial for optimized multi-robot coordination using this
approach. These findings suggest that the proposed
method offers a promising strategy for prioritized mo-
tion planning in multi-robot systems, balancing effi-
ciency and safety based on assigned task importance.
Future research directions include an in-depth evalua-
tion of BB-PSO against a broader set of optimization
algorithms, given that the greedy strategy was less ef-
fective in minimizing collisions. Additionally, explor-
ing methods for dynamically adjusting robot priorities
based on real-time performance metrics or changing
mission objectives, along with extending the model
to incorporate task parameterizations, could enhance
robot autonomy.
ACKNOWLEDGEMENTS
This research was supported in part by the Univer-
sity of Alberta-Tecnologico de Monterrey Seed Grant
Program, under project ”Intelligent Distributed Con-
trols for Multi-Agent Autonomous Systems for Safe
Interaction with Humans”.
REFERENCES
Alonso-Mora, J., Breitenmoser, A., Rufli, M., Beardsley,
P., and Siegwart, R. (2013). Optimal reciprocal col-
lision avoidance for multiple non-holonomic robots.
In Distributed autonomous robotic systems: The 10th
international symposium, pages 203–216. Springer.
Banik, S., Banik, S. C., and Mahmud, S. S. (2025). Path
planning approaches in multi-robot system: A review.
Engineering Reports, 7(1):e13035.
Canny, J. (1988). The complexity of robot motion planning.
MIT press.
Chen, Y., Wang, Y., Li, B., and Kamiya, T. (2024). Multi-
robot navigation based on velocity obstacle prediction
in dynamic crowded environments. Industrial Robot:
the international journal of robotics research and ap-
plication, 51(4):607–616.
Fiorini, P. and Shiller, Z. (1998). Motion planning in dy-
namic environments using velocity obstacles. The in-
ternational journal of robotics research, 17(7):760–
772.
Guo, M., Haque, A., Huang, D.-A., Yeung, S., and Fei-Fei,
L. (2018). Dynamic task prioritization for multitask
learning. In Proceedings of the European conference
on computer vision (ECCV), pages 270–287.
Hiwonder (2025). Jetauto ros robot car. https:
//www.hiwonder.com/products/jetauto?variant=
41201592762455. Accessed: 2025-07-28.
Jathunga, T. and Rajapaksha, S. (2025). Improved path
planning for multi-robot systems using a hybrid prob-
abilistic roadmap and genetic algorithm approach.
Journal of Robotics and Control (JRC), 6(2):715–733.
Kumar, S., Parhi, D. R., and Muni, M. K. (2023). Path plan-
ning and obstacle avoidance of multi-robotic system
in static and dynamic environments. Proceedings of
the Institution of Mechanical Engineers, Part B: Jour-
nal of Engineering Manufacture, 237(9):1376–1390.
Latombe, J. (1991). Robot motion planning, volume 124
of The Kluwer international series in engineering and
computer science. Kluwer.
Najm, H. T., Ahmad, N. S., and Al-Araji, A. S. (2024). En-
hanced path planning algorithm via hybrid woa-pso
for differential wheeled mobile robots. Systems Sci-
ence & Control Engineering, 12(1):2334301.
Nasir, N. M., Ghani, N. M. A., Nasir, A. N. K., Ahmad,
M. A., and Tokhi, M. O. (2025). Neuro-modelling
and fuzzy logic control of a two-wheeled wheelchair
system. Journal of Low Frequency Noise, Vibration
and Active Control, 44(1):588–602.
Paikray, H., Das, P., and Panda, S. (2021). Optimal multi-
robot path planning using particle swarm optimiza-
tion algorithm improved by sine and cosine algo-
rithms. Arabian Journal for Science and Engineering,
46(4):3357–3381.
Saha, M. and Isto, P. (2006). Multi-robot motion planning
by incremental coordination. In 2006 IEEE/RSJ In-
ternational Conference on Intelligent Robots and Sys-
tems, pages 5960–5963.
Sanchez, G. and Latombe, J.-C. (2002). Using a prm plan-
ner to compare centralized and decoupled planning for
multi-robot systems. In Proceedings 2002 IEEE In-
ternational Conference on Robotics and Automation
(Cat. No.02CH37292), volume 2, pages 2112–2119
vol.2.
Silv
´
erio, J., Calinon, S., Rozo, L., and Caldwell, D. G.
(2018). Learning task priorities from demonstrations.
IEEE Transactions on Robotics, 35(1):78–94.
Tian, S., Li, Y., Kang, Y., and Xia, J. (2021). Multi-robot
path planning in wireless sensor networks based on
jump mechanism pso and safety gap obstacle avoid-
ance. Future Generation Computer Systems, 118:37–
47.
Van den Berg, J., Lin, M., and Manocha, D. (2008). Re-
ciprocal velocity obstacles for real-time multi-agent
navigation. In 2008 IEEE international conference on
robotics and automation, pages 1928–1935. Ieee.
Yang, Z., Li, J., Yang, L., Wang, Q., Li, P., and Xia, G.
(2023). Path planning and collision avoidance meth-
ods for distributed multi-robot systems in complex dy-
namic environments. Mathematical Biosciences and
Engineering, 20(1):145–178.
ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics
316