A New Sliding Mode Control Proposal with a Clegg Integrator for a

Mobile Manipulator

Pablo Proa

, Paulo Leica

and Gabriela Andaluz

Escuela Polit

ecnica Nacional, Departamento de Automatizacion y Control Industrial, Quito, Ecuador

Keywords:

Mobile Manipulator, Sliding Mode Control, Clegg Integrator, Trajectory Tracking, Discontinuous Control,

Chattering Reduction, Nonlinear Control.

Abstract:

This article presents a novel control strategy for trajectory tracking in mobile manipulators. The proposed

method combines a conventional Sliding Mode Controller (SMC) with a reset-based integrator, speciﬁcally

a Clegg integrator, applied to the discontinuous component of the sliding surface. The system under study

consists of a mobile platform with dynamic behavior and a robotic arm modeled kinematically. The main

objective is to improve tracking performance and reduce control signal oscillations, particularly under abrupt

reference changes and external disturbances. A reference trajectory with an inclined square shape is used

to challenge the controller with sudden directional transitions. To evaluate the effectiveness of the proposed

approach, both the classical SMC and the SMC+Clegg controllers are implemented and tested under the

same conditions. The performance is analyzed using standard indices such as Integral Square Error (ISE),

Integral Absolute Error (IAE), and Total Variation of the control signal (TVu). Results show that the proposed

controller achieves improved trajectory tracking with reduced overshoot and chattering, while maintaining

robustness to disturbances. Stability is formally demonstrated using Lyapunov theory. The positive impact of

the Clegg integrator is highlighted in the discontinuous control component, allowing for reduced control effort

without compromising tracking quality or disturbance rejection.

1 INTRODUCTION

The modeling of mobile manipulators is commonly

performed using state-space representations, where

inverse Jacobian matrices are employed to compute

the joint velocities required to follow a desired end-

effector trajectory. Since the mobile platform typi-

cally has greater mass than the robotic arm, a dynamic

model is used for the base and a kinematic model for

the manipulator to simplify the formulation while pre-

serving accuracy (Haddadin et al., 2022; Widhiada

et al., 2020; Delgado et al., 2022). Reference trajec-

tories with abrupt changes are often applied to test

the robustness and reactivity of controllers under de-

manding conditions (You et al., 2019; Kemp et al.,

2022).

A wide range of control techniques has been pro-

posed for mobile manipulators, including PID, null-

space optimization, fuzzy logic, and sliding mode

control (SMC) (Salinas et al., 2018; Moreno et al.,

https://orcid.org/0000-0002-6902-7151

https://orcid.org/0000-0002-5385-1920

https://orcid.org/0000-0002-1822-6943

2021). More recently, hybrid control approaches

have been explored to improve interaction perfor-

mance and adaptability, incorporating learning-based

impedance tuning (Zhao et al., 2022) and coordinated

actuation mechanisms (Gan et al., 2022). PID con-

trollers are extensively used in industry due to their

simplicity and effectiveness, although in robotic ap-

plications they are often embedded into hybrid strate-

gies (Zangina et al., 2020; Maung et al., 2024). A

key limitation of PID controllers lies in the integral

windup phenomenon, which can degrade system per-

formance by introducing overshoots and increasing

settling times (Hitit et al., 2023; Okelola et al., 2020;

Chaudhary, 2024).

Reset-based techniques have emerged to address

this issue. One notable solution is the Clegg in-

tegrator (CI), a nonlinear integrator that resets its

state when the error derivative crosses zero. The

CI reduces the accumulation of the integral term,

thereby limiting overshoot and improving transient

performance (Beerens et al., 2022; Gholipour et al.,

2015; Kolar and Lazar, 2021). Recent developments

have extended this concept through soft-reset con-

Proaño, P., Leica, P. and Andaluz, G.

A New Sliding Mode Control Proposal with a Clegg Integrator for a Mobile Manipulator.

DOI: 10.5220/0013719900003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 301-308

ISBN: 978-989-758-770-2; ISSN: 2184-2809

301

trollers, which approximate hard-reset behavior using

continuous-time differential inclusions. These con-

trollers preserve passivity properties and offer im-

proved stability guarantees under convex Lyapunov

conditions, facilitating their application in robotic

systems (Le and Teel, 2021; Teel, 2022). . In re-

cent work by Proa

no et al. (Proa

no et al., 2024), the

use of a Clegg integrator in a PID-type sliding surface

demonstrated faster settling, reduced chattering, and

improved overall performance compared to conven-

tional SMC and PID strategies. The reset action was

shown to affect only the discontinuous component of

the SMC, resulting in a smoother control signal with-

out compromising the system’s robustness.

Sliding Mode Control remains a robust strategy

for handling modeling uncertainties and external dis-

turbances. It consists of a continuous term that

maintains system convergence on the sliding sur-

face and a discontinuous term responsible for driv-

ing the state toward it. The latter, however, tends

to introduce high-frequency oscillations, or chatter-

ing, which several studies have sought to mitigate us-

ing smoothed switching functions and hybrid surfaces

(Gude et al., 2024; Demim et al., 2023; Li et al.,

2024). Recent advancements have further explored

chattering reduction through higher-order and adap-

tive SMC strategies (V and Manthati, 2024), as well

as the use of chattering-attenuation disturbance ob-

servers (CADOB), which effectively suppress high-

frequency components in the disturbance estimation

without degrading control performance (Yim et al.,

2023).

This paper proposes a sliding mode control strat-

egy that incorporates a Clegg-type integrator into the

sliding surface. The reset action aims to mitigate

windup, reduce overshoot, and improve settling time.

The controller is implemented on a mobile manipu-

lator and evaluated under setpoint changes and exter-

nal disturbances. Performance indices are calculated

to compare the proposed method with conventional

strategies. The main contributions include improved

response time, reduced overshoot, enhanced recovery

from disturbances, and ease of implementation in sys-

tems that already use PID architectures.

2 MOBILE MANIPULATOR

MODEL

Before implementing the proposed control strategies,

it is essential to understand the structure and behavior

of the mobile manipulator. This system consists of a

mobile platform, modeled using a dynamic approach,

and a robotic arm, described through a kinematic

model. This section presents both models, which en-

able an accurate representation of the system’s evolu-

tion in response to control signals and reference tra-

jectories.

A graphical representation of the mobile manipu-

lator used in the present work is shown in Figure 1.

Figure 1: Mobile manipulator with three degrees of free-

dom, (Vizuete et al., 2017).

Where l

represents the vertical distance from the

ground to the base of link 1 of the manipulator; l

, and l

are the lengths of the manipulator links; a

denotes a point of interest introduced to eliminate the

non-holonomic constraint; and b is the distance from

the center of the mobile platform to link 1. The pa-

rameter a has no physical structure but is geometri-

cally deﬁned to lift the non-holonomic restriction of

the platform’s motion model. The variables θ

, θ

and θ

correspond to the rotation angles of links l

, and l

, respectively. The coordinates x and y rep-

resent the position of the mobile robot’s base, and ψ

denotes its orientation, while u and ω represent the

linear and angular velocities of the mobile platform,

respectively. Finally, x

, y

, and z

deﬁne the po-

sition of the end-effector with respect to the origin of

the coordinate system.

The position of the end-effector (x

, y

, z

) as

a function of the system’s angles and parameters is

computed using the following expressions:

= x + b cos(ψ)

+ cos(θ

+ ψ)(l

cos(θ

) + l

cos(θ

+ θ

))

(1)

= y + b sin(ψ)

+ sin(θ

+ ψ)(l

cos(θ

) + l

cos(θ

+ θ

))

(2)

= l

+ l

sin(θ

) + l

sin(θ

+ θ

) (3)

The kinematic behavior of the mobile platform is

described by the following equations:

˙x = u cos ψ − aωsinψ (4)

˙y = u sin ψ + aωcos ψ (5)

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

302

ψ = ω (6)

Where x and y denote the position of the mobile

robot base, and ψ represents its orientation. The vari-

able u corresponds to the linear velocity of the mobile

platform, while ω denotes its angular velocity.

The kinematics of the mobile manipulator h is de-

termined by:

= J

˙q (7)

Where J

is the Jacobian matrix that relates the

generalized velocities ˙q = [u, ω,

]

to the

Cartesian velocity of the end-effector. The vector

= [x

, y

, z

]

represents the Cartesian position

of the end-effector in the task space, and is used to

describe its spatial motion relative to the global coor-

dinate system.

The Jacobian matrix J

, using the trigonometric

shorthand deﬁned in the implementation, is given by:





−aS

− bS

− S

+ l

) −S

+ l

) −C

+ l

) −l

+ bC

+ l

) C

+ l

) −S

+ l

) −l

0 0 0 l

+ l





(8)

Where C

= cos(ψ) and S

= sin(ψ); C

cos(θ

) and S

= sin(θ

); C

= cos(θ

+ ψ) and

= sin(θ

+ ψ); and C

= cos(θ

+ θ

) and

= sin(θ

+ θ

Each row of J

corresponds to a Cartesian direc-

tion of the end-effector (x

, y

, and z

), while each

column is associated with one of the generalized ve-

locities: u (linear), ω (angular), and

(joint

velocities of the manipulator).

Given that the mass of the robotic arm is consider-

ably smaller than that of the mobile platform, a kine-

matic model is used for the arm and a dynamic model

for the mobile platform.



˙u











−





−





uω −













(9)

Where [B] = [B

, B

]

is the vec-

tor of identiﬁed parameters of the robot, u

is the con-

trol input associated with the linear velocity of the

mobile platform, and ω

is the control input associ-

ated with its angular velocity.

The ﬁnal model of the mobile manipulator is ob-

tained by combining the kinematic model of the arm,

presented in Eq. (7), with the dynamic model of the

mobile platform, given in Eq. (9). This results in the

complete representation summarized in Eq. (10).







˙x

˙y

˙z

˙u













+ ωJ





−





u +

−





uω −





ω +







(10)

where J

represents the elements of the Jacobian ma-

trix described in Eq. (8), which maps the generalized

velocities to the Cartesian velocity of the end-effector.

3 DESIGN OF THE PROPOSED

CONTROLLER

This section presents the development of the con-

trollers. First, a sliding mode controller for the mo-

bile manipulator is derived, and then the concept of

a Clegg integrator is incorporated into its sliding sur-

face.

3.1 Sliding Mode Controller for Mobile

Manipulator

To compute the control inputs, the inverse kinematics

of the mobile manipulator is calculated.

U = J

(11)

Where U = [u

, ω

]

is the vector of

control inputs generated through inverse kinematics,

and J

is the pseudoinverse of the Jacobian matrix

, used to map the desired Cartesian velocity of the

end-effector to the generalized control inputs. The

pseudoinverse is computed using the Moore–Penrose

formulation as:

= J

)

−1

(12)

As described in the previous section, a sliding

mode controller consists of a continuous component

and a discontinuous component U

. To compute

the continuous component, a sliding surface must ﬁrst

be deﬁned. In this work, a proportional-integral (PI)

type surface is used:

s = e

+ λ

dt (13)

A New Sliding Mode Control Proposal with a Clegg Integrator for a Mobile Manipulator

303

Where e

is the tracking error, deﬁned as the

difference between the desired trajectory and the

actual end-effector position, i.e., e

= h

− h

, e

]

; h

represents the desired Cartesian tra-

jectory of the end-effector; and λ

is a positive tuning

parameter that determines the convergence rate of the

sliding surface.

To satisfy the sliding condition, the derivative of

the sliding surface must be equal to zero. Therefore,

the time derivative of Eq. (13) is computed as:

˙s = ˙e

+ λ

= 0 (14)

Since the tracking error is deﬁned as e

= h

−h

its time derivative is given by:

˙e

−

(15)

Substituting Eq. (15) into Eq. (14), the sliding sur-

face derivative becomes:

˙s =

−

+ λ

= 0 (16)

Solving for

yields:

+ λ

(17)

Equation (17) provides the desired Cartesian ve-

locity of the end-effector required to stay on the slid-

ing surface. By substituting this expression into the

inverse kinematics relation in Eq. (11), the continu-

ous component of the sliding mode control law is ob-

tained as:

= J



+ λ



(18)

To obtain the discontinuous component of the con-

troller, the Lyapunov stability concept is directly ap-

plied.

According to Lyapunov’s direct method, if there

exists a scalar function V , continuously differentiable

and positive deﬁnite, such that its time derivative

along the system trajectories

V is negative deﬁnite,

then the equilibrium point at the origin is globally

asymptotically stable.

Let V =

s, which satisﬁes V > 0 for all s ̸= 0,

since s

s represents the squared norm of the vector s.

If s = 0, then V = 0, as the norm of the zero vector

is zero. The time derivative of V is given by

V =



˙s

s + s

˙s



= s

˙s.

The error derivative in Eq. (14) is decomposed

as ˙e

−

. Then, using the expression from

Eq. (7),

is replaced by J

U, and this substitution

is used to rewrite the sliding surface derivative.

V = s



− J

U + λ



(19)

If U

SMC

is considered as the sum of its continuous

and discontinuous components, that is, U

SMC

= U

, and the expression for U

from Eq. (18) is used,

the following is obtained:

V = −s

(20)

To ensure that

V < 0, the discontinuous compo-

nent is deﬁned as:

= J

sign(s) (21)

where k

is a positive scalar or diagonal gain matrix

that adjusts the intensity of the switching action. The

matrix J

denotes the pseudoinverse of the Jacobian

matrix J

, and is used to project the control action

from Cartesian space back to the generalized coordi-

nates of the system. This operation allows the gen-

eration of appropriate control inputs that achieve the

desired behavior of the end-effector in task space.

However, using the sign(s) function may cause

chattering and excessive effort in the actuators of the

mobile manipulator. Therefore, a smoothed version is

used instead:

= J

∥s∥ + δ

(22)

where δ is a small positive scalar that smooths the

discontinuity and reduces chattering effects. A larger

value of δ increases the smoothness of the control sig-

nal but compromises the speed at which the system

reaches the reference.

Replacing the smoothed expression of U

into the

derivative of the Lyapunov function yields:

V = −s

∥s∥ + δ

(23)

Assuming that J

≈ I, this simpliﬁes to:

V = −k

∥s∥ + δ

(24)

Since k

> 0, it follows that

V < 0, which implies

that s → 0 as t → ∞. From (13), and by introducing

the change of variable ρ =

dt, we obtain:

0 =

ρ + λ

ρ (25)

In order for the system solutionisfy ρ → 0, it is

required that λ

> 0. Consequently, ρ =

dt → 0,

which implies that e

→ 0 as t → ∞.

The complete control law can be expressed in a

compact form as:

SMC

= J



+ λ

∥s∥ + δ



(26)

3.2 Sliding Mode Control Proposal with

a Clegg Integrator

The approach proposed in this work uses a Clegg inte-

grator in the sliding surface. Figure 2 presents a block

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

304

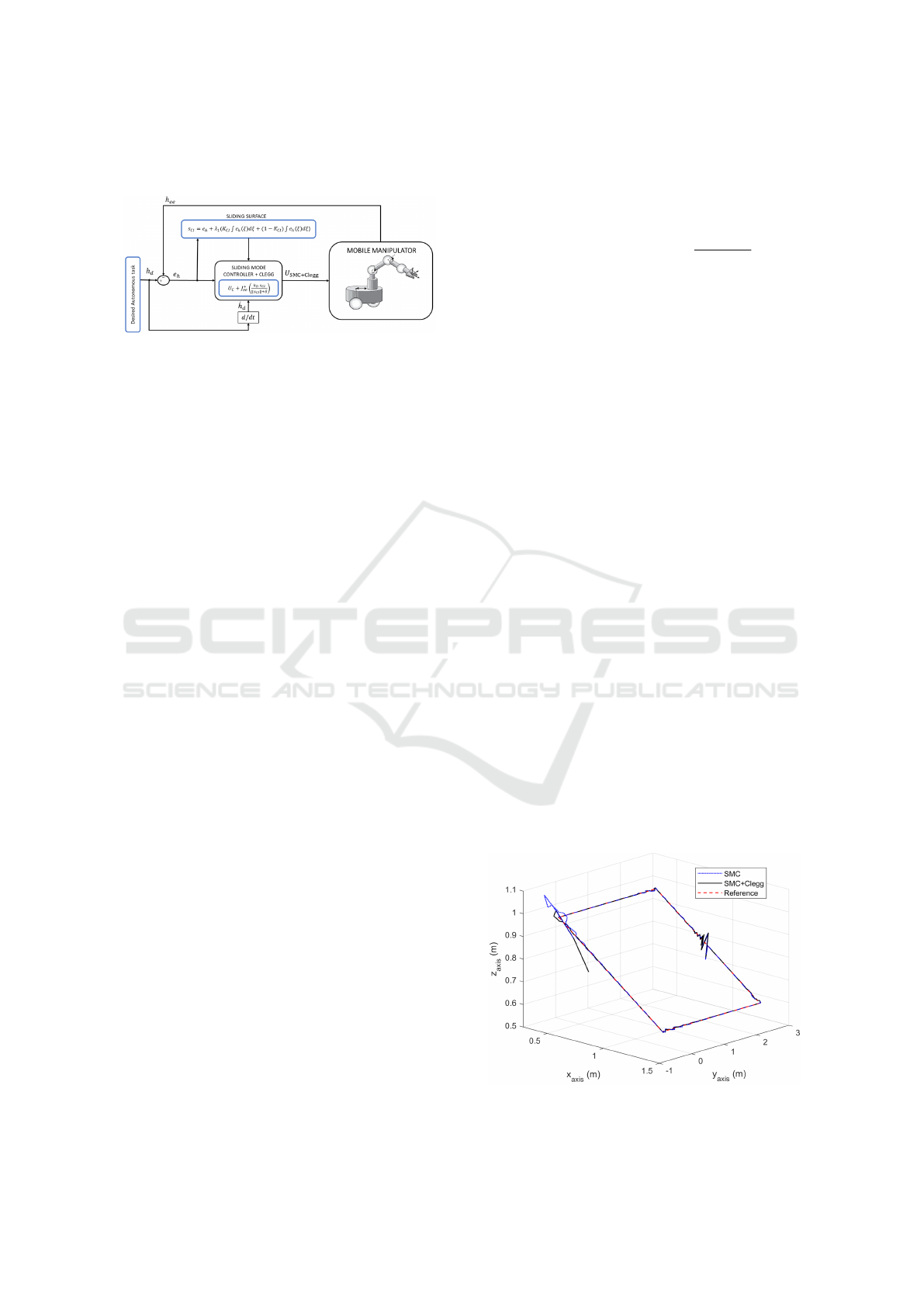
diagram of the overall control strategy, which will be

detailed in the following sections.

Figure 2: SMC+Clegg control scheme.

The resulting sliding surface, incorporating a

Clegg integrator, is expressed as:

= e

+ λ

(ξ)dξ

+ (1 − K

)

(ξ)dξ

(27)

Where K

is a scalar gain that determines the con-

tribution of the Clegg integrator in the sliding surface.

It must be bounded in the range 0 ≤ K

≤ 1, where

= 1 corresponds to a full Clegg integrator and

= 0 to a conventional integrator. The variable ξ

is used as the integration variable to avoid confusion

with the upper limit t, and represents the intermediate

time over which the error signal is integrated. The re-

set time t

is updated whenever the derivative of the

tracking error ˙e

crosses zero; this mechanism elimi-

nates the accumulation of past control actions and re-

sets the integrator, thereby reducing windup effects.

To avoid spurious resets caused by high-frequency

noise, a moving average ﬁlter with a window of ﬁve

sampling intervals was applied to ˙e

prior to evaluat-

ing the reset condition.

Since the continuous component was obtained

based on the sliding condition, which requires the

time derivative of the sliding surface to be zero, the

Clegg integrator has no effect on the continuous part

of the controller. This is because the integral term

in the sliding surface expression disappears when dif-

ferentiating. As a result, the continuous component

of a conventional SMC controller and that of the

SMC+Clegg controller are the same. Therefore, the

stability analysis of the continuous part presented in

the previous section also applies to the proposed con-

troller.

However, the discontinuous component of the

controller directly depends on the sliding surface ex-

pression, which includes the Clegg integrator. There-

fore, the effects of the Clegg integrator have a direct

impact on the discontinuous control action, inﬂuenc-

ing both the chattering behavior of the system and its

settling time.

The complete control law, using the Clegg-

integrated sliding surface, is deﬁned as:

SMC+Clegg

= J



+ λ

∥s

∥ + δ



(28)

The simulation parameters used for the model and

controller are as follows: the manipulator link lengths

are l

= 0.4 m, l

= 0.25 m, and l

= 0.25 m; the

vertical offset is l

= 0.2 m; the distances a and b

are both set to 0.13 m. The dynamic coefﬁcients

used in the model are B

= 0.2604, B

= 0.2509,

= −4.99 × 10

−4

, B

= 0.9965, B

= 0.00263, and

= 1.0768. The control parameters include a slid-

ing surface slope λ

= 28, Clegg integrator reset pro-

portion K

= 0.5, smoothing parameter δ = 0.8, and

sliding mode gain k

= 11.5.

4 RESULTS AND DISCUSSION

This section presents the results of the tests per-

formed. A single experiment was conducted, con-

sisting of trajectory tracking combined with an ex-

ternal disturbance to evaluate the performance of

the conventional SMC controller and the proposed

SMC+Clegg approach. The selected trajectory is an

inclined-square path that includes sharp corners and

sudden reference changes, designed to assess the con-

trollers’ performance under abrupt directional transi-

tions and varying orientations.

As shown in Figure 3, the results of the tracking

for the inclined-square trajectory are presented. The

reference trajectory is shown in red, the response us-

ing the conventional SMC controller is shown in blue,

and the response of the proposed SMC+Clegg inte-

grator in the sliding surface is shown in black.

Figure 3: Tracking results for the inclined-square trajectory.

A New Sliding Mode Control Proposal with a Clegg Integrator for a Mobile Manipulator

305

Figure 4 presents the tracking errors along the

three Cartesian axes for the inclined-square trajectory.

The effects of the disturbance introduced into the sys-

tem at t = 15 s can also be observed in the responses.

Figure 4: Tracking errors for the inclined-square trajectory.

Top: error in the x-axis; middle: error in the y-axis; bottom:

error in the z-axis.

As observed in the Figure 4, the introduction of

the Clegg integrator in the sliding surface reduces

both the amplitude and duration of the oscillations.

The proposed approach improves the system’s re-

sponse in terms of trajectory tracking and recovery

after disturbances in the inclined-square trajectory.

To highlight the impact of the proposed method

on the control action, Figure 5 shows the norm of the

control output vectors, with the conventional SMC

controller in blue and the SMC+Clegg controller in

black.

The greatest inﬂuence of the Clegg integrator oc-

curs in the sliding surface, which is directly associ-

ated with the discontinuous component of the con-

trol law. As shown in Figure 5(a), the norm of U

is signiﬁcantly reduced when using the SMC+Clegg

controller, indicating a more moderate control effort

during transients. This reduction is more clearly ob-

served in the zoomed view in Figure 5(b), where sharp

variations are effectively attenuated. Figures 5(c)

and 5(d) present the norm of the total control signal

and its zoomed view, respectively, showing that the

beneﬁts of the proposed strategy extend to the overall

control action, particularly during abrupt changes in

the reference or in the presence of disturbances.

It is important to clarify that, although the dis-

continuous term is bounded due to the smoothing pa-

rameter applied to the switching function, the integral

term in the sliding surface may still accumulate error

during persistent transients. This accumulation can

delay convergence and intensify the control action be-

fore correction occurs. By resetting the integral com-

ponent whenever the error derivative crosses zero, the

Clegg integrator mitigates this form of windup in the

sliding surface, contributing to faster recovery and

improved control smoothness during abrupt transi-

tions.

Figure 5: Norm of the controller vector: (a) discontinuous

component U

, (b) zoomed view of U

, (c) total control

signal, and (d) zoomed view of the total control signal.

Likewise, Figure 5(d) shows that noticeable dif-

ferences between both controllers emerge primarily

during abrupt reference changes or in the presence

of disturbances. This behavior aligns with expecta-

tions, since the discontinuous component—where the

Clegg integrator is applied—is activated mainly un-

der signiﬁcant tracking errors. During steady-state

operation, when the system remains close to the ref-

erence, the control action is dominated by the contin-

uous component, leading to similar behavior for both

controllers.

To evaluate the performance of the controller,

three standard indices were used: the Integral Square

Error (ISE), the Integral Absolute Error (IAE), and

the Total Variation of the control signal (TVu). These

metrics were applied to quantify the tracking accuracy

and control effort of each controller. Table 1 summa-

rizes the results obtained for both controllers, includ-

ing the percentage improvement achieved by the pro-

posed SMC+Clegg controller relative to the conven-

tional SMC controller. Additionally, since the Clegg

integrator is applied in the discontinuous part of the

control law, the TVu was also computed speciﬁcally

for that component to assess its isolated effect on con-

trol smoothness.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

306

Table 1: Performance comparison for the inclined-square

trajectory.

Metric SMC SMC+Clegg ∆ (%)

IAE 0.21846 0.12332 43.55

ISE 0.01685 0.01377 18.30

TVu 7.51519 6.52225 13.21

TVu (U

) 2.39366 1.40371 41.36

As evidenced by the results, the proposed

SMC+Clegg controller achieved notable improve-

ments in all performance indices. The IAE was re-

duced by over 43%, and the total variation of the

discontinuous control signal (U

) decreased by more

than 41%, indicating a smoother and more efﬁcient

control effort. Although the reduction in ISE and

overall TVu was more moderate, improvements of

18% and 13%, respectively, still reﬂect enhanced

tracking precision and reduced control aggressive-

ness. Importantly, resetting the integral component

did not compromise the system’s ability to reject dis-

turbances. In this study, a reset proportion of 50%

= 0.5) was employed, balancing convergence

speed with control signal smoothness. This value was

selected empirically based on iterative testing, as it

provided a satisfactory trade-off between responsive-

ness and chattering attenuation. Nonetheless, system-

atic tuning or optimization of K

may further im-

prove performance and is considered for future work.

5 CONCLUSIONS

This work presented a sliding mode control strategy

that incorporates a Clegg integrator into the sliding

surface. The controller was implemented on a mo-

bile manipulator combining the kinematic model of

the arm and the dynamic model of the platform.

The system was evaluated using an inclined-

square trajectory and external disturbances to test ro-

bustness. Compared to the conventional SMC, the

proposed controller showed improved performance,

with reduced overshoot duration and oscillations,

smoother control signals, and effective mitigation of

chattering. These improvements were reﬂected in the

IAE, ISE, and TVu indices.

Stability is formally ensured via Lyapunov’s direct

method. The Clegg integrator only affects the discon-

tinuous part of the control law, which is active mainly

during transient phases, leaving the continuous com-

ponent stable during steady-state.

Future work may include experimental validation

and extension to systems with higher complexity or

nonlinearities. It should be noted that the current re-

sults are limited to simulation only. Therefore, prac-

tical aspects such as sensor noise, actuator saturation,

and discretization effects must be considered in future

implementations, as they may affect the reset behav-

ior and control smoothness.

Additionally, this work focused exclusively on

the Clegg integrator due to its simplicity and

proven effectiveness. A comparative analysis with

other reset strategies—such as First-Order Reset

Elements (FORE) or Generalized Reset Elements

(GFORE)—was not conducted and remains an im-

portant direction for future research. Nonetheless, the

proposed strategy relies on standard Jacobian inver-

sion and integrator modiﬁcation, which facilitates its

application in embedded systems with typical sensing

and actuation capabilities.

Moreover, extensions of sliding mode control

such as higher-order sliding mode (HOSMC) and

homogeneity-based designs were not considered in

this study. These approaches offer improved conver-

gence properties and enhanced robustness, and their

integration with reset-based strategies could further

improve system performance, representing a valuable

direction for future exploration.

REFERENCES

Beerens, R., Bisofﬁ, A., Zaccarian, L., Nijmeijer, H.,

Heemels, M., and van de Wouw, N. (2022). Reset

pid design for motion systems with stribeck friction.

IEEE Transactions on Control Systems Technology,

30(1):294–301.

Chaudhary, B. (2024). Anti-windup strategy for interval

positive linear systems with input saturation. Inter-

national Journal of Dynamics and Control, 12:2842–

2849.

Delgado, M., Morales, R., Garc

ıa, J., and P

erez, L. (2022).

Motion planning for mobile manipulators—a system-

atic review. Machines, 10(2):97.

Demim, F., Rouigueb, A., Belaidi, H., Messaoui, A. Z.,

Bensseghieur, K. L., Allam, A., Benatia, M. A., Nouri,

A., and Nemra, A. (2023). Smooth sliding mode

control based technique of an autonomous underwa-

ter vehicle based localization using obstacle avoid-

ance strategy. In Proceedings of the 20th Inter-

national Conference on Informatics in Control, Au-

tomation and Robotics (ICINCO 2023), pages 529–

537. SCITEPRESS – Science and Technology Publi-

cations.

Gan, D., Fu, J., Lin, H., Yang, H., Rastgaar, M., Min, B.-

C., and Voyles, R. (2022). Actuation-coordinated mo-

bile parallel robots with hybrid mobile and manipula-

tion functions. Journal of Mechanisms and Robotics,

14(4):041005.

Gholipour, E., Aref, M. M., and Fateh, M. M. (2015). 2-dof

pid with reset controller for 4-dof robot arm manip-

ulator. In 2015 3rd RSI International Conference on

A New Sliding Mode Control Proposal with a Clegg Integrator for a Mobile Manipulator

307

Robotics and Mechatronics (ICRoM), pages 704–709.

IEEE.

Gude, J. J., Di Teodoro, A., Agudelo, D., Herrera, M.,

Rinc

on, L., and Camacho, O. (2024). Sliding mode

control design using a generalized reduced-order frac-

tional model for chemical processes. Results in Engi-

neering, 24:103032.

Haddadin, S., Albu-Sch

affer, A., and Hirzinger, G. (2022).

A holistic approach to reactive mobile manipulation.

IEEE Transactions on Robotics, 38(1):3–22.

Hitit, Z. Y.,

Ismet Koc¸er, Kus¸, G., Arslan, N. Z., Dal,

E. P., and Koz, H. (2023). Optimal pid control

with anti-windup in neutralization process. Interna-

tional Advanced Researches and Engineering Jour-

nal, 7(3):138–145.

Kemp, C. C., Edsinger, A., Clever, H. M., and Matule-

vich, B. (2022). The design of stretch: A compact,

lightweight mobile manipulator for indoor human en-

vironments. In 2022 International Conference on

Robotics and Automation (ICRA), pages 3150–3157.

Kolar, A. and Lazar, M. (2021). Anti windup pid control

of discrete systems subject to actuator saturation. In

2021 60th IEEE Conference on Decision and Control

(CDC), pages 5104–5109, Austin, TX, USA. IEEE.

Le, J. H. and Teel, A. R. (2021). Passive soft-reset con-

trollers for nonlinear systems. In 2021 60th IEEE

Conference on Decision and Control (CDC), pages

5320–5325.

Li, X., Wang, Y., Liu, Y., Liu, Y., and Liu, Y. (2024). A

novel hybrid control strategy for a class of nonlinear

systems with input saturation. Heliyon, 10(9):e2590.

Maung, L. M. M., San, A. M., Myint, W. M., Win, W. Y.,

and Soe, M. T. (2024). Analysis of the pid con-

troller parameters for a surface mobility platform mo-

bile robot. PLATFORM - A Journal of Engineering,

8(2):29–40. Creative Commons CC BY 4.0.

Moreno, G. P., la Cruz, N. D. D., Ortiz, J. S., and Andaluz,

V. H. (2021). Human-robot collaborative control for

handling and transfer objects. In Applied Technolo-

gies, volume 1388 of Communications in Computer

and Information Science, pages 96–110. Springer.

Okelola, M. O., Aborisade, D. O., and Adewuyi, P. A.

(2020). Performance and conﬁguration analysis

of tracking time antiwindup pid controllers. Jur-

nal Ilmiah Teknik Elektro Komputer dan Informatika

(JITEKI), 6(2):20–29.

Proa

no, P., D

ıaz, R., Chill

an, C., Medina, J., Chamorro, W.,

and Zu

niga, J. (2024). Sliding mode control proposed

using a clegg integrator for speed control of a three-

phase induction motor. In Proceedings of the XXXII

Conference on Electrical and Electronic Engineering,

volume 77, page 8. MDPI.

Salinas, L. R., Santiago, D., Slawi

nski, E., Mut, V. A.,

Chavez, D., Leica, P., and Camacho, O. (2018). P+d

plus sliding mode control for bilateral teleoperation of

a mobile robot. International Journal of Control, Au-

tomation and Systems, 16(4):1927–1937.

Teel, A. R. (2022). Continuous-Time Implementation of Re-

set Control Systems, pages 27–41. Springer Interna-

tional Publishing, Cham.

V, V. D. and Manthati, U. B. (2024). Advanced strategies for

chattering reduction in sliding mode-controlled bidi-

rectional cuk converters. In 2024 IEEE 1st Interna-

tional Conference on Green Industrial Electronics and

Sustainable Technologies (GIEST), pages 1–5.

Vizuete, R., Torres, J. A., and Leica, P. (2017). Trajectory

tracking based on containment algorithm applied to

a formation of mobile manipulators. In Proceedings

of the 14th International Conference on Informatics

in Control, Automation and Robotics (ICINCO 2017),

Volume 1, pages 122–131.

Widhiada, W., Santhiarsa, I. G. N., and Partha, C. G. I.

(2020). Design of motion control for mobile robot

manipulator. International Journal of Mechanical En-

gineering and Robotics Research, 9(11):1509–1514.

Yim, J., You, S., Lee, Y., and Kim, W. (2023). Chattering at-

tenuation disturbance observer for sliding mode con-

trol: Application to permanent magnet synchronous

motors. IEEE Transactions on Industrial Electronics,

70(5):5161–5170.

You, Y., Fan, Z., Chen, W., Zhu, G., Qiu, B., Xin, J.,

Chen, J., Deng, F., Hou, Y., Liang, W., and Fu, R.

(2019). Design and implementation of mobile ma-

nipulator system. In 2019 IEEE 9th Annual Interna-

tional Conference on CYBER Technology in Automa-

tion, Control, and Intelligent Systems (CYBER), pages

113–118.

Zangina, U., Buyamin, S., Abidin, M. S. Z., Mahmud, M.

S. A., and Hasan, H. S. (2020). Non-linear pid con-

troller for trajectory tracking of a differential drive

mobile robot. Journal of Mechanical Engineering

Research and Developments, 43(7):255–270. ISSN:

1024-1752, CODEN: JERDFO.

Zhao, J., Giammarino, A., Lamon, E., Gandarias, J. M.,

Momi, E. D., and Ajoudani, A. (2022). A hy-

brid learning and optimization framework to achieve

physically interactive tasks with mobile manipulators.

IEEE Robotics and Automation Letters, 7(3):8036–

8043.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

308