Simultaneous Learning of State-to-State Minimum-Time Planning and

Control

Swati Dantu

, Robert P

eni

cka

and Martin Saska

Department of Cybernetics, Faculty of Electrical Engineering, Czech Technical University in Prague, Czech Republic

Keywords:

Unmanned Aerial Vehicle, Planning and Control, Reinforcement Learning.

Abstract:

This paper tackles the challenge of learning a generalizable minimum-time ﬂight policy for UAVs, capable of

navigating between arbitrary start and goal states while balancing agile ﬂight and stable hovering. Traditional

approaches, particularly in autonomous drone racing, achieve impressive speeds and agility but are constrained

to predeﬁned track layouts, limiting real-world applicability. To address this, we propose a reinforcement

learning-based framework that simultaneously learns state-to-state minimum-time planning and control and

generalizes to arbitrary state-to-state ﬂights. Our approach leverages Point Mass Model (PMM) trajectories

as proxy rewards to approximate the true optimal ﬂight objective and employs curriculum learning to scale

the training process efﬁciently and to achieve generalization. We validate our method through simulation

experiments, comparing it against Nonlinear Model Predictive Control (NMPC) tracking PMM-generated

trajectories and conducting ablation studies to assess the impact of curriculum learning. Finally, real-world

experiments conﬁrm the robustness of our learned policy in outdoor environments, demonstrating its ability to

generalize and operate on a small ARM-based single-board computer.

1 INTRODUCTION

Unmanned Aerial Vehicles (UAVs) are becoming in-

creasingly used in applications that beneﬁt from fast

and agile ﬂight between given goals, such as inspec-

tion (Chung et al., 2021), surveillance (Tsai et al.,

2023), and humanitarian search and rescue (Alotaibi

et al., 2019). In these scenarios, the ability to ﬂy be-

tween desired positions as quickly as possible is cru-

cial for maximizing efﬁciency. The problem of ﬂying

a drone to a target location in minimum time typically

involves two key aspects: (1) planning a minimum-

time trajectory and (2) controlling the drone such that

it accurately follows the planned trajectory. Success-

fully solving this problem allows UAVs to navigate at

high speeds and thus efﬁciently ﬁnish e.g. an inspec-

tion mission.

Solving for planning and control together while

achieving minimum-time ﬂight is, however, challeng-

ing due to several fundamental reasons. UAVs have

highly nonlinear dynamics and must be controlled at

the edge of their actuation limits to achieve the fastest

https://orcid.org/0009-0003-8895-3462

https://orcid.org/0000-0001-8549-4932

https://orcid.org/0000-0001-7106-3816

possible motion. Unlike stable hovering or slow navi-

gation, agile ﬂight demands precise control under ex-

treme conditions, where any model mismatches or ex-

ternal disturbances can lead to catastrophic failures.

A signiﬁcant challenge remains in designing an algo-

rithm, in our case a learning-based planner-controller

leveraging Deep Reinforcement Learning (DRL), that

can generalize to arbitrary starting and ending states,

and thus can solve simultaneously the state-to-state

planning and control for general purpose ﬂight. This

is in contrast, e.g., with existing learning-based ap-

proaches for UAV racing (Kaufmann et al., 2023) that

have been designed to work only with predeﬁned gate

sequences.

Prior work on learning-based UAV ﬂight has pri-

marily focused on speciﬁc racing scenarios (Kauf-

mann et al., 2023), achieving impressive performance

but failing to generalize beyond small deviations in

predeﬁned tracks (Song et al., 2021a). While recent

advances demonstrate the ability to learn ﬂight poli-

cies in a matter of seconds (Eschmann et al., 2024) or

adapt to different UAV conﬁgurations (Zhang et al.,

2024), these approaches have been validated only un-

der near-hover conditions or moderate speeds. The

key limitation remains the lack of a robust, learning-

based minimum-time planner-controller that can gen-

Dantu, S., P

eni

cka, R. and Saska, M.

Simultaneous Learning of State-to-State Minimum-Time Planning and Control.

DOI: 10.5220/0013716800003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 283-291

ISBN: 978-989-758-770-2; ISSN: 2184-2809

283

Figure 1: Illustration from real-world ﬂight: quadrotor in

ﬂight using proposed learned policy.

eralize to arbitrary start-goal positions while main-

taining agility in general ﬂight conditions.

To bridge this gap, we propose a approach for

learning-based minimum-time ﬂight by effectively

solving both planning and control with a single pol-

icy that generalizes to arbitrary start-goal conﬁgura-

tions. We leverage Deep Reinforcement Learning ap-

proach that incorporates two key ideas: (1) leveraging

Point Mass Model (PMM) trajectories as proxy re-

wards, ensuring that the learning objective closely ap-

proximates the true performance metric of minimum-

time ﬂight (Teissing et al., 2024), and (2) employing

a curriculum learning strategy to progressively scale

the learning process, enabling the policy to handle in-

creasingly large position variations in agile ﬂight and

at the same time be able to hover smoothly. To the

best of our knowledge, this is the ﬁrst work that in-

tegrates these concepts into a reinforcement learning

framework for UAV minimum-time ﬂight, achieving

a balance between hovering stability and high-speed

manoeuvrability.

We evaluate the proposed approach in both sim-

ulation and real-world experiments. In simulation,

we compare our learned policy against Nonlinear

Model Predictive Control (NMPC) tracking PMM-

generated trajectories over various maneuvers, in-

cluding straight-line, zigzag, and semicircular paths,

demonstrating comparable ﬂight times while main-

taining more stable execution. We show that the cur-

riculum learning signiﬁcantly improves convergence

and performance compared to conventional reinforce-

ment learning. Finally, real-world tests validate our

policy’s robustness in outdoor environments, show-

casing its ability to control a small agile drone with

limited compute power as shown in Figure 1.

2 RELATED WORKS

Recently, learning-based approaches have shown

promising outcomes for diverse tasks of minimum-

time planning and control. One of the learning-

based approaches (Song et al., 2021b), designed for

drone racing scenarios, leverages deep reinforcement

learning framework with additional privileged infor-

mation for high-speed racing drones reaching speeds

of ∼17m/s to navigate through gates autonomously.

Similarly, (Song et al., 2023) additionally include per-

ception awareness for navigation in cluttered envi-

ronments to optimize for ﬂight efﬁciency and visual

awareness. Perception awareness has also shown re-

markable progress in drone racing (Kaufmann et al.,

2023) to achieve performance at the level of the best

human pilots. However, these works have been only

designed for speciﬁc race tracks with minimum per-

turbations (as seen in (Song et al., 2021b)) and do not

generalize for state-to-state agile ﬂight.

The prior methods are limited to a single task of

navigation through race tracks. To address this limita-

tion, (Xing et al., 2025) presented a multi-Task DRL

framework with a shared physical dynamics across

tasks through shared actor and separate critic for each

task. The authors provided a single policy that is ca-

pable of performing multiple tasks: stabilizing, track-

ing a racing trajectory, and velocity tracking, without

the need for separate policies. Yet, without an explicit

transition mechanism between different ﬂight modes

(e.g., switching between tracking a racing trajectory

and stabilizing task mid-ﬂight).

Learning-based control methods have also been

shown to adapt to different quadrotor dynamics with-

out manual tuning. The work presented in (Zhang

et al., 2023) introduces a DRL based near-hover posi-

tion controller that adjusts control gains in real-time

that showed a rapid adaptation to quadrotors with

mass variations up to 4.5 times along with distur-

bances such as external force, payloads or disparities

in drone parameters. The authors of (Zhang et al.,

2024) combined imitation learning (for a warm start)

and reinforcement learning to ﬁne-tune control in re-

sponse to changing dynamics. This work demon-

strated adaptation to disturbances arising from an off-

center payload and external wind for quadrotors with

mass differences and various propeller constants.

Deep reinforcement learning has also shown im-

mense promise for landing a quadrotor. The authors

of (Kooi and Babuška, 2021) illustrated landing of a

quadrotor on an inclined surface by using PPO with

sparse rewards. Prior to this, (Polvara et al., 2018)

presented the use of DRL for landing on ground mark-

ers with low resolution images, while (Rodriguez-

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

284

Ramos et al., 2019) showed the possibility of landing

on a moving platform.

The work presented in (Eschmann et al., 2024)

elucidated the feasibility of real-time learning by

training an off-policy asymmetric actor-critic RL

framework within 18s on a consumer-grade laptop

with demonstration of successful real-world ﬂight

with minimal tuning. Previously, (Hwangbo et al.,

2017) successfully showed waypoint following using

an approach based on Deterministic Policy Optimiza-

tion (DPG). However, the aforementioned methods do

not consider the minimum-time objective. Our pro-

posed algorithm tackles this problem by designing a

learning-based planner-controller optimized for min-

imizing time, capable of generalizing across varying

start and goal positions. Our policy is not restricted

to a single task, capable of seamlessly transitioning

between waypoint ﬂight and stable hovering.

3 PROBLEM FORMULATION

AND METHODOLOGY

In this section we present the quadrotor dynamics

considered during the training and deployment of our

proposed method, formulate the control problem and

explain the choice of observation and action spaces

together with design of applied rewards.

3.1 System Dynamics

The quadrotor is modeled with state x =

[p, q, v, ω, Ω]

which consists of position p ∈ R

velocity v ∈ R

, unit quaternion rotation q ∈ SO(3),

body rates ω ∈ R

, and the rotors’ rotational speed

Ω. The dynamics equations are

p = v , (1a)

q =

q ⊙





, (1b)

v =

R(q) (f

+ f

)

+ g , (1c)

ω = J

−1

(τ − ω ×Jω) , (1d)

where ⊙ denotes the quaternion multiplication, R(q)

is the quaternion rotation, f

is the drag force vector

in the body frame, m is the mass, J is diagonal inertia

matrix, and g denotes Earth’s gravity. The speeds of

the propellers Ω are modelled as a ﬁrst-order system,

Ω =

mot

(Ω

− Ω) with Ω

being the commanded

speed and k

mot

the time constant.

The collective thrust f

and torque τ

are calcu-

lated as:









, (2)

τ =





√

2 (f

− f

+ f

)

√

2 (−f

− f

+ f

)

κ (f

− f

+ f

− f

)





, (3)

where κ is the torque constant and l is the arm length.

Here, individual motor thrusts f

are functions of the

motor speeds using the thrust coefﬁcient c

(Ω) =



· Ω



. (4)

3.2 Task Formulation

The minimum-time planning and control problem is

formulated in the reinforcement learning (RL) frame-

work using a Markov Decision Process (MDP) repre-

sented as a tuple (S, A, P, R, γ). The action a

∈ A

is executed at every time step t to transition the agent

from the current state s

∈ S to next state s

t+1

with

the state transition probability P(s

t+1

, a

) receiv-

ing an immediate reward r

∈ R.

The objective of deep reinforcement learning is to

optimize the parameters θ of a neural network policy

so that the learned policy maximizes the expected

discounted reward. The objective function is formu-

lated as

∗

= arg max

∞

t=0

. (5)

3.3 Observation and Action Spaces

The observation space is deﬁned as the vector o

, R

, p

, ω

, ϕ

, a

t−1

] ∈ R

which corresponds to

linear velocity of the quadrotor, rotation matrix, rela-

tive position of the quadrotor to that of the goal posi-

tion, input body rates around each axis of the quadro-

tor, relative heading of the quadrotor to that of the

goal and the action executed at the previous time step.

The agent is such that the observation is mapped

to the action consisting of collective thrust and body

rates around each of the axes. This deﬁnes the action

space to be a

= [τ

, ω

3.4 Reward Shaping

The objective of deep reinforcement learning is to

maximize the cumulative discounted reward. To this

end, our rewards consist of two main components,

one direct, simple function-based rewards for posi-

tion and velocity, and one capturing proxy reward

Simultaneous Learning of State-to-State Minimum-Time Planning and Control

285

via the usage of point-mass model (PMM)(Teissing

et al., 2024) trajectories to consider the minimum-

time state-to-state objective.

3.4.1 Direct Rewards

These rewards are designed to consider various as-

pects that are crucial for both hovering and the

minimum-time state-to-state objective. In this paper,

we consider total direct reward (r

) to be the sum of

the following components.

• Distance to Goal: r

= K



1 −

∥p

−p

∥



• Heading: r

= K

|ϕ

− ϕ

• Stay at Goal: r

= K

· s

), where s

∥p

− p

t−1

∥, s

= ∥p

− p

∥

• Acceleration: r

= K

∥a

∥

• Angular Velocity: r

= K

• Thrust Smoothing: r

= K

|τ

− τ

t−1

• Commanded Angular Velocity: r

= K

|ω

−

t−1

where p ∈ R

, a

∈ R

⊯

, ϕ

∈ [−π, π], ω

∈ R

⊯

are

the current position, acceleration, heading and angu-

lar acceleration of the UAV at time t, p

∈ R

, ϕ

∈

[−π, π] are the position and heading of the desired

goal. G is the acceptable convergence radius from the

goal point. ω

∈ R

, ω

t−1

∈ R

are the commanded

velocities and τ

, τ

t−1

are the commanded thrusts at

times t, t − 1. K

, K

are the

scaling factors.

The Distance to Goal reward acts as an indica-

tor for the quadrotor to move towards the goal, which

is especially valuable during the exploration phase.

Heading reward awards if the quadrotor moves to-

wards the heading goal and penalises it if not by a

factor of the absolute difference between the current

heading and the goal heading. The Stay at Goal re-

ward keeps the quadrotor at the goal by rewarding

if the movement direction vector of the quadrotor is

aligned with the vector towards the goal. The Acceler-

ation and Angular Velocity rewards penalize if either

of these quantities are too high. These rewards are

essential in ﬁnding the balance between stable hover-

ing and agile start-to-goal ﬂight. We observed that, in

the absence of these penalties, the quadrotor demon-

strated effective agile start-to-goal ﬂight but failed to

maintain stable hovering. These reward components

are crucial for enabling consistent multi-goal behav-

ior. The Thrust Smoothing and Commanded Angu-

lar Velocity rewards are temporal smoothing rewards.

They penalise the quadrotor if the change is too high

within immediate time steps of particular commanded

values. This ensures the outputs of the policy do not

contain any sharp perturbation which could cause in-

stability during ﬂight.

3.4.2 Proxy Reward with PMM

In order to drive the minimum state-to-state objec-

tive, we use trajectories generated by the PMM plan-

ner (Teissing et al., 2024) to compute proxy reward

to closely approximate the true performance objec-

tive while providing feedback at every time step.

The proxy reward is also instrumental in combining

the planning and control objective for the learning

process. The PMM planner planner generates the

minimum-time trajectories over multiple waypoints

within milliseconds by utilizing a point-mass model

of the UAV combined with thrust decomposition al-

gorithm that enables the UAV to utilize all of its col-

lective thrust.

A time-optimal PMM trajectory segment can be

described as:

= p

+ v

, v

= v

+ a

= p

+ v

, v

= v

+ a

(6)

where p

, v

∈ R are the start position and velocity,

, v

∈ R are the end position and velocity, t

, t

∈

R are the time durations of the corresponding sub-

segments of the trajectory and

∈ {a

min

, a

max

}, i = 1, 2, a

∈ R, (7)

are the optimal control inputs. a

= a

is omitted as

it is equivalent to t

= 0 or t

= 0. This omission

leaves two two combinations of possible values for

and a

Analytical solutions to the equations (6) can be

derived, revealing a total of four possible solutions.

For each combination of a

and a

values, two solu-

tions exist. The ﬁnal solution is selected based on the

criteria that all unknowns must be real numbers and

that the real-world constraint of non-negative times,

≥ 0 and t

≥ 0, is met.

We sample a PMM trajectory generated between

the initial and goal position. The proxy reward r

P M M

is deﬁned as

P M M

= k

P M M

∥p

−p

P M M

∥+k

P M M

∥v

−v

P M M

∥

(8)

where p

, v

describe the state of UAV at time t and

P M M

, v

P M M

are position and velocity values sam-

pled from PMM trajectory generated between the ini-

tial and goal position. k

P M M

, k

P M M

are scaling fac-

tors.

This reward incentivises the quadrotor to track the

PMM trajectory akin to a linear MPC tracking the tra-

jectory.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

286

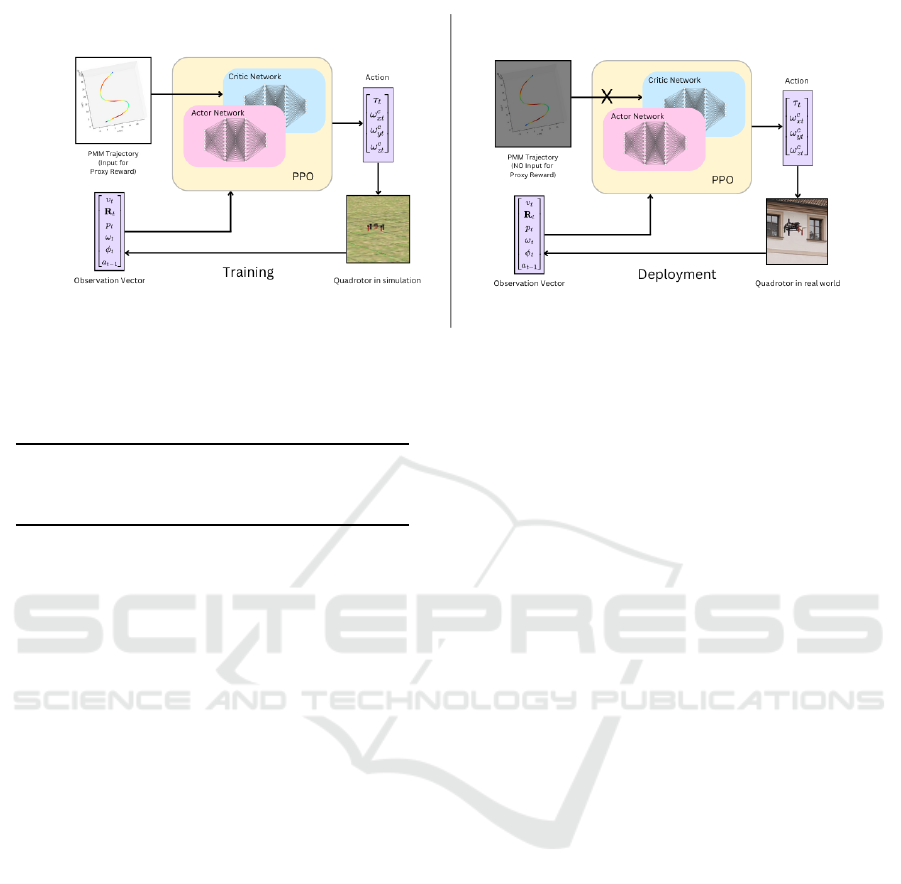
Figure 2: System Overview: We train the network with the trajectories generated through PMM planner as a proxy reward

for minimum-time state-to-state objective. The network later does not have access to these trajectories during deployment.

Table 1: Values of the rewards scaling parameters.

0.2 K

-1.0 K

0.2

-0.15 K

0.25 K

0.4

0.35 k

P M M

-3.0 k

P M M

-0.3

4 IMPLEMENTATION DETAILS

This section details the speciﬁcations of the simula-

tion environment we used for training and evaluation,

the details of the hardware equipment used for the

real-world experiments along with the network archi-

tecture and implementation details of the proposed al-

gorithm.

4.1 Simulation Environment

We use an in-house developed simulator for training

and testing of our control policies. The inputs to our

policy are linear velocity of the quadrotor, rotation

matrix, relative position of the quadrotor to that of the

goal position, input body rates around each axis of the

quadrotor, relative heading of the quadrotor to that of

the goal, and the action executed at the previous time

step. The state of the quadrotor (position, velocity,

rotation matrix, linear and angular velocities) comes

from the simulation platform and the reference PMM

trajectories are generated at the simulated time point.

The policy outputs mass-normalized collective thrust

and the body rates. The maximum duration of each

of the simulated environments is 5s with early termi-

nation if the quadrotor goes out of the bounds of the

simulated environment. The simulation step size is

1ms and the control frequency is set to 100Hz.

We integrate the trained RL algorithm into the

multirotor Unmanned Aerial Vehicle control and es-

timation system developed by the Multi-robot Sys-

tems Group (MRS) at the Czech Technical University

(CTU) (Bá

ca et al., 2021), (He

rt et al., 2023). For the

simulated experiments, we use the existing multiro-

tor dynamics simulation tools available in the system

(He

rt et al., 2023).

4.2 Hardware Speciﬁcations

We utilize a custom-built agile quadrotor with a di-

agonal motor-to-motor span of 300 mm and a total

weight of 1.2 kg. It is controlled by our open-source

MRS system architecture (He

rt et al., 2023) operat-

ing on a Khadas Vim3 Pro single-board computer.

The quadrotor has a CubePilot Cube Orange+ ﬂight

controller with PX4 ﬁrmware acting as the low-level

controller. It is powered by a 4S Lithium Polymer

battery. We use Holybro F9P RTK GNSS module

on the quadrotor for the state estimation. It receives

real-time corrections from a base station, which are

combined with the ﬂight controller’s IMU to generate

odometry for the system.

4.3 Policy Training

We use Proximal Policy Optimization (PPO) algo-

rithm (Schulman et al., 2017), a ﬁrst order policy gra-

dient method to train our agent. Although PPO is

popular for its simplicity in implementation, our task

is challenging due to the large dimensionality of the

search space and the complexity of learning two dis-

tinctly different behaviours. Therefore, we emphasize

important details that allowed us to achieve a policy

capable of planning and control simultaneously.

Simultaneous Learning of State-to-State Minimum-Time Planning and Control

287

4.3.1 Network Architecture

We represent the control policy with a deep neu-

ral network. We use PPO (Schulman et al., 2017)

network architecture with 2 hidden layers with 256

ReLU nodes. The learning rate is linearly decreased

starting from 5e −4 ending at 2e −5. Discount factor

γ is set to 0.99. The algorithm is set to collect 2000

experiences from each environment into the batch.

Since parallelise the training with 500 environments

the total batch size is 1 million. Such a large batch

size is needed to encapsulate the different behaviour

in a large observation space.

4.3.2 Parallelization

We trained our agent in simulation with 500 environ-

ments in parallel to increase the speed of the data col-

lection process. Additionally, we were able to lever-

age this parallelization process to diversify the data

collected by interacting with the environment. Since

training requires signiﬁcantly different environment

interactions for ﬂying in minimum-time between start

and goal and hover at a setpoint, rollouts could be per-

formed with multiple, diverse environments to learn a

generalizing policy.

4.3.3 Randomized Initialization and Dynamics

The training aims to learn simultaneously minimum-

time planning and control. To this end, we ran-

domize initial setpoint in position and heading to en-

sure exploration of necessary areas of state space.

The position is randomly sampled within the interval

[−20, 20]m and the heading is randomly sampled in

the interval [−π, π] radians.

Furthermore, to ensure robustness, for each

episode, the quadrotor’s mass and inertia are random-

ized. These are used to imitate variations caused in

the quadrotor parameters due to disturbances caused

by environmental factors such as wind. The mass and

inertia are both randomized by 30%.

4.3.4 Curriculum Strategy

Having a large(40m) sampling range, that is essen-

tial for learning state-to-state generalizing behaviour,

makes the problem incredibly challenging to learn.

Therefore, we employ a curriculum approach to

achieve the successful learning of desired objectives.

The training is divided into 4 sub-tasks. The task

difﬁculty increases with every stage in the curricu-

lum. In the ﬁrst stage, the start position (in the be-

ginning of each episode) is sampled from the interval

of [−1, 1]m for each of X, Y, Z axes. This ensures

that the state space is small enough for successful ex-

ploration and helps the quadrotor learn the behaviour

of moving towards the goal considering PMM trajec-

tory as reference, which is given as proxy reward.

The stage is stepped up once the RSME error cal-

culated between the reached position after the rollout

and the goal gets below 2 for 100 sampled trajectories.

The position is sampled in the intervals of [−5, 5]m

,[−10, 10]m ,[−20, 20]m for all the 3 axes in the sec-

ond, third, and the fourth sub-tasks respectively. The

heading is sampled from the interval [−π, π] radians

for all the stages of the curriculum training.

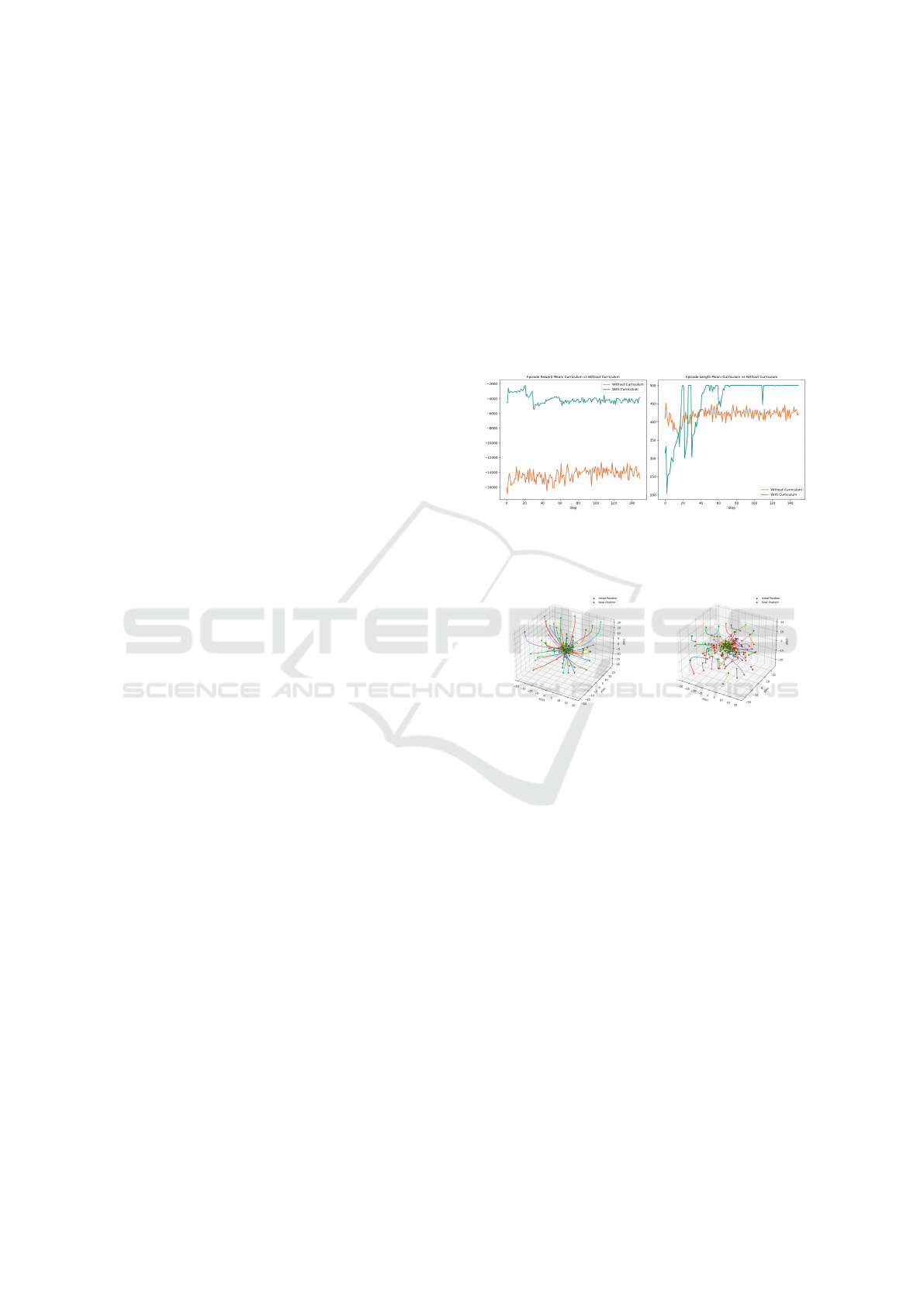
Figure 3: Comparison of mean rewards (left) and episode

lengths (right) for policies trained with curriculum (green)

and without curriculum (orange).

(a) With curriculum (b) Without curriculum

Figure 4: Visualization of typical desired quadcopter trajec-

tories in 3D space during simulated tests with curriculum

and without curriculum. We sampled 100 initial positions.

The goal conditions of all trajectories are hovering at the

origin.

5 EXPERIMENTAL RESULTS

In this section, we outline the details of the exper-

iments we conducted to validate our experiments.

We begin by establishing the importance of the cur-

riculum approach by evaluating the same objective

learned with and without curriculum. Subsequently,

we evaluate the performance of our method against a

set of baseline methods in a controlled simulation en-

vironment. Eventually, we show the deployment of

our controller on a real quadrotor (see Fig. 1) to vali-

date the robustness of our approach.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

288

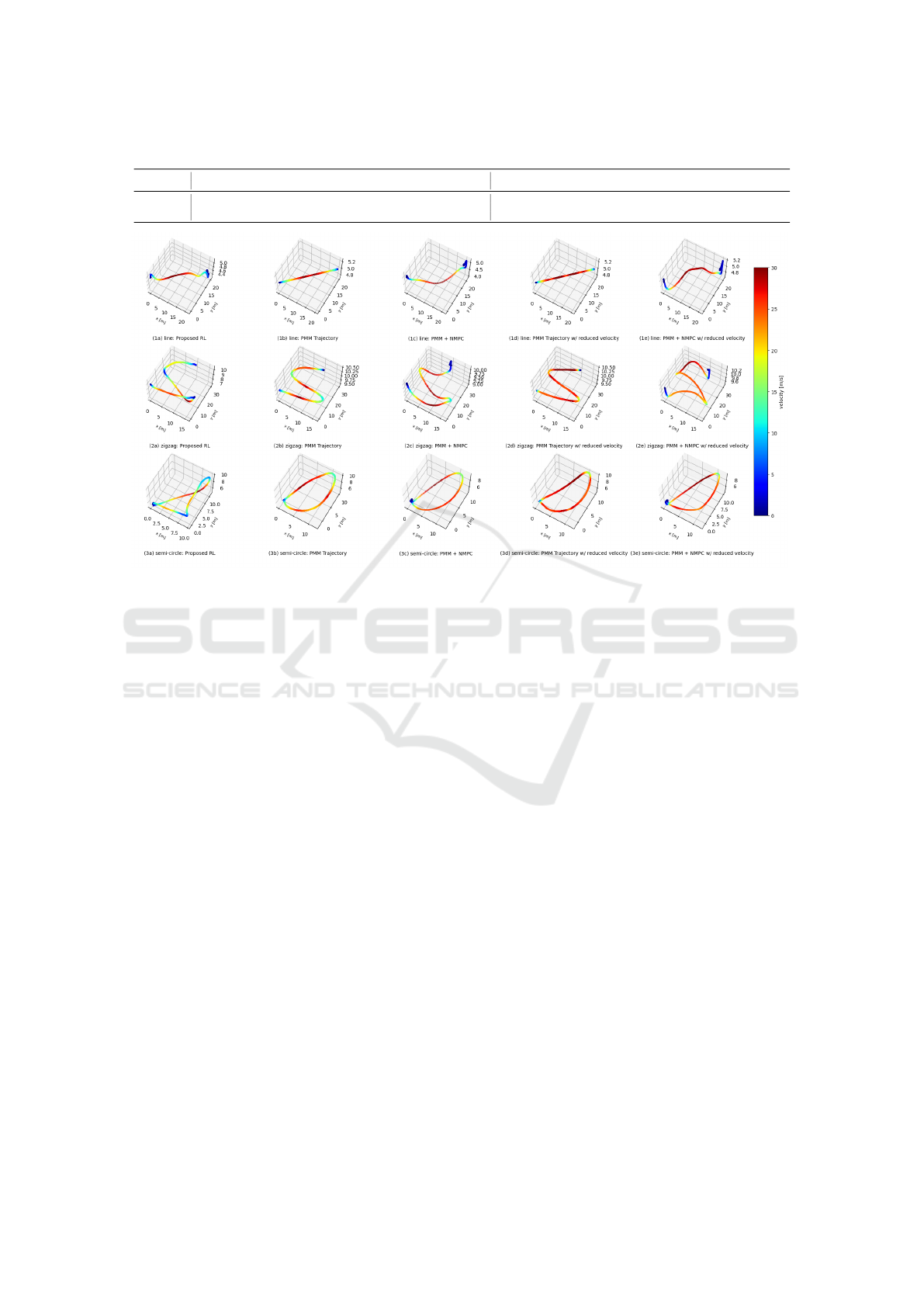
Table 2: Comparision of Flight Times and Maximum Velocity wrt baseline.

Trajectory

Flight time in seconds Maximum Velocity in m/s

Proposed RL PMM + NMPC (Foehn et al., 2021) PMM + NMPC w/ reduced velocity Proposed RL PMM + NMPC (Foehn et al., 2021) PMM + NMPC w/ reduced velocity

line 4.239 3.119 4.127 17.20 28.8 20.1

zigzag 7.924 5.092 7.503 14.5 22.6 15.9

3D semi-circle 8.169 5.614 8.202 12.8 19.0 12.5

Figure 5: Velocity Proﬁles of proposed RL controller along with the generated PMM trajectories and NMPC tracking perfor-

mance. The PMM trajectories with full and reduced velocities along with NMPC performance are shown.

5.1 Simulation Experiments

5.1.1 Ablation Studies

We compare the performance of the RL policy ob-

tained when the training scheme contains curriculum

and also when it is absent. To maintain consistency,

we trained both of these polices with an objective to

reach the same goal position when starting at a ran-

dom initial position obtained from sampling a space

spanning 40 x 40 x 40 m. Both the policies have ac-

cess to proxy reward in the form of PMM trajecto-

ries during training. They are trained for 3000 mil-

lion time steps with the hyperparameters detailed in

section 3.4 and scaling factors for rewards speciﬁed

in Table 1. The training scheme used is the only sole

distinction between the polices.

The results of the ablation studies are visualized

through Figures 3 and 4. The learning approach with

curriculum converges compared to training solely

with the conventional approach. It could be observed

from Fig. 3 that both the mean cumulative discounted

reward as well as the mean episode length are higher

with the use of the curriculum approach, substantiat-

ing the convergence of the proposed approach. This

is more evident from the visualizations of 100 roll-

outs with each of the approaches shown in Fig. 4. The

policy with the curriculum training paradigm success-

fully learns the objective while conventional RL fails

to do so.

5.1.2 Comparison with Baseline

We choose 3 trajectories: line, zigzag, and slanted

semicircle as shown in Fig. 5 to evaluate the perfor-

mance against the Nonlinear Model Predictive Con-

troller (NMPC) (Foehn et al., 2021) tracking the tra-

jectory generated by the PMM planner. Identical

waypoints were provided to both the PMM planner

and the proposed RL-based planner-controller. Sub-

sequently, the trajectory generated by the PMM plan-

ner—tracked by an NMPC controller—and that pro-

duced directly by the proposed RL planner-controller

are evaluated. These curves together encapsulate the

common manoeuvrers a UAV is expected to execute

in the majority of applications.

Despite providing the same velocity and acceler-

ation constraints to the PMM during training of the

proposed RL algorithm and for the NMPC controller,

we observe a signiﬁcant loss in performance using the

proposed algorithm. The proposed RL algorithm has

to learn diametrically opposite behaviours of hover-

ing and agile ﬂight over a large distance. Therefore,

the proposed RL algorithm learns to accommodate the

opposing behaviours and realize a stable behaviour

with smaller speed. To further substantiate this, we

compared the performance of the proposed RL con-

troller to NMPC tracking the PMM trajectories with

Simultaneous Learning of State-to-State Minimum-Time Planning and Control

289

reduced velocity. The velocity proﬁles for the trajec-

tories ﬂown are shown in Fig. 5. When we matched

the maximum velocity of the PMM trajectory to that

of the proposed RL controller, the ﬂight times are

comparable as seen in Table 2. It is also interesting to

note that since the proposed RL controller was trained

on state-to-state trajectories, the path it takes between

two waypoints is straighter when compared to the tra-

jectory generated by the PMM planner, as shown in

the Figures 6 and 7.

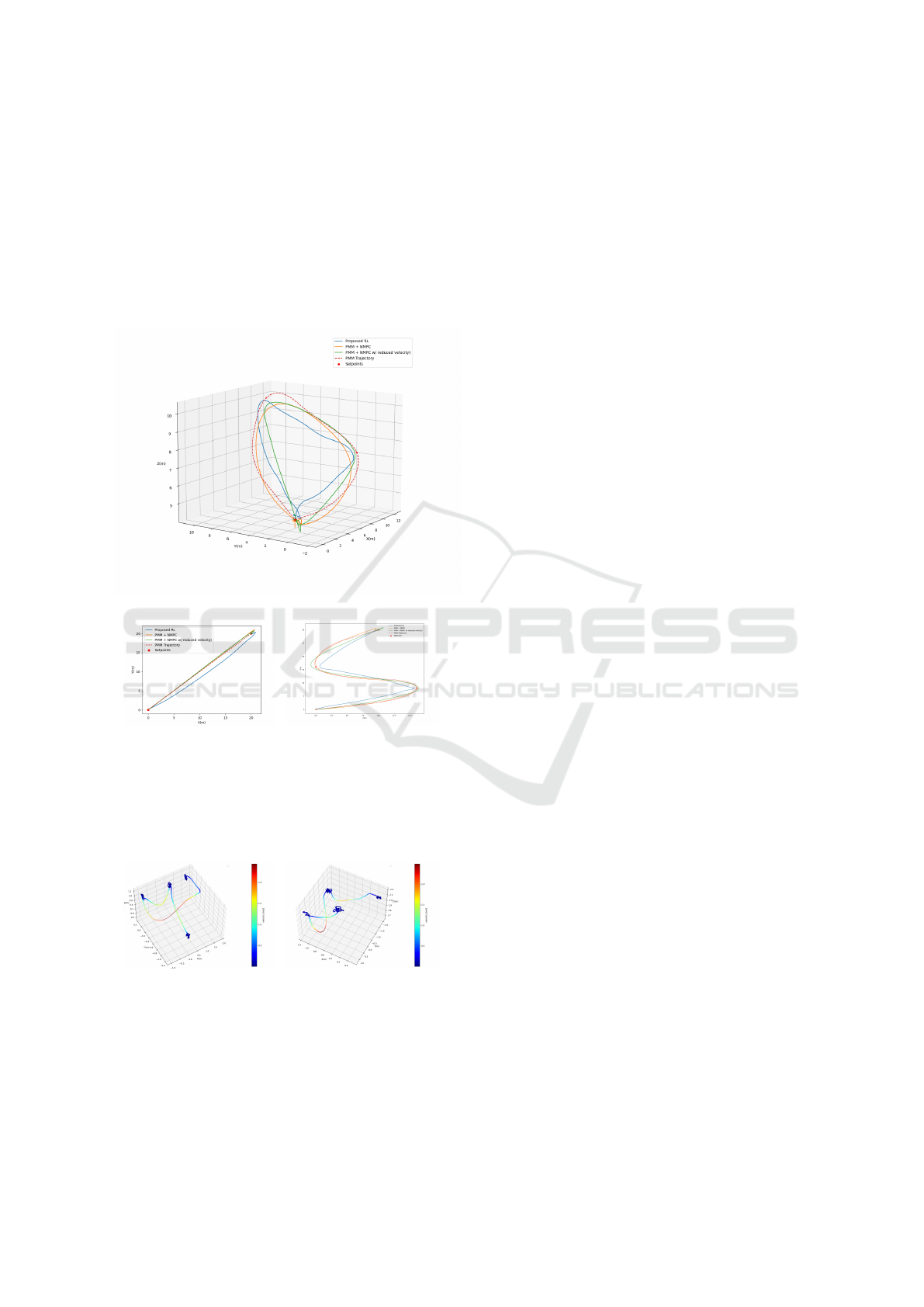
Figure 6: Comparison of path of the proposed RL algorithm

with the baseline for the waypoints of a semi-circle.

(a) line (b) zigzag

Figure 7: Comparison of path of the proposed RL algorithm

with the baseline for the waypoints of line and zigzag curve.

5.2 Real World Experiments

(a) Run 1 (b) Run 2

Figure 8: Performance of the proposed RL planner-

controller between arbitrary way points in the real world.

After verifying the proposed solution in simula-

tion, we conducted experiments in the real world. We

gave random goal waypoints to our controller to test

the robustness of the generalization of the proposed

controller. Due to constraints in space with the out-

door testing environment, we were only able to input

goal points maximally 2m far. Therefore, we were

only able to reach a maximum speed of 2.5 m/s.

Our proposed solution was able to hover stably

and reach the given way points successfully in two

different runs as shown in Fig. 8 which showcases an

ability of sim-to-real transfer. On the other hand, we

observe loss of altitude initially. We believe this is due

to the aggressive nature of the policy and mismatch in

the PID control coefﬁcients in the lower-level control

and communication delays between the simulated en-

vironment and the real-world system. This shows the

ability of our controller to be robust against the mis-

matches, which is a consequence of artiﬁcially intro-

ducing system mismatches by randomizing the mass,

inertia and gravity coefﬁcient during training.

6 CONCLUSION

In this work we introduced a reinforcement learning

framework that enables quadrotors to perform gen-

eralizable, minimum-time ﬂights between any given

start and goal states. Unlike traditional methods in au-

tonomous drone racing that rely on predeﬁned track

layouts, this approach focuses on balancing agile

ﬂight with stable hovering. The key innovation lies in

using Point Mass Model (PMM) trajectories as proxy

rewards to approximate the optimal ﬂight objective.

Additionally, curriculum learning is employed to en-

hance training efﬁciency and generalization. The pro-

posed method is validated through simulations, where

it is compared against Nonlinear Model Predictive

Control (NMPC) tracking PMM-generated trajecto-

ries. Ablation studies further highlight the beneﬁts of

curriculum learning. Finally, real-world outdoor ex-

periments demonstrate the robustness and adaptabil-

ity of the learned policy, conﬁrming its effectiveness

in various challenging scenarios. In the future, we

would like to conduct experiments over longer dis-

tances to better understand the potential of the ap-

proach and its full transferability to the real world.

ACKNOWLEDGMENT

The authors thank Ond

rej Procházka for helping

with the real-world experiments. This work has

been supported by the Czech Science Foundation

(GA

CR) under research project No. 23-06162M,

by the European Union under the project Robotics

and Advanced Industrial Production (reg. no.

CZ.02.01.01/00/22_008/0004590) and by CTU grant

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

290

no SGS23/177/OHK3/3T/13.

REFERENCES

Alotaibi, E. T., Alqefari, S. S., and Koubaa, A. (2019).

Lsar: Multi-uav collaboration for search and rescue

missions. IEEE Access, 7:55817–55832.

Bá

ca, T., Petrlík, M., Vrba, M., Spurný, V., Pe

cka, R.,

rt, D., and Saska, M. (2021). The mrs uav system:

Pushing the frontiers of reproducible research, real-

world deployment, and education with autonomous

unmanned aerial vehicles. Journal of Intelligent &

Robotic Systems, 102(26).

Chung, H.-M., Maharjan, S., Zhang, Y., Eliassen, F., and

Strunz, K. (2021). Placement and routing optimiza-

tion for automated inspection with unmanned aerial

vehicles: A study in offshore wind farm. IEEE Trans-

actions on Industrial Informatics, 17(5):3032–3043.

Eschmann, J., Albani, D., and Loianno, G. (2024). Learn-

ing to ﬂy in seconds. IEEE Robotics and Automation

Letters, 9(7):6336–6343.

Foehn, P., Romero, A., and Scaramuzza, D. (2021). Time-

optimal planning for quadrotor waypoint ﬂight. Sci-

ence Robotics, 6(56):eabh1221.

rt, D., Bá

ca, T., Pet

rá

cek, P., Krátký, V., Pe

ní

cka,

R., Spurný, V., Petrlík, M., Vrba, M., Zaitlík, D.,

Stoudek, P., Walter, V., Št

epán, P., Horyna, J., Pritzl,

V., Srámek, M., Ahmad, A., Silano, G., Licea, D. B.,

Štibinger, P., Nascimento, T., and Saska, M. (2023).

MRS Drone: A Modular Platform for Real-World De-

ployment of Aerial Multi-Robot Systems. Journal of

Intelligent & Robotic Systems, 108(64):1–34.

Hwangbo, J., Sa, I., Siegwart, R., and Hutter, M.

(2017). Control of a quadrotor with reinforcement

learning. IEEE Robotics and Automation Letters,

2(4):2096–2103.

Kaufmann, E., Bauersfeld, L., Loquercio, A., Müller, M.,

Koltun, V., and Scaramuzza, D. (2023). Champion-

level drone racing using deep reinforcement learning.

Nature, 620(7976):982–987.

Kooi, J. E. and Babuška, R. (2021). Inclined quadro-

tor landing using deep reinforcement learning. In

2021 IEEE/RSJ International Conference on Intelli-

gent Robots and Systems (IROS), pages 2361–2368.

Polvara, R., Patacchiola, M., Sharma, S., Wan, J., Manning,

A., Sutton, R., and Cangelosi, A. (2018). Autonomous

quadrotor landing using deep reinforcement learning.

Rodriguez-Ramos, A., Sampedro, C., Bavle, H., de la

Puente, P., and Campoy, P. (2019). A deep reinforce-

ment learning strategy for uav autonomous landing on

a moving platform. Journal of Intelligent & Robotic

Systems, 93(1-2):351–366.

Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and

Klimov, O. (2017). Proximal policy optimization al-

gorithms.

Song, Y., Shi, K., Penicka, R., and Scaramuzza, D. (2023).

Learning perception-aware agile ﬂight in cluttered en-

vironments. In 2023 IEEE International Conference

on Robotics and Automation (ICRA), pages 1989–

1995.

Song, Y., Steinweg, M., Kaufmann, E., and Scaramuzza, D.

(2021a). Autonomous drone racing with deep rein-

forcement learning. In 2021 IEEE/RSJ International

Conference on Intelligent Robots and Systems (IROS),

pages 1205–1212. IEEE.

Song, Y., Steinweg, M., Kaufmann, E., and Scaramuzza, D.

(2021b). Autonomous drone racing with deep rein-

forcement learning. In 2021 IEEE/RSJ International

Conference on Intelligent Robots and Systems (IROS),

pages 1205–1212.

Teissing, K., Novosad, M., Penicka, R., and Saska, M.

(2024). Real-time planning of minimum-time trajec-

tories for agile uav ﬂight. IEEE Robotics and Automa-

tion Letters, 9(11):10351–10358.

Tsai, H.-C., Hong, Y.-W. P., and Sheu, J.-P. (2023). Com-

pletion time minimization for uav-enabled surveil-

lance over multiple restricted regions. IEEE Trans-

actions on Mobile Computing, 22(12):6907–6920.

Xing, J., Geles, I., Song, Y., Aljalbout, E., and Scara-

muzza, D. (2025). Multi-task reinforcement learning

for quadrotors. IEEE Robotics and Automation Let-

ters, 10(3):2112–2119.

Zhang, D., Loquercio, A., Tang, J., Wang, T.-H., Malik, J.,

and Mueller, M. W. (2024). A learning-based quad-

copter controller with extreme adaptation.

Zhang, D., Loquercio, A., Wu, X., Kumar, A., Malik, J., and

Mueller, M. W. (2023). Learning a single near-hover

position controller for vastly different quadcopters. In

2023 IEEE International Conference on Robotics and

Automation (ICRA), pages 1263–1269.

Simultaneous Learning of State-to-State Minimum-Time Planning and Control

291