A Context-Enriched Hybrid ARIMAX–Deep Learning Framework for

Robust Cryptocurrency Price Forecasting

Gerasimos Vonitsanos

, Andreas Kanavos

and Phivos Mylonas

Computer Engineering and Informatics Department, University of Patras, Patras, Greece

Department of Informatics, Ionian University, Corfu, Greece

Department of Informatics and Computer Engineering, University of West Attica, Athens, Greece

Keywords:

Cryptocurrency, Bitcoin Forecasting, Time Series Forecasting, Hybrid Models, ARIMAX, LSTM, Deep

Learning, Ensemble Learning, Financial Time Series, Market Sentiment.

Abstract:

The inherent volatility and nonlinear dynamics of cryptocurrency markets pose substantial challenges to ac-

curate price forecasting. This paper proposes a novel context-enriched hybrid modeling framework that inte-

grates classical time series analysis with deep learning techniques to enhance prediction accuracy for Bitcoin

price movements. A comprehensive evaluation is conducted on ARIMA, ARIMAX, Support Vector Machines

(SVM), and Long Short-Term Memory (LSTM) networks using high-resolution market data from 2019 to

2024. The framework leverages exogenous variables—such as trading volume, market capitalization, and

moving averages—to enrich model inputs and capture contextual signals. Experimental results demonstrate

that hybrid conﬁgurations, particularly ARIMAX-based models, consistently achieve the lowest Root Mean

Squared Error (RMSE) and highest coefﬁcient of determination (R

), closely tracking real market trends.

These ﬁndings conﬁrm the effectiveness of combining statistical rigor with the nonlinear learning capabilities

of deep architectures. Furthermore, the study highlights the potential of extending this approach with ensem-

ble strategies for even greater robustness. This work contributes to the development of accurate, data-driven

forecasting tools for decision-making in highly dynamic and speculative digital asset markets.

1 INTRODUCTION

The emergence of digital currencies has profoundly

transformed the structure of contemporary ﬁnancial

systems, evolving rapidly from specialized techno-

logical innovations into integral components of global

transaction infrastructures. Among these, cryptocur-

rencies—digital tokens underpinned by blockchain

protocols and cryptographic mechanisms—have gar-

nered substantial attention due to their trans-

parency, decentralization, and resilience to tamper-

ing (Narayanan et al., 2016). Bitcoin, launched in

2009, established the foundation for a diverse and

fast-growing ecosystem now comprising over 5,000

active cryptocurrencies, including major platforms

such as Ethereum (ETH) and Ripple (XRP) (Pinte-

las et al., 2020). The scale and speed of this evolution

underscore the rise of a dynamic and highly volatile

market landscape, attracting increasing interest from

both speculative investors and academic researchers

(Livieris et al., 2018).

One of the most challenging yet consequential

problems in this domain is the accurate forecasting

of cryptocurrency prices. Despite the intrinsic volatil-

ity of these assets and their sensitivity to exogenous

shocks, the ability to model and predict price trajec-

tories remains of critical importance. Accurate pre-

diction models can inform strategic investment deci-

sions, guide macro-ﬁnancial policy, and yield deeper

insights into the behavioral dynamics governing digi-

tal ﬁnancial ecosystems (Urquhart, 2016).

The academic literature has largely converged on

two principal paradigms to address this forecasting

challenge. The ﬁrst treats cryptocurrency valuation

as a classical time series problem, employing econo-

metric techniques such as the Auto-Regressive Inte-

grated Moving Average (ARIMA) model. These ap-

proaches leverage temporal autocorrelation and his-

torical structure to extrapolate future trends. While

statistically grounded and interpretable, traditional

models often struggle to capture the nonlinear and dy-

namic nature of cryptocurrency price movements, es-

pecially in the presence of high-frequency noise.

In contrast, machine learning ap-

Vonitsanos, G., Kanavos, A. and Mylonas, P.

A Context-Enriched Hybrid ARIMAX–Deep Learning Framework for Robust Cryptocurrency Price Forecasting.

DOI: 10.5220/0013713700003985

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Web Information Systems and Technologies (WEBIST 2025), pages 257-266

ISBN: 978-989-758-772-6; ISSN: 2184-3252

257

proaches—particularly deep learning—offer ﬂexible,

data-driven alternatives capable of modeling com-

plex, nonlinear temporal dependencies. Deep neural

networks, including architectures such as Long

Short-Term Memory (LSTM) networks, are designed

to extract hierarchical patterns from sequential data,

demonstrating strong predictive capabilities across

various noisy and volatile time series domains

(LeCun et al., 2015; Siami-Namini et al., 2018).

Nevertheless, the interplay between data char-

acteristics and model architecture introduces further

challenges. Cryptocurrency markets are notably in-

ﬂuenced by external variables, including macroeco-

nomic indicators, policy shifts, and investor senti-

ment (Trigka et al., 2022). The integration of such

exogenous variables into forecasting models can sig-

niﬁcantly enhance predictive power (Saravanos and

Kanavos, 2023a; Saravanos and Kanavos, 2023b).

Consequently, hybrid modeling techniques that com-

bine the statistical rigor of classical methods with the

representational power of deep learning architectures

have emerged as promising solutions.

Unlike previous works that either rely solely on

statistical models or purely on deep learning ar-

chitectures, this paper introduces a novel Context-

Enriched Hybrid Modeling Framework that jointly

leverages exogenous contextual features and com-

bines the strengths of both approaches (Savvopou-

los et al., 2018). The framework is implemented

from scratch and rigorously evaluated on a four-year

dataset, ensuring reproducibility and methodological

clarity. Furthermore, the study sets the foundation for

future extensions involving ensemble strategies that

can further enhance robustness in volatile markets.

This study advances the state of the art by propos-

ing a hybrid modeling framework that integrates sta-

tistical and deep learning approaches for cryptocur-

rency price prediction. Speciﬁcally, we incorporate

exogenous variables such as trading volume, market

capitalization, and moving averages into ARIMAX

and LSTM models to enable multivariate, context-

aware forecasting. This integration aims to balance

model interpretability with forecasting accuracy, par-

ticularly under conditions of structural shifts and non-

stationary behavior. Experimental results demon-

strate that the hybrid framework outperforms stan-

dalone statistical or deep learning models across mul-

tiple performance metrics, offering superior align-

ment with actual market trends.

The remainder of the paper is structured as fol-

lows. Section 2 reviews relevant literature and prior

developments in cryptocurrency forecasting. Sec-

tion 3 outlines the data preprocessing pipeline and

core methodological components. Section 4 presents

the implementation details of the hybrid framework.

Section 5 reports and analyzes the experimental re-

sults. Finally, Section 6 summarizes key ﬁndings and

discusses avenues for future research.

2 RELATED WORK

Cryptocurrency price forecasting has attracted con-

siderable academic attention in recent years, driven

by the unique characteristics of digital asset markets,

including high volatility, nonstationarity, and sensitiv-

ity to exogenous signals. A diverse range of modeling

techniques has been explored, spanning traditional

statistical methods, classical machine learning algo-

rithms, deep learning architectures, and hybrid frame-

works. This section provides a structured overview of

existing research, highlighting its respective strengths

and limitations.

Early efforts in this domain predominantly em-

ployed statistical models such as the Auto-Regressive

Integrated Moving Average (ARIMA), which offered

interpretability and a principled foundation for cap-

turing linear temporal dependencies. Applications

of ARIMA to cryptocurrency prices conﬁrmed its

ease of use but also revealed signiﬁcant limitations in

handling nonlinearities and abrupt structural changes

(Alahmari, 2019; Pintelas et al., 2020).

To overcome these shortcomings, machine learn-

ing algorithms such as Support Vector Machines

(SVMs) and Random Forests were introduced. These

models exhibited greater ﬂexibility in handling high-

dimensional feature spaces, often incorporating price-

derived indicators, trading volume, and technical met-

rics. Nevertheless, their lack of native temporal mod-

eling constrained their ability to capture sequential

dependencies critical to time series forecasting (Der-

bentsev et al., 2020).

This limitation led to the adoption of deep learning

architectures, particularly Recurrent Neural Networks

(RNNs) and their gated variants such as Long Short-

Term Memory (LSTM) and Gated Recurrent Units

(GRU). These models are designed to learn long-

range temporal dependencies and nonlinear transfor-

mations, making them well-suited for volatile ﬁnan-

cial environments. LSTM-based approaches have

demonstrated superior predictive accuracy over clas-

sical models in various cryptocurrency prediction

tasks, effectively coping with noise and abrupt regime

changes (Zoumpekas et al., 2020).

Comparative studies have further shown that GRU

networks often achieve similar performance lev-

els to LSTM while offering reduced computational

complexity, thus making them suitable for latency-

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

258

sensitive applications (Siami-Namini et al., 2018).

Additional work has emphasized the generalization

capabilities of deep recurrent models across differ-

ent cryptocurrencies and their applicability to high-

frequency data (LeCun et al., 2015). A compre-

hensive evaluation of Multilayer Perceptrons (MLP),

RNNs, LSTMs, and Bidirectional LSTMs applied to

large-scale time series conﬁrmed that recurrent ar-

chitectures consistently outperform feedforward net-

works, while also providing insights into data pre-

processing and network design for ﬁnancial forecast-

ing tasks (Vonitsanos et al., 2023; Vonitsanos et al.,

2024).

More recent developments include hybrid ap-

proaches that integrate statistical decomposition

techniques—such as trend and seasonality extrac-

tion—with deep neural networks. These methods aim

to leverage the denoising and interpretability bene-

ﬁts of statistical models alongside the representational

power of deep architectures, thereby improving gen-

eralization across nonstationary regimes (Narayanan

et al., 2016).

Within this category, ARIMAX represents a no-

table extension of ARIMA that incorporates exoge-

nous features, providing improved predictive accu-

racy by capturing external market signals alongside

autoregressive patterns. This approach has been

shown to be effective in modeling nonlinearities when

external indicators such as market capitalization, trad-

ing volume, and moving averages are available.

Furthermore, economic analyses have emphasized

the signiﬁcant inﬂuence of exogenous factors—such

as market sentiment, macroeconomic indicators, and

investor behavior—on cryptocurrency price dynam-

ics (Ciaian et al., 2016; Corbet et al., 2019). These

studies highlight the importance of incorporating con-

textual variables into forecasting models, as external

information can substantially improve predictive per-

formance in volatile markets.

In addition to hybrid models, recent research

has also begun to investigate ensemble learning

techniques—such as bagging, boosting, and stack-

ing—that combine multiple forecasting algorithms to

exploit their complementary strengths. These ensem-

ble approaches have been shown to reduce prediction

variance and improve robustness under high volatil-

ity conditions (Livieris et al., 2020). The demon-

strated stability of ensemble-based architectures sug-

gests they are a promising extension to hybrid frame-

works.

Similarly, research on context-aware forecasting

has indicated that incorporating sentiment indica-

tors derived from social media and news sources

can further enhance model accuracy (Saravanos and

Kanavos, 2025). These ﬁndings underscore the value

of combining both market-derived and external con-

textual signals to achieve more reliable predictions.

In summary, while traditional and deep learn-

ing models have each contributed important in-

sights to cryptocurrency forecasting, limitations re-

main—particularly in handling external variables,

regime shifts, and data sparsity. Recent research

highlights the promise of hybrid and ensemble

frameworks that integrate statistical foundations with

context-aware deep learning architectures. Building

on these ﬁndings, the present study proposes a multi-

variate context-enriched hybrid framework that lever-

ages ARIMAX and LSTM models, aiming to improve

forecasting accuracy under volatile and nonstationary

market conditions.

3 METHODOLOGY

This section presents the methodological founda-

tion of the proposed cryptocurrency price pre-

diction framework, integrating traditional statisti-

cal modeling, machine learning, and deep learn-

ing techniques. Four modeling paradigms are con-

sidered: Auto-Regressive Integrated Moving Aver-

age (ARIMA), Generalized Autoregressive Condi-

tional Heteroskedasticity (GARCH), Support Vec-

tor Machines (SVM), and Long Short-Term Memory

(LSTM) networks. Each model is evaluated individ-

ually and in hybrid conﬁgurations to assess forecast-

ing accuracy under different data dynamics, includ-

ing linear trends, volatility clustering, and long-range

temporal dependencies.

3.1 Auto-Regressive Integrated Moving

Average (ARIMA)

The ARIMA model is a foundational technique for

univariate time series forecasting, designed to cap-

ture autocorrelations under the assumptions of linear-

ity and stationarity. Represented as ARIMA(p, d,q),

the model includes autoregressive terms (p), differ-

encing operations (d), and moving average terms (q),

each serving to capture distinct temporal properties.

The general forecasting equation, applied after differ-

encing the original time series Y

d times to achieve

stationarity (denoted as y

), is given by:

ˆy

= µ +

∑

i=1

t−i

∑

j=1

t− j

(1)

where ˆy

is the predicted value, µ is a constant term, φ

are the autoregressive coefﬁcients, θ

are the moving

A Context-Enriched Hybrid ARIMAX–Deep Learning Framework for Robust Cryptocurrency Price Forecasting

259

average coefﬁcients, and e

t− j

represents the residual

errors assumed to be white noise with zero mean and

constant variance. Parameter selection was performed

via a grid search minimizing the Akaike Informa-

tion Criterion (AIC), ensuring the optimal trade-off

between model complexity and goodness of ﬁt (Box

et al., 2015; Shumway and Stoffer, 2017).

ARIMA’s simplicity and interpretability have long

justiﬁed its use in ﬁnancial time series forecasting.

However, its reliance on stationarity assumptions,

Gaussian-distributed residuals, and inability to ac-

commodate exogenous variables reduce its effective-

ness in cryptocurrency markets (Azari, 2019; Petric

et al., 2016). It is thus primarily used in this study as

a benchmark for more advanced approaches (Boller-

slev, 1986).

3.2 Auto-Regressive Integrated Moving

Average with Exogenous Variables

(ARIMAX)

The ARIMAX model extends ARIMA by incorporat-

ing external predictors that enhance the modeling of

market dynamics. The general form is:

= c +

∑

i=1

t−i

∑

j=1

t− j

+ βX

+ ε

(2)

where y

is the predicted price, X

is a vector of exoge-

nous features (trading volume, market capitalization,

and moving averages), φ

and θ

are AR and MA co-

efﬁcients, and ε

is the residual. Here, β represents

the vector of regression coefﬁcients associated with

the standardized exogenous features X

, which were

normalized to ensure numerical stability and compa-

rability in estimation.

This integration allows ARIMAX to capture both

the autoregressive structure of the price series and

contextual signals from market indicators, which ex-

plains its superior performance in the experimental re-

sults (B

ohme et al., 2015).

3.3 Generalized Autoregressive

Conditional Heteroskedasticity

(GARCH)

To model time-varying volatility and capture cluster-

ing effects in ﬁnancial returns, the GARCH model is

employed. Unlike ARIMA, which focuses on mean

behavior, GARCH models the conditional variance of

the residuals from a ﬁtted mean equation. The inno-

vation process ε

is assumed to be conditionally nor-

mally distributed:

| ψ

t−1

∼ N (0, h

) (3)

where h

is the conditional variance and ψ

t−1

rep-

resents the information set up to time t − 1. The

GARCH(p, q) model deﬁnes h

as:

= α

∑

i=1

t−i

∑

j=1

t− j

(4)

with α

> 0, α

≥ 0, and β

≥ 0 (Fałdzi

nski et al.,

2020; Franses and Dijk, 1996). GARCH models are

particularly useful for capturing volatility clustering

and excess kurtosis in return distributions. However,

they assume stationarity and may not fully account for

nonlinear dependencies or external shocks.

Although the GARCH model was evaluated, its

results are not included in the ﬁnal comparison be-

cause it failed to outperform ARIMA in prelimi-

nary tests and demonstrated instability under non-

stationary market conditions. Nevertheless, its abil-

ity to model volatility clustering remains valuable and

motivates future work on volatility-augmented hy-

brid frameworks (Fałdzi

nski et al., 2020; Selmi et al.,

2018).

3.4 Support Vector Machines (SVM)

Support Vector Machines are supervised learning

models used for both classiﬁcation and regression.

In time series forecasting, SVMs are typically im-

plemented through Support Vector Regression (SVR),

which aims to ﬁnd a function f (x) that has at most ε

deviation from the actual observed values and is as

ﬂat as possible (Cortes and Vapnik, 1995; Sch

olkopf

and Smola, 2002; Smola and Sch

olkopf, 2004). The

SVR optimization problem is formulated as:

min

w,b,ξ,ξ

∗

∥w∥

∑

i=1

(ξ

+ ξ

∗

) (5)

subject to:

− ⟨w, x

⟩ − b ≤ ε + ξ

⟨w, x

⟩ + b − y

≤ ε + ξ

∗

, ξ

∗

≥ 0

(6)

where C is a regularization parameter controlling the

penalty for deviations larger than ε, and ε deﬁnes an

insensitive zone where errors are not penalized. An

RBF (Radial Basis Function) kernel was employed

to capture nonlinear relationships in the feature space

(Keerthi and Lin, 2003). SVMs perform well in high-

dimensional settings and are robust to overﬁtting, but

their effectiveness in time series forecasting is limited

by their inability to model temporal dependencies un-

less additional engineering (e.g., lagged inputs) is ap-

plied (Pisner and Schnyer, 2020; Vapnik, 1999).

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

260

3.5 Long Short-Term Memory (LSTM)

Networks

LSTM networks are a type of Recurrent Neural Net-

work (RNN) speciﬁcally designed to address the van-

ishing gradient problem and model long-range tem-

poral dependencies in sequential data. Each LSTM

cell includes input, output, and forget gates that reg-

ulate the ﬂow of information across time steps. The

key equations governing an LSTM unit are:

= σ(W

· [h

t−1

, x

] + b

) (7)

= σ(W

· [h

t−1

, x

] + b

) (8)

= tanh(W

· [h

t−1

, x

] + b

) (9)

= f

∗C

t−1

+ i

∗

(10)

= σ(W

·[h

t−1

, x

]+b

), h

= o

∗tanh(C

) (11)

where W

∗

and b

∗

represent the weight matrices and

bias vectors for the respective gates, while tanh is

used as the activation function for candidate cell

states. The gates f

, i

, and o

regulate information re-

tention, input, and output at each time step, enabling

the network to capture both short- and long-term de-

pendencies in the data (Pintelas et al., 2020; Staude-

meyer and Morris, 2019).

For this study, the LSTM architecture consisted of

two hidden layers with 64 and 32 units respectively,

followed by a dense output layer. The network was

trained using the Adam optimizer with a learning rate

of 0.001, batch size of 32, and early stopping to pre-

vent overﬁtting.

Although the present study evaluates ARIMAX

and LSTM separately, their outputs can conceptually

be combined in an ensemble or hybrid formulation:

ˆy

= λ ˆy

ARIMAX

+ (1 − λ) ˆy

LSTM

(12)

where ˆy

ARIMAX

and ˆy

LSTM

are the predictions from

ARIMAX and LSTM models respectively, and λ is

a weighting parameter that could be optimized. This

formulation motivates future research on stacked hy-

brid and ensemble frameworks.

4 IMPLEMENTATION

4.1 Dataset

The dataset was stored in a Comma-Separated Values

(CSV) format, containing columns such as timeOpen,

timeClose, timeHigh, timeLow, open, high, low,

close, volume, marketCap, and timestamp. The

timestamps provide the precise data capture period,

while each column offers a distinct perspective on the

market’s daily activity, including opening and closing

prices, intraday highs and lows, traded volume, and

overall market capitalization.

The dataset was sourced from CoinMarketCap, a

reputable provider of cryptocurrency market statis-

tics, ensuring accuracy and reliability. To enhance

data integrity, all records were cross-validated with

alternative public sources and checked for anomalies

such as duplicated rows or inconsistent timestamps.

Preprocessing steps included handling missing val-

ues, aligning time zones, correcting irregularities, and

normalizing features where necessary. A 7-day mov-

ing average was also computed as an additional ex-

ogenous feature for the ARIMAX model.

For model training and evaluation, the dataset was

divided into training (80%) and testing (20%) sub-

sets using a chronological split to avoid data leakage.

Feature scaling was applied using Min-Max normal-

ization for machine learning models (SVM, LSTM)

to improve numerical stability during optimization.

These preprocessing measures ensured a clean, con-

sistent dataset suitable for both statistical and deep

learning approaches.

The ﬁnal dataset covered Bitcoin’s daily market

activity from September 2019 to February 2024, rep-

resenting more than four years of continuous data. Its

richness and breadth provided a strong foundation for

evaluating intricate price trends and testing the mod-

els under various market conditions, including peri-

ods of extreme volatility and regime shifts.

4.2 Tools

The predictive models were implemented using

Python, leveraging Scikit-learn and TensorFlow as the

primary frameworks. Scikit-learn was used for tradi-

tional machine learning algorithms and preprocessing

pipelines, offering robust implementations of statisti-

cal models and feature scaling methods (Silaparasetty,

2020). TensorFlow was employed for the develop-

ment of LSTM networks, as it provides optimized ten-

sor operations, GPU acceleration, and scalable model

deployment capabilities.

The experimental environment consisted of a

Linux-based system with an Intel Core i7 proces-

sor, 32GB RAM, and an NVIDIA RTX 3060 GPU.

Python 3.10 was used with Scikit-learn 1.4 and Ten-

sorFlow 2.15, ensuring compatibility with the latest

library features. All experiments were executed un-

der controlled conditions with ﬁxed random seeds to

guarantee reproducibility.

A Context-Enriched Hybrid ARIMAX–Deep Learning Framework for Robust Cryptocurrency Price Forecasting

261

5 EXPERIMENTAL EVALUATION

This section presents a comprehensive evaluation of

the proposed hybrid modeling framework and its con-

stituent models under real-world cryptocurrency mar-

ket conditions. The objective is to assess predictive

accuracy, robustness, and the ability of each model to

capture the nonlinear and volatile nature of Bitcoin

price movements. The evaluation combines quan-

titative metrics, statistical tests, and visual analyses

to provide a holistic comparison of ARIMA, ARI-

MAX, SVM, and LSTM. In addition to performance

benchmarking, residual diagnostics are used to vali-

date model adequacy, and the results are interpreted

in the context of market dynamics and model design.

5.1 Experimental Setup

To ensure a consistent and fair comparison, all models

were trained and evaluated on the same dataset com-

prising daily Bitcoin market data from September 24,

2019, to February 6, 2024. The dataset was divided

into training (80%) and testing (20%) subsets using a

chronological split to avoid look-ahead bias. Prepro-

cessing steps included handling missing values, con-

verting timestamps to datetime format, and normaliz-

ing features for machine learning models to improve

optimization stability.

Model-speciﬁc hyperparameters were tuned using

grid search: ARIMA and ARIMAX orders (p, d, q)

were selected based on the lowest Akaike Informa-

tion Criterion (AIC); SVM used an RBF kernel with

C = 10 and γ = 0.01; and the LSTM network was

trained with a dropout rate of 0.2, early stopping, and

50 epochs. Although cross-validation is not straight-

forward in time series, a walk-forward validation ap-

proach was also tested to conﬁrm model stability.

5.2 Statistical Tests

The four models evaluated in this study span statisti-

cal, machine learning, and deep learning paradigms.

ARIMA is a univariate model that forecasts future

values based on past observations and their errors.

It operates under the assumption of stationarity, thus

requiring differencing for non-stationary time series.

ARIMAX extends ARIMA by incorporating exoge-

nous variables—speciﬁcally volume, market capi-

talization, and a 7-day moving average of closing

prices—allowing the model to learn from additional

market indicators and potentially improve predictive

performance. SVM for regression was implemented

using an RBF kernel, enabling the model to capture

complex, non-linear relationships in the data. Lastly,

LSTM networks, a variant of recurrent neural net-

works (RNNs), were employed due to their ability

to learn long-range dependencies in sequential data

and handle the inherent volatility and noise present in

cryptocurrency markets.

To conﬁrm model validity, several statistical di-

agnostics were performed. The Augmented Dickey-

Fuller (ADF) test conﬁrmed that differencing ren-

dered the time series stationary, meeting ARIMA’s

assumptions. The Jarque-Bera test revealed resid-

uals deviated from normality, justifying the adoption

of nonlinear models. The Ljung-Box test and ACF

plots showed that residual autocorrelation was negli-

gible in ARIMAX but persisted in ARIMA, highlight-

ing the superior speciﬁcation of the former.

5.3 Model Comparison

To assess and visualize each model’s forecasting ac-

curacy, predicted values were compared with actual

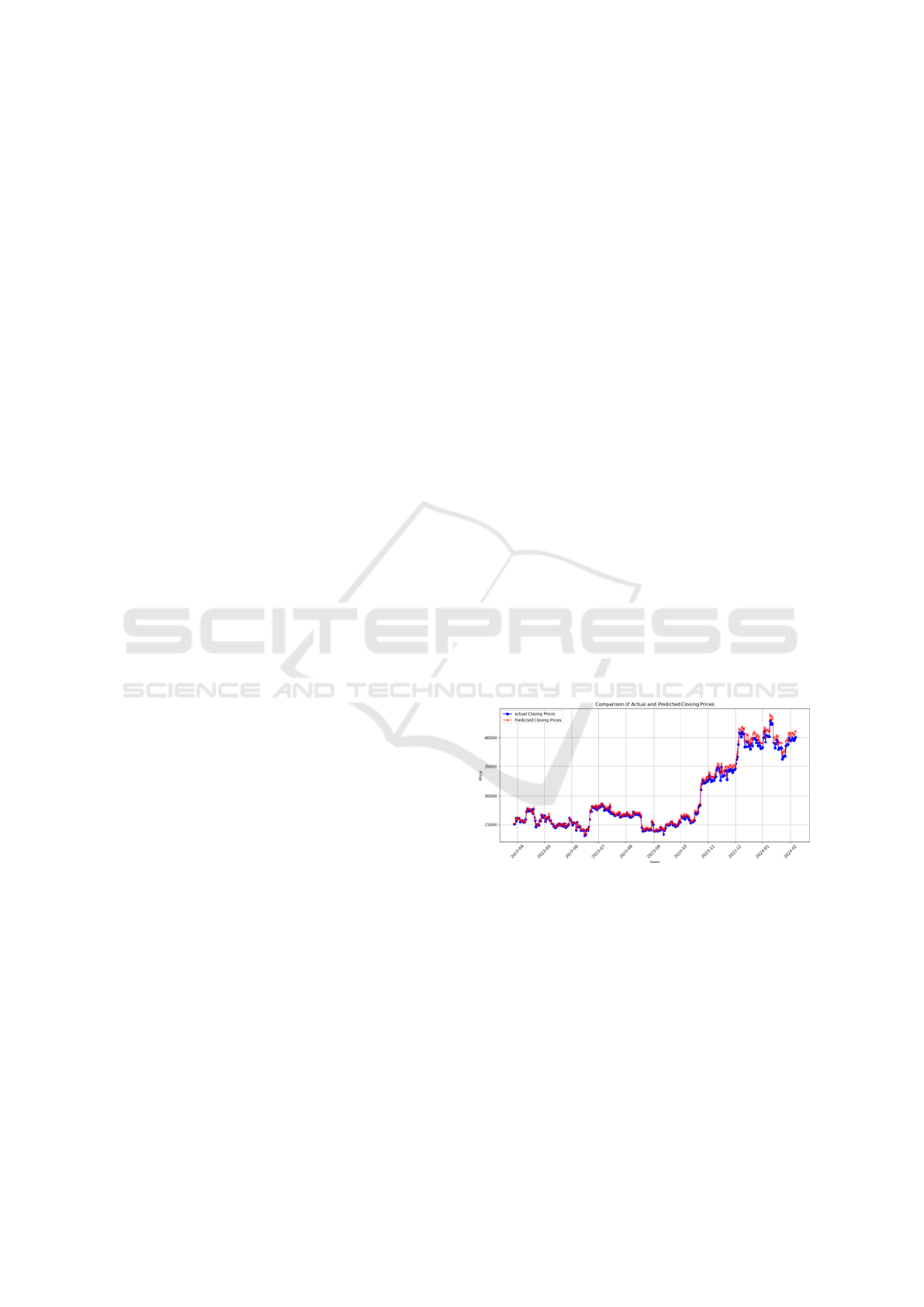
Bitcoin prices. Figure 1 presents the predictions of

ARIMAX, SVM, and LSTM models against observed

data. ARIMAX demonstrates the highest alignment

with real market trends, particularly during periods of

sharp price movements. LSTM also exhibits robust

performance, capturing nonlinear patterns but occa-

sionally lagging in extreme ﬂuctuations. The SVM

model performs adequately but tends to underreact to

sudden changes, underscoring the difﬁculty of model-

ing high-volatility assets with non-temporal methods.

Figure 1: Comparison of predicted vs. actual Bitcoin prices

using ARIMAX, SVM, and LSTM models. ARIMAX

demonstrates the closest alignment with real market trends,

followed by LSTM.

Additionally, Figure 2 illustrates the historical Bit-

coin price series, contextualizing the high volatility

and irregular seasonal trends present in the dataset.

These ﬂuctuations emphasize the complexity of cryp-

tocurrency forecasting and the importance of models

capable of adapting to structural shifts.

Finally, Figure 3 displays histograms and Q-Q

plots of ARIMA residuals. The skewness and heavy

tails conﬁrm a departure from Gaussianity, supporting

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

262

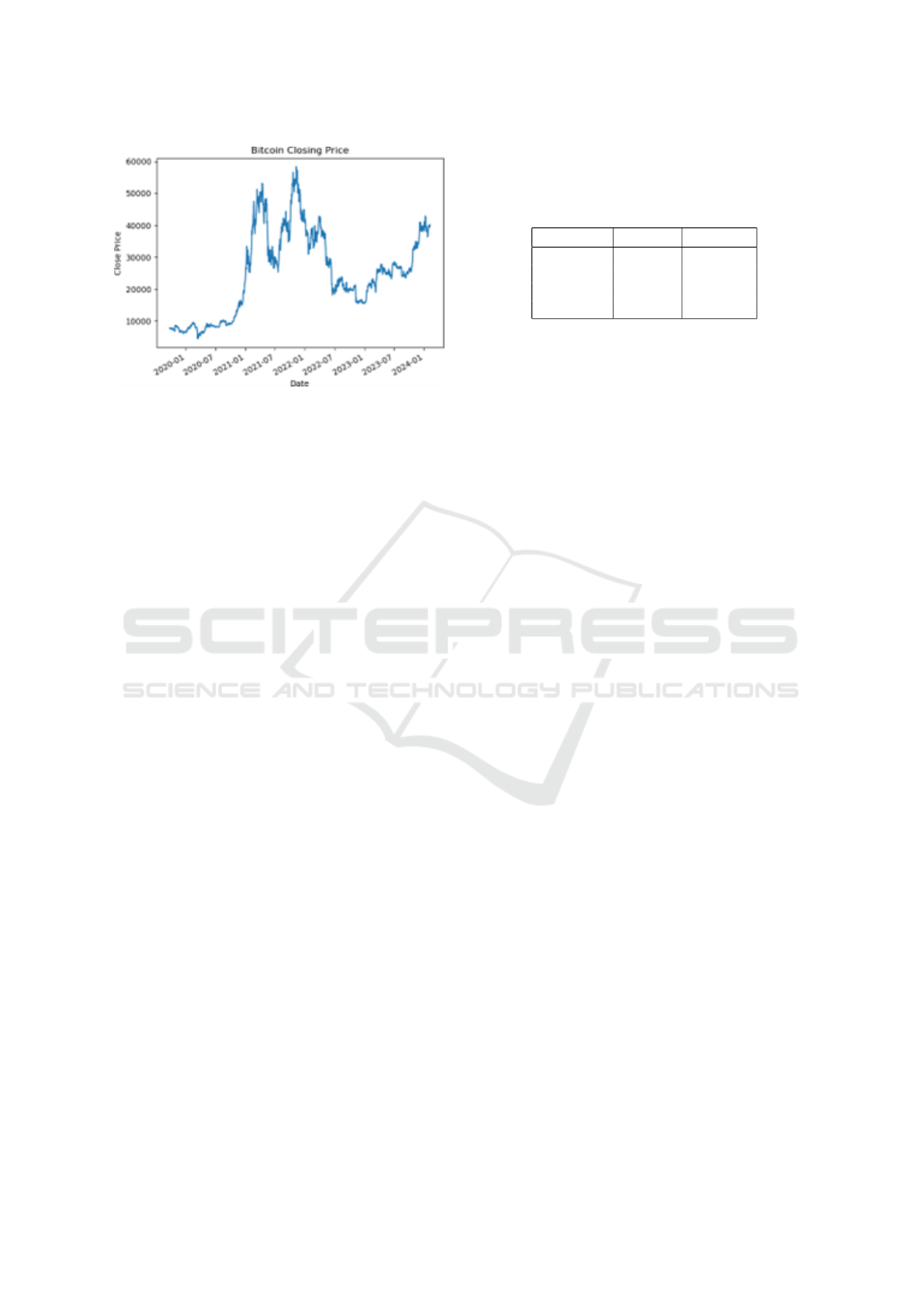
Figure 2: Daily closing prices of Bitcoin from 2019 to 2024.

The time series exhibits high volatility and irregular pat-

terns.

the use of ARIMAX and LSTM, which better accom-

modate nonlinear and non-Gaussian structures.

5.4 Evaluation Metrics

The models were evaluated using two key quantita-

tive metrics for a robust comparison. The Root Mean

Squared Error (RMSE measures the average magni-

tude of the prediction error and is particularly sensi-

tive to large deviations, making it effective for high-

lighting signiﬁcant inaccuracies. The R

Score, also

known as the Coefﬁcient of Determination, indicates

the proportion of variance in the dependent variable

explained by the model, thus providing a measure of

its explanatory power.

In addition to these metrics, further statistical di-

agnostics were explicitly applied to the ARIMA and

ARIMAX models. The Augmented Dickey-Fuller

(ADF) test was employed to assess the stationarity of

the time series data, which is a critical assumption for

the validity of these models. To evaluate whether the

residuals followed a normal distribution, the Jarque-

Bera test was conducted. Furthermore, the Ljung-

Box test and Autocorrelation Function (ACF) plots

were used to detect any autocorrelation remaining in

the residuals, ensuring the adequacy and reliability of

the model ﬁt.

Table 1 presents the performance metrics for each

forecasting model. The evaluation used the Root

Mean Squared Error (RMSE) and the Coefﬁcient of

Determination (R

score). Among all models, ARI-

MAX achieved the best performance with the low-

est RMSE and the highest R

value, indicating strong

predictive accuracy and generalization capability. The

SVM model also demonstrated solid performance,

slightly outperforming the LSTM model. In contrast,

the ARIMA model yielded signiﬁcantly higher er-

rors, underscoring its limitations in capturing Bitcoin

prices’ complex and volatile behavior.

Table 1: Performance Metrics of Forecasting Models.

Model RMSE R

Score

ARIMA 7012.59 –

ARIMAX 508.45 0.9920

SVM 793.32 0.9806

LSTM 943.17 0.9732

The superior performance of ARIMAX can be

attributed to its ability to integrate external mar-

ket indicators that traditional ARIMA cannot ex-

ploit. While LSTM captures nonlinear dependen-

cies, it lacks explicit contextual awareness, which

explains its slightly lower performance. This ob-

servation suggests that models capable of combin-

ing autoregressive structure with contextual informa-

tion—either through exogenous variables or advanced

architectures—offer a distinct advantage.

5.5 Discussion

The experimental ﬁndings provide clear evidence of

the advantages of integrating exogenous variables

and nonlinear learning mechanisms in cryptocurrency

forecasting. Among all evaluated models, ARIMAX

consistently delivered the most accurate predictions,

as reﬂected by the lowest RMSE and highest R

val-

ues. This improvement stems from the model’s capac-

ity to incorporate additional market context—such as

trading volume and capitalization—which allowed it

to adapt more effectively to market ﬂuctuations com-

pared to ARIMA. The residual diagnostics further

conﬁrmed that ARIMAX reduced autocorrelation and

non-normality in errors, reinforcing its suitability for

highly volatile ﬁnancial time series.

While LSTM achieved strong performance by

capturing nonlinear dependencies and long-term tem-

poral relationships, it underperformed relative to

ARIMAX in certain volatile segments. This behav-

ior can be attributed to the sensitivity of deep learn-

ing models to noise and abrupt structural changes, as

well as their reliance on large amounts of training data

for robust generalization. Nevertheless, the model

successfully identiﬁed complex patterns missed by

purely statistical models, indicating that its integra-

tion in hybrid or ensemble frameworks could further

enhance predictive stability.

The SVM model, although computationally efﬁ-

cient and robust in moderately volatile regions, strug-

gled to react to sudden price spikes. This limitation

arises from its lack of explicit temporal modeling and

dependence on lagged features. However, its strong

A Context-Enriched Hybrid ARIMAX–Deep Learning Framework for Robust Cryptocurrency Price Forecasting

263

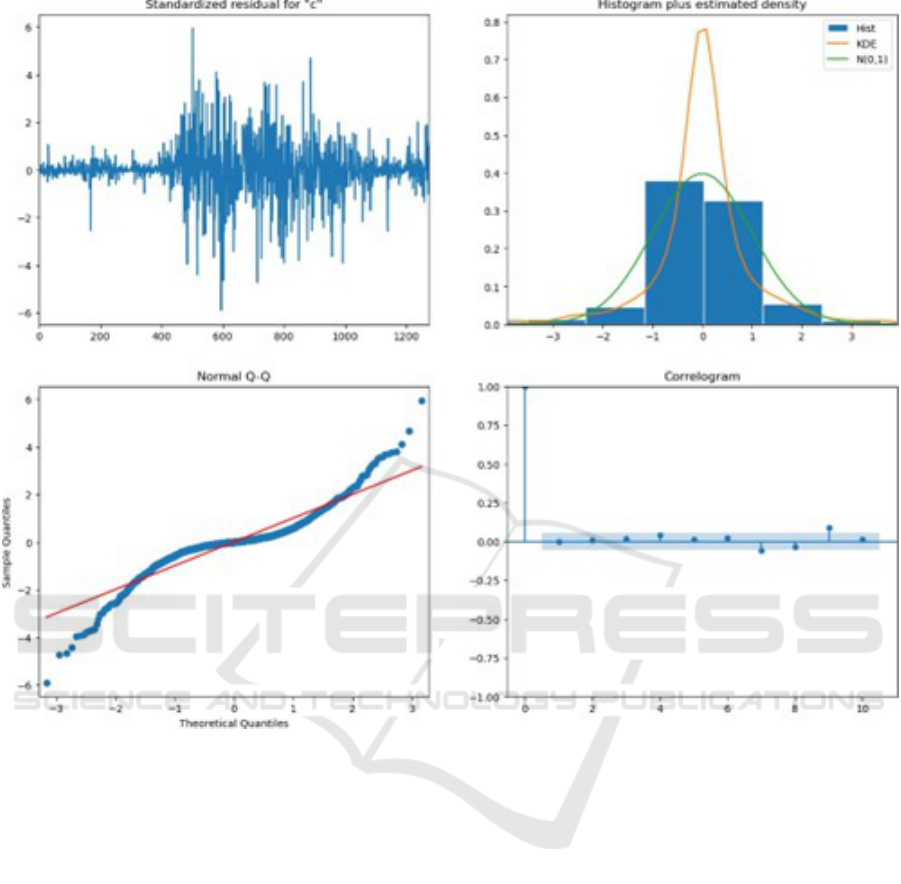
Figure 3: Histogram and Q-Q plot of ARIMA residuals. The residuals exhibit skewness and heavy tails, deviating from

normality, which supports the adoption of models like ARIMAX and LSTM that handle nonlinear and non-Gaussian patterns

more effectively.

performance relative to ARIMA highlights the value

of nonlinear regression techniques even in the absence

of sequential modeling.

Overall, the results validate the central hypoth-

esis of this study: models that combine statisti-

cal interpretability with contextual awareness outper-

form both purely statistical and purely data-driven

approaches. The superior performance of ARIMAX

suggests that incorporating external variables is criti-

cal in capturing the dynamics of cryptocurrency mar-

kets. These ﬁndings align with previous research ad-

vocating hybrid and ensemble approaches as promis-

ing directions for ﬁnancial forecasting. The insights

gained here motivate future work involving stacked

architectures, attention-based mechanisms, and adap-

tive ensembles to achieve even greater robustness in

such chaotic environments.

6 CONCLUSIONS AND FUTURE

WORK

This research set out to investigate how different

modeling paradigms can be effectively applied to

the challenging task of cryptocurrency price forecast-

ing, with a particular focus on Bitcoin. By compar-

ing classical statistical models (ARIMA, ARIMAX)

with machine learning and deep learning approaches

(SVM, LSTM), we provided a comprehensive eval-

uation of their respective capabilities under volatile

market conditions. The extensive experimental anal-

ysis on a multi-year dataset revealed several important

ﬁndings.

First, our results conﬁrmed that purely statistical

approaches such as ARIMA, while interpretable and

computationally efﬁcient, fail to capture the nonlin-

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

264

earities and abrupt structural changes typical of cryp-

tocurrency markets. In contrast, the ARIMAX model,

by incorporating exogenous variables such as market

capitalization, trading volume, and moving averages,

demonstrated superior performance in aligning fore-

casts with real market trends. Deep learning mod-

els, particularly LSTM, also achieved competitive re-

sults due to their ability to model long-term tempo-

ral dependencies. Yet they were more sensitive to

volatility and required careful regularization to avoid

overﬁtting. The SVM approach provided a middle

ground, offering reasonable accuracy with lower com-

putational cost, making it suitable in contexts where

efﬁciency is prioritized.

The comparative analysis highlights that hybrid

approaches leveraging both statistical rigor and non-

linear learning capabilities achieve the best trade-off

between interpretability and accuracy. This ﬁnding is

consistent with recent research advocating for hybrid

models in ﬁnancial time series forecasting. Moreover,

the evaluation metrics (RMSE, R

) and residual di-

agnostics validated the robustness of our ARIMAX-

based conﬁguration, which outperformed other mod-

els in capturing market behavior even during periods

of high turbulence.

While the proposed hybrid framework has demon-

strated strong predictive performance, several promis-

ing directions remain for further improvement. One

particularly important extension involves the adoption

of ensemble learning techniques. Ensembles, such

as stacking, boosting, and bagging, combine multi-

ple models to leverage their complementary strengths

and reduce individual weaknesses. In volatile mar-

kets like Bitcoin, where single-model predictions of-

ten suffer from instability, ensemble methods could

smooth forecasts, improve robustness against outliers,

and enhance generalization. For example, an ensem-

ble that integrates ARIMAX’s interpretability with

LSTM’s capacity to learn complex patterns could pro-

duce predictions that are both accurate and stable.

Beyond simple voting or averaging, meta-learning

strategies that optimize the combination weights dy-

namically could be explored to adapt to evolving mar-

ket regimes.

Furthermore, extending the current approach to

include transformer-based architectures with atten-

tion mechanisms would allow the model to capture

long-range dependencies more efﬁciently than tradi-

tional recurrent networks. Similarly, incorporating

external signals such as social media sentiment, reg-

ulatory news, and macroeconomic indicators could

enrich the context provided to the models, enabling

them to react more accurately to market events. Ex-

panding the dataset to cover additional cryptocurren-

cies would also test the generalizability of the frame-

work across different asset classes and market struc-

tures.

Finally, from an applied perspective, integrat-

ing the developed models into real-time trading sys-

tems and stress-testing them against historical mar-

ket shocks would provide practical insights into their

usability in production environments. The inclusion

of probabilistic forecasts, risk quantiﬁcation, and ex-

plainability techniques (e.g., SHAP values) could fur-

ther bridge the gap between academic research and

industry deployment.

In summary, this work conﬁrms the value of hy-

brid frameworks enriched with contextual features

for cryptocurrency forecasting and lays the founda-

tion for future studies incorporating ensemble and

attention-based architectures. Such advances promise

to further improve predictive accuracy and robust-

ness, thereby contributing to the development of data-

driven decision-support systems in ﬁnancial markets.

REFERENCES

Alahmari, S. A. (2019). Using machine learning ARIMA

to predict the price of cryptocurrencies. ISC Inter-

national Journal of Information Security, 11(3):139–

144.

Azari, A. (2019). Bitcoin price prediction: An ARIMA ap-

proach. CoRR, abs/1904.05315.

ohme, R., Christin, N., Edelman, B., and Moore, T.

(2015). Bitcoin: Economics, technology, and gover-

nance. Journal of Economic Perspectives, 29(2):213–

238.

Bollerslev, T. (1986). Generalized autoregressive condi-

tional heteroskedasticity. Journal of Econometrics,

31(3):307–327.

Box, G. E. P., Jenkins, G. M., Reinsel, G. C., and Ljung,

G. M. (2015). Time Series Analysis: Forecasting and

Control. John Wiley & Sons.

Ciaian, P., Rajcaniova, M., and d’Artis Kancs (2016). The

economics of bitcoin price formation. Applied Eco-

nomics, 48(19):1799–1815.

Corbet, S., Lucey, B., Urquhart, A., and Yarovaya, L.

(2019). Cryptocurrencies as a ﬁnancial asset: A sys-

tematic analysis. International Review of Financial

Analysis, 62:182–199.

Cortes, C. and Vapnik, V. (1995). Support-vector networks.

Machine Learning, 20(3):273–297.

Derbentsev, V., Matviychuk, A., and Soloviev, V. N. (2020).

Forecasting of cryptocurrency prices using machine

learning. In Advanced Studies of Financial Technolo-

gies and Cryptocurrency Markets, pages 211–231.

Springer.

Fałdzi

nski, M., Fiszeder, P., and Orzeszko, W. (2020). Fore-

casting volatility of energy commodities: Comparison

A Context-Enriched Hybrid ARIMAX–Deep Learning Framework for Robust Cryptocurrency Price Forecasting

265

of garch models with support vector regression. Ener-

gies, 14(1):6.

Franses, P. H. and Dijk, D. V. (1996). Forecasting stock

market volatility using (non-linear) garch models.

Journal of Forecasting, 15(3):229–235.

Keerthi, S. S. and Lin, C.-J. (2003). Asymptotic behaviors

of support vector machines with gaussian kernel. Neu-

ral Computation, 15(7):1667–1689.

LeCun, Y., Bengio, Y., and Hinton, G. E. (2015). Deep

learning. Nature, 521(7553):436–444.

Livieris, I. E., Kanavos, A., Vonitsanos, G., Kiriakidou, N.,

Vikatos, A., Giotopoulos, K. C., and Tampakas, V.

(2018). Performance evaluation of an SSL algorithm

for forecasting the dow jones index stocks. In 9th In-

ternational Conference on Information, Intelligence,

Systems and Applications (IISA), pages 1–8. IEEE.

Livieris, I. E., Pintelas, E., Stavroyiannis, S., and Pinte-

las, P. E. (2020). Ensemble deep learning models for

forecasting cryptocurrency time-series. Algorithms,

13(5):121.

Narayanan, A., Bonneau, J., Felten, E. W., Miller, A., and

Goldfeder, S. (2016). Bitcoin and Cryptocurrency

Technologies - A Comprehensive Introduction. Prince-

ton University Press.

Petric

a, A.-C., Stancu, S., and Tindeche, A. (2016). Limi-

tation of arima models in ﬁnancial and monetary eco-

nomics. Theoretical & Applied Economics, 23(4).

Pintelas, E., Livieris, I. E., Stavroyiannis, S., Kotsilieris, T.,

and Pintelas, P. E. (2020). Investigating the problem

of cryptocurrency price prediction: A deep learning

approach. In 16th IFIP WG 12.5 International Con-

ference on Artiﬁcial Intelligence Applications and In-

novations (AIAI), volume 584 of IFIP Advances in In-

formation and Communication Technology, pages 99–

110. Springer.

Pisner, D. A. and Schnyer, D. M. (2020). Support vector

machine. In Machine Learning, pages 101–121. Else-

vier.

Saravanos, C. and Kanavos, A. (2023a). Forecasting stock

market alternations using social media sentiment anal-

ysis and deep neural networks. In 14th International

Conference on Information, Intelligence, Systems &

Applications (IISA), pages 1–8. IEEE.

Saravanos, C. and Kanavos, A. (2023b). Forecasting stock

market alternations using social media sentiment anal-

ysis and regression techniques. In International Con-

ference on Artiﬁcial Intelligence Applications and In-

novations (AIAI), volume 677 of IFIP Advances in

Information and Communication Technology, pages

335–346. Springer.

Saravanos, C. and Kanavos, A. (2025). Forecasting

stock market volatility using social media senti-

ment analysis. Neural Computing and Applications,

37(17):10771–10794.

Savvopoulos, A., Kanavos, A., Mylonas, P., and Sioutas,

S. (2018). LSTM accelerator for convolutional object

identiﬁcation. Algorithms, 11(10):157.

Sch

olkopf, B. and Smola, A. J. (2002). Learning With Ker-

nels: Support Vector Machines, Regularization, Op-

timization, and Beyond. Adaptive Computation and

Machine Learning Series. MIT Press.

Selmi, R., Tiwari, A. K., and Hammoudeh, S. (2018). Efﬁ-

ciency or speculation? a dynamic analysis of the bit-

coin market. Economics Bulletin, 38(4):2037–2046.

Shumway, R. H. and Stoffer, D. S. (2017). Arima models.

In Time Series Analysis and Its Applications, pages

75–163. Springer.

Siami-Namini, S., Tavakoli, N., and Namin, A. S. (2018).

A comparison of ARIMA and LSTM in forecasting

time series. In 17th IEEE International Conference on

Machine Learning and Applications (ICMLA), pages

1394–1401. IEEE.

Silaparasetty, N. (2020). The tensorﬂow machine learning

library. In Machine Learning Concepts with Python

and the Jupyter Notebook Environment: Using Ten-

sorﬂow 2.0, pages 149–171. Springer.

Smola, A. J. and Sch

olkopf, B. (2004). A tutorial on

support vector regression. Statistics and Computing,

14(3):199–222.

Staudemeyer, R. C. and Morris, E. R. (2019). Understand-

ing LSTM - a tutorial into long short-term memory

recurrent neural networks. CoRR, abs/1909.09586.

Trigka, M., Kanavos, A., Dritsas, E., Vonitsanos, G., and

Mylonas, P. (2022). The predictive power of a twitter

user’s proﬁle on cryptocurrency popularity. Big Data

and Cognitive Computing, 6(2):59.

Urquhart, A. (2016). The inefﬁciency of bitcoin. Economics

Letters, 148:80–82.

Vapnik, V. (1999). An overview of statistical learning

theory. IEEE Transactions on Neural Networks,

10(5):988–999.

Vonitsanos, G., Kanavos, A., Grivokostopoulou, F., and

Sioutas, S. (2024). Optimized price prediction of

cryptocurrencies using deep learning on high-volume

time series data. In 15th International Conference

on Information, Intelligence, Systems & Applications

(IISA), pages 1–8. IEEE.

Vonitsanos, G., Kanavos, A., and Mylonas, P. (2023). De-

coding gender on social networks: An in-depth anal-

ysis of language in online discussions using natural

language processing and machine learning. In IEEE

International Conference on Big Data, pages 4618–

4625.

Zoumpekas, T., Houstis, E. N., and Vavalis, M. (2020).

ETH analysis and predictions utilizing deep learning.

Expert Systems with Applications, 162:113866.

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

266