Multi-Objective Policy Optimization for Effective and Cost-Conscious

Penetration Testing

Xiaojuan Cai

1 a

, Lulu Zhu

1 b

, Zhuo Li

1 c

and Hiroshi Koide

2 d

Department of Information Science and Technology, Information Science and Electrical Engineering, Kyushu University,

Fukuoka, Fukuoka, Japan

Section of Cyber Security for Information Systems, Research Institute for Information Technology, Kyushu University,

Fukuoka, Fukuoka, Japan

Keywords:

Internet Security, Penetration Testing, Reinforcement Learning, Constrained Optimization.

Abstract:

Penetration testing, which identiﬁes security vulnerabilities before malicious actors can exploit them, is essen-

tial for strengthening cybersecurity defenses. Effective testing helps discover deep, high-impact vulnerabilities

across complex networks, while efﬁcient testing ensures fast execution, low resource utilization, and reduced

risk of detection in constrained or sensitive environments. However, achieving both effectiveness and efﬁ-

ciency in real-world network environments presents a core challenge: deeper compromises often require more

actions and time. At the same time, excessively conservative strategies may miss critical vulnerabilities. This

work addresses the trade-off between maximizing attack performance and minimizing operational costs. We

propose a multi-objective reinforcement learning framework that minimizes costs while maximizing rewards.

Our approach introduces a Lagrangian-based policy optimization scheme in which a dynamically adjusted

multiplier balances the relative importance of rewards and costs during learning. We evaluate our method

on benchmark environments with varied network topologies and service conﬁgurations. Experimental results

demonstrate that our method achieves successful penetration performance and signiﬁcantly reduces time costs

compared to the baselines, thereby improving the adaptability and practicality of automated penetration testing

in real-world scenarios.

1 INTRODUCTION

Penetration testing is an essential defense strategy in

cybersecurity, which identiﬁes network vulnerabili-

ties before malicious actors exploit them. Penetra-

tion testing involves simulating realistic attack scenar-

ios, such as unauthorized access, lateral movement,

or privilege escalation, to assess the security posture

of systems, networks, or applications (Teichmann and

Boticiu, 2023; Jeff and Kala, 2024; Hayat and Gatlin,

2025).

As the complexity of network systems grows, the

increasing cybersecurity challenges make penetration

testing play a more critical role, especially in cloud in-

frastructures, IoT deployments, and software-deﬁned

environments (Skandylas and Asplund, 2025; Ankele

et al., 2019). In these dynamic and complex network

https://orcid.org/0009-0009-4242-8420

https://orcid.org/0009-0001-5889-1374

https://orcid.org/0000-0002-0602-7664

https://orcid.org/0009-0008-7111-8053

environments, the effectiveness of penetration testing

refers to discovering high-impact vulnerabilities and

reaching sensitive targets. Effective penetration test-

ing policies help identify vulnerabilities before the

deployment of network systems and avoid severe ﬁ-

nancial loss (Bandar Abdulrhman Bin Arfaj, 2022;

Fadhli, 2024; Caddy, 2025). On the other hand, pen-

etration testing must be efﬁcient. The reason is that

penetration testing policies have to identify vulnera-

bilities in sensitive, dynamic, or large-scale systems,

while time, bandwidth, stealth, and resource usage are

all constrained (Li et al., 2025b; Kong et al., 2025;

Li et al., 2025a). Efﬁcient testing minimizes risks,

avoids unnecessary exposure, and ensures real-world

practicality (Zennaro and Erd

odi, 2023).

However, effectiveness and efﬁciency are often

in conﬂict for penetration testing policies. Achiev-

ing deeper compromises typically demands more time

and incurs higher risk, while overly conservative

strategies may terminate early or fail to identify seri-

ous vulnerabilities (Erd

odi and Zennaro, 2022; Pham

et al., 2024; Luo et al., 2024). Balancing this trade-off

374

Cai, X., Zhu, L., Li, Z. and Koide, H.

Multi-Objective Policy Optimization for Effective and Cost-Conscious Penetration Testing.

DOI: 10.5220/0013713400003985

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Web Information Systems and Technologies (WEBIST 2025), pages 374-385

ISBN: 978-989-758-772-6; ISSN: 2184-3252

remains a central challenge in the design of automated

penetration testing systems.

To enhance the effectiveness, various automated

penetration testing techniques have been proposed.

Traditional rule-based penetration testing methods of-

ten rely on developers’ background knowledge and

conventional rule-based testing techniques (Ankele

et al., 2019; Raj and Walia, 2020; Malkapurapu

et al., 2023; Jeff and Kala, 2024; Skandylas and As-

plund, 2025; Wieser et al., 2024). However, design-

ing scalable and adaptive testing methods for com-

plex systems remains an open and pressing research

challenge. DL-based approaches have been applied

to penetration testing, particularly in IoT environ-

ments, to improve automation and accuracy (Koroni-

otis et al., 2021). Recent advances in deep learning

(DL) have shown promise in simulating complex at-

tack behaviors and automatically assessing system se-

curity (Koroniotis et al., 2021; Alaryani et al., 2024;

Deng et al., 2024; Antonelli et al., 2024; Kong et al.,

2025; Nakatani, 2025). Nevertheless, adopting DL

in real-world penetration testing still faces challenges

such as limited generalization and training data de-

pendency.

To further improve effectiveness while increasing

efﬁciency, reinforcement learning (RL) has been in-

creasingly used for penetration testing. RL models

penetration testing as a sequential decision-making

process, where an agent learns to exploit vulnerabil-

ities through trial-and-error interactions with a simu-

lated environment (Hoang et al., 2022; Bianou and

Batogna, 2024; Ahmad et al., 2025). Many prior

works have shown strong results (Cody et al., 2022;

Li et al., 2025a; Yao et al., 2023; Li et al., 2024a;

Zhou et al., 2025; Pham et al., 2024; Li et al., 2025b;

Yang et al., 2024; Zennaro and Erd

odi, 2023; Li et al.,

2024b), mainly because once state and action spaces

are well-deﬁned, the learned testing policy can scale

across scenarios with limited manual effort, as suc-

cessful exploit outcomes drive reward signals. How-

ever, most RL-based methods optimize a single ob-

jective, typically about task success, which makes it

challenging to balance effectiveness and efﬁciency.

As a result, jointly optimizing for both penetration

success and operational cost remains a critical yet un-

derexplored direction.

To address the conﬂict and explicitly balance the

trade-off between effectiveness and efﬁciency in pen-

etration testing, this paper proposes a multi-objective

RL-based framework for optimizing penetration test-

ing policies that aims to improve testing effectiveness

while minimizing operational costs. Unlike classical

RL approaches that focus exclusively on reward max-

imization, our method jointly optimizes two objec-

tives: attack-speciﬁc rewards and time-sensitive costs.

To balance these competing objectives, we incorpo-

rate a Lagrangian multiplier, which is dynamically ad-

justed during policy training. When the accumulated

cost exceeds a high level, the agent shifts its behav-

ior to prioritize cost reduction; conversely, when costs

remain low, the agent emphasizes reward maximiza-

tion. This adaptive mechanism enables efﬁcient and

cost-aware penetration strategies in complex network

environments.

We validate our method through comprehensive

experiments on the Network-Attack-Simulator bench-

mark. To evaluate performance across varying lev-

els of complexity, we select three tasks that differ in

the number of hosts, service conﬁgurations, sensitiv-

ity levels, and network topologies. The experimental

results show that our method signiﬁcantly improves

penetration testing effectiveness and efﬁciency by ex-

ploring 3,475 more unique penetration paths, while

reducing the operational time cost by 88.27% over

the best-performing baseline method in an advanced

complex network environment. For more implemen-

tation details and experimental results, please refer to

our public repository in https://github.com/cxjuan/pe

netration test.

2 BACKGROUND

We learn a Lagrangian-based and multi-objective RL

policy to maximize rewards, minimize costs, and

adaptively balance the trade-off between them during

penetration testing. This section outlines the model-

ing and algorithmic background.

2.1 Markov Decision Process

An Markov Decision Process (MDP) is formally de-

ﬁned by a tuple (S, A, P, R, γ), where, S is the set

of possible states, A is the set of available actions,

P(s

′

|s, a) is the transition probability function repre-

senting the probability of transitioning to state s

′

from

state s after taking action a, R(s, a) is the reward func-

tion, indicating the immediate reward received after

taking action a in state s, γ ∈ [0, 1) is the discount fac-

tor, which balances the importance of immediate and

future rewards.

2.2 Reinforcement Learning

Reinforcement Learning (RL) is a learning paradigm

where an agent interacts with an environment to

learn a policy that maximizes cumulative rewards

Multi-Objective Policy Optimization for Effective and Cost-Conscious Penetration Testing

375

over time (Chadi and Mousannif, 2023). The en-

vironment is typically modeled as a Markov Deci-

sion Process (MDP), which provides a mathematical

framework for sequential decision-making under un-

certainty (Sutton and Barto, 2018; Chadi and Mou-

sannif, 2023).

At each time step t, the agent observes the cur-

rent state s

∈ S , selects an action a

∈ A based on

its policy π(a|s), receives a reward r

= R(s

, a

), and

transitions to a new state s

t+1

∼ P(·|s

, a

). The goal

of the agent is to learn a policy π that maximizes the

expected return:

∞

∑

t=0

R(s

, a

)

To evaluate policies, the action value functions is

commonly used by following demonstrations:

(s, a) = E

∞

∑

t=0

R(s

, a

) | s

= s, a

= a

A policy is considered optimal if it achieves the

highest possible expected return from any initial state.

The corresponding optimal value functions, V

∗

(s) and

∗

(s, a), satisfy the Bellman optimality equations.

Various RL algorithms, such as Q-learning, policy

gradients, and actor-critic methods, aim to approxi-

mate these optimal value functions or policies through

interaction with the environment (Wang et al., 2022).

2.3 Constrained Markov Decision

Process (CMDP)

While standard MDPs aim solely to maximize re-

wards, many real-world applications, such as penetra-

tion testing and robotics, require satisfying additional

constraints, such as limited time, energy, or risk ex-

posure (Li, 2023). The Constrained Markov Decision

Process (CMDP) (Altman, 1999) extends the MDP

framework by introducing one or more cost functions.

A CMDP is deﬁned as (S , A, P, R, C, γ, d), where

C(s, a) is a cost function and d is a cost threshold.

The objective is to ﬁnd a policy π that maximizes the

expected cumulative reward while satisfying the con-

straint on cumulative cost:

max

∞

∑

t=0

R(s

, a

)

subject to E

∞

∑

t=0

C(s

, a

)

≤ d.

2.4 Deep Q-Networks (DQN)

DQN is constructed on the concept of Q-learning.

The Q-learning algorithm seeks to learn the opti-

mal action-value function Q

∗

(s, a), which satisﬁes the

Bellman optimality equation:

∗

(s, a) = E

′



R(s, a) +γ max

′

∗

′

, a

′

)



Deep Q-Networks (DQN) (Mnih et al., 2013) ap-

proximate Q

∗

(s, a) using a neural network parameter-

ized by θ, denoted as Q

(s, a). The network is trained

to minimize the temporal difference (TD) loss:

L(θ) = E

(s,a,r,s

′

)∼D

∗

′

(s, a) −Q

(s, a))

where θ

′

denotes the parameters of a target network

that is periodically updated from θ, s

′

is the next state

of s by executing action a, a

′

is the action with the

highest predicted return and is selected by the policy

in state s

′

, and D is a replay buffer storing past transi-

tions to improve sample efﬁciency and stability.

DQN has achieved notable success in various do-

mains such as Atari games and network intrusion de-

tection, but it is inherently designed for reward maxi-

mization without considering cost or constraints (Guo

et al., 2025; Dana Mazraeh and Parand, 2025; Xu

et al., 2025).

3 METHODOLOGY

3.1 Policy Optimization Objectives

Each episode yields a sparse reward and one or more

cost signals for constraint violations. At each step, the

policy receives a state vector that summarizes the net-

work’s status, including connectivity, services, privi-

leges, and alerts. Based on this input, action values for

expected returns are estimated. The highest-valued

action is selected and executed.

Actions include scanning, exploiting, privilege es-

calation, and lateral movement. These actions are dis-

crete and tailored to penetration testing. Each action

incurs a ﬁxed cost of 1, while a reward of 100 is only

given upon successful penetration, with no intermedi-

ate rewards during the testing phase.

Our approach aims to learn a policy that consis-

tently selects actions that maximize cumulative re-

wards while minimizing cumulative costs per episode,

leading to efﬁcient and constraint-aware penetration

strategies.

To estimate the long-term value and cost associ-

ated with each state-action pair (s

, a

), we compute

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

376

Algorithm 1: Optimizing Penetration Testing Policy with Lagrangian Multiplier.

Input : Environment E, replay buffer B, episodes N, discount factor γ, learning rate η

Output: Optimized policy π

Initialize Q-networks Q

, Q

, and Lagrange multiplier λ ← 1;

Initialize cost history buffer H ←

0 ; // Track episodic costs for averaging

for k ← 1 to N do

Reset environment, get initial state s

;

← 0 ; // Initialize discounted cumulative cost for episode

while episode not terminated do

Select action a

= argmax



, a) − λQ

, a)



; // Trade off reward and penalized cost

Execute a

, observe next state s

t+1

, reward r

, cost c

= 1;

← C

+ γ

; // Update discounted cost

Store transition (s

, a

, r

, c

, s

t+1

) in replay buffer B;

← s

t+1

;

Sample mini-batch from B and update Q

, Q

via Bellman targets ; // Train Q-networks

Append C

to H ;

Compute average cost

C =

|H |

∑

; // Mean episodic cost over history

Update λ ← max



0, λ + η(C

−



; // Projected gradient ascent update

the discounted episodic return and cost as follows:

R(s

, a

) =

N−1

∑

i=0

t+i

C(s

, a

) =

N−1

∑

i=0

t+i

Where r

∈ {0, 200} is the reward at timestep t, c

= 1

is the ﬁxed cost per action, γ ∈ [0, 1) is the discount

factor, T is the length of the episode, N is the number

of time steps from t to end of the episode.

This formulation reﬂects the sparsity of the reward

signal and encourages the agent to reach the pene-

tration goal in as few steps as possible, to minimize

the accumulated operational cost. By jointly learning

from reward and cost signals, our framework guides

the policy toward efﬁcient and stealthy penetration

strategies under predeﬁned operational constraints.

3.2 Optimization of Value and Cost

Functions

Two separate neural networks are used to approximate

the action-value and cost-value functions. Each net-

work takes the current state as input and outputs a vec-

tor representing the estimated value or cost for every

possible action.

Formally, we employ two separate Q-functions:

• Q

(s, a) estimates the expected return (cumulative

reward).

• Q

(s, a) estimates the expected cumulative cost.

These functions are learned using separate Bell-

man equations:

Reward Bellman target:

= R(s, a) + γmax

′

, a

′

Cost Bellman target:

= C(s, a) + γmax

′

, a

′

is the action with the highest action value and cost

in the respective Bellman functions. The above Bell-

man function indicates that, for example, the target

of the value function is computed by the sum of the

current reward and future action returns. Each Q-

function is trained by minimizing the mean squared

temporal difference (TD) error over a batch of transi-

tions:

= E

(s,a,r,s

′

)



(s, a) −y

)



= E

(s,a,c,s

′

)



(s, a) −y

)



This dual-Q learning structure allows us to eval-

uate actions by their expected rewards and the risks

or costs they incur, forming the foundation for

constraint-aware decision-making.

3.3 Lagrangian-Based Multi-Objective

Optimization

Our method adopts a Lagrangian-based primal-dual

optimization framework to enforce cost constraints

during learning. A key distinction of our approach

is that the Lagrange multipliers λ are not only used

during policy optimization but are also directly incor-

porated into the action selection process. That is, the

policy selects actions by maximizing a reward sig-

nal adjusted by the current penalty weights, which

Multi-Objective Policy Optimization for Effective and Cost-Conscious Penetration Testing

377

ensures that the agent explicitly considers constraint

penalties when choosing actions, even during evalua-

tion:

∼ π(a | s

;λ) = argmax

[R(s

, a) −λC(s

, a)].

To enforce long-term constraint satisfaction, the

Lagrange multiplier λ

is modeled as a learnable

scalar and updated using projected gradient ascent

based on the gap between the current episodic cost

and the historical average cost. Speciﬁcally, let i de-

note episode numbers during training, and let k denote

the current episode number. The update rule is:

λ ←



λ + η



−

∑

i=0



, ∀i,

where η is the dual learning rate and [·]

projects onto

the non-negative reals. C

is the episodic cost of the

current episode, compared with the average of history

episodes. If C

is greater than the historical average,

then the λ will increase, strengthening the impact of

costs in action selection. It decreases λ when the cur-

rent episodic cost is lower than its historical average,

allowing the agent to adaptively balance task perfor-

mance and constraint satisfaction over time. Note that

λ is set to 1 when the training starts.

3.4 Multi-Objective Policy Optimization

We frame penetration testing as a constrained

decision-making problem, where the agent aims to

maximize success while minimizing cost. At each

step, it selects actions by maximizing the expected re-

ward minus a cost penalty scaled by a learnable La-

grange multiplier.

Rewards are sparse and only given upon success-

ful exploits, escalations, or goal completion, while

each action incurs a unit cost. Transitions are stored

in a replay buffer to train separate Q-networks for re-

wards and costs. After each episode, the Lagrange

multiplier is updated via projected gradient ascent to

balance performance and constraint adherence.

Through repeated learning, the agent converges to

a cost-aware strategy that optimizes both effective-

ness and efﬁciency. The full procedure is in Algo-

rithm 1.

4 EXPERIMENTS

4.1 Experiment Setup

We build our method on the Network-Attack-

Simulator benchmark

, and evaluate it against six

https://networkattacksimulator.readthedocs.io

state-of-the-art Safe RL baselines across three repre-

sentative environments: gen, small, and hard. gen re-

tains the tiny benchmark’s minimal topology but adds

stochasticity to test generalization. small introduces

more lateral movement paths for moderate complex-

ity. hard features complex zone structures and multi-

ple privilege escalation goals, requiring deeper plan-

ning and cost-sensitive behavior. These tasks as-

sess scalability and constraint-awareness in increas-

ing complexity.

Moreover, we compare with DQN (Mnih et al.,

2013) and set the Lagrange multiplier learning rate

to 1e-3 as well, using the same architecture for both

cost and policy networks. Our RL training process

doubles as penetration testing, with interactions serv-

ing as both learning and evaluation data.

Additionally, we implement two heuristic base-

lines: (i) a random agent selecting uniformly from

the action space, and (ii) a rule-based agent guided by

the logic of Metasploit and tools like Nmap, Nessus,

OpenVAS, Armitage, Wireshark, and Netcat (Ankele

et al., 2019; Raj and Walia, 2020; Malkapurapu et al.,

2023; Jeff and Kala, 2024; Skandylas and Asplund,

2025). Details of these baselines are in the implemen-

tation resources.

4.2 Evaluation of Training Performance

In our experiments, following the strategy of “test-

ing while training”, evaluation is conducted periodi-

cally during the training process. During the experi-

ment, we executed three rounds of penetration testing

in each environment. In each round of testing, we set

the total training budgets to 50,000 and 100,000 steps

for gen, small, and hard, respectively.

In Figure 1, we present the average trends of

episodic returns and costs during the training of base-

lines (e.g., standard DQN, random- and rule-based

method) and the Constrained-DQN penetration test-

ing policies. Each point on the curves represents the

evaluated episodic returns and costs of the policies at

the corresponding time steps. A higher return indi-

cates a greater likelihood of successfully compromis-

ing the network system, while a higher cost reﬂects a

longer task completion time.

Our method, the Constrained-DQN, consistently

outperforms baseline agents by achieving higher cu-

mulative returns and lower episodic costs. In par-

ticular, on the gen, the Constrained-DQN achieves

substantial improvements in both return and cost

throughout the training process. In the more challeng-

ing small and hard tasks, it demonstrates even greater

efﬁciency in earning reward and cost reduction. No-

tably, in hard, compared to DQN and two other base-

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

378

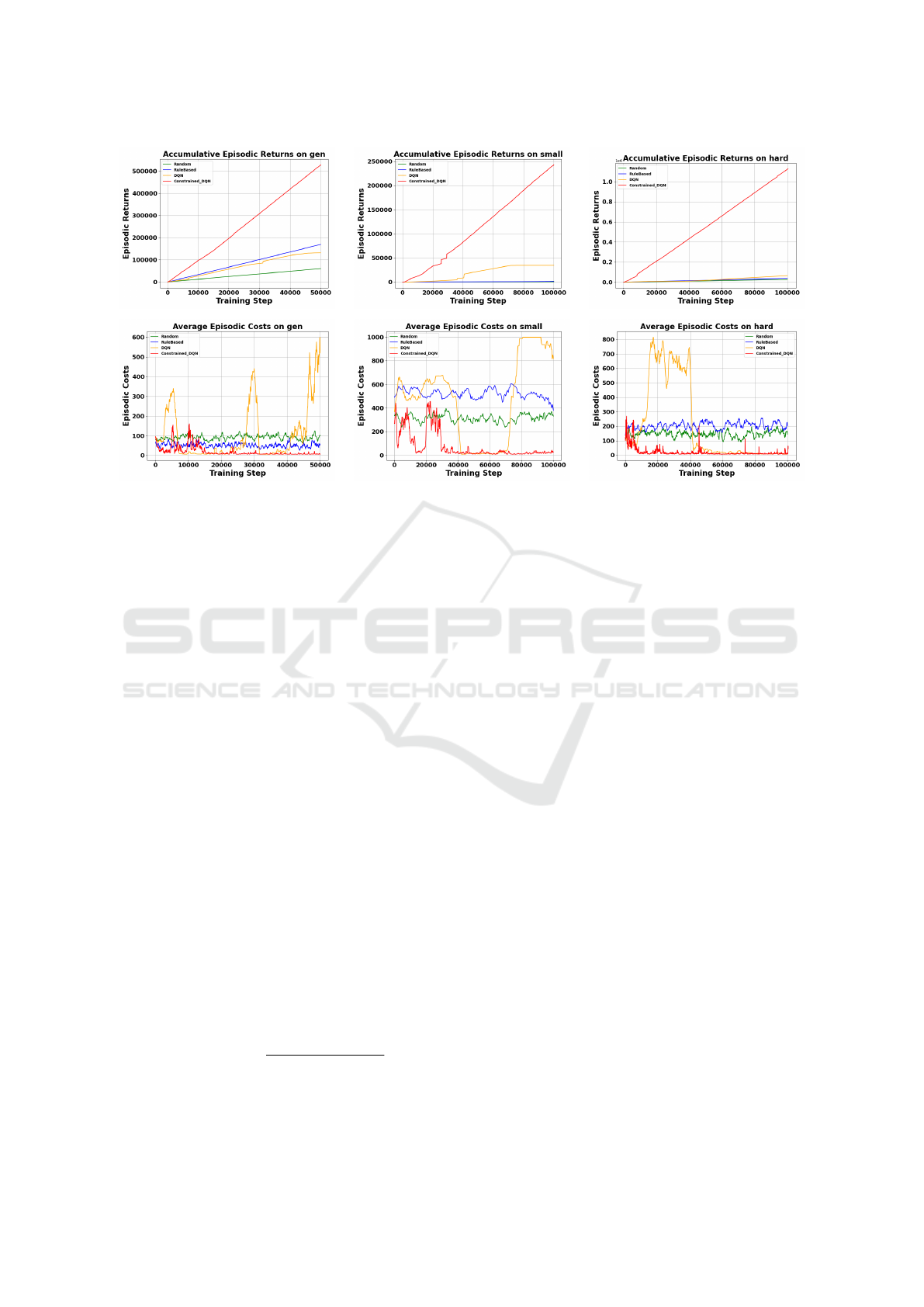
Figure 1: Average trends of episodic returns and costs achieved by random- and rule-based penetration testing method, DQN,

and Constrained-DQN penetration testing policies.

lines, our method shows signiﬁcant capabilities of re-

ducing costs from the early training phases, and out-

performs all baselines in cumulative rewards.

These results indicate that our approach improves

penetration testing effectiveness and efﬁciency by in-

creasing the success rate and reducing the time re-

quired to complete the task.

4.3 Evaluation of Penetration Testing

Performance

We evaluated our proposed method against three

baselines (e.g., standard DQN, random- and rule-

based methods) across three representative penetra-

tion testing tasks with varying difﬁculty levels: gen-

eral (gen), small-scale (small), and complex scenar-

ios (hard). We trained all the methods under identical

conditions with ﬁxed training steps for each task.

To comprehensively evaluate our penetration test-

ing policies, we measure the average number of test-

ing episodes, the number of discovered penetration

paths, path uniqueness and exclusivity, average path

length and cost, and the overall success rate. Unique

paths refer to those that were identiﬁed by our policies

but were absent in the baseline evaluation. The com-

putation of the overall success rate is in the following

equation:

SuccessRate =

|Unique Paths|

|Testing E pisodes|

|Unique Paths| refers to the number of distinct

penetration paths discovered by a method, counted by

eliminating repeated paths within the same method,

and |TestingE pisodes| is the total number of testing

episodes conducted within the same training budget

(i.e., number of steps).

Table 1 summarizes the results, demonstrating

that our method consistently outperforms all baseline

methods across metrics and tasks. In the gen task with

50,000 training steps, our approach achieves an aver-

age of 4,697.0 testing episodes, discovering 4,692.33

penetration paths, 2,258.67 unique paths, and 1,025.0

exclusive paths. It improves the success rate by ap-

proximately 23.72% over the best-performing base-

line (RuleBased), increasing from 3.651% to 4.517%,

while reducing the average cost by 55.57%.

More notably, in the more complex small and hard

tasks, our method shows signiﬁcantly stronger explo-

ration and exploitation capabilities. For instance, in

the hard scenario, it discovers over ﬁve times (com-

pared to Random), seven times (compared to Rule-

Based), and fourteen times (compared to DQN) more

total penetration paths, and six times, four times,

and nine times more unique paths, respectively. It

also achieves nearly a ﬁvefold increase in success

rate compared to the random-based method (4.462%

vs. 0.685%), a threefold increase over the rule-based

method (4.462% vs. 0.987%), and an eightfold in-

crease over DQN (4.462% vs. 0.465%), all while

maintaining the lowest average costs (23.875).

Our method’s effectiveness relies on reducing

penetration testing costs. Speciﬁcally, with the same

training time steps, our method can always ﬁnish the

penetration testing with fewer time steps than the

baselines. This advantage enables our method to test

Multi-Objective Policy Optimization for Effective and Cost-Conscious Penetration Testing

379

Table 1: Averaged penetration testing results of baselines and our method on selected tasks. We consider the random-based

penetration testing method, the rule-based penetration testing method, and DQN as baselines against our Constrained-DQN.

Better results are highlighted in blue.

Tasks

Methods

Training

Steps

Experienced

Episodes

Penetration

Paths

Unique

Paths

Exclusive

Paths

Ave. Path

Lengths

Avg.

Costs

Avg. Success

Rates (%)

gen

Random 50,000 1,090.0 1,088.0 544.0 181.333 91.901 91.743 1.088

RuleBased 50,000 1,894.0 1,892.0 1,825.667 914.333 52.550 52.539 3.651

DQN 50,000 717.667 682.333 456.333 254.333 78.187 105.263 0.913

Ours 50,000 4,697.0 4,692.333 2,258.667 1,025.0 22.592 23.188 4.517

small

Random 100,000 636.0 634.0 317.0 105.66 314.495 314.465 0.317

RuleBased 100,000 381.667 359.667 359.667 182.0 500.421 521.739 0.360

DQN 100,000 318.0 161.333 144.333 96.0 203.193 515.464 0.144

Ours 100,000 1,213.0 1,160.667 1,009.667 625.333 92.916 125.366 1.010

hard

Random 100,000 1,372.0 1,370.0 685.0 228.333 145.943 145.773 0.685

RuleBased 100,000 988.667 986.667 986.66 490.333 203.583 203.528 0.987

DQN 100,000 616.0 513.0 465.333 216.0 184.983 321.888 0.465

Ours 100,000 7,535.0 7,515.333 4,461.667 2,587.0 20.833 23.875 4.462

more episodes within a ﬁxed testing budget. Con-

sequently, our method can detect more penetration

paths. Moreover, we infer that our method tends

to avoid repeatedly exercising the same penetration

paths since we continuously reduce the time costs

during training. Such a mechanism might help dis-

cover more unique penetration paths with short path

lengths.

Overall, the results show that our method effec-

tively discovers penetration paths and generalizes bet-

ter across different task complexities. The high num-

ber of unique and exclusive paths indicates broader

search space coverage, while shorter average path

lengths and lower costs suggest more efﬁcient and

optimal solutions. This strong performance validates

the strength of our approach in automated penetration

testing, highlighting its potential for practical deploy-

ment.

4.4 Hyperparameter Tuning

The learning rate for the Lagrangian multiplier λ is

a critical hyperparameter. It directly inﬂuences how

quickly the agent adjusts its penalty signal in response

to constraint violations. A learning rate that is too

low may result in slow or insufﬁcient updates to λ,

failing to enforce constraints effectively. Conversely,

an overly high learning rate can lead to unstable up-

dates, causing oscillations or divergence in cost man-

agement and policy learning. Thus, tuning this hy-

perparameter is essential to ensure stable convergence

and reliable satisfaction of constraints over training.

Experimental results on the small environment in

Figure 2 show that 1 × 10

−3

achieves the best over-

all performance on episodic returns and relatively

Figure 2: The trends of episodic returns and costs achieved

by our method with different λ learning rates on small.

lower costs than other settings. Based on our statis-

tics, 1 × 10

−3

achieves a high penetration testing suc-

cess rate and the greatest episodic return (7,489.8),

while maintaining the lowest average cost (708.87)

among all tested conﬁgurations. In contrast, the lower

rate 1 × 10

−4

shows slightly reduced task perfor-

mance, with lower returns (2,490.67) and higher costs

(786.62). The highest rate 1 × 10

−2

leads to degraded

performance across the board, including lower return

(2,618.05), and increased cost (871.47), likely due to

unstable λ updates.

5 DISCUSSION

5.1 Analysis of Penetration Strategy

Distribution

We analyze penetration path distributions across tasks

(gen, small, hard) using DBSCAN clustering in Jac-

card similarity space, visualized with Isomap (Sun-

dararajan, 2025; Cheng et al., 2025). Cluster struc-

tures reﬂect strategy similarity, while dispersion indi-

cates behavioral diversity (Sundararajan, 2025).

As shown in Figure 3, each point represents a pen-

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

380

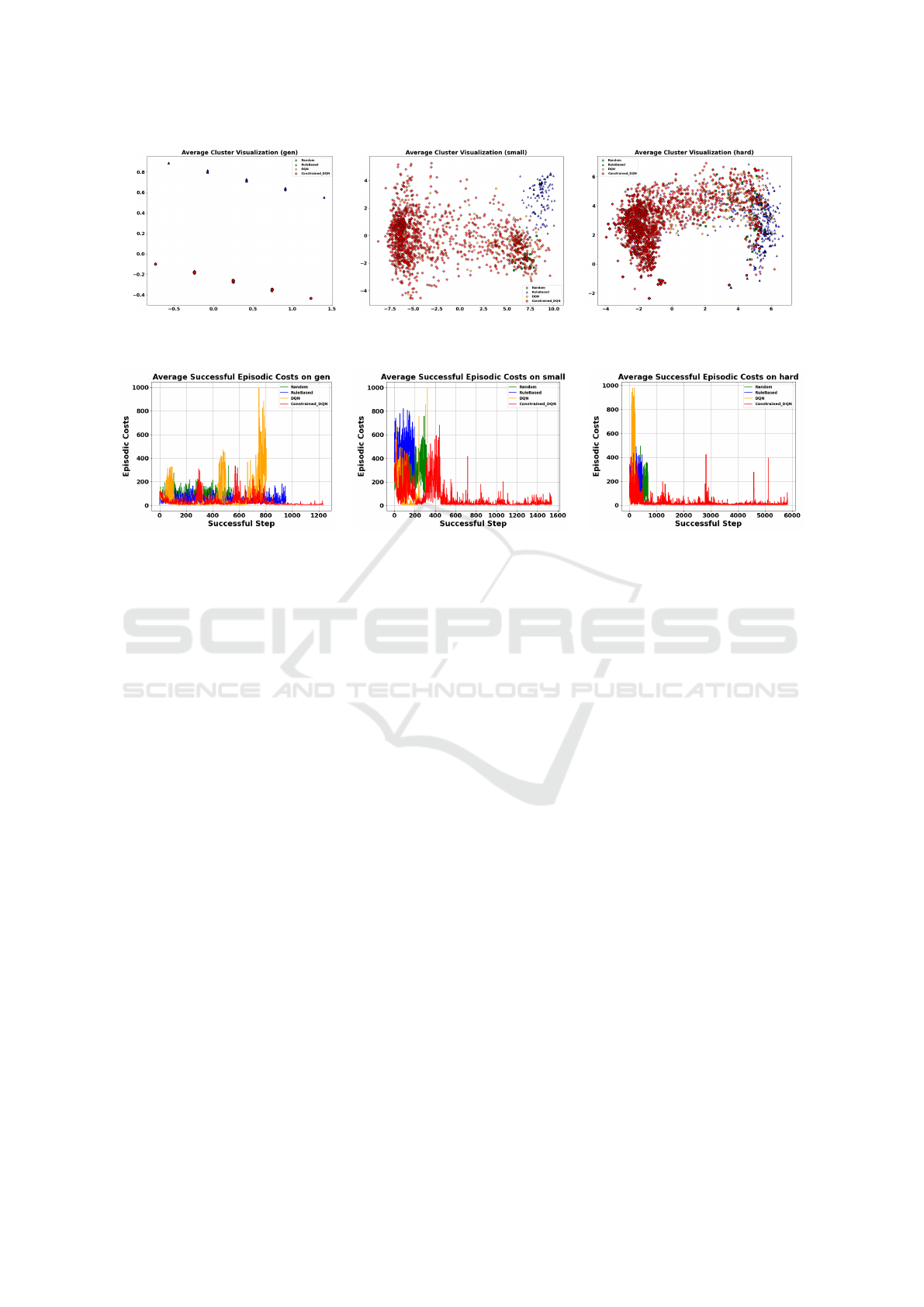
Figure 3: Average trends in the distribution of clusters of penetration test paths using Isomap. Paths are achieved by random-

and rule-based penetration testing method, DQN, and Constrained-DQN penetration testing policies.

Figure 4: Average trends of successful penetration testing episodic costs achieved by random- and rule-based penetration

testing method, DQN, and Constrained-DQN penetration testing policies.

etration path and is embedded according to its Jaccard

similarity to other paths. Tightly grouped points sug-

gest consistent and repeatable strategies, as proximity

indicates high similarity between penetration paths.

In the task of gen, our method induces only 16 clus-

ters, whereas in the more complex small and hard

tasks, it obtains 78 and 478 clusters, respectively. In

contrast, the baseline methods show fewer and less

stable clusters across scenarios. Speciﬁcally, in gen,

random-based method, rule-based method, and DQN

provide 12, 22, and 16 clusters, respectively. Mean-

while, in small, only 2 (Random), 2 (RuleBased), and

15 (DQN) clusters are observed. Meanwhile, in hard,

17 (Random), 8 (RuleBased), and 40 (DQN) clusters

are identiﬁed, respectively.

Notably, the diversity of isolated points in small

and hard shows that our policies are exploratory. It

also indicates that the Constrained-DQN generates a

signiﬁcantly broader and more dispersed distribution

of penetration paths than the baselines.

5.2 Analysis of Lagrangian Multiplier λ

and Costs

As shown in Figure 4, we compare the average

episodic costs of successful penetration testing steps

achieved by the Constrained-DQN and baseline meth-

ods. The results show that our method incurs the low-

est average cost while achieving the highest number

of successful penetration steps. Meanwhile, it consis-

tently achieves a low cost per successful step, indicat-

ing higher efﬁciency compared to the baselines.

We analyze the relationship between the La-

grangian multiplier λ and the average cost per episode

in the gen, small, and hard environments using

the Pearson correlation coefﬁcient (Sedgwick, 2012),

which measures the linear relationship between two

variables. In our context, it reﬂects how the adaptive

λ responds to the cost incurred by the policy during

training.

Across all tasks, we observed positive correlations

between λ and the average cost per episode: in gen,

the correlation is +0.297; in small, it is +0.605; and

in hard, it is +0.236. These results suggest that as the

agent encounters higher costs, the value of λ tends

to increase. This behavior reﬂects the design of our

method: the adaptive adjustment of λ penalizes costly

actions and reduces their selection probability, en-

couraging the agent to avoid inefﬁcient decisions.

The agent learns to prioritize task completion

and cost efﬁciency through this mechanism. Unlike

standard DQN, the random- and rule-based method,

which focuses solely on maximizing returns, our con-

strained formulation incorporates cost-awareness di-

rectly into the policy learning process. This is espe-

cially critical in penetration testing scenarios, where

an agent that reaches the goal without regard for efﬁ-

ciency is of limited practical use. The observed corre-

lations demonstrate that the adaptive λ provides an ef-

Multi-Objective Policy Optimization for Effective and Cost-Conscious Penetration Testing

381

fective internal signal for guiding cost-sensitive learn-

ing.

Overall, we introduce a multi-objective policy op-

timization scheme to learn penetration testing poli-

cies. Our method outperforms baselines in terms of

success rate, cost efﬁciency, and strategic diversity, as

supported by experimental results. While current lim-

itations include the use of a scalar Lagrange multiplier

and reliance on simulated environments, our method

shows potential for real-world, resource-constrained

scenarios such as enterprise or IoT networks.

6 RELATED WORKS

6.1 Rule-Based Penetration Testing

Various tools are preferred among security profes-

sionals and organizations in conﬁgured testing envi-

ronments for traditional penetration testing. For in-

stance, by setting the scope of the penetration testing

to a generic In-Vehicle Infotainment (IVI) system, the

authors of (Wieser et al., 2024) focus on the Wi-Fi in-

terface of the IVI model to reveal vulnerabilities that

could allow attackers to crash the system, access data,

or manipulate settings. Their study demonstrates ef-

fective testing methods tailored to the automotive en-

vironment to address the unique security challenges

in vehicular networks.

Moreover, works of (Ankele et al., 2019; Raj and

Walia, 2020; Malkapurapu et al., 2023; Jeff and Kala,

2024; Skandylas and Asplund, 2025) analyze the per-

formance of the Metasploit Framework in conjunc-

tion with other popular penetration testing tools (e.g.,

Nmap, Nessus, OpenVAS, Armitage, Wireshark, and

Netcat). The results show that a ﬂexible and modular

architecture enables a comprehensive range of test-

ing scenarios. (Ankele et al., 2019) extracts meta-

data from diagrams and models commonly used in

typical software development processes to automate

threat modeling, security analysis, and penetration

testing without prior detailed security knowledge in a

large-scale IoT/IIoT network. This approach reduces

the reliance on deep security expertise and addresses

the scalability limitations of manual approaches in

complex industrial systems. In addition, (Malkapu-

rapu et al., 2023) discussed that a large and active

community ensures that open-source Metasploit re-

ceives frequent updates and shared resources. The

authors detail Metasploit’s modular design, extensive

exploit database, and integration capabilities, demon-

strating its utility in automating and enhancing secu-

rity assessments. Furthermore, to address the grow-

ing need for scalable and expert-independent secu-

rity testing, the authors in (Skandylas and Asplund,

2025) formalize the problem of penetration testing

as an architectural-level problem and propose a self-

organizing, architecture-driven automation tool for

penetration testing (ADAPT). They successfully ap-

plied their method to real-world environments such

as Metasploitable2/3 and virtual training networks.

6.2 Deep Learning-Based Penetration

Testing

The powerful ability to process large amounts of data

and identify patterns enables DL models to efﬁciently

and automatically simulate complex attack scenarios

and assess security posture during penetration test-

ing. The authors of (Koroniotis et al., 2021) aim to

address the limitations of existing penetration test-

ing tools in detecting zero-day vulnerabilities in IoT

environments due to the diversity of data generated,

hardware limitations, and environmental complexity.

Hence, they provide a deep learning-based framework

(LSTM-EVI) for vulnerability identiﬁcation in smart

IoT environments. Evaluated using real-time data

on a smart airport testbed, the framework achieves

outstanding accuracy in detecting scanning attacks.

Meanwhile, in the work of (Alaryani et al., 2024), an

AI-enabled penetration testing platform (PentHack)

is designed to enhance the development of cyberse-

curity knowledge. The platform integrates the Large

Language Model (LLM) with a user-friendly GUI to

automate testing procedures and enhance user learn-

ing outcomes while supporting educational and prac-

tical applications in cyberwarfare and security. More-

over, the authors of (Deng et al., 2024) propose PEN-

TESTGPT, an LLM-powered automated penetration

testing framework that leverages domain knowledge

and a modular, self-interacting architecture to address

context loss challenges. Their proposal shows strong

performance on real-world targets, which achieves a

228.6% task-completion improvement over GPT-3.5

on benchmark penetration testing tasks.

To improve the efﬁciency and adaptability of ex-

ploration in complex network environments, the au-

thors of (Kong et al., 2025) proposed VulnBot, an au-

tonomous penetration testing framework based on a

multi-agent collaborative architecture. The VulnBot

enables agents to share knowledge and coordinate at-

tacks to address the limitation of a lack of task co-

ordination and excessive unstructured output. Addi-

tionally, in the work of (Nakatani, 2025), a frame-

work called RapidPen utilizes LLM to discover vul-

nerabilities and exploits autonomously. In RapidPen,

the LLM helps synthesize new command inputs based

on contextual understanding of the target and its con-

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

382

ﬁguration. As a result, a report on the progress of

the penetration test (e.g., logs, vulnerabilities found,

commands used to obtain a shell) can be obtained by

providing the target IP address and shows strong ef-

fectiveness in discovering and exploiting vulnerabili-

ties autonomously without human intervention.

Furthermore, the work of (Antonelli et al., 2024)

improves the efﬁciency of data mining in the pene-

tration testing of web applications through semantic

clustering techniques. The authors utilize advanced

embedding models, such as Word2Vec and Univer-

sal Sentence Encoder, to convert word list entries

into vector representations. These vectors are then

grouped using a semantic similarity-based clustering

algorithm. The resulting clusters provide the basis for

an intelligent next-word selection strategy that signif-

icantly improves the performance of traditional brute-

force cracking methods in various web applications.

6.3 Reinforcement Learning-Based

Penetration Testing

By viewing penetration testing as an ongoing

decision-making process, RL agents can learn the op-

timal attack strategies to increase the efﬁciency and

coverage of penetration testing. (Cody et al., 2022)

propose an RL method for discovering data exﬁltra-

tion paths in enterprise networks using attack graphs.

Their penetration testing scenario assumes that the

stolen data is seeking a stealthy exﬁltration. The au-

thors design the reward function of the RL agent to

favor low-detection paths, showing promising results

in large-scale environments. Moreover, the authors

of (Li et al., 2025a) introduce a novel framework for

formalizing and reﬁning attack patterns involving dis-

junctive, conjunctive, and hybrid causal relationships

among actions (TTCRT). By modeling these dynam-

ics as Markov Decision Processes, the framework en-

ables deep RL algorithms to discover optimal attack

paths accurately.

Otherwise, since the intelligent-led penetration

testing approaches often assume static environments,

the authors of (Yao et al., 2023; Li et al., 2024a) apply

RL in a dynamic defense environment and evaluate

with the scenario of CyberBattleSim. Results show

reduced agent performance and convergence in dy-

namic scenarios, highlighting the need for a balanced

exploration-exploitation strategy. To improve conver-

gence speed and continuous adaptation in dynamic

scenarios, the authors in the work of (Li et al., 2024a)

capture observed scenario changes to help penetration

testing agents make decisions based on historical ex-

perience. Meanwhile, the work of (Zhou et al., 2025)

addressed the challenge of non-stationarity in real-

world autonomous penetration testing. The authors

propose SCRIPT, a scalable continual RL framework.

SCRIPT enables agents to learn large-scale tasks se-

quentially, leveraging prior knowledge (positive for-

ward transfer) while mitigating catastrophic forget-

ting through new task learning and knowledge con-

solidation processes.

To tackle partial observability in penetration test-

ing, EPPTA (Li et al., 2025b) introduces a state-

estimation module within an asynchronous RL frame-

work, achieving up to 20 times faster convergence

than prior methods. To overcome limited test cov-

erage and repetitive behaviors, CLAP (Yang et al.,

2024) proposes a coverage-driven RL framework with

Chebyshev-based strategy diversiﬁcation, improving

efﬁciency and scaling to networks with up to 500

hosts. In addition, works of (Zennaro and Erd

odi,

2023; Li et al., 2024b; Pham et al., 2024) provide

efforts for an efﬁcient penetration testing. The au-

thors of (Zennaro and Erd

odi, 2023) explore the ap-

plication of RL to penetration testing through model-

ing realistic, goal-driven attack processes to capture-

the-ﬂag (CTF) scenarios, focusing on the trade-off

between model-free learning and the use of domain

knowledge. Compared to knowledge-guided agents

with predeﬁned heuristics, the results show that in-

tegrating limited prior knowledge can reduce learn-

ing time. A knowledge-informed RL approach for

leveraging reward machines to encode domain knowl-

edge into the RL process was proposed later (Li et al.,

2024b). Their approach improves learning efﬁciency

and interpretability by guiding the agent with struc-

tured symbolic rewards rather than relying solely on

trial-and-error. It highlights combining human knowl-

edge with RL for more efﬁcient, goal-directed attack

strategies. (Pham et al., 2024) automates the post-

exploitation phase in penetration testing. Unlike treat-

ing exploitation as an end goal, the authors focus on

evaluating the security level of a system by systemat-

ically exploring post-exploitation actions. The results

show high success rates with fewer attack steps in a

complex network environment.

7 CONCLUSION

This work presents a reinforcement learning pen-

etration testing framework that employs a multi-

objective policy optimization scheme based on con-

strained DQN to jointly maximize penetration test-

ing efﬁciency and minimize operational cost through

adaptive Lagrangian multiplier λ. Experiments

on three penetration testing environments, gen,

small, and hard in Network-Attack-Simulator bench-

Multi-Objective Policy Optimization for Effective and Cost-Conscious Penetration Testing

383

mark, showed that the proposed method consistently

achieves higher success rates, larger coverage returns,

and more reductions in episode cost compared with

standard DQN, random- and rule-based penetration

testing methods. Statistically signiﬁcant positive cor-

relations between λ and incurred cost conﬁrm that the

dual update mechanism guides the agent to perform

lower-cost actions without sacriﬁcing exploit quality.

These results demonstrate that constrained reinforce-

ment learning is a practical avenue for scalable, efﬁ-

cient, and effective automated penetration testing in

real-world, resource-limited environments.

Our future work focuses on a broader considera-

tion of improving penetration testing efﬁciency. At

ﬁrst, we will upgrade the Lagrangian multiplier λ

from a learnable scalar to a neural network. A more

complex λ helps improve the granularity and accu-

rately measure the impact of costs on selecting actions

under different states. Furthermore, we will focus

on extending our method to more complex network

systems, such as cloud-based platforms or software-

deﬁned networks, to improve its scalability and real-

world applicability.

ACKNOWLEDGEMENTS

This work is supported by Hitachi Systems, Ltd.

REFERENCES

Ahmad, T., Butkovic, M., and Truscan, D. (2025). Using

reinforcement learning for security testing: A system-

atic mapping study. In 2025 IEEE International Con-

ference on Software Testing, Veriﬁcation and Valida-

tion Workshops (ICSTW), pages 208–216.

Alaryani, M., Alremeithi, S., Ali, F., and Ikuesan, R. (2024).

Penthack: Ai-enabled penetration testing platform for

knowledge development. European Conference on

Cyber Warfare and Security, 23:27–36.

Altman, E. (1999). Constrained Markov Decision Pro-

cesses, volume 7. CRC Press.

Ankele, R., Marksteiner, S., Nahrgang, K., and Vallant,

H. (2019). Requirements and recommendations for

iot/iiot models to automate security assurance through

threat modelling, security analysis and penetration

testing. CoRR, abs/1906.10416.

Antonelli, D., Cascella, R., Schiano, A., Perrone, G., and

Romano, S. P. (2024). “dirclustering”: a semantic

clustering approach to optimize website structure dis-

covery during penetration testing. Journal of Com-

puter Virology and Hacking Techniques, 20(4):565–

577.

Bandar Abdulrhman Bin Arfaj, Shailendra Mishra, M. A.

(2022). Efﬁcacy of unconventional penetration testing

practices. Intelligent Automation & Soft Computing,

31(1):223–239.

Bianou, S. G. and Batogna, R. G. (2024). Pentest-ai, an

llm-powered multi-agents framework for penetration

testing automation leveraging mitre attack. In 2024

IEEE International Conference on Cyber Security and

Resilience (CSR), pages 763–770.

Caddy, T. (2025). Penetration testing. In Jajodia, S., Sama-

rati, P., and Yung, M., editors, Encyclopedia of Cryp-

tography, Security and Privacy, pages 1786–1787,

Cham. Springer Nature Switzerland.

Chadi, M.-A. and Mousannif, H. (2023). Understanding

reinforcement learning algorithms: The progress from

basic q-learning to proximal policy optimization.

Cheng, Y.-Y., Fang, Q., Liu, L., and Fu, X.-M. (2025).

Developable approximation via isomap on gauss im-

age. IEEE Transactions on Visualization and Com-

puter Graphics, pages 1–11.

Cody, T., Rahman, A., Redino, C., Huang, L., Clark, R.,

Kakkar, A., Kushwaha, D., Park, P., Beling, P., and

Bowen, E. (2022). Discovering exﬁltration paths us-

ing reinforcement learning with attack graphs. In 2022

IEEE Conference on Dependable and Secure Comput-

ing (DSC), pages 1–8. IEEE.

Dana Mazraeh, H. and Parand, K. (2025). An innova-

tive combination of deep q-networks and context-free

grammars for symbolic solutions to differential equa-

tions. Engineering Applications of Artiﬁcial Intelli-

gence, 142:109733.

Deng, G., Liu, Y., Mayoral-Vilches, V., Liu, P., Li, Y.,

Xu, Y., Zhang, T., Liu, Y., Pinzger, M., and Rass, S.

(2024). PentestGPT: Evaluating and harnessing large

language models for automated penetration testing. In

33rd USENIX Security Symposium (USENIX Security

24), pages 847–864, Philadelphia, PA. USENIX As-

sociation.

Erd

odi, L. and Zennaro, F. M. (2022). Hierarchical re-

inforcement learning for efﬁcient and effective auto-

mated penetration testing of large networks. Journal

of Intelligent Information Systems, 59(3):375–393.

Fadhli, M. (2024). Comprehensive analysis of penetration

testing frameworks and tools: Trends, challenges, and

opportunities : Analisis komprehensif terhadap frame-

work dan alat penetration testing: Tren, tantangan,

dan peluang. Indonesian Journal of Electrical En-

gineering and Renewable Energy (IJEERE), 4(1):15–

22.

Guo, C., Zhang, L., Thompson, R. G., Foliente, G., and

and, X. P. (2025). An intelligent open trading system

for on-demand delivery facilitated by deep q network

based reinforcement learning. International Journal

of Production Research, 63(3):904–926.

Hayat, T. and Gatlin, K. (2025). Ai-powered ethical hack-

ing: Rethinking cyber security penetration testing.

Preprint on ResearchGate.

Hoang, L. V., Nhu, N. X., Nghia, T. T., Quyen, N. H.,

Pham, V.-H., and Duy, P. T. (2022). Leveraging

deep reinforcement learning for automating penetra-

tion testing in reconnaissance and exploitation phase.

In 2022 RIVF International Conference on Comput-

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

384

ing and Communication Technologies (RIVF), pages

41–46.

Jeff, V. and Kala, K. (2024). Penetration testing:

An overview of its tools and processes. Interna-

tional Journal of Research Publication and Reviews,

5(3):4346–4353.

Kong, H., Hu, D., Ge, J., Li, L., Li, T., and Wu, B. (2025).

Vulnbot: Autonomous penetration testing for a multi-

agent collaborative framework.

Koroniotis, N., Moustafa, N., Turnbull, B., Schiliro, F.,

Gauravaram, P., and Janicke, H. (2021). A deep

learning-based penetration testing framework for vul-

nerability identiﬁcation in internet of things environ-

ments. In 2021 IEEE 20th International Conference

on Trust, Security and Privacy in Computing and

Communications (TrustCom), pages 887–894.

Li, Q., Wang, R., Li, D., Shi, F., Zhang, M., Chattopad-

hyay, A., Shen, Y., and Li, Y. (2024a). Dynpen: Auto-

mated penetration testing in dynamic network scenar-

ios using deep reinforcement learning. IEEE Transac-

tions on Information Forensics and Security, 19:8966–

8981.

Li, S., Huang, R., Han, W., Wu, X., Li, S., and Tian, Z.

(2025a). Autonomous discovery of cyber attack paths

with complex causal relationships among optional ac-

tions. IEEE Transactions on Intelligent Transporta-

tion Systems, pages 1–15.

Li, S. E. (2023). Reinforcement Learning for Sequential

Decision and Optimal Control. Springer Singapore.

Li, Y., Dai, H., and Yan, J. (2024b). Knowledge-informed

auto-penetration testing based on reinforcement learn-

ing with reward machine. In 2024 International Joint

Conference on Neural Networks (IJCNN), pages 1–9.

Li, Z., Zhang, Q., and Yang, G. (2025b). Eppta: Efﬁcient

partially observable reinforcement learning agent for

penetration testing applications. Engineering Reports,

7(1):e12818.

Luo, F.-M., Tu, Z., Huang, Z., and Yu, Y. (2024). Efﬁcient

recurrent off-policy rl requires a context-encoder-

speciﬁc learning rate. In Globerson, A., Mackey, L.,

Belgrave, D., Fan, A., Paquet, U., Tomczak, J., and

Zhang, C., editors, Advances in Neural Information

Processing Systems, volume 37, pages 48484–48518.

Curran Associates, Inc.

Malkapurapu, S., Abbas, M. A. M., and Das, P. (2023). Ex-

ploring the capabilities of the metasploit framework

for effective penetration testing. In Data Science and

Network Engineering, volume 655 of Lecture Notes in

Networks and Systems, pages 457–471. Springer Na-

ture Singapore.

Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,

Antonoglou, I., Wierstra, D., and Riedmiller, M.

(2013). Playing Atari with deep reinforcement learn-

ing. arXiv preprint arXiv:1312.5602.

Nakatani, S. (2025). Rapidpen: Fully automated ip-to-shell

penetration testing with llm-based agents.

Pham, V.-H., Hoang, H. D., Trung, P. T., Quoc, V. D., To,

T.-N., and Duy, P. T. (2024). Raiju: Reinforcement

learning-guided post-exploitation for automating se-

curity assessment of network systems. Computer Net-

works, 253:110706.

Raj, S. and Walia, N. K. (2020). A study on metasploit

framework: A pen-testing tool. In 2020 International

Conference on Computational Performance Evalua-

tion (ComPE), pages 296–302.

Sedgwick, P. (2012). Pearson’s correlation coefﬁcient. Bmj,

345.

Skandylas, C. and Asplund, M. (2025). Automated penetra-

tion testing: Formalization and realization. Computers

& Security, 155:104454.

Sundararajan, S. (2025). Multivariate Analysis and Ma-

chine Learning Techniques: Feature Analysis in Data

Science Using Python. Transactions on Computer

Systems and Networks. Springer Singapore, 1 edition.

Sutton, R. S. and Barto, A. G. (2018). Reinforcement Learn-

ing: An Introduction. MIT Press.

Teichmann, F. M. and Boticiu, S. R. (2023). An overview

of the beneﬁts, challenges, and legal aspects of pene-

tration testing and red teaming. International Cyber-

security Law Review, 4(4):387–397.

Wang, P., Liu, J., Zhong, X., Yang, G., Zhou, S., and Zhang,

Y. (2022). Dusc-dqn:an improved deep q-network for

intelligent penetration testing path design. In 2022 7th

International Conference on Computer and Commu-

nication Systems (ICCCS), pages 476–480.

Wieser, H., Sch

afer, T., and Krauß, C. (2024). Penetra-

tion testing of in-vehicle infotainment systems in con-

nected vehicles. In 2024 IEEE Vehicular Networking

Conference (VNC), pages 156–163.

Xu, C., Du, J., Lai, B., Wang, H., Zheng, H., Dai, T., Liang,

Z., and and, Y. Y. (2025). Design and implementation

of an intelligent penetration security assessment sys-

tem based on graph neural network (gnn) technology.

Journal of Cyber Security Technology, 0(0):1–13.

Yang, Y., Chen, L., Liu, S., Wang, L., Fu, H., Liu, X., and

Chen, Z. (2024). Behaviour-diverse automatic pene-

tration testing: a coverage-based deep reinforcement

learning approach. Frontiers of Computer Science,

19(3):193309.

Yao, Q., Wang, Y., Xiong, X., and Li, Y. (2023). Intelligent

penetration testing in dynamic defense environment.

In Proceedings of the 2022 International Conference

on Cyber Security, CSW ’22, page 10–15, New York,

NY, USA. Association for Computing Machinery.

Zennaro, F. M. and Erd

odi, L. (2023). Modelling penetra-

tion testing with reinforcement learning using capture-

the-ﬂag challenges: trade-offs between model-free

learning and a priori knowledge. IET Information Se-

curity, 17(3):441–457.

Zhou, S., Liu, J., Lu, Y., Yang, J., Zhang, Y., Lin, B., Zhong,

X., and Hu, S. (2025). Script: A scalable contin-

ual reinforcement learning framework for autonomous

penetration testing. Expert Systems with Applications,

285:127827.

Multi-Objective Policy Optimization for Effective and Cost-Conscious Penetration Testing

385