MultiFlags: A Probabilistic Framework for Article-Based Size Advice in

Fashion E-Commerce

Matthias Sp

ath

1,∗

, Andrea Nestler

1,∗

, Henry B

oddeker

1,∗

, Leonidas Lefakis

, Yevgeniy Puzikov

Rodrigo Weffer

, Nour Karessli

, Nadja Klein

and Reza Shirvany

Zalando SE, Berlin, Germany

Technische Universit

at Dortmund, Germany

Keywords:

Fashion, Article-Based Size Advice, Recommendation Systems, Size and Fit, Size-Related Returns,

E-Commerce, Probabilistic Framework.

Abstract:

Accurately modeling the size behavior of fashion articles at scale is a critical task for fashion e-commerce.

However, it has proven to be highly challenging due to inconsistent sizing systems across countries, inconsis-

tent garment design processes, and brand-speciﬁc sizing speciﬁcations. Widespread methods in the ﬁeld focus

primarily on giving customers rudimentary size recommendations (e.g., we recommend you size S) based

on the customers’ purchase behavior and/or their size and ﬁt preferences. These approaches fail to take into

account the size and ﬁt behavior of the article, for example their design cut, shape, material, etc. (or at best

treat it with simplistic ad hoc assumptions), and in turn, not effectively reducing the high volume of online

article returns due to size and ﬁt. In this work, we propose a theoretically-motivated probabilistic framework,

MultiFlags, which can signiﬁcantly reduce size-related returns in fashion e-commerce thanks to modeling

multiple aspects of article’s size and ﬁt behavior. We also highlight how this framework enables a principled

approach to article-based size advice, while leveraging data from multiple modalities. The results validate

the competitiveness of the proposed framework in the state-of-the-art in several size advice scenarios that are

critical for fashion e-commerce. The framework is deployed in production in a large e-commerce site, serving

millions of customers and driving signiﬁcant results.

1 INTRODUCTION

The rise and steady growth of fashion e-commerce

has introduced customers to a novel shopping expe-

rience. On the one hand, customers are enabled to

browse and search clothing items from a multitude of

brands and different trends simply from their phones.

On the other hand, they can no longer physically inter-

act with the clothing items. In order to aid customers

in navigating this new shopping environment, a host

of fashion-focused algorithmic products have been

developed in recent years (see Jaradat et al. (Jaradat

et al., 2022) and references therein).

One of the main challenges in choosing the right

clothing item to wear is its size, which has been

shown to be a major factor in returning clothes and

shoes (C, 2014). In the brick-and-mortar experience,

a customer typically has access to a ﬁtting room to try

∗

These authors contributed equally to this research.

clothes and shoes on before purchasing them, and to

shop attendants or family and friends who can give

feedback on the right size and ﬁt of the item. In

online fashion, purchasing clothes and shoes in the

wrong size not only will result in that article be-

ing returned, it most importantly will cause frustra-

tion to the customer, increase CO2 emissions, reduce

proﬁtability for the online shop, and increase logisti-

cal costs and delivery trucks on the roads. Consid-

ering the CO2 emissions, for example, a recent e-

commerce carbon report indicates that reducing one

return could cut a whooping ∼ 0.99 kg of CO2 equiv-

alent emissions (Aso, 2020). Considering that mil-

lions of clothes and shoes are returned each year in

online fashion due to size and ﬁt issues, the CO2

impact of reducing the size related returns is signif-

icant. In fact, these effects are pivotal today and in

coming years where returns are seeing a steady in-

crease (Choi, 2016). We consider the size-related re-

turns, in theory, to be an unnecessary hassle, espe-

Späth, M., Nestler, A., Böddeker, H., Lefakis, L., Puzikov, Y., Weffer, R., Karessli, N., Klein, N. and Shirvany, R.

MultiFlags: A Probabilistic Framework for Article-Based Size Advice in Fashion E-Commerce.

DOI: 10.5220/0013709900004000

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2025) - Volume 1: KDIR, pages 313-322

313

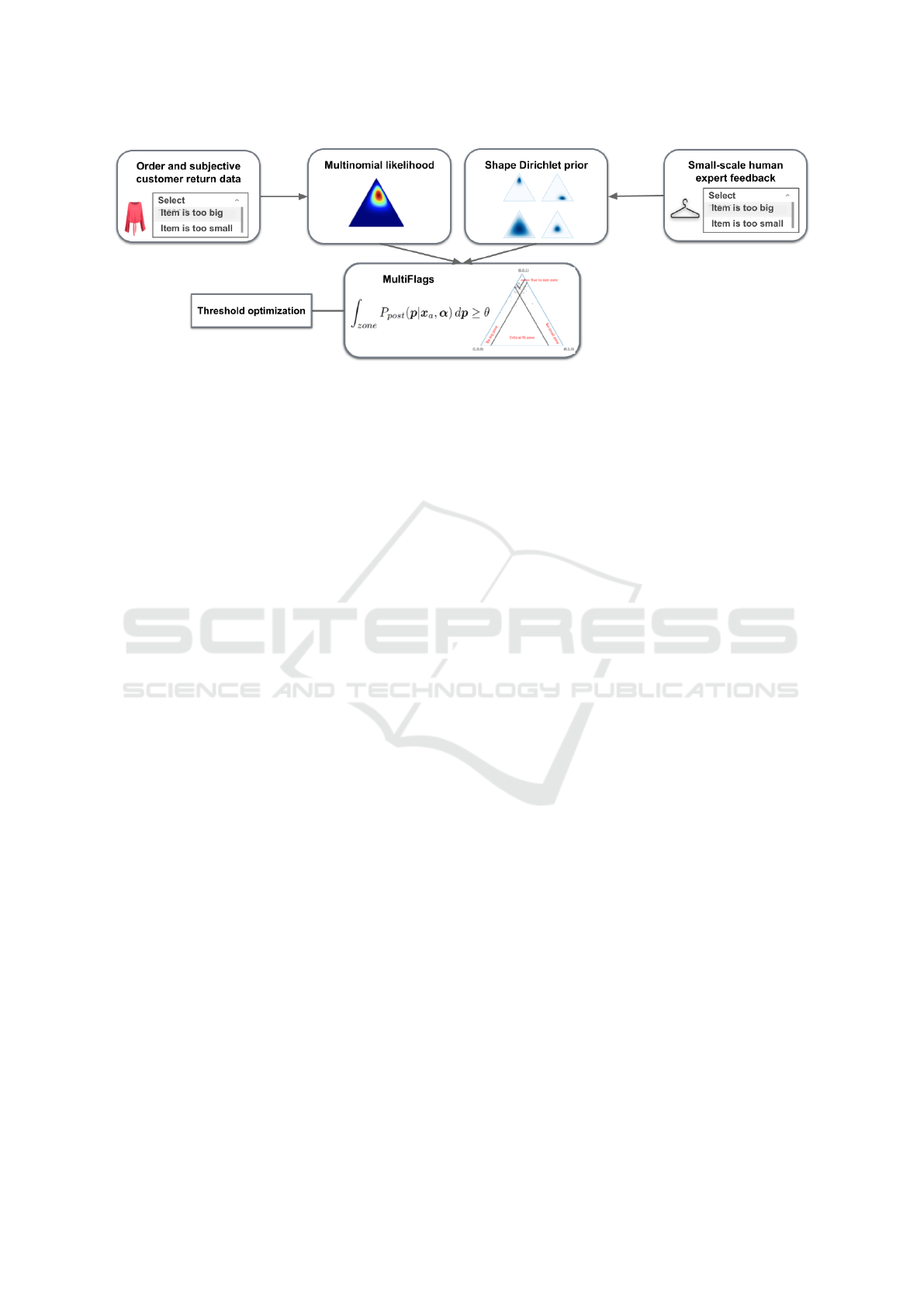
Figure 1: High level overview of the new article-based size advice framework MultiFlags.

cially considering that the customers are often satis-

ﬁed with all other attributes of their order (e.g., item’s

color, price, material, delivery, etc.) and only due to

the fact that the ordered size of the clothes or shoes

does not ﬁt them, they have no choice but to re-

turn the item. This is an unsolved problem today in

fashion e-commerce due to: the lack of standardized

sizing systems (e.g., discrepancies in a medium size

across different brands), incompatible sizing varia-

tions (e.g., the difference between EU and UK sizes),

the prevalence of vanity sizing (intentional mislabel-

ing to make customers feel smaller, e.g., make cus-

tomers believe they are a size 6 when in reality they

are a size 8), inconsistent size charts (e.g., conﬂict-

ing measurements for the same size across brands),

limited size range (e.g., excluding plus-size or petite

options), variations in body shapes (e.g., inadequate

consideration of different proportions), inconsistent

ﬁt (e.g., the same size ﬁtting differently in different

styles), and insufﬁcient size information in product

descriptions.

Addressing these challenges requires the imple-

mentation of creative solutions to enhance the siz-

ing experience and improve overall customer satis-

faction in the realm of online fashion. Prior work on

developing algorithmic products to assist customers

often focuses on providing personalized size recom-

mendations, relying rather on customers’ personal

data (Lefakis et al., 2021; Yuan et al., 2021), or their

prior purchases (Hajjar et al., 2020; Sheikh et al.,

2019; Lasserre et al., 2020), and often without con-

sidering the articles’ sizing issues (Guigour

es et al.,

2018; Sembium et al., 2017; Sembium et al., 2018;

Dogani et al., 2019; Abdulla and Borar, 2017; Ab-

dulla et al., 2019). This approach to size advice ex-

cludes customers without a purchase history or cus-

tomers who buy for others within a single account.

A notable exception is SizeFlags (Nestler et al.,

2021) where articles are “ﬂagged” as too-big and too-

small based on historic customer returns for this arti-

cle, expert assessments, and the ﬁt issue probability

assessment of an image based convolutional neural

network, SizeNet (Karessli et al., 2019). Such advice

allows customers to decide whether to go “one size

down” or “one size up” compared to the usual size

they would be purchasing. In this work, we present

a novel joint probabilistic framework, called Multi-

Flags, which similarly provides article-based size ad-

vice. MultiFlags leverages a multinomial-Dirchlet

model to build a recommender system that eliminates

the need for separate treatment of the article size is-

sues while relaxing the limiting assumptions made in

previous works. Figure 1 shows a high level overview

of the framework and is detailed in Section 3.

2 RELATED WORK

2.1 Size Recommendations

Previous work on the issue is mostly focused on sug-

gesting a speciﬁc size of an article for the customer’s

preferences, i.e. size recommendation. Abdulla and

Borar (Abdulla and Borar, 2017) formulate the rec-

ommendation task as binary classiﬁcation, circum-

venting data sparsity by learning article latent repre-

sentations from categorical features including brand,

size, occasion, etc. Customer representations are built

by aggregating article vectors from their order his-

tory. Sembium et al. (Sembium et al., 2017) pro-

pose a latent factor model for customers and products,

corresponding to their physical true size. Sheikh et

al. (Sheikh et al., 2019) exploit the correlations be-

tween different categories in a scalable deep learn-

ing system that can ingest broader article and cus-

tomer features, while Dogani et al. (Dogani et al.,

2019) leverage transfer learning from brand to prod-

uct level. Hajjar et al. (Hajjar et al., 2020) further

extend this ability and explicitly consider the sequen-

tial and temporal nature of the problem by applying

KDIR 2025 - 17th International Conference on Knowledge Discovery and Information Retrieval

314

an attention-based model. Inspired by advancements

in the computer vision ﬁeld, Lasserre et al. (Lasserre

et al., 2020) utilize a meta-learning approach that ef-

ﬁciently learns new customer sizes with little order

data. Other approaches further deal with extreme

cases of cold-start customers with little or no purchase

history using physical body-related features (Lefakis

et al., 2021; Yuan et al., 2021). From another angle

on the problem, computer vision techniques and arti-

cle measurement data are used to learn article ﬁt and

body shape compatibility (Hidayati et al., 2018; Hsiao

and Grauman, 2020). With the aim of simulating the

in-store customer ﬁtting experience, recent efforts de-

veloped virtual try-on solutions to visualize garments

on a target body. While 3D methods (Bhatnagar et al.,

2019; Patel et al., 2020) accurately render garments

on virtual avatars, they often require expensive real

body scans. Overcoming this requirement, generative

adversarial models are used to warp clothing items on

a target person in 2D images (Han et al., 2018; Dong

et al., 2019; Issenhuth et al., 2019; Pecenakova et al.,

2022; Pang et al., 2024), however, the physical feasi-

bility of such methods in real-life applications is not

guaranteed. There have been earlier Bayesian models

in the size and ﬁt space focused on personal size rec-

ommendation. Sembium et al. (Sembium et al., 2018)

used Bayesian inference to ﬁnd the best article size

for a given customer, by modelling the joint posterior

of a customer’s true size and article sizes by using

the purchase histories. Guigour

es et al. (Guigour

et al., 2018) use a similar strategy by modelling the

joint probability distribution of return and article size

in a hierarchical model. Size recommendation poses

several challenges. Some approaches require sensi-

tive customer information, such as height and weight,

or scans of the customer’s physical body to be able

to generate recommendations or simulate the ﬁtting

experience (Yuan et al., 2021; Lefakis et al., 2021;

Bhatnagar et al., 2019; Patel et al., 2020).

2.2 Article-Based Size Advice

The status quo on article-based size advice is that

the existing state-of-the-art is notably and sadly very

sparse, where only a handful of publications focus on

the critical article-level size advice capability uncon-

ditioned on a target customer’s orders or body proper-

ties (Nestler et al., 2021; Karessli et al., 2019; Baier,

2019; Misra et al., 2018), which is key in alleviating

the issues with data sparsity, sizing systems and the

customer-speciﬁc cold start problem. This has been

approached by analyzing customer reviews (Baier,

2019; Misra et al., 2018), and by evaluating cold-

start articles with a computer vision-based teacher-

student framework (Karessli et al., 2019). Building

on that work, (Nestler et al., 2021) propose Size-

Flags, a method capable of incorporating different

priors and evaluated on a large-scale A/B test sce-

nario showing SizeFlags reduce the size-related re-

turn rate across different fashion categories of tex-

tile and shoes. Due to space limitations, we do not

provide a detailed description of SizeFlags (Nestler

et al., 2021) and refer the reader to the original paper.

In short, SizeFlags (Nestler et al., 2021) is reducing

size-related returns by providing article-based size ad-

vise with the recommendation of selecting a larger/

smaller size when the article runs small/ large. It

models the probability of an article being too-small or

too-big separately, using two separate Beta-Binomial

distributions. This implies the assumption of inde-

pendence between the probability of an article be-

ing too-big or too-small, which is unlikely to hold in

practice and constitutes one of the main limitations of

SizeFlags (Nestler et al., 2021) . Furthermore, Size-

Flags (Nestler et al., 2021) uses point estimates for

predictive posterior calculation and does not estimate

the conﬁdence of the model in its predictions.

2.3 Baselines for Size-Related Return

Reduction

To our knowledge, SizeFlags (Nestler et al., 2021)

is the only state-of-the-art approach that has demon-

strated a positive impact on reducing size-related re-

turns—the key objective of this line of work in fash-

ion e-commerce—and will therefore serve as our

baseline for article-based size advice. Other article-

based size advice approaches have neither claimed

nor have been evaluated by their authors in terms

of reducing size-related returns, making them not di-

rectly applicable as baselines for the MultiFlags ap-

proach. Previous approaches using personalized rec-

ommenders as described in Section 2.1 are often eval-

uated based on acceptance rate (usually deﬁned as the

share of sales where a customer follows the recom-

mendation and keeps it). This in turn is not possible

for article-based size advice like the presented Mul-

tiFlags, because the true size of the customer is un-

known, so it remains unclear whether the customer

followed the advice or not.

To provide a broader context beyond article-

based advice, we also consider a personalized size-

recommendation paradigm outlined in Section 2.2 for

comparison, which utilizes the meta-learning method-

ology proposed by Lasserre et al. (Lasserre et al.,

2020). In this approach, the individual customer gets

a direct size recommendation (e.g., ”We recommend

size S”) that is dependent on both the customer and

MultiFlags: A Probabilistic Framework for Article-Based Size Advice in Fashion E-Commerce

315

the article. This allows us to frame the new algo-

rithm described in this paper against both article-

based and personalized recommendation approaches

(Section 4.3).

The scarcity of prior research on data science so-

lutions for reducing size-related returns underscores

the urgent need for advancements in this area. This

paper addresses this gap by presenting a novel, com-

prehensive solution that not only overcomes existing

limitations but also makes a signiﬁcant contribution

to the ﬁeld through our probabilistic framework and

its demonstrably impactful results.

3 MULTIFLAGS: A MULTI-CLASS

SIZE ADVICE ALGORITHM

The aim of the proposed MultiFlags approach is to

lower size-related returns in fashion e-commerce by

providing article-based size advice to the customer. It

leverages the article’s sales and return reason informa-

tion, such as ”too small” and ”too big”, which is typi-

cally collected in fashion e-commerce. The output is a

ﬂag that provides the customer with additional sizing

information on the article, such as ”This article runs

large, we recommend going one size down”. Optional

additional input for the model is used as prior infor-

mation and can be based on expert knowledge on the

article or visual sizing cues based on models such as

SizeNet (Karessli et al., 2019). The prior information

can help raising ﬂags faster and earlier in the product

life cycle, so that customers can beneﬁt early on. The

approach is illustrated in Figure 1. MultiFlags ad-

dresses the limitations described in Section 2.2, lead-

ing to novelty in ﬁve points: 1) Instead of using sepa-

rate models, the estimation of all ﬂags is uniﬁed into

a single model, acknowledging the dependence be-

tween an article being too-big (tb; an article ﬁts bigger

than expected) or too-small (ts; an article ﬁts smaller

than expected). 2) The approach naturally gives rise

to two new ﬂag types, namely true-to-size (tts; an arti-

cle has good ﬁt in their indicated size.) and critical-ﬁt

(cf; an article is ts and tb at the same time) when the

probability vertex is split into different zones. 3) The

framework provides a principled approach to include

prior information. 4) The model has a ﬂagging logic

based on conﬁdence and 5) the model is extendable to

prior mixtures and hyperpriors.

3.1 A Uniﬁed Probabilistic Framework

The framework leverages a conjugate Bayesian

Model with a Dirichlet prior p|α ∼ Dir(α).

The return realizations x = (x

, x

tts

) (with x

number return reasons k ∈ {tb,ts}; x

tts

= number

sales −x

− x

) given p = (p

, p

tts

) (class prob-

ability vector with

∑

k∈Ω

= 1) are modelled using

a multinomial likelihood x|p ∼ Mult(p). Thus, the

probability density functions of the likelihood P(x|p)

and prior P

prior

(p|α) read as

P(x|p) =

tts

, (1)

prior

(p|α) =

B(α)

∏

i∈Ω

−1

, (2)

where B(α) is the multivariate Beta function, Ω =

{ts, tb, tts} is the set of indices. The posterior proba-

bility density function, by conjugacy, is deﬁned as

post

(p|x, α) =

P(x|p)P

prior

(p|α)

∥ · ∥

(3)

= P

prior

(p|x + α) (4)

B(x + α)

∏

i∈Ω

+α

−1

. (5)

Note that, while SizeFlags (Nestler et al., 2021)

computes a score value for each ﬂag directly and then

compares to a threshold for raising a ﬂag, MultiFlags

estimates the posterior probability, determining ﬂags

at a later step.

3.2 Estimation of the Posterior

Probability

We deﬁne the observed size-related return rate srr

(a)

of a given article a ∈ C that belongs to a fashion cate-

gory C ⊂ C

all

(e.g. jeans, shirts, shoes) as

srr

(a) =

, k ∈ {tb,ts}. (6)

with n the number of sales. The true size-related re-

turn rate srr

⋆

(a) of an article is unknown, but we

know that the higher the number of article orders n,

the more conﬁdent we are that srr

(a) is close to

srr

⋆

(a):

srr

⋆

(a) = lim

n→∞

srr

(a). (7)

Each fashion category C poses different size and

ﬁt challenges. Therefore, we evaluate each article

against its category.

The mean and the standard deviation

C ,k

:= mean({srr

(a)}

a∈C

), (8)

C ,k

:= std({srr

(a)}

a∈C

), (9)

for k ∈ {ts, tb} differ for each category. For example,

C ,k

of the category C = C

t−shirt

is in general much

smaller than µ

C ,k

with C = C

dresses

as t-shirts are less

KDIR 2025 - 17th International Conference on Knowledge Discovery and Information Retrieval

316

complex in terms of ﬁt than dresses, which results in

a lower size-related return rate.

Based on the category averages µ

C ,k

and standard

deviations σ

C ,k

, we deﬁne the zones that are interest-

ing for the different ﬂag types. The tb/ts zone is de-

ﬁned by the srr

⋆

(a) of an article a being more than

one standard deviation σ

C ,k

above the category mean

C ,k

for k ∈ {ts, tb} (red and green zone in Figure 2).

The cf zone is deﬁned by having both the srr

⋆

(a) and

srr

⋆

(a) above the category speciﬁc mean (blue zone

in Figure 2). The tts zone is deﬁned exactly opposite

by having both the srr

⋆

(a) and srr

⋆

(a) below the cat-

egory speciﬁc mean (yellow zone in Figure 2). The

four zones are the most obvious approach to zoning

the probability vertex and hence naturally give rise to

the two new ﬂag types. The four zones result in the

following logic for k ∈ {tb,ts}:

a is k ⇔ srr

⋆

(a) ≥ µ

C ,ts

+ σ

C ,k

a is cf ⇔ srr

⋆

(a) ≥ µ

C ,ts

srr

⋆

(a) ≥ µ

C ,tb

a is tts ⇔ srr

⋆

(a) ≤ µ

C ,ts

srr

⋆

(a) ≤ µ

C ,tb











(10)

Example 1. Let us illustrate the zoning rules (10)

with one example for a real world category C

, which

has an average size-related return rate µ

C ,k

= 10% for

k ∈ {tb,ts}, meaning 10% of sold items are returned

as too-big or too-small each. The standard deviations

are σ

C ,tb

= 0.05 and σ

C ,ts

= 0.06. C

contains more

than 100000 different articles.

In practice srr

⋆

for k ∈ {tb, ts} is not known, but

let’s suppose we pick one article a ∈ C

with a high

srr

⋆

(a) = 33% and low srr

⋆

(a) = 8%. The article a

has an exceeding amount of too-small returns in the

category C

with srr

⋆

(a) = 33% ≥ µ

C ,ts

+ σ

C ,ts

10% + 6% = 16%. At the same time this article

shows a usual too-big returns since srr

⋆

(a) = 8% ≤

C ,tb

+ σ

C ,tb

= 10% + 5% = 15%. This article would

therefore be a suitable too-small candidate. But we do

not know the true return rate. Therefore we integrate

over the probability distribution in the zone deﬁned by

C,k

and σ

C,k

for k ∈ {tb,ts} to get a conﬁdence mea-

surement. Based on this, we decide whether the item

is actually marked as too-small. This number helps

us to make a conﬁdent decision as to whether an item

will be ﬁnally be labeled as too-small. This approach

is outlined in the next paragraph.

With deﬁnition (10), for a given article a ∈ C with

return realization x and ﬁxed parameter α, the proba-

bilities are deﬁned as

= P (p

≥ µ

C ,ts

+ σ

C ,ts

= l

(1)

), (11)

= P (p

≥ µ

C ,tb

+ σ

C ,tb

= l

(2)

c f

= P (p

≥ µ

C ,ts

= l

(1)

c f

, p

≥ µ

C ,tb

= l

(2)

c f

tts

= P (p

≤ µ

C ,ts

= u

(1)

tts

, p

≤ µ

C ,tb

= u

(2)

tts

With the zone boundaries u

(i)

and l

(i)

from (11) and

additionally u

(i)

= 1 for k ̸= tts and l

(2)

= l

(1)

= l

(i)

tts

0 we get ∀k ∈ Ω

and i ∈ {1, 2}

(1)

(2)

post

(p|x, α) d p (12)

For each k ∈ Ω

(=Ω∪{c f }) this results in a posterior

probability P

∈ [0, 1], which can be interpreted as the

probability that srr

⋆

(a) of an article a is within the

speciﬁed zone. For example, P

= 97% implies that,

based on the current return realizations of the article,

it’s 97% likely that the srr

⋆

(a) is within the too-small

zone. With this approach the posterior probability can

be interpreted as a conﬁdence measure in the ﬂag.

Figure 2: (Bottom Left) The different zones are deﬁned

based on their respective µ

C,k

and σ

C,k

(Top Right) Probability density distribution for a too-small

ﬂagged article a ∈ C

In Figure 2 we illustrate the different zones on the

probability vertex and re-visit the Example 1 with cat-

egory C = C

and article a ∈ C

with srr

⋆

(a) = 33%

and srr

⋆

(a) = 8%. Assuming return realizations x +

α = (8.4, 2.9, 28.5) (e.g. based on return observations

x = (6, 0, 6) and prior α = (2.4, 2.9, 22.5)), the poste-

rior zone value integrates to P

= 97%, P

= 0.01%,

c f

= 1% and P

tts

= 1%. Here we used the prior con-

centration parameter α = α

⋆

which will be described

in the next Section 3.3.

The approach MultiFlags raises a ﬂag when P

≥

θ ∈ [0, 1]. In Section 4.1 we will show how an optimal

threshold θ

⋆

= θ for raising a ﬂag can be determined.

3.2.1 Computational Complexity and Efﬁcient

Integration Methods

The biggest bottleneck is the numerical integration to

get the posterior probability P

(x(a

), α

) in equation

MultiFlags: A Probabilistic Framework for Article-Based Size Advice in Fashion E-Commerce

317

(12). To increase efﬁciency, the double integration of

the two free parameters is performed only in zones

with overlap, reducing the runtime by a factor of 10.

Zones that depend on one parameter are integrated us-

ing the marginal distribution of the Dirichlet distribu-

tion. To derive the marginal distribution of a Dirich-

let distribution with three dimensions, we use the

deﬁnition of conditional probability after integrating

the third dimension, f (p

, p

) = f (p

) × f (p

Rewriting the equation shows that the marginal is a

Beta distribution,

1−p

∼ Beta(α

, α

), which

has a closed-form cumulative density function, so the

numerical integration is not necessary. When the too-

small and too-big zones overlap, we calculate the in-

dividual zones using the marginal Beta distributions,

and handle the overlap separately. To reduce the time,

the full computation is parallelized on a distributed

computing system, i.e. Spark, on a cluster with 8

workers and 8 cores each, taking 3 hours for several

million articles.

3.3 Estimation of the Parameter α

3.3.1 Estimation Based on Category Sales and

Return Data

All articles within a category C have similar size-

related return properties, which can be incorporated

as a prior in the Bayesian approach, as µ

C ,k

and σ

C ,k

for k ∈ {tb,ts} are known at the time of calculation.

To estimate the concentration parameter α for

the prior, we use the Dirichlet-Multinomial distribu-

tion. It is a closed-form compound distribution of

the Dirichlet and multinomial distribution, where the

variable p of the Dirichlet distribution is integrated

out. With A =

∑

k∈Ω

and the Gamma function Γ()

the likelihood function reads

f (x|α, n) =

P(x|p)P

prior

(p|α)d p

Γ(A)Γ(n +1)

Γ(n + A)

∏

k∈Ω

Γ(x

+ α

)

Γ(α

)Γ(x

+ 1)

(13)

The parameter α = α

⋆

for each category C can be

estimated using the maximum likelihood method

⋆

= argmax

∏

a∈C

f (x|α, n). (14)

Applying method (14) for the category C

in Ex-

ample 1, we obtain the optimal solution α

⋆

(2.4, 2.9, 22.5). This problem is solved by a combined

Gradient-Newton method.

3.3.2 Estimation Based on Prior Information

We aim to have articles ﬂagged as early as possible

to ensure both customers and the business beneﬁt re-

spectively from the supportive advice and the lower

return rates thanks to those early ﬂags. Using the prior

information as outlined here helps to tackle the cold-

start problem for articles where not enough return in-

formation is available and aims at raising ﬂags with

less processed returns available. For MultiFlags we

introduce prior information from human expert feed-

back from fashion models. The feedback is based on

fashion models who try on articles before they are ac-

tivated on the platform to provide ﬁrst hand feedback

on a subset of articles. They provide size and ﬁt feed-

back similar to the customer return information, indi-

cating whether an article runs ”too small”, ”too big”

or ”true to size”. The averaged feedback of multiple

human models for the same article is used to estimate

the article-speciﬁc prior parameters.

Let C

exp

(k) ⊂ C be the subset of all articles a

for which the feedback of the fashion models is ex-

actly k (i.e. f eedback(a) ≡ k for k ∈ {tb, ts,tts}).

Then, similar to equation (14), the Expert Prior

⋆

exp

(k)

= α can be determined via the maximum like-

lihood method. Revisiting Example 1 with category

C = C

and focusing on all articles with human ex-

pert feedback C

exp

(k), the maximum likelihood ap-

proach for articles with too-small human expert feed-

back (k ≡ ts) results in the concentration parameters

= 6.3, α

= 2.2, and α

tts

= 15.0.

4 MULTIFLAGS: DATA AND

RESULTS

MultiFlags is compared to the state-of-the-art bench-

mark for article-based size advise, SizeFlags (Nestler

et al., 2021) . The comparison creates an additional

complexity that goes beyond the complexity of bench-

marking against no size advise at all, as the compari-

son of the two models, gives rise to four distinct cases,

namely when a ﬂag is added by MultiFlags (Added),

dropped by MultiFlags (Dropped) or when both ap-

proaches raise the same ﬂag (Same) or a different ﬂag

(Different) for the same article. A graphical overview

of these four sets can be found in Figure 3. In the

coming sections we will focus on the evaluation of

the Same, Dropped and Added ﬂags as the number of

Different ﬂags is close to zero and negligible in our

experiments.

The following evaluation of the models is sep-

arated into two sections: Section 4.1 addresses the

Same and Dropped ﬂags, by optimizing the θ thresh-

old, which was introduced in Section 3.2, on a train-

ing set and evaluating the results on a holdout set via

Difference-in-Differences approach. Section 4.2 ex-

tends the evaluation of the two models to the Added

KDIR 2025 - 17th International Conference on Knowledge Discovery and Information Retrieval

318

Figure 3: The comparison of the two approaches gives rise

to the Same, Different(Diff ), Dropped and Added ﬂags.

ﬂags via A/B test. Finally, Section 4.3 discusses the

complementary effects between our article-based ap-

proach and personalized size recommendations.

4.1 Threshold Optimization and

Holdout Set Performance

Evaluation

4.1.1 Datasets

The data acquisition is based on the return process

of the e-commerce platform. Customers can return

articles at no charge with or without providing a re-

turn reason from a predeﬁned list of reasons. With

respect to size or ﬁt, customers have the possibility

to state ”The item is too small” or ”The item is too

big” among other non-size-related options (such as

”The item isn’t as described”, ”The item is too ex-

pensive” etc.). The dataset used is a random subset of

anonymized data coming from two years [June 2021

- May 2023] of article purchases and returns of a ma-

jor fashion e-commerce platform for multiple Euro-

pean countries. It contains the sales and return infor-

mation for 3.6 million textile articles. The additional

prior information was available for ∼ 5000 articles for

the human expert feedback. The top ﬁve categories

are dresses, knitwear, jerseys, blouses, trousers and

these together make up 55% of articles in the dataset.

We highlight that this method is applicable for most

fashion e-commerce platforms as it requires a dataset

that contains only the sales as well as ”too small” and

”too big” returns on an article level, which fashion e-

commerce platforms typically collect.

To our knowledge, from publicly available fash-

ion datasets (fas, 2022), only two are relevant for the

size topic in fashion, ‘ModCloth’ and ‘RentTheRun-

Way’ (Misra et al., 2018). These contain fashion

products with ﬁt labels, however, both datasets lack

the sales and return information required to test the

proposed approach and for drawing any conclusion

on reducing size-related returns.

We perform a training-test split and use the ﬁrst

year of data [June 2021 - May 2022] for parameter op-

timization as outlined in Section 4.1.3 and the second

year [June 2022 - May 2023] for the results presented

in Section 4.1.4. MultiFlags is tested experimentally

by running the algorithm on the second year of histor-

ical data (holdout set), where the results of the refer-

ence model SizeFlags (Nestler et al., 2021) are also

known.

4.1.2 Evaluation Method DiD

Given the lack of a ground truth, the causal effect of

showing size advice to customers can only be cap-

tured through the relative reduction of size-related

returns (srr

red

) of the two approaches. The nearest

neighbor Difference-in-Differences (DiD) approach

of Nestler et al. (Nestler et al., 2021) is used as

a quasi-experimental signal of the srr

red

by a ﬂag.

This method, originally presented in Heckmann et

al. (Heckman et al., 2019), compares the srr

red

for

articles which received a ﬂag against similar articles

which did not receive a ﬂag over a time frame of 6

weeks before and after raising the ﬂag. We aggre-

gate the srr

red

to calculate the number of saved re-

turns per article. It is important to note, that srr

red

cannot be calculated with DiD for all ﬂags M (θ) that

are raised by MultiFlags with ﬁxed threshold θ, as

M (θ) includes new ﬂags for which no historical re-

sults exist. It is, however, possible to calculate the

srr

red

for all SizeFlags (Nestler et al., 2021) S that

have already been shown to the customers. It follows

that srr

red

can be calculated for the two subsets Same

= S ∩ M (θ) and Dropped = S \ M (θ). The addi-

tional ﬂags for which we cannot calculate the srr

red

via the DiD method are denoted by Added and are

A/B tested in Section 4.2. The sets are illustrated in

Figure 3.

4.1.3 Threshold Optimization on Training Set

The practical approach outlined here focuses on deter-

mining θ for comparing the proposed approach with

SizeFlags (Nestler et al., 2021) . We use the data over

a period of one year [June 2021 - May 2022] and ﬁnd

the best value which satisﬁes two constraints:

(i) θ ∈ [0.5, 1], which corresponds to the probabil-

ity that the true size-related return rate srr

⋆

(a) is

within the respective zone is above the threshold

of 0.5, i.e. P

≥ 0.5, k ∈ {ts,tb, c f , tts}, with P

from equation (11).

(ii) Find θ as such that the overall srr rate

srr

red

(M (θ)) is reduced as much as possible.

Choosing a high value of θ implies that MultiFlags

M (θ) raises ﬂags only when it is very conﬁdent about

the prediction. With θ

⋆

= 1, M (θ) raises only ≈ 5K

tb and ts ﬂags, which is ≈ 30 times less than the num-

ber of ﬂags raised by SizeFlags (Nestler et al., 2021)

MultiFlags: A Probabilistic Framework for Article-Based Size Advice in Fashion E-Commerce

319

S in the same timeframe. Therefore, to ﬁnd the opti-

mal value of θ, the effectiveness per single ﬂag based

on (i) needs to be balanced vs. the total number of

ﬂags.

Figure 4: The highest srr reduction is achieved for θ → 1.

Figure 4 shows that for θ ∈ [0.5, 1] the srr reduc-

tion varies only slightly, providing a relatively free

choice of θ value in that range. Given the free choice

of θ in the speciﬁed range and in order to be able to

compare S vs. M (θ) on equal footing, we select θ as

such that

1. we achieve a balance between the groups Dropped

and Added (|M (θ)| ≈ |S|) and

2. the ﬂag recall R(θ) =

|Same(θ)|

|S |

should be as large

as possible.

By using grid search, we found θ

⋆

= 0.695 to be

the optimal value, resulting in |M (θ)| ≈ |S| with

the numbers of Dropped and Added balanced (Fig-

ure 5), and the ﬂag recall R(0.695) = 78.2% sufﬁ-

ciently high.

Figure 5: For θ = 0.695 there are as many ﬂags in Added as

in Dropped.

With the resulting θ

⋆

, we also see a ﬁrst indication

that M (θ

⋆

) performs well on the cold-start problem,

as the necessary number of returns needed to raise a

ﬂag are smaller in the case of S (ˆr

= 161 vs. ˆr

165).

4.1.4 Results on Holdout Set

We evaluate MultiFlags M := M (θ) with ﬁxed θ =

0.695 vs. SizeFlags (Nestler et al., 2021) S on the

holdout set. Despite both sets covering all four sea-

sons by choosing one year for the training and the

holdout set each, both sets are slightly different. The

holdout set contains 2.6 million articles, which is

9.3% more than in the training set and the number of

SizeFlags (Nestler et al., 2021) |S | = 176386 is 5.5%

higher than in the training set. With |M | = 193103,

M contains 9.5% more ﬂags than S . M raises

144378 Same ﬂags and achieves a recall of 81.9%

compared to S , showing that it performs equally well

as on the training set. The number of Dropped is

32008 and Added is 48 725. The same DiD approach

is used to calculate the srr

red

. Similar to the train-

ing set, the size-related return reduction of the group

Same with srr

red

= 3.8% is greater than the reduction

of the group Dropped with srr

red

= 2.8% . Lastly,

M requires ˆr

= 151 returns to raise a ﬂag versus

ˆr

= 166 for S , indicating a more than 10% improve-

ment in terms of speed for M , potentially increasing

the average number of saved returns per item over an

extended period, by offering a ﬂag earlier in the arti-

cle’s life cycle.

4.1.5 New Flags Critical-Fit and True-to-Size

In addition to the results in comparison with the Size-

Flags (Nestler et al., 2021) S baseline, we explore

the results obtained for the new ﬂags offered by Mul-

tiFlags M , critical-ﬁt and true-to-size. M raises

62 408 critical-ﬁt ﬂags on the holdout set. These en-

able new actionable information for customers about

articles with difﬁcult ﬁt and provide new opportuni-

ties for businesses. Note that critical-ﬁt denotes ill ﬁt

of an article, because it does not ﬁt the majority of the

customers, which is a problem that can be addressed

in several ways. Depending on the criticality of the

ﬁt issue, businesses can, for instance, down-sort the

article in it’s catalog views, exclude the articles from

discovery, communicate the article to brands for their

improvement, or ultimately remove the article from

the assortment. M raised 159 411 true-to-size ﬂags,

which enable high conﬁdence for customers when se-

lecting a size; contrary to the articles with a critical-ﬁt

ﬂag, businesses are able to up-sort such articles in the

article ranking shown to the customers.

4.2 A/B Test Evaluation Against

Article-Based Size Advice

The ﬂags added by the M approach have been A/B

tested against S . As those ﬂags are added, it’s an

A/B test where a ﬂag from M shown to the treat-

ment group is compared to the same article without

a ﬂag from S shown to the control group. The A/B

test was performed November 2023 to January 2024

KDIR 2025 - 17th International Conference on Knowledge Discovery and Information Retrieval

320

in the whole textile category with more than 132 000

customers and 150 000 orders per group from 12 dif-

ferent countries. The A/B test demonstrated that the

size-related return rate was signiﬁcantly reduced by

M (−4.5% relative change, p-value < 0.001). The

biggest impact was observed in the category of full

body garments (e.g. dresses and tracksuits; −7.3%),

followed by upper garments (e.g. shirts and pullovers;

−3.6%) and lower garments (e.g. pants and skirts;

−2.1%). The A/B test also showed an increase in se-

lection orders (in which a customer orders multiple

sizes of the same article; +4.4%) for the treatment

group and a reduction of cost-intensive re-orders (in

which a customer returns an article and re-orders in a

different size; −6.3%).

Table 1: Added ﬂags by MultiFlags M show the strongest

srr reduction.

Group Dropped Same Added

Evaluation DiD DiD A/B test

Dataset Holdout Holdout Production

Srr reduction 2.8% 3.8% 4.5%

The results of Section 4.1 and 4.2 are summa-

rized in Table 1. The DiD results show that the ﬂags

dropped by M have a clearly lower srr reduction than

Added and Same. We highlight that for the sake of

this study we chose a single global θ such that the

number of ﬂags each method raises is roughly equal.

Within this context it is important to note that though

Dropped have a positive srr reduction (as estimated

by DiD), Added have an even larger srr reduction (as

estimated by the A/B test), and consequently for the

same number of ﬂags we expect a higher overall srr

reduction by M . Furthermore, if we wish to reduce

the number of Dropped ﬂags, this can be achieved

by lowering the θ parameter or even having differ-

ent θ

for each ﬂag k. The choice here depends,

amongst other considerations, on the aggressiveness

of the strategy.

4.3 Complementary Effects with

Personalized Size Recommendations

MultiFlags M requires only article-level information

and as such it is available for all customers shopping

that ﬂagged article without limitations or needs with

respect to customer data. In contrast, size recom-

menders leverage the combined data from both cus-

tomers and articles and as such are only available to

customers from whom the size matching optimization

given an article is conﬁdently achieved thanks to a

pre-requisite depth level in the customer data. In other

words, M marks only those articles with a sizing ﬂag

that exhibit a systemic sizing behavior (e.g., articles

that run too large) and enables all customers to im-

prove their sizing choices on those articles and reduce

sizing returns. However, most articles display regular

sizing behavior. This is precisely where size recom-

menders play a crucial role: providing customers with

personalized size advice when no size ﬂag is avail-

able, ensuring comprehensive size guidance through-

out the product catalog. This indicates that both ap-

proaches are not interchangeable but rather comple-

mentary solutions, which will be the subject of future

work.

5 CONCLUSION

A probabilistic framework was presented to build

theoretically motivated article-based size advice so-

lutions, with a conﬁdence measure for the raised

ﬂags. This framework enables the true-to-size and

critical-ﬁt ﬂags, which can be leveraged in practical

approaches for businesses. With empirical results,

the strengths of the approach were shown: the pro-

posed approach reduces size-related returns signiﬁ-

cantly more than SizeFlags (Nestler et al., 2021) base-

line. Fewer returns save the customer time as the

return process can be time consuming and also im-

prove sustainability and environmental footprint. Fu-

ture work involves experimenting with different prior

setups for including more signals (e.g., leveraging

sentiment analysis of reviews, leveraging LLMs to

gather richer return information) and developing the

approach into hierarchical recommender system.

REFERENCES

(2019/2020). Asos operational carbon report.

(2022). Fourth workshop on recommender systems in fash-

ion.

Abdulla, G. M. and Borar, S. (2017). Size recommendation

system for fashion e-commerce. In Machine Learning

Meets Fashion Workshop at ACM SIGKDD Confer-

ence on Knowledge Discovery and Data Mining.

Abdulla, G. M., Singh, S., and Borar, S. (2019). Shop your

right size: A system for recommending sizes for fash-

ion products. In Companion Proceedings of The 2019

World Wide Web Conference.

Baier, S. (2019). Analyzing customer feedback for product

ﬁt prediction. arXiv.

Bhatnagar, B. L., Tiwari, G., Theobalt, C., and Pons-Moll,

G. (2019). Multi-garment net: Learning to dress 3d

people from images. In Proceedings of the IEEE/CVF

International Conference on Computer Vision.

MultiFlags: A Probabilistic Framework for Article-Based Size Advice in Fashion E-Commerce

321

C, R. (2014). How Fashion Ecommerce Retailers Can Re-

duce Online Returns. Econsultancy.

Choi, T.-M. (2016). Analytical Modeling Research in Fash-

ion Business. Springer.

Dogani, K., Tomassetti, M., Vargas, S., Chamberlain, B. P.,

and Cnudde, S. D. (2019). Learning embeddings for

product size recommendations. In eCOM@SIGIR.

Dong, H., Liang, X., Shen, X., Wang, B., Lai, H., Zhu, J.,

Hu, Z., and Yin, J. (2019). Towards multi-pose guided

virtual try-on network. In 2019 IEEE/CVF Interna-

tional Conference on Computer Vision (ICCV), pages

9025–9034.

Guigour

es, R., Ho, Y. K., Koriagin, E., Sheikh, A.-S.,

Bergmann, U., and Shirvany, R. (2018). A hierarchi-

cal Bayesian model for size recommendation in fash-

ion. In Proceedings of the 12th ACM Conference on

Recommender Systems, pages 392–396. ACM.

Hajjar, K., Lasserre, J., Zhao, A., and Shirvany, R. (2020).

Attention gets you the right size and ﬁt in fashion. In

14th Conference on Recommender Systems. ACM.

Han, X., Wu, Z., Wu, Z., Yu, R., and Davis, L. S. (2018).

Viton: An image-based virtual try-on network. In Pro-

ceedings of the IEEE conference on computer vision

and pattern recognition, pages 7543–7552.

Heckman, J., Ichimura, H., and Todd, P. (2019). Match-

ing as an econometric evaluation estimator: Evidence

from evaluating a job training programme. The Re-

view of Economic Studies, 64(4):605–654.

Hidayati, S. C., Hsu, C.-C., Chang, Y.-T., Hua, K.-L., Fu,

J., and Cheng, W.-H. (2018). What dress ﬁts me best?

fashion recommendation on the clothing style for per-

sonal body shape. In 26th ACM International Confer-

ence on Multimedia.

Hsiao, W.-L. and Grauman, K. (2020). Vibe: Dressing for

diverse body shapes. In Computer Vision and Pattern

Recognition.

Issenhuth, T., Mary, J., and Calauz

enes, C. (2019).

End-to-end learning of geometric deformations of

feature maps for virtual try-on. arXiv preprint

arXiv:1906.01347.

Jaradat, S., Dokoohaki, N., Pamp

ın, H. J. C., and Shirvany,

R. (2022). Fashion Recommender Systems, pages

1015–1055. Springer US, New York, NY.

Karessli, N., Guigoures, R., and Shirvany, R. (2019).

SizeNet: Weakly supervised learning of visual size

and ﬁt in fashion images. In Proceedings of the IEEE

Conference on Computer Vision and Pattern Recogni-

tion Workshop.

Lasserre, J., Sheikh, A.-S., Koriagin, E., Bergmann, U.,

Vollgraf, R., and Shirvany, R. (2020). Meta-learning

for size and ﬁt recommendation in fashion. In SIAM

International Conference on Data Mining (SDM20).

Lefakis, L., Koriagin, E., Lasserre, J., and Shirvany,

R. (2021). Towards user-in-the-loop online fashion

size recommendation with low cognitive load. In

Dokoohaki, N., Jaradat, S., Corona Pamp

ın, H. J., and

Shirvany, R., editors, Recommender Systems in Fash-

ion and Retail, pages 59–76, Cham. Springer Interna-

tional Publishing.

Misra, R., Wan, M., and McAuley, J. (2018). Decompos-

ing ﬁt semantics for product size recommendation in

metric spaces. In Proceedings of the 12th ACM Con-

ference on Recommender Systems, RecSys ’18, New

York, NY, USA.

Nestler, A., Karessli, N., Hajjar, K., Weffer, R., and Shir-

vany, R. (2021). SizeFlags: Reducing size and ﬁt re-

lated returns in fashion e-commerce. In Proceedings

of the 27th ACM SIGKDD Conference on Knowledge

Discovery & Data Mining.

Pang, K., Zou, X., and Wong, W. (2024). Learning visual

body-shape-aware embeddings for fashion compati-

bility. In Proceedings of the IEEE/CVF Winter Con-

ference on Applications of Computer Vision (WACV),

pages 8056–8065.

Patel, C., Liao, Z., and Pons-Moll, G. (2020). Tailor-

net: Predicting clothing in 3d as a function of human

pose, shape and garment style. In Proceedings of the

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition.

Pecenakova, S., Karessli, N., and Shirvany, R. (2022). Fit-

gan: Fit- and shape-realistic generative adversarial

networks for fashion. In 26th International Confer-

ence on Pattern Recognition (ICPR) 2022. arXiv.

Sembium, V., Rastogi, R., Saroop, A., and Merugu, S.

(2017). Recommending product sizes to customers.

In Proceedings of the Eleventh ACM Conference on

Recommender Systems, RecSys ’17, New York, NY,

USA.

Sembium, V., Rastogi, R., Tekumalla, L., and Saroop, A.

(2018). Bayesian models for product size recommen-

dations. In Proceedings of the 2018 Web Conference.

ACM.

Sheikh, A.-S., Guigour

es, R., Koriagin, E., Ho, Y. K., Shir-

vany, R., and Bergmann, U. (2019). A deep learn-

ing system for predicting size and ﬁt in fashion e-

commerce. In Proceedings of the 13th ACM Confer-

ence on Recommender Systems. ACM.

Yuan, Y., Park, M.-J., and Huh, J.-H. (2021). A proposal for

clothing size recommendation system using chinese

online shopping malls: The new era of data. Applied

Sciences, 11(23).

KDIR 2025 - 17th International Conference on Knowledge Discovery and Information Retrieval

322