High-Precision Contour Tracking for Mobile Manipulators in Large-Scale

Industrial Applications

Buu Hai Dang Trinh

, Daniel Heß

and Christof R

ohrig

IDiAL – Institute for the Digital Transformation of Application and Living Domains,

Dortmund University of Applied Sciences and Arts, Dortmund, Germany

Keywords:

Mobile Manipulator, Artiﬁcial Landmarks, Contour Tracking, Trajectory Control, High-Precision Localization.

Abstract:

Industrial manipulators are limited in their workspace due to mechanical constraints, which pose signiﬁcant

challenges in large-scale industrial applications. Expanding a robot’s workspace often involves deploying

additional stationary manipulators or integrating linear axes, both of which increase installation costs and system

complexity without gaining much ﬂexibility. A more effective and ﬂexible solution is to integrate industrial

manipulators onto mobile platforms. To support this research, the authors developed a mobile manipulator

system consisting of a mobile platform driven by two Differential Drive Steering Units and an industrial

robotic arm with six Degrees of Freedom (DoF). This conﬁguration provides the system with nine DoF in its

conﬁguration space, substantially extending the workspace compared to conventional ﬁxed-base manipulators.

A trajectory control method is proposed to ensure smooth, low-vibration, and high-precision motion during

operation. To enable accurate localization, a cost-effective method based on a 2D laser sensor and artiﬁcial

landmarks is introduced. Furthermore, a high-precision contour tracking algorithm is developed to monitor the

position of the end-effector relative to the workpiece. The proposed methods are validated through real-world

experiments, demonstrating millimeter-level accuracy in both positioning and tracking.

1 INTRODUCTION

Manipulators are widely used in manufacturing due to

their exceptional ﬂexibility, precision, and efﬁciency.

Owing to their ability to seamlessly integrate with a

wide range of end-effectors, manipulators can be pro-

grammed to perform diverse tasks, including heavy,

hazardous, and dangerous operations that pose poten-

tial risks to human workers, thereby enhancing work-

place safety and reducing the likelihood of occupa-

tional accidents. Furthermore, they are capable of

maintaining high levels of precision and repeatability,

ensuring consistent product quality and reliability in

production lines with stringent tolerance requirements.

With the ﬂexibility to be integrated into automated pro-

duction systems, combined with sensors and advanced

technologies, manipulators play a pivotal role in the ad-

vancement of smart manufacturing lines, thus promot-

ing comprehensive industrial automation in modern

industries.

Nevertheless, these manipulators are inherently

limited in their workspace as a result of mechani-

https://orcid.org/0009-0008-3661-3569

https://orcid.org/0000-0002-4627-8951

https://orcid.org/0000-0002-3286-3703

Figure 1: MobileRobot: Omnidirectional mobile platform

with a 6-DoF manipulator.

cal constraints such as joint conﬁgurations, structural

dimensions, and arm length. In applications involv-

ing the processing of large-scale components — such

as those encountered in shipbuilding, aerospace, and

wind turbine manufacturing — the required workspace

often exceeds the reach and ﬂexibility of stationary ma-

nipulators.

A common approach to overcoming workspace

limitations is the strategic deployment of additional sta-

Trinh, B. H. D., Heß, D. and Röhrig, C.

High-Precision Contour Tracking for Mobile Manipulators in Large-Scale Industrial Applications.

DOI: 10.5220/0013709500003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 60-71

ISBN: 978-989-758-770-2; ISSN: 2184-2809

tionary manipulators throughout the work area. How-

ever, this approach considerably increases installation

costs and system complexity, particularly with respect

to coordination and control. Another widely used so-

lution is the integration of linear axes — commonly

referred to as the seventh axis — onto which a single

manipulator is mounted and can traverse along a pre-

deﬁned track. For example, systems like the KUKA

KL 1500 extend the working range of a robot with-

out requiring multiple manipulators (KUKA Robotics,

2025). However, this conﬁguration only allows move-

ment along one axis and is not ﬂexible when the

workspace or task changes. Adjusting the system usu-

ally requires extra mechanical work and reprogram-

ming. Mobile manipulators, which combine indus-

trial manipulators with autonomous mobile platforms,

are increasingly recognized as a promising solution

to overcome the inherent workspace limitations (Gh-

odsian et al., 2023). Nevertheless, the development

of such systems poses signiﬁcant challenges, as it re-

quires maintaining high positioning accuracy and op-

erational efﬁciency while addressing the uncertainties

introduced by both the mobile base and the manipula-

tor (Sereinig et al., 2020).

Industrial mobile manipulators typically operate in

highly structured environments where object positions

are ﬁxed and predetermined. This setup enables more

predictable, stable, and efﬁcient navigation and opera-

tion. Unlike those used in service or domestic appli-

cations, they must meet strict accuracy requirements

— particularly at the end-effector — for tasks such

as gripping, welding, painting, and assembly (Gawel

et al., 2019). Since the end-effector’s pose results from

the combined kinematics of the mobile base and the

manipulator, any inaccuracy in the platform’s move-

ment can compromise overall task performance.

As part of this research, a mobile manipulator sys-

tem was designed combining a mobile platform driven

by two Differential Drive Steering Units (DDSUs)

and a 6-DoF industrial robotic arm (see Fig. 1). This

conﬁguration enables the platform to achieve omnidi-

rectional movement while retaining the advantages of

conventional wheels. Compared to Mecanum wheels,

the DDSU-based platform signiﬁcantly reduces vibra-

tions, thereby enhancing the system’s accuracy and

stability. We performed a measurement of the dis-

placement of the Tool Center Point (TCP) position

caused by vibrations generated by the platform dur-

ing the linear phase at 800 mm/s, as illustrated in

Fig. 2. The results demonstrate that the DDSU-based

platform generates signiﬁcantly lower vibrations than

the Mecanum-wheeled platform, leading to improved

end-effector stability and positioning accuracy. Fur-

thermore, we have presented a system control model

to address the kinematic constraints of DDSUs. While

these units enable omnidirectional movement, they in-

troduce speciﬁc limitations that require careful control

to maintain accurate and efﬁcient system performance

(Heß et al., 2023).

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Offset (in mm)

Time (in seconds)

Mecanum Platform

DDSU Platform

Figure 2: Displacement of base and TCP positions during

linear motion.

The localization of mobile manipulators within the

workspace is essential for performing tasks accurately.

However, advanced localization systems based on

3D Light Detection and Ranging (LiDAR) sensor

or motion capture systems are often prohibitively

expensive and may not be feasible for many in-

dustrial environments. Radio-based localization

technologies, such as Ultra-Wideband (UWB), offer

high positioning accuracy and low latency, making

them an attractive alternative. Nevertheless, UWB

still encounters signiﬁcant challenges in complex

industrial environments due to signal interference and

multipath propagation. The performance of UWB can

degrade considerably in enclosed areas with metallic

structures or dense machinery, where signal reﬂections

and obstructions are prevalent (Delamare et al., 2020).

The main contributions of this paper are as follows:

A mobile manipulator system, integrating an indus-

trial six-DoF robotic arm with a mobile platform

driven by two DDSUs, has been developed to sig-

niﬁcantly expand the workspace for large-scale

industrial applications.

A trajectory control method for the mobile ma-

nipulator has been proposed that ensures smooth,

low-vibration coordinated motion while fully con-

sidering the kinematic and mechanical constraints

of the DDSU-driven platform.

A cost-effective localization method based on a

2D laser sensor and artiﬁcial landmarks has been

introduced.

A contour tracking algorithm has been devel-

High-Precision Contour Tracking for Mobile Manipulators in Large-Scale Industrial Applications

oped to achieve high-precision control of the end-

effector position relative to the workpiece during

the entire task execution.

The proposed methods have been validated in real-

world scenarios, demonstrating that the mobile

manipulator system achieves millimeter-level posi-

tioning and tracking accuracy.

2 RELATED WORK

A variety of mobile manipulator systems have been

developed to overcome the workspace limitations of

stationary robots. Representative systems include

KUKA’s KMR iiwa and KMR QUANTEC, both of

which integrate omnidirectional platforms with KUKA

industrial arms. Another example is RB-KAIROS+, a

mobile manipulator from Robotnik Automation that

combines an omnidirectional base with the UR5e,

UR10e, or UR16e collaborative robotic arms. These

systems are designed for ﬂexible industrial and intral-

ogistics applications. Additionally, researchers at the

Dortmund University of Applied Sciences and Arts

developed OmniMan, a mobile manipulator system for

human-robot collaboration in intralogistics (R

ohrig

and Heß, 2020).

All of these systems use Mecanum-wheeled plat-

forms, which allow for omnidirectional movement in

narrow spaces. Mecanum wheels consist of driven

hubs combined with free-spinning rollers mounted at

an angle to the wheel axis, allowing the platform to

move in any direction. However, these rollers gener-

ate vibrations during motion, which can reduce the

system’s stability and accuracy and negatively affect

production quality (Bae and Kang, 2016).

Zhewen et al. proposed combining Mecanum

wheels with a dedicated suspension system to min-

imize vibrations and improve comfort (Zhewen et al.,

2024). In addition to Mecanum wheel-based designs,

omnidirectional platforms can be implemented using

steered standard wheels. An overview of such plat-

forms is provided (Jacobs, 2018). Wheel modules

enabling omnidirectional motion can be designed ei-

ther with active steering motors (Jacobs et al., 2012)

or using differential drive mechanisms (Jacobs and

Schaefer, 2020).

3 PROBLEM FORMULATION

In this paper, the problems of motion control, localiza-

tion, and contour tracking for a large-scale industrial

mobile manipulator system, designed speciﬁcally for

automated welding of large objects are addressed. The

system consists of a six DoF robotic arm mounted

on an omnidirectional mobile platform driven by two

DDSUs. The robotic arm enables full six DoF spatial

manipulation, allowing precise control of position and

orientation in three-dimensional space. In addition,

the omnidirectional platform provides planar mobil-

ity, enabling two-dimensional translation and rotation.

Consequently, the entire mobile manipulator system

exhibits a total of nine DoF in its conﬁguration space.

Therefore, the mobile welding manipulator (MWM) is

an overdetermined system where the additional DoF

in conﬁguration space can be used to optimize the mo-

tion of the MWM. The welding path is speciﬁed in

the three-dimensional Cartesian space of the MWM’s

operational workspace. To maintain weld quality, the

welding torch is required to track this path at predeter-

mined linear and angular velocities. Since the weld-

ing path may extend beyond the reachable workspace

of the robotic arm, it is necessary for the arm and

the mobile platform to coordinate their movements

synchronously. The forward kinematics of a mobile

manipulator can be generally formulated as:

p = f (q), with p =













, and q =





. (1)

Where

denotes the pose of the mobile manip-

ulator’s tool frame with respect to the world frame,

such that

p ∈ R

× SO(3)

. The vector q represents

the generalized coordinates in the conﬁguration space

(C-space), consisting of the 2D pose of the mobile

platform, deﬁned as

= (x

,θ

)

, where

∈

× S

, and the joint angles of the manipulator arm,

given by

= (θ

,...,θ

)

. The inverse kinematics,

crucial for trajectory planning and control, can thus be

expressed as:

q = f

−1

(p) (2)

The inverse kinematics problem of the system is

overdetermined because it has more degrees of free-

dom than required to deﬁne the end-effector pose.

This leads to multiple possible joint conﬁgurations

for the same task, which can be resolved using numer-

ical methods to optimize motion in the conﬁguration

space. In addition, the system’s redundancy not only

improves motion efﬁciency and safety but also extends

the manipulator’s reachable workspace beyond the

physical limitations of the arm alone.

The omnidirectional mobile platform, driven by

two DDSUs, can simultaneously translate along the

- and

-axes and rotate about the

-axis, thereby pro-

viding full mobility in the 2D plane. The world frame

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

is a ﬁxed reference frame used to describe the task

space. The MWM operates within this workspace,

and its motion is expressed relative to

. The robot

frame

is a coordinate frame that is rigidly attached

to the mobile platform, with its origin located at the

geometric center of the platform (see Fig. 3).

Figure 3: Pose deﬁnition of the mobile manipulator in the

world p

and robot frame F

The pose of the mobile platform relative to the

world frame is deﬁned as

= (x

,θ

)

, where

and

represent the position in the 2D plane, and

the heading angle around the orthogonal

-axis. This

coordinate setup allows for a clear separation between

global task planning in the world frame and local con-

trol actions in the robot frame. The platform’s pose

serves as a critical reference for deﬁning its veloc-

ity, localization, and control inputs within the world

frame. However, for control implementation, these

quantities are generally transformed and expressed in

the robot frame

, where they are more convenient

and consistent to manage in motion control schemes.

The transformation of velocities from the robot frame

to the world frame is performed using the platform’s

heading angle (θ = θ

˙p

= R(z,θ) ˙p

, ⇒ ˙p

= R

−1

(z,θ) ˙p

with ˙p





˙x

˙y





, ˙p





˙x

˙y





and R(z, θ) =





cosθ −sinθ 0

sinθ cosθ 0

0 0 1





(3)

To determine the necessary wheel velocities and steer-

ing angles that enable the platform to achieve a desired

motion in the robot frame, the inverse kinematics of the

platform is formulated as a set of nonlinear equations:



˙φ



= f

( ˙p

), (4)

where

• ˙p

= ( ˙x

, ˙y

θ)

is the velocity of the platform

over the ground described in the robot frame.

• ˙φ = (

,...,

)

is the vector of wheel angu-

lar velocities.

• β = (β

,β

,...,β

)

is the vector of wheel steer-

ing angles.

The forward kinematics can be obtained by using

a nonlinear least-squares approach

˙p

= f

−1



˙φ



, (5)

In contrast to the overdeterminacy in the mobile

manipulator, the over-actuated drive structure of the

platform cannot be used to achieve additional degrees

of freedom in C-space. The overdeterminacy of the

platform is subject to motion constraints, which must

be satisﬁed to avoid additional wheel slip.

The global localization of the MWM is performed

using a 2D LiDAR sensor combined with strategically

placed artiﬁcial landmarks around the workspace of

the MWM. A localization algorithm processes the Li-

DAR and landmark data to estimate the pose of the

platform relative to the world coordinate frame

The localization algorithm processes the LiDAR mea-

surements and the known locations of these landmarks

to estimate the platform’s pose relative to the world

coordinate frame F

Although the localization system achieves an ac-

curacy of a few centimeters, this level of precision

remains insufﬁcient to meet the stringent requirements

of industrial applications. Furthermore, the global

localization system is affected by environmental inter-

ference, landmark occlusions, and the limited scanning

range of the LiDAR, leading to reduced stability dur-

ing operation. For the welding task, high-precision

contour tracking of the target workpiece is required to

ensure accurate torch positioning along the welding

path. Since the global localization system alone cannot

guarantee the required accuracy at the end-effector, a

2D proﬁle scanner is mounted at the end-effector to

support local contour tracking. This sensor does not di-

rectly provide contour information, but instead returns

proﬁle data as a set of distance measurements captured

along the scanning line. Therefore, additional data

processing is necessary to reconstruct and accurately

estimate the object’s contour.

By combining global localization with contour

tracking, the system is capable of performing high-

precision manipulation tasks with enhanced accuracy

and operational stability.

High-Precision Contour Tracking for Mobile Manipulators in Large-Scale Industrial Applications

4 PROPOSED LOCALIZATION

METHOD

4.1 Overview and Requirements

Accurate localization of the mobile platform is a fun-

damental prerequisite for performing high-precision

manipulation tasks in large-scale industrial applica-

tions. In structured and static environments, Adaptive

Monte Carlo Localization (AMCL) offers an efﬁcient

and cost-effective solution for mobile platform local-

ization. However, its accuracy remains limited, with

position errors often reaching several tens of centime-

ters. Although the integration of QR codes on the

ﬂoor improves localization accuracy, it still fails to

meet the stringent requirements of industrial applica-

tions. This limitation becomes even more critical in

large and dynamic environments, where noise, mov-

ing obstacles, and changes in the environment further

degrade accuracy (Wang et al., 2021).

For contour tracking applications such as welding,

the system requires centimeter-level localization accu-

racy of the mobile base to ensure stable and precise

end-effector control. Improved base accuracy mini-

mizes the need for manipulator compensation, thereby

enhancing the stability and quality of the weld path.

4.2 Localization Architecture

In this project, the NAV245 2D LiDAR sensor (SICK

AG, Germany) is employed for environmental percep-

tion and distance measurement. The sensor covers

270

◦

scanning ﬁeld with an angular resolution of

0.001

◦

for reﬂectors and

0.25

◦

for raw contour data.

Operating at 25 Hz, the sensor completes a full scan

in 40 ms and supports a maximum detection range of

50 m, depending on the target’s properties. According

to the manufacturer, for reﬂector-based data, the typi-

cal systematic measurement error is

10 mm, while

the statistical error is 8 mm (SICK AG, 2022). These

features enable precise and low-latency positioning of

the robot in large indoor environments using only a

single sensor.

Artiﬁcial landmarks are constructed using RA3-

class microprismatic retroreﬂective foil, which enables

incident laser beams to be returned directly to the sen-

sor regardless of the angle of incidence. This full-cube

microprism technology achieves remission values of

up to 3,000%, which is considerably higher than the

maximum 100% remission of natural surfaces. As

a result, measurements on reﬂectors provide higher

precision and signal stability, making them ideal for

landmark-based localization in indoor environments.

The odometry system is derived from the DDSU

developed by G

otting KG. Each DDSU integrates a

pseudo-incremental encoder providing 65,535 pulses

per revolution for wheel rotation measurement of

the foure active wheels of both DDSUs, and a steer-

ing angle encoder with 4,096 pulses per revolution

for accurate steering position feedback. These high-

resolution sensors provide precise relative motion es-

timation of the mobile platform. However, while the

high-resolution encoders ensure low-noise and high-

frequency odometry data, the odometry data tends to

accumulate errors over time due to wheel slip and in-

tegration drift. Fig. 4 illustrates the overall pipeline

of the proposed high-precision and robust localization

system.

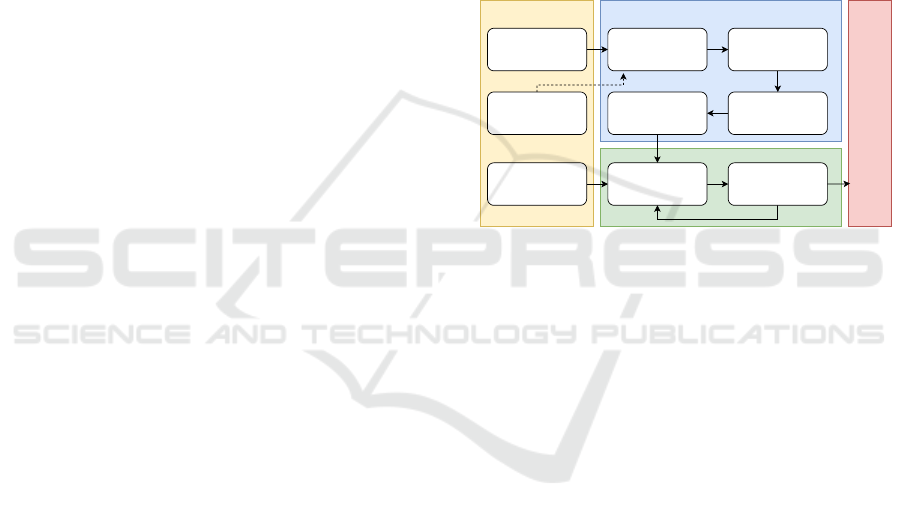
LiDAR Data

(Distance & Intensitty)

Landmark Map

Wheel Odometry Data

(Local Frame)

Landmark Detection &

Identification

GDOP Calcutation &

Trilateration

Coordinate

Transformation

Platform Pose Estimation

(Global frame)

EKF-Based Fusion

(Prediction & Correction)

Estimated Platform Pose

(Global frame)

Perception Pose Estimation

Sensor Fusion & Correction

Platform

Control

Figure 4: Overview of the proposed localization architecture.

The Perception module is responsible for contin-

uously collecting distance and intensity information

from a 2D LiDAR scanner as well as odometry data

from wheel encoders. The Pose Estimation module

utilizes LiDAR data in combination with a previously

generated landmark map containing known global po-

sitions of all landmarks in the workspace. This enables

the system to accurately detect and identify the land-

marks present in the current scan. Once the landmarks

are identiﬁed, the module calculates the Geometric Di-

lution of Precision (GDOP) to evaluate how the spatial

conﬁguration of the landmarks relative to the sensor

affects the accuracy of the position estimation. The

GDOP metric guides the selection of the most suitable

landmark-set for trilateration, ensuring improved esti-

mation reliability. The trilateration method is used to

estimate the global position of the scanner. Finally, by

applying a coordinate transformation, the global pose

of the mobile platform is determined.

Trilateration can achieve high positioning accuracy

when landmarks are correctly identiﬁed and the dis-

tance measurements are sufﬁciently reliable. However,

in practice, these measurements are often affected by

noise and environmental conditions. Due to its sen-

sitivity, even small errors can result in signiﬁcant de-

viations in position estimation. To improve localiza-

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

tion accuracy and robustness, an Extended Kalman

Filter (EKF) is employed to fuse the landmark-based

position estimates with the robot’s internal odometry.

Through this process, the system effectively compen-

sates for odometry drift and minimizes the impact of

environmental noise on LiDAR-based measurements,

ensuring consistent pose estimation over time. Finally,

the global pose generated by the Sensor Fusion & Cor-

rection module is transmitted to the system controller

for platform control.

4.3 Localization Algorithm

To ensure the availability of a sufﬁcient number of

reference landmarks for position estimation, a total of

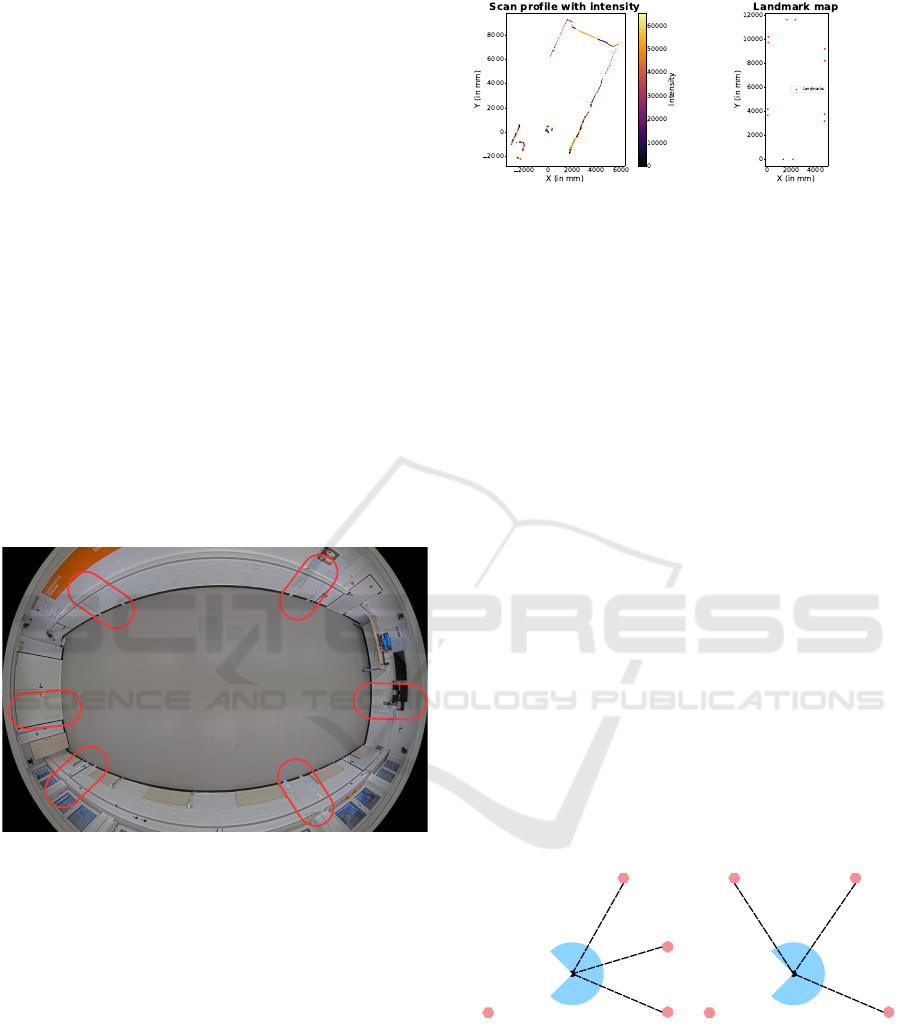
12 artiﬁcial landmarks were mounted on the laboratory

walls (see Fig. 5). The positions of these landmarks

were determined by combining measurements from a

Vicon motion tracking system and the NAV245 LiDAR

scanner, which signiﬁcantly reduced errors compared

to manual measurement methods. The landmarks were

strategically arranged in distinct pairs, ensuring that

the distance within each pair was unique.

Artificial landmarks

Figure 5: Landmark setup for the experimental environment.

In each scan cycle, the LiDAR sensor generates a

scan proﬁle representing the relative positions of all

points detected within its ﬁeld of view (see Fig. 6a).

The artiﬁcial landmarks are characterized by signiﬁ-

cantly higher reﬂection intensity compared to natural

surfaces. By applying a predeﬁned intensity threshold,

the system is able to distinguish the artiﬁcial landmarks

from other objects. Once detected, these landmarks

are matched against the stored landmark map (see

Fig. 6b) to determine their identities. As a result of

this process, each successfully identiﬁed landmark is

associated with both its relative position with respect

to the LiDAR sensor and its global position within the

workspace.

The global position of the LiDAR scanner is es-

timated using the Trilateration method. This method

(a) LiDAR scan proﬁle

(b) Reference landmark map

Figure 6: Required data for the Pose Estimation Module.

utilizes the measured distances between the scanner

and three previously identiﬁed artiﬁcial landmarks, lo-

cated at

M = (x

)

N = (x

)

, and

K = (x

)

The distances to these landmarks, denoted as

and

, are measured by the LiDAR scanner. The scan-

ner’s position

(x,y)

is then determined by solving the

following system of nonlinear equations:







(x − x

)

+ (y − y

)

= r

(x − x

)

+ (y − y

)

= r

(x − x

)

+ (y − y

)

= r

(6)

The accuracy of position estimation using the Tri-

lateration method depends on the geometric arrange-

ment of the landmarks relative to the LiDAR sensor.

In cases where the landmarks have an unfavorable

geometric conﬁguration (see Fig. 7a)—such as when

the reference landmarks are closely spaced or aligned

along a straight line—even small errors in distance

measurements can result in signiﬁcant position es-

timation errors (Li et al., 2020). Therefore, to im-

prove estimation accuracy and minimize the inﬂuence

of measurement noise, only landmark combinations

with an optimal geometric conﬁguration (see Fig. 7b)—

characterized by a low GDOP—are selected for the

Trilateration process.

Landmark

(a) High GDOP

Landmark

(b) Low GDOP

Figure 7: Relationship between the arrangement of the land-

marks and the GDOP value.

The GDOP is calculated using the observation ma-

trix

, which contains the direction vectors from the

LiDAR sensor to the landmarks, according to the fol-

High-Precision Contour Tracking for Mobile Manipulators in Large-Scale Industrial Applications

lowing equation:

GDOP =

trace



−1



with A =







x − x

y − y

... ...

x − x

y − y







and r

(x − x

)

+ (y − y

)

(7)

The global orientation of the LiDAR is calculated

using the atan2 function based on the relative posi-

tions of the detected landmarks and the LiDAR’s es-

timated position. By applying geometric coordinate

transformation to the global pose of the LiDAR, the

global pose of the mobile platform can be accurately

estimated. This pose is then used as an input for the

Sensor Fusion & Correction module, where it will be

fused with odometry data using the EKF to enhance

the accuracy and robustness of the position estimation.

For the implementation of the EKF, the state vector is

deﬁned as:

= (x

,θ

)

= f (x

t−1

), (8)

where u

is the control input vector at time

, repre-

senting the measured relative motion of the mobile

platform in its local coordinate frame, obtained from

odometry data. The process noise w

models uncer-

tainties in the motion model and is assumed to follow

a zero-mean Gaussian distribution to account for er-

rors such as wheel slip and odometry drift. In the

prediction step, the state is propagated based on the

control input, and the covariance is updated to reﬂect

the uncertainty:

t|t−1

= f



t−1|t−1



(9)

t|t−1

= A

t−1|t−1

+ W

(10)

where

t|t−1

is the predicted state covariance matrix,

representing the uncertainty of the state after the pre-

diction step. A

and W

are the Jacobians of the motion

model with respect to the state and the process noise,

respectively. Q

is the process noise covariance ma-

trix, representing the uncertainties introduced by the

system dynamics and odometry errors.

The correction step is triggered immediately after

the global pose of the mobile platform is calculated

from the LiDAR measurements. It is performed using

the following set of equations:

= z

− h



t|t−1



(11)

t|t

t|t−1

+ k

(12)

= P

t|t−1



t|t−1

+ V



−1

(13)

t|t

= (I − K

t|t−1

(14)

Here, the measurement function



t|t−1



maps the

predicted state into the measurement space. The resid-

ual

is calculated as the difference between the actual

measurement

and the predicted measurement. The

Kalman gain

is computed to balance the uncer-

tainties between the predicted state and the measure-

ment, considering the measurement noise covariance

. The updated state estimate

t|t

represents the cor-

rected global pose of the mobile platform at time

combining the prediction from odometry with the cor-

rection from the LiDAR measurements.

5 TRAJECTORY CONTROL AND

CONTOUR TRACKING

5.1 Contour Tracking Algorithm

Based on the pre-deﬁned plan, the motion controller

of the mobile manipulator guides the TCP along the

processing trajectory. However, factors such as wheel

slippage, uneven terrain, joint backlash, and structural

ﬂex can lead to deviations between the planned and

actual trajectory of the TCP. To ensure precise task

execution, an algorithm is required to accurately de-

tect these deviations. A 2D laser proﬁle scanner is

mounted on the same end-effector as the welding torch

to capture the contour proﬁle near the tool. It is ori-

ented such that the scanning area is angled forward in

the direction of motion, allowing it to detect the proﬁle

of the area just ahead of the tool path (see Fig. 8a). In

T-joint welding applications, the weld seam is located

at the intersection of the vertical and horizontal plates.

To accurately identify the seam, the laser scanner must

have a ﬁeld of view that includes parts of both surfaces

(see Fig. 8b).

Movement direction

Laser scanner

Tool

Contour

(a) Frontal view

act,h

act,v

Movement direction

Laser scanner

Tool

Contour

(b) Lateral view

Figure 8: Tool and Sensor Arrangement for Contour Track-

ing.

During each scan cycle, the laser proﬁle scanner

captures a two-dimensional depth proﬁle of the target

surface. Each proﬁle consists of a sequence of dis-

crete data points, with each point containing three key

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

values: the x-coordinate, representing the horizontal

position along the scan line; the z-coordinate, indicat-

ing the measured height relative to the scanner; and

the intensity. The overall workﬂow of the system for

detecting the machining point and adjusting the trajec-

tory, based on laser proﬁle data, is illustrated in Fig. 9.

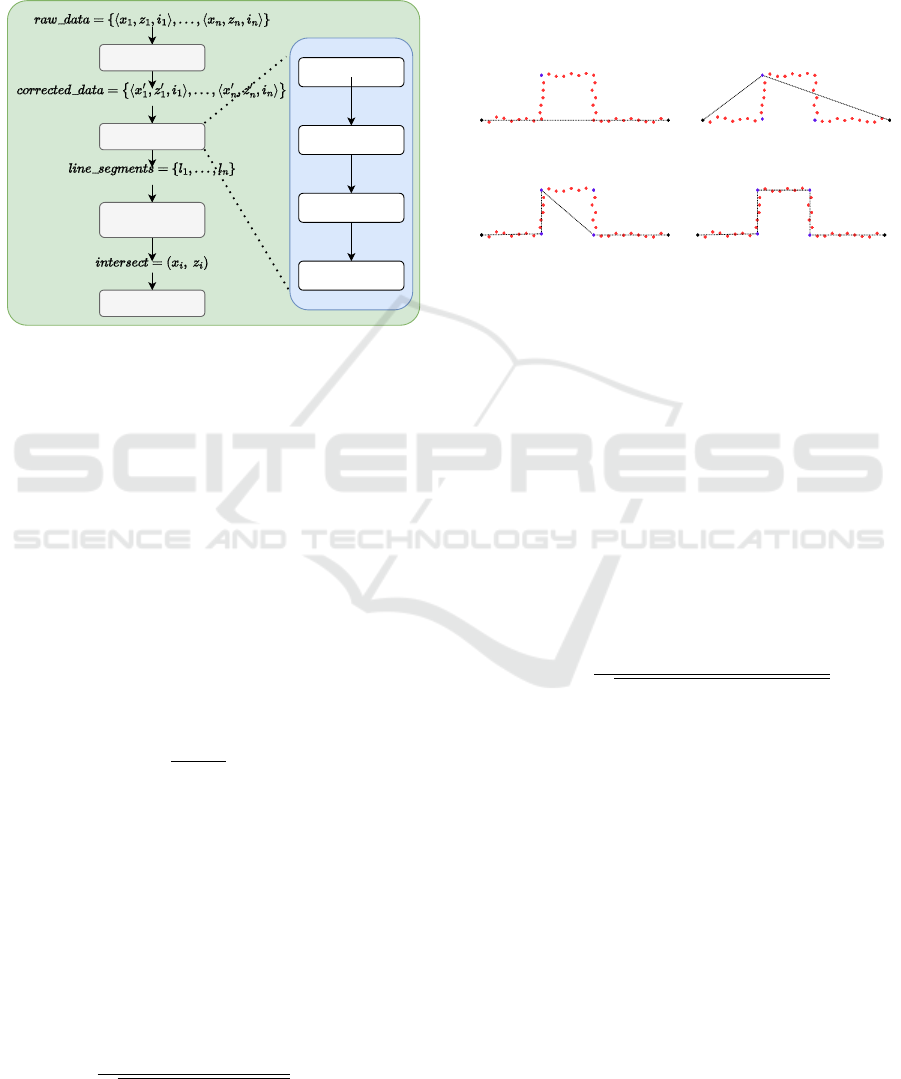
Preprocessing

Line Extraction

Line Filtering

& Intersection

Tool path

adjustment

Detect

Breakpoints

Line

Estimation

Check

Fit

Linear

Regression

Figure 9: Workﬂow for welding position detection and tra-

jectory adjustment using laser proﬁle data.

Before any computation is performed, the raw laser

proﬁle data must be preprocessed. Irrelevant or unreli-

able points—typically characterized by low intensity

values—are removed. This helps reduce noise and

ensures that only meaningful surface features are used

in the next steps. To reduce measurement noise in

the distance measurements, a simple linear smoothing

ﬁlter is applied. This ﬁlter gives the current value

the highest weight, while still considering the adjacent

values to reduce local noise. The stability of break-

point detection and line ﬁtting is improved through this

ﬁltering approach. Such ﬁltering enhances the quality

of breakpoint detection and the ﬁtting of line segments

that follow.

′

= 0.2d

i−1

+ 0.6d

+ 0.2d

i+1

with d

+ x

(15)

The lines are extracted using the Split-and-Merge

algorithm. This algorithm provides a recursive ap-

proach for segmenting point data into linear compo-

nents. In the ﬁrst step, a line

is drawn between the

ﬁrst and last points of the currently considered set of

points. Next, all points between the current start and

end points are evaluated, and the orthogonal distance

from each point d

to l is computed.

=⃗v ·



− x

− z



with ⃗v =

− z

)

+ (x

− x

)



− z

− x



(16)

If the maximum distance exceeds a predeﬁned

threshold, the corresponding point is classiﬁed as an

outlier with respect to the current line segment

. The

point set is then split at this location, and the algo-

rithm is recursively applied to the resulting subsets.

The recursion terminates once all points in a segment

lie within the threshold distance from their respective

ﬁtted line. As shown in Figure 10, the black lines are

ﬁtted to the red points.

(x , z )

s s

(x , z )

e e

1.Split

(a)

1. Split

2. Split 2. Split

(b)

1. Split

2. Split 2. Split

3. Split

(c)

1. Split 3. Split

2. Split 2. Split

(d)

Figure 10: Stepwise representation of the operation of the

recursive line extraction method.

Breakpoint analysis allows the segmentation of

laser proﬁle data into geometrically consistent sections,

such as areas where the surface changes direction or

curvature. Performing this analysis before applying

the recursive splitting process helps reduce unneces-

sary iterations and improves the overall efﬁciency of

line extraction. In this paper, the Bearing Angle (BA)

method (Harati and Siegwart, 2007) is used to detect

geometric discontinuities. This approach computes a

bearing angle value at each scan point based on consec-

utive distance measurements and the scanner’s angular

resolution α. This bearing angle is deﬁned as:

′

− d

′

i−1

cos(α)

′2

+ d

′2

i−1

− 2d

′

i−1

cos(α)

(17)

A breakpoint is detected at point

if the absolute dif-

ference between two consecutive BA values exceeds a

predeﬁned threshold:

− BA

i−1

≥ θ

threshold

(18)

The result of the split phase is a set of data subsets,

where each subset is assumed to be well approximated

by an individual straight line. However, to avoid over-

ﬁtting—that is, generating too many segments due to

excessive sensitivity to small noise—additional valid-

ity checks are required. These include, for example,

verifying whether each segment contains a sufﬁcient

number of points.

After the data has been segmented through the split

phase, each subset is processed independently to es-

timate the best-ﬁtting straight line. This is done by

High-Precision Contour Tracking for Mobile Manipulators in Large-Scale Industrial Applications

applying linear regression to the points within each

segment (Arras and Tomatis, 1999). The resulting

line is then reformulated in Hesse normal form, which

is particularly useful for subsequent geometric opera-

tions. The Hesse parameters are computed using the

following equations:

α = atan2



−

∑

i=1

(¯z − z

)( ¯x − x

)

∑

i=1

(¯z − z

)

( ¯x − x

)



(19)

p = ¯x · cos(α) + ¯z · sin(α) (20)

Here,

¯x

and

¯z

denote the mean values of the co-

ordinates of the respective point set. The computed

line minimizes the orthogonal distance to the input

points, providing a robust and consistent representa-

tion for downstream processing, such as computing

the intersection between two adjacent line segments.

Once the intersection of two neighboring ﬁtted lines is

determined, it is used as a control point to update the

trajectory of the welding tool.

5.2

Trajectory Tracking Control Scheme

The proposed control scheme for trajectory tracking

of the MWM is illustrated in Fig. 11. Based on the

Cartesian weld path, the motion planner computes

the complete trajectory

q(t) = (q

(t),q

(t))

in the

conﬁguration space. The motion interpolator computes

the current state and its derivatives for each time step

in t to ensure smooth and continuous motion.

The platform’s motion controller is based on our

previously proposed control scheme for Mecanum-

driven omnidirectional platforms (R

ohrig et al., 2017).

The underlying kinematic model of the MWM is also

adopted from our earlier work on redundant mobile

manipulators, as presented in (Heß et al., 2023). The

platform control consists of pose control, platform

kinematics, odometry, localization, and DDSU con-

trol. The platform kinematics are derived from the

platform’s motion model. The DDSU controller con-

trols the steering angle

and the velocity

for both

DDSUs based on differential drive kinematics using

the angular velocities

˙φ

of the four driven wheels.

Odometry is computed using the wheel encoder values

and the measured passive steering angles

. Local-

ization is performed by fusing the odometry with data

from a SICK NAV245 LiDAR.

The tracking of the weld path is done by a laser

sensor that measures the deviation from the weld path.

Since the robotic arm is much more precise and dy-

namic than the robotic platform, the tracking control

uses the arm to control the deviation from the weld

path. The deviation is measured in the end-effector

coordinate frame, hence the end-effector Jacobian

) =

∂f(q)

∂q



3×3



) ˙q

(21)

is used to control the deviation. The tracking control

scheme is based on the well known Resolved-Rate

Motion Control (see (Corke, 2023)). When the arm

correction

∆q

becomes large, the motion planner cal-

culates a new trajectory to correct the platform’s pose

and reduce ∆q.

6 EXPERIMENTAL EVALUATION

To validate the proposed algorithm, two experiments

were conducted: one assessing the accuracy of the mo-

bile platform, and the other evaluating contour tracking

in a welding task.

6.1 Experimental Setup

The MWM used for the experiments described here

comprises a platform equipped with two DDSUs and

a KUKA KR 6 R900-2 robotic arm, controlled via a

KRC5 controller. An embedded PC running a real-

time Linux operating system that connects the mo-

bile platform’s DDSUs via Controller Area Network

(CAN) bus and the manipulator’s KRC5 controller

via real-time Ethernet. Serving as a centralized real-

time control system, the system controller PC synchro-

nizes the setpoints of all components in real time to

ensure coordinated operation. Every 200 ms, the SICK

NAV245 LiDAR provides a full

270

◦

scan, which is

used by the platform controller as feedback for the

pose control loop (see Fig. 11). The scanCONTROL

3012-100 laser proﬁle sensor, mounted on the same

end-effector as the welding torch, is used in Trajectory

Tracking to enable closed-loop control of the robotic

arm. In the experimental setup, the T-joint is simu-

lated using an L-shaped proﬁle instead of two separate

workpieces (see Fig. 12). For ground truth compari-

son, the MWM’s global pose is obtained via a Vicon

motion capture system, which offers high-precision

6-DoF tracking.

6.2 Experimental Results

In order to evaluate the effectiveness of the proposed

localization method, we applied a series of algorithms

to the dataset obtained from the NAV245 laser scanner.

The localization accuracy improved progressively with

each enhancement in the algorithmic pipeline. Trilater-

ation served only as the baseline, producing the largest

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

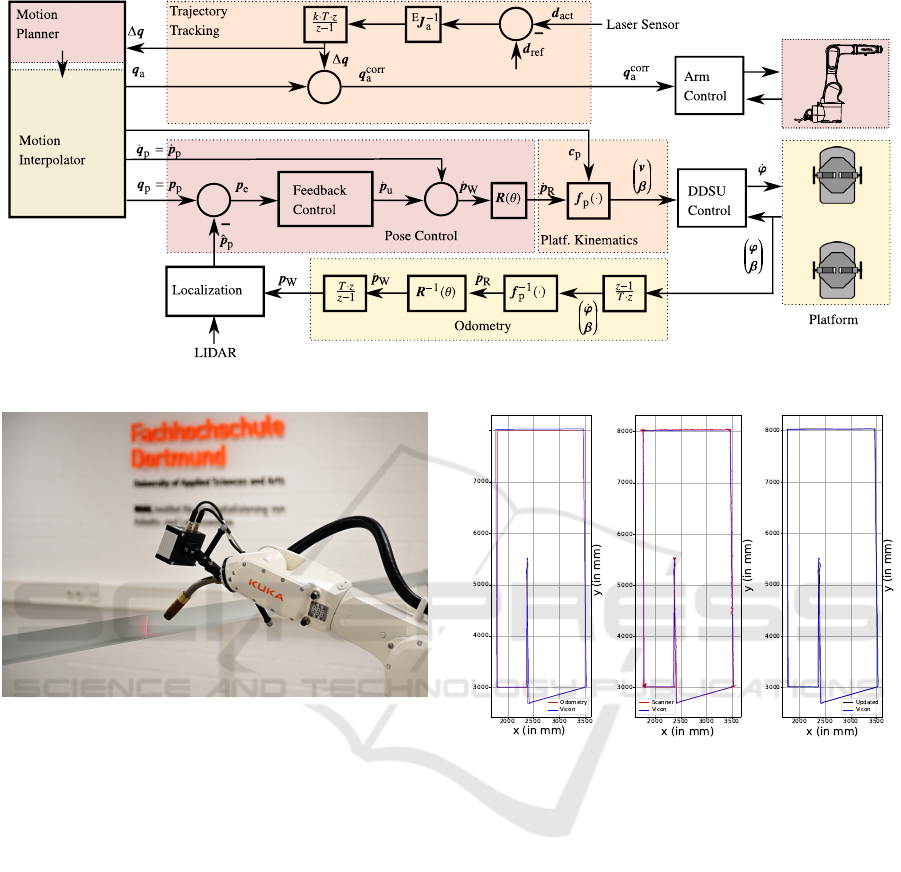
Figure 11: Block diagram for tracking a welding path with MWM.

Figure 12: Simulation of T-Joint weld using L-Proﬁle.

variance in position estimates. Incorporating the opti-

mal geometric conﬁguration of the detected landmarks

— based on GDOP analysis — signiﬁcantly reduced

the standard deviation, minimized measurement noise,

and produced position estimates that were more stable

and more tightly clustered around the true location.

Next, the MWM was driven along a predeﬁned

trajectory. During this motion, both odometry data and

scan measurements were recorded. Figure 13 show the

estimated trajectory using (a) raw odometry data, (b)

trilateration with GDOP, and (c) sensor fusion com-

bining odometry with trilateration + GDOP using an

Extended Kalman Filter. Each method was compared

against ground-truth data obtained from a Vicon mo-

tion capture system.

Due to wheel slippage and integration drift, the

trajectory estimated from odometry diverges signiﬁ-

cantly from the ground truth. By contrast, trilateration

enhanced with GDOP ﬁltering yields a trajectory that

more closely aligns with the actual path. However,

residual noise remains—particularly in turning seg-

8000

(a) Using odometry

data.

(b) Using Trilatera-

tion + GDOP.

GDOP + EKF.

Figure 13: Comparison of estimated trajectories using differ-

ent methods.

ments or in areas with limited landmark coverage—

likely due to suboptimal geometric conﬁgurations for

trilateration. The EKF-based data fusion method effec-

tively mitigates these errors, signiﬁcantly enhancing

the accuracy and stability of mobile platform localiza-

tion.

To demonstrate the effectiveness of the EKF-based

localization approach, Figure 14 presents the absolute

differences between the estimated and ground-truth

values over time. The odometry-only method resulted

in Root Mean Square Errors (RMSE) of 24.32 mm

(

), 24.23 mm (

), and 0.01299 rad (

). In contrast,

the EKF-based fusion signiﬁcantly reduced these er-

rors, achieving RMSEs of 8.15 mm (

), 8.77 mm (

and 0.00497 rad (

). These results highlight the ro-

bustness and precision of the proposed fusion method

High-Precision Contour Tracking for Mobile Manipulators in Large-Scale Industrial Applications

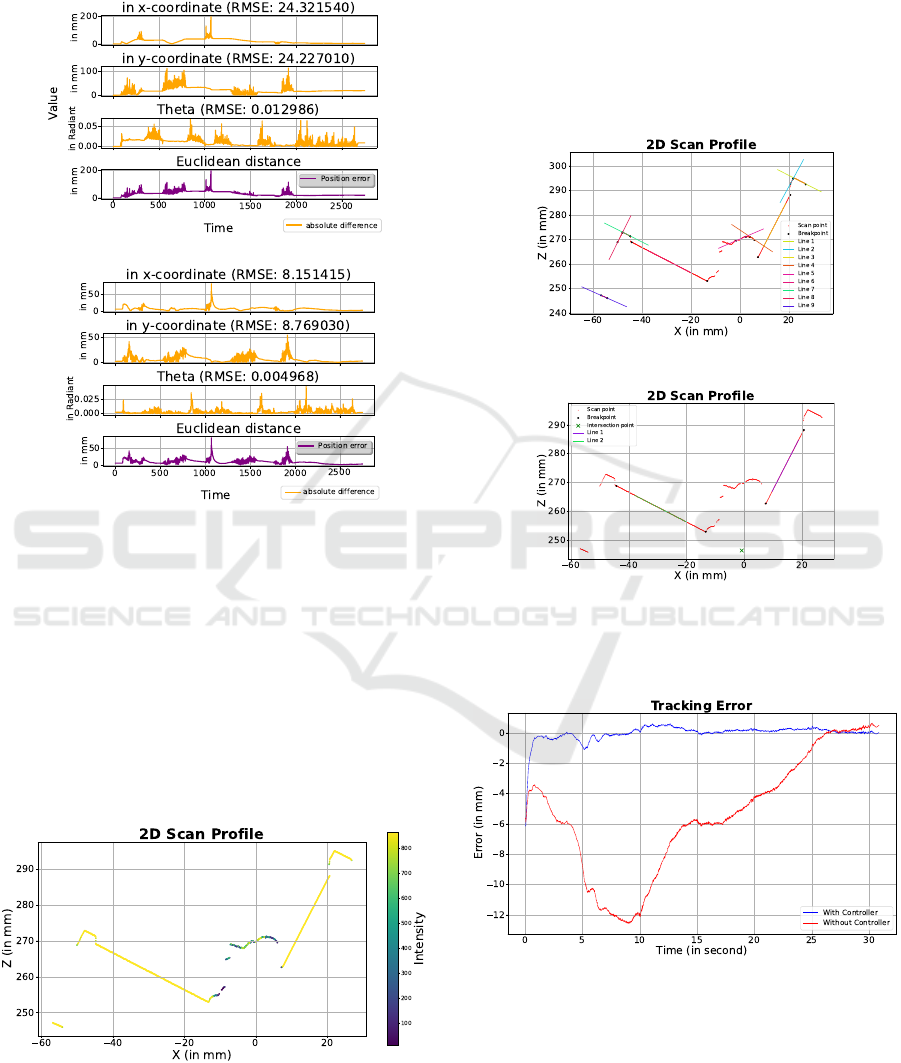
in dynamic operating scenarios. However, for pre-

cise end-effector control during welding, local contour

tracking is required.

(a) Using Odometry

Value

(b) Using EKF

Figure 14: Absolute error between estimated and ground-

truth values.

Contour tracking aims to accurately detect the ma-

chining point, which, in the context of simulated T-

joint welding, refers to the intersection line between

two metal plates. Maintaining precise and continuous

alignment between the welding torch and this intersec-

tion line is a critical factor that determines the quality

and stability of the weld. Figure 15 illustrates a typi-

cal depth and intensity proﬁle acquired from the 2D

proﬁle laser.

Figure 15: Depth and Intensity Proﬁle from 2D Laser Scan.

The raw scan proﬁle is processed to extract line

segments using the proposed contour tracking algo-

rithms, as shown in Figure 16a. In the ﬁnal step, the

intersection of relevant line segments is computed to

determine the precise machining point, as shown in

Figure 16b. This intersection point is then used to

regulate the relative position between the laser sensor

and the workpiece. Since both the torch and the sensor

are mounted on the same end-effector, this adjustment

also determines the relative position between the torch

and the workpiece.

(a) Breakpoint detection and line segmen-

tation

(b) Intersection point estimation

Figure 16: Estimation of the precise machining point through

line extraction and intersection of 2D scan proﬁle data.

Figure 17: Tracking error over time.

Figure 17 illustrates the deviation of the torch from

the welding path during motion. While the MWM

moves along the workpiece, the mobile platform main-

tains global localization using LiDAR, and the robotic

arm compensates for any deviations from the prede-

ﬁned weld path. The blue curve represents the tracking

error with active contour tracking using laser sensor

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

feedback, whereas the red curve shows the error with-

out such feedback control. The tracking system ef-

fectively corrects deviations of the platform, which

reach up to 12 mm in this experiment. The blue curve

shows that the deviation does not exceed 2 mm when

the tracking controller is used.

7 CONCLUSION

In this paper, we presented a MWM designed for high-

precision contour tracking in large-scale industrial en-

vironments. The proposed system combines a 6-DoF

robotic arm suitable for welding tasks with an omnidi-

rectional mobile platform driven by DDSUs, allowing

for smooth and stable motion with reduced vibration.

The DDSUs contain kinematic constraints that must

be considered in motion planning and control. Each

unit has a limited steering angle and can be driven

in two different conﬁgurations by changing the direc-

tion of the wheel speeds. The entire weld trajectory

is planned in Cartesian space, with explicit consid-

eration of the motion constraints introduced by the

DDSU-driven platform. To achieve accurate localiza-

tion, an Extended Kalman Filter fuses LiDAR data

with wheel odometry, resulting in a centimeter-level

pose estimate. However, this level of accuracy is in-

sufﬁcient for high-precision welding. Therefore, a 2D

laser proﬁle scanner mounted on the end-effector is

used to detect the machining point and measure de-

viations from the weld path. Since the robotic arm

is signiﬁcantly more accurate and dynamic than the

mobile platform, the tracking controller uses the arm

to adjust the torch trajectory in order to compensate

for deviations from the weld path.

Experimental results conﬁrm that the proposed tra-

jectory tracking control scheme achieves millimeter-

level accuracy at the end-effector relative to the work-

piece, satisfying the precision requirements of indus-

trial welding applications.

REFERENCES

Arras, K. and Tomatis, N. (1999). Improving robustness and

precision in mobile robot localization by using laser

range ﬁnding and monocular vision. pages 177 – 185.

Bae, J.-J. and Kang, N. (2016). Design optimization of a

mecanum wheel to reduce vertical vibrations by the

consideration of equivalent stiffness. Shock and Vibra-

tion, 2016:1–8.

Corke, P. (2023). Manipulator Velocity, pages 307–331.

Delamare, M., Boutteau, R., Savatier, X., and Iriart, N.

(2020). Static and dynamic evaluation of an uwb local-

ization system for industrial applications. Sci, 2:23.

Gawel, A., Blum, H., Pankert, J., Kr

amer, K., Bartolomei,

L., Ercan Jenny, S., Farshidian, F., Chli, M., Gramazio,

F., Siegwart, R., Hutter, M., and Sandy, T. (2019). A

fully-integrated sensing and control system for high-

accuracy mobile robotic building construction.

Ghodsian, N., Benfriha, K., Olabi, A., Gopinath, V., and

Arnou, A. (2023). Mobile manipulators in industry 4.0:

A review of developments for industrial applications.

Sensors, 23.

Harati, A. and Siegwart, R. (2007). A new approach to

segmentation of 2d range scans into linear regions.

pages 2083–2088.

Heß, D., Trinh, D., R

ohrig, C., and Parys, M. (2023). Mo-

bilerobot: Control of a redundant kinematic using

drive-steering modules for mobile manipulation.

Jacobs, T. (2018). Omnidirectional robot undercarriages

with standard wheels - a survey. pages 1–6.

Jacobs, T., Connette, C., and H

agele, M. (2012). Design

of wheel modules for non-holonomic, omnidirectional

mobile robots in context of the emerging control prob-

lems. pages 1–4.

Jacobs, T. and Schaefer, E. (2020). Design of compact om-

nidirectional wheel modules with internal differential

kinematics. In ISR 2020; 52th International Sympo-

sium on Robotics, pages 1–7.

KUKA Robotics (2025). Roboter Linearein-

heiten. KUKA Robotics. Available online:

https://www.kuka.com/de-de/produkte-leistungen/

robotersysteme/roboterperipherie/lineareinheiten

(accessed on 5 June 2025).

Li, B., Zhao, K., and Shen, X. (2020). Dilution of precision

in positioning systems using both angle of arrival and

time of arrival measurements. IEEE Access, 8:192506–

192516.

ohrig, C. and Heß, D. (2020). Mobile Manipulation for

Human-Robot Collaboration in Intralogistics, pages

1–20.

ohrig, C., Heß, D., and K

unemund, F. (2017). Motion

controller design for a mecanum wheeled mobile ma-

nipulator.

Sereinig, M., Werth, W., and Faller, L.-M. (2020). A review

of the challenges in mobile manipulation: systems

design and robocup challenges. e & i Elektrotechnik

und Informationstechnik, 137:1–12.

SICK AG (2022). NAV245-10100 Product Datasheet. SICK

AG, Waldkirch, Germany. Available online: https:

//www.sick.com/1074308 (accessed on 15 May 2025).

Wang, J., Li, C., Li, B., Pang, C., and Fang, Z. (2021).

High-precision and robust localization system for mo-

bile robots in complex and large-scale indoor scenes.

International Journal of Advanced Robotic Systems,

18(5):17298814211047690.

Zhewen, Z., Hongliu, Y., Chengjia, W., Pu, H., and Jiangui,

W. (2024). A comprehensive study on mecanum wheel-

based mobility and suspension solutions for intelligent

nursing wheelchairs. Scientiﬁc Reports, 14.

High-Precision Contour Tracking for Mobile Manipulators in Large-Scale Industrial Applications