Possibilistic Extension of Dom ain Information System (DIS) Framework

Deemah Alomair

1,2 a

and Ridha Khedri

1 b

Department of Computing and Software, McMaster University, Hamilton, Canada

Department of Computer Information Systems, Imam A bdulrahman Bin Faisal University, K.S.A.

Keywords:

Uncertainty, Incomplete Information, Knowledge Representation and Reasoning, Ontology Modelling,

Ontologies, Possibilistic Logic, Ontology Reasoning.

Abstract:

Uncertainty poses a signiﬁcant challenge in ontology-based systems, manifesting in forms such as incomplete

information, imprecision, vagueness, ambiguity, or inconsistency. This paper addresses this challenge by

introducing a quantitative possibilistic approach to manage and model incomplete information systematically.

Ontologies are modelled using the Domain Information System (DIS) framework, which is designed to handle

Cartesian data structured as sets of tuples or lists, enabling the construction of ontologies grounded i n the

dataset under consideration. Possibility theory is employed to extend the DIS framework, enhancing its ability

to represent and reason with incomplete information. The proposed extension captures uncertainty associated

with instances, attributes, relationships, and concepts. Furthermore, we propose a reasoning mechanism within

DIS that leverages necessity-based possibilistic logic to draw inferences under uncertainty. The proposed

approach is characterized by its simplicity. It improves the expressiveness of DIS-based systems, introducing

a foundation for ﬂexible and robust decision-making in the presence of incomplete information.

1 INTRODUCTION

One of the primary challenges in knowledge-based

systems, particularly those that rely on ontologies

for domain reasoning, is managing un c ertainty stem-

ming f rom incomplete informatio n. I n dataset-driven

ontologies, data is contextualized to deﬁne con-

cepts, relationships, and instances. However, real-

world applications frequently suffer from missing

or partial informa tion, leadin g to epistemic uncer-

tainty (Sentz and Ferson, 2002). This type of un-

certainty a ffects instance classiﬁcation, attribute re-

liability, relationship strength, and concept validity.

When unaddressed, such uncertainty can render on-

tologies either overly rigid, failing to a c commodate

partial knowledge, or misleading, by permitting un-

justiﬁed inferences. Effectively managing uncer-

tainty is therefore essential to ensure the expressive-

ness, reliability, and ad aptability o f onto logy-ba sed

systems, especially in the context of decision sup-

port or auto mated reasoning systems. To illustrate,

consider a customer service ontology; the con c ept

PositiveFeedback

may depend on attributes like

Satisfaction

Quality

, and

ResponseTime

. If one

https://orcid.org/0000-0001-9397-9999

https://orcid.org/0000-0003-2499-1040

of these values is m issing or partially available, classi-

cal inference systems may fail to classify an instance

PositiveFeedback

or do so incorrectly. This

highlights the n eed f or a framework that can represent

and reason under partial kn owledge.

This pap er introdu c es a quantitative possibilistic

extension to the Domain Information System (DIS)

framework (Marinache et al., 2 021) to represent and

reason und e r partial knowledge. DIS is a bottom-

up, data-centric formalism that constructs ontologies

from datasets, structurally separating the domain on-

tology from the data view and linking them via a map-

ping operator. Unlike Description Logic (DL)-based

ontologies, which separate th e A-Box and T-Box log-

ically, DIS achieves this separation structurally and

grounds the ontology in data, red ucing data-ontology

mismatches. DIS is useful for aligning ontologies

with real-world datasets, which makes it particularly

effective fo r domains where ontologies must be gen-

erated or ada pted from existing data sources, im-

proving modularity, transparency, and maintainability

in ontology design. In contr ast to tra ditional ontol-

ogy languages like Web Ontology L a nguage (OWL),

which struggle to directly represent mereological re-

lationships in Cartesian d atasets (i.e., the structured

data itself) without complex extensions, DIS lever-

108

Alomair, D. and Khedri, R.

Possibilistic Extension of Domain Information System (DIS) Framework.

DOI: 10.5220/0013706800004000

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2025) - Volume 2: KEOD and KMIS, pages

108-119

ISBN: 978-989-758-769-6; ISSN: 2184-3228

ages cylindric algebra and Boolean algebra to model

both data structures an d conceptual part-whole re-

lations. This enables more natural and robust han-

dling of mereological reasoning within structured

data. However, the original DIS mod el does not cap-

ture domain uncertainty and information uncertainty.

The propo sed approach overcomes this by associating

each ontological componen t with quantiﬁed cer tainty.

Unlike vagueness or imprecision, the fo-

cus here is on un certainty due to incomplete-

ness, typically addressed via probability theory

(e.g., (Laha and Rohatgi, 2020)), possibility th eory

(e.g., (Dubois and Prade, 2015)), or Dempster–Shafer

theory (e.g., (Sentz and Ferson, 2002)), as discussed

in (Alomair et al., 2025). I n this study, possibility

theory is adopted and rationale behind this selection

is explained in the section 5.

The proposed appro ach models uncertainty across

all key ontological elem e nts: attributes, concepts, re-

lationships, and instances. The key contributions of

this paper are as follows:

1. Modelling Uncertainty of Attributes: Introduc es a

necessity-based mapping from the d ataset’s attributes

to ontology concepts.

2. Modelling Uncertainty of In stances: Proposes an

instance distribution relation (SV

), allowing a datum

(instance) to be assigned to multiple sorts (attributes)

with varying degrees of certainty.

3. Modelling Uncertainty of Relationships: Intro-

duces necessity-based relationship, wh ich allows re-

lationships to hold with varying levels of certainty.

4. Modelling Uncertainty of Concepts: Reﬁnes the

construction of datascape concepts (which depend on

available data values) by incorporating uncertainty

modelling into their data-specializing predicate.

5. Possibilistic Reasoning for Uncertainty -Aware I n-

ference: Develops a reasoning mechanism within

the DIS framework, leveraging necessity-based pos-

sibilistic logic to support inference under incomplete

informa tion.

The paper is structured as follows: Section 2 in-

troduces foundational theor ie s. Section 3 presents the

integration of possibilistic componen ts into the DIS

framework, followed by uncertainty-aware reasoning

in Section 4. Section 5 reviews relate d work and of-

fers a discussion. Section 6 concludes the paper and

outlines futur e directions.

2 PRELIMINARIES

This section reviews uncertainty in ontolog y, intro-

duces possibility theor y a nd possibilistic logic, and

presents the theoretical background of the DIS frame-

work.

2.1 Uncertainty and Ontolog y

Information imperfection includes incompleten ess,

imprecision, vagueness, ambiguity, and inconsis-

tency (Ma et al. , 2013; Bosc and Prade, 1997). The

paper adopts a broad interpretation, consid ering

uncertainty as arising from any of these deﬁ-

ciencies, as adopted in (Anand and Kumar, 2022;

Ceravolo et al., 2008). Incompleteness arises when

informa tion is partial. This creates uncertainty about

which interpretation of a statement to rely on, of-

ten addressed by calculating an estimation degree

for possible worlds (Straccia, 2013). Imprecision

refers to the lack of exactness, occurring when data

is expressed in approxima te or qualitative terms in -

stead o f prec ise values (Ma et al., 2013). Vagueness

emerges when terms or concepts lack clear bound-

aries (Straccia and Bobillo, 2017). Ambiguity ar ises

from multiple interpreta tions (Ma et al., 2013), and

inconsistency involves contradictions, such as con-

ﬂicting statements (Bosc and Prade, 1997).

An extensive review of uncertainty mod-

elling in domain ontologies is presented

in (Alomair et al. , 2025). The survey examines

over 550 stud ie s published between 2010 and 202 4

on this topic. A guidin g taxonomy is p roposed,

classifying o ntological uncertainty into concept

uncertainty an d information uncertainty. This clas-

siﬁcation supports the systematic id entiﬁcation of

uncertainty types across ontological frameworks and

the selection of appropriate formalisms to manage

them. Concept uncertainty involves uncertainty of

relationships, uncertainty of attributes deﬁning a

concept, and unc ertainty due to semantic ambigu ity,

where context inﬂuences the interpretatio n of a

concept. Information unc ertainty concerns asso-

ciating instance s with concepts or re la tions. The

identiﬁed unce rtainties are a ttributed to incomplete,

imprecise, vague, or inconsistent information. Then,

various formalisms are presented to manage these

uncertainties. This taxonomy offers a structured ap-

proach to understanding and addressing uncertainty

in o ntology-driven systems. A visual r e presentation

of the taxonomy is shown in Figure 1.

2.2 Possibility Theory and Possibilistic

Logic

Possibility theory m odels incomplete and inconsistent

knowledge using qualitative (ordinal) or quantitative

(numerical) approaches (Dubois and Prade, 2015).

Possibilistic Extension of Domain Information System (DIS) Framework

109

Figure 1: Ontological Uncertainty Taxonomy.

The q ualitative approach ranks events withou t nu-

merical degree (e.g., ”highly possible”, ”possible”, or

”less possible”), while the quantitative approach as-

signs a numerical degree to represent degrees of pos-

sibility. Possibility distribution represents an agent’s

knowledge a bout the world by assigning plausibility

degrees to states in a set S, which may be ﬁnite or in-

ﬁnite. Formally, it is a function π : S → L, where L is

a totally ordered scale (often [0,1]). The value π(x)

expresses how plausible the state x ∈ S. A value of

π(x) = 0 means state x is imp ossible, while π(x) = 1

means it is fully plausible. If S is exhaustive, at least

one state must have plausibility 1. The possibilis-

tic framework captures both comp lete and inco mplete

knowledge. Complete knowledge is represented by

assigning possibility 1 to a sin gle state and 0 to all

others. Complete ignorance is mo deled by assign-

ing possibility 1 to all states, indicating that any state

could be true. The possibility distribution forms the

basis for deﬁning possibility and necessity measures

over any sub set X ⊆ S:

Π(X) = sup

x∈X

π(x) and N(X) = inf

x/∈X

(1 − π(x)), (1)

where Π(X) indicates feasibility, and N(X) expresses

certainty (Alola et al., 201 3). The measures are dual

via: N(X) = 1 − Π(X

′

), where X

′

is the comp le -

ment of X . Possibility measures follow the maxitiv-

ity a x iom: Π(A ∪ B) =

max

(Π(A),Π(B)), while ne-

cessity measure satisﬁes the dual minitivity axiom:

N(A ∩ B) =

min

(N(A),N(B)). The necessity degree

for the union o f two sets satisﬁes th e following pr op-

erty, expressed a s (Dubois and Prade, 2014):

N(A ∪ B) ≥

max

(N(A),N(B)) (2)

Unlike probab ility theory, which quantiﬁes

likelihood, possibility theory evaluates feasibility.

In (Zadeh, 1999), a distinction betwe en possibility

and probability theories has been made through an

example of ”Hans is ea ting eggs for breakfast”. In

his example, the possibility distribution of (π

(3) =

1) suggests it is en tirely possible for Hans to eat

three eggs, but the probability (P

(3) = 0.1) indicates

this outcome is statistically rare. Th is demonstrates

that high possibility does n ot imply high probabil-

ity, though an impossible event (π

(u) = 0) has zero

probability (P

(u) = 0).

Possibility theory underpins possibilistic lo gic,

which we limit here to necessity-based possibilistic

logic (Dubois et al., 1994; Dubois and Prade, 2014;

Nieves et al., 2007). In this logic, a formula is a pair

(θ,α), where θ is a classical ﬁrst-order logic formula,

and α ∈ [0, 1] is a certainty or priority degree. Th is

pair indicates that θ is certain at least to level α, (i.e.,

N(θ) ≥ α). Th e interval [0,1] can be replaced by

any linearly ordered scale. Standard lim it conditions

hold: Π(⊥) = N(⊥ ) = 0, Π(⊤) = N(⊤) = 1, where

⊥ and ⊤ denote contradiction and tautology, re spec-

tively. In the formal system of this logic, the follow-

ing properties hold: N(θ ∧ γ) =

min

({N(θ),N(γ)})

and N(θ ∨ γ) ≥

max

({N(θ),N(γ)}), where θ and γ

are formulae. One of its ma in rules is the weakest

link resolution rule:

(¬θ ∨ γ,α),(θ ∨ δ,β) ⊢ (γ ∨ δ,

min

(α,β)), (3)

Here, the conclusio n’s certainty is the smallest among

the premises, reﬂecting that an inference chain is lim-

ited by its weakest premise.

The weighted minimum and maximum

operations, introdu ced in (Grabisch , 1998;

Dubois and Prade, 1986) within the framework

of possibility the ory, generalize the standard

min

and

max

functions to account for elements from different

contexts, each associated with a distinct weight of

importance. These op erations reﬁne aggregation by

modulating the inﬂuence of each element based on

its assigned weight.

Let X = {x

,· ·· ,x

} be a set of criteria. Let a

and

be, respectively, the score and the weight of impor-

tance attributed to criterion x

such that Σ

i=1

= 1.

Then we have:

Weighted Min

,· ·· ,a

) =

min

(i | 1 ≤ i ≤ n :

max

((1 − w

),a

)).

This formulation ensures that elements w ith lower

weights con tribute less to the overall minimum com-

putation. Similarly, the operation

Weighted Max

given by:

Weighted Max

,· ·· ,a

) =

max

(i | 1 ≤ i ≤ n :

min

)).

KEOD 2025 - 17th International Conference on Knowledge Engineering and Ontology Development

110

2.3 Domain Information System

DIS is an ontology framework consisting of

three primary components (Marinache et al., 2021;

Marinache, 2025): Domain Ontology View (DOnt)

O, Domain Data View (DDV) A, and mapping func-

tion τ linking A to O, forming the structure D =

(O,A,τ).

The DOnt, O = (C ,L, G), is composed of three el-

ements. The concept structure C = (C,⊕,e

), which

is a commutative idempoten t monoid where the ca r-

rier set C includes an em pty concept (e

), a set of

atomic co ncepts (T ) derived directly from d a ta set at-

tributes, and composite concepts forme d using the ⊕

operator. The Boolean la ttice L = (L, ⊑

) organizes

concepts hierar chically based on a natural order ⊑

deﬁned as c

⊑

⇐⇒ c

⊕ c

= c

. Lastly, the set

of rooted graphs G pr ovides additional expressiveness

by capturing concepts and relations beyond those de-

ﬁned by the lattice structure. Each roo ted graph G

) consists of a set o f vertices C

⊆ C, a set of

edges R

, and a root vertex t

∈ L.

The D DV, A = (A,+,⋆,−,0

,{c

}

k∈U

), is

formalized as a diagonal-free cylindric algebra, whe re

U is a ﬁnite set of sorts (the universe). The main

notion of this view is sor t, which corresponds to a n

attribute in the dataset. The ordered pair of a sort

and its value is known as

Sorted Value

(

). A

set of

with a ma ximum of one

for each sort

forms

Sorted Datum

(

S Datum

). The carrier set A

consists of

Sorted Data

(

S Data

), structured as a set

S Datum

. The cylindriﬁcation operators c

are in-

dexed by the sorts used in the data, corresponding to

the elements o f L, the carrier set of the Boolean lattice

L. For a deeper under standing of cylindric algebra,

readers are referred to ( Imieli´nski and Lipski, 1984).

The ﬁnal component of DIS is the mapp ing func-

tion τ : A → L, which links the elements of A in DDV

to their corresponding conc epts in the Boolean lattice

L within DOnt. To deﬁne τ, several helper opera-

tors in troduced, one of which is the helper map ping

operator η : U → L. This ensures a one-to-one corre-

spondence between the sorts in DDV and the atomic

concepts in the Boolean lattice of DOnt. Ensuring

a seamless mapping from data attributes to ontology

concepts: η(S

attr

) = attr, where S

attr

and attr are a

sort and an atomic concept, respectively.

In DIS, concepts ar e categoriz ed based on their de -

pendence on objective reality or data elem e nts, lead -

ing to the distinction between objective concepts and

datascape concepts, de noted by C

. Objective con-

cepts exist independently of any dataset. For instance,

consider the objective statemen t ∃(x | x ∈ Animal :

Pet(x)). The concept Pet remains valid regardless

of wheth er supporting data is available. In contrast,

datascape conce pts rely on data for their deﬁnition

and existence. For instance, consider the modiﬁed

example ∃(x | x ∈ Animal : Active

Pet(x)). The con-

cept Active

Pet, deﬁned as a pet that exercises fo r at

least one hour daily, depen ds on a speciﬁc data source

such as d a ily ac tivity log s. If such data is unavailable

or does not meet the require d con ditions, the concept

cannot be re alized. Formally, a datascape concept in

a DIS is deﬁned as follows:

Deﬁnition 1 (From (Alomair and Khedri, 2025),

Datascape Concept). Let D = (O, A,τ) be a g iven

DIS. For a carrier set A in A and a lattice L in

O, a datascape concept C

is deﬁned as follows:

def

= {a | τ(a) ∈ L ∧ Φ(a)}, where a ∈ A and Φ

is a data-specializing predicate expressed in Disjunc-

tive Normal Form (DNF). This predicate Φ is given

by: Φ(a) =∨ (i | 1 ≤ i ≤ N : Ψ

(a)), with N is a

natural nu m ber, and each conjunctive clau se Ψ

(a)

is deﬁned as: Ψ

(a) =∧ ( j | 1 ≤ j ≤ M : Ω

(i, j)

(a)),

where M is a n atural number and Ω

(i, j)

(a) = ( f

(i, j)

(a·

sort

name

(i, j)

),c

(i, j)

) ∈ R

(i, j)

, where f

(i, j)

∈ F , and

F = {⊕,e

,⊤

,+,⋆,−,0,1,τ,cyl} is the set of func-

tion symbols, c

(i, j)

is a gro und term in the DIS lan-

guage, and R

(i, j)

is a relator.

Based on the above deﬁnition, we deﬁne the oper-

ation ⊕ as an operation on concepts.

Deﬁnition 2. Let D = (O,A, τ) be a given DIS. Let

= {a | τ(a) ∈ L ∧ Φ

(a)}, and C

= {a | τ(a) ∈

L ∧ Φ

(a)} be two d atascape concepts deﬁned on D.

We have C

⊕C

∪ C

= {a | τ(a) ∈ L ∧ (Φ

(a) ∨ Φ

(a))}.

The structure of the C

⊕ C

is that of a datas-

cape as (Φ

(a) ∨ Φ

(a)) is in DNF and the othe r con-

ditions stipulated by Deﬁnition 1 are satisﬁed. More-

over, the empty concept e can be perceived as a datas-

cape concept deﬁned as e = {a | τ(a) = e

∧ false} =

0. Hence, if we take, for a given DIS, C

is the set of

datascape concepts, then (C

,⊕,e

) is a commutative

monoid due to the pr operties of set union.

Illustrative Example of DIS Construction. We co n-

sider a

CustomerService

dataset with the attr ibutes:

Satisfaction

Quality

, and

ResponseTime

. The

correspo nding DIS structure is built as follows:

1. Lattice construction: Each dataset attribute

is mapped to an atomic concept: τ =

{(

Quality

Status

),(

ResponseTime

Duration

(

Satisfaction

Comfort

)}. Then the rest of the

Boolean lattice is generated, where each node rep-

resents a possible composition of atom ic con cepts

(e.g.,

status Tenure

Status

⊕

Duration

Possibilistic Extension of Domain Information System (DIS) Framework

111

2. Objective roote d graph concept: Rooted graphs

enrich the ontology beyond lattice nodes.

One such objective concept is

Feedback

rooted at

CustomerService

, and deﬁned ab-

stractly as follows:

Feedback

def

= {a | τ(a) ∈

CustomerService

3. Datascape rooted graph concept: A rooted graph

concept might be a datascape concept, in which

its deﬁnition depends o n data. For exam-

ple, the concept

PositiveFeedback

can be

deﬁned as:

PositiveFeedback

= {a | τ(a) ∈

CustomerService

∧ a.

Satisfaction

≥ 0.6}.

The predicate here indicates tha t an instance a of

the

Satisfaction

attributes sho uld have a value

greater than or equa l to 0.6.

4. Construc tion of the domain data view: An ex-

ample of

is (

Quality

Good

). An exam-

ple of

S Datum

is dt 1 = {(

Quality

Good

(

ResponseTime

Fast

), (

Satisfaction

Yes

)}.

An example o f

S Data

is a = {dt 1,dt n}.

5. Building the whole DI S system: The D IS is then

formed by (O,A,τ). A full illustration of the DIS

structure is shown in Figure 2.

Figure 2: Customer Service DIS Framework.

3 UNCERTAINTY MODELLING

IN DIS FRAMEWORK

In this section, we extend the DIS fram ework to

handle uncertainty by addressing two key que stions:

What type o f unce rtainty can be modelled, and where

in the DIS framework it can be introduced. As note d

in section 1, we focus on incomplete information and

adopt possibility theory as the formalism.

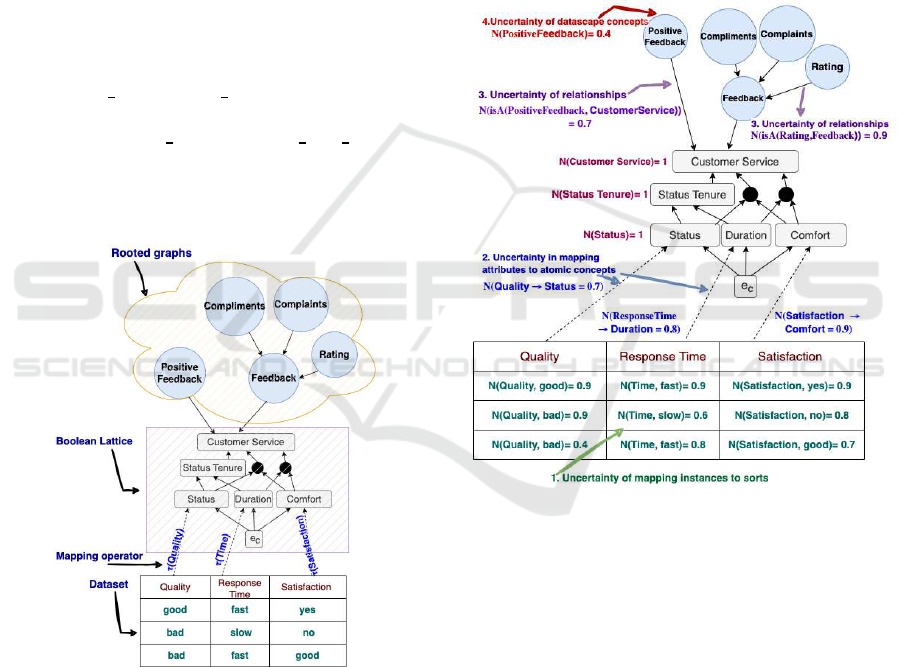
To illustrate where uncertainty can arise, Figure 3

shows an example using a customer service dataset.

Database attributes may assign values, introducing

uncertainty of instances. These attributes are mapped

via the operator τ (shown by arrows) to atomic con-

cepts introducing uncertainty of attributes. The lat-

tice is further expanded with multiple rooted gra phs,

such as

PositiveFeedback

and

Feedback

, introduc-

ing uncertainty of concep ts. The

Feedback

graph in-

cludes specialized c oncepts like

Rating

, with arrows

indicating sem a ntic paths among th e se concepts, cap-

turing the uncertainty of relationships.

Figure 3: Necessity Degrees Assigned to D I S.

Since the focus is on uncertain ty due to incom-

plete info rmation, it is cru cial to distinguish between

data and inform a tion. In our formalism, a datu m is

strictly a raw value witho ut any assigned context (e.g.,

the num ber 3.7 isolated fr om metadata, units, or se-

mantics). At this stage, it has no uncertainty; Un-

certainty arises only when contextual interpretation is

applied (e.g., labelling 3.7 as “sensor voltage reading

with ±0.2 error”). We acknowledge that the broader

literature often tr eats data as implicitly contextualized

(and th us uncertain), but our formalism explicitly sep-

arates raw values from their con textua l layers. It is

also important to emphasize that the assigned degree

is explicitly interpreted as a measure of certainty, not

as a degree of truth or graded quality. For this reason,

we ad opt necessity-based possibilistic logic, wh e re

KEOD 2025 - 17th International Conference on Knowledge Engineering and Ontology Development

112

necessity degrees directly cor respond to the degree of

certainty. This interpretation aligns naturally with our

setting, in which the degree reﬂects the certainty in

the existence of concep ts, in instance- to-concept and

attribute-to-concept associa tions, and in th e presence

of relationships. In our approach, we examine four

types of uncer ta inty:

1. Uncertainty of mapping in sta nces to sorts: When

mapping a value to a sort(attribute), for example, as

indicated in Figure 3, the

Quality

attribute being as-

signed values like

Good

Bad

, with a necessity de-

gree reﬂecting the degree of certainty with which the

value belongs to a given sort. For instan ce, assigning

(

Good

,0.9) to

Quality

indicates that for this particu-

lar instanc e, it is 0.9 certain that the

Quality

Good

2. Uncertainty in mapping attributes to atomic con-

cepts: When mapping a sort to a lattice concept, such

as associating

Quality

with the

Status

concept as

Quality

→

Status

) = 0.7 .

3. Uncertainty of relationships: When deﬁning rela-

tionships am ong r ooted graph concepts, like the rela-

tionship betwe e n

Rating

and

Feedback

is associated

with N(

isA

(

Rating

Feedback

)) = 0.9.

4. Uncertainty of datascape concepts: This

uncertainty arises when a concept is deﬁned

in terms of data co nditions that may them-

selves be unc e rtain. For example, consider

the datascape concept

PositiveFeedback

, de-

ﬁned as

PositiveFeedback

= {a | τ(a) ∈

CustomerService

∧ a.

Satisfaction

≥ 0.6}.

Here, the condition (Φ(a) = a.

Satisfaction

≥ 0.6)

is the data-specializing predicate that character-

izes the concept. In our fram ework, the necessity

degree of the datascape concept itself, that is, the

degree to which the concept

PositiveFeedback

holds in the presence of incomplete inform ation, is

derived dir e ctly from the necessity with which its

data-specializing predicate is satisﬁed.

The ﬁrst three types of uncertainty that are listed

above are given by the domain expert, while the last

one is calculated .

3.1 Uncertainty of Mapping Instances

to Sorts

In the traditional DIS framework, data records

(instances) are typically assigned to sorts (attributes)

through a certain mapping fun ction. Th is assign-

ment is

: V → U, where V is a ﬁnite set of

values assigned to the sort, and U is a ﬁnite set

of sorts (the universe). For example, consider a

customer service database presented in Figure 3,

where the a ttribute

Quality

can take values such

Good

and

Bad

. The traditional mapping function

would assign these values to the

Quality

sort,

(

Good

) =

Quality

and

(

Bad

) =

Quality

However, u ncertainty brings nondeterminism in this

mapping, as a value might be assigned to several

sorts with some degree of certainty. Hence, to

account for the uncertainty in these assignments,

we introduce a new relatio n called the instance

distribution relation, deno ted SV

, and deﬁned as

⊆ V × U × [0,1]. The r elation SV

relates a

data value to sor ts and necessity degree tha t represent

the degree of certainty in the assignment. A da ta

value might be assigned to several sorts with varying

degrees of certainty. In the example, the instance

distribution relation could re turn values like: SV

{ (

Good

Quality

,0.9)),(

Bad

Quality

,0.9)),

(

Bad

Quality

,0.4)),(

Good

Satisfaction

,0.7))}.

Here, the data value

Good

is assigned to the

Quality

sort with a certainty of 0.9, while the value

Bad

assigned to the same sort with two different certainty

degrees: 0.9 and 0.4. These reﬂect varying contexts,

such as different data records, whe re assignment

certainty d iffers. Although the notation does n ot

explicitly represent context, it is implicitly captured

through association with different instances. Add i-

tionally,

Good

is assigned to the

Satisfaction

sort

with a certainty of 0.7. This extension enables the

framework to better reﬂect un certainty by accommo-

dating varying degrees of certainty in data-to-sort

assignments.

3.2 Uncertainty in Mapping Attributes

to Atomic Concepts

As previously discussed in subsection 2.3, the DI S

framework deﬁnes the helper mapping operator η :

U → L, which assigns each sort (attributes) in U to its

correspo nding atom ic concept in the Boolean lattice.

Similar to the uncertainty of instances, uncertainty in

attribute mapping introduces non-determinism when

associating sorts with atomic lattice concepts. To ac-

count for this, we deﬁne the mapping distribution re-

lation η

, which captures the uncertainty in this map-

ping. The relation η

⊆ U × L × [0,1] is provided

by a domain expert, and assigns a necessity degree to

each potential mapping.

Consider th e customer service database presented

in Figur e 3, where the m a pping operators η are de-

ﬁned as follows:

η(

Quality

) =

Status

,η(

Satisfaction

) =

Comfort

,η(

ResponseTime

) =

Duration

Possibilistic Extension of Domain Information System (DIS) Framework

113

In this mapping, the sorts

Quality

Satisfaction

and

ResponseTime

correspo nd to the atomic con-

cepts

Status

Comfort

, and

Duration

, respectively.

To capture the uncertainty in the se mappings, the

mapping distribution relation η

assigns a necessity

degree to each a ssocia tion:

(

Quality

) = (

Status

, 0.7),

(

Satisfaction

) = (

Comfort

, 0.9),

(

ResponseTime

) = (

Duration

, 0.8).

These degrees indicate the degree of certainty in each

mapping, allowing the DIS framework to handle the

uncertainty in the alignment betwee n data attributes

and ontology concepts.

3.3 Uncertainty of Relationships

Within the DIS framework, there are relationships be-

tween the co ncepts of rooted graphs and a parthood

relationship between the concepts of the Bo olean lat-

tice. The parthood re la tionship ⊑

forms the rela-

tionship between objective concepts given in the lat-

tice. The existence of this relationship among lat-

tice concepts is certain, as they are constructed by

a Cartesian construction from the ato mic concepts.

In othe r terms, a concept k

is considered a

partOf

another concept k, if k

is a Cartesian projection of

k or if its atomic structur e is a subset of that of k.

However, the relations among the concepts of the

rooted g raph might be uncertain. Given a rooted

graph G

= (C

), C

⊆ C, R

⊆ C

× C

, t

∈ L,

its relation is transformed to give each edge a neces-

sity degree. We extend R

to a necessity-based R

Hence, R

⊆ R

× [0,1], which incorporates nece ssity

degrees to quantify the degree of cer ta inty associated

with each relationship.

In the customer service database illustrated

in Figure 3, the relation o f the rooted graph, denoted

by R

, is the following: R

{(

isA

(

PositiveFeedback

CustomerService

)),

(

isA

(

Complaints

Feedback

)),

(

isA

(

Rating

Feedback

)),

(

isA

(

Feedback

CustomerService

)),

(

isA

(

Compliments

Feedback

))}

Hence, the relations R

is given as follows: R

= {

(

isA

(

PositiveFeedback

CustomerService

),0.4),

(

isA

(

Complaints

Feedback

),1),

(

isA

(

Rating

Feedback

),0.9)

(

isA

(

Feedback

CustomerService

),0.5),

(

isA

(

Compliments

Feedback

),0.7)}

These necessity degrees quantify the degree of cer-

tainty in each relationship, enabling the framework

DIS to systematically capture and reason about un-

certainty in relational structures.

3.4 Uncertainty of Datascape Concepts

If we examine the elementary predicate Ω

(i, j)

(a),

which is used in building the data-spec ia lizing pre di-

cate Φ(a) of a datascape concept and which is equal

to ( f

(i, j)

(a·

sort name

(i, j)

),c

(i, j)

) ∈ R

(i, j)

, we ﬁnd that

there are two sources of uncertainty. The ﬁrst comes

from mapping a datum a to a sort due to the usage

of the term a ·

sort name

(i, j)

, an d th e second comes

from the relator R

(i, j)

used in Ω

(i, j)

(a). He nce, by

capturing these two sources of uncertainty, we capture

the uncertain ty of th e d a ta scape concept. For that, we

adopt the weighted minim um function, previously de-

ﬁned in subsection 2.2. The weights of instance map-

ping w

inst

, and the weight of the relationship w

rel

assign relative importanc e to the necessity measures

(a) and R

(a), with w

inst

+ w

rel

= 1. Then, we

have the following inductive procedur e for calculat-

ing the nec essity degree N

Φ(a)

of a datascape concept

having Φ as its data-specializing predicate.

Procedure 3.1 (Necessity Degree of a Datascape

Predicate). Let D = (O,A, τ) be a given DIS. Let

= {a | τ(a) ∈ L ∧ Φ(a)} be a datascape con-

cept that is deﬁned within D, and has Φ as its spe -

cializing predicate. For a given element a ∈ A, let

δ = (w

inst

= w

Wrel

) ∨



(SV

(a) ≤ (1 − w

inst

)) ∧

(i, j)

(a) ≤ (1 − w

Wrel

))



. The n ecessity degree

N(Φ(a)) is computed indu ctively as follows:

• Base cases:

1. N(true) = 1;

2. N(false) = 0.

3. N(Ω

(i, j)

(a)) =











min



(a),R

(i, j)

(a)



, if δ = true,

min

max



(1 − w

inst

),SV

(a)



max



(1 − w

rel

),R

(i, j)

(a)



, otherwise.

• Inductive cases:

1. Conjunction of atomic predicates:

N(Ψ

(a)) = min



j | 1 ≤ j ≤ M : N(Ω

(i, j)

(a))



2. Disjunction of conjunctive clauses:

N(Φ(a)) = max



i | 1 ≤ i ≤ N : N(Ψ

(a))



KEOD 2025 - 17th International Conference on Knowledge Engineering and Ontology Development

114

In the base case, the necessity degree of ea ch

atomic pr edicate is consid ered. The necessity degree

of the ground terms true and false are , respectively,

1 and 0. For the elementa ry term Ω

(i, j)

(a) forming

Φ(a), we have several cases:

• When we have equal weights of all the criteria, then

the weights are omitted in determining N(Ω(a)).

• When both the certainty of a m a pped to its sort

is below 1 minus the weight assigned to the map-

ping, and the certainty of the relator R

(i, j)

(a) used

in Ω is also below 1 minus the weight assigned to

the relationship, then the weights are also omitted.

Hence, when (SV

(a) ≤ (1 − w

inst

) and R

(i, j)

(a) ≤

(1 − w

Wrel

) m eans that the importance or inﬂuence of

the mapping of instances to sorts and the relator in the

overall-uncertainty determination outweighs the level

of uncertainty a ssoc ia ted with it. That is why we ig-

nore the weights in this case.

We can extend the necessity degree function to the

datascape concepts as follows: N(C

)

def

= N(Φ) =

max



a | a ∈ A : N(Φ(a))



, where C

= {a | τ(a) ∈

L ∧ Φ(a)} is a datascape concept that is deﬁned

within a DIS D. We take the

max

of the individual

necessity degrees due to the union property described

earlier in Equation 2.

For o bjective concepts in the lattice, the composi-

tion operator ⊕ enables the formation of new concepts

by comp osing existing ones i.e., creating composite

concepts f rom the set of atomic concepts T . Writing

k = k

⊕ k

means that concept k is constructed by

the Cartesian product of concepts k

and k

. These

concepts are certain and carry no unce rtainty. An al-

ternative way to consider uncertainty in an objective

concept is considering its specializing predicate that

is always true, hence its certainty degree is 1.

4 REASONING ON

POSSIBILISTIC DIS

FRAMEWORK

We discuss several reasoning tasks and their govern-

ing inference rules for deriving conclusions in differ-

ent reason ing scenarios. These tasks are concept sat-

isﬁability and concept subsumption. Each of which is

explained in detail. We use N to denote the n ecessity

degree function.

4.1 Concept Satisﬁability

In this subsection, we examine concept satisﬁability

in necessity-based reasoning within the DIS frame-

work, distinguishing between the objective and the

datascape concept satisﬁability.

In the classical DIS framework, a datascape con-

cept is considere d satisﬁable if its corresponding data

values exist within the carrier set of the DDV. How-

ever, in the necessity-b a sed extension of DIS, we in-

troduce the necessity degree to account for incom-

plete information of the data specializin g predicate

(Φ(a)), which deﬁn e s the datascape concept. In

this extended framework, a datascape concept C

deemed satisﬁable if ther e exists a t least one instance

a ∈ C

such that the necessity degree N(a,C

) of this

instance is strictly greater than zero. Therefore, a

datascape concept is satisﬁable if and only if its ne-

cessity degree is strictly greater than zero, indicating

that there is sufﬁcient data support for the con c ept’s

existence.

Deﬁnition 3. Let D = (O,A, τ) be a given DIS. Let

= {a | τ(a) ∈ L ∧ Φ(a)} be a datascape concept

that is deﬁned within D, with Φ(a) as its data spe-

cializing predicate. The datascape concept C

is sat-

isﬁable, denoted by stsfd(C

), if and only if ∃(a |

a ∈ A : N(Φ(a)) > 0 ).

For objective concepts within the Boolean lattice,

their certainty is inheren tly guaranteed, as they are

directly linked to the DDV of the DIS under con-

sideration. Thus, their satisﬁability is inherently en-

sured, m eaning they are both valid and certain to ex-

ist. The satisﬁability of a c omposite concept is also

guaran teed, as its atomic components have a degree

of necessity of one. In this case, the combin a tion of

their necessity degree results in the composite con-

cept also having a necessity degree of one, ensuring

its satisﬁability. If, from another perspective, one sees

objective conc epts as con cepts that are independent

of datasets, which translates into a data specializing

predicate equivalent to true, then using Deﬁnition 3

and Procedure 3.1(item 1), one infers that its n eces-

sity degree is also equal to one.

Claim 4.1. Let C

and C

be datascape concepts

deﬁned in a given DIS. Let Φ

(a) and Φ

(a) be their

data specializing predicates, respectively. We have

stsfd(C

⊕C

) ≡ stsfd(C

) ∨ stsfd(C

Proof. The concepts C

and C

are two da tas-

cape concepts. Hence, by Deﬁnitio n 1 and for D =

(O,A,τ) is a given DIS, we can write C

and C

as follows: C

def

= {a | τ(a) ∈ L ∧ Φ

(a)}, a nd

def

= {a | τ(a) ∈ L ∧ Φ

(a)}.

Then, we have

stsfd

⊕C

)

≡ h Deﬁnition 2 i

stsfd

{a | τ(a) ∈ L ∧ (Φ

(a) ∨ Φ

(a))}

Possibilistic Extension of Domain Information System (DIS) Framework

115

≡ h Deﬁnition 3: Satisﬁability of datascape

concept i

∃(a | a ∈ A : N(Φ

(a)) > 0 ∨ N(Φ

(a)) > 0 )

≡ h Axiom Distributivity f or ∨ i

∃(a | a ∈ A : N(Φ

(a)) > 0 )

∨ ∃(a | a ∈ A : N(Φ

(a)) > 0 )

≡ h Deﬁnition 3 i

stsfd

) ∨

stsfd

)

Example 4.1 (Satisﬁability of a Datas-

cape Conce pt). Consider the data scape con-

cept PositiveFeedback = {a | τ(a) ∈

CustomerService ∧ a.Satisfaction ≥ 0.6}.

Thus, this concept consists of a single atomic predi-

cate: Ω(a) = (a.Satisfaction ≥ 0.6). Assume

the following information is provide d by a domain

expert:

• Instance distribution relation:

) = (Good,(Satisfaction,0.7))

• Relator necessity degree: R

) = (Good ≥

0.6, 0.8)

• Wig hts of importance : w

inst

= 0.4, w

Wrel

= 0.6

Then, usin g Procedure 3.1, we compute the necessity

degree of the atomic predicate:

min



max(1 − w

inst

,SV

)), max(1 − w

Wrel

))



= min (max(0.6, 0.7), max(0.4,0.8)) = 0.7

Since Φ(a) consists of just this atomic predicate, we

have:

N(C

) = N(Φ(a)) = N(Ω(a

)) = 0.7

By Deﬁnition 3, the concept is satis-

ﬁable because N(Φ(a)) > 0. Hence:

stsfd(PositiveFeedback) holds.

4.2 Necessity-Based Subsumption

In general, we say that a concept C

subsumes a con-

cept C

if every instance of C

is in C

. In c la ssical

DIS, we have an additional kind o f subsumptio n re-

lationship. It is the

partOf

relationship, denoted by

⊑

, that exists among the mem bers of the Boolean

lattice. When we write C

⊑

, it indicates that the

instances of C

are obtained through the projection of

correspo nding instances of C

on the attributes deﬁn-

ing C

. In this case, we say that C

subsumes C

. The

formal deﬁnition of DIS based subsumption is given

below:

Deﬁnition 4. Given a DIS D = (O,A, τ). Let C

and

be two concepts in the set of concepts of D. We

say that C

⊑ C

iff one of the conditions holds:

1. C

∈ L ∧ C

⊑

2. C

and C

are two datascape concepts with data

specializing predicates Φ

and Φ

, respectively and

∀(a | a ∈ A : Φ

(a) =⇒ Φ

(a)).

3. C

∈ L and C

is a datascape concept. We have

) ∈ R

∗

, where R

∗

is the reﬂexive transitive c lo-

sure of a relation R of the graph roote d at C

Deﬁnition 4 formalizes conce pt subsumption in

DIS, covering both objective and datascape con c epts.

First, if C

and C

are objective con c epts in the ontol-

ogy lattice, subsumption h olds if C

⊑

, meanin g

is structurally more speciﬁc than C

per the lat-

tice order, reﬂecting the traditional subclass relation

of the lattice hierarchical struc ture. Second, if both

are datascape concepts deﬁned by data specializing

predicates Φ

and Φ

, then C

⊑ C

holds if ∀a ∈ A,

the implication Φ

=⇒ Φ

is satisﬁed. T his ensures

all instances satisfying C

also satisfy C

. Third, if

is an objective concept and C

is a datascape, sub-

sumption ho lds if a path exists from C

to C

in the

reﬂexive-transitive closure R

∗

of relation R. Notably,

all concepts in the graph rooted at C

are considered

a spec ialization of C

. Subsumption is a partial order

(reﬂexive, antisymmetric, transitive) over c oncepts, as

stated in the following claim.

Claim 4.2. Given a DIS D = (O,A,τ), the subsump-

tion relation on the set of concepts in D is a partial

order.

Proof. We provide a proof for each case of the sub-

sumption relation as given in Deﬁnition 4.

1. In the ﬁrst case, the subsumption relation is iden-

tical to the

partOf

(i.e., ⊑

) relation. The latter sat-

isﬁes the pro perties required for subsumption (reﬂex-

ivity, tr ansitivity, and anti-symmetry) because it is de-

ﬁned on a Boolean lattice, which is itself a p artially

ordered set (poset) (Mar inache, 2025).

2. In the seco nd case, the subsumption relation ⊑

deﬁnes a partial order over the datascape concepts.

This is due to the proper ties of the logical =⇒

operation that satisﬁes the properties of partial or-

der (Gries and Schne ider, 1993, Pages 57-59 ).

3. In the third case, subsumption is interpreted as

membersh ip to the reﬂexive transitive closure R

∗

. It

is established that a reﬂexive transitive closure on an

acyclic graph is a partial order. Indeed, the rooted

graphs a re acyclic, as furthermor e each is a Directed

Acyclic Gr aph (DAG).

KEOD 2025 - 17th International Conference on Knowledge Engineering and Ontology Development

116

In the context of necessity-based subsumption,

the subsumption ne cessity degree is determined by a

domain expert. In addition, as the transitivity of sub-

sumption applies, the degree of transitive subsum p-

tion is governed by the weakest link resolution rule,

presented previously in subsection 2.2. T his approach

to possibilistic transitivity reasoning has bee n adopted

in prior research (e.g., (Mo hamed et al., 2018;

Benferhat and Bouraoui, 201 5)) and has shown effec-

tiveness in han dling uncertainty within possibilistic

ontologies.

Claim 4.3. Let D = (O,A, τ) be a DIS. Let C

, C

and C

be concepts deﬁned in D. Let

⊑

= {(C

) | C

∈ C ∧ C

⊑ C

}

and R

⊑

is its corresponding necessity relation. We

have:

((C

),α) ∈ R

⊑

∧ ((C

),β) ∈ R

⊑

=⇒ ((C

),min(α,β)) ∈ R

⊑

Proof. ((C

),α) ∈ R

⊑

∧ ((C

),β) ∈ R

⊑

≡ h Deﬁnition of R

⊑

) ∈ R

⊑

∧ (C

) ∈ R

⊑

∧ N((C

)) = α ∧ N((C

)) = β

=⇒ h Transitivity of R

⊑

and the weakest link

resolution rule (Equation 3) i

) ∈ R

⊑

∧ N((C

)) =

min

(α,β)

≡ h Deﬁnition of R

⊑

((C

min

(α,β)) ∈ R

⊑

The nece ssity- based subsumptio n between objec-

tive c oncepts (

partOf

relation) invariably assumes

a necessity degree of 1, since the parthood rela-

tion among lattice concepts is considered fully cer-

tain i.e., N(

partOf

) = 1, as indicated previously

in subsection 3.3. This certainty extends naturally to

the transitivity of

partOf

relation, wher eby the mini-

mum necessity degree comp uted over a chain of part-

hood relations, among lattice concepts, gives a degree

of 1.

Example 4.2 (Transitivity of Concept Subsump-

tion in DIS). Let C

= Complaints, C

Feedback, C

= CustomerService be three

concepts deﬁned in given DIS. Suppose the following

necessity-based subsump tion relationships are pro-

vided by the domain expert:

{((Complaints,Feedback),0.6),

((Feedback,CustomerService),0.8)} ⊆ R

⊑

By Claim 4.3, the transitive subsumption relation

holds with:

N(Complaints,CustomerService) = 0.6

5 RELATED WORK AND

DISCUSSION

This section reviews ontology mo delling approaches

that handle uncertainty using possibility theory, an d

explains our choice of this formalism.

In possibilistic DL-based approaches, u ncertainty

is modelled by assigning necessity or possibility

degrees to ontology axioms at different levels. For

instance, Pb-π-DL-Lite (Boutouhami et al., 2017)

assigns ne c essity degrees only to ABox assertions,

allowing uncertain instance membership such as

(

Status

Good

) = 0.9 in the

CustomerService

domain, without modelling uncertainty at concept

or relationship levels. The work of (Sun, 2013)

focuses o n uncertainty at the TBox level, as-

signing necessity degrees to TBox axioms such

as N(

isA

(

Rating

Feedback

)) = 0.8, yet does

not support uncertain instance classiﬁcation

or data-driven concept deﬁnitions. Similarly,

studies such as (Benferhat and Bouraoui, 2015;

Benferhat et al., 201 4; Qi et al., 2011) extend pos-

sibilistic logic to both TBox and A Bo x axioms,

enriching the expressiveness by allowing weighted

axioms at multiple levels; however, their frameworks

still assume that concepts like

PositiveFeedback

are deﬁned and do not enable concept deﬁnitions

directly derived fro m data (i.e., datascape concepts).

The study of (Mohamed et al., 2018) further incor-

porates possibility distributions over interpretations,

adding expressiveness to represent uncertainty about

models themselves, but does not provide mechanisms

to ground concepts in uncertain data attributes or

integrate gra ded uncertainty at the attribute-concept

mapping level.

At the language level, (Saﬁa and Aicha, 2014)

propose extending Web Ontology Language 2

(OWL2) with possibilistic annotations, enablin g un-

certainty representation in both concepts and in-

stances. Using the

CustomerService

example, on e

could an notate a concept like

PositiveFeedback

, or

an instances like

Fast

with possibility degree s, yet

the approach still requires concepts to be pre-deﬁned

and does not suppo rt automatic or context-aware con-

struction of co ncepts from data conditions. Finally,

the work of (Ben Salem et al., 2018) assigns possibil-

ity degrees directly to concepts outside DL seman-

tics, like assigning possibility degree to the concept

PositiveFeedback

, but does not address un certainty

propagation from attribute data to instances or mode l

uncertainty in relationships or attribute m appings.

In contrast, our DIS-based framework uniquely in-

tegrates uncertainty at all levels: attributes, instances,

relationships, and d ata-driven concepts. For exam ple,

Possibilistic Extension of Domain Information System (DIS) Framework

117

we model uncertain attribute-conce pt mappings such

as N(

Quality

→

Status

) = 0.7, uncertain in stance-

concept classiﬁcation like (

Good

,0.9), and relation-

ships such as N(

isA

(

Rating

Feedback

)) = 0.9. Our

datascape concept

PositiveFeedback

is deﬁned by

a data-specializing predicate reﬂecting the actual sat-

isfaction values, allowing uncertainty in satisfaction

data to propagate naturally to the mem bership degree

PositiveFeedback

concept. This uniﬁed, data-

grounded modelling allows more expressive, context-

aware reasoning abou t u ncertain information com-

pared to existing possibilistic ontology methods.

From a methodological standpoint, choosing an

uncertainty formalism requires alignment with the

modelling goals and constraints of the framework.

While several candidates exist, including probabilis-

tic approaches and Dempster-Shafer Theory (DST),

we ad opt possibility theor y for its suitability to

our framework. Probability theory enforces the

additivity axiom, requiring the sum of probabil-

ities for mutually exclusive events in a universe

of discour se to equal one even under insufﬁcient

data (Kovalerchuk, 2017), leading to challenges in ac-

curately repr esenting uncertainty. In contrast, possi-

bility theory relaxes this constraint, making it more

suitable for the proposed a pproach. This ratio-

nale is supported by several possibilistic on tology

frameworks (e.g., (Bal-Bourai and Mokhtari, 2016;

Boutouha mi et al., 201 7)). Regarding DST, it is

primarily designed for belief fusion from multi-

ple sources (Mc Clean, 2003), whereas our approach

derives certainty from a single source. More-

over, DST typically assigns belief to sets of hy-

potheses rather than individual ones, making it

more suitable for representing gro up-level uncer-

tainty. In co ntrast, the DIS framework deman ds ﬁne-

grained c e rtainty assignments to individual attributes,

values, and relationships (Sentz a nd Ferson, 2002;

Gordon and Shortliffe, 1984). Possibility th eory di-

rectly supports this by enabling necessity degree s to

annotate speciﬁc elements, making it a natural ﬁt for

our ontology-based model.

6 CONCLUSION AND FUTURE

WORK

This paper presents a pr incipled extension of the

DIS framework to support reasonin g under incom-

plete information using necessity-based possibilis-

tic logic. Unlike most ontology-based systems that

assume complete information, our approach mod-

els uncertainty across instance s, attributes, relation-

ships, and concept deﬁnitions, e nabling ﬁne-grained,

graded reasoning. A key advantage is replacing bi-

nary infere nces with necessity-valued conclusions, al-

lowing cautious reasoning with p a rtial information.

Overall, this approach provid es a structured fou n-

dation for possibilistic reasoning in ontology- based

systems advancing more expressive a nd uncertain ty-

aware knowledge representations essential for robust

decision-making in complex, data-limited contexts.

We are currently auto mating necessity-

based reasoning tasks using the Domain Infor-

mation System Extended Language ( D ISEL)

tool (Wang et al., 2022). Future work will focu s on

automating necessity d egre e assignment via machine

learning, integrating fuzzy logic to handle impreci-

sion, developing a scalable reasoning engine, and

applying the framework to rea l-world domains. Once

the automation is in place, we plan to use DISEL to

reason over data collected f rom network secu rity pre-

vention mechanisms. This data is often unce rtain an d

originates from diverse sources with varying levels of

reliability. Fu rthermore, this data originates from log

ﬁles, whether structured or semi-structur e d, making

it well-suited for DIS modelling. The goal is to pre-

process and clea n the d ata (Khedri et al., 2013), then

apply the proposed reasoning framework to facilitate

reliable and context-aware security de cision-making

in highly dynamic and complex uncertain landscapes.

REFERENCES

Alola, A., Tunay, M., and Alola, U. (2013). Analysis of

possibility theory for reasoning under uncertainty. In-

ternational Journal of Statistics and Probability, 2:12.

Alomair, D. and Khedri, R. (2025). Towards a cartesian

theory of ontology domain adequacy. Synthese, pages

1–12. Submitted for publication on July. 25, 2025.

Alomair, D. , Khedri, R ., and MacCaull, W. (2025). A com-

prehensive review of uncertainty modelling i n domain

ontologies. ACM Computing Surveys, pages 1–35.

Accepted with minor revision.

Anand, S. K. and Kumar, S. (2022). Uncertainty analysis in

ontology-based knowledge representation. New Gen-

eration Computing, 40(1):339–376.

Bal-Bourai, S. and Mokhtari, A. (2016). Poss-SROIQ(D):

Possibilistic description logic for uncertain geo-

graphic information. In Trends in Applied Knowledge-

Based Systems and Data Science, pages 818–829,

Cham. Springer International Publishing.

Ben Salem, Y., Idoudi, R., E ttabaa, K. S., Hamrouni, K.,

and Soleiman, B. (2018). Mammographie image

based possibilistic ontological representation. In (AT-

SIP) 4th International Conference, pages 1–6.

Benferhat, S. and Bouraoui, Z. (2015). Min-based possi-

bilistic DL-Lit e. Journal of Logic and Computation,

27(1):261–297.

KEOD 2025 - 17th International Conference on Knowledge Engineering and Ontology Development

118

Benferhat, S., Bouraoui, Z., and Tabia, K. (2014). On

the revision of prioritized DL - Lite knowledge bases.

In Scalable Uncertainty Management, pages 22–36,

Cham. Springer International Publishing.

Bosc, P. and Prade, H. (1997). An Introduction to the F uzzy

Set and Possibility Theory-Based Treatment of Flex-

ible Queries and Uncertain or Imprecise Databases,

pages 285–324. Springer US, Boston, MA.

Boutouhami, K., Benferhat, S., Khellaf, F., and Nouioua, F.

(2017). U ncertain lightweight ontologies in a product-

based possibility theory framework. International

Journal of Approximate Reasoning, 88:237–258.

Ceravolo, P., Damiani, E., and Leida, M. (2008). Which

role for an ontology of uncertainty? In International

Workshop on Uncertainty Reasoning for the Semantic

Web, volume 423.

Dubois, D., Lang, J., and Prade, H. (1994). Possibilistic

logic. Handbook of logic in artiﬁcial intelligence and

logic programming, pages 439–513.

Dubois, D. and Prade, H. (1986). Weighted minimum and

maximum operations in fuzzy set theory. Information

Sciences, 39(2):205–210.

Dubois, D. and Prade, H. (2014). Possibilistic logic—an

overview. Handbook of t he History of Logic, 9:283–

342.

Dubois, D. and Prade, H. (2015). Possibility theory and it s

applications: Where do we stand? Mathware and Soft

Computing Magazine, 18.

Gordon, J. and Shortliffe, E. H. (1984). The dempster-

shafer theory of evidence. Rule-Based Expert Sys-

tems: The MYCIN E xperiments of the Stanford

Heuristic Programming Project, 3(832-838):3–4.

Grabisch, M. (1998). Fuzzy Integral as a Flexible and Inter-

pretable Tool of Aggregation, pages 51–72. Physica-

Verlag HD, Heidelberg.

Gries, D. and Schneider, F. B. (1993). A logical approach

to discrete math. Springer-Verlag, Berlin, Heidelberg.

Imieli´nski, T. and Li pski, W. (1984). The relati onal model

of data and cylindric algebras. Journal of Computer

and System Sciences, 28(1):80–102.

Khedri, R., Chiang, F., and S abri, K. E. (2013). An alge-

braic approach for data cleansing. In the 4th EUSPN,

volume 21 of Procedia Computer Science, pages 50 –

59. Procedia Computer Science.

Kovalerchuk, B. (2017). Relationships Between Probabil-

ity and Possibility Theories, pages 97–122. Springer

International Publishing, Cham.

Laha, R. G. and Rohatgi, V. K. (2020). Probability theory.

Courier Dover Publications.

Ma, Z. M., Zhang, F., Wang, H., and Yan, L. (2013).

An overview of fuzzy description logics for the se-

mantic web. The Knowledge Engineering Review,

28(1):1–34.

Marinache, A. (2025). Syntax and Semantics of Domain

Information System and its usage in conjecture veriﬁ-

cation. PhD thesis, School of Graduate S tudies, Mc-

Master University, Hamilton, Ontario, Canada.

Marinache, A., Khedri, R., LeCl ai r, A., and MacCaull, W.

(2021). DIS: A data-centred knowledge representa-

tion formalism. In (RDAAPS) 2021: A Big Data Chal-

lenge, pages 1–8.

McClean, S. I. (2003). Data mining and knowledge discov-

ery. In Encyclopedia of Physical Science and Technol-

ogy (Third Edition), pages 229–246. Academic Press,

New York, third edition edition.

Mohamed, R., Loukil, Z., and Bouraoui, Z. (2018).

Qualitative-based possibilistic el ontology. In PRIMA

2018: Principles and Practice of Multi -Agent Sys-

tems, pages 552–559, Cham. Springer International

Publishing.

Nieves, J. C., Osorio, M., and Cort´es, U. (2007). Semantics

for possibilistic disjunctive programs. In LPNMR: 9th

International C onference, Tempe, AZ, USA, May 15-

17, 2007. Proceedings 9, pages 315–320. Springer.

Qi, G., Ji, Q., Pan, J. Z., and Du, J. (2011). E xtending

description logics with uncertainty reasoning i n possi-

bilistic logic. International Journal of Intelligent Sys-

tems, 26(4):353–381.

Saﬁa, B.-B. and Aicha, M. (2014). Poss-OWL 2: Possibilis-

tic extension of OWL 2 for an uncertain geographic

ontology. Procedia Computer Science, 35:407–416.

Sentz, K. and Ferson, S. (2002). Combination of evidence

in Dempster-Shafer theory, volume 4015. Sandia Na-

tional Laboratories Albuquerque.

Straccia, U. (2013). Foundations of Fuzzy Logic and Se-

mantic Web Languages. Chapman & Hall/CRC.

Straccia, U. and Bobillo, F. (2017). From Fuzzy to An-

notated Semantic Web Languages, pages 203–240.

Springer International Publishing, Cham.

Sun, S. (2013). A novel semantic quantitative description

method based on possibilistic logic. Journal of Intel-

ligent & Fuzzy Systems, 25:931–940.

Wang, Y., Chen, Y., Alomair, D., and K hedri, R. (2022).

DISEL: A language for specifying DIS-based ontolo-

gies. In (KSEM) 2022, Lecture Notes in Artiﬁcial In-

telligence, pages 1–16, Singapore. Springer.

Zadeh, L. (1999). Fuzzy sets as a basis for a theory of pos-

sibility. Fuzzy Sets and Systems, 100:9–34.

Possibilistic Extension of Domain Information System (DIS) Framework

119