FOPID-Based Trajectory Control for an Unmanned Aerial

Robotic Manipulator

Gabriela M. Andaluz

, Zahid Nazate

, Paulo Leica

and Guillermo Palacios-Navarro

Departamento de Automatización y Control Industrial, Escuela Politécnica Nacional, Quito 170525, Ecuador

Department of Electronic Engineering and Communications, University of Zaragoza, Teruel 44003, Spain

Keywords: Aerial Manipulators, Fractional-Order PID, FOPID Control, UMA, Trajectory Tracking, UAV-Based

Manipulation.

Abstract: This work presents a Fractional Order PID (FOPID) control strategy for trajectory tracking of an Unmanned

Aerial Manipulator (UAM), proposed as an alternative to the conventional PID controller. Unlike classical

integer-order controllers, the FOPID design enables more flexible tuning of the aerial manipulator’s kinematic

response by introducing five independent tuning parameters. This added flexibility enhances system stability

and improves robustness against abrupt reference changes. The controller parameters are optimized through

Integral of Squared Error (ISE) minimization to ensure efficient performance. Simulation results confirm that

the FOPID controller achieves superior trajectory tracking accuracy compared to the conventional PID.

Specifically, the ISE values obtained with the FOPID reflect reductions of 23.46%, 24.99%, and 15.35% in

the tracking errors along the 𝑥, 𝑦 and 𝑧̃ directions, respectively. These results validate the effectiveness of the

FOPID approach in improving the control performance of unmanned aerial manipulators.

1 INTRODUCTION

Unmanned Aerial Manipulators (UAMs) integrate

the mobility of Unmanned Aerial Vehicles (UAVs)

with the manipulation capabilities of robotic arms,

posing significant control challenges due to their high

nonlinearities, strong couplings, and external

disturbances. Although full dynamic models offer

accuracy (Carvajal et al., 2024), their complexity

restricts real-time implementation. Consequently,

some approaches adopt decoupled dynamics

(Sharma et al., 2025), (Zhang et al., 2021) or treat the

robotic arm as a disturbance (Zheng et al., 2023).

Within this framework, kinematic models offer a

suitable alternative for achieving precise trajectory

tracking at low computational cost, particularly in

low-speed operation scenarios.

Classical integer-order PID controllers have been

extensively applied in robotics due to their simplicity

and ease of implementation (Moya et al., 2016;

Mundheda et al., 2023), but they exhibit significant

https://orcid.org/0000-0002-1822-6943

https://orcid.org/0009-0009-4826-9475

https://orcid.org/0000-0002-5385-1920

https://orcid.org/0000-0002-8408-1280

limitations when dealing with external disturbances,

parametric variations, and nonlinearities (Leica et al.,

2017), especially in systems such as UAMs. To

address these shortcomings, various PID extensions

have been proposed, including adaptive schemes

(Ghamari et al., 2022), sliding mode controllers

(Noordin et al., 2022), fuzzy logic-based controllers

(Cao et al., 2022), and sigmoid-based control

structures (Suid & Ahmad, 2022). Nonetheless, all of

these strategies still operate under the constraints of

integer-order dynamics.

Fractional-order control theory generalizes the

classical PID framework by allowing non-integer

orders in the integral and derivative operators, thus

introducing two additional degrees of freedom that

enhance tuning flexibility and the ability to model

real-world systems more accurately (Torvik &

Bagley, 1984). FOPID controllers have demonstrated

superior performance in diverse robotic applications.

For example, in robotic manipulators, FOPID

schemes have been integrated with neural networks

Andaluz, G. M., Nazate, Z., Leica, P. and Palacios-Navarro, G.

FOPID-Based Trajectory Control for an Unmanned Aerial Robotic Manipulator.

DOI: 10.5220/0013706200003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 227-234

ISBN: 978-989-758-770-2; ISSN: 2184-2809

227

(Mohamed et al., 2023), applied in iterative model-

free control (Zhang et al., 2021), combined with

sliding mode control (Noordin et al., 2022), and tuned

using nature-inspired algorithms such as the Bat

algorithm (A. Faraj & Mohammed Abbood, 2021) or

optimization-based methods (Ghamari et al., 2022).

In the UAVs, FOPID controllers have been improved

tracking precision and robustness against parametric

uncertainties using micro-integral operators

(Delgado-Reyes et al., 2024; Li et al., 2023).

Experimental comparisons with adaptive schemes

further confirm their superiority over classical PID

(Timis et al., 2022). In UAMs, FOPID has been

combined with predictive and sliding mode control

strategies, yielding significant improvements in

disturbance rejection and trajectory tracking (Shao et

al., 2025; Zheng et al., 2023). However, many of

these approaches assume accurate knowledge of the

system dynamics, which remains a practical

limitation due to the inherent complexity of UAM

platforms. Based on the literature, FOPID controllers

have demonstrated significant advantages in

precision and robustness against disturbances and

uncertainties, with successful applications in aerial

and ground robotics (UAVs and UGVs), particularly

in scenarios with wind gusts, payload variations,

friction, and model inaccuracies (Cajo et al., 2019).

Nevertheless, their implementation in UAM systems

remains limited, despite the high potential fractional-

order control offers for this domain.

This work proposes the design and

implementation of a fractional-order PID (FOPID)

controller, formulated using the Caputo fractional

derivative operator, applied to the kinematic model of

a UAM composed of a quadrotor and a 3-DOF robotic

arm. Unlike previous approaches that rely on

complex dynamic models with high real-time

computational costs, the proposed method enables

efficient and precise trajectory tracking control under

abrupt reference changes. The results demonstrate

significant improvements over classical PID

controllers, exhibiting smoother and more robust

responses, thereby positioning the FOPID as an

effective alternative for robust kinematic control of

UAMs. The main contributions of this work are: i) a

novel application of FOPID control in aerial

manipulators, providing a foundation for future

research; and ii) a control strategy that does not

require an exact system model, making it particularly

suitable for platforms like UAMs, whose dynamics

are complex and highly coupled.

The article is organized as follows: Section 1

presents a review of FOPID controllers and the

contributions of this work; Section 2 describes the

modeling of the manipulator, the quadrotor and

UAM; Section 3 details the PID and FOPID

controllers along with the stability analysis; Section 4

presents the obtained results; and Section 5

summarizes the study’s conclusions.

2 SYSTEM MODELING

2.1 Quadrotor Modeling

For this work, an aerial manipulator composed of a

quadrotor equipped with a 3-DOF robotic arm is

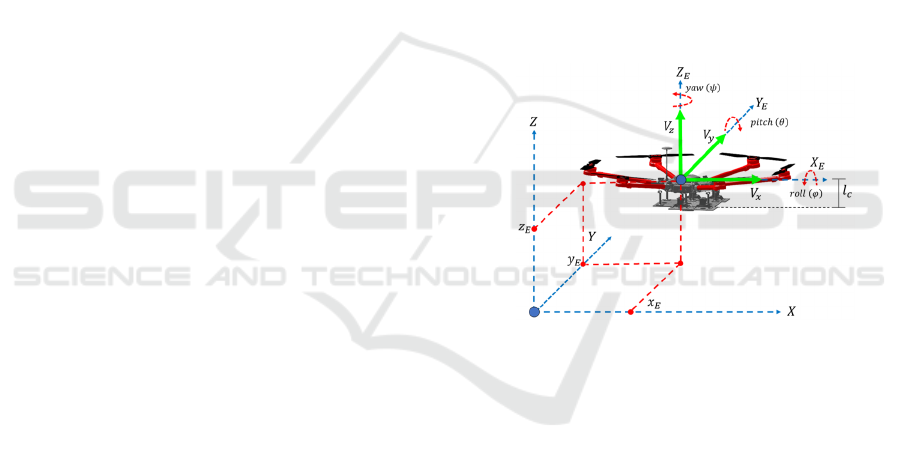
considered, as illustrated in Figure 1. Under the

assumption of operation around equilibrium, it is

assumed that the roll and pitch angles are negligible,

which allows simplifying the quadrotor kinematics by

considering only translations in the horizontal plane

and a constant yaw orientation (Guayasamín et al.,

2018).

Figure 1: Quadrotor Robot.



𝑥



𝑦



𝑧





cos 𝜓−sin 𝜓 0

sin 𝜓 cos 𝜓 0

001



𝑉



𝑉



𝑉



,





where 𝑉



, 𝑉



and 𝑉



are the linear velocities of the

quadrotor,



𝑥



, 𝑦



, 𝑧







represents the position with

respect to the quadrotor’s 𝑋, 𝑌 and 𝑍 axes, 𝜓 is the

rotation angle of the quadrotor about the 𝑍-axis, and

𝑙



is the vertical distance from the quadrotor’s base to

its center of mass.

2.2 Robotic Arm Modeling

A 3-DOF robotic arm is considered, as shown in

Figure 2. By applying the Denavit-Hartenberg

algorithm, the system’s forward kinematic model is

determined (Guayasamín et al., 2018), which is

expressed as follows:

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

228

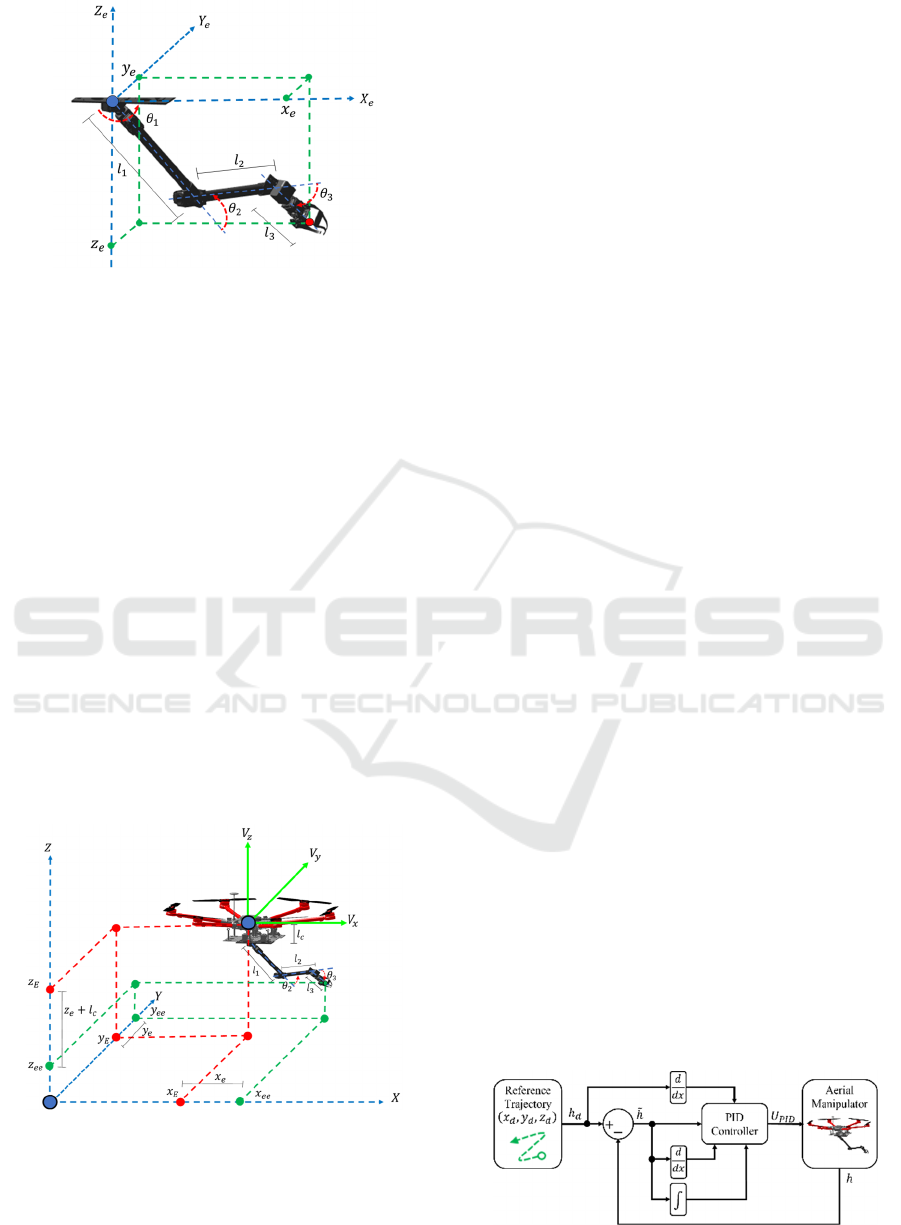
Figure 2: 3-DOF Robotic Arm.



𝑥



𝑦



𝑧





cos 𝜃





𝑙



cos 𝜃



𝑙



cos



𝜃



𝜃







sin 𝜃





𝑙



cos 𝜃



𝑙



cos



𝜃



𝜃







−𝑙



sin 𝜃



−𝑙



sin 𝜃



𝑙



sin



𝜃



𝜃





.





The parameters 𝑙



, 𝑙



, and 𝑙



denote the link

lengths, 𝜃



, 𝜃



, and 𝜃



are the joint angles, and



𝑥



, 𝑦



, 𝑧







represents the position of the

manipulator’s end-effector with respect to the 𝑋



, 𝑌



and 𝑍



axes.

2.3 Aerial Manipulator Modeling

The robotic system is formed by coupling the

quadrotor with the previously described robotic arm.

To obtain the combined model, it is considered that

the end-effector’s position is now influenced by the

quadrotor’s position, such that the end-effector

position is given by



𝑥



, 𝑦



, 𝑧











𝑥





𝑥



, 𝑦



𝑦



, 𝑧



𝑧



𝑙







, where



𝑥



, 𝑦



, 𝑧





denotes the position of the aerial manipulator’s end-

effector in 𝑋, 𝑌, and 𝑍 axes.

Figure 3: Unmanned Aerial Manipulator Robot.

It is considered that there exists an angle 𝜃



influenced by the quadrotor’s yaw orientation 𝜓 and

the angle 𝜃



of the first joint of the robotic arm, such

that 𝜃



𝜃



𝜓 . Based on these considerations, the

kinematic model of the UAM is given by:

ℎ



𝐽𝑈,





The vector ℎ







𝑥



, 𝑦



, 𝑧







represents the

time derivative of the position of the end-effector of

the aerial manipulator. The input vector of the system

is defined as 𝑈𝑉



, 𝑉



, 𝑉



, 𝜓



, 𝜃





, 𝜃





, 𝜃









where

𝜓



is the angular velocity of the quadrotor around the

Z-axis. The angular velocities of each joint of the

robotic arm are 𝜃





, 𝜃





, and 𝜃





The matrix 𝐽 is the Jacobian of the complete

system and is defined as:

𝐽

⎣

⎢

⎡

𝐶

𝜓

−𝑆

𝜓

−𝑆

𝜃

𝜓

𝐿

𝐶

−𝑆

𝜃

𝜓

𝐿

𝐶

−𝐶

𝜃

𝜓

𝐿

𝑆

−𝑙

𝐶

𝜃

𝜓

𝑆

𝜃

𝑆

𝜓

𝐶

𝜓

𝐶

𝜃

𝜓

𝐿

𝐶

𝜃

𝜓

𝐿

𝐶

−𝑆

𝜃

𝜓

𝐿

𝑆

−𝑙

𝑆

𝜃

𝜓

𝐶

𝜃

𝐿′

𝐶

𝑙

𝐶

𝜃

⎦

⎥

⎤

𝑻





The equivalent nomenclature is 𝐶



cos 𝜓,

𝑆



sin 𝜓, 𝑆







sin



𝜃



𝜓



, 𝐶





cos 𝜃



𝑆





sin 𝜃



, 𝐶









cos



𝜃



𝜃





, 𝐶









cos



𝜃



𝜓



, 𝑆









sin



𝜃



𝜃





, 𝐿





𝑙



𝐶







𝑙



𝐶









, 𝐿





𝑙



𝑆





𝑙



𝑆









, and 𝐿′







−𝑙



𝐶





𝑙



𝐶









3 CONTROLLERS

This section analyzes the stability of the control laws

using Lyapunov functions. The tracking error is

defined as ℎ



ℎ



−ℎ, where ℎ



𝑥



, 𝑦



, 𝑧







represents the actual position of the end-effector, and

ℎ







𝑥



, 𝑦



, 𝑧







denotes the desired position of

the end-effector, which may vary over time.

3.1 PID Controller

The classical PID control scheme is illustrated in

Figure 4.

Figure 4: PID Control Scheme.

FOPID-Based Trajectory Control for an Unmanned Aerial Robotic Manipulator

229

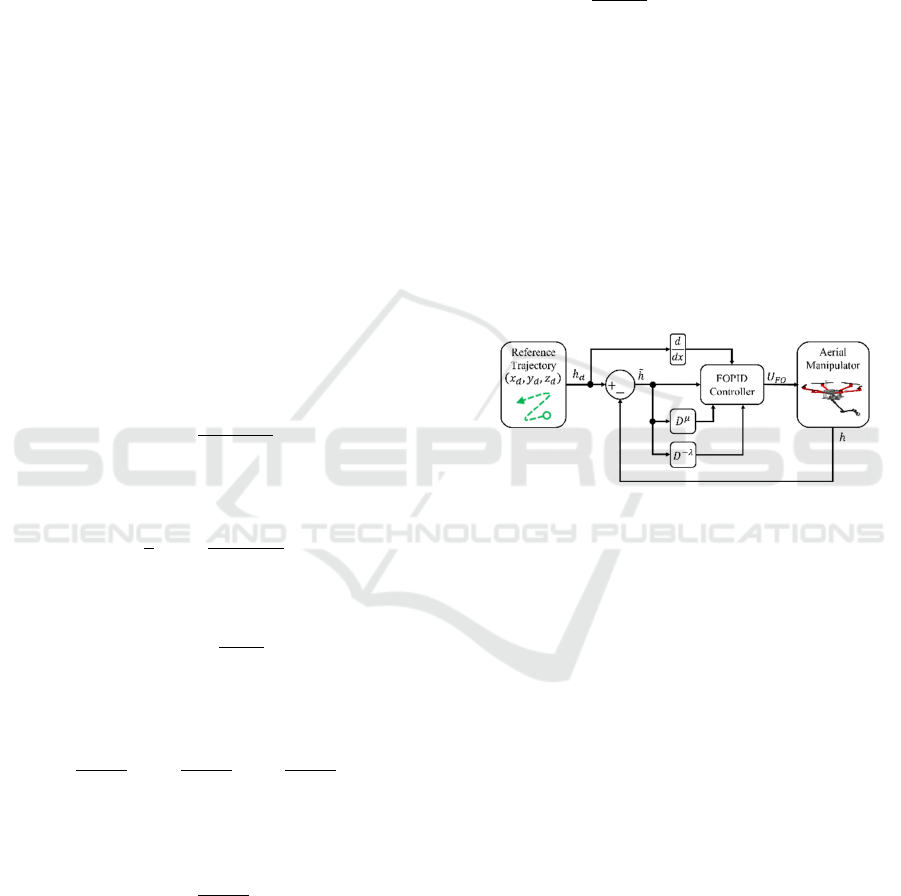
A PID-type control law is proposed for trajectory

tracking of the UAM (Li et al., 2023), given by:

𝑈



𝐽

ℎ





𝑘



ℎ



𝑘



ℎ



𝑑𝑡𝑘



ℎ





.





The gains 𝑘



, 𝑘



, 𝑘



0 represent the PID

controller parameters, respectively, and ℎ



ℎ



−ℎ

is the tracking error. Defining the integral term as 𝑧



ℎ



𝑑𝑡, with 𝑧ℎ



, the above expression can be

rewritten as:

𝑈



𝐽



ℎ





𝑘



ℎ



𝑘



𝑧𝑘



ℎ











The time derivative of the tracking error is

ℎ





ℎ





−ℎ



and combining this with the kinematic model (3), we

obtain:

ℎ





ℎ





−𝐽𝑈.





Assuming perfect velocity tracking, i.e., 𝑈𝑈



and substituting (6) into (7), the closed-loop system

becomes:

ℎ





−𝑘



ℎ



−𝑘



𝑧−𝑘



ℎ









Solving for ℎ





, we obtain:

ℎ





−

𝑘



ℎ



𝑘



𝑧



1 𝑘









The following Lyapunov candidate function is

proposed:

𝑉

ℎ





ℎ





𝑘





1 𝑘





𝑧



𝑧.





Its time derivative is given by:

𝑉



ℎ



𝑇

ℎ







𝑘

𝑖



1𝑘

𝑑



𝑧

𝑇

𝑧







Substituting (9) into (11) and expanding the terms

yields:

𝑉



−

𝑘



1 𝑘



ℎ





ℎ



−

𝑘



1 𝑘



ℎ





𝑧

𝑘



1 𝑘



𝑧



ℎ







Since ℎ





𝑧𝑧



ℎ



, the cross terms cancel out,

resulting in:

𝑉



−

𝑘



1 𝑘



ℎ





ℎ







This expression guarantees that ℎ



and z are

bounded, i.e., ℎ



∈𝐿



and 𝑧∈𝐿



. To demonstrate

that the errors converge to zero, LaSalle’s invariance

principle is applied. The invariant set is defined as:

𝑆ℎ



, 𝑧∈ℝ



𝑥ℝ



: 𝑉



0→ℎ



0. (14)

Thus, ℎ



0 , and since 𝑧ℎ



0, it follows that

𝑧𝑐𝑜𝑛𝑠𝑡. Therefore, the system’s solutions

converge to the largest invariant set contained in 𝑆,

namely:

𝑀ℎ



, 𝑧: ℎ



0, 𝑧𝑐𝑜𝑛𝑠𝑡. (15)

Given that







(





)

𝑧



𝑧→𝑐𝑜𝑛𝑠𝑡, and considering

that 𝑉 is decreasing, it is concluded that ℎ



→0 as 𝑡→

∞. This result demonstrates the asymptotic stability

of the system under the proposed PID control law.

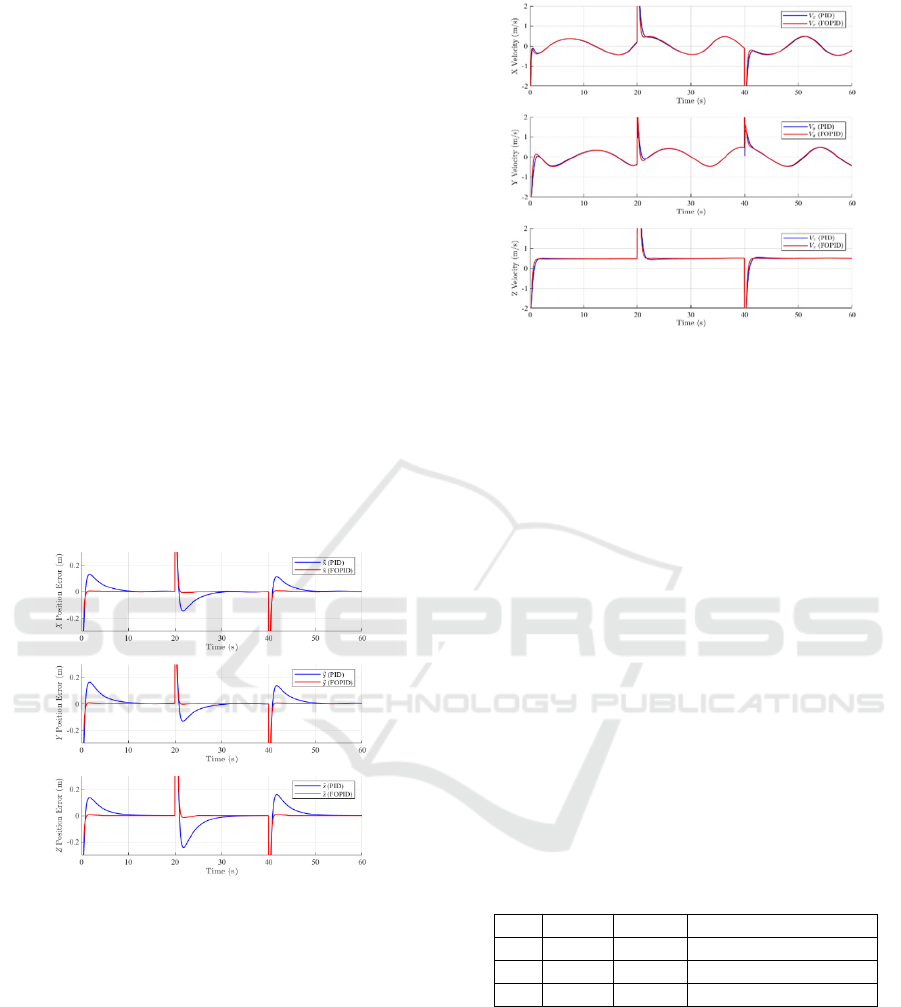
3.2 Fopid Controller

For the design of the fractional-order PID controller

(FOPID), the Caputo definition is adopted (Shah &

Agashe, 2016), as it enables the derivative and

integral actions of the controller to be represented

through fractional-order operators applied to the

tracking error. The proposed control scheme is

illustrated in Figure 5.

Figure 5: FOPID control scheme.

The proposed control law is defined as (A. Faraj

& Mohammed Abbood, 2021):

𝑈



𝐽

ℎ





𝑘



ℎ



𝑘



𝐷



ℎ



𝑘



𝐷



ℎ



.

(

)

The gains 𝑘



, 𝑘



, 𝑘



0 represent the PID

controller parameters, and 𝐷



denotes the fractional

differential or integral operator of order 𝑛 , and ℎ



the tracking error. The state 𝑧



𝐷



ℎ



is defined as

the fractional integral of order 𝜆∈0,1, such that

ℎ



𝐷



𝑧



, while the state 𝑧



𝐷



ℎ



corresponds to

the fractional derivative of order 𝜇 ∈0,1 with ℎ







𝐷



𝑧



. By substituting these expressions into (15),

the control law can be rewritten as:

𝑈



𝐽

ℎ





𝑘



ℎ



𝑘



𝑧



𝑘



𝑧



.

(

)

Assuming perfect velocity tracking, we have 𝑈

𝑈



. Replacing (17) into the kinematic model (3), the

closed-loop dynamics are obtained as:

ℎ





−𝑘

𝑝

ℎ



−𝑘

𝑖

𝑧

𝑖

−𝑘

𝑑

𝑧

𝑑

(

)

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

230

To analyze stability, the following Lyapunov

candidate function is proposed:

𝑉



ℎ





ℎ



𝑘



𝑧





𝑧



𝑘



𝑧





𝑧



(

)

By differentiating (19) with respect to time, we

obtain:

𝑉





= ℎ





ℎ





+ 𝑘



𝑧





𝑧



+ 𝑘



𝑧





𝑧



(

)

Considering the fractional relationships:: 𝑧











ℎ



𝑑𝑡= ℎ



= 𝐷



𝑧



, and 𝑧





ℎ



= ℎ





𝐷



𝑧



; and substituting into (20), we get:

𝑉





= ℎ





ℎ





+ 𝑘



𝑧





𝐷



𝑧



+ 𝑘



𝑧





𝐷



𝑧



(

)

Given the previously defined state variables, the

Lyapunov derivative can be rewritten as:

𝑉





= ℎ





ℎ





+ 𝑘



𝑧





ℎ



+ 𝑘



𝑧





ℎ





(

)

Substituting (18) into (22) and expanding, we obtain:

𝑉





= −𝑘



ℎ





ℎ



−𝑘





𝑧





𝑧



−𝑘



1+𝑘



𝑧





ℎ



−𝑘



𝑘



𝑧





𝑧



(

)

Applying Young's inequality to bound the cross

terms:

𝑧





ℎ



≤

𝑧





𝑧



+ ℎ





ℎ



.

(

)

𝑧





𝑧



≤

𝑧





𝑧



+ 𝑧





𝑧



.

(

)

Rewriting (23) in terms of inequalities, we obtain:

𝑉





≤−𝑘



ℎ





ℎ



−𝑘





𝑧





𝑧



−







1+𝑘



𝑧





𝑧



+ ℎ





ℎ



−











𝑧





𝑧



+ 𝑧





𝑧



. (26)

Developing (26) leads to:

𝑉





≤−𝐾





ℎ





ℎ



−𝐾





𝑧





𝑧



−𝐾





𝑧





𝑧



(

)

where 𝐾





= 𝑘









1+𝑘



 , 𝐾





= 𝑘











1+𝑘



+











, and 𝐾















, are strictly

positive constants.

Since 𝑉





≤0 , the system is Lyapunov stable.

Furthermore, the positivity of the coefficients

guarantees that ℎ



, 𝑧



, 𝑧



→0 as 𝑡→∞, confirming

the asymptotic convergence of the tracking error

under the proposed FOPID controller.

4 TESTS AND RESULTS

This section presents the simulation results

corresponding to the two proposed control

algorithms: classical PID and fractional-order PID

(FOPID). The objective is to compare the

performance of each controller under identical

operating conditions. Quantitative evaluation is

carried out using the Integral of Squared Error (ISE)

performance index applied to the tracking error in

each coordinate of the aerial manipulator’s end-

effector.

The desired trajectory for the end-effector was

defined as: ℎ



(

𝑡

)



𝑥



, 𝑦



, 𝑧









𝑐𝑜𝑠

(

𝑡/2

)

+2,

𝑠𝑖𝑛

(

𝑡/2

)

+2 , 𝑡/2





. The simulation was run for

60 s. Additionally, to assess the controllers'

adaptability to abrupt changes, a disturbance was

introduced in the desired trajectory between 20 s and

40 s, consisting of a constant increment of 2 m applied

to each coordinate.

Both controllers employed the same PID gains,

with values 𝑘



=3, 𝑘



=0.1, and 𝑘



=1, which

were obtained through a tuning process based on the

minimization of the ISE index. For the FOPID

controller, the fractional orders 𝜆 and 𝜇, associated

with the integral and derivative actions respectively,

were incorporated. These values were selected using

heuristic methods aimed at improving performance

relative to the classical PID. The values used were

𝜆=0.1 and 𝜇=0.8 . Under these conditions,

simulations were conducted for both control schemes,

comparing the tracking errors and the resulting ISE

indices across the three coordinates.

Figure 6: End-Effector Trajectory under PID and FOPID

Control.

Figure 6 shows the evolution of the end-effector

trajectories under classical PID and FOPID control,

compared to the desired trajectory. It can be observed

that both controllers are capable of achieving the

FOPID-Based Trajectory Control for an Unmanned Aerial Robotic Manipulator

231

desired trajectory; however, the FOPID exhibits

faster convergence and a smoother response,

especially when facing abrupt changes in the

reference.

Figure 7 depicts the temporal evolution of the

position error in each coordinate of the end-effector

under classical PID and FOPID control. The errors

are displayed within a bounded range of  0.3 m to

facilitate comparison of the dynamic behavior of the

controllers. Peaks in the error occur simultaneously in

both strategies and correspond to the abrupt changes

in the desired trajectory applied between 20 s and 40

s, with magnitudes being practically equal.

Nonetheless, the FOPID demonstrates a significantly

superior ability to correct the error. While the PID

requires approximately 10 s to nullify the error after

the reference change, the FOPID achieves the desired

tracking within about 1 s. Overall, the PID controller

exhibits an underdamped behavior with error

overshoots and longer settling times. In contrast, the

FOPID provides a faster and smoother response,

effectively eliminating the error without notable

overshoot.

Figure 7: Position errors.

Figure 8 shows three of the seven control signals

generated by each controller, corresponding to the

linear velocities of the aerial manipulator. These

signals are plotted within a 2 m/s range to facilitate

a clearer comparison of their dynamic differences. It

can be observed that, at steady state, both control

strategies reach similar values, indicating that the

control signals converge to the same regime.

However, during the transients caused by the

reference changes at 20 s and 40 s, slight differences

appear. The FOPID tends to generate smoother and

less oscillatory signals, whereas the PID exhibits

more abrupt responses, consistent with its less

damped behavior observed in the position error.

Figure 8: Linear velocity control signals.

5 DISCUSSION

The results obtained show that the FOPID controller

implemented performs better than the PID controller,

considering that the calibration parameters

(proportional, derivative, and integrator) were the

same for both controllers. Table 1 presents the

performance indices ISE derived from the position

errors in the three coordinates (𝑥, 𝑦, 𝑧) for both

controllers, along with the relative percentage

improvement achieved by the FOPID. The

quantitative analysis reveals that the FOPID

consistently reduces the ISE values across all

coordinates, indicating more accurate tracking of the

desired trajectory. On average, the FOPID improves

performance by 21.27 %, relative to the PID, which

supports its faster and smoother response, as also

observed in the trajectories shown in Figure 6 and the

error evolution in Figure 7.

Table 1: ISE Resulting ISE for Each Controller.

ISE PID FOPID % Improvement

𝑥 1.5526 1.1884 23.46%

𝑦 1.9318 1.4490 24.99%

𝑧

2.5807 2.1846 15.35%

These results validate the effectiveness of the

fractional orders 𝜆 and 𝜇 in enhancing the dynamic

behavior of the system by enabling finer tuning of the

controller, particularly in scenarios involving abrupt

changes in the reference trajectory. The

implementation of the FOPID controller entails

increased complexity in tuning, as it requires

adjusting five parameters instead of the three used in

the classical PID controller. To simplify this process,

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

232

an efficient sequential tuning strategy was applied:

first, the PID parameters were tuned, followed by the

optimization of the fractional orders. This approach

reduces the search space and facilitates improved

system performance. While these results confirm the

efficacy of the kinematic approach under ideal

conditions, it is acknowledged that its performance

may degrade in scenarios where the payload or

manipulator arm dynamics significantly influence the

UAV's behavior. In such cases, future work should

consider extending the approach to incorporate

coupled dynamic models or robust control.

6 CONCLUSIONS

Based on the obtained results, it is evident that the

FOPID controller demonstrated superior performance

compared to the classical PID, achieving faster and

more precise trajectory tracking with reduced

oscillations. This improvement was also observed in

response to abrupt changes in the reference trajectory,

to which both controllers were subjected. The FOPID

achieved a 21.27% improvement in the ISE compared

to the classical PID. Although the FOPID requires

tuning of five parameters compared to three in the

classical controller, this provides greater flexibility in

the adjustment process. Overall, the results validate

the use of the FOPID as an efficient solution for

trajectory tracking control of aerial manipulators

under demanding conditions. Furthermore, since this

control approach is model-free, it opens a future

research avenue for aerial manipulators, focusing on

robust and adaptive FOPID strategies to compensate

for the complex dynamics of these robots.

As future work, we propose to extend the

approach to schemes that incorporate coupled

dynamics of the aerial manipulator, in order to

evaluate how the dynamics of the arm affect the

robotic system. The implementation of robust

controllers based on FOPID will be analyzed.

ACKNOWLEDGEMENTS

The authors would like to express their sincere

gratitude to the Escuela Politécnica Nacional for the

financial support provided for research, development,

and innovation through the project PIS-23-09:

Artificial Intelligence Techniques Applied to an

Aerial Manipulator in Semi-structured Environments.

The authors also acknowledge the support from the

Universidad de las Fuerzas Armadas ESPE through

the project PIEX-DACI-ESPE-24: Autonomous

Control of Aerial Manipulator Robots. Finally, the

authors are grateful to the ARSI and GIECAR

research groups for their valuable theoretical

contributions and technical support throughout the

development of this work.

REFERENCES

A. Faraj, M., & Mohammed Abbood, A. (2021). Fractional

order PID controller tuned by bat algorithm for robot

trajectory control. Indonesian Journal of Electrical

Engineering and Computer Science, 21(1), 74.

https://doi.org/10.11591/ijeecs.v21.i1.pp74-83

Cajo, R., Mac, T., PLaza, D., Copot, C., Keyser, D., &

Ionescu, C. (2019). A Survey on Fractional Order

Control Techniques for Unmanned Aerial and Ground

Vehicles. 66864–66878. https://doi.org/10.1109/AC

CESS.2019.2918578

Cao, G., Zhao, X., Ye, C., Yu, S., Li, B., & Jiang, C. (2022).

Fuzzy adaptive PID control method for multi-

mecanum-wheeled mobile robot. 2019–2029.

https://doi.org/10.1007/s12206-022-0337-x

Carvajal, C. P., Andaluz, G. M., Andaluz, V. H., Roberti,

F., Palacios-Navarro, G., & Carelli, R. (2024).

Multitask control of aerial manipulator robots with

dynamic compensation based on numerical methods.

Robotics and Autonomous Systems, 173, 104614.

https://doi.org/10.1016/j.robot.2023.104614

Delgado-Reyes, G., Valdez-Martínez, J. S., Guevara-

López, P., & Hernández-Pérez, M. A. (2024). Hover

Flight Improvement of a Quadrotor Unmanned Aerial

Vehicle Using PID Controllers with an Integral Effect

Based on the Riemann–Liouville Fractional-Order

Operator: A Deterministic Approach. Fractal and

Fractional, 8(11), 634. https://doi.org/10.3390/frac

talfract8110634

Ghamari, S., Narm, H., & Mollaee, H. (2022). Fractional-

order fuzzy PID controller design on buck converter

with antlion optimization algorithm. 340–352.

https://doi.org/10.1049/cth2.12230

Guayasamín, A., Leica, P., Herrera, M., & Camacho, O.

(2018). Trajectory Tracking Control for Aerial

Manipulator Based on Lyapunov and Sliding Mode

Control. 36–41. https://doi.org/10.1109/INCISCOS

.2018.00013.

Leica, P., Camacho, O., Lozada, S., Guamán, R., Chávez,

D., & Andaluz, V. H. (2017). Comparison of control

schemes for path tracking of mobile manipulators. 28,

86–96. https://doi.org/10.1504/IJMIC.2017.085300

Li, J., Chen, P., Chang, Z., Zhang, G., Guo, L., & Zhao, C.

(2023). Trajectory Tracking Control of Quadrotor

Based on Fractional-Order S-Plane Model. Machines,

11(7), 672. https://doi.org/10.3390/machines11070672

Mohamed, M. J., Oleiwi, B. K., Abood, L. H., Azar, A. T.,

& Hameed, I. A. (2023). Neural Fractional Order PID

Controllers Design for 2-Link Rigid Robot

FOPID-Based Trajectory Control for an Unmanned Aerial Robotic Manipulator

233

Manipulator. Fractal and Fractional, 7(9), 693.

https://doi.org/10.3390/fractalfract7090693

Moya, V., Espinosa, V., Chavez, D., Leica, P., & Camacho,

O. (2016). Trajectory tracking for quadcopter’s

formation with two control strategies. 2016 IEEE

Ecuador Technical Chapters Meeting (ETCM), 1–6.

https://doi.org/10.1109/ETCM.2016.7750839

Mundheda, V., Mirakhor, K., Rahul, K. S., & Govindan, N.

(2023). Predictive Barrier Lyapunov Function Based

Control for Safe Trajectory Tracking of an Aerial

Manipulator. 1–6. https://doi.org/10.23919/ECC57647.

2023.10178336.

Noordin, A., Mohd Basri, M. A., & Mohamed, Z. (2022).

Position and Attitude Tracking of MAV Quadrotor

Using SMC-Based Adaptive PID Controller. Drones,

6(9), 263. https://doi.org/10.3390/drones6090263

Shah, P., & Agashe, S. (2016). Review of fractional PID

controller. Mechatronics, 38, 29–41. https://doi.org/

10.1016/j.mechatronics.2016.06.005

Shao, K., Xia, W., Zhu, Y., Sun, C., & Liu, Y. (2025).

Research on UAV Trajectory Tracking Control System

Based on Feedback Linearization Control–Fractional

Order Model Predictive Control. Processes, 13(3), 801.

https://doi.org/10.3390/pr13030801

Sharma, A., Gupta, S., Singh, S. P., Yadav, R. D., Song, H.,

Pan, W., Roy, S., & Baldi, S. (2025). Impedance and

Stability Targeted Adaptation for Aerial Manipulator

with Unknown Coupling Dynamics

(arXiv:2504.01983). arXiv. https://doi.org/10.48550/

arXiv.2504.01983

Suid, M. H., & Ahmad, M. A. (2022). Optimal tuning of

sigmoid PID controller using Nonlinear Sine Cosine

Algorithm for the Automatic Voltage Regulator system.

128, 265–286. https://doi.org/10.1016/j.isatra.2021

.11.037

Timis, D. D., Muresan, C. I., & Dulf, E.-H. (2022). Design

and Experimental Results of an Adaptive Fractional-

Order Controller for a Quadrotor. Fractal and

Fractional, 6(4), 204. https://doi.org/10.3390/fract

alfract6040204

Torvik, P. J., & Bagley, R. L. (1984). On the Appearance

of the Fractional Derivative in the Behavior of Real

Materials. Journal of Applied Mechanics, 51(2), 294–

298. https://doi.org/10.1115/1.3167615

Zhang, X., Xu, W., & Lu, W. (2021). Fractional-Order

Iterative Sliding Mode Control Based on the Neural

Network for Manipulator. Mathematical Problems in

Engineering, 2021, 1–12. https://doi.org/10.1155/

2021/9996719

Zheng, W., Li, Z., Zhan, L., Xiu, B., Zhao, B., & Guo, Z.

(2023). Robust fractional-order fast terminal sliding

mode control of aerial manipulator derived from a

mutable inertia parameters model. 2425, 012009.

https://doi.org/10.1088/1742-6596/2425/1/012009

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

234