Categorical Model Estimation with Feature Selection Using an Ant

Colony Optimization

Tetiana Reznychenko

1 a

, Ev

zenie Uglickich

2 b

and Ivan Nagy

1,2 c

Faculty of Transportation Sciences, Czech Technical University, Na Florenci 25, 11000 Prague, Czech Republic

Department of Signal Processing, Institute of Information Theory and Automation, Czech Academy of Sciences,

Pod vod

arenskou v

ı 4, 18208 Prague, Czech Republic

Keywords:

Categorical Model Estimation, Feature Selection, Ant Colony Optimization, Dimension Reduction.

Abstract:

This paper deals with the analysis of high-dimensional discrete data values from questionnaires, with the

aim of identifying explanatory variables that inﬂuence a target variable. We propose a hybrid algorithm that

combines categorical model estimation with an ant colony optimization scheme for feature selection. The

main contributions are: (i) the efﬁcient selection of the most signiﬁcant explanatory variables, and (ii) the

estimation of a categorical model with reduced dimensionality. Experimental results and comparisons with

well-known algorithms (e.g., random forest, categorical boosting, k-nearest neighbors) and feature selection

techniques are presented.

1 INTRODUCTION

This paper focuses on the analysis of discrete data ob-

tained from questionnaires. Such data sets typically

involve a large number of discrete variables, while

the sample size remains relatively small. This com-

bination presents substantial challenges in applying

standard mathematical techniques for data modeling

and prediction (Alwosheel et al., 2018; F

oldes et al.,

2018), thereby reducing the accuracy of the analysis.

The questionnaires provide an effective way to

understand people’s preferences and are also used

in areas such as social science, transportation sci-

ence, medicine, marketing, and many others. Exam-

ples of speciﬁc applications of questionnaires include:

identifying accident causation factors (Wang et al.,

2023), improving transportation quality (Dell’Olio

et al., 2017), evaluating road quality and safety (Hu

et al., 2022), identifying injury causes (D. Zwahlen

and Pf

afﬂi, 2016), travel behavior analysis, examin-

ing the use of carsharing for various trips (Matowicki

et al., 2021), symptom evaluation, patient evaluation

(Phuong et al., 2023), etc.

The analysis of discrete data involves many statis-

tical approaches, including descriptive statistics, hy-

https://orcid.org/0009-0000-6725-8864

https://orcid.org/0000-0003-1764-5924

https://orcid.org/0000-0002-7847-1932

pothesis testing, and modeling associations between

categorical variables.

In univariate analysis, both nominal and ordinal

variables are explored using proportion estimation,

the chi-square goodness of ﬁt test, and graphical tools

such as bar charts, pie charts, and histograms (Tang

et al., 2012; Agresti, 2018; Falissard, 2012). Bivari-

ate analysis examines the relationships between two

discrete variables. It includes estimating and compar-

ing proportions, using statistical tests such as the chi-

square test of independence (Agresti, 2018; Falissard,

2012), Fisher’s exact test for small samples with nom-

inal data (Agresti, 2018), rank-based measures such

as Goodman and Kruskal coefﬁcients for nominal and

ordinal data (Goodman and Kruskal, 1963; Bergsma

and Lupparelli, 2025). For high-dimensional contin-

gency tables, multivariate methods are applied. The

Cochran-Mantel-Haenszel test enables stratiﬁed anal-

ysis of odds ratios and relative risks (Falissard, 2012),

while simple log-linear models offer a ﬂexible frame-

work to capture complex interactions between cate-

gorical variables (Agresti, 2012; Stokes et al., 2012).

The analysis of discrete data is closely related

to the task of classiﬁcation. Numerous algorithms

have been developed for classiﬁcation. These algo-

rithms encompass decision trees (Azad et al., 2025),

random forest (Biau and Scornet, 2016), logistic re-

gression (Hosmer and Lemeshow, 2000), Bayesian

networks (Congdon, 2005), neural networks (Ag-

Reznychenko, T., Uglickich, E. and Nagy, I.

Categorical Model Estimation with Feature Selection Using an Ant Colony Optimization.

DOI: 10.5220/0013705300003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 1, pages 219-226

ISBN: 978-989-758-770-2; ISSN: 2184-2809

219

garwal, 2018), k-nearest neighbors (Zhang and Li,

2021), naive Bayes classiﬁers (Forsyth, 2019), gra-

dient boosting (Wade and Glynn, 2020), light gradi-

ent boosting machine (Wade and Glynn, 2020), cate-

gorical boosting (Hancock and Khoshgoftaar, 2020),

extreme gradient boosting (Wade and Glynn, 2020),

fuzzy rules (Berthold et al., 2013), genetic algo-

rithms (Reeves, 2010) and model-based methods in-

cluding the use of discrete mixture models such as la-

tent class and Rasch mixture models (Agresti, 2012),

Poisson and negative binomial mixtures (Congdon,

2005), mixtures of Poisson regressions, mixtures of

logistic regressions for binary data (Congdon, 2005),

Poisson-gamma and beta-binomial models (Agresti,

2012; Congdon, 2005) as well as Dirichlet mixtures

(Bouguila and Elguebaly, 2009; Li et al., 2019).

There are also recursive estimation algorithms for cat-

egorical mixtures with prior conjugate Dirichlet dis-

tributions (K

arn

y, 2016).

Discrete data analysis faces challenges such as un-

certainty and large dimensionality in a data set, lead-

ing to an exponential increase in the number of pos-

sible combinations. Two main approaches are used

to handle the high-dimensionality problem: (i) fea-

ture extraction methods such as principal component

analysis (Lovatti et al., 2019) for dimensionality re-

duction, multiple correspondence analysis (Roux and

Rouanet, 2010; Hjellbrekke, 2018) for categorical

data, neural network-based methods; (ii) feature se-

lection methods (Pereira et al., 2018), including L1

regularization (Suykens et al., 2014), random forest

importance (Genuer et al., 2010), categorical boost-

ing importance (Prokhorenkova et al., 2018), etc.

The key challenge is the high-dimensional na-

ture of the explanatory variables (Ray et al., 2021;

Ayesha et al., 2020), which complicates the analysis

and interpretation of the data. Thus, there is a criti-

cal need for effective dimensionality reduction tech-

niques that preserve or enhance classiﬁcation accu-

racy while identifying the subset of variables that are

most informative about the target variable. The spe-

ciﬁc problem addressed in this work is the identiﬁca-

tion of explanatory variables that are statistically as-

sociated with the target variable, enabling a reduction

in the complexity of the model.

This suggests that current methods for discrete

data analysis still require improvement (Jozova et al.,

2021). Inspired by feature selection heuristics used

in ensemble methods such as random forests, we pro-

pose a hybrid approach to reduce the dimensionality

of categorical models while preserving predictive per-

formance. This study introduces a novel method tai-

lored for discrete data sets with the aim of identifying

the most relevant subset of variables. The proposed

solution is based on two key points: (i) a categorical

model estimation, and (ii) a feature selection using ant

colony optimization.

The paper is organized as follows: Section 2

presents the preliminary part, introduces the neces-

sary notation, and reviews the basic facts about both

discrete data coding and the estimation of categori-

cal models. Section 3 is the main part of the paper.

Subsection 3.1 formulates the prediction problem in

general. Subsection 3.2 presents the proposed solu-

tion. The results of illustrative experiments are given

in Section 4, and Section 5 provides conclusions and

future plans.

2 PRELIMINARIES

This section provides a basic concept about the cate-

gorical models and techniques utilized in this paper.

The categorical model has the following form:

f (y|x,α) = α, (1)

where f (·|·) denotes a conditional probability func-

tion; y is a discrete target variable; x = [x

,...,x

]

is the discrete multivariate explanatory variable, and

N is the number of variables; α is a model parameter

which contains the probabilities of individual combi-

nations of the target and explanatory variables.

Model estimation in the standard case is straight-

forward. For multivariate models, vector coding must

ﬁrst be introduced. This process is illustrated using an

example with two variables x

∈ 1,2,3 and x

∈ 1,2,

with all possible combinations and their correspond-

ing codes z summarized in Table 1.

Table 1: The coding of the data set.

1 1 2 2 3 3

1 2 1 2 1 2

z 1 2 3 4 5 6

For the estimation of the categorical model, the

values of y and x are measured, the code z is deter-

mined, and the frequencies of the vector y|z are calcu-

lated. This is illustrated in Table 2, where the values

of y ∈ {1,2} are vertically positioned in the table, and

the encoded values z are horizontally positioned. The

table is normalized so that the sums of entries in the

columns are equal to one. By normalizing, we obtain

probability values for every combination of y

and the

corresponding code z

, which deﬁne the estimated pa-

rameters of the coded model.

Ant Colony Optimization is a metaheuristic al-

gorithm inspired by the behavior of real ants to ﬁnd

the shortest path from a colony to a food source.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

220

Table 2: Estimation of the categorical model.

y/z 1 2 3 4 5 6

y = 1 α

1|1

1|2

1|3

1|4

1|5

1|6

y = 2 α

2|1

2|2

2|3

2|4

2|5

2|6

The main concept of this approach is based on

modeling the environment as a graph G = (V,E),

where V consists of two nodes, namely v

represents

the nest of the ants and v

is the food source. E con-

sists of two links, namely e

, which represents the

short path l

between v

and v

, and e

represents the

long path l

> l

). The real ants lay pheromone on

the paths. Accordingly, we introduce a value p

to de-

note the pheromone intensity on each of the two paths

, i = 1,2.

Each ant starts at v

and selects a path with proba-

bility θ

between the edges e

and e

to reach the food

source v

. If θ

> θ

, the probability of choosing e

is higher. Moreover, as more ants select a particular

path, the corresponding θ

increases. Links that are

not used eventually lose the pheromone and are reset

(Blum, 2005; Fidanova, 2021).

3 CATEGORICAL MODEL

ESTIMATION WITH FEATURE

SELECTION USING AN ANT

COLONY OPTIMIZATION

3.1 Problem Formulation

Consider a categorical model with a discrete target

variable y

and a set of discrete explanatory variables

1;t

2;t

,...,x

N;t

in a discrete time instant t, where

t = 1,2,..,T and T denote the number of records.

The target variable y

and the explanatory variables

= [x

,...,x

]

are measured in time t ≤ T . The

model estimation is performed using training data.

For t > T , we only measure x

and predict the target

using test data.

The aim is to predict a discrete target based on N

explanatory variables x

= [x

,...,x

]

. However,

we assume that not all variables from the vector x

are important for this prediction. The task is to ﬁnd

an optimal selection of variables x

= [x

,..,x

∗

where N

∗

is a pre-selected and ﬁxed, for which the

quality of prediction is best, and there is a function

ϕ : x → Accuracy(x). (2)

We look for optimal selection for which

Accuracy(x) is maximal. This is the optimiza-

tion task. Unfortunately, the criterion function is

discrete with an extremely huge deﬁnition domain.

The optimization method for ant colonies looks like

a possible tool for the solution.

We deﬁne a graph with G nodes, each represent-

ing an individual explanatory variable. The process

begins by randomly selecting a starting node and then

repeatedly choosing the edge with the highest weight

in the S steps. Initially, all edge weights are set to

zero.

Once a path is selected, the variables correspond-

ing to the nodes along this path are used to estimate

the categorical model. The resulting model is evalu-

ated on the basis of its prediction error. Depending

on the evaluation, the edges along the selected path

are updated with new weights. Additionally, all edge

weights are subject to exponential forgetting.

The next step involves randomly selecting a start-

ing point, which is repeated many times until the path

is ﬁxed.

The idea of the proposed solution is to estimate the

categorical model for various subsets of explanatory

variables and to employ ant colony optimization to

identify an optimal subset.

3.2 Overview of the Proposed Solution

The core principle of the hybrid algorithm is to ran-

domly generate P

subsets of unique explanatory

variables. Then, we estimate the parameter α, per-

form the estimation of the K models, and predict the

target variable. Predictive accuracy is used to deter-

mine the quality of the constructed K models and the

efﬁciency of the x

. Based on the accuracy of the

model, using the ant colony optimization scheme, the

inﬂuence weights of the variables are determined. If

the accuracy of the model P

< P

K+1

, we increase

the inﬂuence weight of the variables included in this

subset. Otherwise, we ignore the model. Explaining

variables that are not updated, their inﬂuence weights

are forgotten. The proposed solution includes the fol-

lowing steps:

Algorithm setup:

1. Set a number of features f .

2. Set a coefﬁcient of forgetting β.

Initialization of solution vectors:

1. Randomly create P

subsets that consist of f

number of variables. Exp: f = 3, where P

[5,15,19].

2. Evaluate each entry in P

and calculate the accu-

racy, which is an indicator of the quality of the

categorical model.

3. Calculate the weight of each variable for each so-

lution.

Categorical Model Estimation with Feature Selection Using an Ant Colony Optimization

221

Time loop:

For i = 1,2,..,S:

1. Creating new solutions: randomly select a vec-

tor P

from the set of K solutions. Each vector

represents a subset of selected features. Then a

feature is randomly chosen; for example, consider

= [5,15,19], and suppose that the second ele-

ment, 15, is selected for modiﬁcation. The chosen

feature is then decomposed into a set of alterna-

tive features, which include neighboring variables

such as {11,12,13,15,16,17,18}. From this set,

select the variable that has the highest weight. The

new solution is P

= [5,11,19].

2. Evaluate the solution and update the weights of

the variables.

3. Sort the solutions by accuracy. Variables that are

not used, then their weight is multiplied by the

forgetting coefﬁcient.

Stopping criterion:

Stop the algorithm if the computation does not

modify during m iterations.

end

4 EXPERIMENTS

The experiments were conducted to evaluate the ef-

fectiveness of the proposed method in feature se-

lection and classiﬁcation, comparing its performance

with that of widely used algorithms.

For this purpose, a publicly available data set from

the Kaggle platform (Kaggle, 2019) was used. This

data set is based on a survey of people’s use of on-

line food delivery services. It aims to identify the

factors that are driving the growing demand for these

services, particularly in metropolitan areas. The re-

search focuses on the following aspects: 1) demo-

graphic characteristics of consumers, 2) general be-

havioral patterns in purchasing decisions, and 3) the

inﬂuence of delivery time on consumer preferences.

To ensure a comprehensive understanding of the

characteristics of the sample, the data values were col-

lected using a structured closed-ended questionnaire.

The responses were recorded on a ﬁve-point Likert

scale and the survey included questions that covered a

variety of sociodemographic variables. The distribu-

tion of the participants by these variables is presented

in Table 3.

Before applying machine learning methods, the

data set was thoroughly cleaned. This involved

eliminating special characters, null entries, duplicate

records, and irrelevant content that could negatively

impact the quality of the analysis. The cleaned data

Table 3: Sociodemographic characteristics of the partici-

pants.

Variable Categories

Age range 18–33 years

Gender Male, Female

Marital status Single, Married, Prefer not to say

Occupation Student, Employee, Housewife, Self-employed

Monthly income No income, <Rs.10k, Rs.10k–25k,

Rs.25k–50k, >Rs.50k

Education level Uneducated, School, Graduate,

Postgraduate, Ph.D.

Family size 1–6 members

set used for the ﬁnal analysis consisted of 286 obser-

vations in 45 variables (which are speciﬁed in Table

4). The binary target variable includes class label 1,

which corresponds to ”Yes – I will order online deliv-

ery,” while class label 0 represents ”No – I will not or-

der online delivery.” The data set is imbalanced, with

77.3% of the responses indicating ”Yes” and only

22.7% indicating ”No.” This imbalance poses a chal-

lenge for classiﬁcation models, particularly in main-

taining high performance across both classes. The

data values were recoded for analysis, and the recoded

values are presented in Table 4. Five data sets were

randomly shufﬂed based on the main data set. Each

data set was divided into two subsets: 80% for train-

ing and 20% for testing.

The experiments were performed using Jupyter

Notebook with Python 3.10.12, leveraging well-

established machine learning libraries such as

scikit-learn (www.scikit-learn.org), pandas (pan-

das.pydata.org), and AutoGluon (auto.gluon.ai).

These tools facilitated data preprocessing, model de-

velopment, and performance evaluation. In addition,

Scilab (www.scilab.org) was employed to test and

validate the proposed method, using its capabilities

for numerical analysis and algorithm veriﬁcation.

4.1 Performance Assessment Using

Survey Data Values

In this series of experiments, we focus on determining

the key parameters for building a classiﬁcation model.

One of the conﬁgurations under consideration is

the number of explanatory variables (features) used

to train the model. To investigate this, we vary the

number of features f from 1 to 10. The quality of each

feature selection is evaluated using a score, deﬁned as

the predictive accuracy of the model.

To identify the optimal number of features, the

experiments were conducted in ﬁve data sets. Fig-

ure 1 shows how the model accuracy changes with the

number of features and presents the average accuracy

across all data sets.

As shown, the highest accuracy of 94.1% was ob-

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

222

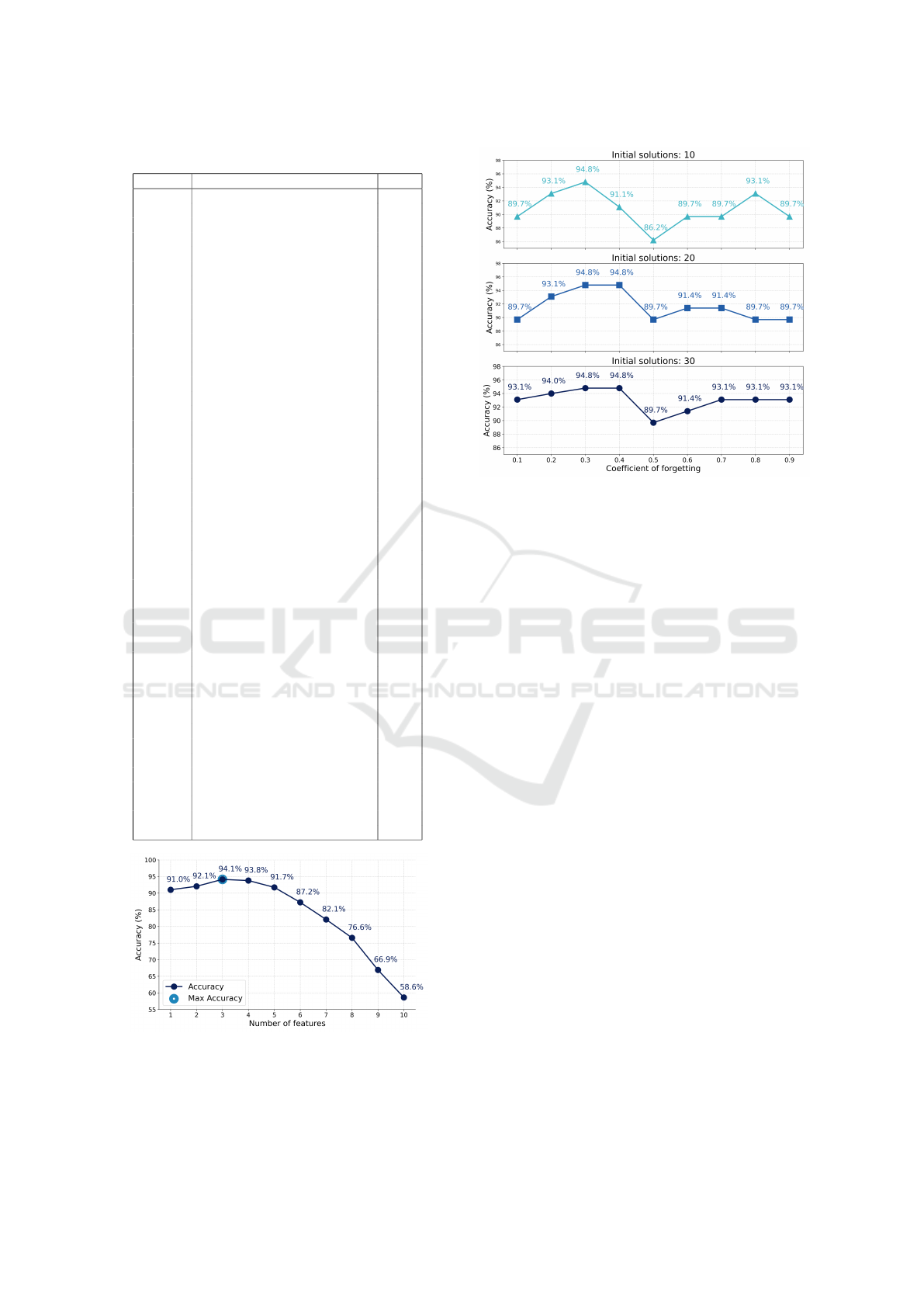
Table 4: Variables and their value ranges.

Variable Name Value

1 Age 1–7

2 Gender 1–2

3 Marital Status 1–3

4 Occupation 1–4

5 Monthly Income 1–3

6 Education 1–5

7 Family Size 1–6

8 Ease and Convenience 1–3

9 Time Saving 1–3

10 More Restaurant Choices 1–3

11 Easy Payment Option 1–3

12 More Offers and Discounts 1–3

13 Good Food Quality 1–3

14 Good Tracking System 1–3

15 Self Cooking 1–3

16 Health Concern 1–3

17 Late Delivery 1–3

18 Poor Hygiene 1–3

19 Bad Past Experience 1–3

20 Unavailability 1–3

21 Unaffordable 1–3

22 Long Delivery Time 1–3

23 Delay in Assigning Delivery Person 1–3

24 Delay in Picking Up Food 1–3

25 Wrong Order Delivered 1–3

26 Missing Item 1–3

27 Order Placed by Mistake 1–3

28 Inﬂuence of Time 1–3

29 Order Time 1–3

30 Maximum Wait Time 1–5

31 Residence in Busy Location 1–3

32 Google Maps Accuracy 1–3

33 Good Road Condition 1–3

34 Low Quantity, Low Time 1–3

35 Delivery Person Ability 1–3

36 Inﬂuence of Rating 1–3

37 Less Delivery Time 1–3

38 High Quality of Package 1–3

39 Number of Calls / Politeness 1–3

40 Freshness 1–3

41 Politeness 1–3

42 Temperature 1–3

43 Good Taste 1–3

44 Good Quantity 1–3

45 Output 0–1

Figure 1: Accuracy comparison with number of features

from 1 to 10.

tained using three features, while using four led to a

Figure 2: Accuracy comparison concerning the forgetting

coefﬁcient and the number of initial candidate solutions,

with the number of features ﬁxed at three.

slightly lower mean accuracy of 93.8%.

Based on this result, the next experiment was con-

ducted to investigate the effect of two parameters on

model performance: the forgetting coefﬁcient β (var-

ied from 0.1 to 0.9) and the number of initial can-

didate solutions P

. For this analysis, the number of

features n

was ﬁxed at three.

As shown in Figure 2, the model achieves the

highest accuracy when the forgetting coefﬁcient β is

in the range of 0.2 to 0.4. Moreover, increasing the

number of initial candidate solutions to 30 leads to

improved predictive accuracy, indicating that greater

diversity in initialization improves model accuracy.

4.2 Models Comparison

The goal of these experiments is to evaluate and com-

pare established machine learning algorithms to de-

termine which perform best on discrete data. A set

of baseline algorithms was selected for comparison

with the proposed method, including random for-

est (RF), categorical boosting (CatBoost), k-nearest

neighbors (KNeighbors), light gradient boosting ma-

chine (LightGBM), an extended variant of LightGBM

with increased model capacity (LightGBMLarge), ex-

treme gradient boosting (XGBoost), and a neural net-

work implemented using the FastAI library (Neu-

ralNetFastAI). All experiments and model evalua-

tions were conducted using the AutoGluon library

(auto.gluon.ai).

The model parameters were ﬁxed according to the

previous analysis: the number of features was set to

Categorical Model Estimation with Feature Selection Using an Ant Colony Optimization

223

three, the forgetting coefﬁcient to 0.3, and the number

of initial candidate solutions to 30.

Table 5 summarizes the classiﬁcation accuracy

of each model. The proposed method achieved the

highest average accuracy of 94.1%, outperforming all

other models. CatBoost followed with 90.7%, Ran-

dom Forest with 90.3%, and KNeighbors with 90.0%.

Table 5: Comparison of the performance of algorithms on

ﬁve data sets.

Algorithm DS 1 DS 2 DS 3 DS 4 DS 5 Average

Proposed method 94.8% 93.1% 93.1% 93.1% 96.6% 94.1%

CatBoost 94.8% 87.9% 91.4% 89.7% 89.7% 90.7%

RandomForest 94.8% 89.7% 89.7% 87.9% 89.7% 90.3%

KNeighbors 93.1% 87.9% 89.7% 89.7% 89.7% 90.0%

LightGBM 96.6% 89.7% 89.7% 82.8% 86.2% 89.0%

XGBoost 90.0% 87.9% 87.9% 87.9% 84.5% 87.6%

NeuralNetFastAI 91.4% 79.3% 86.2% 87.9% 82.8% 85.5%

LightGBMLarge 84.5% 82.8% 86.2% 84.5% 87.9% 85.2%

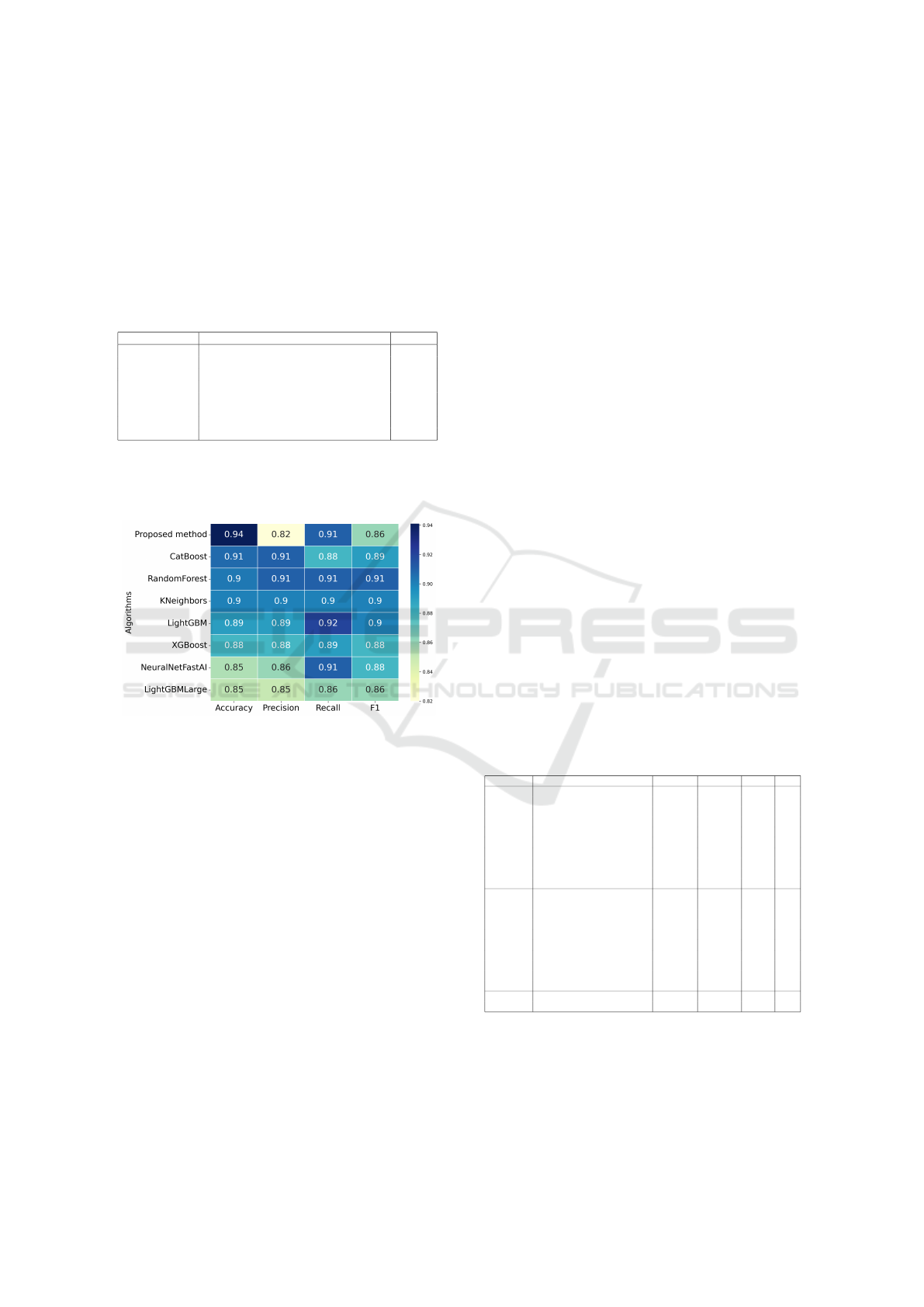
Figure 3 presents a heat map summarizing the av-

erage performance of each model in four key evalua-

tion metrics: accuracy, precision, recall, and F1 score.

Figure 3: Average performance metrics for each classiﬁca-

tion model.

Models such as Random Forest and CatBoost

achieve precision and recall values near 0.91, leading

to the highest F1 scores 0.91. The proposed method

achieves a recall 0.91. However, its precision 0.82 is

lower than that of other models.

In this experiment, all machine learning algo-

rithms except the proposed method were applied to

the full set of input variables. Challenges associ-

ated with the dataset’s high dimensionality will be

addressed in subsequent experiments that aim to im-

prove performance and reduce the number of input

features.

4.3 Feature Selection

This stage aims to conduct experiments using a re-

duced set of variables to achieve efﬁcient classiﬁca-

tion. Feature selection was applied to identify the

most informative variables from the full set.

As discussed in Subsection 4.2, Random Forest

and CatBoost demonstrated the highest classiﬁcation

performance among the baseline models. Therefore,

feature importance selection methods tailored to each

algorithm were employed. For Random Forest, im-

portance scores were computed using the Mean De-

crease in Impurity (as implemented in scikit-learn).

For CatBoost, the default feature importance method

– PredictionValuesChange (catboost.ai) – was used.

Two conﬁgurations of the proposed hybrid

method were evaluated. The model setup followed the

best-performing parameters from earlier experiments:

a forgetting coefﬁcient β of 0.3 and 30 initial candi-

date solutions. The number of selected variables was

set to 3 for the ﬁrst conﬁguration and 4 for the second.

Feature sets ranging in size from one to nine were

established for each algorithm. The results are pre-

sented in Table 6. Random Forest achieved an accu-

racy of 91.4% with seven variables, where the preci-

sion was 0.90, the recall and the F1 score decreased

to 0.81 and 0.84, respectively. CatBoost achieved an

improved accuracy of 93.1% with an F1 score of 0.87.

The results of the proposed method applied to

different subsets of variables are shown in Table

6. When using the variables set {9,22,37,42}, the

model achieved the highest accuracy of 94.8%, with

a precision of 0.90, recall of 0.82, and an F1 score

of 0.86. This indicates effective overall performance.

In contrast, using a smaller subset of three features

{9,17,21} led to a slight decrease in performance.

The model achieved the accuracy of 93.1%, a preci-

sion of 0.89, a recall of 0.73, and an F1 score of 0.80.

Table 6: Comparison of model performances with different

feature sets.

Algorithm Selected variables Accuracy Precision Recall F1

RF all variables 91.4% 0.91 0.90 0.91

10 84.5% 0.77 0.66 0.69

10, 11 84.5% 0.77 0.66 0.69

10, 11, 12 82.8% 0.72 0.72 0.72

10, 11, 12, 9 87.9% 0.82 0.75 0.78

10, 11, 12, 9, 14 87.9% 0.82 0.75 0.78

10, 11, 12, 9, 14, 1 84.5% 0.77 0.66 0.69

10, 11, 12, 9, 14, 1, 21 91.4% 0.90 0.81 0.84

10, 11, 12, 9, 14, 1, 21, 30 89.6% 0.88 0.76 0.80

10, 11, 12, 9, 14, 1, 21, 1, 30, 13 89.7% 0.88 0.76 0.80

CatBoost all variables 89.7% 0.89 0.89 0.89

8 89.7% 0.94 0.73 0.78

8, 9 86.2% 0.80 0.71 0.74

8, 9, 1 81.0% 0.67 0.57 0.58

8, 9, 1, 12 84.5% 0.77 0.66 0.69

8, 9, 1, 12, 2 86.2% 0.83 0.67 0.71

8, 9, 1, 12, 2, 17 93.1% 0.96 0.82 0.87

8, 9, 1, 12, 2, 17, 9 91.4% 0.95 0.77 0.83

8, 9, 1, 12, 2, 17, 9, 23 89.7% 0.94 0.73 0.78

8, 9, 1, 12, 2, 17, 9, 23, 11 89.7% 0.94 0.73 0.78

PM 9, 17, 21 93.1% 0.89 0.73 0.80

9, 22, 37, 42 94.8% 0.90 0.82 0.86

Table 7 presents the classiﬁcation performance of

the Random Forest and CatBoost models when ap-

plied to feature subsets selected by the proposed hy-

brid method (PM). The models were evaluated on fea-

ture subsets selected by the proposed method.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

224

Table 7: Performance of models with selected features us-

ing the proposed method.

Algorithm Selected variables Accuracy Precision Recall F1

Random Forest with PM 9, 17, 21 93.1% 0.91 0.85 0.88

Random Forest with PM 9, 22, 37, 42 94.8% 0.93 0.90 0.91

CatBoost with PM 9, 17, 21 93.1% 0.91 0.85 0.88

CatBoost with PM 9, 22, 37, 42 94.8% 0.93 0.90 0.91

Both models achieved their highest accuracy of

94.8% when using the feature subset 9, 22,37,42,

with precision, recall, and F1 score of 0.93, 0.90,

and 0.91, respectively. When a reduced subset of

three features 9, 17, 21 was used, accuracy slightly de-

creased to 93.1% for both Random Forest and Cat-

Boost. The corresponding precision, recall, and F1

score also declined to 0.91, 0.85, and 0.88, respec-

tively.

4.4 Discussion

This study aimed to validate the proposed method

and select a subset of explanatory variables for which

a categorical model can optimally predict the target

variable. This objective was achieved successfully.

The results demonstrated that the method achieves

high accuracy when the optimal subset consists of

only four variables. Moreover, the selected variables

enhanced the performance of both the Random Forest

and CatBoost models.

One limitation of the proposed hybrid algorithm

is its reliance on randomly generating variable sub-

sets, which can increase computational time during

the search for the most relevant subset. Addition-

ally, the method requires careful setting of parameters

such as the subset size and the forgetting coefﬁcient,

which may reduce the performance of a model. De-

spite these limitations, the algorithm has the potential

to analyze questionnaire data in ﬁelds such as market-

ing, the social sciences, and transportation research,

where identifying a reduced set of informative cate-

gorical variables is essential.

5 CONCLUSION

This study focused on analyzing discrete data ob-

tained from questionnaires. The paper presented the

hybrid method for categorical model estimation with

feature selection using an ant colony optimization.

The proposed method was applied to discrete ques-

tionnaire data to select a subset of explanatory vari-

ables to predict the target variable. To assess the

effectiveness of the presented method, experiments

were conducted.

The main contributions of this study are the iden-

tiﬁcation of a relevant set of variables – achieved

by evaluating multiple categorical models using ant

colony optimization – and the reduction of the

model’s dimensionality. Further work will focus on

improving and optimizing the search for relevant vari-

ables, which will enhance both the speed of determi-

nation and the accuracy, thereby increasing the efﬁ-

ciency in solving complex tasks.

In general, the proposed method shows potential

as a useful tool in practical tasks related to question-

naire data analysis, where preserving information in

high-dimensional discrete models is important.

ACKNOWLEDGEMENTS

This paper was funded by the project

SGS25/096/OHK2/2T/16 from the Student Grant

Competition of the Czech Technical University in

Prague, Faculty of Transportation Sciences.

European Funding: Under grant 101096884, Lis-

ten2Future is co-funded by the European Union.

Views and opinions expressed are however those of

the author(s) only and do not necessarily reﬂect those

of the European Union or Chips Joint Undertaking.

Neither the European Union nor the granting author-

ity can be held responsible for them. The project is

supported by the CHIPS JU and its members (includ-

ing top-up funding by Austria, Belgium, Czech Re-

public, Germany, Netherlands, Norway and Spain.

National Funding: This project has also received

national funding from the Ministry of Education,

Youth and Sports of the Czech Republic (MEYS) un-

der grant agreement No 9A22004.

REFERENCES

Aggarwal, C. C. (2018). Neural Networks and Deep Learn-

ing: A Textbook. Springer.

Agresti, A. (2012). Categorical Data Analysis. John Wiley

& Sons, 3rd edition.

Agresti, A. (2018). An Introduction to Categorical Data

Analysis. Wiley, 3rd edition.

Alwosheel, A., Cranenburgh, S. V., and Chorus, C. G.

(2018). Is your dataset big enough? sample size re-

quirements when using artiﬁcial neural networks for

discrete choice analysis. Journal of Choice Modelling,

28:167–182.

Ayesha, S., Hanif, M. K., and Talib, R. (2020). Overview

and comparative study of dimensionality reduction

techniques for high dimensional data. Information Fu-

sion, 59:44–58.

Azad, M., Nehal, T. H., and Moshkov, M. (2025). A novel

ensemble learning method using majority based vot-

ing of multiple selective decision trees. Computing,

107(1):42.

Categorical Model Estimation with Feature Selection Using an Ant Colony Optimization

225

Bergsma, W. and Lupparelli, M. (2025). Editorial for spe-

cial issue on categorical data analysis. Metrika, pages

1–3.

Berthold, M. R., Wiswedel, B., and Gabriel, T. R. (2013).

Fuzzy logic in knime – modules for approximate rea-

soning. International Journal of Computational Intel-

ligence Systems, 6(1):34–45.

Biau, G. and Scornet, E. (2016). A random forest guided

tour. Test, 25(2):197–227.

Blum, C. (2005). Ant colony optimization: Introduction and

recent trends. Physics of Life Reviews, 2(4):353–373.

Bouguila, N. and Elguebaly, W. (2009). Discrete data clus-

tering using ﬁnite mixture models. Pattern Recogni-

tion, 42(1):33–42.

Congdon, P. (2005). Bayesian Models for Categorical Data.

John Wiley Sons.

D. Zwahlen, C. J. and Pf

afﬂi, M. (2016). Sleepiness, driv-

ing, and motor vehicle accidents: a questionnaire-

based survey. Journal of Forensic and Legal Medicine,

44:183–187.

Dell’Olio, L., Ibeas, A., de O

na, J., and de O

na, R.

(2017). Public transportation quality of service: Fac-

tors, models, and applications. Elsevier.

Falissard, B. (2012). Analysis of Questionnaire Data with

R. Chapman & Hall/CRC, Boca Raton.

Fidanova, S. (2021). Ant colony optimization. In Ant

Colony Optimization and Applications, pages 3–8.

Springer International Publishing, Cham.

Forsyth, D. (2019). Applied Machine Learning. Springer.

oldes, D., Csisz

ar, C., and Zarkeshev, A. (2018). User

expectations towards mobility services based on au-

tonomous vehicle. In 8th International Scientiﬁc Con-

ference CMDTUR, pages 7–14.

Genuer, R., Poggi, J. M., and Tuleau-Malot, C. (2010).

Variable selection using random forests. Pattern

Recognition Letters, 31(14):2225–2236.

Goodman, L. A. and Kruskal, W. H. (1963). Measures of

association for cross classiﬁcations iii: approximate

sampling theory. Journal of the American Statistical

Association, 58(302):310–364.

Hancock, J. T. and Khoshgoftaar, T. M. (2020). Catboost

for big data: an interdisciplinary review. Journal of

Big Data, 7(1):94.

Hjellbrekke, J. (2018). Multiple Correspondence Analysis

for the Social Sciences. Routledge.

Hosmer, D. W. and Lemeshow, S. (2000). Applied Logistic

Regression. Wiley-Interscience, 2nd edition.

Hu, Y., Li, Y., Huang, H., Lee, J., Yuan, C., and Zou,

G. (2022). A high-resolution trajectory data driven

method for real-time evaluation of trafﬁc safety. Acci-

dent Analysis & Prevention, 165:106503.

Jozova, S., M. Matowicki, O. Pribyl, M. Z. S. O., and Zi-

olkowski, R. (2021). On the analysis of discrete data

ﬁnding dependencies in small sample sizes. Neural

Network World, 31(5):311.

Kaggle (2019). Online food delivery

preferences-bangalore region. Available:

https://www.kaggle.com/datasets/benroshan/online-

food-delivery-preferencesbangalore-region.

arn

y, M. (2016). Recursive estimation of high-order

markov chains: Approximation by ﬁnite mixtures. In-

formation Sciences, 326:188–201.

Li, Y., Schoﬁeld, E., and G

onen, M. (2019). A tutorial on

dirichlet process mixture modeling. Journal of Math-

ematical Psychology, 91:128–144.

Lovatti, B. P., Nascimento, M. H., Neto,

A. C., Cas-

tro, E. V., and Filgueiras, P. R. (2019). Use of random

forest in the identiﬁcation of important variables. Mi-

crochemical Journal, 145:1129–1134.

Matowicki, M., Pribyl, O., and Pecherkova, P. (2021). Car-

sharing in the czech republic: Understanding why

users chose this mode of travel for different purposes.

Case Studies on Transport Policy, 9(2):842–850.

Pereira, R. B., Plastino, A., Zadrozny, B., and Merschmann,

L. H. (2018). Categorizing feature selection methods

for multi-label classiﬁcation. Artiﬁcial Intelligence

Review, 49:57–78.

Phuong, N. T., Hoang, P. V., Dang, T. M., Huyen, T. N. T.,

and Thi, T. N. (2023). Improving hospital’s quality

of service in vietnam: the patient satisfaction eval-

uation in multiple health facilities. Hospital Topics,

101(2):73–83.

Prokhorenkova, L., Gusev, G., Vorobev, A., Dorogush,

A. V., and Gulin, A. (2018). Catboost: unbiased boost-

ing with categorical features. In Advances in Neural

Information Processing Systems, volume 31.

Ray, P., Reddy, S. S., and Banerjee, T. (2021). Various

dimension reduction techniques for high dimensional

data analysis: a review. Artiﬁcial Intelligence Review,

54(5):3473–3515.

Reeves, C. R. (2010). Genetic algorithms, pages 109–139.

Roux, B. L. and Rouanet, H. (2010). Multiple Correspon-

dence Analysis, volume 163. Sage.

Stokes, M. E., Davis, C. S., and Koch, G. G. (2012). Cate-

gorical Data Analysis Using SAS. SAS Institute, 3rd

edition.

Suykens, J. A., Signoretto, M., and Argyriou, A. (2014).

Regularization, Optimization, Kernels, and Support

Vector Machines. CRC Press.

Tang, W., He, H., and Tu, X. M. (2012). Applied Cat-

egorical and Count Data Analysis. Chapman and

Hall/CRC.

Wade, C. and Glynn, K. (2020). Hands-On Gradient Boost-

ing with XGBoost and scikit-learn: Perform accessi-

ble machine learning and extreme gradient boosting

with Python. Packt Publishing Ltd.

Wang, W., Wang, Y., Wang, G., Li, M., and Jia, L. (2023).

Identiﬁcation of the critical accident causative factors

in the urban rail transit system by complex network

theory. Physica A: Statistical Mechanics and its Ap-

plications, 610:128404.

Zhang, S. and Li, J. (2021). Knn classiﬁcation with one-

step computation. IEEE Transactions on Knowledge

and Data Engineering, 35(3):2711–2723.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

226