From Traditional to Intelligent: The Theoretical Foundations,

Method Comparisons, and Challenges of Stock Price Prediction

Models

Qiancheng Rong

School of Mathematics and Statistics, The University of Sydney, Camperdown, New South Wales 2006, Australia

Keywords: Machine Learning; Deep Learning; Stock Price Prediction.

Abstract: Stock prices are a fundamental component of financial markets, encapsulating collective investor expectations

and serving as a crucial basis for economic decision-making. The accurate prediction of price movements

remains a longstanding challenge in financial research, driven by the complex, nonlinear, and dynamic nature

of market behavior. With the proliferation of high-frequency financial data and advancements in

computational methodologies, a diverse array of predictive models has been developed, ranging from

traditional statistical techniques to sophisticated machine learning algorithms. This paper aims to provide a

comprehensive review of the principal methodologies and recent advancements in stock price forecasting. It

covers traditional statistical approaches such as Support Vector Machines (SVM), Random Forests (RF),

Long Short-Term Memory networks (LSTM), Convolutional Neural Networks (CNN), and Reinforcement

Learning (RL). By examining the underlying mechanisms, performance metrics, and implementation

challenges, this paper offers a structured perspective on the diverse methodologies employed in stock price

prediction, which contributes to a deeper understanding of their theoretical foundations and key characteristics.

1 INTRODUCTION

Stocks are a fundamental financial instrument that

represents a share of ownership in a company.

Investors holding stocks thereby become partial

owners and are entitled to a proportional claim on the

company’s assets and profits. In the stock market,

prices are determined by a confluence of factors,

including supply and demand dynamics, market

sentiment, and corporate performance. In the global

financial arena, forecasting stock prices has long been

a central challenge in both theoretical and practical

investment research, as prediction accuracy directly

influences investment decisions, risk management,

and capital allocation (Sun et al., 2020; Sun et al.,

2019; Raza et al., 2014).

Traditional time series models, such as the

AutoRegressive Integrated Moving Average

(ARIMA) model, have historically provided robust

tools for stock price forecasting. In recent years, the

advent of big data, the exponential growth in

computational power, and the rapid development of

https://orcid.org/0009-0007-3613-8473

Artificial Intelligence techniques have ushered in

significant advancements in stock price prediction.

Emerging methodologies are gradually dominating

this field involving Support Vector Machines (SVM),

Random Forests (RF), Long Short-Term Memory

networks (LSTM), Convolutional Neural Networks

(CNN), and Reinforcement Learning (RL). These

models not only possess the capacity to automatically

mine hidden patterns from vast datasets but also

exhibit commendable flexibility and precision when

processing long-term dependencies and non-

stationary data.

This paper aims to present a summary of recent

research developments in stock price prediction. This

research meticulously examines the effectiveness and

limitations of both traditional statistical approaches

and contemporary methods from machine learning,

deep learning, and reinforcement learning, evaluating

and comparing each technique in practical

applications. Furthermore, the paper will analyse the

prevailing challenges and potential future directions

in this rapidly evolving field. Through a critical

660

Rong, Q.

From Traditional to Intelligent: The Theoretical Foundations, Method Comparisons, and Challenges of Stock Price Prediction Models.

DOI: 10.5220/0013703700004670

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Data Science and Engineering (ICDSE 2025), pages 660-666

ISBN: 978-989-758-765-8

comparative discussion of these diverse approaches,

the goal is to offer the academic community and

industry practitioners a comprehensive and profound

perspective, thereby fostering further innovation and

application in the realm of stock price forecasting.

2 STOCK PREDICTION BASED

ON MACHINE LEARNING

MODELS

2.1 Stock prediction based on Machine

Learning Models

2.1.1 SVM Model

SVM endeavor to find an optimal hyperplane in the

feature space that maximizes the margin between

itself and the nearest data points (the support vectors).

For linearly separable cases, a straightforward linear

boundary suffices; however, when dealing with

nonlinearly separable data, kernel functions (such as

the Radial Basis Function or polynomial kernels) are

employed to map the data into a higher-dimensional

space where a linear separation is achievable.

In many stock prediction studies, researchers treat

future price movements as a classification problem—

dividing outcomes into “upward” or “downward

” trends—by leveraging features such as technical

indicators, trading volume, and fundamental data.

This method is prized for its relative simplicity,

interpretability, and its capacity to capture nonlinear

signals. Alternatively, Support Vector Regression

(SVR) is used to directly forecast stock returns or

prices by minimizing prediction errors within a

predefined tolerance, while the kernel trick allows it

to effectively model nonlinear relationships.

Compared to traditional linear regression, SVR

generally exhibits enhanced robustness in noisy

environments and complex data structures, yielding

superior predictive performance.

SVM is further acclaimed for its strong

generalization ability, primarily due to its strategy of

maximizing the classification margin. This approach

minimizes training errors while bolstering

performance on unseen data by reducing sensitivity to

noise, thereby mitigating overfitting — an essential

attribute given the inherent uncertainty in financial

markets. The versatility of kernel methods makes

SVM particularly apt for financial applications, as

they enable the implicit mapping of data into higher-

dimensional spaces where nonlinear patterns become

linearly separable. In addition, the SVM model was

suggested to perform better than the Linear

Regression model by a review study (Kontopoulou et

al., 2023).

On the downside, the effectiveness of SVM is

highly contingent on the appropriate choice of kernel

function and the fine-tuning of hyperparameters.

Inadequate parameterization can severely impair

model performance, and the tuning process can be

both time-consuming and computationally intensive.

The running efficiency is estimated to be affected by

the training period and process of large amounts of

data (Kontopoulou et al., 2023). Moreover, solving

the quadratic programming problem intrinsic to SVM,

especially with nonlinear kernels, escalates

computational demands as data volumes increase,

potentially necessitating distributed computing or

approximation methods for efficiency. This

computational overhead can present a bottleneck in

real-time trading applications. Finally, despite partial

interpretability through support vectors, the overall

decision-making process in high-dimensional spaces

often remains opaque, a “black-box” characteristic

that is problematic in financial contexts where clear

rationale is crucial for risk management and

regulatory oversight.

2.1.2 Random Forest Model

RF employs a bootstrap sampling strategy, whereby

multiple sub-samples are drawn with replacements

from the original dataset. Each sub-sample is then

used to train an individual decision tree. This

approach ensures that each tree is trained on a slightly

different subset of the data, which, when aggregated,

reduces the overall model variance and mitigates the

risk of overfitting. In the domain of stock price

forecasting, Random Forest can be utilized to frame

the prediction problem as a classification task – for

instance, predicting whether a stock’s price will rise

or fall. The RF classifier leverages a

multidimensional feature set (including historical

prices, trading volumes, technical indicators, and

fundamental metrics) to discern the directional

movement of stocks, thereby generating actionable

buy and sell signals. Simultaneously, Random Forest

is also applicable in a regression context, where it

models historical data to produce continuous

forecasts of future stock prices or returns, serving as

quantitative inputs for investment decision-making.

RF model offers an alternative approach by

adeptly handling nonlinear relationships — a critical

advantage given the multifactorial nature of stock

prices. By constructing an ensemble of decision trees,

each derived from a randomly selected subset of

From Traditional to Intelligent: The Theoretical Foundations, Method Comparisons, and Challenges of Stock Price Prediction Models

661

features, RF can effectively capture diverse nonlinear

patterns. This ensemble method not only enhances

long-term predictive accuracy by identifying hidden

patterns but also inherently performs feature selection

through metrics (Majumder & Hossain, 2019). Such

mechanisms diminish the impact of noisy or

redundant variables and facilitate the extraction of the

most predictive features, thereby streamlining the

model. Additionally, the aggregation of predictions

across multiple trees confers robustness, mitigating

the influence of outliers and ensuring stability in

volatile market conditions.

Conversely, the computational complexity and

resource demands of RF can hinder system

responsiveness and deployment efficiency. Although

parallel processing can alleviate some of these

concerns, constructing, selecting features for, and

aggregating predictions from numerous trees

becomes computationally onerous with high-

dimensional and large-scale data. This challenge is

particularly acute in real-time forecasting scenarios,

where frequent model updates are required.

Furthermore, while RF can output feature importance

rankings, the composite nature of its decision-making

process renders it less interpretable, thereby

complicating risk assessment and undermining

stakeholder confidence. In high-dimensional

contexts, the presence of substantial noise or

redundant features may further impair RF

performance, despite its built-in random feature

selection.

2.2 Stock prediction based on Deep

Learning Models

2.2.1 LSTM Model

LSTM networks capitalize on gated mechanisms —

specifically the input, forget, and output gates — to

control information flow within each cell. This design

allows LSTM to effectively propagate gradients

across long sequences, thereby capturing long-term

dependencies essential for forecasting in financial

markets, where historical price trends, trading

volumes, and volatility may have prolonged effects

on future movements.

LSTM ’ s capacity for automatic feature

extraction obviates the need for elaborate manual

engineering, enabling it to discern critical patterns

from raw time series data, and a study proposed that

the prediction error can be reduced by incorporating

feature-attention mechanisms (Xavier, 2019).

Through successive layers of nonlinear

transformation, LSTM can convert raw inputs into

deep, predictive representations that underpin

subsequent forecasting or decision-making tasks.

Moreover, its ability to dynamically adjust hidden

states in response to evolving market conditions

enhances its robustness during periods of heightened

volatility.

Nonetheless, research has demonstrated that

relying solely on historical closing prices as a singular

feature is insufficient for forecasting stock trends,

causing LSTM networks typically require a large

volume of data to effectively extract relevant

features, and insufficient or noisy datasets may hinder

their ability to capture complex temporal dynamics

(Yan & Yang, 2021). Rigorous data preprocessing

including normalization, denoising, and stabilization

is often necessary to optimize performance, thereby

imposing higher demands on data quality and

processing. Furthermore, the computational and

training costs associated with deep LSTM

architectures are significant, often necessitating

Graphics Processing Unit (GPU)acceleration and

distributed computing — especially when high-

frequency data are involved. Extended training cycles

can thus become a bottleneck for real-time

applications. Hyperparameter tuning in LSTM

networks is equally challenging, as performance is

highly sensitive to factors such as network depth,

hidden unit count, learning rate, batch size, and

regularization; suboptimal configurations can lead to

overfitting and compromised generalization. Lastly,

despite its strengths, the internal decision processes of

LSTM remain relatively opaque compared to

classical statistical models, which can be a critical

drawback in financial settings where interpretability

is paramount.

2.2.2 CNN Model

Convolutional Neural Networks (CNN) have also

been applied to stock prediction by exploiting their

ability to automatically extract local features via

convolutional and pooling operations. In this context,

CNNs can capture short-term volatility patterns from

time series data. An innovative approach involves

transforming time series data into visual formats —

such as candlestick charts or heat maps—and applying

CNN-based image analysis to detect latent patterns

that inform stock price forecasts. This methodology

leverages CNNs’ well-established prowess in image

processing to achieve effective predictive

performance. Additionally, CNNs have been utilized

in intelligent stock selection strategies, where

multifactor features are extracted to classify or score

ICDSE 2025 - The International Conference on Data Science and Engineering

662

stocks, thereby aiding in the identification of

promising investment opportunities.

From an advantages perspective, CNNs benefit

from parameter sharing and sparse connectivity

(Zheng et al., 2024), which dramatically reduce the

number of parameters, enhance training efficiency,

and lower the risk of overfitting—especially in high-

dimensional settings. Their aptitude for discerning

local patterns and short-term fluctuations is

particularly valuable for capturing transient price

trends relevant to short-term trading. CNN can be

employed to predict stock prices by analyzing images

that represent stock price trends (Zheng et al., 2024).

However, CNNs are inherently limited in their

ability to model long-term dependencies, as they are

primarily designed for spatial rather than temporal

data. Consequently, relying solely on CNNs may be

insufficient for capturing the extended temporal

dependencies characteristic of stock price

movements. Moreover, deep CNN architectures

demand extensive training data and substantial

computational resources, and their “ black-box ”

nature further complicates interpretability, potentially

leading to challenges in aligning model outputs with

sound investment decisions.

2.3 Reinforcement Learning Model

RL is a paradigm that learns optimal decision-making

policies through continuous interaction with a

dynamic environment. Its fundamental principle is to

enable an agent to perform actions within an

environment, receive corresponding rewards, and

iteratively refine its strategy to maximize cumulative

returns. In stock trading scenarios, the environment is

typically constructed from historical prices, trading

volumes, and technical indicators; actions may

include buying, selling, or holding a stock; and the

reward function is often defined in terms of realized

profits (or losses). State space design involves

assembling a state vector from historical stock data

and relevant indicators, while the action space is

frequently discretized (e.g., 0 for hold, 1 for buy, 2 for

sell). Moreover, the reward function can be defined

either in terms of single-trade profits or cumulative

returns—often adjusted for risk using measures such as

the Sharpe ratio.

On the positive side, RL emphasizes the

autonomous extraction of effective trading strategies

from raw data, reducing the need for extensive

manual intervention. Once trained, an RL model can

rapidly adapt to real-time market conditions by

evaluating the current state and executing appropriate

buy or sell decisions, thus enhancing both the

timeliness and efficiency of trade execution (Dang,

2020). Furthermore, RL models have the capacity to

dynamically update their strategies to accommodate

evolving market volatility. By integrating risk control

metrics (such as maximum drawdown or the Sharpe

ratio) into the reward function, the agent is

encouraged not only to maximize returns but also to

maintain a prudent risk profile. In contrast to

supervised learning approaches, RL does not require

vast quantities of pre-labeled data and profitable

trading strategies can be developed even with only a

few hundred samples, which is an advantage when

labeled data is scarce or costly to obtain (Dang, 2020).

However, several challenges and limitations

temper the application of RL in stock price prediction.

Firstly, RL methods typically exhibit low sample

efficiency, requiring a substantial number of

interactions to converge on an optimal policy — a

significant drawback in financial markets where

effective samples may be limited. Training instability

and the risk of overfitting further complicate the use

of RL, as market noise, non-stationary data, and

poorly designed reward functions can lead the model

to overfit historical patterns, thereby undermining its

performance in live trading (Sahu et al., 2023).

Moreover, deep reinforcement learning models are

computationally intensive, with large numbers of

parameters and lengthy training periods that demand

significant computational resources (e.g., GPUs),

potentially impeding real-time application.

Additionally, the design of a robust and balanced

reward function — which accurately reflects real

trading profits while incorporating risk management—

is inherently complex. An ill-conceived reward

function may steer the agent away from desirable

trading behavior (Sahu et al., 2023). Finally, the “

black-box” nature of RL models often results in

limited interpretability, which can reduce investor

confidence and complicate regulatory oversight.

3 COMPARISON AND

EVALUATION

Model evaluation is a critical component in stock

price forecasting. Diverse evaluation criteria allow

for a multidimensional assessment of a model’s

performance, thereby guiding model fine-tuning and

strategy enhancement.

From Traditional to Intelligent: The Theoretical Foundations, Method Comparisons, and Challenges of Stock Price Prediction Models

663

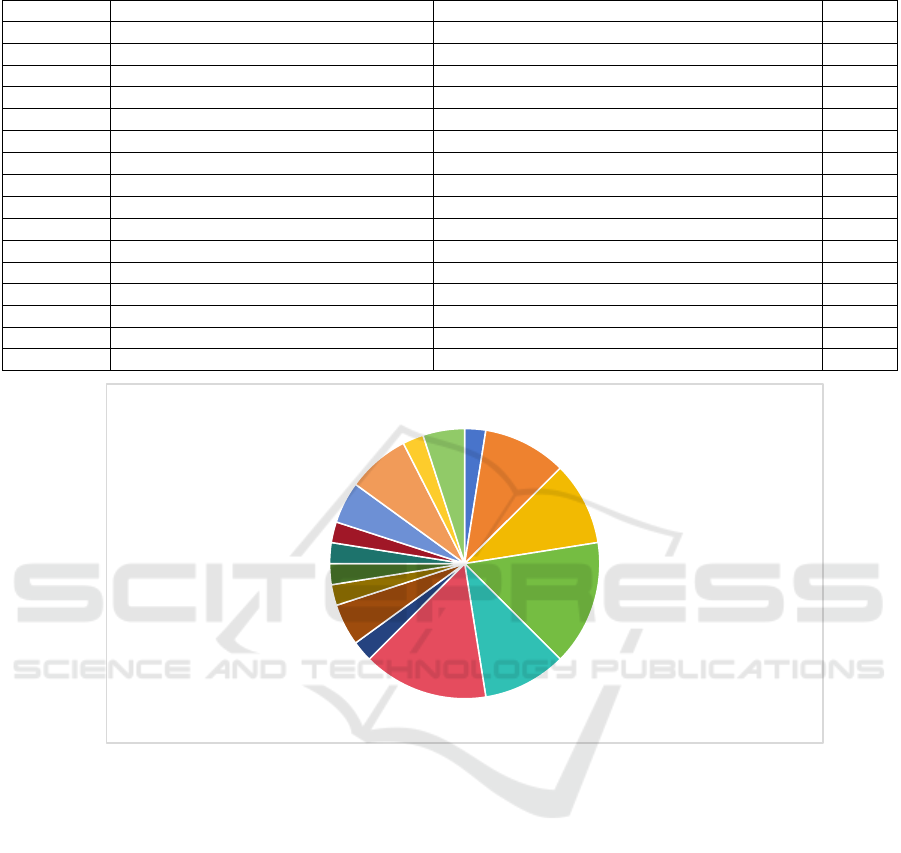
Table 1: Evaluation method of selected studies.

Model Citation Evaluation Metho

Yea

ARIMA

(

Altan & Karasu, 2019

)

MPE, MAPE 2020

ARIMA

(

Budiharto, 2021

)

MSE, MAE, RMSE,MAPE 2021

ARIMA (Carapuço et al., 2018) Accurac

2020

SVM (Chen & Huang, 2021) MSE, RMSE, MAE 2019

SVM (Dhyani et al., 2020) MSE, MAE, AUC, Accuracy, Recall 2020

SVM (Ganesan & Kannan, 2021)

MSE, RMSE, MAE,



2019

(

Ghosh et al., 2019

)

RMSE, MAPE, MBE 2020

LSTM (Gururaj et al., 2019)

RMSE, MAE,



2020

LSTM

(

Khan & Al

hulaiakh, 2020

)

Error Values 2019

LSTM

(

Nti et al., 2020

)

Accurac

, RMSE, 2021

CNN (Oncharoen & Vateekul, 2018) Accuracy, Precision, Recall, F1 Score 2021

CNN (Patil et al., 2020) RMSE, MAE, MAPE 2020

CNN (Qiu et al., 2020) F-measure, Return Rate, Sharpe Ratio 2018

(

Shin et al., 2019

)

Return Rate 2018

(

Tsantekidis et al., 2020

)

Shar

e Ratio 2019

(

h et al., 2020

)

Shar

e Ratio 2020

Figure 1: Occupation for each evaluation method of selected studies. (Picture credit: Original).

Table 1 and Figure 1 indicate that the vast

majority of stock price forecasting models can be

evaluated using conventional statistical metrics. In

contrast, RL models are predominantly assessed by

risk-adjusted performance indicators such as the

Sharpe Ratio and Return Rate. The fundamental

distinction lies in the training process: RL models

iteratively refine their decision-making strategies

through trial-and-error interactions with the

environment rather than merely minimizing

prediction error. Consequently, one may

preliminarily infer that RL possesses certain

advantages over other models.

4 CONCLUSIONS

Initially, this paper provides a systematic review of

the theoretical underpinnings and practical

applications of various forecasting models,

elucidating their respective strengths and limitations.

Subsequently, it consolidates several evaluation

methodologies employed in prior studies, which

tentatively demonstrate the superiority of RL-based

approaches. Given the inherent complexity and

nonlinearity of financial markets, as well as the

specific constraints associated with individual

models, this review advocates for future research to

adopt hybrid and ensemble techniques — such as

ARIMA-LSTM models—that can effectively capture

MPE

MAPE

MSE

RMSE

Accuracy

MAE

AUC

Recall

MBE

Error Values

Precision

F1 Score

Return Rate

Sharpe Ratio

F-measure

R^2

ICDSE 2025 - The International Conference on Data Science and Engineering

664

both linear trends and nonlinear dynamics. Moreover,

future investigations should leverage big data and

multimodal information to explore more adaptive

dynamic strategies and efficient training methods,

ultimately furnishing robust theoretical and empirical

support for investment decision-making and risk

management.

By integrating these advancements, researchers

and practitioners can develop more resilient and

interpretable forecasting frameworks, enhancing

predictive accuracy and robustness in real-world

financial applications. As financial markets continue

to evolve, a multidisciplinary approach that

synergizes machine learning, econometrics, and

domain-specific expertise will be crucial in shaping

the next generation of intelligent financial forecasting

systems.

REFERENCES

Altan, A., & Karasu, S. 2019. The effect of kernel values in

support vector machine to forecasting performance of

financial time series. The Journal of Cognitive Systems,

4(1), 17-21.

Budiharto, W. 2021. Data science approach to stock prices

forecasting in Indonesia during Covid-19 using Long

Short-Term Memory (LSTM). Journal of Big Data,

8(1).

Carapuço, J., Neves, R., & Horta, N. 2018. Reinforcement

learning applied to Forex trading. Applied Soft

Computing, 73, 783–794.

https://doi.org/10.1016/j.asoc.2018.09.017

Chen, Y.-C., & Huang, W.-C. 2021. Constructing a stock-

price forecast CNN model with gold and crude oil

indicators. Applied Soft Computing, 112(107760),

107760.

Dang, Q. V. 2020. Reinforcement learning in stock trading.

In H. Le Thi, H. Le, T. Pham Dinh, & N. Nguyen (Eds.),

Advanced computational methods for knowledge

engineering (Vol. 1121, pp. 311–322). Springer, Cham.

Dhyani, B., Kumar, M., Verma, P., & Jain, A. 2020. Stock

Market Forecasting Technique using Arima Model.

International Journal of Recent Technology and

Engineering, 8(6), 2694–2697.

Ganesan, A., & Kannan, A. 2021. Stock Price Prediction

using ARIMA Model. International Research Journal of

Engineering and Technology.

Ghosh, A., Bose, S., Maji, G., Debnath, N., & Sen, S. 2019,

September 26. Stock Price Prediction Using LSTM on

Indian Share Market. Easychair.org; EasyChair.

Gururaj, V., V R, S., & Ashwini K, D. 2019. Stock Market

Prediction using Linear Regression and Support Vector

Machines. International Journal of Applied

Engineering Research, 14(8), 1931–1934.

Khan, S., & Alghulaiakh, H. 2020. ARIMA Model for

Accurate Time Series Stocks Forecasting. International

Journal of Advanced Computer Science and

Applications, 11(7).

Kontopoulou, V. I., Panagopoulos, A. D., Kakkos, I., &

Matsopoulos, G. K. 2023. A Review of ARIMA vs.

Machine Learning Approaches for Time Series

Forecasting in Data Driven Networks. Future Internet,

15(8), 255. https://doi.org/10.3390/fi15080255

Majumder, Md. M. R., & Hossain, Md. I. 2019, February 1.

Limitation of ARIMA in extremely collapsed market:

A proposed method. IEEE Xplore.

Nti, I. K., Adekoya, A. F., & Weyori, B. A. 2020. Efficient

Stock-Market Prediction Using Ensemble Support

Vector Machine. Open Computer Science, 10(1), 153–

163.

Oncharoen, P., & Vateekul, P. 2018. Deep Learning Using

Risk-Reward Function for Stock Market Prediction.

Proceedings of the 2018 2nd International Conference

on Computer Science and Artificial Intelligence - CSAI

’18.

Patil, P., Wu, C.-S. M., Potika, K., & Orang, M. 2020. Stock

Market Prediction Using Ensemble of Graph Theory,

Machine Learning and Deep Learning Models.

Proceedings of the 3rd International Conference on

Software Engineering and Information Management.

Qiu, J., Wang, B., & Zhou, C. 2020. Forecasting stock

prices with long-short term memory neural network

based on attention mechanism. PLOS ONE, 15(1),

e0227222.

Raza, S. A., Jawaid, S. T., & Hussain, A. 2014. Risk and

investment decisions in stock markets: evidence from

four Asian countries. International Journal of

Managerial and Financial Accounting, 6(3), 227-250.

Sahu, S. K., Mokhade, A., & Bokde, N. D. 2023. An

Overview of Machine Learning, Deep Learning, and

Reinforcement Learning-Based Techniques in

Quantitative Finance: Recent Progress and Challenges.

Applied Sciences, 13(3), 1956.

Shin, H.-G., Ra, I., & Choi, Y.-H. 2019. A Deep

Multimodal Reinforcement Learning System

Combined with CNN and LSTM for Stock Trading.

2019 International Conference on Information and

Communication Technology Convergence (ICTC).

Sun, Y., Jin, Q., Cheng, Q., & Guo, K. 2019. New tool for

stock investment risk management: Trend forecasting

based. Industrial Management & Data Systems.

Sun, Y., Jin, Q., Cheng, Q., & Guo, K. 2020. New tool for

stock investment risk management: Trend forecasting

based on individual investor behavior. Industrial

Management & Data Systems, 120(2), 388-405.

Tsantekidis, A., Passalis, N., Toufa, A.-S., Saitas-Zarkias,

K., Chairistanidis, S., & Tefas, A. 2020. Price Trailing

for Financial Trading Using Deep Reinforcement

Learning. IEEE Transactions on Neural Networks and

Learning Systems, 32, 1–10.

Vijh, M., Chandola, D., Tikkiwal, V. A., & Kumar, A.

2020. Stock Closing Price Prediction using Machine

Learning Techniques. Procedia Computer Science,

167(167), 599–606.

Xavier, A. 2019, January 22. Predicting stock prices with

LSTM - Neuronio - Medium. Medium; Neuronio.

From Traditional to Intelligent: The Theoretical Foundations, Method Comparisons, and Challenges of Stock Price Prediction Models

665

https://medium.com/neuronio/predicting-stock-prices-

with-lstm-349f5a0974d4

Yan, Y., & Yang, D. 2021. A Stock Trend Forecast

Algorithm Based on Deep Neural Networks. Scientific

Programming, 2021(7510641), 1–7.

Zheng, J., Xin, D., Cheng, Q., Tian, M., & Yang, L. 2024.

The Random Forest Model for Analyzing and

Forecasting the US Stock Market in the Context of

Smart Finance.

ICDSE 2025 - The International Conference on Data Science and Engineering

666