A Study on the Impact of Decision Tree and Multiple Regression on

Study Time Optimization and Performance

Tianyu Fu

School of Computing, Clemson University, 821 McMillan Rd, Clemson, U.S.A.

Keywords: Study Time Allocation, Academic Performance Predication, Multiple Linear Regression, Decision Tree

Algorithm, Machine Learning in Education.

Abstract: Student achievement is affected by a variety of factors, such as study time, prior grades, extracurricular

activities, hours of sleep, and a number of practice problems. In this paper, multiple linear regression model

and decision tree models are used for modeling and analysis. The results of multiple linear regression showed

that prior grades, study time, and the number of practice problems were significant factors affecting students'

performance, with students' study time having a highly significant positive effect on students' academic

performance. In addition, the decision tree model further indicates the different trends of students'

performance under changes in study time for different prior achievement intervals, which provides data

support for the development of personalized learning strategies. Based on the findings, this paper provides

recommendations for optimizing students' time management, enhancing after-school exercise practice, and

developing individualized learning plans for students at different achievement levels. Future research could

introduce additional variables, such as mental health and family support, to improve the predictive power of

the model and inform education policy optimization.

1 INTRODUCTION

In the modern education system, unequal distribution

of educational resources and difficulties in the time

management of students have become important

factors affecting academic performance. With the

networking of educational resources and the

popularization of advanced data analysis methods,

rational planning, and optimization of students' study

time to bridge the resource gap and enhance learning

efficiency have become a core topic of educational

research. The need to optimize study time is further

highlighted by the fact that, against the backdrop of

increasing global competition, students are faced with

a significant increase in the pressure to advance to the

next level of education, a heavy load of coursework

and varying degrees of independent learning ability.

The study of how to improve students' performance

index through scientific learning strategies not only

contributes to students' academic success but also

provides a practical basis for the development of

educational policies and the improvement of teaching

methods. This study focuses on the effects of study

https://orcid.org/ 0009-0004-6173-1111

time and practice problems on students' academic

performance under different academic foundation

conditions, and explores how machine learning-based

models can provide suggestions for optimizing study

strategies for students with different academic

foundations. By analyzing data on how study time is

allocated, the number and type of practice problems,

and students' learning outcomes in different academic

contexts, this study aims to reveal the relationship

between these factors and provide data to support the

development of individualized learning programs.

In recent years, researchers have utilized

algorithms that commonly use machine learning to

predict student academic performance and explore

the factors that influence it. For example, Verma’s

team made use of different machine learning

algorithms to predict student academic performance

based on real-world data, which includes academic

history and student habits. Their research was

indicating the potential of educational data mining in

helping students optimize their study patterns (Verma

et al. 2022). Similar to Verma, Rajendran’s team also

used multiple techniues,including multinomial

624

Fu, T.

A Study on the Impact of Decision Tree and Multiple Regression on Study Time Optimization and Performance.

DOI: 10.5220/0013703000004670

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Data Science and Engineering (ICDSE 2025), pages 624-631

ISBN: 978-989-758-765-8

logistic regression, artificial neural networks, random

forests, gradient boosting, and methods to predict

GPA based on socio-demographic, school-related

factors, and individual student variables (Rajendran

et al., 2022) . The study showed that students' healthy

lifestyle is positively related with academic

performance, while poor lifestyle such as chronic

negative emotions and stress negatively affects

academic performance, with no significant effect of

gender factor. Other research group also applied

machine learning algorithms to predict undergraduate

students' final exam grades based on their midterm

scores. Their prediction model achieved an accuracy

of 70–75% and the potential of educational data

mining for early identification of poor academic

performance students were highlighted (Yağcı,

2022). In addition, Martey investigated the

relationship between study time and performance

using an optimized Support Vector Regression (SVR)

model combined with Recursive Feature Elimination

(RFE) and found that SVR performs best with an

accuracy of R² value of 0.97, which is higher than

methods such as Decision Tree and Random Forest

(Martey et al., 2024). The impact of students' mental

health on academic performance is of equal concern.

Elshewey research group investigated the

relationship between levels of depression, attention

deficit hyperactivity disorder (ADHD ), and course

grades (Elshewey et al., 2024). Specifically, they used

a random forest algorithm for the data analysis, and

the results revealed that student psychological status,

hours of sleep, and social relationships have a

significant impact on academic success. They

suggested that psychological support should be

provided for students. Additionlly, Support Vector

Machine was also implemented to the predicting

students academic performance. Recent research has

demonstrated that student academic performance

was effectively predicted by the Time Management

Skills data from the Time Structure Questionnaire

(TSQ), which achived 80% accuracy by using a

Linear Support Vector Machine model (Khoudier et

al., 2023). Similarly, Other Researchers also explored

the Time Management Skills data from the Time

Structure Questionnaire (TSQ) to predict student

academic performance. They used Linear Support

Vector Machine which finally achieved 80%

accuracy in academic performance prediction and

84% in English performance(Rimadana et al. 2019).

Other Reseacher did similarwork by implementing

Extreme Gradient Boosting (XGBoost) that can

predict student academic performance with 97.12%

accuracy. The final output was highlighting the

impact from social and demographic on student

successs (Ojajuni et al. 2021). To improve

predicational model’s stabilities, lots of resrach team

made use of different methods. Some researchers

introduced a graph-based ensemble machine learning

approach that integrated supervised method with

unsupervised methods to improve model’s stability

and accuracy in student performance prediction, and

eventually outperformed traditional models by up to

14.8% (Wang et al. 2021). Lastly, researcher also

used the output of machine learning model to guide

them construct customized education. Researchers

conducted a comprehensive review of personalized

learning in smart and customized education, which

emphasized role of personalized learning by

integrating large-scale education with individualized

learning.(Wu et al. 2022).

The goal of this study was to explore the impact

of study time on student performance and to suggest

personalized learning strategies based on data

analysis.

This paper is structured as follows: the second

section describes the research methodology,

including data collection, variable selection, and

model construction; The third section presents the

results of the study and analyzes the trends in the

performance of students in different achievement

zones under changes in study time; Part IV discusses

the findings of the study and makes recommendations

for dynamically adapting instructional strategies;

Finally, Part V summarizes the contributions of this

study and future research directions.

2 DATA AND METHODS

2.1 Data Sources

2.1.1 Data Source

The data was obtained from the website Kaggle. The

file contains several variables related to student

performance with specific characteristics as shown in

Table 1.

Table 1 Data variables in Multiple Linear Regression

Model

Parameters Meanings

Hours Studied Total number of hours per

week that students spend

stud

Previous Scores Student's test scores at the

revious level

Extracurricular

Activities

Whether the student

articipates in

A Study on the Impact of Decision Tree and Multiple Regression on Study Time Optimization and Performance

625

extracurricular activities

(

Yes/No

)

Sleep Hours Average number of hours

of sleep per day for

students

Sample Question Papers

Practiced

Number of practice

problems completed by

students

Performance Index Target variable, a

measure of overall

student performance

2.1.2 Data Characteristics

The data has continuous variables Hours Studied,

Previous Scores, Sleep Hours, Performance Index,

and subtyped variables Extracurricular Activities also

suitable for studying the combined effect of different

variables on student performance.

2.1.3 Reasons for Choice

The dataset covers multiple aspects of key factors that

influence student performance and can be used to

analyze the influences on academic performance as

well as predict student achievement.

2.2 Methodologies

2.2.1 Linear Regression Model

Multiple linear regression is a machine learning and

statistical method that measures the effects of

multiple variables on a target variable and the

interactions between multiple variables

simultaneously. In this study, variables including

Hours Studied, Previous Scores, Extracurricular

Activities, Sleep Hours, and Sample Question Papers

Practiced were used as independent variables, and the

Performance Index was used as the target variable.

Practiced) were used as independent variables, and

the Performance Index was used as the target

variable.

In addition to multiple regression modeling,

decision tree modeling is an important statistical tool

for studying student performance. Decision trees can

categorize students' performance in different tiers,

revealing the pattern of influence of the different

variables above on students' performance in a non-

linear manner. In this study, a decision tree model was

constructed using Hours Studied and Previous Scores

as input variables and Performance Index as the target

variable. Building a decision tree model centers on

determining the rules for dividing the data and

identifying the key factors that best differentiate

student performance. The decision tree can

automatically select the most influential variables in

the modeling process and construct a tree structure so

that different combinations of variable characteristics

correspond to different results on student

performance.

2.2.2 Model Concepts

Multiple regression models were applied to analyze

the combined effects of multiple independent

variables (e.g., hours of study, prior grades,

extracurricular activities, hours of sleep, and a

number of practice problems) on the Performance

Index (PI) of student achievement. The error term (ϵ)

in the model represents other factors that cannot be

explained by these variables.

Decision tree modeling was applied to analyze the

path of influence of two independent variables such

as length of study, and prior grades) on the different

tiers of the division and of the Performance Index (PI)

of student achievement. The tree structure

characterizes the model, which recursively divides

the training dataset and generates decision rules based

on the range of values of different variables to predict

the values of the student performance index. The

value of each leaf node represents the value of the

predicted target variable (Performance Index), while

each split node shows the variable that has the

greatest impact on that split point and its threshold.

2.2.3 Model Benefits

Multiple regression models have a strong analytical

ability to consider the effects of multiple factors on

student performance simultaneously and reveal the

interactions between variables. By calculating the

regression coefficients (β), the model can

quantitatively assess the extent to which each variable

contributes to student performance, enabling the

researcher to specify which factors have the greatest

impact on student academic performance. In addition,

the multiple regression model has a strong predictive

ability, which can predict the future performance of

students based on existing data and provide a

scientific basis for the development of personalized

learning plans. Due to the high flexibility of the

model, the researcher can adjust the variables

according to the demand or introduce new

characteristic variables (e.g., socio-economic

background) to further optimize the analytical effect

of the model, thus improving the accuracy and

applicability of the prediction.

The decision tree model is more interpretable and

can be visualized by dividing the rules to show how

the two variables, length of study and prior grades,

ICDSE 2025 - The International Conference on Data Science and Engineering

626

have an impact on the student's performance index.

Compared to multiple linear regression, decision tree

models can present different groups and conditions

affecting student performance through different

levels of splitting, which can provide more

personalized guidance for student learning.

2.2.4 Best Subset Selection for Multiple

Linear Regression (MLR)

The subsets of all variables were combined using the

Treg subsets function to find the combination of

variables with the highest adjusted R² to ensure model

simplicity and explanatory power. A subset of all

variables was combined using the regsubsets function

to find the combination of variables with the highest

adjusted R², ensuring model simplicity and

explanatory power. Regarding the use of the

variables, Hours. Studied was not forced to be

included in the model, but it may be very important

for the prediction of the effect and is therefore marked

as “ ”. The previous score (Previous.Scores) was

likewise not forced into the model, but was selected

in most of the models, suggesting that it had less of

an effect on the target variable, and was therefore also

labeled as “ ”. Extracurricular Activities were not

forced into the model and were only selected in some

of the models, implying that their relationship with

the target variable may not be significant.

Sleep.Hours was likewise not forced into the model

and was not selected in most models, indicating that

it had less of an effect on the target variable, hence

the absence of the flag. Finally, the number of

practice sample papers

(Sample.Question.Papers.Practiced) was not forced

into the model, but it may be very important for the

prediction effect and is therefore marked as “ ”.

By exhaustive algorithm to taste the different

number of combinations of parameters, the final five-

parameter model has the highest goodness-of-fit

effect (R² = 0.9887523) therefore the five-parameter

model works best.

2.2.5 Comparison of Multiple Linear

Regression Models and Analysis of

Variance (ANOVA)

When making model selection, in addition to

focusing on the overall model's goodness of fit (e.g.,

R² or adjusted R²), it is necessary to further assess the

contribution of each variable to the explanatory

power of the model. By introducing or removing

specific variables, quantitative assessment using

model comparison and analysis of variance

(ANOVA) can test whether they significantly affect

the explanatory power of the target variable

(Performance. Index).

In this analysis, the significance of the

enhancement of the explanatory power of the model

with the introduction of Extracurricular. Activities

and Sleep. Hours were tested. Specifically, the need

to retain all variables was assessed by constructing

two models: a full model with all variables included

(Full Model) and a simplified model with both

variables removed (Reduced Model) as well as

through F-tests on both the full and simplified models

to ensure statistical significance of the models.

H0: The introduced variable has no significant

effect

H1: The introduced variable has a significant

effect

The ANOVA test showed that the inclusion of

Extracurricular. Activities and sleep. Hours

significantly increased the model's ability to explain

the target variable (Performance. Index) (F=898.28,

p<0.001). Therefore, the original hypothesis H0 is

rejected and Extracurricular. Activities and Sleep.

Hours are considered as significant variables. The

original hypothesis H0 is rejected.

2.2.6 Decision Tree Model Training

Firstly, to divide the dataset, the (train_test_split)

method was used. The original dataset is divided into

a training set and a test set, and the trainer randomly

selects 70% of the original data (test_size=0.7). The

test set randomly selects 30% of the original data

(test_size=0.3), and the random seed is set to 42

(random_state=42) to ensure the reproducibility of

the results.

Secondly, to select characteristics and target

variables, the feature variables, features, as 'Hours

Studied' and 'Previous Scores', representing the total

study duration and previous academic performance,

were defined respectively. The target variable, target,

corresponds to the student’s Performance Index.

Extract the relevant columns, X_train and y_train,

from the training set and assign them to X and y,

respectively, for model training.

Lastly, to train the Decision Tree Model, the

model is trained using Decision Tree Regressor. To

mitigate overfitting, the maximum tree depth is

constrained to 3 max_depth=3, ensuring controlled

model complexity. Additionally, to enhance the

model’s stability and reproducibility, the random seed

is set to 42 (random_state=42).

A Study on the Impact of Decision Tree and Multiple Regression on Study Time Optimization and Performance

627

3 ANALYSES OF RESULTS

3.1 Multiple linear regression model results

Table 2

esults of Multiple Linear Regression Analysis

Variable Estimate Std. Error t-value Pr(>|t|)

Interprect

-34.075588 0.127143

-268.01 <2e-16

Hours

Studied

2.852982

0.007873

362.35 <2e-16

Scores

1.018434

0.001175

866.45 <2e-16

Extracurric

ular

Activities

0.612898

0.040781

15.03

<2e-16

Sleep

Hours

0.480560

0.12022

39.97

<2e-16

Sample

Question

Papers

Practiced

0.193802

0.007110

27.26

<2e-16

The significance of the multiple linear regression

model body is high as the model has an F-value of

1.757e+05 and the corresponding p-value is also less

than 2.2e-16 (Table 2). The R² value of 0.9888 as well

as the value of the adjusted R

is slightly 0.9887,

which proves that the model can account for most of

the variance in the target variable as well as maintains

a high level of robustness and validity when dealing

with complex data.

3.2 Residual analysis of multiple linear

regression models

The standardized residual distribution indicates that

the model meets the linear regression assumptions

and the residuals are uniformly distributed without

significant bias.

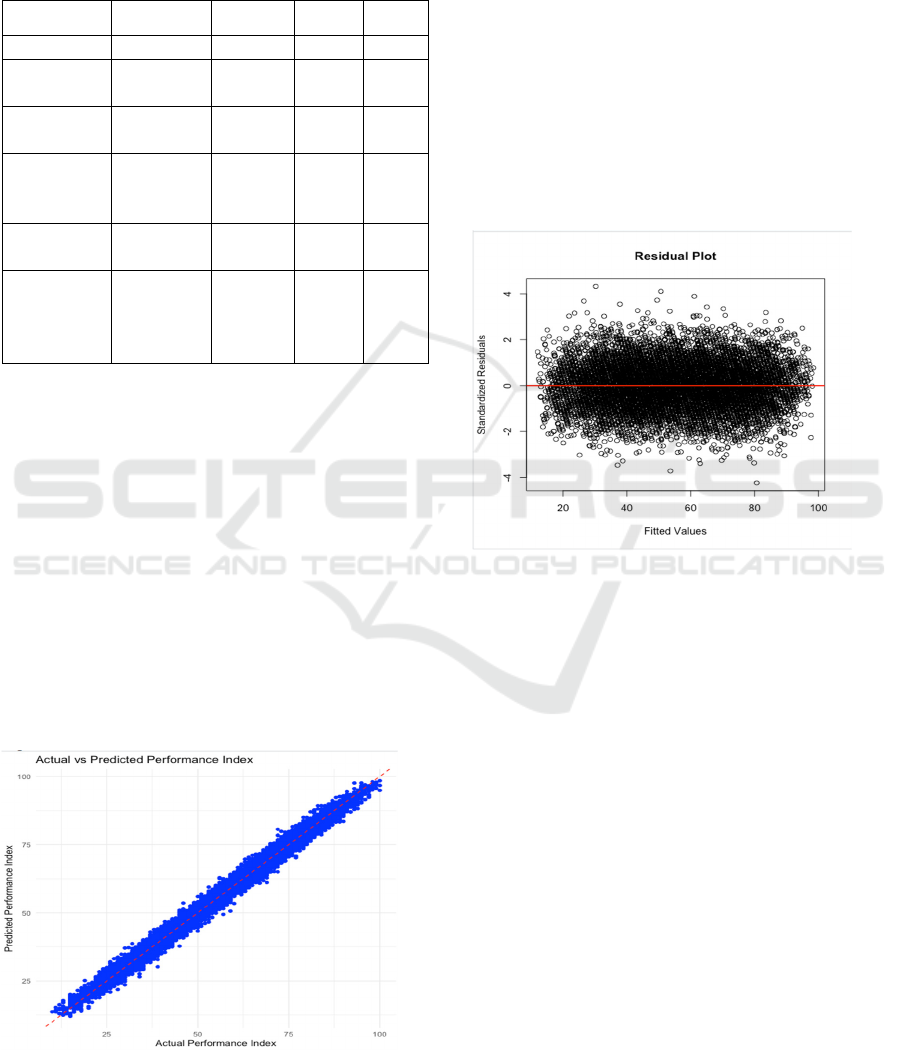
Figure 1: Comparison of actual and predicted values

(Picture credit : Original)

Figure 1 illustrates the relationship between the

actual values of the Student Performance Index and

the predicted values of the multiple linear regression

model. As can be seen in Figure 1, the data points are

tightly and linearly distributed around the diagonal

line (red dashed line). The red dashed line represents

the ideal prediction line, and the dense distribution of

data points on both sides of this line indicates a small

deviation between the predicted and actual values.

The accuracy of the model's predictions of the

Student Performance Index was high. Figure 1

visually illustrates the high accuracy and strong

explanatory power of the model in predicting student

performance indices, supporting the previous

conclusions about the significance of the model.

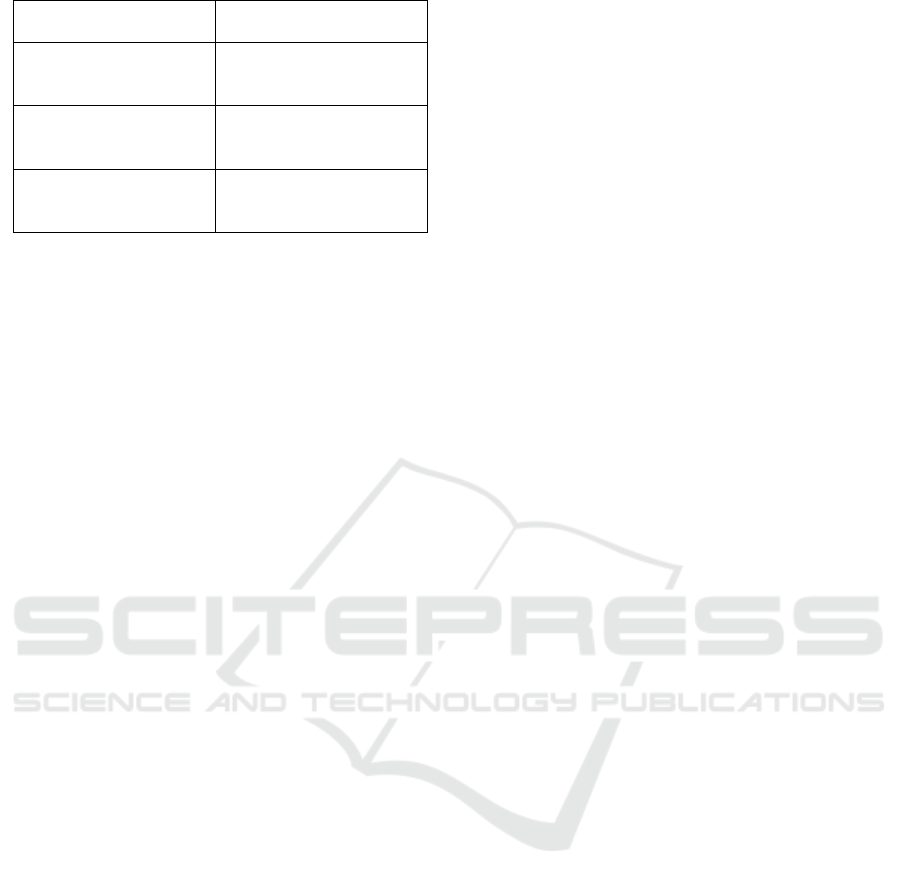
Figure 2: Residual Plot(Picture credit : Original)

Figure 2 illustrates the distribution between the

normalized residuals and the predicted values. As

seen in Figure 2, most of the residuals are distributed

above and below 0 and are scattered randomly with

no clear pattern or trend. The residuals are

predominantly distributed between [-4, 4], which

indicates a moderate error margin. The model's

residual distribution satisfies the basic assumptions of

linear regression, and the model's predictive and

explanatory power is high and relatively robust.

3.3 Analysis of Decision Tree Model Results

3.3.1 Program Code

Use decision_tree.predict(X_test) to predict the test

set X_test and get the predicted value y_pred.

ICDSE 2025 - The International Conference on Data Science and Engineering

628

3.3.2 Decision Tree Decision Rules

Based on the partitioning logic of the decision tree

model, the specific rules by which a student's

Previous Scores and Hours Studied contribute to the

prediction of the Performance Index are as follows:

Rule 1: When Previous Scores are less than or

equal to 69.50 and less than or equal to 55.50, the

predicted Performance Index is 25.84 if Hours

Studied is less than or equal to 4.50; if Hours Studied

is greater than 4.50, the predicted Performance Index

is 38.79.

For the mutual benefit and protection of Authors

and Publishers, it is necessary that Authors provide

formal written Consent to Publish and Transfer of

Consent ensures that the publisher has the Author’s

authorization to publish the Contribution.

Rule 2: If a student's Prior Scores are less than or

equal to 69.50 and greater than 55.50, the Predicted

Performance Index will vary depending on the Hours

Studied. Specifically, when hours studied are less

than or equal to 4.50 hours, the predicted

Performance Index is 41.11; when hours studied are

greater than 4.50 hours, the predicted Performance

Index increases to 53.42.

Rule 3: If a student's Previous Scores are greater

than 69.50 and also less than or equal to 84.50, the

predicted Performance Index will vary depending on

the Hours Studied. Specifically, when the learning

time is less than or equal to 4.50 hours, the predicted

Performance Index is 55.81, while when the learning

time is greater than 4.50 hours, the predicted

Performance Index increases to 68.43.

Rule 4: If a student's Previous Scores are greater

than 69.50 and also greater than 84.50, the predicted

Performance Index will vary depending on the Hours

Studied. Specifically, when the learning time is less

than or equal to 4.50 hours, the predicted

Performance Index is 70.87, while when the learning

time is greater than 4.50 hours, the predicted

Performance Index increases to 83.76.

3.3.3 Decision Tree Modelling Performance

Using the mean_squared_error function, calculate the

Mean Squared Error (MSE) between the actual value

y_test and the predicted value y_pred. The result of

the calculation is 38.808, which indicates that the

mean squared error between the predicted and actual

values is low.

Using the r2_score function, the coefficient of

determination (R² Score) for the model was

calculated. An R² value of 0.895 indicates that the

model explains approximately 89.5% of the variance

of the target variable, Performance Index.

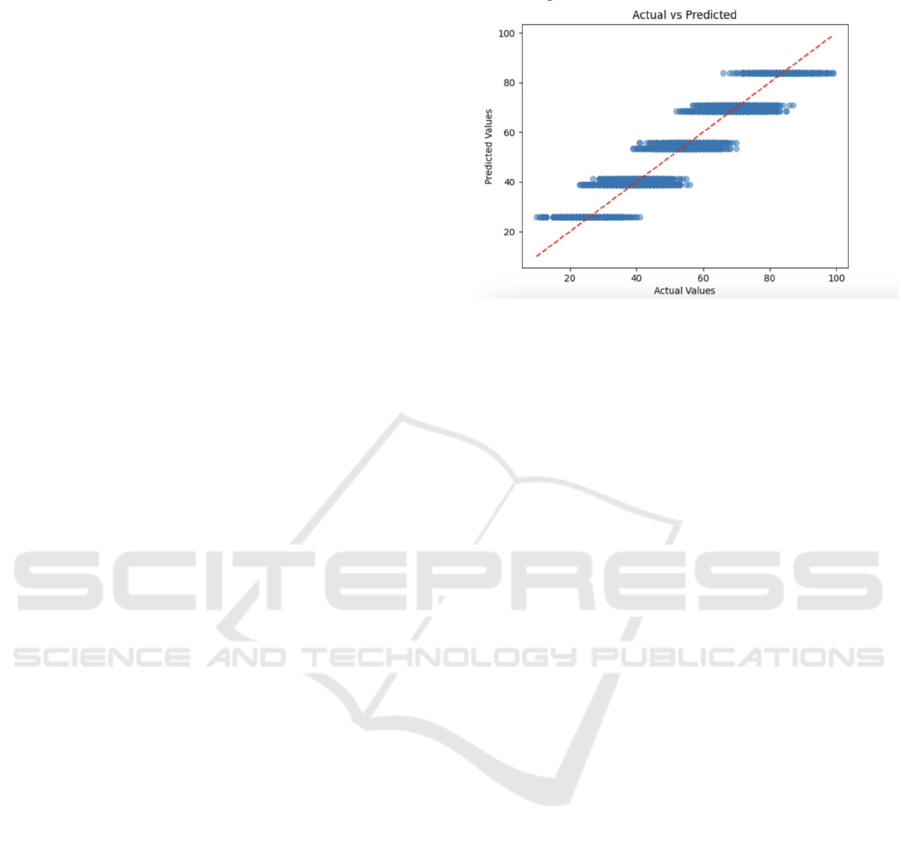
Figure 3. Decision Tree Predicted vs. Actual (Actual vs

Predicted)(Picture credit : Original)

Figure 3 illustrates the predicted versus actual

values of the model's student performance index

(Performance Index). The blue scatter represents the

predicted value and the red dotted line represents the

actual value, the overlapping part means that the

predicted value is exactly equal to the actual value.

As can be observed from Figure 3, most of the scatter

distributions are close to the red dashed line,

indicating that even though some of the scatters are

skewed, especially in the lower and higher intervals,

the model predicts a high degree of fit between the

student performance index (Performance Index) and

the actual values.

4 DISCUSSION AND

RECOMMENDATIONS

4.1 Discussion

This study shows that the effect of the amount of time

spent studying on students' performance indices is

significant and that students devoting more time to

studying is usually associated with higher academic

achievement. We hope you find the information in

this template useful in the preparation of your

submission. This emphasizes the critical role that the

investment of study time plays in academic success.

The classification results of the decision tree model

showed that students with less study time had lower

performance indices, indicating that time 3

management has a significant impact on academic

performance. In addition, research has shown that

students' prior achievement is a significant predictor

of future academic performance. Therefore,

providing students with the necessary and adequate

learning support at the beginning of their academic

A Study on the Impact of Decision Tree and Multiple Regression on Study Time Optimization and Performance

629

careers is necessary and important to promote long-

term academic success. In addition, the study

revealed that the number of practice problems of the

students was positively correlated with the

performance index, suggesting that the students'

after-school practice activities play an important role

in knowledge consolidation and academic

competence enhancement. However, although

multiple linear regression and decision tree models

demonstrated better predictive power in this study,

their explanatory power is still limited by the

completeness of the data. This study did not consider

incorporating variables into the model such as

physical health factors, psychological factors, and

family environment that may affect academic

performance, which may have reduced the

generalizability of the findings.

4.2 Recommendation

Based on these findings, this study makes the

following recommendations. First, students can plan

their study time wisely through time management

tools or course guidance. Schools and educational

institutions should also provide training for students

to enhance their time management skills and learning

effectiveness. Second, for students with poor prior

performance, schools should provide personalized

tutoring, allocating different study time to different

students based on their prior performance, and

progressively helping them build a solid academic

foundation at an early stage. For example, among

students with prior scores in the 69.5 - 84.5 range,

studying for more than four hours significantly

increased the performance index. Based on this,

educational institutions can implement precise

intervention strategies for this specific group. For

example, students in this zone are encouraged to add

an additional 1-2 hours of study time per day. At the

same time, schools can utilize the data monitoring

system to track changes in students' learning time and

dynamically adjust the content and difficulty of

teaching to ensure that students' learning efficiency

will not be reduced while their learning time is

increased.

In addition, schools should enrich students' after-

school practices by providing a variety of high-

quality practice questions or mock exams to help

students strengthen their knowledge acquisition and

enhance their academic performance. Meanwhile,

future research should explore more factors that

influence academic performance, such as mental

health, family support, and social activities, in order

to fully analyze the impact of these variables on

student learning outcomes. Finally, to further

improve the predictive accuracy and applicability of

the model, subsequent studies could collect a larger

and more diverse range of student data and attempt to

use more sophisticated machine learning models,

such as random forest or deep learning, to improve

the explanatory power and generalization of the

model. These improvements not only optimize the

learning strategies of individual students, but also

provide a scientific basis for educational policy-

making and contribute to the overall improvement of

academic outcomes.

5 CONCLUSIONS

This study analyzed the effects of several factors on

students' academic performance by modeling with

decision trees and multiple linear regression and

found that study time, previous grades, and the

number of practice problems were the most important

influences. Student performance can be effectively

enhanced by optimizing study plans, focusing on

practice and maintaining good habits. Although the

model showed good predictive performance, there are

still limitations in this study, such as the modeling of

the model did not consider factors such as mental

health and family environment. Future studies should

incorporate more variables and combine more

sophisticated machine learning models (e.g., vector

machines and random forests) to enhance the

predictive power. In addition, validation under

different countries' education systems contributes to

the generalizability of the study. The findings of this

study not only help students to develop efficient study

plans, but also provide empirical support for the

optimization of educational policies and teaching

methods.

REFERENCES

Elshewey, A. M., Ibrahim, A., Abdelhamid, A. A., Eid, M.

M., Singla, M. K., and Farhan, A. K., 2024.

Understanding the impact of mental health on academic

performance in students using random forest and

stochastic fractal search with guided whale

optimization algorithm. Journal of Artificial

Intelligence in Engineering Practice, 1(1):66–82.

Khoudier, M. M. E., Abdelnaby, R. H. M., Eldamnhoury,

Z. M., Abouzeid, S. R. A., El-Monayer, G. K., Enan, N.

M., El-Ghamry, A., Fouad, K., and Moawad, I., 2023.

Prediction of student performance using machine

learning techniques. In NILES 2023, 5th Novel

ICDSE 2025 - The International Conference on Data Science and Engineering

630

Intelligent and Leading Emerging Sciences Conference,

pages 333–338. IEEE.

Martey, E. M., Abdullah, A., and Appiah, O., 2024.

Predicting student academic performance using an

optimised regression machine learning model. In

ICAST 2024, IEEE 9th International Conference on

Adaptive Science and Technology, volume 9, pages 1–

7. IEEE.

Ojajuni, O., Ayeni, F., Akodu, O., Ekanoye, F., Adewole,

S., Ayo, T., Misra, S., and Mbarika, V., 2021.

Predicting student academic performance using

machine learning. In ICCSA 2021, 21st International

Conference on Computational Science and Its

Applications, pages 481–491. Springer.

Rajendran, S., Chamundeswari, S., and Sinha, A. A., 2022.

Predicting the academic performance of middle- and

high-school students using machine learning algorithms.

Social Sciences Humanities Open, 6(1):100357.

Rimadana, M. R., Kusumawardani, S. S., Santosa, P. I., and

Erwianda, M. S. F., 2019. Predicting student academic

performance using machine learning and time

management skill data. In ISRITI 2019, International

Seminar on Research of Information Technology and

Intelligent Systems, pages 511–515.

Verma, U., Garg, C., Bhushan, M., Samant, P., Kumar, A.,

and Negi, A., 2022. Prediction of students’ academic

performance using machine learning techniques. In

MECON 2022, International Mobile and Embedded

Technology Conference, pages 151–156. IEEE.

Wang, Y., Ding, A., Guan, K., Wu, S., and Du, Y., 2021.

Graph-based ensemble machine learning for student

performance prediction. arXiv preprint

arXiv:2112.07893.

Wu, S., Cao, Y., Cui, J., Li, R., Qian, H., Jiang, B., and

Zhang, W., 2024. A comprehensive exploration of

personalized learning in smart education: From student

modeling to personalized recommendations. arXiv

preprint arXiv:2402.01666.

Yağcı, M., 2022. Educational data mining: Prediction of

students’ academic performance using machine

learning algorithms. Smart Learning Environments,

9(1):11.

A Study on the Impact of Decision Tree and Multiple Regression on Study Time Optimization and Performance

631