Predicting Stock Closing Prices: A Random Forest Model Using

Fundamental, Technical, Risk, and Macroeconomic Indicators

Jiafan Liu

School of Finance, Guangdong University of Finance & Economics, Guangzhou, Guangdong, China

Keywords: Random Forest, Stock Price Prediction, Multi-Factor, Quantitative Trading.

Abstract: Accurate stock price prediction is crucial for investors and the economy, yet it remains challenging due to

market volatility and the limitations of traditional quantitative trading strategies, which struggle to capture

nonlinear relationships. This study employs a Random Forest (RF) model to enhance stock closing price

prediction ability by integrating fundamental, technical, risk, and macroeconomic indicators. Using stock data

from the Chinese A-share market's CSI300 and CSI1000 indices spanning January 2015 to December 2023,

the model was trained after preprocessing for missing values and standardization. The evaluation utilized

Root Mean Square Error (RMSE), R², and K-Fold Cross-Validation to ensure accuracy and reliability. The

model achieved high prediction accuracy, with an RMSE of 8.09 and R² of 0.9927 for BYD Co., Ltd. closing

price prediction, and similarly strong performance across 663 other stocks. These findings highlight the

effectiveness of combining macro and risk indicators within an RF framework, offering invaluable insights

for developing robust quantitative trading strategies that leverage machine learning to address complex market

dynamics.

1 INTRODUCTION

The stock market is a vital cog of the economic

machine. For the overall economy of a country, it

reflects, to a significant extent, the supply and

demand of market capital and the economic

trajectory; thus, it is often called the "barometer of the

economy". Nevertheless, since the market’s

pronounced volatility, the intricacies of the

investment decision-making process, and the

interference of myriad external factors, securing

investments that yield excessive returns remains a

profoundly challenging endeavor.

Traditional quantitative trading strategies employ

mathematical models and statistical analyses to

automatically discern investment opportunities,

effectively mitigating emotional biases in decision-

making, achieving excess returns, and reducing

investment risks (Sun, Wang, & An, 2023). However,

the preponderance of quantitative trading strategies

relies on conventional factor models, typically

utilizing fixed-weight factors such as fundamental

and technical indicators for stock selection. Notable

examples include the widely recognized Three-factor

https://orcid.org/0009-0001-6706-2703

Model and the Capital Asset Pricing Model (Sharpe,

1964; Fama & French, 1993). These quantitative

trading strategies, due to their reliance on fixed rules

and models, exhibit certain limitations, such as their

inability to effectively capture nonlinear relationships

between factors or to constantly adapt in real time to

trading environments characterized by heightened

complexity and uncertainty (Deng et al., 2016).

In the age of computer science and big data,

researchers have explored the application of machine

learning methodologies to stock trading (Rundo et al.,

2019; Bhandari, 2022; Zheng et al., 2020). Among

these, random forest (RF), a form of ensemble

learning, has garnered favor in stock price prediction

and quantitative trading due to its capacity to handle

vast datasets, capture nonlinear relationships,

facilitate feature selection, and mitigate overfitting

(Biau & Scornet, 2016). By integrating diverse

features, RF offers a multifaceted predictive

framework, yielding relatively accurate and stable

forecasting outcomes.

Scholars have conducted comparative analyses of

RF and Long Short-Term Memory (LSTM) models in

the context of stock price prediction and quantitative

612

Liu, J.

Predicting Stock Closing Prices: A Random Forest Model Using Fundamental, Technical, Risk, and Macroeconomic Indicators.

DOI: 10.5220/0013702800004670

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Data Science and Engineering (ICDSE 2025), pages 612-618

ISBN: 978-989-758-765-8

trading. Utilizing data from the S&P 500 index, these

studies revealed that, in the absence of pronounced

white noise, the RF model exhibits a smaller bias in

forecasting stock prices compared to LSTM. This

also demonstrates a superior capacity to accurately fit

price variations and respond more swiftly to price

fluctuations (Wu, 2024). In terms of quantitative

investment, Ma et al. integrated machine learning

models with traditional portfolio optimization

techniques, proposing a stock selection methodology

based on RF and support vector regression (SVR)

(Ma, Han, & Wang, 2021). This approach was

benchmarked against deep learning models, such as

LSTM networks and convolutional neural networks

(CNNs). Their experimental findings indicate that

machine learning models outperform conventional

time-series models in the stock pre-selection process.

Notably, when applied to Mean-Variance (MV) and

Omega portfolio optimization frameworks, the RF

model demonstrated superior predictive efficacy.

This study underscores that RF, as a robust regression

and classification tool, can effectively furnish reliable

predictive information for quantitative strategies,

particularly during the stock pre-selection phase.

Furthermore, Rasekhschaffe & Jones explored the

application of machine learning techniques in stock

selection, highlighting the RF's advantages in

managing multiple complex factors and nonlinear

relationships (Rasekhschaffe & Jones, 2019).

Although there has been some research on the

application of RF in stock prediction and quantitative

investment, how to integrate factors from different

sectors to effectively and accurately predict stock

prices is still a challenging topic. Compared to the

conventional application of machine learning in stock

price prediction, this study innovatively employs a

number of factors, including fundamental, technical,

risk, and macroeconomic indicators, to develop a

sophisticated RF model that can maximize the

utilization of information from bond market and

macroeconomy, aiming to capture as much valuable

market context as possible to yield a precise price

prediction.

The subsequent sections of this paper are

structured as follows. Section 2 will show the source

of the data and the descriptive statistics of the data,

followed by a brief introduction to how data

preprocessing was conducted in this study. Then, the

author will explain the basic principles of the random

forest model and how it was applied in this study. In

Section 3, the author will present the results of this

paper and conduct cross-validation. The last section

summarizes the whole paper.

2 DATA AND METHOD

2.1 Data Collection and Description

The data in this study are obtained from the CCER

and RESSET databases, covering samples from

January 1, 2015, to December 31, 2023. The sample

includes the constituent stocks of the CSI300 and

CSI1000 indices, which respectively represent the

companies with large and small market value in the

Chinese A-share market. The constituent stocks of

these indices are selected to analyze the predicted

performance of the RF algorithm with different

market capitalizations and liquidity under multi-

dimensional factors. The collected data include the

closing price of each stock every Friday and the data

corresponding to each factor. The factors used in this

study are divided into four types: fundamental

factors, technical factors, macroeconomic factors and

risk factors. The specific abbreviations and notations

are shown in Table 1.

Table 1: Abbreviations and notations.

Classification Abbreviation Notation

Fundamental

indicators

PE_Ratio Price-to-Earnings Ratio

PB_Ratio Price-to-Book Ratio

BM_Ratio Book-to-Market Ratio

Current_Ratio Measuring a company's short-term debt repayment ability

Quick_Ratio

Measuring a company's ability to pay its short-term liabilities without

rel

on inventor

Cash_Ratio The coverage of the company's cash holdings to short-term liabilities

Predicting Stock Closing Prices: A Random Forest Model Using Fundamental, Technical, Risk, and Macroeconomic Indicators

613

ROE Return on Equity, measuring profitability of a company's shareholders

Technical indicators

Momentum_4w Momentum factor, calculating the historical return over the past 4 weeks

Volatility_4w

Volatility factor, calculating the stock price volatility over the past 4

weeks

Volume_Change

Volume variation factor, calculating the difference from the previous

tradin

's volume

RSI Relative Strength Index

Macroeconomic

indicators

CPI_Growth Consumer Price Index (Month-on-month growth rate)

GDP_Growth Gross Domestic Product (Month-on-month growth rate)

Exchange_Rate

(USD)

RMB exchange rate (Based on USD)

Interest_Rate Benchmark Interest Rate

Risk indicators

Beta Measuring the correlation of individual stocks with the market as a whole

Default_Count Number of debt defaults

RMER Relative market excess return

Stock price Closing_price Closing price every Friday

2.2 Data Pre-processing

Data preprocessing is a key step to ensure that the RF

model can be effectively trained and predicted. The

data preprocessing in this study mainly includes

missing value processing and standardization

processing. Due to the complexity of financial market

data, missing values are common in a dataset.

Missing values of macro indicators are filled by the

time series interpolation method. For example, for the

monthly CPI sample, this study uses interpolation to

fill it into weekly data; for the quarterly GDP sample,

it fills it into weekly data. Missing values of

fundamental factors, technical factors, and risk

factors are handled by the linear filling method to

avoid the impact of days gap between two trading

days. After filling in all missing values, several

statistical characteristics of sample data are presented

through tables and graphs. Table 2 is the descriptive

statistics of all variables.

Table 2: Descriptive statistics of the dataset.

count mean std

Closing_price 363973 24.4785 57.9591

PE_Ratio 363973 67.6010 844.7043

PB_Ratio 363973 4.4241 32.4917

BM_Ratio 363973 1.4291 15.4509

Current_Ratio 363973 2.2972 2.4149

Quick_Ratio 363973 1.8550 2.2438

Cash_Ratio 363973 0.8232 1.3121

ROE 363973 0.0554 0.3888

Momentum_4w 363973 0.0028 0.1389

Volatility_4w 363973 1.2798 3.4418

Volume_Change 363973 96337 109895380

RSI 363973 47.9334 11.6070

CPI 363973 1.0013 0.0041

GDP_Growth 363973 1.0132 0.0219

Interest_Rate 363973 0.0245 0.0055

Beta 363973 1.1373 0.3595

Default_Count 363973 0.0176 0.3313

RMER 363973 -0.0007 0.0590

Exchange_Rate

(

USD

)

363973 6.7385 0.2678

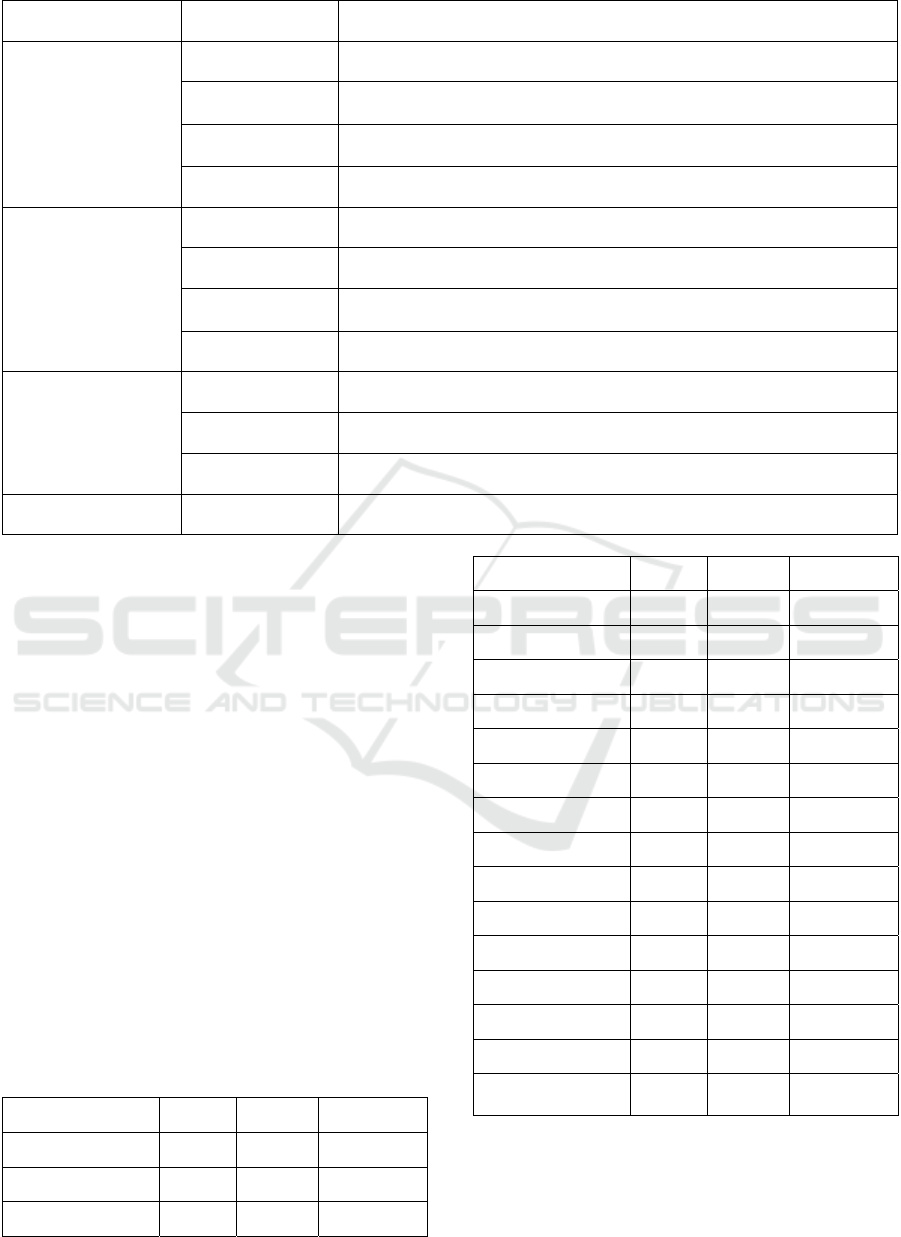
For the relevant data of macro indicators, Figure

1 shows the data of the two indicators CPI_Growth

and GDP_Growth. The left y axis represents the CPI

growth rate, the right y axis represents the GDP

growth rate, and the x axis represents time. The CPI

ICDSE 2025 - The International Conference on Data Science and Engineering

614

growth rate fluctuates prominently, especially around

2016, 2018 and 2020, while the GDP growth rate is

generally stable, but there are also obvious

fluctuations in 2020.

Figure 1: Line chart of CPI_Growth & GDP_Growth.

(Picture credit: Original)

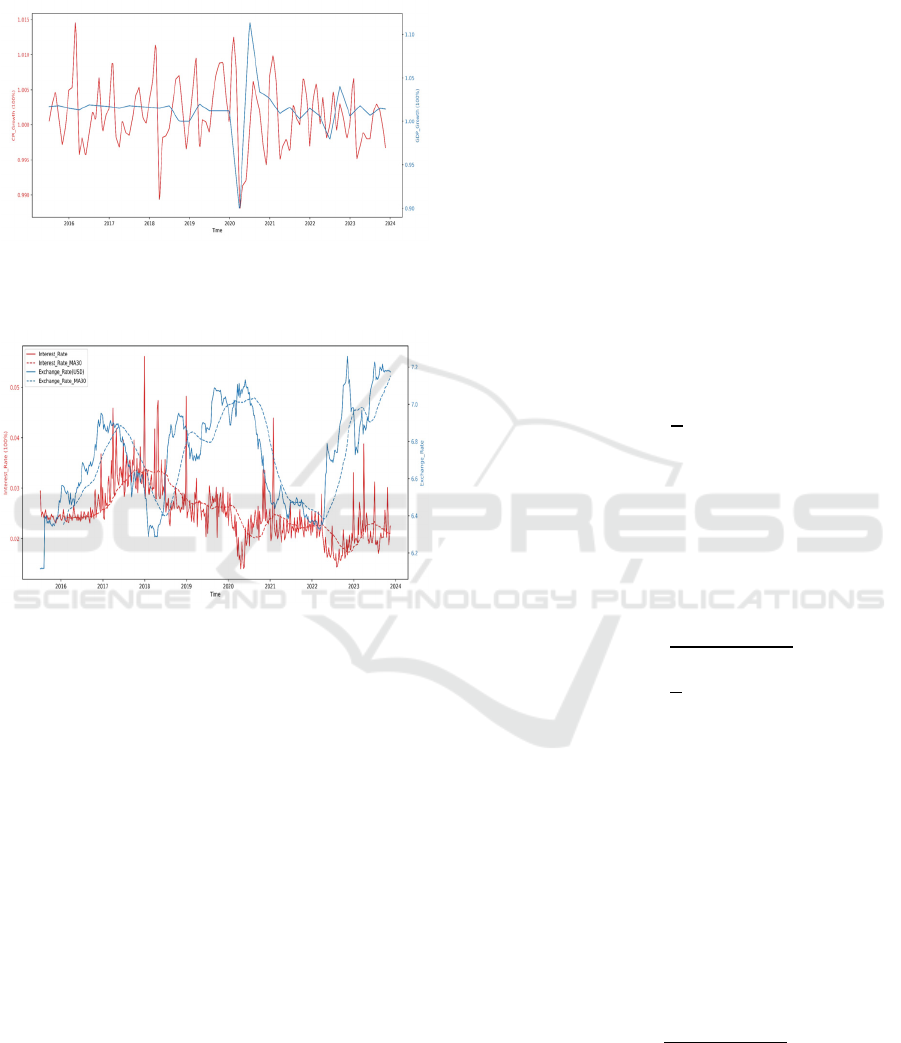
Figure 2: Line chart of Interest_Rate & Exchange_Rate.

(Picture credit: Original)

Figure 2 shows the time series changes of the

benchmark interest rate and exchange rate x (1 USD

-- x RMB). Two y axes are used in the figure,

representing the different dimensions of the two

indicators. The red solid line represents the

fluctuation of the interest rate, and the blue solid line

represents the change of the exchange rate. Both are

equipped with a 30-day moving average (dashed line)

to show a smooth trend. As can be seen from Figure

2, the interest rate fluctuates greatly, while the

exchange rate fluctuates relatively stable. Therefore,

the author believes that interest rates and exchange

rates, as important macroeconomic factors in

quantitative trading, will play a crucial role in stock

price prediction.

In financial data, the differences in the dimension

of various factors may lead to deviations when

training machine learning models. Therefore, after

filling in all missing values, the author standardized

all data (except weekly closing prices) to ensure that

data of different dimensions can be used in the same

model.

3 MODEL

This study uses RF regression to forecast the closing

price of stocks. Subsequently, the author will

introduce the basic principles of the RF model, as

well as the model training and testing process of this

study. RF regression is an ensemble learning method

that improves the accuracy and stability of the model

by building multiple decision trees and combining

their prediction results. Each decision tree is trained

on a random (using the boosted sampling method)

sample in the original dataset and split into branches

using randomly selected features. The prediction

result of RF regression is the average of the prediction

results of all decision trees. Its calculation principle is

represented by formula (1),

y

y













Where 𝑇 is the number of decision trees and 𝑦



 is

the prediction of the 𝑡-th decision tree.

Indicators such as Root Mean Square Error

(RMSE) and R² measure whether the prediction

results of RF regression are accurate. The formula (2)

is the equation for calculating RMSE,

𝑅𝑀𝑆𝐸



𝑛





𝑦



𝑦

















where 𝑦



is the true value of the 𝑖-th data point; 𝑦





is the predicted value; 𝑛 is the number of data points.

The prediction error of the model is positively

correlated with the RMSE value. This indicator is

generally used in conjunction with the coefficient 𝑅



which is a statistic indicator that measures the

correlation between the true values and the

predictions, namely, the proportion of the variability

explained by the model to the total variability. The

formula (3) is the equation of calculating 𝑅



𝑅



1

∑

𝑦



𝑦𝑖









∑

𝑦



𝑦













Predicting Stock Closing Prices: A Random Forest Model Using Fundamental, Technical, Risk, and Macroeconomic Indicators

615

Its value ranges from 0 to 1. An accurate model

needs to have a high fit and a low prediction error,

that is, a high 𝑅



and a low RMSE.

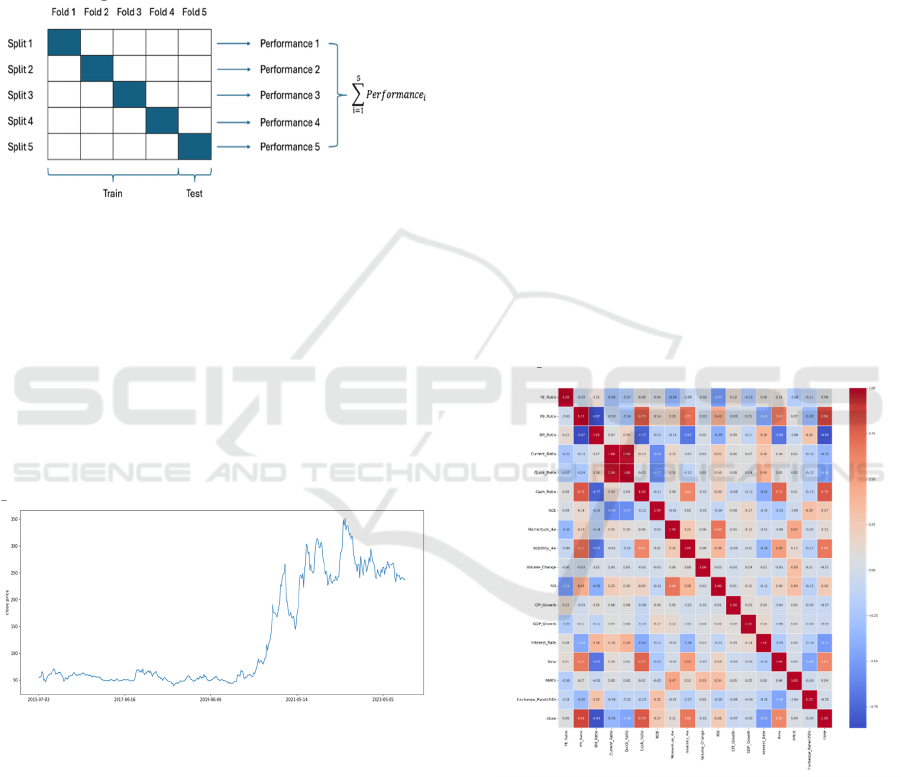
Finally, the author employed the K-Fold Cross-

Validation to test the stability and reliability of the

model by training and testing the model multiple

times, to avoid the situation where the model

performs well on the training set but performs poorly

in actual applications (also called overfitting). Figure

3 shows the process when 𝐾5.

Figure 3: K-Fold Cross-Validation. (Picture credit:

Original)

4 RESULTS AND DISCUSSION

This study first selects BYD Co., Ltd. (002594.SZ)

stock in the stock pool as representative, trains and

evaluates the RF model to verify the effectiveness of

the RF regression framework in stock prediction.

Figure 4 shows the tendency of this stock's Closing-

price.

Figure 4: BYD stock's closing price. (Picture credit:

Original)

The price of the stock rose significantly around

2020, and the volatility increased. The author

performs Z-score standardization on the relevant data

of the stock and randomly divides it into training sets

and test sets at a ratio of 4:1.

After data preprocessing, this paper conducted a

correlation analysis on the data, and the results are

shown in Figure 5. The PB_Ratio has the most

significant correlation with the closing price, with a

correlation coefficient of 0.858. A high price-to-book

ratio usually reflects the market's recognition of the

company's asset value, which aligns with normal

rules; The BM_Ratio and the closing price show a

strong negative correlation because when the book

value is high relative to the market value, the

corresponding stock price is relatively low; the

company's abundant cash may enhance market

confidence and drive up stock prices, so the

correlation coefficient between Cash_Ratio and the

closing price is 0.792. Other variables with high

correlation with closing prices include Interest_Rate

and Beta. Regarding the collinearity problem between

variables, the correlation coefficient between

PB_Ratio and BM_Ratio is -0.867, which is strongly

collinear (inverse relationship), and it is necessary to

avoid including them in the model at the same time;

while the correlation coefficient between the

Current_Ratio and Quick_Ratio is 0.978 (highly

redundant), so just keep one of them. Other variables

(such as PE_Ratio and Volume_Change) have a weak

correlation with the closing price, which means that

they may not have a significant impact on the

predictive ability of the model. However, they can

still provide some contextual information, so it may

be useful to include them as secondary features to

capture potential interactions.

Figure 5: Correlation heat map. (Picture credit: Original)

The RF model is trained after removing variables

that are not suitable for model training. Considering

the size of the dataset, the author uses 100 decision

trees to form an RF regression model. The

comparison between the predicted closing price and

the actual closing price is shown in Figure 6.

ICDSE 2025 - The International Conference on Data Science and Engineering

616

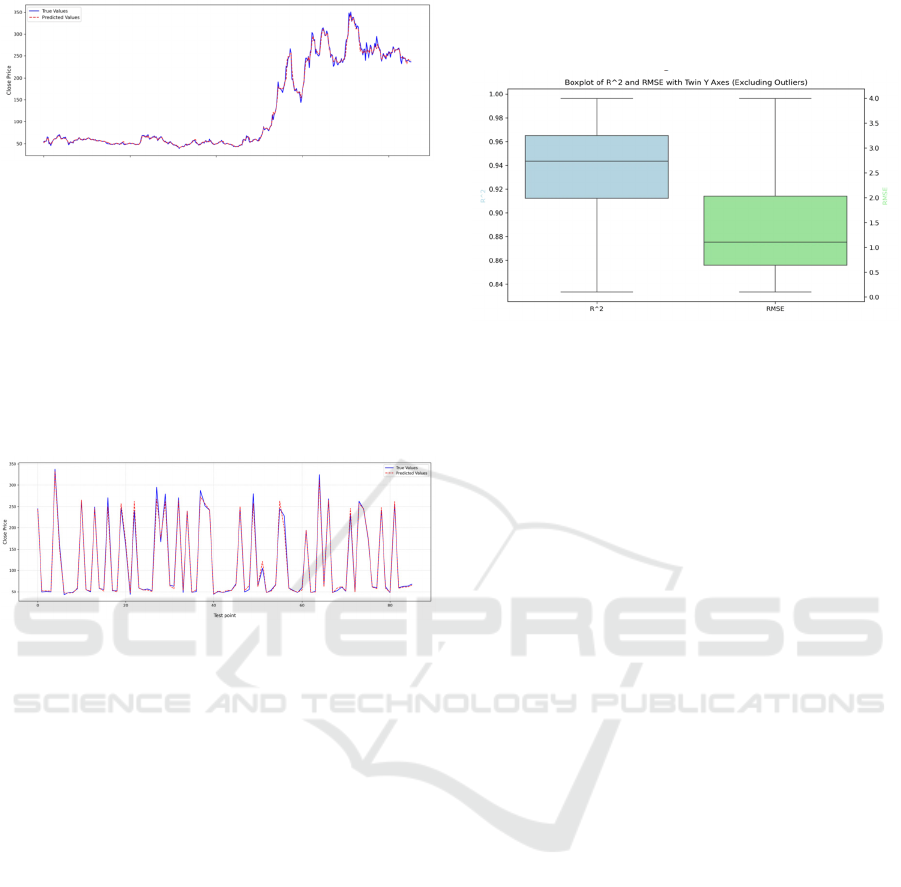
Figure 6: Forecasting performance of RF regression.

(Picture credit: Original)

The test outcomes of the test set are shown in Figure

7. The closing price predicted by the model is

basically close to the actual closing price. The RMSE

Score of the model is 8.09, which is relatively small

compared to the dimension of the closing price,

demonstrating that the prediction error of the model

is small; the 𝑅



of the model is 0.9927, which is close

to 1, presenting that the model has a good fitting

effect.

Figure 7: Forecasting performance of RF regression.

(Picture credit: Original)

To evaluate the generalization ability of the RF

model, the author applies K-Fold Cross-Validation

technique. After calculation, the RMSE of each fold

is: 8.13, 8.31, 7.94, 11.22, 9.62, and the average is

about 9.04. The range of RMSE values shows that the

performance of the model is relatively consistent, but

there are some differences in its predictions in

different data splits. This may be because the stock

has fluctuated greatly after 2020, resulting in different

characteristics of the training and test sets for each

fold. Generally, if the model performs very well on

the training set, but the performance on the cross

validation or test set varies greatly, then there may be

overfitting. However, from the results, the changes in

RMSE are not particularly extreme, so there is no

obvious sign that the model is overfitting on the

training set.

In addition to the experiments on the stock of

BYD Co., Ltd., the author also extends the model to

other constituent stocks in the CSI300 and CSI1000

indices (some stocks have fewer observations; stocks

with less than 300 observations are removed, leaving

663 stocks that meet the requirements), and used the

same training and testing process to predict other

stocks and calculate the RMSE and 𝑅



values for

each stock, shown in Figure 8.

Figure 8: Box plots of RMSE and 𝑅



. (Picture credit:

Original)

In the box plot on the left, the median of 𝑅



about 0.942, the first quartile (25%) is about 0.912,

and the third quartile (75%) is about 0.965, indicating

that most of the data are concentrated in this range,

indicating that the goodness of fit of most stocks is

close to a high level. The box plot on the right shows

that the median of RMSE is about 1.111, indicating

that the prediction errors of most stocks are

concentrated at this level. Considering the dimension

of stock closing prices, this value is relatively small,

indicating that the prediction errors of most models

are small. In conclusion, the RF regression model's

performance in other stocks is similar to that of BYD

stock. It can better recognize and utilize both long-

term and short-term trends of stocks, and the model

shows strong generalization ability.

5 CONCLUSIONS

This study investigated the effectiveness of an RF

regression model in predicting stock prices in the

Chinese A-share market, specifically for the

constituent stocks of the CSI300 and CSI1000

indices. The model utilized a range of different and

innovative indicators, including fundamental,

technical, macroeconomic, and risk factors, and was

trained and tested using data from January 2015 to

December 2023. The integration of macroeconomic

and risk factors, alongside traditional indicators,

enhances the model’s capacity to capture complex

market dynamics, as evidenced by correlation

analyses highlighting the influence of variables like

the Price-to-Book Ratio. The main findings showed

that the random forest approach achieved high

prediction accuracy, as evidenced by low RMSE and

Predicting Stock Closing Prices: A Random Forest Model Using Fundamental, Technical, Risk, and Macroeconomic Indicators

617

high R² values. For example, the model performed

with an RMSE of 8.09 and an R² of 0.9927 for BYD

Co., Ltd., with similar success for other stocks in the

sample. K-Fold Cross-Validation further confirmed

the robustness and generalization ability of the model,

showing consistent performance without overfitting.

Future studies could explore the following.

Initially, by analysing the feature importance of each

indicator, dynamically indicators selecting methods

could be used to boost predictive power. Furthermore,

researchers can investigate additional indicators to

make the prediction more accurate and reliable.

Finally, tuning parameters like tree depth or number

of trees may be able to enhance model performance.

REFERENCES

Bhandari, H. N., Rimal, B., Pokhrel, N. R., Rimal, R.,

Dahal, K. R., & Khatri, R. K. 2022. Predicting stock

market index using LSTM. Machine Learning with

Applications, 9, 100320.

Biau, G., & Scornet, E. 2016. A random forest guided tour.

Test, 25, 197-227.

Deng, Yue, Feng Bao, Youyong Kong, Zhiquan Ren, and

Qionghai Dai. 2016. Deep direct reinforcement

learning for financial signal representation and trading.

IEEE Transactions on Neural Networks and Learning

Systems, 28(3), 653–664.

Fama, Eugene F., & Kenneth R. French. 1993. Common

risk factors in the returns on stocks and bonds. Journal

of Financial Economics, 33(1), 3–56.

Ma, Y., Han, R., & Wang, W. 2021. Portfolio optimization

with return prediction using deep learning and machine

learning. Expert Systems with Applications, 165,

113973.

Rasekhschaffe, K. C., & Jones, R. C. 2019. Machine

learning for stock selection. Financial Analysts Journal,

75(3), 70-88.

Rundo, F., Trenta, F., Di Stallo, A. L., & Battiato, S. 2019.

Machine learning for quantitative finance applications:

A survey. Applied Sciences, 9(24), 5574.

Sharpe, William F. 1964. Capital asset prices: A theory of

market equilibrium under conditions of risk. The

Journal of Finance, 19(3), 425–442.

Sun, Shuo, Rundong Wang, & Bo An. 2023. Reinforcement

Learning for Quantitative Trading. ACM Trans. Intell.

Syst. Technol. 14(3), Article 44 (June 2023), 29 pages.

Wu, Haoyuan. 2024. Comparison of Random Forest and

LSTM in Stock Prediction. Advances in Economics,

Management and Political Sciences, 86, 28-34.

10.54254/2754-1169/86/20240936.

Zheng, L., Pan, T., Liu, J., Ming, G., Zhang, M., & Wang,

J. 2020. Quantitative trading system based on machine

learning in Chinese financial market. Journal of

Intelligent & Fuzzy Systems, 38(2), 1423-1433.

ICDSE 2025 - The International Conference on Data Science and Engineering

618