Multi-Time Scale Prediction of US Stock Index: A Feature Selection

Based Approach Using LSTM and Random Forest

Xiaomin Xia

Department of Electrical and Electronic Engineering, The Hong Kong Polytechnic University, Hong Kong, China

Keywords: LSTM, Random Forest, Feature Selection, Stock Index Prediction.

Abstract: The prediction of stock market indices presents significant challenges owing to their inherent complexity and

nonlinearity. Nevertheless, the swift advancement of artificial intelligence, coupled with its extensive

utilization within the financial sector, equips investors with robust tools for the analysis of market trends. This

research employs the Yahoo Finance API to obtain historical data pertaining to the S&P 500 index. It

subsequently implements data preprocessing techniques, feature selection methodologies, and machine

learning models, specifically Random Forest (RF) and Long Short-Term Memory (LSTM), to forecast trends

over short-term (1-week), mid-term (5-week), and long-term (30-week) horizons. Experimental results

indicate that RF performs better for short-term predictions, while LSTM excels in mid- and long-term

forecasting. The study also compares different methods for handling missing data, this paper uses removing

missing values method in order to simplify the preprocessing workflow. By eliminating irrelevant variables

through feature selection, the prediction accuracy is further improved. This study demonstrates an effective

workflow combining automated feature selection and machine learning algorithms, aiding investors in making

more informed decisions and providing a basis for future research on hybrid models.

1 INTRODUCTION

The inherent complexity and volatility of the stock

market present significant challenges in accurately

predicting market prices. Nevertheless, the rapid

advancements in artificial intelligence (AI) and its

increasing integration within the financial sector have

led investors to increasingly depend on AI-driven

tools for the analysis of market patterns and trends.

By comprehending the fundamental mechanics of the

market and employing automated buy-sell strategies,

investors are better positioned to make informed and

profitable decisions. Numerous researchers and

institutions are now utilizing machine learning

algorithms to process extensive datasets and adapt to

the ever-changing market conditions.

A stock index represents a subset of the stock

market and serves as a measure of its overall

performance. Its value reflects the performance of the

constituent stock within the market and is commonly

used to indicate the shared characteristics of a group

of assembled companies. The trends and trading

strategies for stock index prediction can be indicated

https://orcid.org/0009-0009-8308-2091

by technical indicators as characteristics (Hao, 2023).

By incorporating these indicators as new features

applied with a feature selection method, a more

accurate market direction can be predicted. However,

some variables are not associated with the response

and may even cause unnecessary complexity.

Therefore, the application of advanced approaches,

such as feature selection methods is essential to

exclude irrelevant variables (James et al., 2013).

In this study, the Yahoo Finance API was

employed to obtain historical data for the S&P 500

index, identified by its ticker symbol ^GSPC. This

API facilitates the acquisition of public financial

market data through a user-friendly interface. The

finance library's download function was utilized to

automate the data acquisition and processing over a

designated time frame, incorporating features such as

opening price, high price, low price, closing price,

and trading volume. This methodology obviates the

necessity for manual data entry, and the retrieved data

was successfully stored as SP500.csv.

The objective of this paper is to implement a

Feature Selection Method to identify critical figures

604

Xia, X.

Multi-Time Scale Prediction of US Stock Index: A Feature Selection Based Approach Using LSTM and Random Forest.

DOI: 10.5220/0013702700004670

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Data Science and Engineering (ICDSE 2025), pages 604-611

ISBN: 978-989-758-765-8

from a set of 35 original technical indicators.

Utilizing the optimal feature set, the Random Forest

(RF) and Long Short-Term Memory (LSTM)

machine learning algorithms were applied to forecast

the average closing values over 1-week, 5-week, and

30-week horizons. A comparative analysis of the

error rates of these two algorithms reveals that RF

demonstrates superior performance in short-term

predictions, whereas LSTM is more adept at

capturing long-term trends.

The primary contributions of this research include

the development of a data preprocessing pipeline, a

comparative analysis of the two algorithms, and the

practical implications of the findings in real-world

scenarios. Initially, daily prices were aggregated into

weekly average prices to mitigate redundancy. Three

methodologies for addressing missing values —

deletion, mean imputation, and median imputation—

were evaluated based on their respective error rates.

Subsequently, normalization was applied to scale the

data into an appropriate range for machine learning

algorithms. The Feature Selection method was

employed to identify key technical indicators, thereby

enhancing predictive performance by excluding

irrelevant variables.

Furthermore, by contrasting the performance of

the RF and LSTM algorithms, this paper forecasts the

average closing value of the S&P 500 index,

elucidating the distinct advantages of each algorithm

in terms of error rates. Lastly, the proposed workflow

aims to assist investors in making more informed

decisions by leveraging automated feature selection

and prediction techniques, ultimately contributing to

enhanced profitability.

2 LITERATURE REVIEW

The research conducted by Htun et al. underscores the

significance of identifying essential features that can

impact the efficacy of machine learning algorithms

(Htun, Biehl, & Petkov, 2023). Venkatesh et al.

examined two principal methodologies for

Dimensionality Reduction (DR), specifically Feature

Selection (FS) and Feature Extraction (FE). The

authors concluded that the FS approach presents

advantages in managing static datasets, decreasing

model complexity, and alleviating the risk of model

overfitting (Venkatesh & Anuradha, 2019).

Ji et al. implemented wavelet denoising to

enhance technical indicators and proposed a two-

stage feature selection technique aimed at adaptively

optimizing 18 original technical indicators (Ji et al.,

2022). By integrating this methodology with the RF

model, their findings indicated an improvement in F1

scores while simultaneously reducing redundant

features. A comparable approach was utilized by

Peng et al., who employed three feature selection

algorithms: Sequential Forward Floating Selection

(SFFS), Tabu Search (TS), and Least Absolute

Shrinkage and Selection Operator (LASSO) (Peng et

al., 2021).

Bhuriya et al. formulated a linear regression

model utilizing a set of inputs derived from

mathematical equations for predictive analysis. Their

model incorporated open price, high price, low price,

and volume as independent variables, with the closing

price designated as the dependent variable. A

comparative analysis of the linear regression model

against polynomial regression and Radial Basis

Function (RBF) methods demonstrated that linear

regression yielded superior results (Bhuriya et al.,

2017).

Pawar et al. introduced the application of

recurrent neural network (RNN) and LSTM

algorithms for portfolio management. The results

indicated that the RNN-LSTM model achieved

greater accuracy in comparison to traditional machine

learning algorithms (Pawar, Jalem, & Tiwari, 2019).

Ghosh et al. conducted a comparative analysis of

stock price directional movements utilizing LSTM

and Reinforcement Learning (RL). They proposed a

multi-feature framework that incorporated returns

associated with closing prices, opening prices, and

intraday prices. The findings revealed that LSTM

outperformed RF in terms of daily return calculations

(Ghosh, Neufeld, & Sahoo, 2022).

Nonlinear methodologies, including tree-based

algorithms and neural network paradigms, have been

demonstrated to be effective in predicting stock prices

(Tan, Yan, & Zhu, 2019). RF is a versatile technology

applicable to both regression and classification tasks

(Vijh et al., 2020). Yin et al. proposed the D-RF-RS

method to optimize RF, achieving significant

enhancements in average accuracy and illustrating the

advantages of RF in medium- and long-term trend

forecasting (Yin et al., 2023). Additionally, Chen et

al. investigated a combination of a Genetic Algorithm

(GA) for feature selection and an LSTM neural

network, with the GA-LSTM model exhibiting robust

performance in time series prediction tasks (Chen &

Zhou, 2020). This paper employs RF and LSTM

methodologies for comparative analysis, capitalizing

on their respective strengths in stock market

prediction.

Multi-Time Scale Prediction of US Stock Index: A Feature Selection Based Approach Using LSTM and Random Forest

605

3 METHODOLOGY

3.1 Data Description

The S&P500 is a representative index in the US stock

market. The dataset used in this study spans from

January 2, 2020, to December 31, 2024. The dataset

consists of 6 columns, they are Date, Open, Close,

High, Low, and Volume. Table 1 demonstrates an

overview of the S&P500 dataset. These features

collectively provide a comprehensive view of market

dynamics and are used as input for the subsequent

analysis and modeling.

Table 1: Part of the dataset for the stock of S&P500.

DATE OPEN HIGH LOW CLOSE VOLUME

2020/1/2 3244.67 3258.14 3235.53 3257.85 3459930000

2020/1/3 3226.36 3246.15 3222.34 3234.85 3484700000

2020/1/6 3217.55 3246.84 3214.64 3246.28 3702460000

2020/1/7 3241.86 3244.91 3232.43 3237.18 3435910000

2020/1/8 3238.59 3267.07 3236.67 3253.05 3726840000

3.2 Data Pre-processing

The United States stock market is characterized by

the lack of regular trading activities during weekends

and holidays. A time series is defined as a sequence

of data points organized in chronological order at

consistent intervals, allowing for the analysis and

processing of the data as discrete-time data. By

utilizing weekly average statistics and calculating the

mean price and volume, fluctuations in daily data can

be mitigated, thereby yielding a more stable trend

signal. The formulation for calculating the average

weekly closing price is presented in Equation (1).

Weekly Average =  P











n represents the actual trading days in one week

excluding holidays, represents the price on the i-th

trading day. If the number of trading days in a week

is less than 5 days, the formula calculates the average

based only on the price data of the actual trading days.

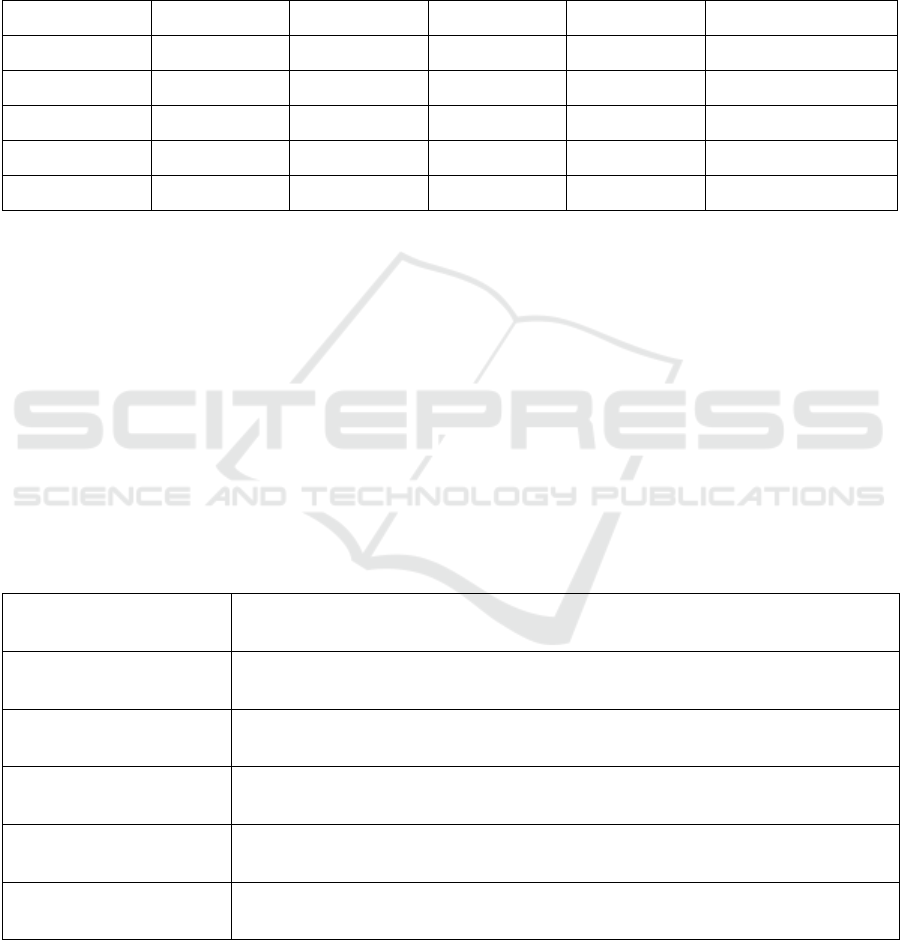
The following Figure 1 illustrates the Weekly

Average Candlestick Chart of the same dataset.

Table 2: 35 Technical Indicators Used in This Study.

Category Indicators

Trend-Following EMA_12, SMA_20, MACD, Signal Line, MACD Histogram, TEMA, DEMA,

LINEARREG, SAR, APO, HT_TRENDLINE, ADX, PSAR

Momentum RSI,KDJ_K,KDJD,STOCHK,STOCHD,Momentum,ROC,CMO, PPO,CCI,ULTOSC

Volatility ATR, BOLL Middle, BOLL_Upper, BOLLLower, WILLR, TRANGE, MIDPRICE

Volume-Based OBV, MFI, ADOSC

Average Typical Price TYPPRICE

ICDSE 2025 - The International Conference on Data Science and Engineering

606

Figure 1: Weekly Average Candlestick Chart (2020-2024). (Picture credit: Original).

Figure 2: Distribution of Some Technical Indicators. (Picture credit: Original).

In the field of financial technical analysis,

technical indicators contain mathematical

calculations based on historical price and total

volume (Murphy, 1999). To predict stock index price,

35 indicators were introduced as shown in Table 2.

As the diagram shows in Figure 2, the indicators

follow the normal distribution.

Then for missing values inside the dataset, there

are three ways to deal with missing values. One is

calculating the average value, one is using the median

to fill in the missing part, and one is deleting all the

missing values. To determine which missing value

processing method performs the best, two evaluation

methods are applied. Observing normal distribution is

one method, the other method calculates the mean

square error (MSE), accuracy, and cross-validation.

After that, in this paper, the linear transformation

of the dataset is carried out by the normalization

method, and the original data is mapped to the range

of 0 to 1.

Furthermore, this study performs a feature

correlation analysis on the dataset through p-value

verification. By examining the correlation between

the selected features and the target feature (closing

price), the p-value serves as a statistically derived

measure of significance, acting as a threshold to

determine whether the observed relationships are due

to chance. A p-value below 0.05 indicates a

Multi-Time Scale Prediction of US Stock Index: A Feature Selection Based Approach Using LSTM and Random Forest

607

significant correlation, while features with p-values

exceeding 0.05 are considered spurious and are

subsequently excluded. The specific results of this

analysis are detailed in Table 3, which illustrates that

the features employed in this study are significantly

correlated with the target features.

The Pearson Correlation Coefficient (r) shows the

strength of linear correlation, where the value ranges

from 0 to 1. Table 3 below summarizes the features

selected based on their correlation strength and

statistical significance.

Table 3: Selected Features Based on Correlation Strength and P-value.

Correlation Stren

th Selected Features

Strong Correlation:

𝑟

≥0.9, 𝑝<0.05

P-TYPPRICE, EMA_12, SMA20, BOLLMiddle, BOLL_Upper, BOLLLower, TEMA,

DEMA, LINEARREG, MIDPRICE, HT_TRENDLINE, OBV

Moderate Correlation:

0.9 >

𝑟

≥ 0.7, 𝑝 < 0.05

MACD, Signal Line, SAR, PSAR

3.3 Cross-Validation

In this research, the cross-validation method utilized

is referred to as Holdout Validation, which is

executed using the 'train-test split' technique. The

dataset was partitioned into a training set and a testing

set, with 80% of the data designated for training and

the remaining 20% for testing. Both RF and LSTM

models were trained on the training set, and the test

set was subsequently employed to evaluate the

models' performance. The following metrics were

calculated to assess the models: the coefficient of

determination (R²), which evaluates the goodness of

fit between the predicted and actual values, with a

score closer to 1 indicating superior model

performance; Mean Absolute Error (MAE), which

measures the average absolute difference between

predicted and actual values; and Root Mean Squared

Error (RMSE), which assesses prediction error by

calculating the square root of the Mean Squared Error

(MSE) to revert the error to its original scale.

4 RESULTS

4.1 Missing Value Analysis

The average of MSE calculated by Cross-Validation

(CV) is used to evaluate the generalization ability, the

smaller the CV Mean MSE value the better

performance. As shown in Table 4, different methods

show various results. Removing missing values

performs the best in terms of cross-validation mean

squared error. However, its performance on the test

set is weaker than mean imputation and median

imputation, with a test MSE of 0.2926.

Table 4: Comparison of Missing Value Processing Methods.

Metho

MSE CV Mean MSE CV Mean F1-Score

Mean Im

utation 0.2630 0.2892 0.5230

Median Im

utation 0.2653 0.2890 0.5258

Removing Missing Values 0.2926 0.2881 0.5390

In this paper removing missing values method is

used. Both CV Mean MSE and CV Mean F1-Score

show better generalization ability. This method is a

straight forward and efficient approach as the

proportion of missing data is small. It avoids the

potential biases introduced by imputation techniques

compared to mean or median imputation. In addition,

it simplifies the preprocessing workflow, making it

more robust and less prone to errors during the

analysis process.

4.2 Performance Comparison RF and

LSTM Models

The results are presented in Tables 5 and 6, which

illustrate the predictive performance of the RF and

LSTM models in forecasting future values over 1-

week, 5-week, and 30-week horizons.

The results are presented in Tables 5 and 6, which

illustrate the predictive performance of the RF and

LSTM models in forecasting future values over 1-

week, 5-week, and 30-week horizons. These metrics,

ICDSE 2025 - The International Conference on Data Science and Engineering

608

including 𝑅



, MAE, and RMSE, provide a

comprehensive evaluation of the accuracy and

reliability of each model. As demonstrated in Tables

5 and 6, it is evident that the RF model outperforms

in predicting future data over a 1-week horizon.

However, its performance declines as the

prediction horizon lengthens, with an 𝑅



of 0.7923

for the 30-week prediction. In contrast, LSTM

outperforms RF in 5 weeks and 30 weeks forecasts,

achieving an 𝑅



of 0.9535 for 5 weeks and 0.9003 for

30 weeks.

Table 5: RF Performance Comparison.

Target

𝑅



MAE RMSE

1 Wee

0.948776 0.028975 0.039593

5 Weeks 0.917610 0.035706 0.052539

30 Weeks 0.792345 0.046047 0.075173

Table 6: LSTM Performance Comparison.

Target

𝑅



MAE RMSE

1 Wee

0.929212 0.036475 0.046543

5 Weeks 0.953484 0.032979 0.039477

30 Weeks 0.900300 0.043782 0.052088

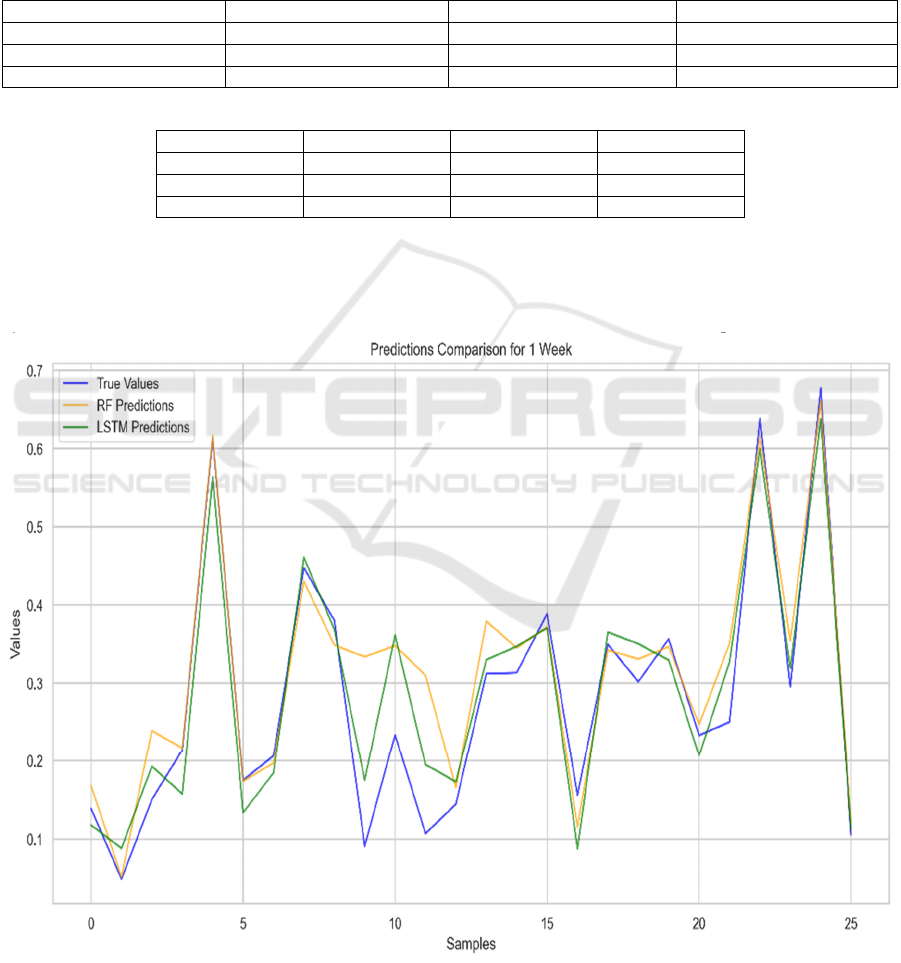
The predictive performance of both models is

further illustrated in Figures 3, 4, and 5, which

compare the true values against the predictions made

by the RF and LSTM models for the 1-week, 5-week,

and 30-week horizons, respectively. These figures

provide a visual representation of how well the

models capture the underlying trends and fluctuations

in the data across different temporal scales.

Figure 3: Comparison of Model Predictions and True Values for 1-week.(Picture credit: Original).

Multi-Time Scale Prediction of US Stock Index: A Feature Selection Based Approach Using LSTM and Random Forest

609

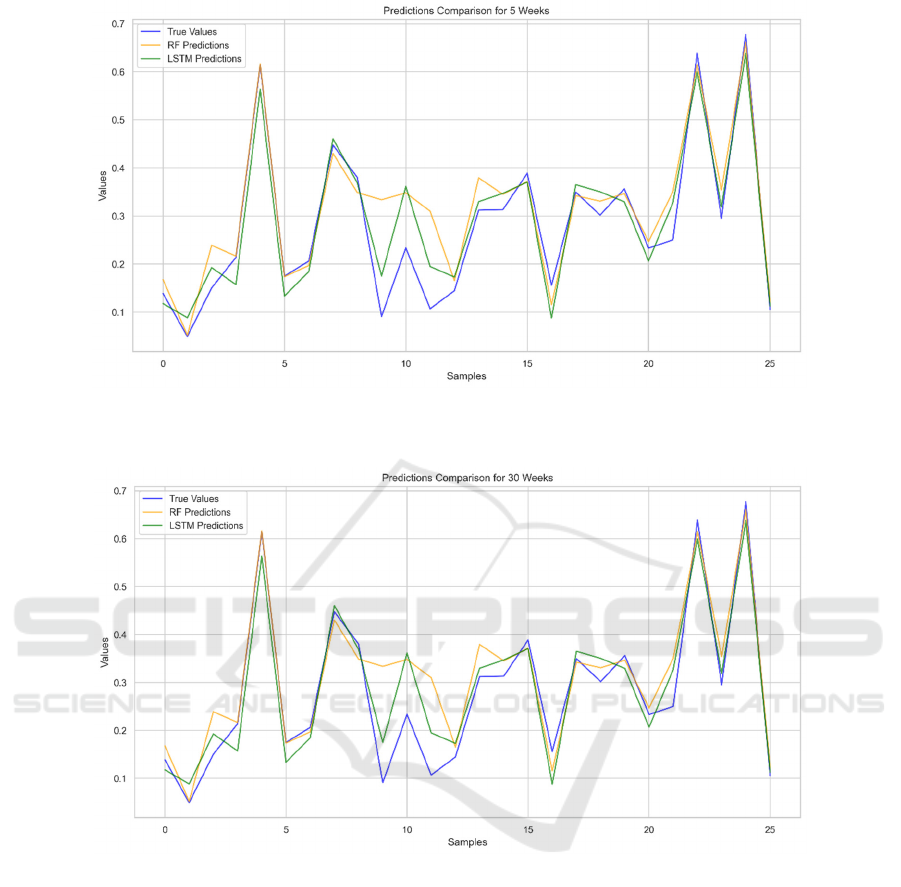
Figure 4: Comparison of Model Predictions and True Values for 5-weeks. (Picture credit: Original).

Figure 5: Comparison of Model Predictions and True Values for 30-weeks. (Picture credit: Original).

LSTM is good in dealing with problems that are

highly related to time series, this model is very good

for prediction on time series. LSTM is a type of RNN

due to its ability to capture long-term dependencies

and temporal patterns in sequential data. The

advantages of LSTM compared to other artificial

neural network models include its ability to preserve

past information for a longer period of time, to be

resistant to vanishing gradient problems, and to

model temporal dependencies better.

Random Forests is a collection of classification and

regression trees, it offers an intuitive method for

predicting outcomes. However, RF often provides

poor accuracy for complex variables.

RF is an ensemble learning method based on decision

trees, commonly used for structured data. It is

characterized by its robustness and high training

efficiency. The model handles noisy data by

averaging the outputs of multiple decision trees,

therefore reducing the risk of overfitting.

LSTM is a variant of RNN designed for time-series

data and captures long-term dependencies effectively.

Hence, for short-term forecasting, RF is preferred due

to its computational efficiency and robustness. For

mid- or long-term predictions, LSTM is more

suitable. It is effective at capturing temporal

dependencies in time-series data. In addition, LSTM

can model the nonlinear dynamics.

ICDSE 2025 - The International Conference on Data Science and Engineering

610

5 CONCLUSIONS

This paper evaluates the predictive performance of

RF and LSTM models for short, mid, and long-term

forecasting tasks. The results show that both models

have distinct strengths and are suitable for different

time series. RF is better at short-term predictions due

to its simplicity and speed, while LSTM is better

suited for mid- and long-term. Future work could

explore hybrid approaches that combine the strengths

of both models to further enhance forecasting

performance.

In the future, advanced hybrid modeling

approaches that integrate the strength of both RF and

LSTM are expected to emerge as a promising

direction. Such models could leverage RF's efficiency

and robustness in handling noisy, structured data and

can be utilized by LSTM with its ability to capture

complete temporal dependencies and nonlinear

dynamics. In addition, there may be a chance to have

various combination machine learning algorithms

integrated together to perform a better prediction task.

Moreover, with the advancement of deep learning

techniques, the rapid growth of large-scale datasets

presents both opportunities and challenges, such as

sensitivity to noise and high training costs. These

challenges may be addressed in the near future

through the implementation of automated feature

engineering techniques in conjunction with artificial

intelligence frameworks, which could significantly

enhance the adaptability of predictive models.

REFERENCES

Bhuriya, D., Kaushal, G., Sharma, A., & Singh, U., 2017.

Stock market predication using a linear regression. In

2017 International Conference of Electronics,

Communication and Aerospace Technology (ICECA),

Vol. 2, pp. 510-513. IEEE.

Chen, S., & Zhou, C., 2020. Stock prediction based on

genetic algorithm feature selection and long short-term

memory neural network. IEEE Access, 9, 9066-9072.

Ghosh, P., Neufeld, A., & Sahoo, J. K., 2022. Forecasting

directional movements of stock prices for intraday

trading using LSTM and random forests. Finance

Research Letters, 46, 102280.

Hao, Y., 2023. Research on Optimization of Stock Index

Prediction Model Based on Random Forest and LSTM

Network. (Master's thesis, Harbin Commercial

University).

Htun, H. H., Biehl, M., & Petkov, N., 2023. Survey of

feature selection and extraction techniques for stock

market prediction. Financial Innovation, 9(1), 26.

James, G., Witten, D., Hastie, T., & Tibshirani, R., 2013.

An introduction to statistical learning. Vol. 112, No. 1.

Springer, New York.

Ji, G., Yu, J., Hu, K., Xie, J., & Ji, X., 2022. An adaptive

feature selection schema using improved technical

indicators for predicting stock price movements. Expert

Systems with Applications, 200, 116941.

Murphy, J. J., 1999. Technical analysis of the financial

markets: A comprehensive guide to trading methods

and applications. Penguin.

Pawar, K., Jalem, R. S., & Tiwari, V., 2019. Stock market

price prediction using LSTM RNN. In Emerging

Trends in Expert Applications and Security:

Proceedings of ICETEAS 2018, pp. 493-503. Springer

Singapore.

Peng, Y., Albuquerque, P. H. M., Kimura, H., & Saavedra,

C. A. P. B., 2021. Feature selection and deep neural

networks for stock price direction forecasting using

technical analysis indicators. Machine Learning with

Applications, 5, 100060.

Tan, Z., Yan, Z., & Zhu, G., 2019. Stock selection with

random forest: An exploitation of excess return in the

Chinese stock market. Heliyon, 5(8).

Venkatesh, B., & Anuradha, J., 2019. A review of feature

selection and its methods. Cybernetics and Information

Technologies, 19(1), 3-26.

Vijh, M., Chandola, D., Tikkiwal, V. A., & Kumar, A.,

2020. Stock closing price prediction using machine

learning techniques. Procedia Computer Science, 167,

599-606.

Yin, L., Li, B., Li, P., & Zhang, R., 2023. Research on stock

trend prediction method based on optimized random

forest. CAAI Transactions on Intelligence Technology,

8(1), 274-284.

Multi-Time Scale Prediction of US Stock Index: A Feature Selection Based Approach Using LSTM and Random Forest

611