Go-Pregel: A User-Friendly Framework for Distributed Graph

Processing

Gabriel Gandour, Celso Massaki Hirata

and Juliana de Melo Bezerra

Department of Computing Science, Instituto Tecnol

ogico de Aeron

autica (ITA), S

ao Jos

e dos Campos, Brazil

Keywords:

Graph, Distributed Processing, Framework, Pregel.

Abstract:

Graphs are widely used for tasks such as visualization and decision-making. When dealing with large-scale

graphs, efﬁcient storage and computation become critical. To address these challenges, distinct tools have

been developed to support the implementation and execution of distributed graph algorithms. These tools

simplify the development process by abstracting the underlying distribution mechanisms, making them largely

transparent to the end user. However, to optimize and extend these implementations, developers must have

a solid understanding of distributed computing concepts, such as communication, coordination, concurrency,

and scalability, which are essential for effectively managing distributed graph processing. This work aims to

explore the fundamental principles of distributed computing in the context of graph processing. To support this,

we introduce Go-Pregel, a framework implemented in Golang and inspired by the core concepts of Google’s

Pregel. The proposed Go-Pregel serves as a ﬂexible experimental platform for both educational and research

purposes, enabling users to better understand the underlying mechanisms of distributed systems and graph

processing.

1 INTRODUCTION

A graph is a data structure that consists of vertices and

edges. A vertex is used to represent an entity, which

can vary depending on the context, and an edge is

used to represent a relationship between two (not nec-

essarily distinct) vertices. A graph is a structure used

to model, study, and understand relationships between

objects, and is particularly useful when handling two

types of tasks: visualization and decision-making.

Regarding data visualization, graphs can represent

data in a clear and easy-to-understand manner. Large

tables and spreadsheets with long lists of relationships

can be seen as graphs, making it easier to ﬁnd patterns

and insights (Michailidis and de Leeuw, 2001). In ge-

ographical maps, roads can be seen as edges that con-

nect different places (vertices). Another popular con-

cept is the knowledge graph. The vertices of a single

knowledge graph represent different types of entities,

such as people, places and objects, and the edges rep-

resent different relationships between these entities,

such as ‘is a friend of’, ‘lives in’ or ‘possesses’ (Peng

et al., 2023).

Decision-making (Li et al., 2022) involves mod-

https://orcid.org/0000-0002-9746-7605

https://orcid.org/0000-0003-4456-8565

eling a problem with graphs, using algorithms to ﬁnd

a solution, and deciding on an action to take based

on the algorithm’s output. The problems that can be

solved using graphs are diverse. One example is ﬁnd-

ing a route that takes a person from one location to

another, preferably using the shortest distance or the

least amount of time. Another example is the Page

Rank problem (Page et al., 1998), which Google ad-

dresses in its search engine. An interesting prob-

lem involving large graphs is encountered by social

networks: community detection (Fortunato and Hric,

2016). Given a set of users and the friendship rela-

tionships among them, the task is to identify which

users should be recommended to each other as poten-

tial connections.

Running an algorithm for a large number of ver-

tices in a graph, even for a simple algorithm, can be

time-consuming, and the machine’s memory might

not be sufﬁcient to store the entire graph. This is why

distributed processing is useful. Splitting the com-

putation across multiple machines can speed up the

processing time, give a faster result, and lower the

amount of memory necessary in a machine to process

the graph.

Numerous researchers and engineers have devel-

oped distributed graph processing models and tools to

Gandour, G., Hirata, C. M. and Bezerra, J. M.

Go-Pregel: A User-Friendly Framework for Distributed Graph Processing.

DOI: 10.5220/0013701000003985

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Web Information Systems and Technologies (WEBIST 2025), pages 149-156

ISBN: 978-989-758-772-6; ISSN: 2184-3252

149

facilitate the implementation and execution of graph

algorithms. Notable solutions include PowerGraph

(Gonzalez et al., 2012), GraphX (Gonzalez et al.,

2014), and Gemini (Zhu et al., 2016). Among the

most prominent are Apache Giraph (Apache, 2020)

and Pregel (Malewicz et al., 2010). Pregel, introduced

by Google, is a distributed graph processing frame-

work that has inﬂuenced the design of several subse-

quent systems, including Apache Giraph.

These tools are designed to address key challenges

in distributed graph processing: scalability, ease of

use, and fault tolerance (Heidari et al., 2018). Scal-

ability refers to the system’s ability to execute graph

algorithms across an arbitrary number of machines.

Ease of use aims to abstract away the complexity

of distributed computing, allowing developers to fo-

cus primarily on the algorithmic logic rather than

low-level implementation details. Fault tolerance en-

sures that the system can recover from node failures

without losing intermediate computation results. De-

spite these strengths, such systems are often treated as

black boxes: users leverage their functionality with-

out a clear understanding of distributed computing

and its internal mechanisms or execution models.

This paper presents the design and implementa-

tion of a framework to support the distributed pro-

cessing of graph algorithms. The primary objective

is to help developers understand key concepts in dis-

tributed computing and learn to transform sequential

algorithms into their distributed counterparts. This

framework, called Go-Pregel, uses Google’s Pregel as

a reference. It is designed to be algorithm-agnostic

and user-friendly, meaning that it is not tailored to

solve a speciﬁc problem but rather provides a general-

purpose platform for implementing and experiment-

ing with a wide range of graph algorithms in a dis-

tributed setting.

The Go-Pregel is developed in Golang, chosen

for its efﬁciency and robust native support for con-

currency, as well as its growing popularity in re-

cent years. To ensure portability and ease of deploy-

ment, the framework is containerized using Docker,

enabling it to run seamlessly across various environ-

ments. In addition, a simple user interface is provided

to help users visualize and understand the intermedi-

ate steps involved in the execution of distributed algo-

rithms.

The remainder of this paper is structured as fol-

lows. Section 2 provides the core concepts of

Google’s Pregel framework. Section 3 introduces the

proposed Go-Pregel framework, describing its archi-

tecture, implementation, and practical usage. Section

4 concludes the paper by discussing broader implica-

tions and outlining directions for future work.

2 PREGEL OVERVIEW

Pregel is a distributed graph processing framework

(Malewicz et al., 2010). It is designed to provide a

simple and scalable model for writing and executing

distributed graph algorithms. The input to a Pregel

program is a graph, and the output is also a graph.

Both vertices and edges can carry user-deﬁned data,

with the data structure determined arbitrarily by the

user. The output graph produced by a Pregel algo-

rithm is often not the ﬁnal solution itself but rather

a transformed graph from which the solution can be

more easily extracted.

Pregel interprets each vertex as an independent

machine, and each vertex is responsible for its part of

the computation. The framework uses the BSP model

(Cheatham et al., 1994) to coordinate the work. This

means that the algorithm is divided into several su-

persteps, where each vertex executes a computation

phase, communicates with other vertices, and then

synchronizes with the other vertices. Each vertex is

unable to read or change the values of other vertices,

but they can read and change their own values at will.

Also, each vertex, in the communication phase, can

send messages to any other vertices, as long as the

target vertex’s ID is known. These messages do not

require a reply, and they are only read in the next su-

perstep. The decisions made in the computation phase

are usually based on the messages received in the pre-

vious superstep, since they are the only way of com-

munication between vertices.

During the computation step, each vertex can vote

to halt and consequently become inactive. When ev-

ery vertex in the graph votes to halt, the Pregel algo-

rithm is considered ﬁnished, and the resulting graph

is written to the output. When a vertex votes to halt,

it is excluded from the computation phase and stops

working, unless it receives a message from another

vertex. When a halted vertex receives a message, it is

automatically reactivated, and its vote to halt is can-

celed. Deciding when a vertex should vote to halt is

the responsibility of the user, and this decision must

be deﬁned according to the logic of the algorithm be-

ing implemented.

When dealing with Pregel, some methods are ex-

pected to be implemented by the user. The ﬁrst is the

Compute method, which is called at the beginning of

every superstep. This method encompasses both the

computation and communication phases of the BSP

(Bulk Synchronous Parallel) model. The user has to

deﬁne the rules for when and how to send messages

to other vertices, using the method SendMessageTo.

The user also has to deﬁne, in the Compute method,

the rules for when a vertex should vote to halt, us-

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

150

ing VoteToHalt. In our proposed framework, we

adopt these conventions when naming correspond-

ing methods, maintaining consistency with the Pregel

programming model.

In Pregel, each vertex is responsible for its own

computation, but it does not mean that each machine

has a single vertex. Instead, the graph is divided

into several partitions (sets of vertices and their out-

edges). Each partition is assigned to a machine, and

the machine executes the Compute method for every

vertex in its partition for every superstep. For the sake

of simplicity, we assume that each machine has only

one partition of the graph.

Pregel uses a master-worker architecture. While

workers are responsible for executing the Compute

method for the vertices in their partition, the master

is responsible for coordinating the work between all

the workers. The master is responsible for distributing

the partitions to the workers, synchronizing the work-

ers, and ordering them to go to the next superstep.

When a worker ﬁnishes the computation and commu-

nication phases, it sends a message to the master ma-

chine, indicating that its superstep has ended. When

all workers are ready to go on to the next superstep,

the master sends a message to every worker, ordering

them to proceed. Until then, the workers stay idle.

In Pregel, fault tolerance is implemented through

checkpoints. A checkpoint is a snapshot of the com-

putation’s state at a given superstep. When a check-

point is saved, each worker logs the values of all ver-

tices in its partition, their incoming messages, and

the corresponding edges and edge values. Since all

computations in a superstep depend solely on this in-

formation, it is possible to resume the execution of

a Pregel algorithm from the last checkpoint in the

event of a failure. When a worker fails, the master

is responsible for detecting the failure and repartition-

ing the graph, starting from the last available check-

point, among the remaining workers. The master then

instructs the workers to resume execution from that

point and continue processing the subsequent super-

steps.

3 A DISTRIBUTED GRAPH

PROCESSING FRAMEWORK

This section presents the Go-Pregel, the distributed

graph processing framework. The framework

was built using Google’s Pregel as a reference

and programmed in Golang (thus the name Go-

Pregel). The project’s repository is available at

https://github.com/GaGandour/Go-Pregel (Gandour,

2024).

Two assumptions were made for this framework.

The ﬁrst is that the work is limited to static directed

graphs. Directed means that edges have a deﬁned di-

rection. Static implies that no vertices or edges are

created or removed during the execution of the algo-

rithms (i.e., the graph topology remains unchanged).

The second assumption is that vertices and edges may

optionally carry associated data, depending on the

problem being addressed. The structure and schema

of this data must be deﬁned by the user.

3.1 Go-Pregel Design

Here we detail the general architecture of the Go-

Pregel framework shown in Figure 1, its components,

and how they interact with each other. The project of-

fers shell scripts that aim to facilitate the use of the

framework. The user needs to write (P0) the algo-

rithm following the distributed processing approach

and start the processing (P1/V1). After being acti-

vated (P2), the master reads the input graph (P3) and

distributes it among workers (P4). Processing contin-

ues with respect to supersteps with commands from

the master (P5), responses from workers (P6a), and a

checkpoint register (P6b). Checkpoints are read (P7)

in case of failure recovery. When processing ﬁnishes,

the master writes the ﬁnal output graph (P8). The vi-

sualizer is then activated (V2) to read the output graph

(V3) and create the associated graph image (V4) to

the user.

The Go-Pregel framework uses a master-worker

architecture, and the master and workers communi-

cate via RPC (Remote Procedure Call). The master

machine in Go-Pregel has three main responsibilities.

The ﬁrst is to partition the graph among the work-

ers, the second is to orchestrate the supersteps, and

the third is to merge the output ﬁles generated by the

workers. These three responsibilities are all managed

by the state machine.

The worker machines, on the other hand, have

simpler responsibilities. The workers have differ-

ent functions that are called by the master via RPC

calls, depending on the master’s current state machine

node. The most important of these functions is the

RunSuperStep function, which loops over the ver-

tices in the worker’s partition and executes the super-

step for each vertex. If the vertex is active or receives

incoming messages (being reactivated), the vertex ex-

ecutes its SuperStep method. After iterating through

all vertices in the subgraph, the worker compiles all

messages that are to be sent from the vertices to other

vertices, and sends them to the appropriate workers.

Finally, the function checks if every vertex has voted

to halt, and sends a reply to the master with this infor-

Go-Pregel: A User-Friendly Framework for Distributed Graph Processing

151

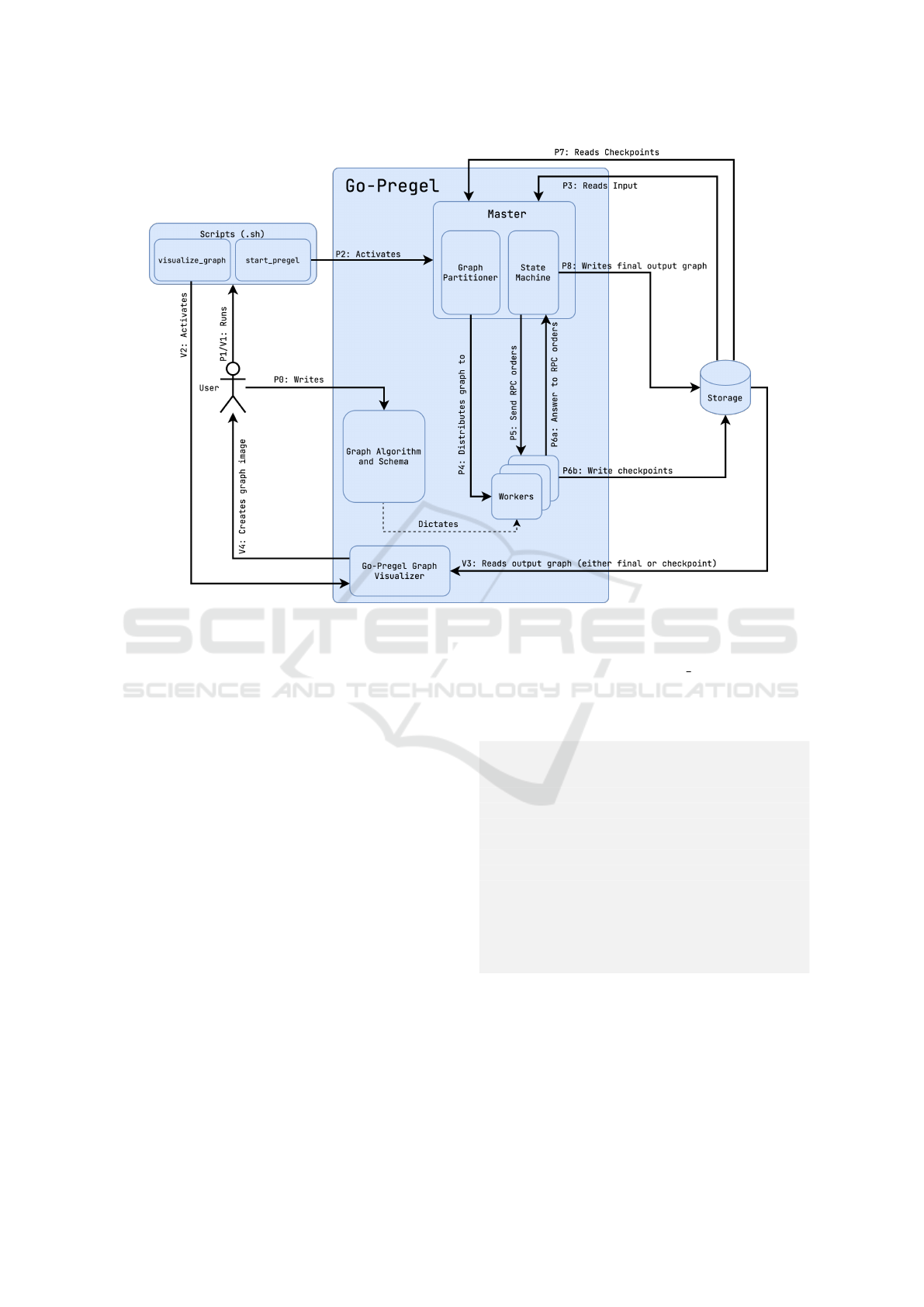
Figure 1: Go-Pregel architecture diagram.

mation.

The visualizer aids the user in understanding the

algorithm’s output and behavior. It is automatically

activated by the Go-Pregel scripts after the algorithm

ﬁnishes and generates an HTML ﬁle with the out-

put graph representation. The visualizer is written

in Python. It uses the json library to read the out-

put graph ﬁle, and the pyvis library to generate the

HTML ﬁle of a graph. The labels of each vertex and

edge are customizable through two functions in a sep-

arate ﬁle.

The input and the output of any Pregel algorithm

are graphs. Since we do not focus on distributed stor-

age, the graphs are stored as a JSON ﬁle in the local

ﬁle system. The project’s repository already comes

with a few graph ﬁles in the graphs/ directory, but

the user is free to create their own. A json graph fol-

lows a speciﬁc schema, as shown in Listing 1. The

Vertices ﬁeld is a map of vertices, where each ver-

tex has an Edges ﬁeld, which is a map of edges. Each

edge has a To ﬁeld, which is the target vertex id. The

Value ﬁeld is a placeholder for the vertex and edge

values, and the schema for these values are deﬁned

by the user. The Value ﬁelds are optional and their

schema (if not empty) depends on the problem to

be solved. After Go-Pregel is run, the output graph

is stored under the src/output graphs/, with the

same structure as in the graphs/ directory.

Listing 1: Input Graph Json Format.

"Vertices": {

"<vertex id>": {

"Value": {

// Vertex Value Schema

"Edges": {

"<edge id>": {

"To": "<target vertex id>",

"Value": {

// Edge Value Schema

}

The graph algorithm executed by Go-Pregel is

programmed by the user by changing two ﬁles in the

project. The ﬁrst ﬁle is the graph types ﬁle, as shown

in Listing 2. It has ﬁve different Golang types that

should be changed depending on the problem and on

how the graph is represented. The ﬁrst two ones are

VertexIdType and EdgeIdType, which are the types

of the vertex and edge IDs, respectively. They can be

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

152

any type, but strings are recommended. The next two

types, VertexValue and EdgeValue, are the values

stored in the vertices and edges. They are the ﬁelds

that contain any persistent information that the user

wants to use in the algorithm. Finally, the last type

to be deﬁned by the user is the PregelMessage type.

This type is the message that is sent from one vertex

to another in the superstep.

Listing 2: Go-Pregel types ﬁle to be modiﬁed by the user.

type VertexIdType string

type EdgeIdType string

type VertexValue struct {

// Fill in here

}

type EdgeValue struct {

// Fill in here

}

type PregelMessage struct {

// Fill in here

}

Listing 3: Go-Pregel methods ﬁle to be modiﬁed by the

user.

func(vertex *Vertex)ComputeInSuperStepZero(){

// Fill in here

If ComputerInSuperStepZero is

the same as Compute, you can

just call Compute with an

empty slice of messages as:

vertex.Compute

([]PregelMessage{})

}

func(vertex *Vertex)Compute

(receivedMessages []PregelMessage) {

// Fill in here

}

The second ﬁle the user has to modify to pro-

gram a Go-Pregel algorithm is the methods ﬁle, as

depicted in Listing 3. This ﬁle has two methods

that should be changed depending on the problem

and how the graph is represented. The ﬁrst one

is the ComputeInSuperStepZero method, which is

called in the ﬁrst superstep. The second one is the

Compute method, which is called in the following su-

persteps. These methods are responsible for interpret-

ing the received messages (if there are any), updating

the vertex value if necessary, deciding if the vertex

should vote to halt or not, and preparing the mes-

sages to be sent to other vertices. In order to write

the ComputeInSuperStepZero and Compute meth-

ods, the user has access to auxiliary methods already

implemented in Go-Pregel.

3.2 Go-Pregel in Practice

Aiming to structure a Go-Pregel algorithm, we ex-

plored the Single Source Shortest Path (SSSP) prob-

lem, which is a classic graph problem that aims to

ﬁnd the shortest path from a source vertex to all other

vertices in a graph. In this problem, each edge has a

positive weight, and the length of a path is the sum of

the weights of the edges that make up the path from

the source vertex to a target vertex. We used a speciﬁc

vertex (in this case, the one with vertex id deﬁned as

zero) as the source for simplicity.

The most common algorithm to solve the SSSP

problem is Dijkstra’s algorithm. However, we noticed

that the order of the graph exploration must follow

the priority queue, making it impossible for us to dis-

tribute it directly in Go-Pregel. To solve the SSSP

problem, we used the Bellman-Ford algorithm, an-

other algorithm with a different approach and time

complexity.

Listing 4: Go-Pregel Value types for the SSSP algorithm.

type VertexIdType string

type EdgeIdType string

type VertexValue struct {

Distance int

Predecessor VertexIdType

}

type EdgeValue struct {

Weight int

}

type PregelMessage struct {

Sender VertexIdType

SenderDistance int

EdgeWeight int

}

In Bellman-Ford’s algorithm, the distances of

each vertex are also initialized in a table dist and set

to inﬁnity, except for the source vertex, which has its

distance set to zero. The algorithm then enters a loop

of N − 1 iterations, where N is the number of vertices

in the graph. Inside this loop, we iterate through all

edges in the graph, and check if the distance of the

edge’s target is greater than the sum of the source’s

distance and the edge’s weight. If positive, the tar-

get’s distance is updated to be equal to the sum of the

other two values. At the end of the loop, the table

dist has the desired distances for the SSSP problem.

Go-Pregel: A User-Friendly Framework for Distributed Graph Processing

153

We developed the code in Go-Pregel as shown in List-

ing 4 and Listing 5.

Listing 5: Go-Pregel methods for the SSSP algorithm.

func (vertex *Vertex)

ComputeInSuperStepZero() {,→

distance := -1

if vertex.Id == "0" {

distance = 0

}

vertex.SetValue(VertexValue{Distance:

distance, Predecessor: ""}),→

for _, edge := range vertex.GetOutEdges()

{,→

vertex.PrepareMessageToVertex(

edge.To,

PregelMessage{

Sender: vertex.Id,

SenderDistance: distance,

EdgeWeight:

edge.Value.Weight,,→

)

}

func (vertex *Vertex)

Compute(receivedMessages []PregelMessage)

{

,→

currentValue := vertex.GetValue()

currentDistance := currentValue.Distance

currentPredecessor :=

currentValue.Predecessor,→

hasChanged := false

for _, message := range receivedMessages

{,→

if message.SenderDistance == -1 {

continue

}

if currentDistance == -1 ||

message.SenderDistance +

message.EdgeWeight <

currentDistance {

,→

hasChanged = true

currentDistance =

message.SenderDistance +

message.EdgeWeight

,→

currentPredecessor =

message.Sender,→

}

if hasChanged {

vertex.SetValue(VertexValue{Distance:

currentDistance, Predecessor:

currentPredecessor})

,→

for _, edge := range

vertex.GetOutEdges() {,→

vertex.PrepareMessageToVertex(

edge.To,

PregelMessage{

Sender: vertex.Id,

SenderDistance:

currentDistance,,→

EdgeWeight:

edge.Value.Weight,,→

)

}

} else {

vertex.VoteToHalt()

}

In the SSSP problem, we are interested in

the Distance and Predecessor ﬁelds of the

VertexValue type. We then customized the visu-

alizer functions. After implementing the Go-Pregel

algorithm for the SSSP problem, we used the pro-

vided scripts to run it and visualize the results. We

used three workers in a small graph whose edges had

weight 1. We had four supersteps executed to end the

algorithm. The visualizer tool’s output is shown in

Figure 2.

As expected, the distance from the source vertex

to itself is zero, and the distances to unreachable ver-

tices are still −1 (inﬁnity). The image also shows the

predecessor of each vertex in the shortest path from

the source vertex. The optimal path from vertex 0 to

vertex 3, for example, can be derived by following the

predecessor ﬁeld, from vertex 3 to vertex 0. The pre-

decessor of vertex 3 is vertex 2, and the predecessor

of vertex 2 is vertex 0. Therefore, the shortest path

from vertex 0 to vertex 3 is going from vertex 0 to

vertex 2, and then from vertex 2 to vertex 3, with a

total distance of 2.

We also tested the fault tolerance of the

framework by using the -failure step

and -checkpoint frequency ﬂags in the

start pregel.sh script. We set the failure

step to 3 and the checkpoint frequency to 2. This

means that one of the workers will fail at superstep 3,

and a checkpoint will be saved every two supersteps.

Listing 6 shows the most important terminal logs.

As expected, the supersteps 0, 1, and 2 were

executed normally, and after superstep 2, the mas-

ter machine ordered the workers to write a check-

point (“write subgraphs”). After that, the workers at-

tempted to execute superstep 3, but one of them failed.

The master machine then noticed the failure, checked

the remaining workers, repartitioned the graph from

the last checkpoint, and ordered the remaining work-

ers to execute superstep 3 again. The algorithm then

continued normally, and the ﬁnal output was the same

as in Figure 2.

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

154

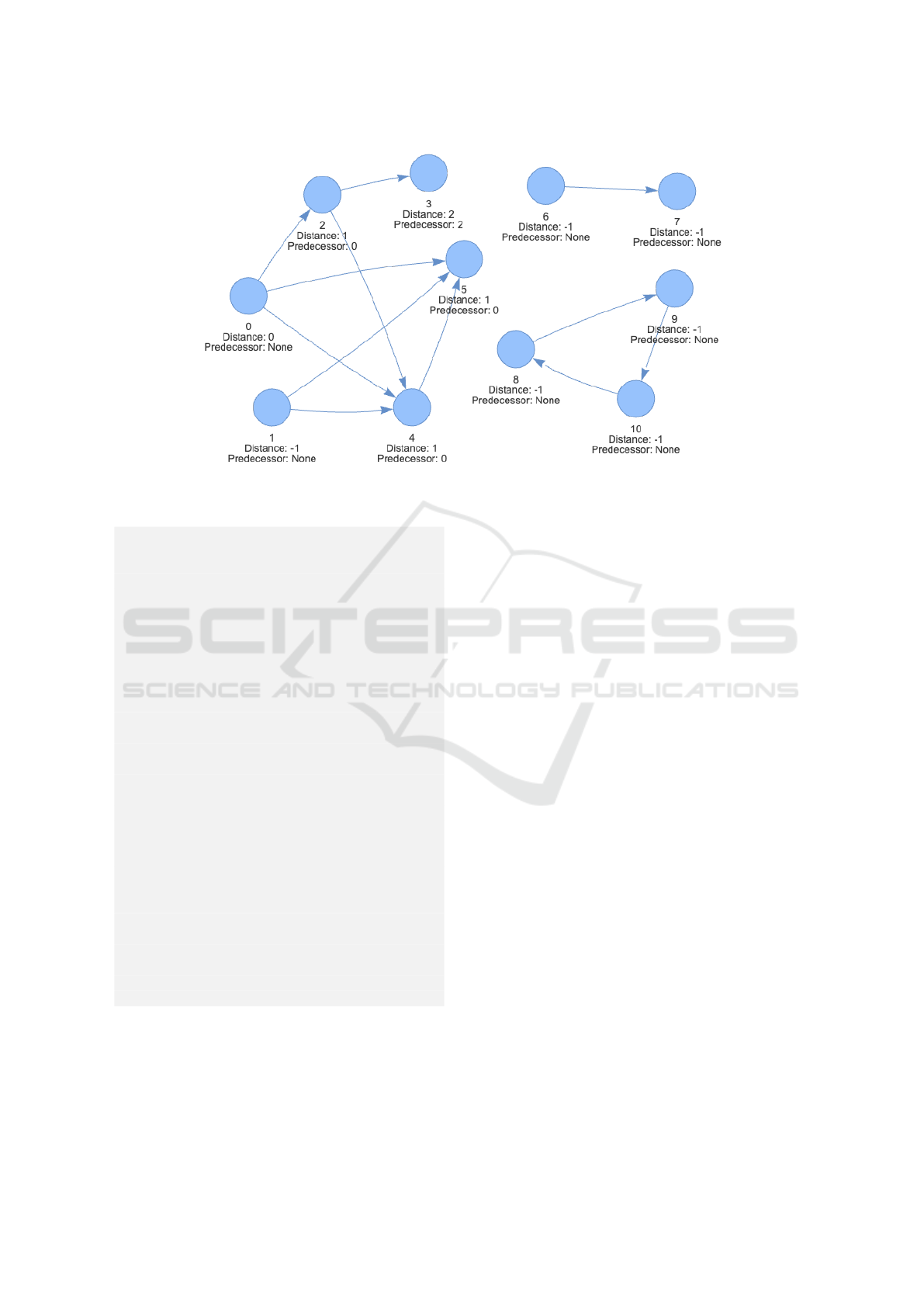
Figure 2: SSSP output generated by the visualizer tool.

Listing 6: SSSP algorithm execution with failure.

$ ./start_pregel.sh -num_workers=3

-graph_file=sssp/graph1.json

-failure_step=3 -checkpoint_frequency=2

,→

(...)

2024/11/09 17:19:29 Partitioning graph between

3 workers,→

2024/11/09 17:19:29 Ordering workers to

execute superstep,→

2024/11/09 17:19:29 Ordering workers to

execute superstep,→

2024/11/09 17:19:29 Ordering workers to

execute superstep,→

2024/11/09 17:19:29 Ordering workers to write

subgraphs,→

2024/11/09 17:19:29 Ordering workers to

execute superstep,→

2024/11/09 17:19:29 Failed to order superstep

to worker. Error: (...),→

2024/11/09 17:19:29 Checking workers

2024/11/09 17:19:29 Failed to check worker

with ID 0. Error: (...),→

(...)

2024/11/09 17:19:29 Next superstep: 3

2024/11/09 17:19:29 Partitioning graph between

2 workers,→

2024/11/09 17:19:29 Ordering workers to

execute superstep,→

2024/11/09 17:19:29 Ordering workers to write

subgraphs,→

(...)

2024/11/09 17:19:29 Pregel finished

We used Go-Pregel to solve three other problems:

to ﬁnd the weakly connected components of a graph,

to deﬁne a topological sort for a graph, and to de-

termine if a graph can be bipartite. The results were

correct in all cases, demonstrating the ﬂexibility and

effectiveness of the Go-Pregel framework for imple-

menting graph algorithms in a distributed manner.

4 CONCLUSIONS

We proposed a simple and easy-to-use framework

called Go-Pregel for distributed graph processing that

proved to work properly. The framework provides

scripts with different options and use cases, along

with an interactive visualization tool that takes any

output graph and displays a customizable represen-

tation of it in a browser. To help developers rea-

son about graph problems and design appropriate dis-

tributed solutions, we aim to deﬁne guidelines for

writing Pregel algorithms. In addition, we plan to ap-

ply Go-Pregel in educational settings to evaluate its

practical effectiveness.

The present version of Go-Pregel includes a fault-

tolerance solution, which is an important feature for

a distributed system. To handle fault tolerance, the

project provides a checkpointing solution similar to

Google’s Pregel system. However, Go-Pregel has a

clear limitation: the graph is not redistributed if a

worker is reactivated after a failure. It would be inter-

esting to implement conditions to decide when node

reconnection is allowed and how to perform graph

repartitioning.

The Go-Pregel framework allows the implemen-

tation of only static graphs, whereas some algorithms

involve changes in the graph topology during the

computation. For example, the Minimum Spanning

Tree problem requires the removal of edges from the

graph, and other algorithms (such as the k-core ﬁnd-

ing problem) demand the removal of vertices. The

Go-Pregel: A User-Friendly Framework for Distributed Graph Processing

155

challenge in implementing dynamic graph process-

ing in Go-Pregel is the need to provide ﬂexibility to

the user without making the framework too complex.

Full ﬂexibility and generality come with the cost of

programming complexity, which can be counterpro-

ductive if the goal of the project is to teach the basics

of distributed graph processing.

Google’s Pregel provides features, such as com-

biners and aggregators, to optimize communication

and enable global coordination during computation.

The Go-Pregel framework comes with a simple com-

biner function that can be modiﬁed by the user if

desired. Being able to measure time effects (for in-

stance, in computational steps or message exchanges)

would be an important feature to motivate the devel-

opers to use combiners in their algorithms. Aggrega-

tors were not implemented in the Go-Pregel, but they

could be an interesting feature to help users solve sim-

ple or even complex problems.

Go-Pregel is an ongoing project. Enhancing the

framework with new features would expand the range

of classic graph problems that can be solved using

our software, offering users greater ﬂexibility and en-

riching their overall learning experience. We argue

that the proposed framework empowers developers

to understand the core principles of distributed sys-

tems and graph processing, moving beyond the use of

black-box tools. Furthermore, it provides a practical

environment for experimenting with new distribution

strategies, serving as a foundation for education and

continued research in scalable graph computing.

REFERENCES

Apache (2020). Apache giraph.

Cheatham, T., Fahmy, A., Stefanescu, D. C., and Valiant,

L. G. (1994). Bulk synchronous parallel computing -

a paradigm for transportable software. Harvard Com-

puter Science Group Technical Report, (TR-36-94).

Fortunato, S. and Hric, D. (2016). Community detection in

networks: A user guide. Physics Reports, 659.

Gandour, G. (2024). Go pregel.

Gonzalez, J. E., Low, Y., Gu, H., Bickson, D., and Guestrin,

C. (2012). Powergraph: Distributed graph-parallel

computation on natural graphs. USENIX Symposium

on Operating Systems Design and Implementation.

Gonzalez, J. E., Xin, R. S., Dave, A., Crankshaw, D.,

Franklin, M. J., and Stoica, I. (2014). Graphx:

Graph processing in a distributed dataﬂow framework.

USENIX Symposium on Operating Systems Design

and Implementation.

Heidari, S., Simmhan, Y. L., Calheiros, R. N., and Buyya,

R. (2018). Scalable graph processing frameworks.

ACM Computing Surveys (CSUR), 51:1 – 53.

Li, X., Meng, K., Qin, L., Lai, L., Yu, W., Qian, Z., Lin, X.,

and Zhou, J. (2022). Flash: A framework for program-

ming distributed graph processing algorithms. 39th

IEEE International Conference on Data Engineering.

Malewicz, G., Austern, M. H., Bik, A. J., Dehnert, J. C.,

Horn, I., Leiser, N., and Czajkowski, G. (2010).

Pregel: a system for large-scale graph processing. In

Proceedings of the 2010 ACM SIGMOD International

Conference on Management of Data, SIGMOD ’10,

page 135–146, New York, NY, USA. Association for

Computing Machinery.

Michailidis, G. and de Leeuw, J. (2001). Data visualiza-

tion through graph drawing. Computational Statistics,

16(3):435–450.

Page, L., Brin, S., Motwani, R., and Winograd, T. (1998).

The pagerank citation ranking: Bringing order to the

web.

Peng, C., Xia, F., Naseriparsa, M., and Osborne, F. (2023).

Knowledge graphs: Opportunities and challenges. Ar-

tiﬁcial Intelligence Review.

Zhu, X., Chen, W., Zheng, W., and Ma, X. (2016). Gem-

ini: A computation-centric distributed graph process-

ing system. USENIX Symposium on Operating Sys-

tems Design and Implementation.

WEBIST 2025 - 21st International Conference on Web Information Systems and Technologies

156