Evaluating Machine Learning Strategies for Credit Risk Anomaly

Detection

Chenxi Hu

Shenzhen Audencia Financial Technology Institute, Shenzhen University, Shenzhen, China

Keywords: Credit Risk Classification, Class imbalance, PCA, Cost-Sensitive Learning, Machine Learning Model.

Abstract: This study addresses class imbalance in credit risk classification and optimizes model performance. One-hot

encoding was applied during data preprocessing, followed by an attempt at dimensionality reduction using

Principal Component Analysis (PCA), although PCA led to poorer results. Cost-Sensitive Learning (CSL)

was used to handle class imbalance. Five machine learning models were evaluated, and results showed that

Support Vector Classifier (SVC) and Logistic Regression performed best in ROC-AUC and F1-Score,

effectively balancing precision and recall. XGBoost achieved the highest recall but had lower precision,

resulting in a lower F1-Score. Random Forest and Neural Networks displayed balanced performance but did

not outperform SVC and Logistic Regression, making SVC and Logistic Regression the recommended models

for credit risk classification. Regarding PCA, the results showed it did not significantly improve model

performance. While some models, such as Neural Networks, showed slight improvements in ROC-AUC and

F1-Score, PCA generally led to a decrease in precision and recall, failing to enhance performance. CSL

improved recall significantly but reduced precision and accuracy. The study mitigated this by optimizing

feature weights, achieving higher recall with minimal precision loss, offering a balanced solution for high-

recall scenarios.

1 INTRODUCTION

Anomaly detection is a critical application in machine

learning, aiming to identify potential abnormal

behaviors from predominantly normal data (Guyon &

Elisseeff, 2003). With advancements in technology

and the exponential growth of data, anomaly

detection has become indispensable across various

industries, particularly in finance, where it plays a

pivotal role in mitigating risks (Hild & Torkkola,

2006). According to a report by the World Bank, the

prevalence of credit anomalies has remained

alarmingly high globally since the 21st century, with

developing countries experiencing disproportionately

higher rates compared to developed nations (Song &

Mei, 2010). This persistent issue undermines

economic stability, underscoring the urgency of

effective credit risk anomaly detection systems in

contemporary society.

However, credit risk anomaly detection faces

significant challenges. First, traditional anomaly

detection methods predominantly rely on binary

https://orcid.org/0009-0003-3960-0548

classification models that assume balanced datasets

(Uğuz, 2011). In reality, credit risks are often

concentrated within minority groups, leading to a

severe class imbalance where "bad" credit cases (e.g.,

defaults) are vastly outnumbered by "good" cases

(Rousseeuw & Van Driessen, 1999). This imbalance

hinders traditional models from accurately

identifying high-risk samples, resulting in suboptimal

recall rates. Second, conventional evaluation metrics,

such as overall accuracy, are ill-suited for imbalanced

credit risk tasks. As highlighted by (Chandola,

Banerjee, & Kumar, 2009), standard metrics fail to

prioritize the detection of truly risky minority-class

samples, which is the primary objective in practical

scenarios. Finally, the era of big data demands

scalable and precise methods to process massive

financial datasets efficiently (World Bank, 2021).

Existing approaches often struggle to balance

computational efficiency with detection accuracy,

necessitating innovative solutions.

The contributions of this study are summarized as

follows: First, this study explores the effectiveness of

436

Hu, C.

Evaluating Machine Learning Strategies for Credit Risk Anomaly Detection.

DOI: 10.5220/0013699000004670

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Data Science and Engineering (ICDSE 2025), pages 436-441

ISBN: 978-989-758-765-8

Cost-Sensitive Learning (CSL) in handling

imbalanced datasets. Second, it investigates high-

performance models suitable for this task, focusing

on identifying those that provide the best results.

Third, the study attempts to reduce feature

dimensionality through PCA, although the results

show that PCA did not optimize the outcome. Finally,

the study optimizes the model by focusing on the

most important features, mitigating the issues caused

by CSL (which significantly improves recall but

usually lowers precision). Through detailed

experiments and research, this work aims to provide

more accurate, efficient, and reliable solutions for

credit risk anomaly detection, offering robust

technical support for risk management in the financial

industry.

2 LITERATURE REVIEW

As a core topic in financial risk management, the

development of credit risk anomaly detection

demonstrates a trend of integrating traditional

statistical methods with modern machine learning

innovations (He & Garcia, 2009). Early credit risk

modeling relied on logistic regression (Mandour &

Chi, 2024), while subsequent advancements

introduced support vector machines (SVM) (Almajid,

2021), random forests (Alam, Shaukat, & Hussain,

2020), and gradient boosting (Fernández et al., 2018).

Despite these advancements, challenges persist in

handling high-dimensional data and mitigating

overfitting, driving innovations in feature engineering

and model optimization.

Feature selection techniques have evolved

significantly. Early work by references (Arora &

Kaur, 2020) emphasized statistical correlation

analysis for dimensionality reduction, later extended

by references (Meinshausen & Bühlmann, 2010)

through domain knowledge integration.

Dimensionality reduction methods such as principal

component analysis (PCA) (Lundberg & Lee, 2017)

address multicollinearity by reconstructing features,

while mutual information and SHAP values ()

optimize feature weighting by quantifying variable

contributions (Altman, 1968; Brown & Mues, 2012).

Traditional statistical approaches, including the

Mahalanobis distance, coexist with machine learning

models like one-class SVM, which expanded

anomaly detection capabilities. Hybrid frameworks

combining gradient boosting with statistical methods

further enhance risk identification reliability

(Fernández et al., 2018).

Recent research highlights system-level integration

of feature engineering, anomaly detection, and model

optimization. For instance, interpretable techniques

like SHAP values balance model performance with

transparency, enabling dynamic risk monitoring that

prioritizes both accuracy and interpretability. These

developments underscore the necessity of holistic

frameworks to overcome the limitations of isolated

methodologies.

3 DATASET AND

METHODOLOGY

3.1 Dataset

The Statlog German Credit Data set is a well-known

dataset in credit risk analysis, containing data from

1,000 individuals, with 20 features and a binary class

label indicating whether the individual is classified as

a "good" or "bad" credit risk. The dataset includes

both numerical and categorical features, such as

credit history, loan purpose, age, employment status,

and housing situation. The goal is to predict the credit

class label based on these features, assess credit risk,

and identify potential financial defaults. The class

distribution is imbalanced, with a ratio of

approximately 3:7 between bad and good credit risks,

presenting a challenge for machine learning models.

Preprocessing techniques, such as feature encoding

and balancing methods, are typically used to improve

model performance. The dataset is widely used in

research for anomaly detection, classification, and

model interpretability, providing a valuable

benchmark for evaluating and comparing different

machine learning algorithms.

3.2 Main Flowchart

Figure 1 shows the flowchart of this study. This work

will compare the performance of five models and

integrate these models to more reliably explore the

optimal features (the identified optimal features will

be used to mitigate the issues caused by CSL). In this

study, the data is processed using one-hot encoding,

resulting in a high-dimensional and sparse dataset.

Although dimensionality reduction through Principal

Component Analysis (PCA) could be intuitively

applied, its effectiveness may be limited. To improve

the model's practicality, specifically to increase

recall, CSL is introduced.

Evaluating Machine Learning Strategies for Credit Risk Anomaly Detection

437

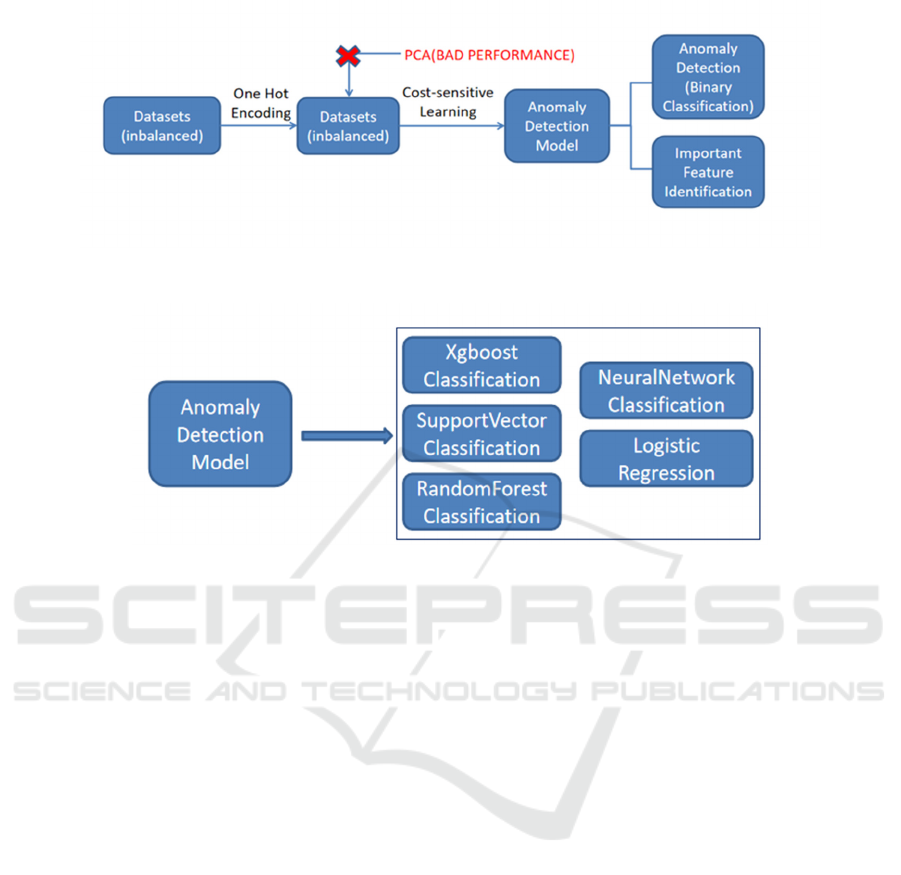
Figure1: CSL Model for Credit Risk Anomaly Detection and Key Feature Identification. (Picture credit: Original)

Figure 2: Multi-Model Analysis for Anomaly Detection: Performance Evaluation and Feature Identification. (Picture credit:

Original)

3.3 Important Feature Identification

Figure 2 displays the five machine learning models

used in this study. For integrating models to select

and weigh important features, the following method

is adopted: by training and evaluating multiple

machine learning models, the most important features

for credit risk prediction are identified. The

evaluation of feature importance relies not only on

model performance (such as AUC values) but also on

the frequency and weighted scores of features across

different models. The weighted score of a feature is

calculated based on its rank and weight in each

model, with the formula as follows:

Weight



RankWeight





Where Rank represents the importance order of

the feature within the model, and Weight reflects the

contribution of the model's performance (e.g., AUC

value) to the feature's importance. Using this method,

the people can identify features that frequently appear

in the top ranks across multiple models and have a

significant impact on prediction outcomes.

In this study, to enhance the impact of specific

features on model training, certain features deemed to

have significant predictive power in credit risk

prediction (boosted_features) were selected and

weighted. First, all features were standardized to

ensure they have the same scale, thus avoiding

unnecessary interference in model training due to

differences in feature scales. Next, the weighting was

applied based on the weights calculated in Equation

(1). By doing so, these boosted features take on a

larger proportion in the training process, encouraging

the model to place more emphasis on their role in the

prediction.

4 RESULT

4.1 Performance of Different Models

From Table 1, in the credit risk classification task,

each model has its own advantages in other

evaluation indicators. Among them, SVC and

Logistic Regression performed well in ROC-AUC

and F1-Score, reaching ROC-AUC of 0.8074 and

0.8015 respectively, indicating that they have a strong

ability to distinguish positive and negative samples.

At the same time, the F1-Score of Logistic Regression

is 0.662, while that of SVC is 0.6569, indicating that

ICDSE 2025 - The International Conference on Data Science and Engineering

438

these two models have good performance in

balancing precision and recall.

Table 1: Performance comparison of various models on different metrics.

Model Accurac

ROC-AUC F1-Score Precision Recall

XGBoost 0.725 0.7557 0.6605 0.5213 0.8305

SVC 0.765 0.8074 0.6569 0.5844 0.75

Random Forest 0.75 0.7961 0.6154 0.5714 0.6667

Neural Networ

0.72 0.7762 0.6316 0.5217 0.8

Logistic Regression 0.76 0.8015 0.662 0.5732 0.7833

Table 2: Feature importance analysis based on frequency, average rank, and weighted score.

Feature Frequenc

Average Ran

Weighted Score (Rank × Weight)

A14 1.0 1.25 4.5

A21 0.5 2.0 4.6

A51 0.5 3.0 7.5

A11 0.5 4.0 10.0

A35 0.5 5.0 11.5

Table 3: Comparison of Logistic Regression performance with and without feature importance.

Model Accurac

ROC-AUC F1 Precision Recall

Logistic Regression

Logistic Regression (Feature Importance)

0.7600

0.7550

0.8015

0.8079

0.6620

0.6629

0.5732

0.5679

0.7833

0.8333

XGBoost performs best in the recall, which is

0.8305 and is suitable for scenarios that pay more

attention to recall in abnormal sample detection, but

its precision is relatively low (0.5213), resulting in a

low F1-Score (0.6605). The comprehensive

performance of random forest and neural network is

relatively balanced, but neither exceeds SVC and

Logistic Regression in any indicator. Therefore, in

this experiment, SVC and Logistic Regression have

more advantages in comprehensive performance and

are recommended choices for credit risk classification

problems.

4.2 Identification and Optimization of

Important Features

4.2.1 Identification of Important Features

The analysis of feature importance revealed that both

qualitative and numerical attributes play a significant

role in credit risk classification. From Table 2, A14

(No Checking Account) emerged as the most

influential, highlighting the importance of a

customer’s existing financial account status.

Additionally, A21 (Duration in Months) and A51

(Credit Amount) demonstrated the relevance of

numerical attributes in assessing creditworthiness.

Furthermore, qualitative features such as A11

(Status of Existing Checking Account) and A35

(Purpose) were identified as key contributors,

indicating that both financial history and the purpose

of credit requests significantly impact model

predictions. These findings underscore the necessity

of incorporating a diverse set of features to effectively

predict credit risk and provide meaningful insights

into customer behavior.

4.2.1 Optimization Based on Important

Features

The optimization results in Table 3 show that by

assigning higher weights to important features, the

problem of a sharp drop in precision when improving

recall is successfully alleviated. In the optimized

model, the recall rate is significantly increased from

0.7833 to 0.8333, while the precision rate only

slightly decreases from 0.5732 to 0.5679, which is a

small drop. This shows that although increasing the

recall rate usually leads to a significant drop in

precision, by optimizing the weight distribution of

important features, the loss of precision can be

controlled within a lower range while ensuring the

increase in recall, thereby better balancing the two.

Evaluating Machine Learning Strategies for Credit Risk Anomaly Detection

439

Table 4: Model Performance Without PCA.

Model Accurac

ROC-AUC F1-Score Precision Recall

XGBoost 0.7800 0.7109 0.5926 0.7447 0.5932

SVC 0.7850 0.7930 0.5981 0.6667 0.5424

Random Forest 0.7950 0.8175 0.5591 0.7647 0.4407

Neural Networ

0.8150 0.8051 0.6838 0.6897 0.6780

Logistic Regression 0.8000 0.8180 0.6364 0.6863 0.5932

Table 5: Model Performance With PCA.

Model Accurac

ROC-AUC F1-Score Precision Recall

XGBoost 0.7350↓ 0.6839↓ 0.5546↓ 0.5500↓ 0.6093↑

SVC 0.7200↓ 0.7595↓ 0.4167↓ 0.5405↓ 0.3390↓

Random Forest 0.7050↓ 0.7285↓ 0.4486↓ 0.5000↓ 0.4068↓

Neural Networ

0.7650↓ 0.8115↑ 0.6843↑ 0.6207↓ 0.6102↓

istic Re

ression 0.7100↓ 0.7763↓ 0.4630↓ 0.5102↓ 0.4237↓

Table 6: Model Performance Without CSL.

Model Accurac

ROC-AUC F1-Score Precision Recall

XGBoost 0.7800 0.7109 0.5926 0.7447 0.5932

SVC 0.7850 0.7930 0.5981 0.6667 0.5424

Random Forest 0.7950 0.8175 0.5591 0.7647 0.4407

Neural Networ

0.8150 0.8051 0.6838 0.6897 0.6780

istic Re

ression 0.8000 0.8180 0.6364 0.6863 0.5932

Table 7: Model Performance With CSL.

Model Accurac

ROC-AUC F1-Score Precision Recall

XGBoost 0.7250↓ 0.7557↑ 0.6605↑ 0.5213↓ 0.8305↑

SVC 0.7650↓ 0.8074↑ 0.6569↑ 0.5844↓ 0.7500↑

Random Forest 0.7500↓ 0.7961↓ 0.6154↑ 0.5714↓ 0.6667↑

Neural Networ

0.7200↓ 0.7762↓ 0.6316↓ 0.5217↓ 0.8000↑

Logistic Regression 0.7600↓ 0.8015↓ 0.6620↑ 0.5732↓ 0.7833↑

4.3 Ablation Experiment

4.3.1 Ablation of PCA

The application of PCA had a notable impact on

model performance (see Table 4,5). Across all

models, there was a general decline in accuracy,

precision, and F1-Score. However, some models,

such as Neural Networks, demonstrated a slight

improvement in ROC-AUC (0.8051 to 0.8115) and

F1-Score (0.6838 to 0.6843). Despite these minor

gains, the overall results indicate that PCA may not

be effective in enhancing model performance for this

specific task, as it often leads to reduced precision and

recall, which are critical metrics in credit risk

anomaly detection.

4.3.2 Ablation of CSL

The application of CSL significantly improved the

recall across all models, demonstrating its

effectiveness in addressing the class imbalance in the

credit risk anomaly detection task (Table 6,7). For

example, XGBoost achieved a recall improvement

from 0.5932 to 0.8305, and SVC saw a similar

increase from 0.5424 to 0.7500. However, this

improvement in recall often came at the expense of

precision and accuracy. The trade-off highlights the

importance of using CSL in scenarios where

identifying the minority class is critical, even if it

means accepting a slight reduction in precision.

5 CONCLUSIONS

Evaluation of the various models revealed distinct

strengths and weaknesses. Logistic Regression and

SVC demonstrated strong overall performance with

high ROC-AUC and a good balance of precision and

recall, making them suitable for general classification

tasks. XGBoost excelled in recall, effectively

identifying high-risk cases, but at the cost of lower

ICDSE 2025 - The International Conference on Data Science and Engineering

440

precision, leading to more false positives. Random

Forest performed well in feature importance analysis

but had lower recall, while Neural Networks provided

balanced performance across metrics, slightly inferior

to SVC and Logistic Regression in maintaining

precision-recall trade-offs.

The application of PCA in credit risk anomaly

detection caused significant information loss,

compromising critical feature relationships and

leading to declines in accuracy, F1-Score, and

precision. Although PCA aims to reduce

dimensionality and enhance efficiency, its use in this

context resulted in sub-optimal performance, failing

to achieve the desired optimization. In contrast, CSL

significantly improved recall across all models,

addressing the need to detect minority-class cases, but

at the expense of precision, resulting in increased

false positives.

A promising solution to these challenges lies in

optimizing the most important features identified

through multi-model integration. By leveraging the

strengths of various models to pinpoint key attributes,

this approach retains essential information and

reduces redundancy, enabling models to achieve a

better balance between recall and precision. This

strategy addresses the practical need for high recall

while mitigating the limitations posed by PCA and

CSL, offering a robust pathway for credit risk

anomaly detection.

REFERENCES

Alam, T. M., Shaukat, K., & Hussain, A. 2020. An

investigation of credit card default prediction in the

imbalanced datasets. IEEE Access, 8, 201270–201283.

Almajid, A. S. 2021. Multilayer perceptron optimization on

imbalanced data using SVM-SMOTE and one-hot

encoding for credit card default prediction. Expert

Systems with Applications, 185, 115642.

Altman, E. I. 1968. Financial ratios, discriminant analysis

and the prediction of corporate bankruptcy. The Journal

of Finance, 23(4), 589–609.

Arora, N., & Kaur, P. D. 2020. A Bolasso-based consistent

feature selection enabled random forest classification

algorithm: An application to credit risk assessment.

Applied Soft Computing, 86, 105936.

Brown, I., & Mues, C. 2012. An experimental comparison

of classification algorithms for imbalanced credit

scoring data sets. Expert Systems with Applications,

39(3), 3446–3453.

Chandola, V., Banerjee, A., & Kumar, V. 2009. Anomaly

detection: A survey. ACM Computing Surveys, 41(3),

1–58.

Fernández, A., García, S., Galar, M., Prati, R. C.,

Krawczyk, B., & Herrera, F. 2018. Learning from

imbalanced data sets (Vol. 10, No. 2018). Cham:

Springer.

Guyon, I., & Elisseeff, A. 2003. An introduction to variable

and feature selection. Journal of Machine Learning

Research, 3, 1157–1182.

He, H., & Garcia, E. A. 2009. Learning from imbalanced

data. IEEE Transactions on Knowledge and Data

Engineering, 21(9), 1263–1284.

Hild, K. E., Erdogmus, D., & Torkkola, K. 2006. Feature

extraction using information-theoretic learning. IEEE

Transactions on Neural Networks, 17(5), 1224–1235.

Lundberg, S. M., & Lee, S. I. 2017. A unified approach to

interpreting model predictions, Nov. arXiv preprint

arXiv:1705.07874.

Mandour, M. A., & Chi, G. 2024. A review study of AI

methods for credit default prediction. Journal of

Artificial Intelligence in Finance, 12(3), 45–67.

Meinshausen, N., & Bühlmann, P. 2010. Stability selection.

Journal of the Royal Statistical Society: Series B, 72(4),

417–473.

Rousseeuw, P. J., & Van Driessen, K. 1999. A fast

algorithm for the minimum covariance determinant

estimator. Technometrics, 41(3), 212–223.

Song, F., Guo, Z., & Mei, D. 2010. Feature selection using

principal component analysis. IEEE Transactions on

Pattern Analysis and Machine Intelligence, 32(3), 547–

561.

Uğuz, H. 2011. A two-stage feature selection method for

text categorization by using information gain, principal

component analysis and genetic algorithm. Expert

Systems with Applications, 38(7), 8747–8753.

World Bank. 2021. Global Financial Development Report

2021: Credit anomalies and economic stability. World

Bank Publications. Retrieved from

https://openknowledge.worldbank.org/handle/10986/3

5430

Evaluating Machine Learning Strategies for Credit Risk Anomaly Detection

441