Comparison of Feature Combinations on Simultaneous Prediction of

Stock Price and Volatility

Wenhan Lu

School of Management, Zhejiang University, Hangzhou, Zhejiang, China

Keywords: Multi-Target Prediction, Feature Combination, Random Forest, Lasso Regression, Mutual Information.

Abstract: Accurate prediction of stock prices and volatility is crucial for informed financial decision-making. However,

traditional models often focus on single-target forecasts, neglecting the connection between price movements

and volatility, which can limit predictive accuracy. Therefore, there is a need for more effective approaches

that can simultaneously predict both stock prices and volatility. This study proposes an innovative method to

address these challenges by using two target variables: the 5-day-ahead closing price and the 5-day high-low

price difference as a measure of volatility. Besides, the study applies three feature selection techniques—

Random Forest, Lasso Regression, and Mutual Information to identify the best features for predicting closing

prices, which are then used to forecast volatility. The results of this study, based on data from Amazon, Google,

and Microsoft over a 10-year period (2015-2025), show that Lasso Regression outperforms the other methods.

It achieved the lowest mean squared error (MSE) across all three companies (Amazon: 0.2485; Google:

0.0323; Microsoft: 5.1805) while maintaining high R² values (above 0.78). The findings highlight Lasso

Regression's ability to balance prediction accuracy and generalizability, offering a computationally efficient

method for multi-target prediction, which improves the practicality of multi-target models for financial

applications.

1 INTRODUCTION

Accurate prediction of stock prices and volatility

remains a critical challenge in financial markets, as

precise forecasting supports investment decisions,

risk management, and portfolio optimization (Shah,

Isah, & Zulkernine, 2019). Previous studies

demonstrate that stock price movements and

volatility are influenced by multiple factors, where

diverse feature characteristics create challenges for

achieving high prediction accuracy (Htun, Biehl, &

Petkov, 2023). Traditional models typically focus on

single-target predictions, often neglecting the

interconnected nature of price changes and volatility.

However, multi-target learning has shown the

potential to enhance accuracy through simultaneous

prediction of related variables. For example,

constrained random forest models have exhibited

robust performance across diverse datasets (Blitsi,

2024).

To address feature selection challenges impacting

prediction accuracy, researchers have developed

https://orcid.org/0009-0007-3434-7706

various effective methods. Random Forest has

emerged as a prominent technique due to its error

estimation capabilities, correlation analysis, and

feature importance scoring (Kursa et al., 2011;

Iranzad et al., 2024). Lasso regression demonstrates

superior performance through exact coefficient

shrinkage to zero (Jovi, Brki, & Bogunovi, 2015;

Muthukrishnan & Rohini, 2016). Mutual Information

(MI), an information theory-based method, measures

nonlinear dependencies between variables and

effectively identifies features with complex

relationships to targets, and examples of these

methods include the forward selection minimal-

redundancy-maximal-relevance (FSMRMR) and

conditional mutual information maximization

(CMIM) methods (Nguyen et al., 2014; Sun et al.,

2019) .

Comparative studies by Nabipour et al. evaluating

nine machine learning models and two deep learning

approaches confirm LSTM's effectiveness in

processing sequential financial data (Nabipour et al.,

2020; Ye, 2024).

430

Lu, W.

Comparison of Feature Combinations on Simultaneous Prediction of Stock Price and Volatility.

DOI: 10.5220/0013698900004670

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Data Science and Engineering (ICDSE 2025), pages 430-435

ISBN: 978-989-758-765-8

This study addresses these challenges by

proposing feature combinations for multi-target

prediction. This study analyzed ten years of stock data

(January 2015 - January 2025) for Amazon, Google,

and Microsoft from Yahoo Finance. Two target

variables are defined: 5-day-ahead closing price and

5-day high-low price differential (volatility proxy).

The methodology follows a sequential process:

Feature Selection for Price Prediction: Three methods

(Random Forest, Lasso Regression, Mutual

Information) identify optimal features for closing

price forecasting. Volatility Prediction: Selected

features from Step 1 are used as inputs for volatility

modeling. The objective of this research is to evaluate

4 different feature combinations for their

effectiveness in simultaneously predicting stock

prices and volatility five days into the future. The

ultimate goal is to identify the optimal feature

combination that yields the most accurate predictions.

2 METHODOLOGY

2.1 Data Description

In this study, stock data was collected from Yahoo for

3 companies including Amazon, Google, and

Microsoft. The time ranges for Amazon, Google and

Microsoft were from 2015.01.01 to 2025.01.01. Table

1 shows part of the dataset for the stock of Google.

Table 1: Part of the dataset for the stock of Google.

Date Open High Low Close Volume

2015/1/2 26.07496452 26.39592813 26.03968897 26.28363971 28951268

2015/1/5 25.53141403 26.05111498 25.49117052 25.99795174 41196796

2015/1/6 24.93967056 25.64593795 24.8944591 25.58755778 57998800

2015/1/7 24.89694405 25.20220556 24.82490104 25.19008214 41301082

2.2 Target Variables

In this study, two target variables were selected for

simultaneous prediction. The first target variable was

the stock closing price five days later, as it reflects the

final outcome of trading activity and provides a

clearer indication of market sentiment. The second

target variable was the price difference between the

highest and lowest prices observed over the same 5-

day period.

Traditional approaches to volatility prediction

typically use the standard deviation of the closing

price over a 5-day period as the target variable.

However, in this study, it was found that the standard

deviation of the closing price over a 5-day period

exhibits a high correlation with the closing price five

days later, which could lead to redundancy in a multi-

target prediction framework. Furthermore, while the

standard deviation is commonly used to measure

market volatility, it is a statistical measure with

relatively limited interpretability. In contrast, the

difference between the highest and lowest prices

offers a more intuitive and direct reflection of price

fluctuation. Therefore, the price difference between

the highest and lowest prices 5 days later was chosen

as the second target variable.

2.3 Feature Engineering

The features included fundamental stock attributes

and technical indicators. The fundamental stock

attributes included Open, Close, High, Low, Volume.

And technical indicators included Simple Moving

Average (SMA), Relative Strength Index (RSI),

Moving Average Convergence Divergence (MACD),

Average True Range (ATR), Chaikin Money Flow

(CMF), Rate of Change (ROC). A table is listed

below to show the calculation of indicators.

In Table 2, the abbreviations used are as follows:

Ct means the day close stock price at time t. Avg

(Gain) means the average day gain in period of 14

days. Avg (Loss) means the average day loss in the

period of 14 days.

Comparison of Feature Combinations on Simultaneous Prediction of Stock Price and Volatility

431

Table 2: Technical indicators and its formulas.

Technical Indicators Calculation and Descri

tion

Simple Moving Average (SMA5)

SMA



















(

The avera

e of the closin

rices over the last 5 da

)

Relative Strength Index (RSI)

RSI = 100 −

100

Avg(Gain)

Avg(Loss)

(

Measures the s

eed and ma

nitude of recent

rice chan

es over 14 da

)

Moving Average Convergence Diver-

gence (MACD)

MACD = EMA



−EMA



(Difference between the 12-day and 26-day exponential moving averages)

Average True Range (ATR)

ATR = Rolling Mean (14) (max (High-Low, High-Close, Low-Close))

(

Measures the volatilit

based on recent hi

h-low-close

rices over 14 da

)

Chaikin Money Flow (CMF)

CMF =

∑

(Money Flow Multiplier Volume)





Rolling Sum of Volume(30)

(

Indicates the bu

and sellin

ressure over 30 da

)

Rate of Change (ROC)

ROC =



−C









(

Measures the

ercenta

e chan

e in

rice over a 12-da

eriod

)

2.4 Feature Selection Methods

Since the closing price of a stock after 5 days was

generally of greater interest compared to its price

volatility over the same period, 3 feature selection

methods were applied to identify the most influential

feature sets for predicting the closing price in 5 days.

The selected feature combinations were then used to

forecast the stock's price volatility 5 days later.

In this study, 3 feature selection methods were

used to help choose feature combinations: Random

Forest, Lasso Regression, Mutual Information.

Random Forest was used to assess the importance

of each feature in predicting the stock price. The

features were then ranked in descending order

according to their importance, and the top 5 most

important features were selected.

Lasso Regression is a regularized linear regression

method that applies L1 regularization to penalize

large coefficients, driving some of them to zero,

thereby performing automatic feature selection. In

this study, Lasso Regression was used to select the

features most relevant for predicting stock price.

Features with non-zero coefficients were identified

and combined into a unified feature set.

Mutual Information was used to evaluate the

dependence between each feature and the stock price.

The features were then ranked in descending order

based on their mutual information scores, and the top

5 most relevant features were selected.

2.5 Test Method

The model’s performance is evaluated using Mean

Squared Error (MSE) and coefficient of

determination (R-squared value). In this study, the R-

squared value was required to exceed 0.65.

2.6 Training and Testing Data

Preparation

The entire dataset was standardized to ensure that all

features and target variables had a mean of 0 and a

standard deviation of 1. Subsequently, the dataset was

split into training and testing sets, with 80% of the

data used for training the model and the remaining

20% reserved for testing the model’s performance.

2.7 Prediction Model

Long Short-Term Memory (LSTM) is a specialized

recurrent neural network designed for processing time

series data. In this study, LSTM was employed as the

predictive model for stock volatility. The input to the

model was a time series tensor with a shape of

(number of samples, 10, number of features), where

each sample consisted of feature data from 10

consecutive days arranged in chronological order.

Firstly, all fundamental stock attributes and technical

indicators were included as input features, and the

LSTM model was used to predict stock volatility,

yielding the MSE and R-squared value. Subsequently,

3 feature selection methods were applied to identify 3

sets of features that had a significant impact on the

stock closing price after 5 days. Each selected feature

set was then used to construct a time series tensor as

input, and the LSTM model was utilized again to make

predictions, obtaining the corresponding MSE and R-

squared value. Figure 1 shows the stock prediction

process using Amazon's stock as an example.

ICDSE 2025 - The International Conference on Data Science and Engineering

432

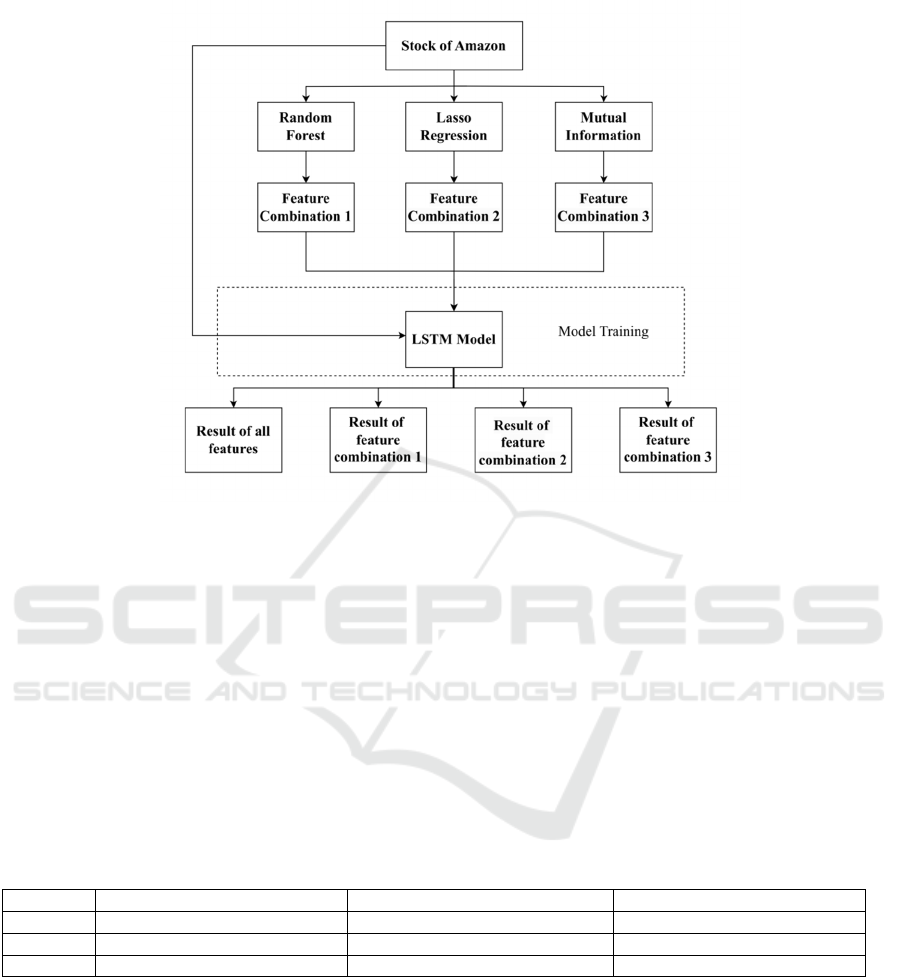
Figure 1: The Predictive Flowchart of Amazon Stock. (Picture credit: Original)

3 RESULT

Table 3 presents a clear comparison of the feature

combinations selected for Amazon, Google, and

Microsoft using different feature selection methods.

Both the Random Forest and Mutual Information

methods consistently identified the same set of

features for all 3 companies, namely Close, SMA5,

High, Low, and Open. In contrast, the Lasso

Regression method selected distinct feature sets

tailored to each company: Amazon was associated

with Open, Close, Volume, and MACD; Google with

Open, Close, RSI, MACD, ATR; and Microsoft with

Open, Close, MACD, CMF, and ROC. These findings

suggest that different feature selection techniques

exhibit notable variability in their selections. The

Random Forest and Mutual Information methods tend

to prioritize a consistent set of features across

different datasets, whereas the Lasso Regression

method appears to adapt feature selection based on the

specific characteristics and dynamics of each dataset.

Table 3: Feature Combinations for Different Companies.

Com

Random Forest Features Lasso Re

ression Features Mutual Information Features

Amazon Close, SMA

, High, Low, Open Open, Close, Volume, MACD Close, SMA

, High, Low, Open

Google Close, SMA

, High, Low, Open Open, Close, RSI, MACD, ATR Close, SMA

, High, Low, Open

Microsoft Close, SMA

, High, Low, Open Open, Close, MACD, CMF, ROC Close, SMA

, High, Low, Open

Since the Random Forest and Mutual Information

feature selection methods identified the exact same

set of features (Close, SMA5, High, Low, and Open)

across all 3 companies, their MSE and R

values were

identical, as shown in Table 4. In 3 companies, the

feature combinations chosen by Random Forest and

Mutual Information feature selection methods

achieved an R

value exceeding 0.98, indicating an

exceptionally high explanatory power. However, their

MSE values were significantly higher than those

obtained using other methods. In contrast, the the

feature combination chosen by Lasso Regression

feature selection method yielded the lowest MSE

values across all 3 companies (Amazon: 0.2485, R

0.9596; Google: 0.0323, R

= 0.9789; Microsoft:

5.1805, R

= 0.7833) Although the R

values of Lasso

Regression were slightly lower than those of the

Random Forest and Mutual Information methods,

they remained at a relatively high level. When all

features were included, the MSE and R

values fell

Comparison of Feature Combinations on Simultaneous Prediction of Stock Price and Volatility

433

between those of the two aforementioned methods

(Amazon: MSE = 7.3282, R

= 0.8589; Google: MSE

= 5.8935, R

= 0.8207; Microsoft: MSE = 5.2499, R

= 0.7804). In terms of predictive performance, while

the features chosen by Random Forest and Mutual

Information methods achieved the highest model fit,

their prediction errors were notably larger. In contrast,

Lasso Regression effectively maintained high

explanatory power while significantly reducing

prediction errors.

Table 4: MSE and R

of feature combinations for companies.

Company

All Features

Random Forest

Features

Lasso Regression

Features

Mutual Information

Features

MSE R

Amazon 7.3282 0.8589 33.9151 0.9875 0.2485 0.9596 33.9151 0.9875

Google 5.8935 0.8207 14.7808 0.9913 0.0323 0.9789 14.7808 0.9913

Microsoft 5.2499 0.7804 55.9238 0.9960

5.1805

0.7833

55.9238

0.9960

4 CONCLUSIONS

The study evaluates the performance of 4 feature

combinations in the simultaneous prediction of stock

closing prices and volatility.A decade-long dataset of

stock market records from 3 companies (Amazon,

Google, and Microsoft) was analyzed. To address

redundancy issues inherent in multi-objective

forecasting frameworks, two distinct target variables

were established: 1) the closing price after 5 days, and

2) the difference between the highest and lowest

prices after 5 days. Given the relative importance of

closing price prediction compared to volatility

forecasting and to reduce parameter bias in multi-

target prediction models, conventional multi-output

approaches were abandoned in favor of a sequential

methodology. Instead, in the study, 3 feature selection

methods helped identify key features for closing price

prediction. Then these selected features were used as

inputs to predict price volatility.

Empirical results revealed company-specific

variations in optimal feature combinations for multi-

objective prediction. However, the feature

combination selected through Lasso Regression

consistently demonstrated superior predictive

performance across all companies compared to

alternative selection methods.

There are still some limitations of this paper. First,

the analytical scope was restricted to three established

feature selection techniques, potentially limiting

comprehensive exploration of the feature space.

Second, the Mutual Information and Random Forest

methods exhibited similar tendencies toward feature

selection, leading to repeated results in feature

combinations.

Future research can build upon this work in

several directions. First, more diverse feature

selection methods could be incorporated, particularly

those leveraging automatic feature extraction

techniques integrated with deep learning. Second,

alternative evaluation metrics, such as return-based

assessments, could be adopted to improve the

practical applicability and robustness of the model.

These avenues of research have the potential to

further enhance the precision of multi-target

prediction models, providing valuable support for

financial decision-making

REFERENCES

Blitsi, A. K. (2024). Multi-target learning with constraints

[Doctoral dissertation, Aristotle University of

Thessaloniki].

Htun, H. H., Biehl, M., & Petkov, N. (2023). Survey of

feature selection and extraction techniques for stock

market prediction. Financial Innovation, 9, 26.

Iranzad, R., & Liu, X. (2024). A review of random forest-

based feature selection methods for data science

education and applications. International Journal of

Data Science and Analytics, 1-15.

Jovi, A., Brki, K., & Bogunovi, N. (2015, May). A review

of feature selection methods with applications. In 2015

38th International Convention on Information and

Communication Technology, Electronics and

Microelectronics (MIPRO) (pp. 1200-1205). IEEE.

Kursa, M. B., & Rudnicki, W. R. (2011). The all relevant

feature selection using random forest. arXiv preprint

arXiv:1106.5112.

Muthukrishnan, R., & Rohini, R. (2016, October). LASSO:

A feature selection technique in predictive modeling for

machine learning. In 2016 IEEE International

Conference on Advances in Computer Applications

(ICACA) (pp. 18-20). IEEE.

Nabipour, M., Nayyeri, P., Jabani, H., Shahab, S., &

Mosavi, A. (2020). Predicting stock market trends using

machine learning and deep learning algorithms via

continuous and binary data; a comparative analysis.

IEEE Access, 8, 150199-150212.

Nguyen, X. V., Chan, J., Romano, S., & Bailey, J. (2014,

August). Effective global approaches for mutual

ICDSE 2025 - The International Conference on Data Science and Engineering

434

information-based feature selection. In Proceedings of

the 20th ACM SIGKDD International Conference on

Knowledge Discovery and Data Mining (pp. 512-521).

Shah, D., Isah, H., & Zulkernine, F. (2019). Stock market

analysis: A review and taxonomy of prediction

techniques. International Journal of Financial Studies,

7(2), 26.

Sun, J., Xiao, K., Liu, C., Zhou, W., & Xiong, H. (2019).

Exploiting intra-day patterns for market shock

prediction: A machine learning approach. Expert

Systems with Applications, 127, 272-281.

Ye, S. (2024). Applying ensemble learning to multiple stock

price predictions: A comparative study. Applied and

Computational Engineering, 50, 189-198.

Comparison of Feature Combinations on Simultaneous Prediction of Stock Price and Volatility

435