Comparative Analysis of Time Series Models for Forecasting the U.S.

Unemployment Rate: A Study of ARIMA, LSTM, and Intervention

Approaches

Yunpeng Li

Bachelor of Business Administration (Hons) Programme, Hong Kong Baptist University, Kowloon, Hong Kong, China

Keywords: Time Series Forecasting, Unemployment Rate Prediction, Economic Events, COVID-19 Pandemic, Machine

Learning Techniques.

Abstract: The unemployment rate reflects the overall health of the labor market and influences monetary and fiscal

strategies. The rapidly changing economic landscape, marked by events like the financial downturn of 2008

and the global health crisis caused by COVID-19, highlights the necessity of stable forecasting models that

capture complex dynamics and structural changes. This research centers on comparing various time series

models to forecast unemployment rates in the United States (ARIMA, LSTM and intervention approaches).

The research collected the US unemployment rate for the 16-24 age group from 1978 to 2023 and applied

time series visualization, seasonal decomposition, and intervention analysis to understand trends and event

impacts. ARIMA and LSTM are developed and evaluated by evaluation measures like MSE, RMSE, MAE,

and MAPE. The study aims to identify which model best captures trends, seasonal patterns, and structural

changes in the labor market. Preliminary findings suggest that LSTM models outperform ARIMA in complex

scenarios due to their ability to learn long-term dependencies. The results of this research will contribute to

improved forecasting methodologies, providing policymakers with more accurate predictions to inform

decision-making processes.

1 INTRODUCTION

The unemployment rate has always been a hot topic

for economists worldwide. As it affects all countries,

forecasting the unemployment rate is critical for

policymakers, economists, and businesses (Douglas,

S., & Zahed, M.,2024). It provides valuable insights

into the overall health of the economy and labor

market trends. The United States unemployment rate,

in particular, is a key economic indicator that

influences monetary policy decisions, fiscal planning,

and business strategies. Over the years, various time

series models have been developed and applied to

predict unemployment rates, each with strengths and

limitations.

Recent studies have highlighted the need for a

comprehensive comparison of different forecasting

models because the performance of these models can

vary significantly depending on economic conditions

and data characteristics. For instance, Douglas and

https://orcid.org/0009-0006-2287-6080

Zahed demonstrated the limitations of using only

ARIMA models for long-term unemployment rate

forecasts, emphasizing the need to consider

alternative approaches (Douglas & Zahed, 2024).

Similarly, Gostkowski and Rokicki compared several

predictive methods, including ARIMA and regression

models, but they did not include more advanced

machine learning techniques such as LSTM

(Gostkowski & Rokicki, 2021).

The rapidly evolving economic landscape,

particularly considering recent worldwide

occurrences, such as the COVID-19 outbreak, has

emphasized the significance of reassessing and

comparing different forecasting models. Traditional

models that performed well in the past may no longer

be as effective in capturing the complex dynamics of

today's labor market. As Barnichon and Nekarda

(2012) noted, models incorporating labor force flow

data can significantly outperform traditional

forecasting approaches, especially during economic

downturns (Barnichon & Nekarda, 2012).

372

Li, Y.

Comparative Analysis of Time Series Models for Forecasting the U.S. Unemployment Rate: A Study of ARIMA, LSTM, and Intervention Approaches.

DOI: 10.5220/0013697600004670

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Data Science and Engineering (ICDSE 2025), pages 372-378

ISBN: 978-989-758-765-8

Predicting unemployment levels is a critical task

for economic policymakers and researchers.

However, the data used by a number of studies is

already outdated, and they didn’t involve the outliers

caused by the pandemic. Various methods have been

employed by many researchers to predict

unemployment rates, including traditional statistical

models and advanced machine-learning techniques.

Previous researchers have used various methods

to predict unemployment trends in the United States,

including traditional ARIMA models, primary

economic signals, and automatic time series modeling

techniques like Autometrics. Guerard, Thomakos,

and Kyriazi built upon earlier work by applying

Autometrics to improve models for real GDP and

unemployment, accounting for structural breaks and

outliers (Guerard, Thomakos & Kyriazi, 2020). Their

study emphasized the effectiveness of adaptive

learning forecasting and the significance of

incorporating leading indicators. However, the

effects of the COVID-19 period were not included in

their research process, which generated a huge impact

on the global unemployment rate.

Shan Zhong analyzed the U.S. real GDP and

unemployment rate data from 1948 to 2023 using

linear and nonlinear regression and ARIMA models

(Zhong, 2023). The study found that nonlinear

regression more accurately represents the relationship

between these two factors. ARIMA forecasts showed

optimistic future trends with GDP growth and low

unemployment but with wide confidence intervals.

Yurtsever proposed a hybrid model combining

LSTM and GRU deep learning techniques to forecast

unemployment rates in the U.S., U.K., France, and

Italy. Generally, the hybrid model outperformed

standalone LSTM and GRU models, except in Italy,

where GRU performed better. This study highlights

the effectiveness of combining different models to

enhance forecasting performance (Yurtsever, 2023).

Other researchers have also explored hybrid

approaches, such as combining ARIMA with

artificial intelligence methods, which have shown

promising results in reducing prediction errors

(Chakraborty et al., 2021; Ahmad et al., 2021).

Additionally, Xiao et al. revisited earlier forecasting

methodologies to explore relationships between

unemployment rates and leading economic indicators

such as data on weekly jobless claims and the U.S.

Leading Economic Indicator (LEI), demonstrating

that incorporating these variables can enhance

predictive accuracy (Xiao et al., 2022). Montgomery

et al. further emphasized that forecasting accuracy

could be improved by combining multiple time series

methods and carefully accounting for structural

breaks in historical data (Montgomery et al., 1998).

Similarly, Dritsakis and Klazoglou applied the Box-

Jenkins methodology extensively to forecast U.S.

unemployment rates, highlighting its effectiveness

but also acknowledging its limitations when

confronted with structural changes or unprecedented

economic shocks (Dritsakis & Klazoglou, 2018).

These findings collectively reinforce the necessity of

exploring diverse forecasting methodologies to better

capture complex labor market dynamics.

This study seeks to fill this research gap by

comparing three well-known time series forecasting

methods to predict unemployment trends in the

United States: ARIMA, LSTM neural networks, and

intervention approaches. By evaluating these diverse

models using the recent data from 1978 to 2023 and

considering their performance across different

economic conditions, this study seeks to point out

which model is best fitted to predict unemployment

trends and offer new perspectives on how effectively

different forecasting approaches perform in the

current financial landscape.

2 DATA AND METHOD

2.1 Data Collection and Description

The dataset used in this analysis contains the

unemployment rate for the 16-24 age group from

December 1978 to July 2023. The data was cleaned

and preprocessed by removing missing values,

converting the date column to a date format, and

arranging the data in chronological order. The dataset

provides a comprehensive view of the trends and

patterns in youth unemployment over more than 40

years.

2.2 Methods and Principles

This study employs several methodologies to analyze

and predict unemployment rates in the United States.

The primary methods are as follows.

2.2.1 Time Series Visualization

Time series visualization is a crucial step in

understanding the behavior of the data over time. This

involves graphically representing the unemployment

rate over time to identify trends, seasonal patterns,

and significant events. Visual inspection helps in

understanding the overall behavior of the data.

Firstly, this study presents a time series graph

depicting unemployment rates among younger age

Comparative Analysis of Time Series Models for Forecasting the U.S. Unemployment Rate: A Study of ARIMA, LSTM, and Intervention

Approaches

373

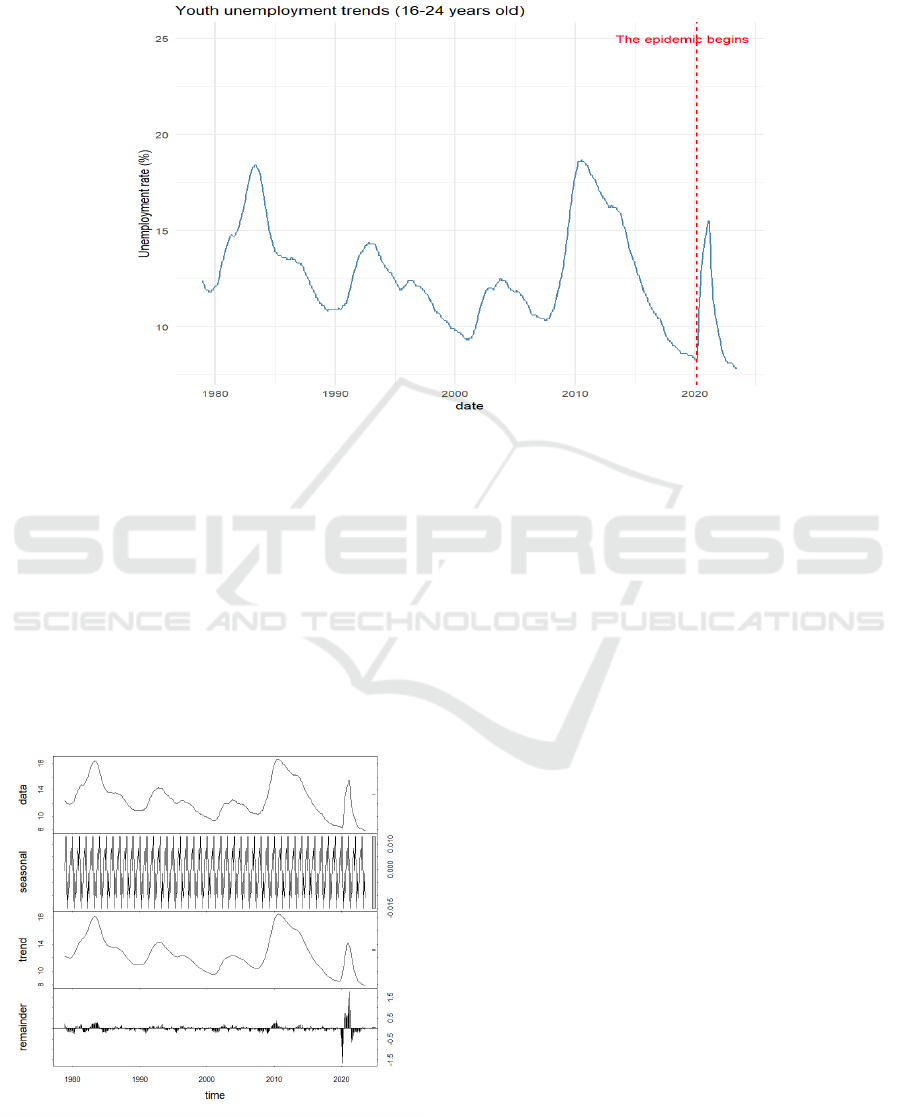
groups. The unemployment rate for the 16-24 age

group was plotted over time, as shown in Figure 1, a

clear trend and seasonal patterns were displayed. A

vertical line was added to mark the start of the

pandemic in March 2020, was marked to observe its

impact on the trend.

Figure. 1 Youth Unemployment Trends (16-24 years old). (Picture credit: Original)

2.2.2 Seasonal Decomposition

Seasonal decomposition, using techniques such as the

STL method, breaks down the time series into its

underlying components: trend, seasonal, and residual.

This decomposition aids in understanding the

underlying structure of the data. In this study, the time

series was decomposed into trend, seasonal, and

residual components using the STL method, as shown

in Figure 2. This provided valuable insights into the

underlying structure of the data.

Figure. 2 Seasonal Decomposition by STL model. (Picture

credit: Original)

2.2.3 Intervention Analysis

Intervention analysis examines how particular

incidents, like the financial crisis in 2008 and the

COVID-19 pandemic, influence changes in

unemployment rates. Intervention analysis helps in

quantifying the effects of these events.

In this paper, a linear regression model was built

to analyze the impact of the financial crisis in 2008

and the 2020 pandemic on the unemployment rate.

The model included dummy variables for these events

and a lagged term of the unemployment rate and also

allowed for the quantification of their impacts on the

unemployment rate at the same time.

2.2.4 ARIMA Model

The ARIMA approach is widely utilized for

forecasting time series data. It integrates

autoregressive (AR), differencing (I), and moving

average (MA) elements to effectively identify linear

dependencies and seasonal variations within the

dataset. In this literature, the ARIMA model was

applied to forecast the unemployment rate. The data

was differenced to achieve stationarity, and the

optimal ARIMA model was selected based on the

AIC values.

2.2.5 LSTM Model

Long Short-Term Memory (LSTM) networks are a

type of recurrent neural network (RNN) that are

ICDSE 2025 - The International Conference on Data Science and Engineering

374

particularly effective for time series forecasting. They

are capable of learning long-term dependencies in the

data. This research applied the LSTM approach to

predict unemployment rates. The dataset underwent

normalization before being divided into training and

testing subsets. The training subset was utilized to

build the model, while the testing subset was

employed to assess its performance.

2.3 Evaluation Metrics

The average squared difference between the expected

and actual values is measured by the Mean Squared

Error, or MSE. It is a frequently used indicator to

assess how well regression models perform.

Root Mean Squared Error (RMSE) is calculated

as the square root of Mean Squared Error (MSE) and

measures the size of prediction errors, expressed in

the original units of the data.

Mean Absolute Error (MAE) calculates the mean

of the absolute differences between observed and

predicted values, and it is more robust against outliers

than MSE.

Mean Absolute Percentage Error (MAPE)

calculates the average of absolute differences

between actual and predicted values expressed as

percentages, offering a relative assessment of

forecasting accuracy.

Mean Absolute Scaled Error (MASE) evaluates a

model's accuracy by comparing its prediction errors

against errors from a simple baseline (naive forecast),

resulting in a standardized performance metric.

3 RESULTS AND DISCUSSION

3.1 Intervention Analysis

The intervention analysis model was designed to

assess the impact of significant events on the

unemployment rate. The results indicate that the 2008

financial crisis had a substantial and statistically

significant impact on the unemployment rate, with a

coefficient of 0.32035. This suggests that the crisis

led to a marked increase in unemployment.

Conversely, the 2020 pandemic had a much smaller

and statistically insignificant impact, with a

coefficient of 0.01223186. This finding may be

attributed to government interventions, such as

stimulus packages and employment support

programs, which mitigated the pandemic's effects on

employment.

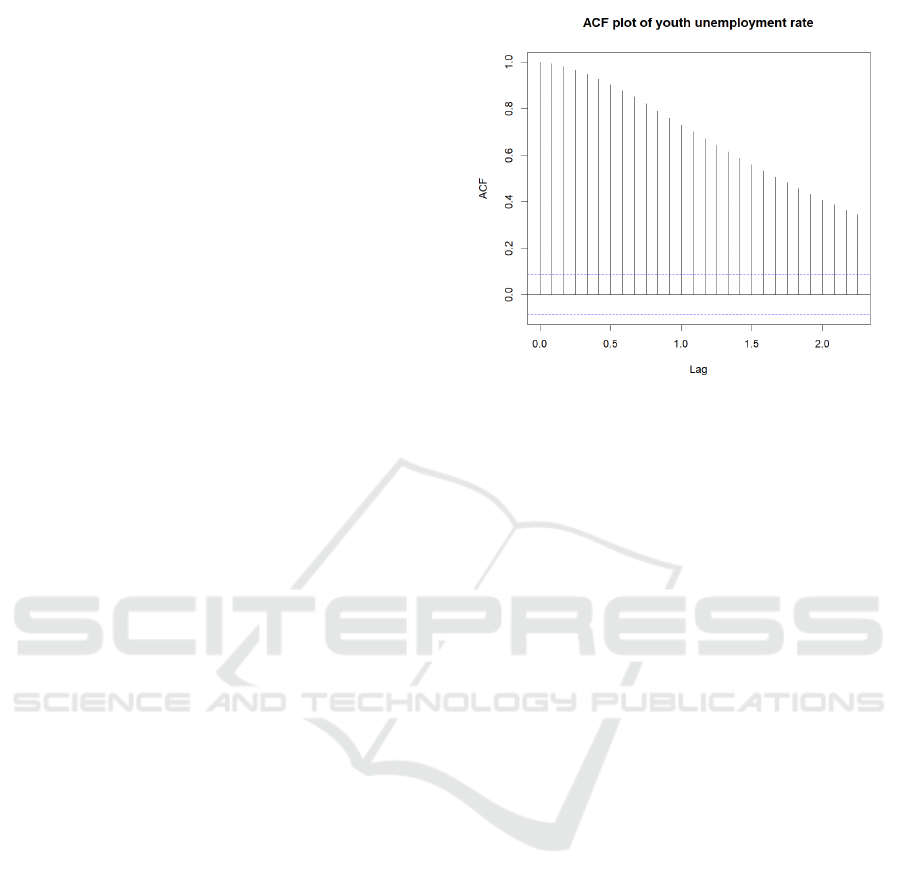
Figure. 3 ACF Plot of Youth Unemployment Rate. (Picture

credit: Original)

Figure. 3 presents the ACF plot for the original

youth unemployment rate data (ages 16-24). The

ACF plot visually represents the correlation between

observations at different lag intervals. The horizontal

axis represents different lag values, while the vertical

axis shows autocorrelation coefficients. The shaded

area indicates the confidence interval bounds;

correlations extending beyond these bounds are

statistically significant. From Figure 3, high initial

autocorrelation is observed that there is a very high

autocorrelation at lag 0 (as expected, always equal to

1), followed by gradually decreasing autocorrelations

at subsequent lags. This indicates strong persistence

in the unemployment rate data, meaning past

unemployment rates heavily influence current rates.

It is also noticeable that notable periodic spikes at

regular intervals (approximately every 12 lags)

suggest clear seasonal patterns. This aligns with

typical labor market dynamics where youth

unemployment rates fluctuate seasonally due to

school calendars, holidays, and seasonal employment

opportunities.

In summary, Figure 3 illustrates that the original

unemployment series is non-stationary due to

persistent trends and seasonal fluctuations. These

characteristics necessitate differencing or other

transformations before applying forecasting models

such as ARIMA.

Comparative Analysis of Time Series Models for Forecasting the U.S. Unemployment Rate: A Study of ARIMA, LSTM, and Intervention

Approaches

375

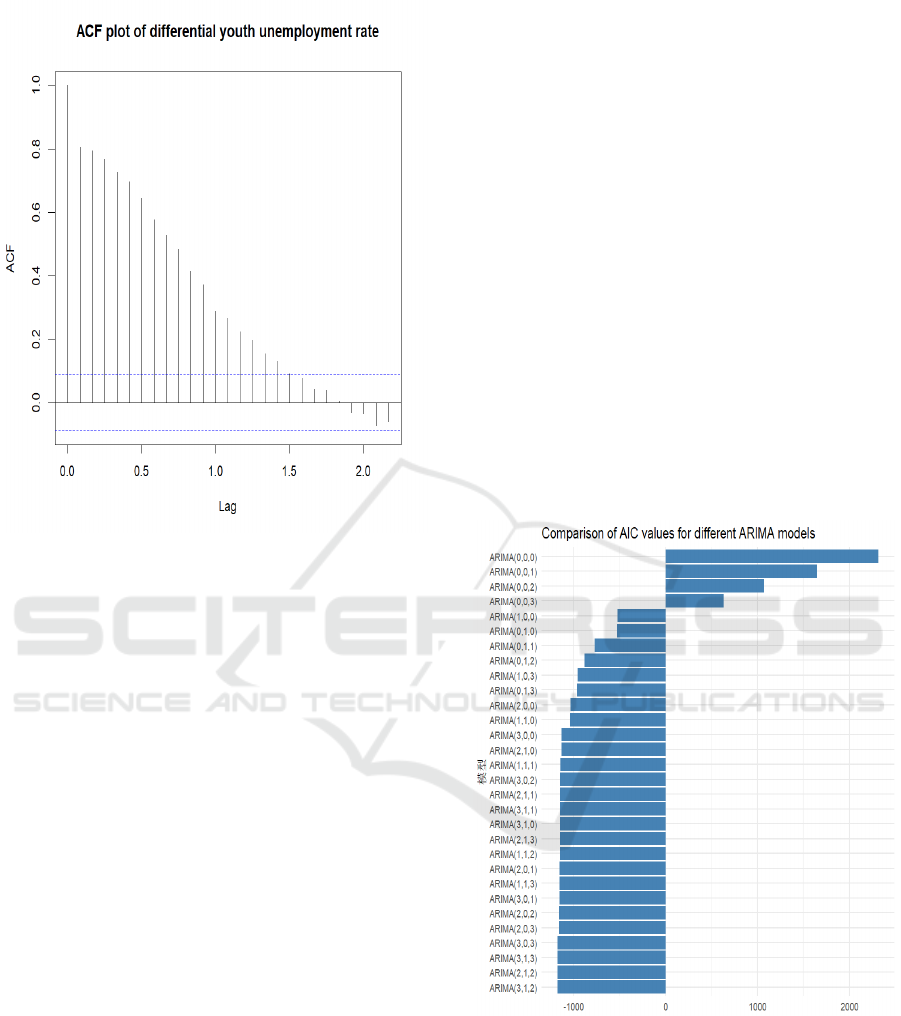
Figure. 4 ACF Plot of Differential Youth Unemployment

Rate. (Picture credit: Original)

Figure 4 shows the ACF plot after applying first-

order differencing to the youth unemployment rate

data. Differencing is a common step in achieving

stationarity by removing trends and stabilizing mean

values. It is observed that there is a significant

reduction in autocorrelation. Compared to Figure 3,

the autocorrelation values drop sharply after

differencing. This substantial reduction indicates that

differencing effectively removed much of the trend

component present in the original data. Furthermore,

unlike Figure 3, Figure 4 displays a rapid decline of

autocorrelation values toward zero after just a few

lags. This rapid decay pattern confirms that

differencing successfully transformed the series into

a stationary one, which is suitable for ARIMA

modeling.

In summary, Figure 4 demonstrates that

differencing has effectively addressed non-

stationarity caused by trends but has not completely

eliminated seasonal effects. Therefore, although

intervention analysis can now be reliably performed

on this stationary series, additional modeling

adjustments may still be beneficial for capturing

remaining seasonal dynamics accurately. These

findings justify using ARIMA models with

differencing (as performed in this study).

3.2 ARIMA Model

Figure 5 below in the research paper provides a

comparative visualization of Akaike Information

Criterion (AIC) values calculated for different

ARIMA models tested during the model selection

process. The ARIMA model selected based on the

lowest AIC value was ARIMA (3,1,2), with an AIC

of -1178.4186. This model was chosen because lower

AIC values suggest a better trade-off between

complexity and explanatory power, which indicates it

achieves an optimal balance between capturing

sufficient patterns in youth unemployment data and

avoiding excessive complexity. Meanwhile, it has the

ability to effectively capture the linear relationships

and seasonal patterns in the data. However, the

model's performance on the test set revealed a

relatively high RMSE of 3.51754016, indicating that

the predictions were not highly accurate. This

suggests that while ARIMA models are useful for

understanding linear trends, they may struggle with

complex or non-linear dynamics.

Figure. 5 Comparison of AIC Values for Different ARIMA

Models. (Picture credit: Original)

3.3 LSTM Model

The LSTM model's performance was evaluated using

RMSE. The RMSE for the LSTM model was

1.030382, which is significantly lower than the

ARIMA model's RMSE on the test set. This indicates

that the LSTM model yielded more precise

ICDSE 2025 - The International Conference on Data Science and Engineering

376

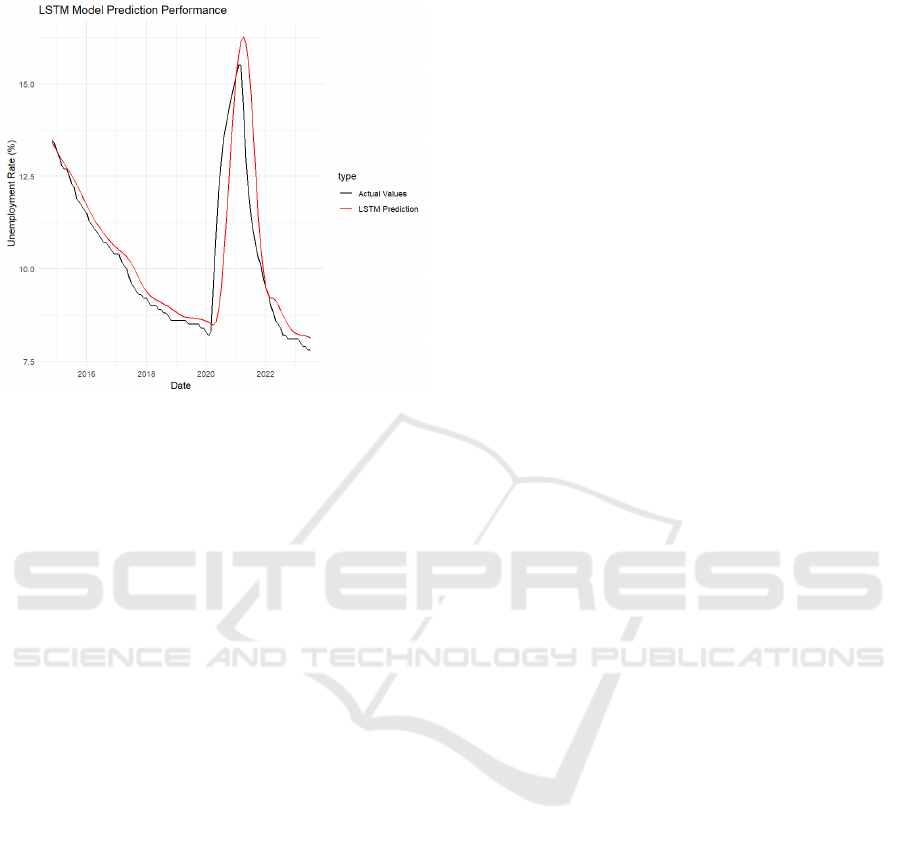
predictions. It demonstrated enhanced performance

compared to the ARIMA model.

Figure. 6 LSTM Model Prediction Performance. (Picture

credit: Original)

However, the LSTM model's predictions, as

shown in Figure. 6, exhibit a hysteresis quality,

indicating a lagged response to changes in the actual

unemployment rate data. This phenomenon can be

attributed to the model's design, which prioritizes

capturing long-term dependencies over immediate

adjustments to new trends. To improve the model's

responsiveness in the future, further research could

focus on refining the model architecture or optimizing

training parameters to better adapt to rapid changes in

economic conditions.

3.4 Comparison of Results

3.4.1 Intervention Analysis

The intervention analysis results indicated clear

differences in the impacts of major economic events

on youth unemployment rates. Specifically, the 2008

Financial Crisis: The unemployment rate increased

significantly during the crisis, as indicated by the

coefficient of 0.32035. The considerable effect of this

event on unemployment rates highlights the necessity

of including external shocks in predictive models. In

contrast, the 2020 Pandemic, with a coefficient of

0.01223186, indicates a negligible impact on the

unemployment rate, which may be due to government

interventions or other factors, such as stimulus

packages, employment subsidies, and targeted

economic support programs implemented during the

pandemic period, which effectively cushioning the

labor market from severe disruptions. The minimal

impact observed may reflect effective policy

interventions, highlighting the need for adaptive

forecasting approaches that account for such factors.

3.4.2 ARIMA Model

Through model selection based on AIC, the ARIMA

(3,1,2) model had the lowest AIC value, indicating it

was the best fit among the models tested and was

suitable for capturing linear relationships and

seasonal patterns present in youth unemployment

data. However, for its prediction Error: The RMSE of

3.51754016 on the test set suggests that the model's

predictions were not very accurate. The high RMSE

suggests limitations in addressing complex scenarios,

particularly when nonlinearities and structural breaks

exist within the historical data.

3.4.3 LSTM Model

In comparison to ARIMA, the LSTM model achieved

a notably lower RMSE of around 1.030382 on test

data. The lower RMSE indicates better performance

in capturing non-linear dynamics. This improved

accuracy highlights LSTM's strength in capturing

long-term nonlinear dependencies and complex

temporal patterns inherent in youth unemployment

rates. Nevertheless, despite its overall better

predictive capability, the LSTM model exhibited a

delayed response or hysteresis effect when reacting to

sudden shifts or structural changes in unemployment

trends.

3.5 Discussion

The results of this study highlight the importance of

selecting appropriate time series models based on the

complexity of the data. While ARIMA models are

effective for linear trends, LSTM models offer

superior performance in scenarios with non-linear

relationships. The intervention analysis underscores

the need to incorporate significant events into

forecasting models to improve accuracy. These

findings have implications for policymakers seeking

to improve their ability to foresee and make well-

informed choices regarding labor market initiatives.

4 CONCLUSIONS

This literature analyses the youth unemployment rate

data using various methods and provides valuable

insights into the trends and impacts of significant

events on the unemployment rate. The intervention

Comparative Analysis of Time Series Models for Forecasting the U.S. Unemployment Rate: A Study of ARIMA, LSTM, and Intervention

Approaches

377

analysis highlighted the significant impact of the

2008 financial crisis, while the 2020 pandemic had a

smaller and statistically insignificant impact. The

ARIMA model provided a baseline for forecasting,

but the LSTM model outperformed it in terms of

prediction accuracy, as indicated by the lower RMSE

value. The results suggest that deep learning models

like LSTM can be more effective for time series

forecasting in complex and non-linear scenarios. This

study has limitations in involving more related

control variables to forecast the unemployment rate in

the US because the unemployment rate is affected by

factors such as different genders, different races, and

the financial crisis period in 2008. If all these highly

correlated factors are included in this research, the

results should be more precise and accurate.

Therefore, the shortcoming of this research is not

taking into account all of these correlated control

variables. Additionally, as the LSTM exhibits a

hysteresis quality, other changes such as adjusting the

model architecture and improving data preprocessing

are required in future studies. In the future, this study

will verify more corresponding factors which perform

a big impact on the unemployment rate. Additionally,

more forecasting models like linear and non-linear

regression models would be applied to get the best-

performing model to predict the unemployment rate

so that governments and policymakers around the

world could look forward to future changes in the

unemployment rate and introduce relevant policies in

advance to stabilize the economic conditions.

REFERENCES

Barnichon, R., & Nekarda, C. J. (2012). The ins and outs of

forecasting unemployment: Using labor force flows to

forecast the labor market. Journal of Economic

Perspectives, 26(3), 45-66.

Douglas, S., & Zahed, M. (2024). Forecasting U.S.

unemployment rates using ARIMA: A time series

analysis from 1948 to 2019. SESUG 2024 Proceedings.

Retrieved from

https://sesug.org/proceedings/sesug_2024_SAAG/Pres

entationSummaries/Papers/148_Final_PDF.pdf

Dritsakis, N., & Klazoglou, P. (2018). Forecasting

unemployment rates in USA using Box-Jenkins

methodology. International Journal of Economics and

Financial Issues, 8(1), 9.

Gostkowski, M., & Rokicki, T. (2021). Forecasting the

unemployment rate: Application of selected prediction

methods. European Research Studies Journal,

XXIV(3), 985-1000.

Guerard, J., Thomakos, D., & Kyriazi, F. (2019). Automatic

time series modeling and forecasting: A replication case

study of forecasting real GDP, the unemployment rate,

and the impact of leading economic indicators. Cogent

Economics & Finance, 7(1), 1-20.

Guerard, J., Thomakos, D., & Kyriazi, F. (2020). Automatic

time series modeling and forecasting: A replication case

study of forecasting real GDP, the unemployment rate

and the impact of leading economic indicators. Cogent

Economics & Finance, 8(1), 1759483.

Montgomery, A. L., Zarnowitz, V., Tsay, R., & Tiao, G. C.

(1998). Forecasting the U.S. unemployment rate.

Journal of the American Statistical Association,

93(442), 478-493.

Xiao, H., Chen, R., & Guerard Jr, J. B. (2022). Forecasting

the U.S. unemployment rate: Another look. Wilmott

Magazine, November, 20-31.

Yurtsever, M. (2023). Unemployment rate forecasting:

LSTM-GRU hybrid approach. Journal for Labour

Market Research, 57(1), 1-9.

Zhong, S. (2023). The research and forecasts on real GDP

growth and the unemployment rate in the United States.

EMFRM, 2023, 159-165.

ICDSE 2025 - The International Conference on Data Science and Engineering

378