Point Cloud Registration for Visual Geo-Referenced Localization

Between Aerial and Ground Robots

Gonzalo Garcia

and Azim Eskandarian

College of Engineering, Virginia Commonwealth University, 601 West Main Street, Richmond, U.S.A.

Keywords:

Monocular Visual SLAM, Autonomous Vehicles, Point Clouds.

Abstract:

Cooperative perception between aerial and ground robots relies on the accurate alignment of spatial data col-

lected from different platforms, often operating under diverse viewpoints and sensor constraints. In this work,

point cloud registration techniques for monocular visual SLAM-generated maps are investigated, which are

common in lightweight autonomous systems due to their low cost and sensor simplicity. However, monocular

visual SLAM outputs are typically sparse and suffer from scale ambiguity, posing signiﬁcant challenges for

map fusion. We evaluate registration pipelines combining coarse global feature matching with local reﬁne-

ment methods, including point-to-plane and plane-to-plane Iterative Closest Point alignments, to address these

issues. Our approach emphasizes robustness to differences in scale, density, and perspective. Additionally, we

assess the consistency of the resulting estimated trajectories to support geo-referenced localization across plat-

forms. Experimental results using datasets from both aerial and ground robots demonstrate that the proposed

methods improve spatial coherence by a factor of over 4 based on statistical metrics, and enable collaborative

mapping and localization in GNSS-intermittent environments. This work can contribute to advancing multi-

robot coordination for real-world tasks such as infrastructure inspection, exploration, and disaster response.

1 INTRODUCTION

Recent advances in autonomous robotics have in-

creasingly emphasized the interaction between aerial

and ground robots for complex tasks such as envi-

ronmental monitoring, infrastructure inspection, and

disaster response (Achtelik et al., 2011; Nex and Re-

mondino, 2014). In these heterogeneous systems, col-

laboration is critically dependent on a shared spatial

understanding of the environment. A central com-

ponent of this is the alignment of 3D data gener-

ated by each platform, typically in the form of sparse

or semi-dense point clouds. However, when relying

on monocular visual Simultaneous Localization and

Mapping (vSLAM) systems (Mur-Artal and Tard

os,

2017), common in lightweight, and low-power plat-

forms, the resulting point clouds are often subject to

scale ambiguity, noise, and viewpoint discrepancies,

making accurate point cloud registration a non-trivial

challenge (Kim and Kim, 2018).

Monocular vSLAM generates 3D maps from a se-

quence of 2D images without requiring depth sen-

https://orcid.org/0000-0001-9968-960X

https://orcid.org/0000-0002-4117-7692

sors or stereo systems, making it ideal for lightweight

aerial and ground autonomous vehicles. However,

due to its reliance on structure-from-motion, monocu-

lar SLAM often produces sparse and scale-ambiguous

point clouds (Scaramuzza and Fraundorfer, 2011).

When both aerial and ground robots use monoc-

ular vSLAM independently, fusing their respective

maps requires robust inter-frame alignment, capable

of compensating for different scales, viewing angles,

and reconstruction densities. This motivates the de-

velopment of point cloud registration techniques that

can operate effectively under such constraints to en-

able cooperative perception and geo-referenced local-

ization (Zhou et al., 2020).

This paper explores point cloud registration meth-

ods tailored for the alignment of monocular SLAM-

generated maps from aerial and ground robots. We

evaluated registration pipelines that combine coarse

feature-based alignment with ﬁne-grained reﬁnement

techniques such as point-to-plane ICP, and plane-to-

plane ICP (Rusinkiewicz and Levoy, 2001), all while

addressing the unique challenges posed by monocular

data, including inconsistent scale and sparse geome-

try. We also investigate the creation and consistency

of estimated trajectories as part of the localization as-

Garcia, G. and Eskandarian, A.

Point Cloud Registration for Visual Geo-Referenced Localization Between Aerial and Ground Robots.

DOI: 10.5220/0013693500003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 211-218

ISBN: 978-989-758-770-2; ISSN: 2184-2809

211

pect of SLAM (Campos et al., 2021).

Our framework emphasizes cross-platform map

fusion by aligning independently generated vSLAM

point clouds into a uniﬁed coordinate system. This

enables collaborative localization, cooperative per-

ception, global map construction, and improved task

coordination between aerial and ground agents. Ex-

perimental indoor results demonstrate the viability of

our approach, showcasing improved alignment accu-

racy and mutual localization despite scale inconsis-

tencies and varying sensor perspectives.

By focusing on vSLAM-based point cloud reg-

istration, this work contributes to enabling more ac-

cessible and lightweight cooperative robotic systems,

empowering teams of monocular camera-equipped

aerial and ground-based autonomous vehicles to share

a uniﬁed understanding of their surroundings with

minimal sensor overhead.

2 VSLAM THEORY

This section reviews the essential theory required for

implementing monocular vSLAM and for compar-

ing two point clouds generated by autonomous ve-

hicles—one ground-based and one aerial—over the

same geographical area. One of the point clouds is

generated while the corresponding robot simultane-

ously estimates its position from a global positioning

system, making this point cloud geo-referenced. A

second point cloud, captured by the other vehicle, is

then registered to the ﬁrst one using point cloud reg-

istration techniques (Jian and Vemuri, 2011). This al-

lows the second set of points to get geo-referenced,

without requiring the second robot to have explicit

knowledge of its own position.

2.1 Monocular VSLAM

SLAM, and in particular monocular visual SLAM,

performs two tightly coupled tasks during its opera-

tion: (1) constructing a 3D map of the environment

based on visual features extracted from a sequence

of images, typically represented as point clouds, and

(2) estimating the camera’s position by localizing it

within the evolving map. These recursive processes

rely heavily on two core concepts derived from stereo

vision: (i) calibrating a pair of consecutive, initially

uncalibrated images, and (ii) estimating the relative

pose (translation and orientation) of the camera be-

tween the two frames.

2.2 Stereo Calibration of Images

Although the theory was originally developed for two

separate cameras in arbitrary poses capturing overlap-

ping scenes, it can also be applied to a single cal-

ibrated camera moving through space, capturing a

sequence of images, and using pairs of consecutive

frames, effectively simulating the condition of spa-

tially separated cameras.

Calibrated stereo, often referred to as simple

stereo, is a special case of the uncalibrated stereo

scenario in which the two cameras are aligned with

identical orientations and a translation restricted to

the horizontal axis of the image plane, known as the

horizontal baseline b. Using the camera projection

matrix (Hartley and Zisserman, 2003), a system of

equations can be derived to estimate the 3D position

(x, y, z) of an object that appears in both images. This

task, known as the Correspondence Problem (Bach

and Aggarwal, 1988), is solved based on the matching

of the pixel coordinates between the two frames:

x =

b(u

− o

)

− u

, y =

b f

− o

)

− u

)

, z =

b f

− u

(1)

with ( f

, f

) the horizontal and vertical components of

the focal length of the camera, (o

, o

), the principal

point, and (u

, v

) and (u

, v

) the pixel coordinates of

the object in the left and right images (considering the

camera is moving from left to right).

When the camera is subjected to an arbitrary mo-

tion, the simple stereo calibration condition is lost,

and it has to be calibrated before applying the equa-

tions in (1). This process is called Image Rectiﬁcation

(Szeliski, 2010).

Image rectiﬁcation in computer vision refers to

the process of transforming images captured from two

different viewpoints so that the corresponding points

now lie on the same horizontal line, that is, they

share the same vertical coordinate v. This transfor-

mation simpliﬁes the correspondence problem by re-

ducing the search for matching points from a two-

dimensional space to a one-dimensional search along

the common lines. As a result, the problem becomes

equivalent to a simple stereo conﬁguration. Rectiﬁ-

cation relies on the principles of Epipolar geometry

(Hartley and Zisserman, 2003).

Once the image pairs are rectiﬁed, the correspon-

dence problem can be addressed to generate candidate

3D points for the point cloud, using information ex-

tracted from each image individually. The key steps

are as follows: 1) Image distortion correction: Radial

distortion is typically corrected using the camera’s in-

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

212

trinsic parameters in (2),

camera





0 o

0 f

0 0 1





(2)

obtained through a process known as camera intrin-

sic calibration (Zhang, 2000). 2) Feature detection:

Salient features such as corners or regions with strong

gradients and textures are identiﬁed in each image.

In this work, 3D point associations are derived using

the Oriented FAST and Rotated BRIEF (ORB) fea-

ture detection method (Rublee et al., 2011). 3) Point

sampling: A uniformly spaced subset of the detected

feature points is selected to ensure even spatial distri-

bution. 4) Feature description: A feature extraction

algorithm, such as SIFT or SURF (Lowe, 2004; Bay

et al., 2006), is applied to compute feature descrip-

tors. These descriptors represent local image patches

around keypoints as numerical or binary vectors, fa-

cilitating reliable matching across views.

The next step involves matching the detected fea-

tures between the two images. This is typically per-

formed by computing the Hamming distances be-

tween all feature descriptors in one image and those

in the other, and then associating pairs based on the

minimum distance. From the resulting set of matched

pairs, the Essential matrix E and the Fundamental ma-

trix F are computed—both of which are fundamental

constructs in Epipolar geometry (Hartley and Zisser-

man, 2003).

2.3 Pose Calculation

Using these matrices, the pose of the camera at the

time the second image was captured can be estimated

relative to its pose during the ﬁrst image. This process

yields the translation components T = [t

, t

]

and

the rotation matrix R, which are essential for gener-

ating the camera’s localization trajectory as it moves

through the environment.

Given a set of matching points shared between the

two images, (u

, v

) and (u

, v

), the Essential matrix

E in (3), and the Fundamental matrix F in (4), can be

estimated by solving the following equation, which

encapsulates the principles of Epipolar geometry:





−T

−1

| {z }





= 0 (3)









= 0 (4)

Once the Essential matrix E is determined, the

Epipolar constraint further deﬁnes the following re-

lationship:

E =





0 −t

−t













| {z }

(5)

This constraint (5) enables the recovery of the rel-

ative camera pose—speciﬁcally, the translation vec-

tor T and rotation matrix R, between the two views,

by doing singular value decomposition. This pose

estimation process is repeated across consecutive or

near-consecutive pairs of frames. By chaining the re-

sulting transformations, a 3D trajectory of the camera

can be constructed over time, representing the local-

ization component of the vSLAM system.

2.4 Point Cloud Registration Concept

Once the two point clouds are generated, the registra-

tion process can be initiated. The ﬁrst point cloud,

produced by the ground vehicle, is geo-referenced

through an external positioning system that provides

accurate location data. The second point cloud, cap-

tured by the aerial drone, lacks global positional infor-

mation. The goal is to geo-reference the drone’s point

cloud by aligning it with the car’s geo-referenced map

using point cloud registration techniques.

The registration method employed in this work is

the Iterative Closest Point (ICP) algorithm, a widely

used technique for aligning two 3D point clouds. The

objective of ICP is to estimate the rigid transforma-

tion—comprising rotation and translation—that best

aligns a source point cloud to a target point cloud

by establishing point-to-point correspondences. The

standard ICP pipeline involves the following steps:

(1) Initial Alignment: Begin with an initial transfor-

mation guess, typically the identity matrix or a prior

estimate; (2) Closest Point Matching: For each point

in the source cloud, identify the closest point in the

target cloud; (3) Transformation Estimation: Com-

pute the rigid transformation that minimizes the mean

squared error between matched point pairs; (4) Apply

Transformation: Update the source point cloud using

the estimated transformation; and (5) Iteration: Re-

peat steps 2 through 4 until convergence, deﬁned by a

threshold on the error reduction or a maximum num-

ber of iterations.

Several ICP variants exist based on the error met-

ric used, (Rusinkiewicz and Levoy, 2001). In partic-

ular, point-to-plane ICP minimizes the distance from

each point in the source cloud to the tangent plane

deﬁned by the corresponding point and its local sur-

face normal in the target cloud. This approach lever-

ages surface geometry for improved convergence, es-

pecially in structured environments. Plane-to-plane

Point Cloud Registration for Visual Geo-Referenced Localization Between Aerial and Ground Robots

213

ICP extends this concept by incorporating planar ap-

proximations in both point clouds, minimizing the

misalignment between corresponding local surface

patches: Given a ﬁxed point cloud p

, and a pair-wise

matched moving point cloud q

, i = 1 . . . N, plane-to-

plane ICP estimates the 3D rigid transformation A

A =



R T

0 1



(6)

by minimizing the following cost function in terms of

tangent planes around each pair of points, p

and q

E(R, T) =

∑

i=1



− (R · p

+ T))

⊤



⊤

∥

⊤

∥



(7)

with n

and n

the surface normals at them. These

variants enhance robustness and accuracy in scenar-

ios involving sparse or noisy data, such as those gen-

erated by monocular vSLAM. These transformations

deﬁne the pose of the second point cloud relative to

the reference frame of the ﬁrst point cloud, aligning

the two datasets within a common coordinate system.

Figure 1 shows a pipeline of the process, including

data collection, point cloud creation, map and trajec-

tory determination, registration, geo-referencing, and

alignment:

Figure 1: Pipeline of the Visual Geo-referenced Localiza-

tion via Point Cloud Registration.

3 EXPERIMENT SETUP

The proof of concept for this cooperative percep-

tion research was conducted indoors using two au-

tonomous vehicles: a small ground robot and a nano-

drone. The ground vehicle is the Wiﬁbot Lab V4

(https://www.wiﬁbot.com), a four-wheel drive plat-

form, and the aerial platform is the Crazyﬂie 2.1 +, a

lightweight nanodrone (www.bitcraze.io). These plat-

forms are illustrated in Figures 2 and 3. The Crazyﬂie

2.1+ weighs only 27 grams and measures less than 5.5

inches from rotor to rotor, making it ideal for indoor

experimentation and agile ﬂight.

Figure 2: Nano Drone Crazyﬂie 2.1+.

Both vehicles navigate autonomously through the

lab, collecting visual data from the same surrounding

area. Each robot is equipped with an onboard cam-

era for performing its own monocular vSLAM com-

putations. In addition, both are capable of determin-

ing their positions via an external positioning system.

This system consists of a ceiling-mounted camera that

tracks each vehicle as it moves and is connected to a

Lab computer that processes the video feed and com-

putes their positions.

Figure 3: White markers centroids are tracked to obtain the

robot position and heading.

A MATLAB script running on the Lab’s computer

initializes the tracking process. For the drone, a single

white marker is placed at its center. For the ground

vehicle, two white markers are afﬁxed to the top of

the robot. These markers are detected and tracked us-

ing an alpha-beta ﬁlter that relies on black-and-white

contrast with the background during the experiments

(see Figure 3). By calculating the centroids of these

markers, the system can estimate the ground robot’s

position and heading.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

214

Figure 4: Grayscale converted image from Figure 3 (before

threshold Comparison).

Marker detection and tracking begin by convert-

ing the RGB image to grayscale, followed by apply-

ing a pixel-value threshold determined through exper-

imentation. Using the previously estimated marker

positions, a rectangular mask is applied to the binary

image to discard detections outside these predeﬁned

regions. An additional ﬁltering step checks that the

pixel count for each detected marker falls within a

speciﬁed range. The grayscale image is shown in Fig-

ure 4 (before applying the threshold). Small spuri-

ous detections are removed, while larger regions, such

as intersection boundaries, remain visible. To pre-

vent interference from these unwanted detections, a

masking procedure is applied once marker tracking

is initialized. This masking ﬁlters out all detections

outside a rectangular region centered on the mark-

ers. These rectangles, with sizes determined by ex-

periment, move dynamically with the markers as the

alpha-beta ﬁlter predicts and updates their estimated

positions over time, maintaining the rectangles cen-

tered on the detected markers.

The test is designed as follows: The ground vehi-

cle navigates following a trajectory while recording a

video of its surroundings. This video is processed to

generate a point cloud and a trajectory, which are ref-

erenced to the initial orientation of the camera. These

can then be geo-referenced to the Lab’s origin by us-

ing the external positioning system. As a feature of

vSLAM, the ﬁrst camera orientation is maintained

as the reference for all subsequent poses. This geo-

referenced point cloud will serve as the baseline for

geo-referencing the drone’s point cloud. The drone

processes its own video similarly but does not rely

on external positioning data; instead, it registers the

point cloud with the point cloud of the ground vehicle

to correct its pose and achieve geo-referencing. The

externally calculated position of the drone, obtained

by the Lab’s positioning system, is only used in this

work to validate the precision of this approach. The

objective is to obtain a geo-referenced trajectory of an

autonomous vehicle through point cloud registration

with an existing geo-referenced point cloud of the en-

vironment. It is important to note that the roles of the

autonomous vehicles are interchangeable and could

be reversed.

4 EXPERIMENTAL RESULTS

This Section presents the main results of the research.

4.1 Fixed Point Cloud Calculation

Figure 5: Car trajectory. The starting point is at the left.

Figure 5 shows the trajectory of the ground vehicle

during the visual mapping obtained by the Lab po-

sitioning system. The effect of radial distortion pro-

duced by the camera can be seen, which is corrected

internally during the tracking process. The car started

on the lower left side of the image and moved to the

right while following the white lane, at a nearly con-

stant speed. It took a video of the scene to its right.

The position of the car is the midpoint between the

two markers, and the heading (not shown here) is ob-

tained by the angle subtended by them (Figure 3).

In this case, the ﬁrst robot is required to serve as

a reference for the point cloud registration of the sec-

ond robot. For the integrity of these tests, it is as-

sumed that the surrounding scene remains unchanged

between the times the two videos are recorded.

As mentioned above, during the motion of the car,

a video sequence (that is, a series of images) is cap-

tured of the surroundings of the Laboratory, speciﬁ-

cally on the right side of the vehicle. The camera is

Point Cloud Registration for Visual Geo-Referenced Localization Between Aerial and Ground Robots

215

Figure 6: Superposition of Images Covering the Span of the

Video Captured from the Car.

mounted in such a way that it is rotated 90 degrees

to the right from the forward direction of the car. To

provide an idea of the scene perceived by the robot

while moving, a rough panoramic view was created

by quickly stitching together the ﬁrst, last, and inter-

mediate frames from the video. This panoramic com-

posite is shown in Figure 6.

Figure 7: Point Cloud and Trajectory (starting at the right

of the graph) Captured by vSLAM from Car.

The video captured by the car, along with its cor-

responding positional data, is processed to generate a

point cloud that is geo-referenced to the Lab’s coordi-

nate system. The intrinsic matrix of the camera K

car

used for this computation, is obtained by a prior cal-

ibration process with ( f

= 479.75, f

= 479.92, o

323.18, o

= 177.88) in pixels. The video consisted

of 388 grayscale images, each with a resolution of

640 × 360 pixels. Figure 7 displays the point cloud

generated from this video. The resulting 3D points

are geo-referenced to the Lab’s coordinate system us-

ing the global position of the car.

4.2 Moving Point Cloud Calculation

The drone ﬂew over the same region of the Lab, using

its onboard camera to capture the surrounding envi-

ronment. It took off vertically to a height of approx-

imately 0.5 meters, then moved horizontally like the

ground vehicle, before landing vertically. Figure 8

shows the trajectory of the drone, as recorded by the

Lab’s positioning system. The drone video had 399

Figure 8: Drone’s ﬂight trajectory. The starting point is to

the left of the Trajectory.

Figure 9: Superposition of Images Covering the Span of the

Video Captured from the Drone.

images with a resolution of 324 × 244 pixels. Its in-

trinsic matrix K

drone

is given by ( f

= 180.95, f

180.94, o

= 159.23, o

= 155.72).

A panoramic view is shown in Figure 9. Feature

extraction and matching between consecutive frames

are a critical part of the vSLAM process.

Feature extraction returns descriptors, along with

their corresponding locations from a binary or inten-

sity image. These descriptors are computed from the

pixels surrounding each interest point, which is de-

ﬁned by a single-point location representing the cen-

ter of a local neighborhood. The speciﬁc method used

to extract descriptors depends on the class or type of

the input points provided.

Then the matching step is used to identify and

match corresponding feature descriptors between two

sets of interest points extracted from images. It com-

pares the feature vectors and ﬁnds pairs that are most

similar according to a speciﬁed distance metric, such

as Hamming or Euclidean distance. The output is a

set of index pairs indicating which features from the

ﬁrst image match those in the second image, enabling

tasks like image alignment, object recognition, and

3D reconstruction. Figure 10 shows the detected fea-

tures in two consecutive frames and their matching,

taken by the drone before taking off.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

216

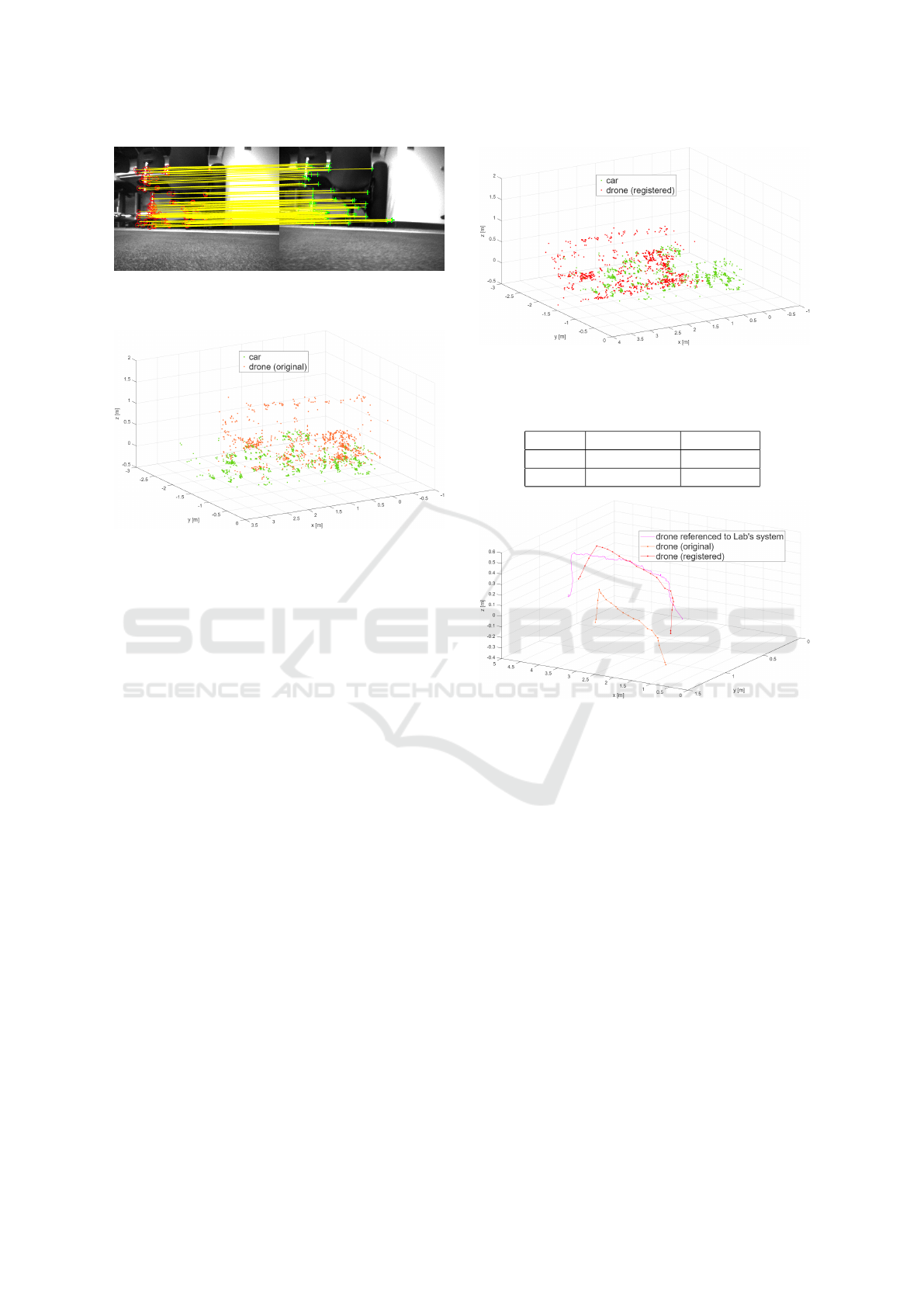
Figure 10: Detected and Matched Features in two Consec-

utive Frames from the Drone’s Camera.

Figure 11: Original Point Cloud Captured by Drone, and

Captured from the Car.

The point cloud obtained by the drone, refer-

enced with respect to its initial pose (i.e., not geo-

referenced), is shown in Figure 11, superimposed on

the point cloud generated by the car.

4.3 Point Cloud Registration

The registration performed by ICP algorithms gives

the following 3D rigid transformation (8), from (6):

A =



R T

0 1









0.995 −0.027 −0.097 −0.808

0.071 0.875 0.479 −0.261

0.072 −0.483 0.872 0.388

0 0 0 1







(8)

Figure 12 shows the car’s point cloud alongside

the drone’s point cloud after registration. Finally,

the 3D rigid transformation from (8) is used to geo-

reference the drone’s trajectory as calculated by vS-

LAM. This transformed trajectory is then reposi-

tioned within the Lab’s reference frame for compar-

ison. Figure 13 illustrates the following: (1) the

drone’s position with respect to the Lab, as measured

by the Lab’s external positioning system; (2) the orig-

inal vSLAM-based drone trajectory, without the cor-

rection; and (3) the geo-referenced drone trajectory,

obtained by applying the 3D transformation to the vS-

LAM output.

Mean Absolute Error (MAE) and Root Mean

Square Error (RMSE) metrics were calculated be-

tween the ﬂown trajectory referenced to the lab

Figure 12: Registered Point Cloud from the Drone, and

Point Cloud from the Car.

Table 1: MAE and RMSE Metrics.

Metric Uncorrected Corrected

MAE 0.45 [m] 0.10 [m]

RMSE 0.46 [m] 0.09 [m]

Figure 13: Drone trajectory Referenced to the Lab’s Coor-

dinate System.

(ground truth), and both the uncorrected and corrected

ones, using the horizontal phase of the trajectories.

The results are shown in Table 1.

The corrected trajectory shows an improvement

in alignment with the Lab-based trajectory (ground

truth) by a ratio greater than 4 : 1, compared to the

uncorrected one, although some deviations remain.

The point cloud registration enables a successful geo-

referenced correction of the drone’s trajectory.

5 DISCUSSION AND

CONSIDERATIONS

Future advancements should focus on addressing the

following challenges to transition current research

into practical, real-world applications: (1) Environ-

mental Robustness: Future work should focus on en-

hancing the pipeline’s robustness to dynamic envi-

ronmental changes like moving objects, varying illu-

Point Cloud Registration for Visual Geo-Referenced Localization Between Aerial and Ground Robots

217

mination, and occlusions. Investigating adaptive ﬁl-

tering or robust feature matching will be crucial for

maintaining performance and understanding failure

modes in the face of temporal inconsistencies. (2)

Computational Efﬁciency: Optimizing the pipeline

for real-time operation on embedded platforms is a

key next step. Exploring incremental registration, par-

allel computing, or hardware acceleration can reduce

latency, enabling live collaborative localization and

mapping, and balancing accuracy with computational

demands. (3) Uncertainty and Scalability: Quantify-

ing uncertainties in transformations and trajectories is

essential for downstream tasks. Propagating registra-

tion errors and integrating conﬁdence metrics will im-

prove decision-making. Additionally, extending the

approach to fuse point clouds from multiple hetero-

geneous robots requires addressing scalability, con-

sistency, and conﬂict resolution.

6 CONCLUSIONS

This work presented a comprehensive study on point

cloud registration techniques tailored for visual geo-

referenced localization between aerial and ground

robots using monocular visual SLAM data. It was

demonstrated that combining coarse feature-based

alignment with ﬁne-grained ICP reﬁnements effec-

tively overcomes challenges associated with scale

ambiguity, sparse data, and viewpoint discrepancies

typical of monocular SLAM outputs. The experi-

mental evaluation on heterogeneous robotic platforms

conﬁrmed that the approach improves map fusion ac-

curacy and enables consistent trajectory estimation,

crucial for cooperative perception and navigation in

environments with GNSS-denied or intermittent con-

ditions. These results highlight the potential of the

registration pipelines to enhance multi-robot coordi-

nation and collaborative mapping, supporting many

applications. Future work will focus on real-time im-

plementation and scalability to larger teams and dy-

namic environments.

REFERENCES

Achtelik, M., Bachrach, A., He, R., Prentice, S., and Roy,

N. (2011). Stereo vision and laser odometry for au-

tonomous helicopters in gps-denied indoor environ-

ments. In Unmanned Systems Technology XIII, vol-

ume 8045, page 80450H. SPIE.

Bach, W. and Aggarwal, J. K. (1988). Motion Understand-

ing: Robot and Human Vision. Springer Science &

Business Media, New York.

Bay, H., Tuytelaars, T., and Van Gool, L. (2006). Surf:

Speeded up robust features. Computer Vision – ECCV

2006, pages 404–417.

Campos, C., Elvira, R., Rodriguez, J. J. G., Montiel, J.

M. M., and Tard

os, J. D. (2021). Orb-slam3: An

accurate open-source library for visual, visual-inertial

and multi-map slam. IEEE Transactions on Robotics,

37(6):1874–1890.

Hartley, R. and Zisserman, A. (2003). Multiple View Geom-

etry in Computer Vision. Cambridge University Press,

2nd edition.

Jian, B. and Vemuri, B. C. (2011). Robust point set regis-

tration using gaussian mixture models. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

33(8):1633–1645.

Kim, G. and Kim, A. (2018). Scan context: Egocentric spa-

tial descriptor for place recognition within 3d point

cloud map. In 2018 IEEE/RSJ International Confer-

ence on Intelligent Robots and Systems (IROS), pages

4802–4809. IEEE.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision, 60(2):91–110.

Mur-Artal, R. and Tard

os, J. D. (2017). Orb-slam2:

An open-source slam system for monocular, stereo,

and rgb-d cameras. IEEE Transactions on Robotics,

33(5):1255–1262.

Nex, F. and Remondino, F. (2014). Uav for 3d mapping

applications: a review. Applied Geomatics, 6(1):1–15.

Rublee, E., Rabaud, V., Konolige, K., and Bradski, G.

(2011). Orb: An efﬁcient alternative to sift or surf. In

2011 International Conference on Computer Vision,

pages 2564–2571.

Rusinkiewicz, S. and Levoy, M. (2001). Efﬁcient variants

of the icp algorithm. In Proceedings Third Interna-

tional Conference on 3-D Digital Imaging and Mod-

eling, pages 145–152. IEEE.

Scaramuzza, D. and Fraundorfer, F. (2011). Visual odome-

try [tutorial]. IEEE Robotics & Automation Magazine,

18(4):80–92.

Szeliski, R. (2010). Computer Vision: Algorithms and Ap-

plications. Springer, London.

Zhang, Z. (2000). A ﬂexible new technique for camera cal-

ibration. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 22(11):1330–1334.

Zhou, B., Wang, K., Wang, S., and Shen, S. (2020). Ro-

bust map merging for multi-robot visual slam in dy-

namic environments. IEEE Transactions on Robotics,

36(6):1649–1665.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

218