Localized Thermal Analysis for Sportswear via Wind Tunnel Testing

Xiaoyi Cai

, Zixiang Hu

and Peng Zhou

Department of Mechanical and Aerospace Engineering, The Hong Kong University of Science and Technology,

Clear Water Bay, Kowloon, Hong Kong SAR, China

Keywords: Sportswear, Thermal Comfort, Wind Tunnel, Convective Heat Transfer Coefficient, Thermal Insulation.

Abstract: Thermal comfort of sportswear is critical for optimizing athletic performance and improving safety. However,

current research on the convective heat transfer coefficient (h) between fabrics and the air flow remains

limited, especially in terms of its local analysis. In this study, a thermal cylinder which simulates human limb

was developed to evaluate the fabrics' thermal insulation (I

) and h (both local and global values) in the wind

tunnel. The wind speed ranged from 2 to 8 m/s, and the stretch ratio (SR) from 1.1 to 2.0. The results show

that for both fabrics, the local h reaches a minimum around θ = 80°–90°, while the local I

peaks near θ =

120°. The effects of SR and wind speed on I

and h are also reported. This work offers a practical method for

quantifying the heat transfer characteristics of stretched fabrics, providing theoretical guidance for sportswear

design and thermal regulation strategies in wind environment.

1 INTRODUCTION

Thermal performance of sportswear is a critical factor

influencing both athletes' competitive performance

and physiological safety (Domenico et al., 2022). On

one hand, effective heat dissipation from the body

surface improves thermal comfort, which is important

for endurance, concentration, and neuromuscular

efficiency during exercise. On the other hand,

inadequate thermal regulation can lead to the

accumulation of metabolic heat and moisture,

increasing the risk of thermal stress, dehydration, and

heat-related illnesses (Douzi et al., 2020; Reilly et al.,

2006). Therefore, a comprehensive understanding of

the thermal performance of sportswear is essential for

designing garments and providing guidance for

enhancing athletes' competitive performance.

Research on evaluating the thermal performance

of sportswear mainly focuses on the thermal

insulation (I

) and evaporative resistance (R

Several researchers have investigated the influence of

fabric physical parameters on thermal insulation and

evaporative resistance, including factors such as

fabric layer and yarn type. A common conclusion

from these studies is that thermal insulation tends to

increase with increasing fabric thickness and the

https://orcid.org/0009-0005-4430-8095

https://orcid.org/0009-0005-5227-9888

volume ratio of air layer. Using heated thermal

manikins, Wang et al. (2012; 2016) and Fan et al.

(2008) studied the effects of body motion, body

regions, and sweat rates on the global evaporative

resistance. Similarly, Preet et al. (2018; 2023)

explored the body-related factors, including sweat

composition and concentration. The impact of

varying wind conditions on thermal insulation and

evaporative resistance has also been studied (Hu et al.,

2016; Cui et al., 2016); however, the maximum wind

speed in these works was limited to 1.5 m/s. Research

on fabrics' It and Ret under static or low wind speed

conditions are listed in Table 1.

In real-world athletic activities such as cycling,

wind speeds usually exceed 5 m/s. Under such

conditions, convective heat transfer plays a

significant role in thermoregulation. Therefore,

investigating the convective heat transfer coefficient

(h) is of practical significance for competitive sports

and recreational sports. Although there have been

standardized American Society of Testing Materials

(ASTM) test methods for evaluating thermal

insulation and evaporative resistance of fabrics

(ASTM, 2022; ASTM, 2016), research focusing on

convection heat transfer of fabric remain limited,and

there is still no international testing standards for the

Cai, X., Hu, Z. and Zhou, P.

Localized Thermal Analysis for Sportswear via Wind Tunnel Testing.

DOI: 10.5220/0013689400003988

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 13th International Conference on Sport Sciences Research and Technology Support (icSPORTS 2025), pages 69-78

ISBN: 978-989-758-771-9; ISSN: 2184-3201

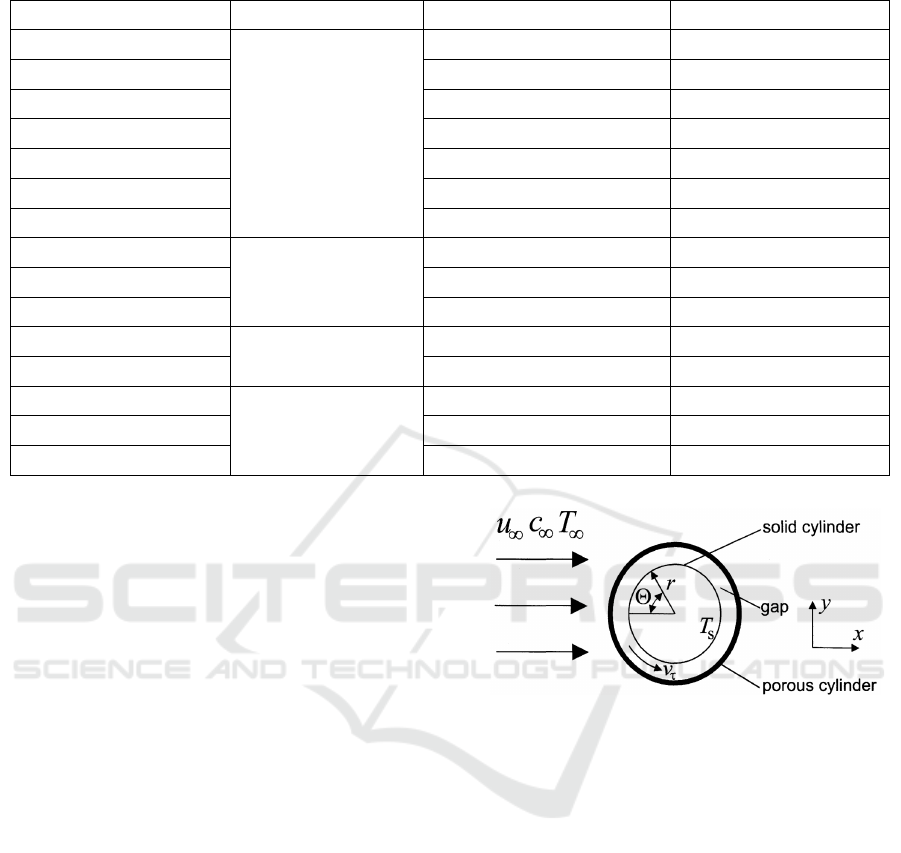
Table 1: Investigation on thermal insulation (I

) and evaporative resistance (R

) of fabric.

Researchers Motivation Method* Variables

Tesinova et al., 2022

Study the effect of

fabric structure or

composition

Commercial instruments Number of layers

Özkan et al., 2023 Commercial instruments Type of yarn

Kumar et al., 2021 Commercial instruments Blend rate of fabrics

Saeed et al., 2022 Commercial instruments Combination of fabrics

Noshro. et al., 2024 Commercial instruments Porosity of fabric

Kumar et al., 2022 Commercial instruments Linear density of fabric

Wang et al., 2017 Thermal manikin Thickness of fabric

Wang et al., 2012

Investigate the factors

related to human

Thermal manikin Body segments

Wang et al., 2016 Thermal manikin Sweating set rate

Fan et al., 2008 Thermal manikin Motions of human

Preet et al., 2018

Study the effect of

sweat components

Commercial instruments Sweat/water

Preet et al., 2023 Commercial instruments Lactate concentration

Wang et al., 2012

Explore the influence of

wind conditions

Thermal manikin Wind speed

Hu et al., 2016 Thermal manikin Wind direction

Cui et al., 2016 Thermal manikin Wind speed

h between fabrics and the air flow. Asawo et al.

(2023)studied the impact of air permeability and wind

speed on thermal insulation and Nusselt number.

Although they compared the thermal properties of

different fabrics, the effect of fabric tightness wasn't

considered. The fabrics used in cycling suits typically

exhibit high elasticity, resulting in notable changes in

surface structure when subjected to stretching (Li et

al., 2025). Researchers already know that such

surface structural variation can affect the flow and

aerodynamic drag (Zheng et al., 2021; Zheng et al.,

2023); it is believed that the change in flow state can

also affect heat transfer performance of fabric (Cai et

al., 2024). Such an effect is not considered in the

conventional thermal characterization of fabrics.

On the other hand, current literature lacks

systematic experimental measurements of the local

convective heat transfer coefficient. Human limbs can

be approximated as cylindrical geometries, where

fabrics experience highly non-uniform flow and

thermal conditions along different circumferential

angles (Θ) at high wind speed (Cai et al., 2025).

Relying solely on overall heat transfer coefficients is

insufficient to accurately estimate fabrics'

thermoregulatory behavior. Although some studies

(Sobera et al., 2003; Gibson et al., 2009) employed

CFD simulations by simplifying fabrics as porous

materials to estimate local Nusselt number, as shown

in Figure 1, such models fail to capture the detailed

structural features of actual fabrics and provide

limited practical guidance.

Figure 1: Physical model of limb-air gap-fabric-air flow

system (Gibson et al., 2009).

In this study, the effects of stretch ratio and wind

speed on the thermal insulation and convective heat

transfer coefficient of fabrics were systematically

investigated. Local measurements were conducted to

elucidate the detailed heat transfer mechanisms, while

global values were analyzed to enable direct

comparison between the two tested fabrics.

2 METHODOLOGY

2.1 Wind Tunnel Facility

The experiment was conducted using an open-jet

wind tunnel in the Aerodynamics and Acoustics

Facility at The Hong Kong University of Science and

Technology. The wind tunnel has a test section area

of 0.6 × 1.35 m

. The flow speed can be adjusted

between 0 and 36 km/h.

icSPORTS 2025 - 13th International Conference on Sport Sciences Research and Technology Support

2.2 Sample Characteristics

In this work, two types of fabrics were selected for

investigation (named Fabric A and Fabric B,

respectively). The fabrics' pattern, 3D profile, and

global surface roughness (Sa) were measured by a 3D

optical profilometer (VR-6000, KEYENCE, Osaka,

Japan), as shown in Table 2. The Sa represents the

average of the absolute values of surface height

deviations from the mean plane over a specified area:

𝑆𝑎=

𝐴



𝑧



𝑥,𝑦

|

d𝑥d𝑦

(1)

To investigate the thermal performance of

sportswear under varying levels of tightness, this

study adopts the stretch ratio (SR) as a quantitative

measure and examines the variations of the

convective heat transfer coefficient h and thermal

insulation I

with respect to SR. The stretch ratio of

fabric is defined as follows (Li et al., 2025):

SR=

𝑃



(2)

where 𝑃



is the original perimeter of fabric, and 𝑃 is

the perimeter of fabric after covering on the cylinder.

Obviously, the larger the SR is, the tighter the

sportswears are.

The lateral orientation corresponds to the

direction orthogonal to the longitudinal grooves. To

ensure consistency across measurements, fabric

samples were mounted onto the cylindrical surface

such that the grooves aligned with the cylinder’s axis

and remained perpendicular to the airflow. The two

cut edges of each fabric piece were stitched together,

with the seam positioned at the rear of the cylinder to

minimize its impact on the surrounding flow field.

2.3 Experimental System

The system is composed of four primary components:

the test section, thermal control system, and data

acquisition system, as shown in Figure 2. Some

detailed information about instruments and

components are listed in Table 3.

2.3.1 Test Section

This section is a cylinder made by resin. Its outer

surface can be covered with various fabrics, emulating

garments worn on human arms and thighs. The inner

surface of the cylinder is equipped with thermocouple

slots and water outlets. As illustrated in Figure 3, the

T-type thermocouples are installed at 10° intervals to

enable the measurement of temperature distribution as

a function of angular position (θ).

Table 2: Samples' characteristics.

Fabric A B

Covered on

cylinder

Pattern

3D profile

(μ

)

114 76

Localized Thermal Analysis for Sportswear via Wind Tunnel Testing

Table 3: Detailed information of the instruments and components used in this work.

Item Model A

licable ran

e Accurac

Resolution

Thermocouple T-type thermocouple -40

–

125℃ ± 0.5℃

–

Infrared camera FLIR-E5 Pro -20

–

400℃ ± 2%*readin

0.1℃

Power mete

NAPUI-PM9817 0.01mA

–

20A ± 0.2% 0.001 mW

Tem

erature re

ulato

ANTHONE -10

–

60℃ ± 0.2% 0.1℃

Data acquisition HIOKI-LR8450 -10

–

50℃

–

0.01℃

Optical profilometer

KEYENCE

-VR 6000

-15 – 30℃ 0.4 μm 0.1 μm

Figure 2: Illustration of experimental system.

2.3.2 Thermal Control System

This system simulates the metabolic heat production

of the human body. A heating film adhered to the

inner surface of cylinder maintains at a certain

temperature, which is controlled by the temperature

regulator (ANTHONE, Xiamen, China). The power

of heating film is measured by a power meter

(NAPUI-PM9817, Dongguan, China). With thermal

insulation plates covering both the top and bottom of

the cylinder, we assume the heat solely dissipates

through the lateral surface of cylinder. This

configuration not only aligns with the actual situation

of human limbs but also facilitates temperature

measurement.

Figure 3: Thermocouples distribution on the cylinder.

2.3.3 Data Acquisition System

It records the temperature and humidity data. The

surface and ambient air temperatures are measured

using thermocouples, while the temperature of the

fabrics' outer surface is measured via an infrared

camera (

FLIR-E5 Pro, America

), as shown in Figure 4.

A humidity sensor is used to measure the ambient

humidity.

Figure 4: Average temperature at θ = 90°.

icSPORTS 2025 - 13th International Conference on Sport Sciences Research and Technology Support

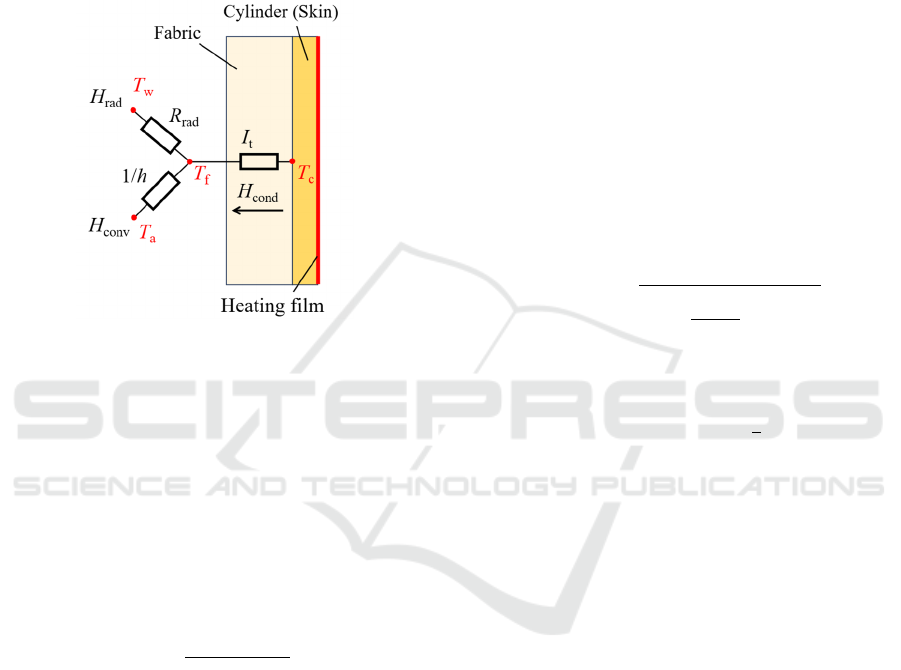
2.4 Formulation

Under the steady-state condition, the power generated

by the heating film H

equals to the heat flux

conducted from the outer surface of cylinder to

fabric’s outer surface (H

cond

). Then the heat flux will

dissipate into the environment via two modes: heat

convection (H

conv

) and thermal radiation (H

rad

Energy balance of fabric is shown in Figure 5.

Figure 5: Energy balance of fabric.

The energy balance relationship can be expressed as

follows:

𝐻



=𝐻



=𝐻



+𝐻



(3)

where H

cond

, H

conv

, and H

rad

represent the steady heat

flux through heat conduction, heat convection, and

thermal radiation. In view of the ratio of fabric

thickness to the curvature, heat conduction within the

fabric can be approximated as one-dimensional

planar conduction. The corresponding formula is

given by:

𝐻



𝐴



∙



𝑇



𝑇





𝐼



(4)

where I

is the thermal insulation of fabric. T

and T

represent temperature of cylinder outer surface and

fabric outer surface, respectively. A

represents the

surface area of fabric. The heat convection and

thermal radiation can be calculated as:

𝐻



=ℎ

𝐴





𝑇



𝑇





(5)

𝐻



𝐴



𝜀𝜎



𝑇





𝑇







(6)

where h, T

, T

, ε, and σ represent convective heat

transfer coefficient, air temperature, wall temperature

(for radiant heat exchange), emissivity of fabric, and

Stefan-Boltzmann constant. In this work, the local

and global values of I

and h can be calculated

combining equations (3) to (6). For local calculation,

𝑇



and 𝑇



are obtained from line-integrated values at

the corresponding θ. For global calculations, 𝑇



and

𝑇



are determined by averaging the values across all θ

angles.

3 RESULTS AND DISCUSSION

3.1 Bare Cylinder Test

For verification, the convective heat transfer

coefficient ℎ of the bare cylinder is measured under

both natural and forced convection conditions (U

2, 4, 6, 8 m/s). The results are compared with the

semi-empirical models to validate the accuracy of our

method. For natural convection, we used the

correlation recommended by Churchill et al. for

comparison (Churchill & Chu, 1975):

𝑁𝑢=

⎩

⎪

⎨

⎪

⎧

0.825+

0.387∙𝑅𝑎

/

1+



0.492

𝑃𝑟



/



/

⎭

⎪

⎬

⎪

⎫



(7)

For forced convection, the correlation developed by

Hilpert was selected (Hilpert, 1933):

𝑁𝑢=𝐶∙𝑅𝑒



∙𝑃𝑟





(8)

where C = 0.193 and m = 0.618 when 4000 < Re <

40000; C = 0.027 and m = 0.805 when 40000 < Re <

400000. As shown in Figure 6(a), the h measured in

this work is 2.45 W/(m

K) under natural convection,

only 1.92% lower than that of Churchill's correlation.

Error bars represent the standard deviation from the

mean of three independent measurements. Although

the deviation increases with airflow velocity, it

remains within an acceptable range. Thus, our

experimental system provides a reliable and accurate

approach for evaluating the thermal performance of

fabrics. Furthermore, we studied the local h at

different θ on the cylinder, as shown in Figure 6(b).

Our results exhibit good consistency with the

previous experimental data (Bergman et al., 2006).

They pointed out that when Re = 10

, the flow

separation occurs at θ ≈ 90°.

3.2 Effect of Stretch Ratio on Fabrics'

Thermal Performance

In this section, the wind speed was fixed at 8 m/s, and

the thermal insulation and convective heat transfer

coefficient were measured for two fabrics under

different stretch ratios (SR = 1.1, 1.4, 1.7, and 2.0).

Localized Thermal Analysis for Sportswear via Wind Tunnel Testing

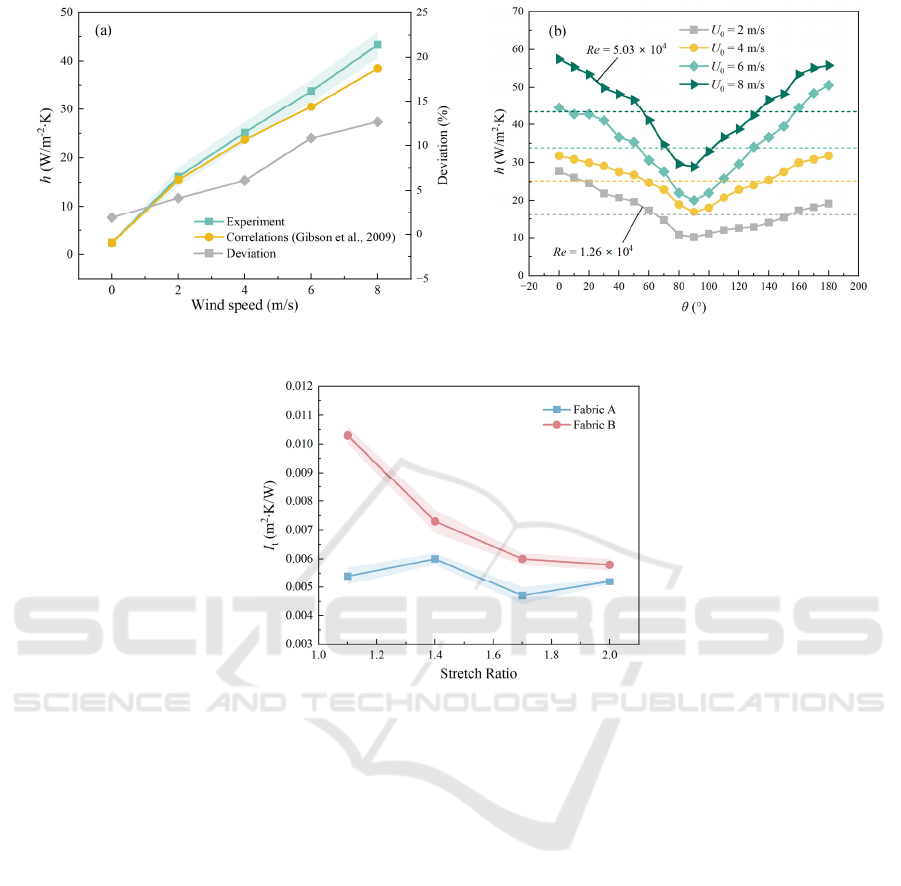
Figure 6: (a) Average and (b) local convective heat transfer coefficient for a bare cylinder.

Figure 7: Comparison of fabrics' thermal insulation at different stretch ratio at 8 m/s.

As shown in Figure 7, the thermal insulation of

Fabric A fluctuated between 0.0047 and 0.006 m

·K/W

with no clear variation tendency. In contrast, the

thermal insulation of Fabric B decreased monoto-

nically from 0.0103 to 0.0058 m

·K/W with increasing

SR. At all tested SR values, the thermal insulation of

Fabric A remained lower than that of Fabric B.

Subsequently, the local thermal insulation at

different θ was investigated, as illustrated in Figure 8.

Both fabrics exhibited a maximum thermal insulation

at θ = 120°, and a minimum at θ = 0° or 180°. At θ =

0°, which corresponds to the front stagnation point, the

incoming airflow impinges directly on the surface and

enhances the interfibrous heat convection, thereby

reducing thermal insulation. A similar effect occurs at

θ = 180° is due to the flow reattachment and turbulence

in the wake region. In contrast, θ = 120° typically lies

within or just beyond the flow separation zone, where

the local flow velocity near the surface is minimal due

to boundary layer detachment. This leads to weakened

convective heat transfer and hence a local maximum in

thermal insulation.

Notice that for Fabric B, the effect of increasing

SR on the thermal insulation's reduction diminished

when the fabric is very tight. As shown in Figure 8(b),

the curves corresponding to SR = 1.7 and 2.0 were

nearly identical, indicating a saturation effect. This

phenomenon can be explained as follows: thermal

insulation is governed by both heat conduction

through the fibers and convective heat transfer

between the interfibrous air and the fiber surfaces. As

the stretch ratio increases, the fabric becomes thinner,

which reduces its thermal conduction resistance.

Simultaneously, the compression of the fabric

decreases the volume fraction of interfibrous air,

thereby suppressing the internal convection. Beyond

a certain SR (e.g., 1.7), further stretching induces

minimal changes in both thickness and internal air

content, leading to a stabilized thermal insulation

performance. However, the thermal insulation of

Fabric A does not stabilize with the increasing SR.

The underlying physical mechanism will be explored

in future studies.

icSPORTS 2025 - 13th International Conference on Sport Sciences Research and Technology Support

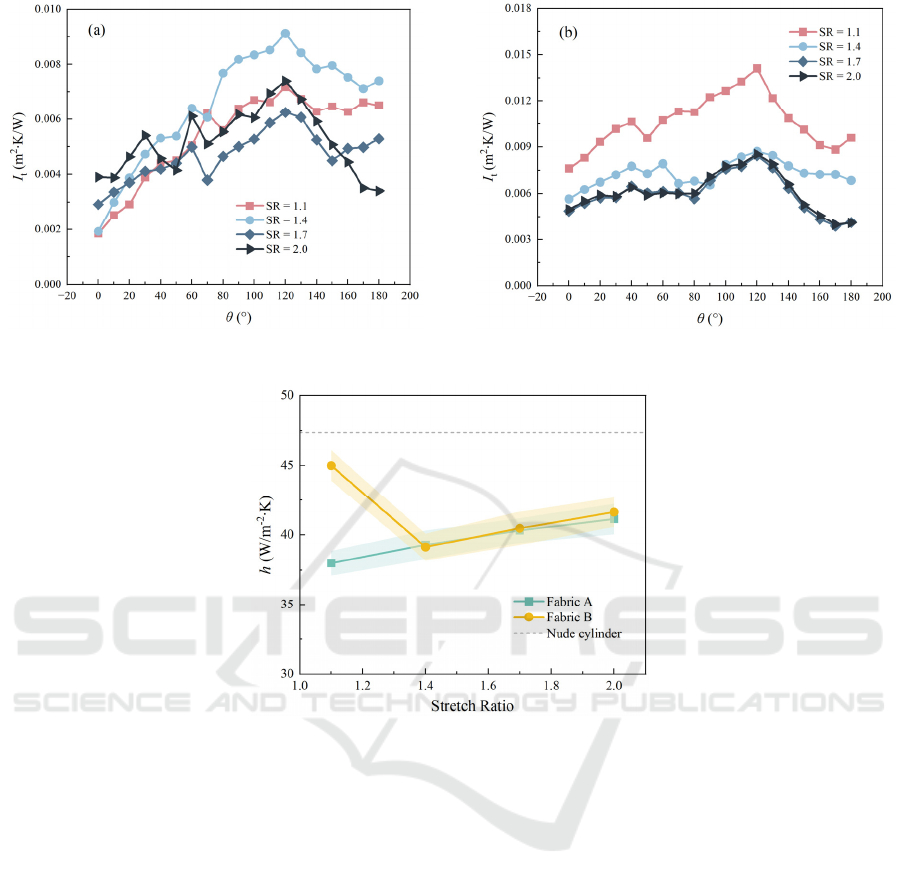
Figure 8: Local value of thermal insulation for (a) Fabric A and (b) Fabric B at different stretch ratio at 8 m/s.

Figure 9: Comparison of convective heat transfer coefficient at different stretch ratio at 8 m/s.

SR also influences the convective heat transfer

coefficient of fabric surface. As shown in Figure 9,

the convective heat transfer coefficient of Fabric A

increases monotonically with SR, with an overall rise

of 8.3% from SR = 1.1 to 2.0. In contrast, although

Fabric B exhibits a similar increasing trend from SR

= 1.4 to 2.0 and shows comparable values to Fabric

A, a significant decrease of 13% is observed when SR

increases from 1.1 to 1.4.

Local analysis reveals the primary cause of the

variations in global value of h. As shown in Figure

10(a), the influence of SR on the convective heat

transfer coefficient of Fabric A is mainly

concentrated within the range of θ = 0°-80°, while the

region from 80°-180° remains almost unaffected. A

similar trend can be observed for Fabric B; however,

at SR = 1.1, its local ℎ in the range of 80°-180° are

significantly higher than those at other SR values,

which accounts for the noticeably higher global h

value. Additionally, it is noted that most curves in

Figure 10 exhibit a minimum at θ = 80°, which is

different from the bare cylinder case where the

minimum occurs at θ = 90°. It suggests that fabric

structure can influence the separation position.

3.3 Effect of Airflow Velocity on

Fabrics' Thermal Performance

In this section, SR is fixed at 1.4 to investigate the

thermal insulation and convective heat transfer

coefficient under varying airflow velocities (U

= 2,

4, 6, 8 m/s). As shown in Figure 11(a), the thermal

insulation of both fabrics decreases with an increasing

airflow velocity. This is because, although airflow

does not affect the intrinsic thermal conductivity of

the fabric, the overall thermal insulation is governed

by both heat conduction through the fibers and heat

convection of the interfibrous air. Higher airflow

enhances inter-fiber convection, thereby reducing the

thermal insulation. Additionally, Figure 11(a) shows

that Fabric A exhibits lower thermal insulation than

Localized Thermal Analysis for Sportswear via Wind Tunnel Testing

Figure 10: Local convective heat transfer coefficient for (a) Fabric A and (b) Fabric B at different stretch ratio at 8 m/s.

Figure 11: Relationship between thermal insulation and wind speed for fabrics A and B (SR = 1.4). (a) Global values

comparison; (b) local value of Fabric A; (c) local value of Fabric B.

Figure 12: Relationship between convective heat transfer coefficient and wind speed for fabrics A and B (SR = 1.4). (a)

Global values comparison; (b) local value of Fabric A; (c) local value of Fabric B.

Fabric B throughout all the tested velocities. Figure

11(b) and (c) present the local distributions of thermal

insulation, from which a similar conclusion to that in

Section 3.2 can be drawn: the local maximum occurs

near θ = 120°.

Figure 12 shows that the convection heat transfer

performance of the two fabrics is nearly identical

across all airflow velocities. Figure 12(b) and (c)

indicate that within the range of 2–8 m/s, both fabrics

maintain a laminar boundary layer, with clear

evidence of flow separation. Notably, at lower airflow

velocities (below 4 m/s), the separation point appears

near θ = 90°, while at higher velocities, it shifts

forward to approximately θ = 80°. This phenomenon

is consistent with the previous results (Bergman,

2006).

3.4 Proportion of Different Thermal

Resistances

This study focuses on heat conduction through the

fabric and convective heat transfer at its surface.

Therefore, radiative heat transfer is neglected in the

icSPORTS 2025 - 13th International Conference on Sport Sciences Research and Technology Support

Figure 13: Total thermal resistance and the proportions of thermal insulation and convective thermal resistance as a function

of (a) stretch ratio and (b) wind speed.

current analysis. The thermal insulation and

convective thermal resistance (1/h) are in series to

obtain the total thermal resistance:

𝑅



=𝐼



ℎ

(9)

Taking Fabric B as an example, we examine how

the total thermal resistance varies with SR and wind

speed, as well as the corresponding changes in the

proportion of each thermal resistance. As shown in

Figure 13(a), the total thermal resistance of Fabric B

tends to decrease with increasing SR. Meanwhile, the

percentage of convective thermal resistance increases

monotonically from 68% to 80%. Figure 13(b) shows

that although the proportion of convective resistance

slightly decreases with increasing wind speed, it

consistently accounts for more than 78% of the total

thermal resistance. These results indicate that within

the studied range (U

= 2 – 8 m/s, SR = 1.1 – 2.0),

enhancing convective heat transfer is a more effective

strategy for improving Fabric B's overall thermal

transfer performance of the fabric.

4 CONCLUSIONS

A thermal cylinder platform fixed in the wind tunnel

was developed to evaluate the heat transfer

performance of sportswear fabrics under varying SR

and wind speeds. The key findings are summarized as

follows:

The I

of Fabric B decreased with increasing SR,

while Fabric A showed no clear trend. An increase in

SR generally enhanced the h for both fabrics,

although Fabric B experienced a notable drop in h

from SR = 1.1 to 1.4.

Higher wind speeds led to the reduction in I

and

increase in h for both fabrics. Across all wind speeds

tested, Fabric A consistently exhibited lower global I

than Fabric B, while the global h of both fabrics

remained nearly identical.

Both fabrics exhibited the maximum I

at θ = 120°

and minimum values at θ = 0° or 180°. With

increasing wind speed, the flow separation point

shifted toward the position with lower θ.

ACKNOWLEDGEMENTS

This work is partially supported by the Hong Kong

Innovation and Technology Commission (No.

ITS/101/23FP). The study was conducted in the

Aerodynamics Acoustics & Noise Control

Technology Centre (aantc.ust.hk).

REFERENCES

ASTM International. (2016). Standard test method for

measuring the evaporative resistance of clothing using

a sweating manikin (ASTM F2370–16). West

Conshohocken, PA: ASTM International.

ASTM International. (2022). Standard test method for

measuring the thermal insulation of clothing using a

heated manikin (ASTM F1291–22). West

Conshohocken, PA: ASTM International.

Bergman, T. L., Lavine, A. S., Incropera, F. P., et al. (2006).

Fundamentals of heat and mass transfer (7th ed.). Wiley.

Cai, X. Y., Li, H. Z., Ma, T., et al. (2024). Size effect on

thermal transport performance of inserted Cu/Cu

bilayer. International Journal of Heat and Mass Transfer,

218, 124784. https://doi.org/10.1016/j.ijheatmasstrans

fer.2023.124784.

Cai, X. Y., Li, H. Z., Zhang, J. Q., et al. (2025). Mechanism

of interfacial thermal resistance variation in

Localized Thermal Analysis for Sportswear via Wind Tunnel Testing

diamond/Cu/CNT tri-layer during thermal cycles.

International Journal of Thermal Sciences, 207C,

109380. https://doi.org/10.1016/j.ijthermalsci.2024.109

380

Churchill, S. W., & Chu, H. H. S. (1975). Correlating

equations for laminar and turbulent free convection from

a horizontal cylinder. International Journal of Heat and

Mass Transfer, 18, 1323–1329. https://doi.org/10.1016/0

017-9310(75)90222-7.

Cui, Z. Y., Fan, J. T., & Wu, Y. S. (2016). A comparative

study on the effects of air gap wind and walking motion

on the thermal properties of Arabian Thawbs and

Chinese Cheongsams. Ergonomics, 59(8), 999–1008.

https://doi.org/10.1080/00140139.2015.1111428.

Domenico, I. D., Hoffmann, S. M., & Collins, P. K. (2022).

The role of sports clothing in thermoregulation,

comfort, and performance during exercise in the heat:

A narrative review. Sports Medicine – Open, 8, 58.

https://doi.org/10.1186/s40798-022-00449-4.

Douzi, W., Dupuy, O., Theurot, D., et al. (2020). Per-

cooling (using cooling systems during physical

exercise) enhances physical and cognitive performance

in hot environments: A narrative review. International

Journal of Environmental Research and Public Health,

17, 1031. https://doi.org/10.3390/ijerph17031031.

Fan, J. T., & Tsang, H. W. K. (2008). Effect of clothing

thermal properties on the thermal comfort sensation

during active sports. Textile Research Journal, 78(2),

111–118. https://doi.org/10.1177/0040517508080046.

Gibson, P. (2009). Modeling heat and mass transfer from

fabric-covered cylinders. Journal of Engineered Fibers

and Fabrics, 4(1), 1–8. https://doi.org/10.1177/1558925

00900400102.

Hilpert, R. (1933). Heat transfer from cylinders.

Ingenieurwes, 4, 215.

Hu, S. R., Zhao, M. M., & Li, J. (2016). Effects of wind

direction on sportswear thermal insulation with various

ease allowance. International Journal of Clothing

Science and Technology, 28(4), 492–502.

https://doi.org/10.1108/IJCST-11-2015-0126.

Kumar, C. B. S., & Kumar, B. S. (2022). Study on thermal

comfort properties of Eri silk knitted fabrics for

sportswear application. Journal of Natural Fibers,

19(14), 9052–9063. https://doi.org/10.1080/15440478.2

021.1982110.

Kumar, D. V., & Raja, D. (2021). Study of thermal comfort

properties on socks made from recycled polyester/virgin

cotton and its blends. Fibers and Polymers, 22(3), 841–

846. https://doi.org/10.1007/s12221-021-0471-6.

Li, X. R., Mao, J. Q. and Zhou, P. (2025). Aerodynamic and

Acoustic Evaluation of a Cylinder Covered by Stretched

Grooved Fabric. AIAA Journal, https://doi.org/10.25

14/1.J065006.

Lu, Y. H., Wang, F. M., Peng, H., et al. (2016). Effect of

sweating set rate on clothing real evaporative resistance

determined on a sweating thermal manikin in a so-

called isothermal condition (T

manikin

= T

International Journal of Biometeorology, 60, 481–488.

http://dx.doi.org/10.1007/s00484-015-1029-3.

Mukhopadhyay, A., Preet, A., & Midha, V. (2018). Moisture

transmission behavior of individual component and

multi-layered fabric with sweat and pure water. The

Journal of The Textile Institute, 109(3), 383–392.

https://doi.org/10.1080/00405000.2017.1348435.

Noshrodkoli, M. R., Mousazadegana, F., Gharehaghaji, A.,

et al. (2024). How porosity of the middle layer can affect

the comfort properties of multi-layer sportswear. The

Journal of The Textile Institute. https://doi.org/10.1080/

00405000.2024.2351668.

Özkan, E. T., Kaplangiray, B., Şekir, U., et al. (2023).

Investigation of the thermal comfort of the sportswear by

standing thermal manikin and thermal imaging

techniques. Journal of Engineered Fibers and Fabrics,

18, 1–12. https://doi.org/10.1177/15589250231180248.

Preet, A., Mukhopadhyay, A., & Midha, V. K. (2023). Impact

of varying lactate concentration in sweat on thermo-

physiological comfort of multi-layered ensembles.

International Journal of Clothing Science and

Technology, 35(2), 266–276. https://doi.org/10.1108/

IJCST-12-2021-0176.

Reilly, T., Drust, B., & Gregson, W. (2006).

Thermoregulation in elite athletes. Current Opinion in

Clinical Nutrition and Metabolic Care, 9(6), 666–671.

https://doi.org/10.1097/01.mco.0000247475.95026.a5.

Saeed, M. A., Safdar, F., Basit, A., et al. (2022).

Development of thermally comfortable clothing for hot

and humid environment. Journal of Natural Fibers,

19(14), 7674–7686. https://doi.org/10.1080/15440478.2

021.1958404.

Sobera, M. P., Kleijn, C. R., & Van den Akker, H. E. A.

(2003). Convective heat and mass transfer to a cylinder

sheathed by a porous layer. AIChE Journal, 49(12),

3018–3028. https://doi.org/10.1002/aic.690491204.

Tamsaki, A., David, T., & David, S. (2023). Measuring

convective heat transfer coefficients and thermal

resistance for protective fabrics using a heated cylinder

in a wind tunnel. The Journal of The Textile Institute,

114(12), 1909–1917. https://doi.org/10.1080/004050

00.2022.2150956.

Tesinova, P., & Atalie, D. (2022). Thermal comfort

properties of sport fabrics with dependency on structure

parameters and maintenance. Fibers and Polymers,

23(4), 1150–1160. https://doi.org/10.1007/s12221-022-

4160-x.

Wang, F. M., Ferraro, S., Lin, L. Y., et al. (2012). Localised

boundary air layer and clothing evaporative resistances

for individual body segments. Ergonomics, 55(7), 799–

812. https://doi.org/10.1080/00140139.2012.668948.

Wang, F. M., Lai, D. D., Shi, W., et al. (2017). Effects of

fabric thickness and material on apparent ‘wet’

conductive thermal resistance of knitted fabric ‘skin’ on

sweating manikins. Journal of Thermal Biology, 70, 69–

76. http://dx.doi.org/10.1016/j.jtherbio.2017.03.004.

Zheng, C. T., Zhou, P., Zhong, S. Y., et al. (2021). An

experimental investigation of drag and noise reduction

from a circular cylinder using longitudinal grooves.

Physics of Fluids, 33, 115110. https://doi.org/10.1063/

5.0070959.

Zheng, C. T., Zhou, P., Zhong, S. Y., et al. (2023). On the

cylinder noise and drag reductions in different Reynolds

number ranges using surface pattern fabrics. Physics of

Fluids, 35, 035111. https://doi.org/10.1063/5.0138074.

icSPORTS 2025 - 13th International Conference on Sport Sciences Research and Technology Support