Multiple-Branch Convolutional Neural Network for SSEC Daily

Return Prediction

Shengxi Jiang

School of Economics Management, Tongji University, Shanghai, China

Keywords: Deep Learning, Stock Market Return, SSEC.

Abstract: This study proposes a Multiple-branch Convolutional Neural Network (MBCNN) model to predict the daily

return direction of the Shanghai Securities Composite Index (SSEC). Due to the complexity and volatility of

financial markets, traditional machine learning methods such as Support Vector Machine (SVM), Random

Forest (RF), Logistic Regression (LR), and Decision Tree (DT) often face limitations in capturing intricate

patterns. To address this, the model leverages multiple feature branches, incorporating historical price data,

global market indicators, and other financial metrics. The effectiveness of MBCNN is evaluated against

classical machine learning approaches, with results demonstrating superior performance in both accuracy and

F-measure metrics. Additionally, the study explores the impact of Principal Component Analysis (PCA) on

model performance, revealing that PCA does not enhance prediction accuracy. Experimental results confirm

that MBCNN outperforms traditional models, offering improved classification capabilities and robustness.

These findings provide valuable insights and a foundation for future research on stock market trend prediction.

1 INTRODUCTION

The capacity to predict trends in stock market indices

is crucial for shaping economic policies and guiding

investment choices (Ayyildiz & Iskenderoglu, 2024).

By predicting the SMI trends, firms can optimize their

planning processes, while investors can enhance the

efficiency of their stock trading activities (Akyildirim

et al., 2022). However, it is quite difficult to forecast

the stock market's price movement because of its

great volatility, dynamic nature, and complexity.

Many scholars have studied this issue. In the

“Efficient Markets Hypothesis”, Nevasalmi’s stated

that all the information of the stock has been reflected

in the current stock price, so the stock price has

nothing to do with historical information, and it is

impossible to predict its price trend. However, the

validity of the Efficient Markets Hypothesis has been

debated in many studies (Nevasalmi, 2020).

According to the Adaptive Market Hypothesis,

markets are flexible and change throughout time,

alternating between efficiency and inefficiency at

various points in time (Lo, 2004). Therefore,

incorporating historical data can increase the

accuracy of stock trend forecast.

https://orcid.org/0009-0002-2578-8714

Several researchers have used machine learning to

the subject of stock prediction as these algorithms

have produced good results in a variety of study

domains. Such as Support Vector Machine (SVM)

(Xiao et al., 2020), Artificial Neural Network (ANN)

(Chen et al., 2017) and random forest (RF) (Weng et

al., 2018), Because of their superior generalization

capabilities, these machine learning algorithms were

successfully utilized to predict financial markets.

Currently, deep learning algorithms, such as long

short-term memory (LSTM), time convolutional

network (TCN) and convolutional neural network

(CNN), are also used in this fields. Ruize Gao et al.

employ CNN to deal with the implications of

evaluating several markets on the goal of market

stock prediction and successfully enhance accuracy

when compared to typical machine learning methods

(Gao et al., 2022).

However, the outcomes of these algorithms are

significantly influenced by the input variables (Gao et

al., 2022). Therefore, many scholars have made a lot

of attempts at feature engineering. Xiao Zhong et al.

add more than 60 relevant features and use Principal

Component Analysis (PCA) to process data and it

significantly improves the model effect (Zhong &

Jiang, S.

Multiple-Branch Convolutional Neural Network for SSEC Daily Return Prediction.

DOI: 10.5220/0013686200004670

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Data Science and Engineering (ICDSE 2025), pages 265-270

ISBN: 978-989-758-765-8

265

Enke, 2019). Ayyildiz et al. combine a variety of

machine learning models with the k-nearest

neighbors (KNN) to forecast changes in stock prices

(Ayyildiz & Iskenderoglu, 2024).

The aim of this study is to predict the daily return

direction of the Shanghai Securities Composite Index

(SSEC) by employing deep learning algorithm. In this

study, a multiple-branch Convolutional neural

network is approached and compared with four

classical machine learning methods including SVM,

RF, Logistic Regression (LR) and Decision tree (DT).

Also, PCA is attempted to be combined with machine

learning algorithms in the hope of improving model

accuracy.

This study consists of five parts. In the second

part, the dataset used in the study is explained. In the

third part, the deep learning algorithm used in this

study is introduced. In the fourth part, the

experimental results of the algorithm are discussed.

Eventually, in the fifth part, the conclusion of the

study is explained.

2 DATA DESCRIPTION

2.1 Introduction of SSEC

This research concentrates on the Shanghai Securities

Composite Index (SSEC), which monitors the

aggregated performance of both A-share and B-share

securities traded on the Shanghai exchange, offering

vital insights into the operational dynamics of China's

capital markets. This research selects a time range

from June 1, 2018 to January 1, 2023 to eliminate bias

produced by a brief amount of time. The dataset

originates from finance.yahoo.com. In Table 1, part

of dataset for the SSEC is presented.

Table 1: Part of dataset for the SSEC.

Date Close High Low Open Volume Stock

2018-06-01 3075.136963 3102.087891 3059.785889 3084.753906 129900 000001.SS

2018-06-04 3091.190918 3098.4021 3076.993896 3083.427002 114600 000001.SS

2018-06-05 3114.206055 3114.769043 3080.045898 3088.008057 118700 000001.SS

2018-06-06 3115.179932 3117.524902 3103.532959 3109.175049 120200 000001.SS

2018-06-07 3109.499023 3128.715088 3105.577881 3121.184082 127800 000001.SS

2.2 Target

This study's prediction target is the daily return

direction. Equations (1), (2), and (3) are used to

compute the three sorts of returns: 𝑅

,

, 𝑅

,

, and

𝑅

,

𝑅

,

𝐶𝑙𝑜𝑠𝑒



−𝐶𝑙𝑜𝑠𝑒



𝐶𝑙𝑜𝑠𝑒







𝑅

,

𝑂𝑝𝑒𝑛



−𝐶𝑙𝑜𝑠𝑒



𝐶𝑙𝑜𝑠𝑒







𝑅

,

𝐶𝑙𝑜𝑠𝑒



−𝑂𝑝𝑒𝑛



𝑂𝑝𝑒𝑛







The close and open prices of the SSEC on trading

day t are shown by the variables 𝐶𝑙𝑜𝑠𝑒



and 𝑂𝑝𝑒𝑛



respectively. Most of the current studies focus on the

prediction of 𝑅

,

, and few predictions

of 𝑅

,

. However, it is also very important for

investors to determine the trend of the stock's opening

price on the next day, so the prediction target of this

study is the direction of 𝑅

,

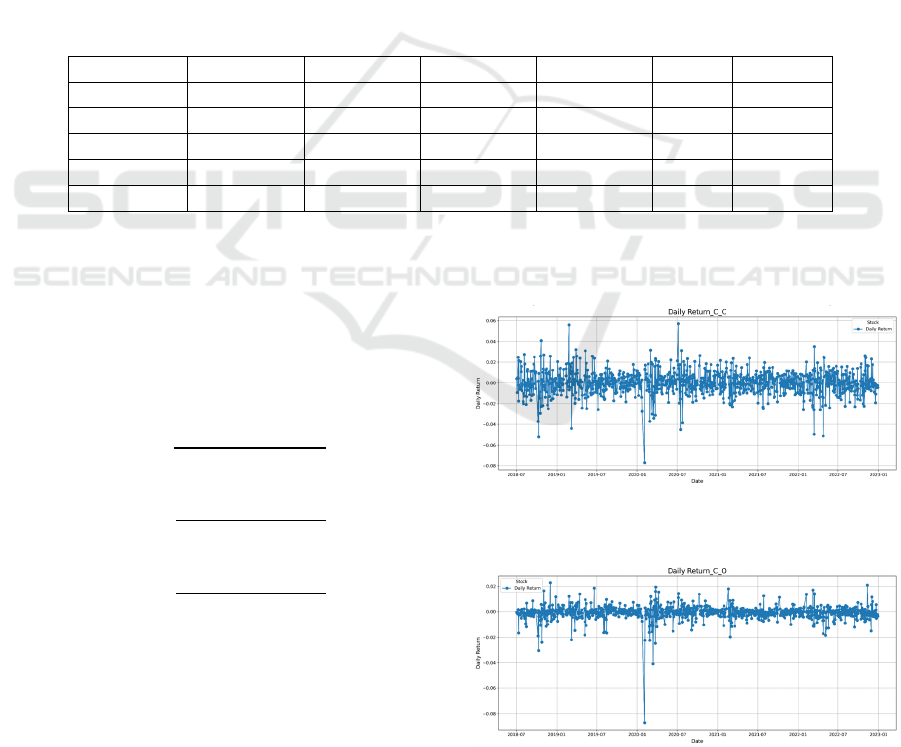
. Figures 1 and 2

show the line graphs of 𝑅

,

and 𝑅

,

over time,

respectively, from which can find that the fluctuation

of 𝑅

,

is smaller compared to that of 𝑅

,

Figure 1: Plot of 𝑅

,

versus time. (Picture credit:

Original)

Figure 2: Plot of 𝑅

,

versus time. (Picture credit:

Original)

ICDSE 2025 - The International Conference on Data Science and Engineering

266

2.3 Features

According to the imperfect efficient market theory,

the more thorough the historical information added,

the more accurate will be. Therefore, this study not

only considers the historical price information of

SSEC, including basic information, the daily return,

the relative difference in percentage and the

exponential moving average, but also takes global

market information, including other 5 major markets,

top 9 companies’ information in SSEC, and other

relevant information like gold and oil price, rate

between countries into account. Total 35 features.

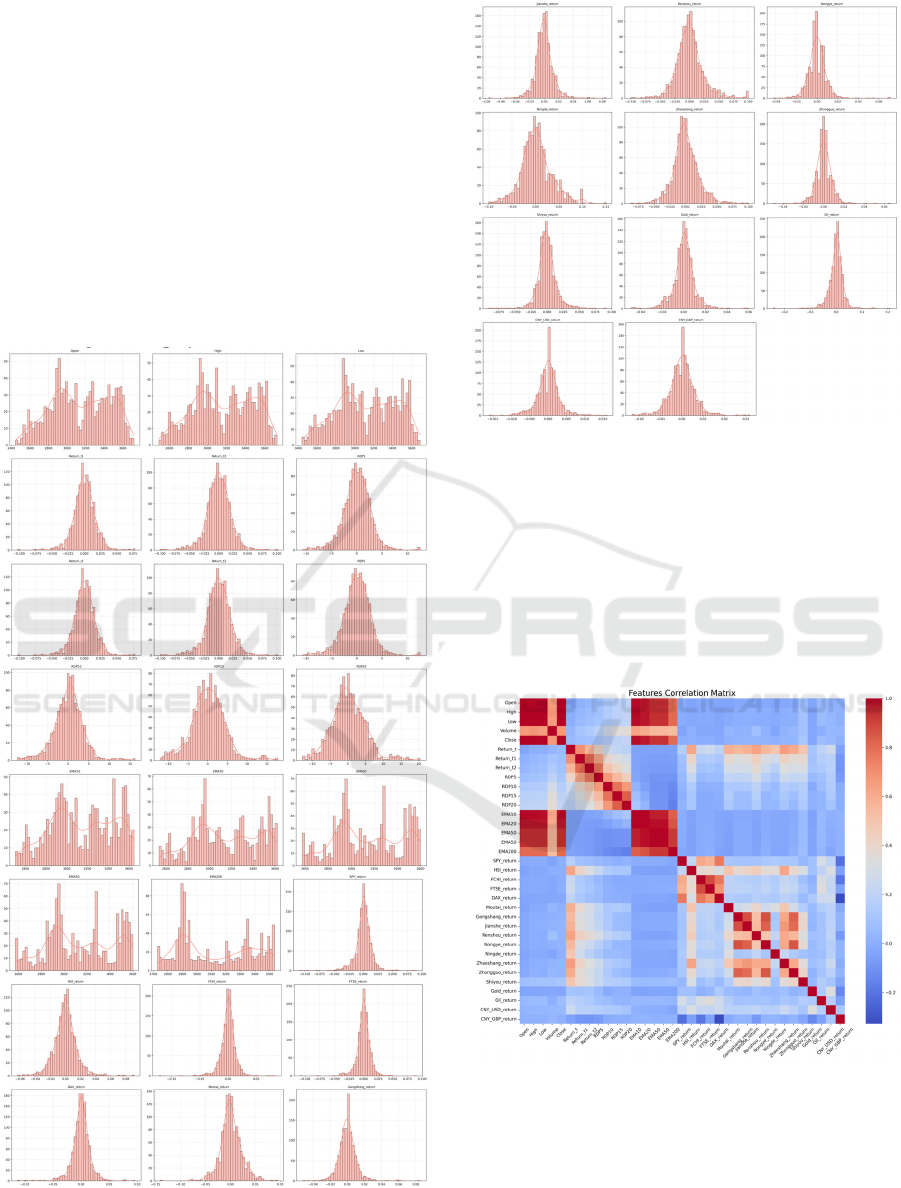
Then, this paper analyses the distribution of each

feature. Figure 3 displays the results.

Figure 3: Distribution of feature. (Picture credit: Original)

From the Figure 3, it can be found that the

distribution of most features is close to normal

distribution, indicating that the data is relatively good.

Then, this paper explored the correlation between

features, and the specific results are shown in Figure

4. The Figure 4 reveals that the correlation coefficient

between features in the same group is lower. This

analysis also provides a basis for subsequent feature

branch selection.

Figure 4: Correlation between features of thermal map.

(Picture credit: Original)

2.4 Principal Component Analysis

Principal Component Analysis (PCA) is a

dimensionality reduction technique that is widely

utilized in machine learning. The fundamental

Multiple-Branch Convolutional Neural Network for SSEC Daily Return Prediction

267

principle involves projecting high-dimensional

datasets via linear dimensionality reduction, while

optimally preserving essential feature characteristics

and reducing the impact of data redundancy and noise

through variance-maximizing coordinate

transformations.

In this study, PCA is used to reduce the

dimensionality of the original features, and then the

new features are input into the four machine learning

models for prediction including SVM, RF, LR and

DT. The performance of these four improved models

will also be compared with the model presented in

this paper.

3 MULTIPLE-BRANCH

CONVOLUTIONAL NEURAL

NETWORK

3.1 Convolutional Neural Network

Convolutional Neural Network (CNN) is a deep

learning model designed for processing structured

data (e.g., images and time series). The core feature

of CNN is the use of convolutional operations to

extract the local features of the data, and then

progressively distill them from the low-level features

to high-level features through a multilayer network.

The network consists of a convolutional layer, an

activation function, a pooling layer and a fully

connected layer. The convolutional layer uses

convolutional kernels to extract features from local

regions of the input data, capturing local spatial

correlations while reducing the number of

parameters.

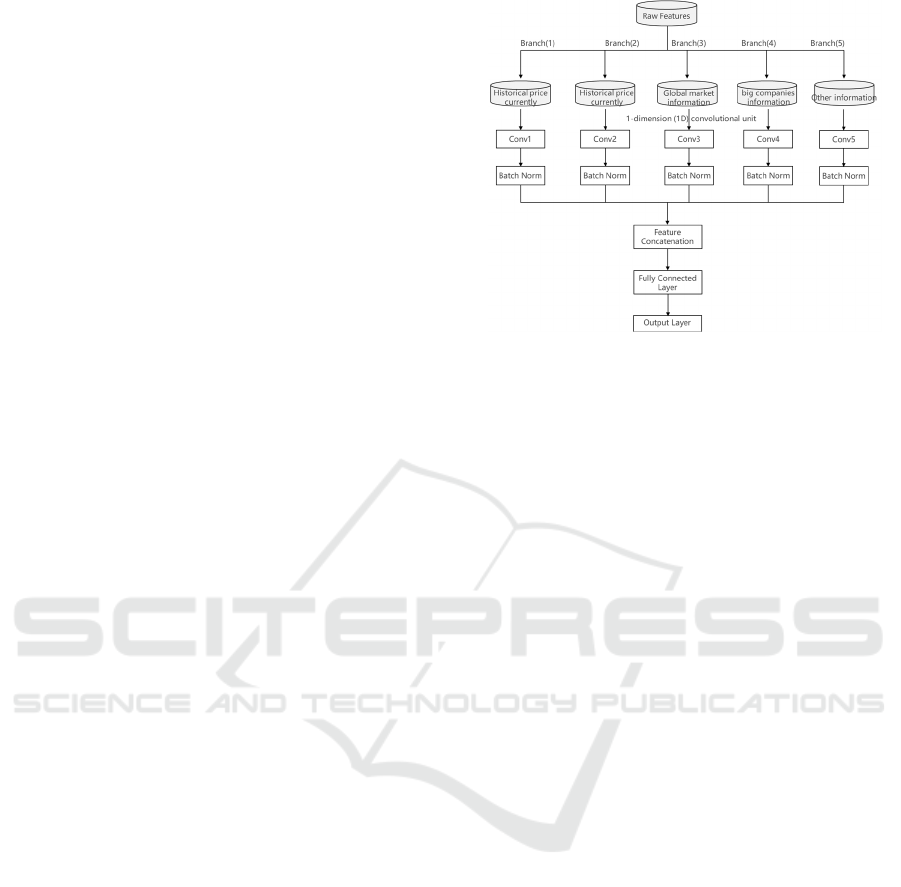
3.2 Framework of MBCNN

In this study, considering that the original features

contain several different dimensional features,

Multiple-branch Convolutional neural network

(MBCNN) is used to perform prediction. The original

features will be divided into 5 groups, each group of

features will be processed by different convolutional

units and standardized. The convolutional

architecture employs weight-sharing branches to

establish global feature correlations and a

convolutional unit is used to extract multiple features.

Then data will enter the Concatenation layer and go

through a dense layer, finally an output layer. The

detailed network structure is shown in Figure 5.

Figure 5: The framework of MBCNN. (Picture credit:

Original)

3.3 Feature Extraction Block of

MBCNN

The features in Branch (1) include important

historical price information ('Open', 'High', 'Low',

'Volume','Close','Return_t','Return_t1','Return_t2').

The features in Branch (2) include the rest historical

price information

('RDP5','RDP10','RDP15','RDP20','EMA10',

'EMA20', 'EMA50', 'EMA50', 'EMA200'). The

reason for dividing the historical information into two

different branches for extraction is that the

information in branch (1) is that the recent

performance of the stock index contains more key

information. The features in Branch (3) include other

major markets information

('SPY_return','HSI_return','FCHI_return','FTSE_retu

rn','DAX_return'). The features in Branch (4) include

information of top 9 companies in SSEC. The features

in Branch (5) include other important information

('Gold_return','Oil_return','CNY_USD_return','CNY

_GBP_return'). Then, to better extract features, this

paper chooses 1-dimension (1D) convolutional unit,

since it has a significantly lower computing cost than

2-dimensional (2D) CNN and is more suitable for

processing time-series data, (Gao et al., 2022). After

that, each block's outputs are normalized by a

normalization layer. The entire features extraction

process is completed.

ICDSE 2025 - The International Conference on Data Science and Engineering

268

4 EXPERIMENT

4.1 Experimental Setting

In this study, four traditional machine learning

models, including DT, SVM, RF, LG, will be

compared and experimented with the MBCNN

proposed in this paper, and their prediction

performances will be evaluated comprehensively by

different metrics. The ratio of the test set for all

experiments was 0.2 and specific experimental

settings can be found in Tables 2 and Table 3.

Table 2: Experimental settings of comparing models.

Comparing

models

Parameter

DT Max depth: 5.

RF Max depth: 5; the number of trees: 100.

SVM Kernel function: rbf; C: 1; degree: 3.

Max iter: 1000; solver: lbfgs; C: 1;

Penalt

: l2.

Table 3: Experimental settings of MBCNN.

Parameter Value

Optimizer Adam

Loss Function Binary crossentropy

Metrics Accuracy

learning rate 0.001

Epochs 100

Batch Size 32

Validation weight 0.2

Test weight 0.2

Class Weights balanced

4.2 Evaluation Metric

This study uses accuracy to assess the performance of

the various models. However, the data set contains

unbalanced data, so the F-measure is chosen as the

second assessment metric (Gunduz et al., 2017;

Hoseinzade & Haratizadeh, 2019).

The source of accuracy and F-measure is the

confusion matrix, which compiles the numbers of

cases that were categorized properly and improperly.

True positive (TP) refers to situations when both the

actual and projected outcomes are “up”, and true

negative (TN) refers to situations where both

predictions and actual results are “down”. False

positive (FP) happens when the real result is “down”

but the forecast is “up”, and false negative (FN)

happens when the actual result is “up” and the

prognosis is “down”. They are calculated by the

Equation (4), Equation (5), Equation (6), Equation

(7).

Precision =

𝑇𝑃

𝑇𝑃 + 𝐹𝑃





Recall =

𝑇𝑃

𝑇𝑃 + 𝐹𝑁





F−Measure=

2 × 𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 × 𝑅𝑒𝑐𝑎𝑙𝑙

𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 + 𝑅𝑒𝑐𝑎𝑙𝑙





Accuracy =

𝑇𝑃 + 𝑇𝑁

𝑇𝑃+𝑇𝑁+𝐹𝑃+𝐹𝑁





4.3 Experimental Result

Table 4 shows the results of the experiment. In

Accuracy metric, MBCNN improves 6.90%, 1.31%,

6.16% and 1.31% over DT, RF, SVM and LR,

respectively. On the F-Measure metric, MBCNN

improves 10.83%, 2.87%, 7.99% and 3.47% over DT,

RF, SVM and LR, respectively. These results show

that MBCNN has better overall performance than

traditional machine learning models in classification

tasks. The data processed by PCA did not have the

expected effect on the prediction performance of the

machine learning models, and this paper argues that

it is related to the structure of the data used, and that

PCA lost the key information of the data or

introduced noise in the process of dimensionality

reduction, which led to a decrease in the prediction

effect of the model.

Table 4: The experimental results.

Model Accuracy Precision Recall F-Measure

DT 0.725 0.662 0.642 0.646

PCA+DT 0.637 0.533 0.728 0.615

RF 0.765 0.726 0.691 0.696

PCA+RF 0.686 0.586 0.716 0.644

SVM 0.730 0.659 0.667 0.663

PCA+SVM 0.642 0.541 0.654 0.592

LR 0.765 0.720 0.667 0.692

PCA+LR 0.662 0.570 0.605 0.587

MBCNN 0.775 0.804 0.852 0.716

To further evaluate the predictive performance of

MBCNN, Receiver Operating Characteristic (ROC)

curves are plotted for each model. The ROC curve is

an important tool used to evaluate the performance of

a binary classification model. It calculates the True

Positive Rate (TPR) and False Positive Rate (FPR)

Multiple-Branch Convolutional Neural Network for SSEC Daily Return Prediction

269

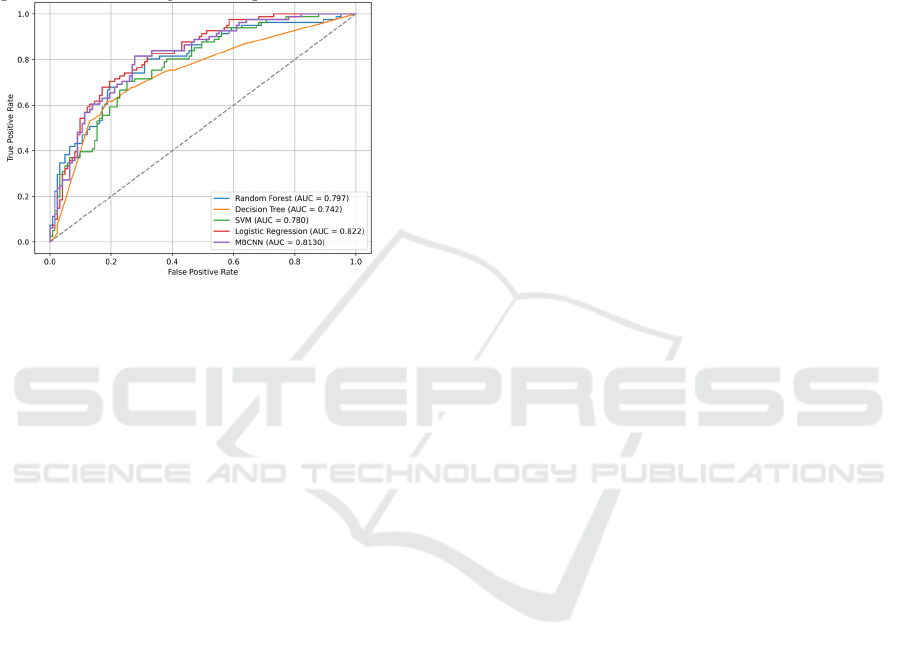
with different thresholds and plots the relationship

between them to measure the overall performance of

the classifier. From Figure 6, it can be seen that the

curve of MBCNN lies above three other traditional

machine learning models, suggesting that it has a

higher TRP at different thresholds and a lower FPR.

And then LR has higher AUC values than MBCNN,

indicating that for the LR model, positive samples are

overall more likely to be assigned higher predictive

probabilities than negative samples.

Figure 6: ROC curves of each model. (Picture credit:

Original)

5 CONCLUSION

In this paper, a deep learning model is proposed to

predict the return direction of SSEC by integrating

different groupings of feature divisions. The first

contribution of this paper is to predict the 𝑅

,

direction of SSEC using deep learning techniques,

which helps investors to make modifications to their

investment decisions for the next day to cope with

changes in the stock market. Second, in this study, the

effect of applying PCA for data processing on model

performance was investigated, which is not able to

improve models’ performance. Third, this paper

proposes the MBCNN model to predict the return

direction of SSEC by extracting 35 features through

multiple branches. And this model is compared with

four traditional machine learning models and the

experimental results show that the model proposed in

this study outperforms the traditional models in terms

of prediction accuracy and F-measure. In terms of

ROC curve performance, the MBCNN model is also

excellent, with AUC=0.812>0.8, which is slightly

lower than that of the LR model (AUC=0.822) but

much better than the other three models.

However, from the results of the ROC curves, it

can be concluded that the shortcoming of this study is

that the performance of the MBCNN model is not as

stable as that of the LR model. Although MBCNN

outperforms LR at a threshold of 0.5, the overall

positive and negative prediction discrimination rate is

not as good as LR. Therefore, Future research can

further improve the branch network structure to make

it better adapt to the input data structure and improve

the prediction performance. Meanwhile, in this

research, PCA did not improve model performance,

most likely because PCA was not applicable to the

data structure of this study. In the future, the people

can further explore the effect of adding

dimensionality reduction algorithms, such as PCA

and KNN, on the performance of the model in the

case of multi-feature.

REFERENCES

Akyildirim, E., Bariviera, A. F., Nguyen, D. K., & Sensoy,

A., 2022. Forecasting high-frequency stock returns: A

comparison of alternative methods. Annals of

Operations Research, 313, 639–690.

Ayyildiz, N., & Iskenderoglu, O., 2024. How effective is

machine learning in stock market predictions. Heliyon,

10(2), e24123.

Chen, H., Xiao, K., Sun, J., & Wu, S., 2017. A double-layer

neural network framework for high-frequency

forecasting. ACM Transactions on Management

Information Systems, 7(4), 1–17.

Gao, R., Zhang, X., Zhang, H., Zhao, Q., & Wang, Y.,

2022. Forecasting the overnight return direction of

stock market index combining global market indices: A

multiple-branch deep learning approach. Expert

Systems with Applications, 194, 116506.

Gunduz, H., Yaslan, Y., & Cataltepe, Z., 2017. Intraday

prediction of Borsa Istanbul using convolutional neural

networks and feature correlations. Knowledge-Based

Systems, 137, 138–148.

Hoseinzade, E., & Haratizadeh, S., 2019. CNNpred: CNN-

based stock market prediction using a diverse set of

variables. Expert Systems with Applications, 129, 273–

285.

Lo, A. W., 2004. The adaptive markets hypothesis. Journal

of Portfolio Management, 30(5), 15–29.

Nevasalmi, L., 2020. Forecasting multinomial stock

returns using machine learning methods. The Journal

of Finance and Data Science, 6, 86–106.

Weng, B., Lu, L., Wang, X., Megahed, F. M., & Martinez,

W., 2018. Predicting short-term stock prices using

ensemble methods and online data sources. Expert

Systems with Applications, 112, 258–273.

Xiao, C., Xia, W., & Jiang, J., 2020. Stock price forecast

based on combined model of ARIMA-LS-SVM. Neural

Computing and Applications, 32, 5379–5388.

Zhong, X., & Enke, D., 2019. Predicting the daily return

direction of the stock market using hybrid machine

learning algorithms. Financial Innovation, 5(1), 1–20.

ICDSE 2025 - The International Conference on Data Science and Engineering

270