A Study of Multi-Objective Optimisation Algorithms

Peiqi Gao

Mathematics and Statistics, Xidian University, Xi`an, Shaanxi Province, 710071, China

Keywords: Multi-Objective Optimisation, AHP Combined with EWM, NSGA-II, PSO.

Abstract: In production activities, the problem often involves the optimisation of multiple objectives, and the traditional

single-objective problem-solving methods are unable to deal with optimisation problems with multiple

objectives. Traditional single-objective optimization methods usually focus on the optimal solution of one

objective function, while multi-objective optimization problems need to consider multiple objective functions

at the same time. This paper offers a comprehensive summary of the approaches to multi-objective

optimization problems and proposes recommendations for future development. Firstly, the development

history of multi-objective optimisation algorithms is reviewed, and then the related concepts of multi-

objective problems, such as pareto optimal solution set, are briefly explained. In this paper, multi-objective

optimisation algorithms are broadly classified into three categories: multi-objective weighting methods,

multi-objective population genetic algorithms, and multi-objective individual evolutionary algorithms. The

advantages and disadvantages of the three main types of methods are analysed by practical examples of the

methods, and suggestions for subsequent improvements are given based on limitations.

1 INTRODUCTION

In engineering and scientific contexts, it's common to

encounter optimisation problems where the goal is to

achieve optimality within a specific domain. These

are referred to as multi-objective optimisation

problems when multiple objectives are involved. For

example, when optimising the purchase of an item,

the decision maker usually has to balance price and

quality.

The solution to multi-objective optimisation

problems is very commonly used in production

activities, and researchers are constantly proposing

new ideas to deal with them. From 1896, Pareto

proposed the optimal solution of pareto to the

beginning of the 20th century, multi-objective

optimisation was introduced into finance and other

fields, marking the gradual formation of the

theoretical basis of multi-objective optimisation;

During the mid-to-late 20th century, scientists and

researchers primarily approached multi-objective

optimization problems by converting them into

single-objective problems, such as: the objective

function weighting method (Xiao, 2011). During the

transition from the 20th to the 21st century,

https://orcid.org/0009-0008-7480-8746

researchers applied population genetic algorithms in

the field of computational intelligence to multi-

objective optimisation. Later individual algorithms,

such as Particle Swarm Optimization Algorithm

(PSO) were applied to multi-objective optimisation.

Since then, new methods have been proposed, such as

Multi-objective Evolutionary Algorithm based on

Decomposition (MOEA/D), but they are not

considered in this paper for the time being.

When dealing with multi-objective optimisation

problems, the main problem is how to make multiple

objectives reach the optimal solution. In the problem,

when one objective is optimized, the performance of

the other objectives usually decreases. This is because

a multi-objective optimization problem involves a

contradiction between the various sub-objectives.

Therefore, a compromise must be made to achieve the

best possible outcome. In other words, there are

solutions that cannot be compared in terms of their

advantages and disadvantages. Consequently,

solutions to multi-objective optimization problems

are not unique. Instead, there exists a set of optimal

solutions, which is referred to as the Pareto optimal

solution set.

Gao, P.

A Study of Multi-Objective Optimisation Algorithms.

DOI: 10.5220/0013680600004670

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Data Science and Engineering (ICDSE 2025), pages 175-181

ISBN: 978-989-758-765-8

175

This paper classifies multi-objective optimisation,

which is often used in scientific experiments, into

three categories, multi-objective weighting method

(which uses weighting to convert a multi-objective

problem into a single-objective problem.), multi-

objective population genetic algorithm (which

introduces multi-objective optimisation into the

framework of genetic algorithms), and multi-

objective individual evolutionary algorithms (which

applies an initial solution to generate a subsequent

solution). The corresponding computational

principles are analysed as well as specific

applications in scientific experiments. Ultimately and

give directions for improvement.

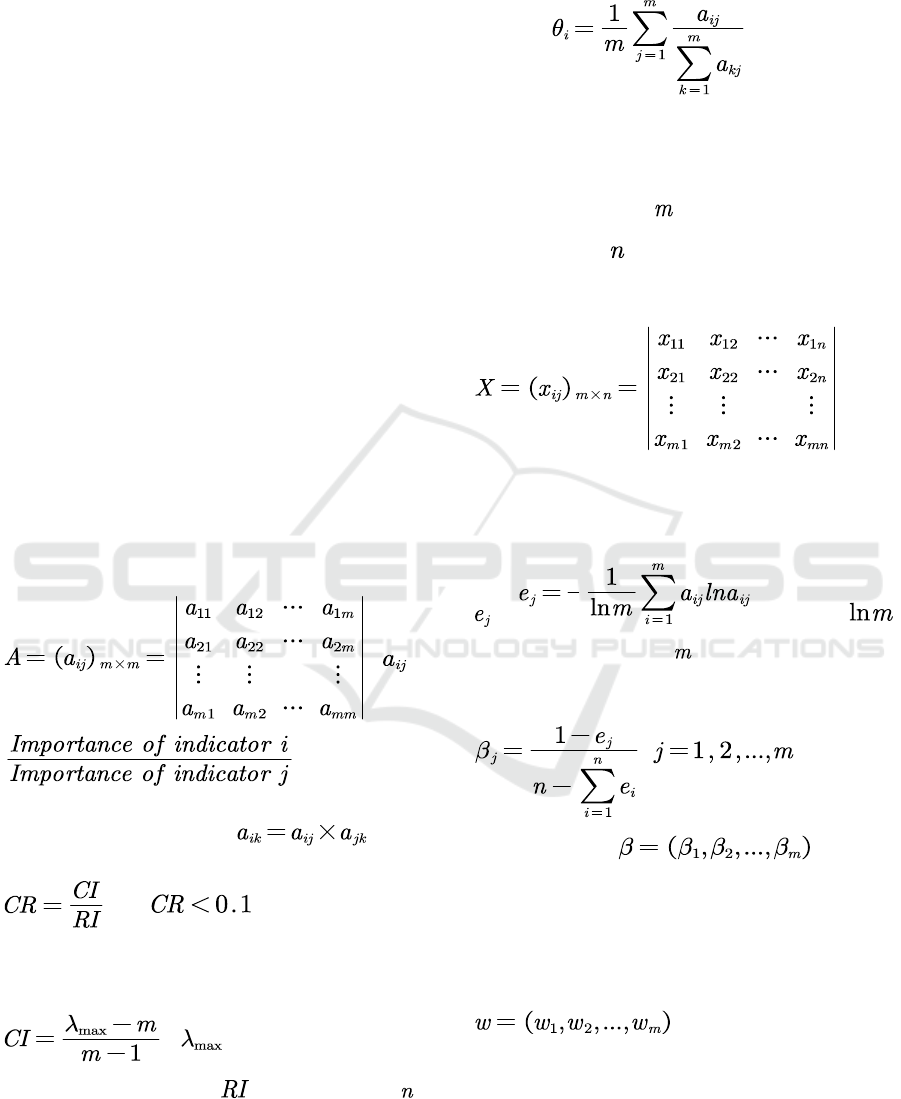
2 MATHEMATICAL

DESCRIPTION

The multi-objective problem can be described in the

following standard form

There are m objective functions, and the variables

involved in decision-making are n-dimensional. The

vector

, which includes through , belongs to

, an n-dimensional space for making decisions.

The variable representing objectives,

, which

includes

through , belongs to , the m-

dimensional space of objectives. Furthermore, there

are

constraints where is less than or equal to

zero

and constraints are

established where

equals zero .

Definition 1 (Feasible Solution) A solution is said

to be feasible if and only if it satisfies the equality

constraints

and the

inequality constraints

in .

The set of all feasible solutions, denoted as

, and

Definition 2 (pareto optimal solution) Assume

that

, is pareto dominated

(dominated as

, ) if

and

. A feasible

solution

is a pareto optimal solution (or non-

dominated solution) if there is no

and the set of all pareto optimal solutions is the set of

pareto optimal solutions

3 MULTI-OBJECTIVE

WEIGHTING METHOD

3.1 Overview of the Weighting Method

The core idea of the weighting method is to convert a

multi-objective optimization problem into a single-

objective one by assigning weights to the various

objective functions. Let’s denote the weights as

and the objective functions as

. By calculating

, the multi-objective optimization problem is

effectively transformed into finding the feasible

solution that maximizes

, thereby identifying the

optimal solution.

The core of the weighting method lies in the

assignment of weights. There are three main

approaches to assigning weights: the subjective

weighting method, the objective weighting method,

and the integrated subjective and objective weighting

method. Among the commonly used subjective

weighting techniques, the Analytic Hierarchy Process

(AHP) and the Grey Analytic Hierarchy Process

(GAHP) are often utilized. However, these methods

are rather rough, and personal subjective factors have

a significant impact on the solution (Guo, 2008).

When it comes to problems requiring higher

precision, the results may not be consistent with the

actual situation.

Objective weighting techniques encompass

methods such as the Entropy Weight Method (EWM)

and Principal Component Analysis (PCA), among

others. This type of method is calculated based on the

data of the program (Wang, 2011). The results are

relatively objective, avoiding the influence of the

evaluator's subjective factors on the weight of the

indicators. Nevertheless, the Entropy Weight Method

(EWM) also has its drawbacks. The weights of the

indicators obtained through it only indicate the

relative intensity of the competition among the

ICDSE 2025 - The International Conference on Data Science and Engineering

176

indicators, rather than the true significance of the

metrics. Moreover, the determination of its weight

relies entirely on the relationship between the

objective data. When the objective data is more

special, the weight will differ from the actual

situation.

The subjective-objective comprehensive

weighting method usually combines the two

approaches mentioned above, such as the Analytic

Hierarchy Process-Entropy Weight Method (AHP-

EWM)(Fei, 2009). However, in the process of

seeking the integrated weights with this method, the

combination is merely a simple synthesis of the

results of the indicators after using each of the

subjective and objective methods to find the weights

of all the indicators.

3.2 Analytic Hierarchy Process-

Entropy Weight Method

Among all weighting methods, the most commonly

used in scientific research is (AHP-EWM) in the

subjective-objective integrated weighting method.

3.2.1 Calculation of Analytic Hierarchy

Process weights

Assume that the judgement matrix

1) Consistency test. Test whether the whole

judgement matrix meets

, by

judging the size of the consistency ratio coefficient

. If , the consistency of

the judgement matrix isn't acceptable, adjustments

are needed to ensure it meets the required

consistency. The consistency coefficient

, is the largest eigenvalue

of the judgement matrix.

is determined by ,

and the specific function value can be obtained

through the relevant table.

2) Calculate the weights by performing column

normalisation followed by arithmetic mean to the

weights,

3.2.2 Calculation of Entropy Weighting

Method Weights

Let there be a total of data points, each data point

corresponds to

objective function values, the

corresponding objective function value of the data

points constitutes an evaluation matrix

The

operation procedure is as follows

Pre-processing of the above matrix such as data

regularisation, normalisation etc.

Calculate the entropy measure of the jth parameter

, , where

denotes the logarithm of

Calculate the entropy value corresponding to the

entropy weights

to get the

entropy weights.

3.2.3 The Final Weights

Multiply the weights of the hierarchical analysis and

entropy weighting methods and then normalise by

multiplication to get the final weights

3.3 Example of the Use of Hierarchical

Analysis-Entropy Weight Method

In practical applications, the hierarchical analysis-

entropy weight method is mainly used in the case of

A Study of Multi-Objective Optimisation Algorithms

177

limited decision-making methods, and Wang Huibin

and others applied this method to photovoltaic power

generation projects. The three main indicators in

photovoltaic power generation are scale, cost, and

benefit (Wang, 2022). The scale is determined by the

installed capacity, the number of hours of power

generation, and the amount of power generated. Cost

is determined by the averageised cost of electricity,

the investment per unit of electricity, and the time to

start earning. Benefits are determined by the internal

rate of return (IRR), which indicates profitability over

the entire operating period, and the net present value

(NPV), which measures net income per unit of

operating time. In this context, all indicators for scale

and benefit are maximizing. Indicators that are

maximized have larger corresponding values, while

those that are minimized have smaller values.

All indicators are normalised (all indicators are

converted into very large ones, which can be inverted)

and then dimensionless. Use Hierarchical Analysis-

Entropy Weighting to get the priority of each

scenario. The prioritisation results were compared

with the results obtained using only Hierarchical

Analysis and only Entropy Weights. The results

obtained were found to be superior.

4 MULTI-OBJECTIVE

POPULATION GENETIC

ALGORITHM

4.1 Overview of Multi-Objective

Population Genetic Algorithms

Over the past 30 years, genetic algorithms

have

developed rapidly. Scientists have applied genetic

algorithms to multi-objective optimisation problems

(Ma, 2007). This has been accompanied by the

introduction of concepts related to the Pareto optimal

solution set. As a result, the success rate of multi-

objective genetic algorithms has been further

guaranteed in terms of their computational results.

The Genetic Algorithm (GA) is a method for

finding optimal solutions, inspired by the biological

principle of "survival of the fittest." In this context,

the fitness value indicates the quality of a solution,

which is reflected by the final function value.

Additionally, GA involves encoding and decoding

operations, where feasible solutions are converted

into strings of characters, such as numbers or letters.

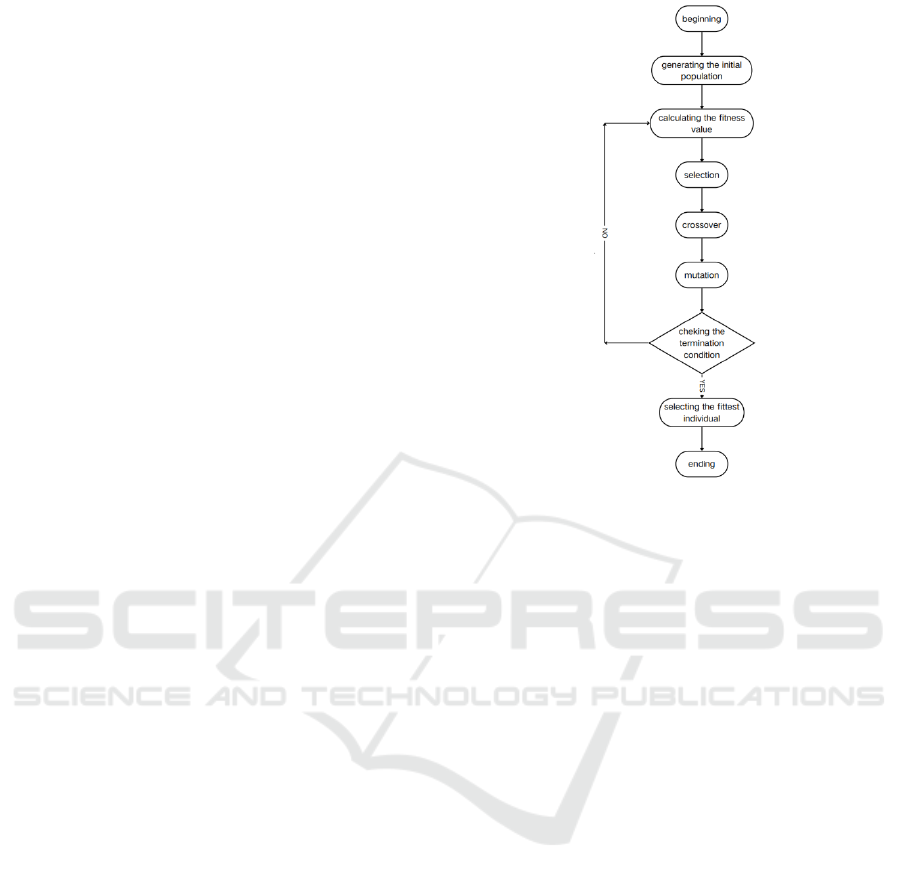
Figure 1: The flow of the genetic framework.(Picture credit :

Original)

The fundamental processes include selection,

recombination, and mutation, in figure 1.

Selection is used to choose better individuals from

the group. It increases the probability of these better

individuals being selected. This can ensure the

convergence of the algorithm. Common selection

methods include the roulette wheel selection method

(RWS). The individual's fitness value is directly

converted into the probability of being selected.

Crossover, where information is exchanged for

multiple parent individuals selected to produce new

child individuals. The diversity of solutions can be

ensured and local convergence due to too fast

convergence can be avoided to some extent. Common

crossover methods include single-point crossover, etc.

mutation, one of the selected parent individuals is

manipulated to produce a new child individual. It also

ensures the diversity of solutions and to some extent

avoids local convergence due to too fast convergence.

However, the difference with crossover is that

crossover requires at least two parent individuals,

while mutation can be achieved with only one parent

individual; at the same time, the probability of

crossover occurring is greater than the probability of

mutation occurring. A common method of mutation

is single point mutation.

ICDSE 2025 - The International Conference on Data Science and Engineering

178

4.2 Non-Dominated Sorting Genetic

Algorithm II (NSGA-II)

The common multi-objective genetic algorithms are

Vector Evaluated Genetic Algorithm (VEGA), Non-

dominated Sorting Genetic Algorithm (NSGA), and

Strength Pareto Evolutionary Algorithm

(SPEA)(Xu,2007). All of these methods use the

framework of genetic algorithms and also apply

pareto dominance relationships, which finally have

significant results in ensuring diversity. However,

although all of these methods employ the framework

of genetic algorithms, the specifics of each step are

different. In the following section, the commonly

used multi-objective genetic algorithm is described in

detail: Non-dominated Sorting Genetic Algorithm II

(NSGA-II)(Gao, 2006)

Perform a fast non-inferiority stratification for the

population

. That is, according to the pareto

dominance relationship, individuals that do not have

dominance relationships with each other are in the

same non-inferiority stratum, where individuals that

are not dominated by any individual are in the first

stratum, those that are only dominated by individuals

in the first stratum are in the second stratum, and so

on until all individuals of the population have been

stratified. Individuals in the same stratum are also a

group of individuals, with the first stratum being the

first group and the second stratum being the second

group. According to the result of non-inferiority

stratification, the population

can be divided into

non-inferiority groups, i.e .,the first

group

is the optimal non-inferiority group of the

population.

Crowding degree calculation, Crowding degree

can indicate the density of individuals in the space.

Assume that the jth non-inferiority group consists of

m individuals. After the jth non-inferiority group is

desorted for the mth objective function value, an

infinite distance is assigned between the first and last

points, and the congestion degree distance for the ith

individual is calculated as

denoting the maximum and minimum values,

respectively

The dominance relation can be further extended

by the crowding degree calculation in step 2). That is,

, i.e., it means that when two solutions belong to the

same non-inferior group, the solution with greater

crowding degree is preferred.

Add the elite strategy in selecting the best

individual. That is, the selection range of individuals

is increased to the concatenation of parents and

children, expanding the search range and making the

algorithm less likely to fall into local optimal

solutions.

4.3 Application of NSGA-II Algorithm

Wang Xi employed the NSGA-II algorithm to tackle

the issue of connecting wind farms to the grid and

expanding the grid, with the aim of reducing costs,

minimizing grid expansion, and lowering pollutant

emissions (Wang, 2011). The final objective is

reached by adjusting the independent variables wind

farm access location, access capacity, and the scheme

of grid expansion.

By comparing the other algorithms, it is

concluded that the NSGA-II ensures the stability of

the algorithm results, i.e., it works well for most of

the cases. At the same time, it does not need a priori

knowledge to get the weights, and the calculation

process is more intelligent.

5 MULTI-OBJECTIVE

INDIVIDUAL EVOLUTIONARY

ALGORITHMS

5.1 Brief Description of Multi-

Objective Individual Evolutionary

Algorithms

In the last fifteen years, population-based algorithms

such as genetic algorithms have not developed

significantly, but some optimisation algorithms based

on individual search mechanisms have developed

rapidly, such as Particle Swarm Optimization (PSO)

(Zhang, 2004), Ant Colony Optimization (ACO)

(Duan, 2004). These algorithms are different from the

mechanism of eliminating individuals in genetic

algorithms, but update and iterate each individual in

the population based on the optimal solution of the

current individual and population. Therefore, this

type of algorithm has more interaction of information

between individuals, and has memory and

consistency for the update route. At the same time,

the update is more flexible and less likely to fall into

local optimal solutions.

A Study of Multi-Objective Optimisation Algorithms

179

5.2 Multi-Objective Particle Swarm

Algorithm

Among the individual-based search mechanism

optimisation methods, the particle swarm algorithm is

more frequently utilized. In this study, we will first

introduce the particle swarm algorithm, and then

describe how to apply the particle swarm algorithm to

multi-objective optimisation problems.

5.2.1 The Particle Swarm Algorithm

The basic particle swarm algorithm is mainly for

single-objective optimisation problems, let

be the

size of the parameter space,

be the size of the

population, and the particle is ,

.The

corresponding velocity

The

best position for this particle so far is

, and the best position for

the whole population is.

According to the iterative formula

where

is the inertia index and is a number

generated by a random process in

. reflecting

the dependence on the previous speed

is the acceleration weight, a number generated

by a random process in

is the stochastic number in is called the

cognitive factor. Reflects dependence on one's own

experience

is the random number in is the social

factor. Reflects the degree of dependence on group

experience

The coordinates of the particles in the population are

updated iteratively until the requirements of the

question are met (either the number of iterations

required or the accuracy required). By observing the

iteration formula

, we can find that the velocity

iteration formula is roughly divided into three parts,

the first part

indicates that it receives the

influence of the last velocity vector, i.e., it is

influenced by its own velocity at the last moment,

which is also known as the memory term. The second

part

Indicates that the velocity of

the particle receives the influence of the vector from

the current position to the particle's optimal point, i.e.,

it indicates that it receives the influence of the

particle's optimal point, which is also known as the

self-cognition term. The third part

indicates that the velocity receives

the influence of the vector from the current individual

position to the group optimal position, which can

reflect the influence of receiving the group optimal

point, also known as the group cognitive term. Also

All are random numbers, which can increase the

diversity of the solution.

5.2.2 Applications of Multi - Objective PSO

For the multi-objective particle swarm algorithm,

since there is no single optimal solution, only the

optimal solution set exists, i.e., The ultimate objective

is to achieve the best possible solutions. Based on the

pareto dominance relation, the population

is divided into two populations, one is the non-

dominated subset

, the other is the dominated

subset

, and the corresponding numbers of

individuals are

. Each

update of the individual coordinates of the particle

population is only for the dominant subset

Determine the dominance relationship between the

updated subset

and the individuals in the non-

dominated subset

, if there is an individual in the

subset

that is dominated by an individual in the

dominated subset

, then replace the corresponding

individual. The update is iterated until the termination

condition (accuracy or number of iterations) is met.

5.3 Application of Multi-Objective

Particle Swarm Algorithm

Gu applied particle swarm optimisation （PSO）to a

Combined Heat and Power (CHP)-based Microgrid

system (Gu, 2012). A Combined Heat and Power

(CHP)-based Microgrid system mainly refers to a

ICDSE 2025 - The International Conference on Data Science and Engineering

180

system that can control the simultaneous production

of electricity and heat. The final objective function is

to minimise the operating cost, carbon monoxide

emission and nitrogen oxide emission. Meanwhile,

the constraints are: battery charging and discharging

balance and surplus supply of heat energy. The

particle swarm algorithm was applied to optimisation

in two cases: a hospital and a school. The final

calculation results were found to be reasonable. It was

concluded that the particle swarm algorithm is widely

used in the field of combined heat and power supply.

6 CONCLUSION

In this paper, the existence of multi-objective

problems is firstly introduced widely, after which the

basic concepts about multi-objective problems, such

as feasible solution sets, are introduced. After that, the

common methods for solving multi-objective

problems are classified into three categories,

describing their mathematical principles and

applications in real life, and comparing the

advantages and disadvantages between different

methods. All three types of methods can be improved.

The main element involved in the weighting

method is the determination of the weight vectors, a

part that is difficult to improve if one wants to make

innovations in the mathematical theory. In addition to

the determination method can be improved, the

weights can be made adaptive, that is, the weights are

not fixed in the arithmetic process, and do not need

human intervention to improve. Multi-objective

population genetic algorithms are also relatively well-

developed at the structural level of the algorithm.

However, the determination of some parameters can

utilize emerging computational methods in recent

years, such as surrogate models and machine

learning. Yet, the choice of specific methods still

needs to be tailored to the specific application

scenario. For the recently emerged multi-objective

individual evolutionary algorithms, there are many

innovations, such as the introduction of the farthest

point from the point and the nearest point in the

iterative formula to avoid the local optimal solution,

as well as the introduction of other particles in the

population to improve the iterative formula and so on.

REFERENCES

Duan, H., Wang, D., Zhu, J., et al., 2004. Progress in the

theory and application research of ant colony algorithm.

Control and Decision Making, (12), pp.1321-

1326+1340.

Fei, Z., 2009. Research on entropy right-hierarchical

analysis method and grey-hierarchical analysis method.

Tianjin University.

Gao, Y., 2006. Research and application of non-dominated

sorting genetic algorithm (NSGA). Zhejiang

University.

Gu, W., Wu, Z., WANG, R., 2012. Multi-objective

operation optimisation of cogeneration-type microgrid

considering pollutant gas emission. Power System

Automation, 36(14), pp.177-185.

Guo, J., Zhang, Z., Sun, Q., 2008. Research and application

of hierarchical analysis. Chinese Journal of Safety

Science, (05), pp.148-153.

Ma, Y., Yun, W., 2012. Research progress of genetic

algorithm. Computer Application Research, 29(04),

pp.1201-1206+1210.

Wang, Y., 2011. Comprehensive evaluation of professional

journals of library and intelligence in mainland China -

A comparative study based on entropy weighting,

principal component analysis and simple linear

weighting. Intelligence Science, 29(06), pp.943-947.

Wang, H., Hu, F., Liu, Y., 2022. Research on multi-

objective decision analysis of photovoltaic power

generation project. Hydropower Generation, 48(10),

pp.99-103.

Wang, X., Zhang, P., 2011. Multi-objective grid planning

for wind farms using NSGA-II hybrid intelligent

algorithm. Chinese Journal of Electrical Engineering,

31(19), pp.17-24.

Xiao, X., Xiao, D., Lin, J., et al., 2011. Research overview

of multi-objective optimisation problems. Computer

Application Research, 28(03), pp.805-808+827.

Xu, L., 2007. Research and application of multi-objective

optimisation problem based on genetic algorithm.

Central South University.

Zhang, L., Zhou, C., Ma, M., et al., 2004. Solving multi-

objective optimisation problems based on particle

swarm algorithm. Computer Research and

Development, (07), pp.1286-1291.

A Study of Multi-Objective Optimisation Algorithms

181