Optimization of Moon Model-Contrastive Federated Learning

Changyu Chen

1,* a

and Weiheng Rao

School of Advanced Engineering, University of Science and Technology Beijing, Beijing, 100083, China

Business School, The University of Sydney, Sydney, 2050, Australia

Keywords: Model-Contrastive Federated Learning, MOON, Temperature, CNN-Transformer Integration.

Abstract: Federated contrast learning has shown great potential in privacy-sensitive scenarios, enabling multiple parties

to train models using their local data, rather than sharing privacy data. Model-contrastive Federated learning

(MOON) effectively improves the accuracy of graphical contrast learning. However, after researching

SimCLR which is a part of the origin of the MOON algorithm, it is found that the MOON federal learning

algorithm does not consider the influence of the change of hyperparameter (temperature) on the accuracy of

its model. This article will focus on the model comparison federated learning framework MOON, and propose

an adaptive temperature control mechanism based on simulated annealing, aiming at the static set limit of its

key hyperparameter, contrast loss temperature (τ). The temperature attenuation function is designed to achieve

global-local optimization of dynamic balance - the initial high-temperature promotion model explores the

global feature space and later low-temperature enhanced local fine-grained optimization. The experiments in

this paper show that the dynamic temperature can slightly improve the accuracy of the MOON model. This

work systematically quantifies the influence of temperature parameters on model contrast federation learning.

1 INTRODUCTION

According to research by the World Innovation and

Change Management Institute, AI is becoming an

important part of human life which constitutes at least

10% of day-to-day activities (World Innovation and

Change Management Insititute, 2024). Intelligent

systems often leverage machine learning capabilities

to enhance their performance(Janiesch et al., 2021).

Meanwhile, the data requirement of deep learning is

huge. However, data is usually stored in different

parties in practice (e.g., companies and self-users).

Due to increasingly stringent privacy laws of different

countries, parties cannot train a model by directly

uploading their data to a centralized server (Voigt &

Bussche, 2017).

Therefore, Federated Learning which is enhanced

to preserve the privacy of individuals’ data appears.

Compared to traditional machine learning, Federated

Learning is a distributed learning framework that

allows multiple entities to work collectively without

sharing sensitive data (Jafarigol et al., 2023). FedAvg

https://orcid.org/0009-0009-4720-133X

https://orcid.org/0009-0005-9297-3567

is one of the popular federated learning algorithms

(Brendan et al., 2016). In each round of the algorithm,

individual participants submit their locally trained

models to the central server, where these models are

integrated to improve the overarching global model.

Therefore, the raw data will not be changed in the

whole process.

Due to the limitation of most deep learning

methods when applying to image datasets, Model-

Optimized Federated Learning (MOON) was

proposed (Li et al., 2021). MOON algorithm proposes

a novel perspective based on FedAvg. Briefly, the

local model is adjusted by reducing the discrepancy

between the representations learned by the local

model and the global model in MOON. By the way,

the accuracy of MOON is significantly greater than

other methods when facing an image dataset (Li et al.,

2021).

This paper presents an improved version of the

MOON algorithm that adjusts the hyperparameter

temperature (τ) to increase the diversity of model

outputs. This paper uses simulated annealing. SA

draws inspiration from the annealing process in

128

Chen, C. and Rao, W.

Optimization of Moon Model-Contrastive Federated Learning.

DOI: 10.5220/0013679800004670

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Data Science and Engineering (ICDSE 2025), pages 128-132

ISBN: 978-989-758-765-8

metallurgy, beginning with an initial solution and a

high temperature. Temperature gradually decreases

as time goes by. This helps fine-tune the model's

outputs and provides a more effective framework for

federated learning, especially in contrastive learning

tasks. This paper also complicates the neural network

structure by introducing the Transformer architecture.

This allows the model to better capture long-range

dependencies and improve the model’s overall

performance.

2 BACKGROUND AND RELATED

WORK

2.1 Federated Learning and MOON

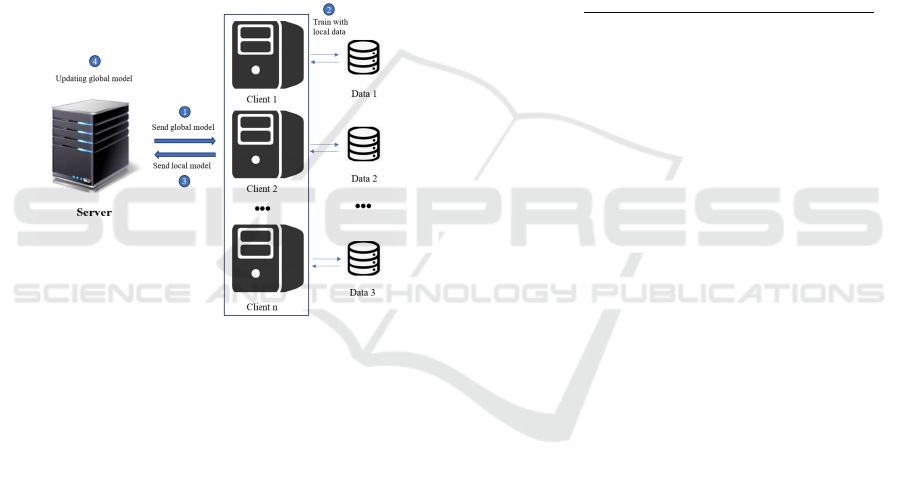
Figure 1: FedAvg framework (Original)

FedAvg is the most commonly used algorithm in

federated learning. The operational framework of

FedAvg is shown in Figure 1. Each round of FedAvg

consists of four steps. First, the server initializes the

global model and sends a global model to all parties.

Each party then uses the local data set to perform a

predetermined round of random gradient (SGD)

descent to update its local model. The parameters of

the local model are sent back to the server after the

update is complete. Finally, after accepting the local

model parameters of all clients, the server aggregates

the parameters by weighted average, thus generating

a new model for the next round of training.

Current research on FedAvg on non-independent

equally distributed data (non-IID) is mainly divided

into two types: improvements to the local training

part (i.e., step 2 of Figure 1) and improvements to

server-side aggregation (i.e., step 4 of Figure 1). This

paper will research and further improve the current

MOON Federation learning algorithm based on

FedAvg, which is an improved method for the local

training part.

The MOON federated learning algorithm is

designed to enhance model performance within

supervised learning contexts by contrast learning.

SimCLR framework is used as the core method of

contrastive learning in the MOON algorithm (Chen et

al., 2020). Therefore, based on FedAvg, a new model

contrastive loss term (i.e., ℓ



) proposed by MOON

has been added to the traditional loss term of

supervised learning (i.e., cross entropy loss ℓ



The aim of ℓ



is to both narrow the difference

between the local model 𝑧 and the global model

𝑧



and extend the difference between the local

model 𝑧 and the last local model 𝑧



. Below is the

formula of ℓ



ℓ



=−𝑙𝑜𝑔

 ((,



)/

 ((,



)/) ((,



)/)

(1)

Where τ represents a temperature parameter.

Therefore, the total loss function has become ℓ=

ℓ



+µℓ



2.2 Simulated Annealing

The Metropolis criterion is the origin of the Simulated

Annealing (SA) algorithm (Chen et al., 2007). SA is

a heuristic random search algorithm. SA's core

principle is to allow a small degree of deterioration

during total search. This is achieved by a probabilistic

mechanism. This mechanism helps SA avoid getting

stuck in a local optimum too early and increases the

chances of finding the global optimum. A large of

studies indicate SA is an effective optimization

technique capable of achieving the optimal solution

with a probability of 1 (Li et al., 2020). In 1983,

Kirkpatrick effectively brought the concept of

annealing into the realm of optimization (Kirkpatrick

et al., 1983). SA is widely used in optimization

problems. It's popular because it can search locally

really effectively and solves problems quickly.

It adds SA during training. SA can boost

exploration and prevent the model from getting stuck

in local optima in federated learning. This helps the

network break free from suboptimal setups and boosts

its generalization performance. This paper integrates

SA into MOON to dynamically adjust

hyperparameter temperature. The code presented in

this paper determines whether to accept a new

temperature by calculating the acceptance probability

between the new and old solutions. The formula for

calculating the acceptance probability of the

hyperparameter temperature is as follows:

Optimization of Moon Model-Contrastive Federated Learning

129

P=

1.0, if new_loss<old_loss

exp



__





,otherwise

(2)

old_loss and new_loss represent the loss values of

the old and new solutions, respectively, and

temperature denotes the current temperature. If the

new solution yields a lower loss than the old one, it is

directly accepted. In another situation, the new

solution is accepted with the probability calculated as

described earlier. In this paper, the temperature

update is closely related to the gradients during

training. Specifically, the updated formula for the

temperature is as follows:

temperature=max



temperature×



1−σ×

__

_



,min_temperature



(3)

current_grad and prev_grad represent the gradient

norms of the current and previous iterations,

respectively. α is a parameter that controls the rate of

temperature change, and ε is a small value used to

prevent division by zero. In this paper, the

temperature adjustment is designed to depend not

only on the cooling rate but also on the variation in

gradients. When the gradient change is large, the

temperature decreases rapidly, reducing the

probability of accepting suboptimal solutions.

Conversely, when the gradient change is small, the

temperature decreases more slowly, maintaining a

higher level of exploration.

2.3 Motivation

The importance of the hyperparameter temperature

(τ) is ignored in MOON federation contrast learning.

In this article, the hyperparameter temperature (τ) will

be emphasized. It is found from formula (1) that the

hyperparameter temperature (τ) is responsible for

controlling the "sensitivity" of similarity calculation

in the contrast loss function, which is similar to the

usage in SimCLR (Chen et al., 2020). The higher

temperature makes the scaling effect smaller, so that

the difference in similarity is not significant, while the

lower temperature has a larger scaling effect, which

can enhance the difference between the similarities.

Therefore, the hyperparameter temperature (τ) plays

an important role in contrast learning.

3 METHOD

3.1 Experiment

This paper refines the neural network model by

integrating Convolutional Neural Networks (CNNs)

and Transformer structures. So that it can

significantly improve the representation capability of

image features. For CIFAR-10, a CNN is first used as

the base encoder. The architecture includes two 3x3

convolutional layers, each followed by a Batch

Normalization layer and a ReLU activation function,

and then a 2x2 max-pooling layer (the first

convolutional layer with 32 channels and the second

convolutional layer with 64 channels). This is

followed by another two 3x3 convolutional layers,

each also followed by Batch Normalization and

ReLU activation, and another 2x2 max-pooling layer

(both convolutional layers have 128 channels), with a

0.1 Dropout added. Finally, the architecture includes

an additional pair of 3x3 convolutional layers, with

each layer accompanied by a Batch Normalization

layer a ReLU activation function, and a 2x2 max-

pooling layer (both convolutional layers have 256

channels).

The Transformer part employs a Transformer

encoder with 6 layers of Transformer encoder layers,

each with a model dimension of 256 and 8 attention

heads. The fully connected layer section first flattens

the feature maps output by the CNN and converts

them into the input format for the Transformer. It then

passes through two linear layers (with a hidden layer

dimension of 256) and ReLU activation functions,

finally output to the target classification dimension,

resulting in 10 output units.

For all methods, it uses the SGD optimizer with a

learning rate of 0.01. The SGD weight decay is

configured at 0.00001, with a momentum of 0.9 and

a batch size of 64. For all federated learning methods,

unless otherwise specified, the number of local

epochs is set to 10. For the CIFAR-10 dataset, the

number of communication rounds was set to 100.

This paper first focuses on adjusting the

temperature hyperparameter to improve the MOON

algorithm. The temperature in the MOON algorithm

controls the degree of softening in contrastive

learning. A lower temperature value makes the

model's representations of different classes more

distinct, while a higher temperature value reduces the

distinction between classes, making clustering easier.

This paper employs the simulated annealing

algorithm to achieve dynamic adjustment, gradually

decreasing the temperature during training to enable

more precise parameter optimization.

This paper proposes an improved acceptance

probability mechanism. When the loss value of the

new solution is lower than that of the current solution,

the new solution is directly accepted. Otherwise, the

acceptance probability is calculated based on the

Metropolis criterion, which is determined by the

ICDSE 2025 - The International Conference on Data Science and Engineering

130

exponential function 𝑒𝑥𝑝((𝑜𝑙𝑑_𝑙𝑜𝑠𝑠 − 𝑛𝑒𝑤_𝑙𝑜𝑠𝑠)/

𝑡𝑒𝑚𝑝𝑒𝑟𝑎𝑡𝑢𝑟𝑒) to decide whether to accept a worse

solution. This update mechanism enables this

algorithm to perform extensive exploration at high

temperatures and progressively converge to get an

improved solution at low temperatures.

To achieve this process, it initiates the

temperature T=1.0 and set the minimum temperature

Tmin=0.001. Within the gradient-based dynamic

temperature adjustment mechanism, the temperature

is modulated by assessing the rate of change of the

current gradient norm relative to the preceding

gradient norm. The formula for updating the

temperature is expressed as 𝑇=𝑀𝐴𝑋(𝑇 ×(1−

𝜎×𝑔𝑟𝑎𝑑_𝑐ℎ𝑎𝑛𝑔𝑒),𝑇𝑚𝑖𝑛), where σ=0.005 serves

as a parameter that governs the extent of temperature

adjustment. This dynamic adjustment mechanism

empowers the algorithm to adaptively regulate the

temperature in accordance with actual model updates,

thus attaining a more optimal equilibrium between

exploration and exploitation.

3.2 Precision Comparison

It adjust the parameter τ to control the strength of

contrastive learning. The test is conducted on the PFL

platform. Table 1 shows the Top-1 test accuracy

achieved with different values of τ on CIFAR-10.

Table 1: Top-1 accuracy with different τ on CIFAR-10.

τ To

-1 Accurac

0.05 66.82%

0.1 67.04%

0.5 66.43%

1.5 66.63%

The results in Table 1 show how the

hyperparameter τ affects model accuracy. Different τ

values lead to big swings in accuracy. This

phenomenon tells us how important τ is in contrastive

learning. Specifically, lower τ makes the model's

representations more distinct between classes. Higher

τ creates more generalized representations, which

might make it harder for the model to distinguish

between classes.

According to this test on PFL, this paper decides

to explore more benefits of dynamically adjusting τ

during training. It integrated SA into the MOON

framework. This method helps with adaptive

temperature control and balances the exploration

access training process. It refines convolutional layers

in the neural network. This allows the MOON model

to capture both local and global features more

effectively. So that it can achieve to enhance the

model's robustness and generalization capability.

It integrates SA and revises convolutional layers

in the MOON codebase. It tests NEW-MOON on

CIFAR-10. The results show that dynamically

adjusting τ through SA boosts the model's

adaptability at different training phases. This adaptive

mechanism helps the model converge better at first

and cut down overfitting finally.

Table 2: Top-1 accuracy between NEW-MOON and

MOON frameworks with different τ on CIFAR-10

τ NEW-MOON Top-1

Accurac

MOON Top-1

Accurac

0.5 68.57% 68.70%

1.0 69.67% 68.54%

1.5 69.31% 68.47%

2.0 69.36% 68.33%

4 DISCUSSION

To gain a deeper understanding of the impact of the

hyperparameter τ on the model's test accuracy, it

introduced a SA algorithm. This algorithm

dynamically adjusts the value of the hyperparameter

to better adapt to changes during the training process.

Our goal is to optimize the contrastive loss function

by allowing the model to focus more on the details of

the training samples in the early stages At the same

time, the model can accelerate convergence. In the

training process, τ is gradually reduced. And the

model begins to pay more attention to global

information, enhancing its generalization capability.

According to our experimental results, this dynamic

adjustment strategy significantly improves the

model's test accuracy. By continuously adjusting τ

generated by the model's feedback during training,

model can successfully mitigate overfitting and

enhance the model's precision.

In addition to the aforementioned aspects, it has

also optimized the neural network architecture by

integrating the Simulated Annealing algorithm with a

deeper neural network structure. The experimental

results demonstrate that this combination yields more

accurate outcomes, particularly in the realm of

hyperparameter tuning. In the training of neural

networks, especially the CNN-Transformer hybrid

model employed in our study, the selection of

hyperparameters is of paramount importance for

performance. Within the MOON algorithm, the

hyperparameter τ optimizes the model's clustering

ability by adjusting the distinguishability of

representations between different classes. By

utilizing Simulated Annealing to dynamically adjust

the temperature, the model can flexibly control the

Optimization of Moon Model-Contrastive Federated Learning

131

intensity of contrastive learning during training,

adapting to the varying needs at different stages and

thereby optimizing performance. This integration

helps achieve more precise training results and

enhances the model's robustness and effectiveness in

practical applications.

However, the study is limited by the use of only

the CIFAR-10 dataset, which consists of small-sized

images (32 × 32) and a limited number of images

(60,000). This may not fully capture the complexity

and diversity of real-world image data. For future

research, this paper suggests expanding the

evaluation on more diverse and more complex

datasets. For example, ImageNet has over 1,000

categories and millions of high-resolution pictures.

Testing on such a dataset will help validate the

model's generalization capability and robustness in

different scenarios.

5 CONCLUSIONS

The temperature parameter τ is a super important

hyperparameter in federated contrastive learning. It

directly determines whether the model performs well

or not. τ controls how smooth and distinct the

similarity distribution is in the contrastive loss

function. If it can tune τ just right, it can boost the

model's training efficiency and ability to generalize.

By finding the perfect step sizes for the model, it can

make the training process smoother and give the

model more confidence when it encounters new

datasets. Conversely, improper settings may result in

unstable training, overfitting, or suboptimal

performance.

This paper demonstrates through experiments that

employing a simulated annealing algorithm to

dynamically adjust τ markedly improves the model's

adaptability across different training stages. This

dynamic adjustment enhances training stability and

final accuracy, allowing the model to flexibly balance

the learning of local and global information. It

accelerates convergence in the early stages of training

and mitigates overfitting in later stages.

Moreover, this paper optimizes the neural

network model by integrating CNN and Transformer

architectures. This integration enables the model to

more effectively capture both local and global

features of images, thereby achieving higher

performance and generalization ability.

In summary, the MOON federated learning

algorithm proposed in this paper addresses the non-

IID data problem in federated learning through

dynamic temperature adjustment and network

structure optimization. Future research can further

explore the adaptability of temperature parameters

and neural network structures under different datasets

and tasks. Additionally, future work can investigate

how to more efficiently leverage the privacy-

preserving features within the federated learning

framework to promote the application development

of this field.

AUTHORS CONTRIBUTION

All the authors contributed equally and their names

were listed in alphabetical order.

REFERENCES

Brendan, M. H., Moore, E., Ramage, D., Hampson, S., &

Arcas, Blaise Agüera y. 2016. Communication-

Efficient Learning of Deep Networks from

Decentralized Data. ArXiv.org.

Chen, D.-J., Lee, C.-Y., Park, C.-H., & Mendes, P. 2007.

Parallelizing simulated annealing algorithms based on

high-performance computer. Journal of Global

Optimization, 39(2), 261–289.

Chen, T., Kornblith, S., Norouzi, M., & Hinton, G. 2020. A

Simple Framework for Contrastive Learning of Visual

Representations. ArXiv:2002.05709.

Jafarigol, E., Trafalis, T., Razzaghi, T., & Zamankhani, M.

2023. Exploring Machine Learning Models for

Federated Learning: A Review of Approaches,

Performance, and Limitations. ArXiv.org.

Janiesch, C., Zschech, P., & Heinrich, K. 2021. Machine

learning and deep learning. Electronic Markets, 31(31),

685–695. Springer.

Kirkpatrick, S., Gelatt, C. D., & Vecchi, M. P. 1983.

Optimization by Simulated Annealing. Science,

220(4598), 671–680.

Li, Q., He, B., & Song, D. 2021. Model-Contrastive

Federated Learning. ArXiv.org.

Li, Y., Wang, C., Gao, L., Song, Y., & Li, X. 2020. An

improved simulated annealing algorithm based on

residual network for permutation flow shop scheduling.

Complex & Intelligent Systems, 7(3), 1173–1183.

Voigt, P., & Bussche, A. von dem. 2017. The EU General

Data Protection Regulation (GDPR). Springer

International Publishing.

World Innovation and Change Management Insititute.

2024. When Artificial intelligence becomes a part of

life? – World Innovation and Change Management

Institute. Wicmi.ch. https://wicmi.ch/techdata/when-

artificial-intelligence-becomes-a-part-of-life-2/

ICDSE 2025 - The International Conference on Data Science and Engineering

132