MOON-DPAP: Model-Contrastive Federated Learning with

Differential Privacy and Adaptive Pruning

Jiaming Su

School of Information Science and Technology, Northwest University, Xuefu Road, Xi’an, 710127, China

Keywords: Federated Learning, MOON-DPAP, Dynamic Pruning, Dynamic Adjustment of Differential Privacy.

Abstract: Recent years have seen a surge in research on distributed data processing and privacy protection due to the

quick growth of big data and artificial intelligence technology. Federated learning, as a distributed

collaboration framework with privacy protection, has attracted much attention due to its application potential.

However, in practical applications, it faces challenges such as heterogeneous data distribution, high

communication overhead, and insufficient privacy protection, and algorithm improvements are urgently

needed to improve performance and adaptability. This study proposed an improved federated learning

algorithm Model Contrastive Federated Learning-Differential Privacy and Adaptive Pruning (MOON-DPAP),

which improved the efficiency, accuracy, and privacy protection capabilities of federated learning by

introducing dynamic pruning technology, dropout, dynamic adjustment of differential privacy, and

hyperparameter optimization. Experiments show that MOON-DPAP outperforms FedAvg, SCAFFOLD,

MOON, and FedDyn in multiple performance indicators. In heterogeneous data scenarios, it shows higher

accuracy and stability. In scalability tests, the algorithm performance remains superior even when the number

of clients increases. Privacy protection tests verify its security and practicality. MOON-DPAP provides an

innovative solution to the challenges of federated learning in performance improvement and privacy

protection, laying the foundation for its practical application.

1 INTRODUCTION

As distributed data becomes more widely used and

data privacy protection becomes more widely

recognized, federated learning has gradually become

a key technology to solve data silos and privacy

protection needs. It uses distributed devices to

collaboratively train models without disclosing the

actual data and has broad application prospects in the

fields of medicine, finance, and the Internet of Things

(Yang, Liu, & Chen et al., 2019). However, in

practical applications, federated learning faces

challenges such as heterogeneous data distribution,

increased communication and computing overhead,

insufficient privacy protection mechanisms, and poor

accuracy, which limit its promotion.

The earliest federated learning algorithm is

Federated Averaging (FedAvg), which modifies the

global model through weighted averaging and local

training, but it has poor adaptability to device

heterogeneity and non-IID data (McMahan, Moore,

https://orcid.org/0009-0004-1508-227X

& Ramage et al., 2017). To this end, improved

algorithms such as Federated Optimization in

Heterogeneous Networks (FedProx) and Adaptive

Federated Optimization using Adam (FedAdam)

have emerged. FedProx balances the difference

between local updates and global models by

introducing regularization terms, while FedAdam

adjusts the local update step size through adaptive

learning rates, thereby reducing the training

differences between devices (Li, Sahu, & Zaheer et

al., 2020; Reddi, Charles, & Zaheer et al., 2020).

Federated learning offers privacy protection, with

differential privacy and homomorphic encryption

being common techniques used for safeguarding this

fundamental benefit. Although they improve privacy

protection to a certain extent, differential privacy will

impact model accuracy, and the significant

computational complexity of homomorphic

encryption constrains its applicability and

dissemination. Communication efficiency is a key

challenge in federated learning, especially when the

Su, J.

MOON-DPAP: Model-Contrastive Federated Learning with Differential Privacy and Adaptive Pruning.

DOI: 10.5220/0013679100004670

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Data Science and Engineering (ICDSE 2025), pages 82-88

ISBN: 978-989-758-765-8

number of devices is large and frequent

communication leads to inefficiency. Han, Mao and

Dally (2015) proposed that model compression and

quantization techniques can be used to reduce

communication overhead. At the same time, by

increasing the number of local training cycles, the

local update approach can decrease the amount of

communication between the hardware and the server,

but it may lead to local model overfitting and affect

global performance. In federated learning, two

significant issues are device and data heterogeneity.

Due to the differences in computing power and data

distribution of devices, the computational capabilities

of devices are frequently not fully utilized by

conventional federated learning techniques., and may

even lead to the degradation of global model

performance. To this end, researchers have proposed

algorithms based on gradient alignment and adaptive

adjustment of model parameters, aiming to optimize

the contribution between different devices and

improve the global model effect.

Li, He and Song (2021) proposed the Model-

Contrastive Federated Learning (MOON) algorithm,

which represents a significant advancement in the

field of federated learning recently. MOON

effectively mitigates the differences among devices

through a standardized update strategy,

demonstrating strong robustness, especially in

handling non-IID data and device heterogeneity. By

optimizing model synchronization and dynamically

adjusting local models, MOON reduces

communication overhead and enhances efficiency.

Although MOON does not have an inbuilt privacy

protection mechanism, it can be combined with

technologies such as differential privacy to further

enhance privacy protection. Despite its outstanding

performance in multiple experiments, MOON still

faces issues such as communication efficiency and

computational complexity in large-scale systems,

especially in scenarios where data is highly uneven,

and further optimization is still needed.

This study proposes an improved federated

learning algorithm to solve the training efficiency and

performance problems in heterogeneous data

environments. By introducing pruning technology to

reduce redundant calculations and improve

computing efficiency. To safeguard data privacy and

guarantee that training is carried out without

disclosing user information, differential privacy

techniques are employed. In addition,

hyperparameters such as learning rate, regularization

parameter, and local learning rate are dynamically

adjusted to accelerate model convergence and

improve performance. The research goal is to reduce

communication overhead, optimize computing

resources, and improve the stability and robustness of

the model under multi-party heterogeneous data

while ensuring data privacy.

2 ONLINE INTELLIGENT

KINEMATIC CALIBRATION

METHOD

2.1 Question Statement

Suppose there are 𝑁 participants 𝐴



,𝐴



,…,𝐴



, each

participant 𝐴



has a local dataset 𝑋



. The objective is

to secure data privacy while working together to train

a global model 𝜃 through a central server while

protecting data privacy. Because the distribution of

local data is heterogeneous, updates during training

may fluctuate greatly, impacting the model's

performance and rate of convergence. At the same

time, as the number of training rounds increases,

storage and computing costs rise, resulting in a waste

of resources. To this end, improving training

efficiency is essential, reducing redundant computing

and communication overhead, and ensuring that the

model converges quickly and stably under

heterogeneous data while ensuring privacy.

2.2 Model Framework

This paper proposes an improved federated learning

algorithm - MOON-DPAP, which enhances the

model's efficiency and privacy protection capabilities

by introducing pruning, differential privacy, and

dynamic parameter adjustment. Dynamic pruning

reduces redundant parameters and improves

computational efficiency; Dropout alleviates

overfitting and enhances model adaptability;

differential privacy protects data privacy by adding

noise. Additionally, dynamic adjustment of the

learning rate, contrastive loss temperature parameter

𝜏, regularization parameter 𝜇, and local learning rate

accelerates model convergence and optimizes

performance.

In the algorithm process, in every round, the client

receives the global model from the server. The client

trains and updates the model using regional

information, and by comparing the loss, it improves

the similarity between both the regional and global

models. During training, differential privacy protects

data security, and dynamic pruning optimizes the

model structure. After the updated model is uploaded

to the server, the server updates the global model

MOON-DPAP: Model-Contrastive Federated Learning with Differential Privacy and Adaptive Pruning

through weighted averaging and adjusts the

hyperparameters. This process effectively balances

privacy protection and performance improvement.

2.3 Dynamically Adjust Local

Learning Rate and

Hyperparameters

In this research, to increase the effectiveness of model

instruction and the end performance, a cosine

annealing-based learning rate adjustment technique

was applied. The learning rate adjustment follows the

following (1)

𝜂



= 𝜂

min







𝜂

max

− 𝜂

min





1 + 𝑐𝑜𝑠



 



max



(1)

Among them, 𝜂

max

is the initial learning rate,

𝜂

min

is the minimum learning rate, 𝑇

max

is the entire

amount of training rounds and 𝑡 is the current round

number. The core idea of this formula is that the

learning rate starts from 𝜂

max

and gradually decays to

𝜂

min

after training. This strategy gradually decays the

learning rate through the cosine function, thereby

maintaining a high learning rate at the beginning for

more extensive exploration and lowering the learning

rate later on in the training process to achieve fine

optimization. To prevent the learning rate from

excessive decay, this paper sets a lower limit for the

minimum learning rate to ensure that the learning rate

will not fall below this value during training.

In addition, the learning rate adjustment can also

be combined with the dynamic adjustment of other

hyperparameters 𝜏𝜇 to improve the model's

performance and convergence even more. During the

training process, following (2) and (3), it is adaptively

modified based on the current number of rounds.

𝜏



=𝑚𝑎𝑥



𝜏



,𝜏



−𝛼×𝑡



(2)

𝜇



=𝑚𝑖𝑛



𝜇



,𝜇



+𝛽×𝑡



(3)

Tables Among them, 𝜏



and 𝜇



are the

minimum values, 𝜏



and 𝜇



are the maximum

values, and 𝛼 and 𝛽 are the adjustment steps. In non-

IID data scenarios, as training progresses, there will

be a greater disparity between the local and global

models, and the gradual reduction of 𝜏 helps to

narrow this difference. In the early phases of training,

the dynamic rise of 𝜇 can enhance the local model's

contribution to the global model. Later in the training

process, the global model's influence on the final

model progressively grows, resulting in a more

balanced model update.

2.4 Differential Privacy

Differential privacy causes the output to have noise,

making the outputs of any two adjacent data sets

almost indistinguishable. By knowing that the noise's

standard deviation 𝜎 is determined by the gradient

sensitivity Δ𝑓, the privacy budget 𝜖 and the privacy

failure probability 𝛿, we can calculate (4).

𝜎=







2𝑙𝑛

.



(4)

Dynamic privacy adjustment is performed, and

the privacy budget 𝜖



𝑡



gradually decreases with the

training round 𝑡 , where 𝜖



is the initial privacy

budget, 𝑡 is the current training round and 𝑇 is the

total number of training rounds, as shown in (5).

𝜖



𝑡



=𝜖





1−







(5)

Differential privacy technology can effectively

protect the privacy of participants by adding noise to

the gradient update process to guarantee that each

client's local data does not leak into the global model.

2.5 Model Pruning

This paper adopts a method that combines static

pruning and dynamic pruning based on weight

thresholds. The core idea of pruning is to remove

parameters with small absolute weight values. These

parameters have little impact on the model output and

can be considered "redundant". Set the pruning

threshold 𝑇, and the pruning rule of weight 𝑤 is as

follows (6), where 𝑤



represents the pruned weight.

𝑤



=

𝑤, 𝑖𝑓

𝑤

≥𝑇

0, 𝑖𝑓

𝑤

<𝑇

(6)

To gradually increase the pruning ratio during the

training process, a dynamic pruning threshold

adjustment strategy is adopted to gradually increase

the pruning threshold during the training rounds. The

dynamic threshold calculation formula is (7), where

𝑇

min

is the minimum pruning threshold. 𝑇

max

is the

maximum pruning threshold. 𝑇

total

is the total training

rounds. 𝑡 is the current training round.

𝑇



=𝑇

min



𝑇

max

−𝑇

min



⋅





total

(7)

In this way, the pruning ratio is progressively

raised in the final phases of training to lower the

ICDSE 2025 - The International Conference on Data Science and Engineering

model's complexity, while more weights are kept in

the initial phases to stabilize the training.

3 EXPERIMENTAL VALIDATION

AND DISCUSSION

3.1 Experimental Setup

To thoroughly assess the MOON-DPAP algorithm's

performance, this research compares it with several

advanced federated learning algorithms. Specifically,

FedAvg, SCAFFOLD, MOON, and FedDyn are

selected as comparison algorithms (McMahan,

Moore, & Ramage et al., 2017; Karimireddy, Kale, &

Mohri et al., 2020; Li, He, & Song, 2021; Jin, Chen,

& Gu et al., 2023). By comparing with these methods,

the accuracy, speed of convergence, computational

efficiency, and privacy of MOON-DPAP's

performance were all carefully examined.

In the experiment, the FashionMNIST dataset was

selected for testing (Xiao, Rasul, & Vollgraf, 2017).

FashionMNIST is a 28x28 pixel image classification

dataset with 10 categories.

To ensure a fair comparison of each algorithm, the

same network architecture and hyperparameter

Settings are used in all experiments. A Convolutional

Neural Network (CNN) serves as the foundational

model of the FashionMNIST dataset. To be more

precise, the network design is made up of two

convolutional layers, a Max pooling layer, two fully

connected layers, and a ReLU activation function at

the end of each layer.

All algorithms were implemented based on the

PyTorch framework (Paszke, Gross, & Massa et al.,

2019), ensuring the reproducibility and efficiency of

the experiments. All experiments were conducted

under the same hardware environment, with the

hardware configuration being an NVIDIA GPU. The

optimizer used was SGD, with a learning rate of

0.005, a batch size of 32, a local training round of 1,

and a global training round of 200.

To simulate non-independent and identically

distributed data in real-world scenarios, this paper

employs the Dirichlet distribution to generate data

partitions among clients. In the experiments, 20

clients were set up, and in each communication

round, the participation ratio of clients was 1.0, unless

otherwise specified.

3.2 Accuracy Comparison

For MOON-DPAP, the optimal batch size on the

Fashion MNIST dataset is 32. For the hyperparameter

𝜇, the best 𝜇 on the FashionMNIST dataset is 0.01.

Unless otherwise specified, these batch sizes and 𝜇

settings are used in all subsequent experiments in this

paper.

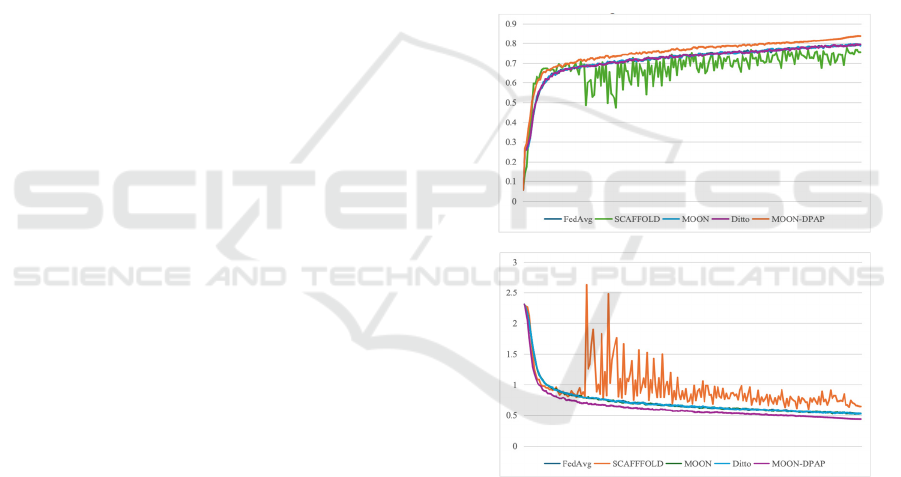
Figure 1 shows the test accuracy and loss of

various methods under the default settings mentioned

above. When comparing different federated learning

methods under the non-IID setting, it can be observed

that MOON-DPAP consistently performs best with

an accuracy of 83.6% and the lowest loss of 0.44

across all tasks. It is 4.7% higher than FedAvg in

average accuracy across all tasks. For MOON and

Ditto, its accuracy is very close to FedAvg. For

SCAFFOLD, its accuracy is much lower than other

federated learning methods.

(a) Accurac

(

)

Loss

Figure 1: Accuracy and loss of different methods in

different rounds on the FashionMNIST dataset

(Photo/Picture credit: Original).

3.3 Security and Privacy Test

The accuracy of the MOON-DPAP algorithm without

differential privacy is marginally higher than that of

the version with differential privacy, as shown in

Figure 2. This indicates that although differential

privacy plays an important role in protecting data

security, differential privacy-introduced noise affects

the model's performance, particularly during the

MOON-DPAP: Model-Contrastive Federated Learning with Differential Privacy and Adaptive Pruning

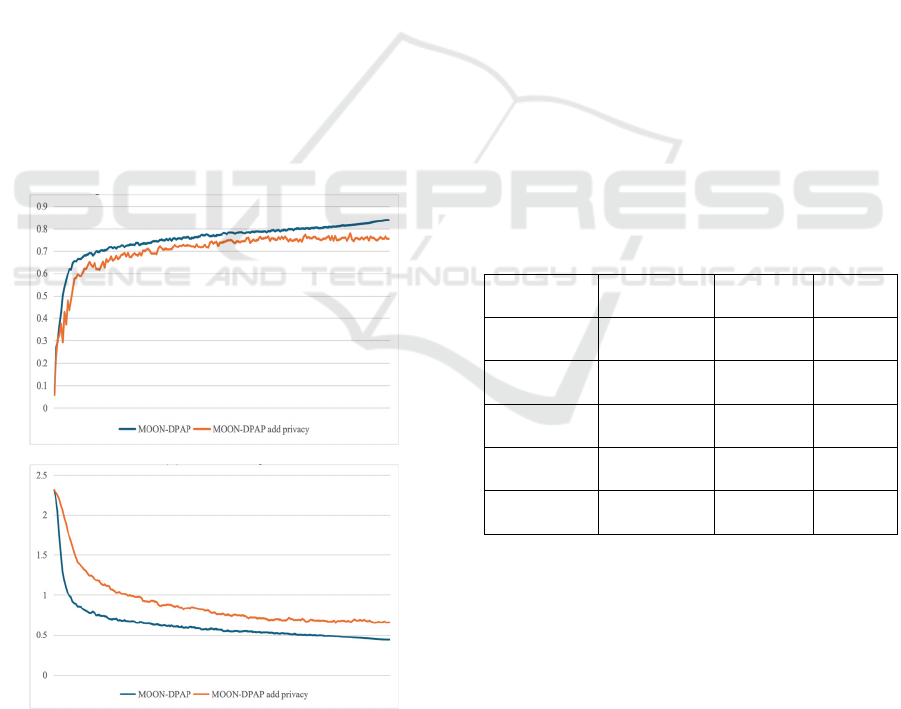
initial training phase. The convergence speed of the

version with differential privacy is slow, while the

version without differential privacy can reach a high

accuracy faster (Dwork & Roth, 2014).

As the training progressed, the version with

differential privacy gradually stabilized, with a final

accuracy of 77% and a loss of 0.71. This shows that

while differential privacy improves data protection, it

also weakens the model's prediction ability. However,

the version with differential privacy showed a

smoother accuracy change curve, showing better

stability.

This outcome illustrates the balance between

differential privacy data security and model

performance. In practical applications, to balance the

impact of privacy protection and model performance,

a fair privacy budget must be chosen based on the

particular case.

In the future, the negative impact of noise

introduced by differential privacy on model

performance will also be a focus of optimization

(Dwork & Roth, 2014). In the future, we can try to

adopt more efficient privacy protection methods, such

as local differential privacy or adaptive noise

strategies, to further optimize the balance between

privacy protection and performance (Duchi, Jordan,

& Wainwright, 2013).

(

)

Accurac

(b) Loss

Figure 2: Comparison of different rounds before and

after adding differential privacy to MOON-DPAP

(Photo/Picture credit: Original).

3.4 Scalability

As shown in Table 1, among all the algorithms,

MOON-DPAP shows strong scalability, and its

accuracy and loss are better than other algorithms in

the case of either 10 or 20 clients, and its performance

is especially more stable in large-scale client

scenarios. This shows that MOON-DPAP can

effectively deal with data heterogeneity and

communication bottlenecks and has better

adaptability. In contrast, FedAvg performs stably

with 10 clients, but the accuracy and loss vary greatly

with 20 clients, showing a lack of scalability. Still, it

is suitable for use in scenarios where the number of

clients is small. FedDyn and SCAFFOLD perform

relatively poorly, especially with 20 clients, showing

a significant drop in performance, indicating their

inadequacy in coping with data heterogeneity and

training imbalance.

According to experimental findings, all

algorithms' performance often declines as the number

of clients rises. This reflects the scalability challenges

of federated learning, especially the increase in

system heterogeneity and communication latency,

which has a significant impact on model training,

leading to a decrease in accuracy and a rise in loss

value.

Table 1: The effect of varying client numbers on the

experiment.

Algorithm

Number Of

Clients

Accuracy Loss

FedAvg

10 53.37% 1.22

20 48.85% 1.34

FedDyn

10 47.97% 1.64

20 43.38% 1.83

SCAFFOLD

10 43.37% 1.51

20 40.37% 1.57

MOON

10 53.65% 1.21

20 49.17% 1.34

MOON-

DPAP

10 62.34% 1.13

20 58.60% 1.26

3.4 Ablation Analysis

To explore how each component affects the model's

performance, this paper conducted an ablation

experiment, gradually removing key components

such as dynamic learning rate adjustment, Dropout,

and pruning, and recorded the changes in accuracy

and loss, as shown in Table 2.

Removing the dynamic learning rate adjustment

significantly degrades the model performance,

ICDSE 2025 - The International Conference on Data Science and Engineering

indicating its important role in optimizing parameter

updates and accelerating convergence. Removing

Although dropout causes a small increase in loss and

a slight fall in accuracy, it is nevertheless crucial for

boosting the model's resilience. After removing

pruning, the performance changes slightly, which is

mainly reflected in improving computational

efficiency, while the direct impact on model

performance is limited. When all three are removed

at the same time, the model performance degrades

significantly, indicating that dynamic learning rate

adjustment is the key factor in improving

performance, and the synergy of the three is

indispensable in improving training efficiency,

optimizing regularization, and accelerating

convergence.

Table 2: Ablation analysis.

Group Ablation Ite

Accurac

Loss

1 Baseline Model 83.71% 0.44

Remove Dynamic

learning rate

ustment

81.03% 0.52

3 Remove Dro

out 80.98% 0.48

4 Remove Prunin

82.94% 0.47

Remove Dropout,

Pruning, Learning

rate Adjustment

78.77% 0.53

4 CONCLUSIONS

This study proposed the MOON-DPAP algorithm and

evaluated its performance in terms of accuracy,

computational efficiency, and privacy protection by

comparing it with federated learning algorithms such

as FedAvg, SCAFFOLD, MOON, and FedDyn.

Experimental results show that MOON-DPAP

exhibits significant advantages in multiple key

dimensions, demonstrating its potential to address the

challenges of federated learning.

Firstly, MOON-DPAP performs well in accuracy,

especially when dealing with scenes with large data

heterogeneity, showing stronger stability and

adaptability. According to the testing results, MOON-

DPAP can successfully handle the problem of

unequal client data distribution, and after several

communication rounds, its ultimate accuracy is

considerably greater than that of other algorithms.

This is because the algorithm's dynamic learning rate

modification, pruning, and dropout methods boost the

model's generalization capabilities in addition to its

rate of convergence. Especially in heterogeneous

environments, the robustness is further improved by

optimizing resource utilization and inhibiting

overfitting.

To preserve excellent model performance and

guarantee user data confidentiality, MOON-DPAP

integrates the differential privacy technique. Despite

the impact of noise introduced by differential privacy

on the model accuracy, MOON-DPAP can still

achieve a good balance between privacy protection

and performance. Experiments show that MOON-

DPAP still has strong applicability in scenarios with

high privacy requirements. In addition, in scalability

tests, MOON-DPAP has demonstrated superior

stability. As the number of clients increases, its

accuracy decreases significantly less than other

algorithms, and it performs better in terms of

computational efficiency, proving its potential in

large-scale federated learning scenarios.

Nevertheless, MOON-DPAP has room for

improvement in personalized learning and privacy

protection, and the lack of a personalization strategy

may affect its performance in heterogeneous data

scenarios, and differential privacy noise also hurts

performance. Future developments could introduce

adaptive noise methods or local differential privacy to

better balance privacy and performance.

As mentioned above, the MOON-DPAP

algorithm performs well in terms of accuracy,

privacy, and scalability, showing strong potential for

practical applications. Future research should

concentrate on optimizing personalized learning and

privacy protection techniques to further improve its

performance and robustness in diverse scenarios.

REFERENCES

Yang, Q., Liu, Y., Chen, T., Tong, Y., 2019. Federated

machine learning: Concept and applications. ACM

Transactions on Intelligent Systems and Technology

(TIST), 10(2), 1-19.

McMahan, B., Moore, E., Ramage, D., Hampson, S., y

Arcas, B. A., 2017, April. Communication-efficient

learning of deep networks from decentralized data. In

Artificial intelligence and statistics (pp. 1273-1282).

PMLR.

Li, T., Sahu, A. K., Zaheer, M., Sanjabi, M., Talwalkar, A.,

Smith, V., 2020. Federated optimization in

heterogeneous networks. Proceedings of Machine

learning and systems, 2, 429-450.

Reddi, S., Charles, Z., Zaheer, M., Garrett, Z., Rush, K.,

Konečný, J., Kumar, S., McMahan, H. B., 2020.

Adaptive federated optimization. arXiv preprint

arXiv:2003.00295.

Han, S., Mao, H., Dally, W. J., 2015. Deep compression:

Compressing deep neural networks with pruning,

MOON-DPAP: Model-Contrastive Federated Learning with Differential Privacy and Adaptive Pruning

trained quantization and huffman coding. arXiv

preprint arXiv:1510.00149.

Li, Q., He, B., Song, D., 2021. Model-contrastive federated

learning. In Proceedings of the IEEE/CVF conference

on computer vision and pattern recognition (pp. 10713-

10722).

Karimireddy, S. P., Kale, S., Mohri, M., Reddi, S., Stich,

S., Suresh, A. T., 2020, November. Scaffold: Stochastic

controlled averaging for federated learning. In

International conference on machine learning (pp.

5132-5143). PMLR.

Jin, C., Chen, X., Gu, Y., & Li, Q. 2023. FedDyn: A

dynamic and efficient federated distillation approach on

Recommender System. In 2022 IEEE 28th

international conference on parallel and distributed

systems (ICPADS) (pp. 786-793). IEEE.

Xiao, H., Rasul, K., & Vollgraf, R. (2017). Fashion-mnist:

a novel image dataset for benchmarking machine

learning algorithms. arXiv preprint arXiv:1708.07747.

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,

Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,

Antiga, L., Desmaison, A., Kopf, A., Yang, E., DeVito,

Z., Raison, M., Tejani, A., Chilamkurthy, S., Steiner,

B., Fang, L., Bai, J., & Chintala, S. 2019. Pytorch: An

imperative style, high-performance deep learning

library. Advances in neural information processing

systems, 32.

Dwork, C., & Roth, A. 2014. The algorithmic foundations

of differential privacy. Foundations and Trends® in

Theoretical Computer Science, 9(3–4), 211-407.

Duchi, J. C., Jordan, M. I., & Wainwright, M. J. 2013. Local

privacy and statistical minimax rates. In 2013 IEEE

54th annual symposium on foundations of computer

science (pp. 429-438). IEEE.

ICDSE 2025 - The International Conference on Data Science and Engineering