Towards Guaranteed Collision Avoidance for Multiple Autonomous

Underactuated Unmanned Surface Vehicles in Restricted Waters

Erick J. Rodr

ıguez-Seda

Department of Weapons, Robotics, and Control Engineering

United States Naval Academy, Annapolis, MD, U.S.A.

Keywords:

Artiﬁcial Potential Field, Collision Avoidance, Multi-Agent Systems, Unmanned Vehicles.

Abstract:

As autonomous surface vessels increasingly operate in restricted and congested waters, the need for dis-

tributed, reactive collision avoidance algorithms becomes more crucial. Traditional avoidance control al-

gorithms are typically conservative, opting for a worst-case scenario approach and restricting the total area

where Unmanned Surface Vehicles (USVs) can navigate. This paper presents a distributed collision avoidance

framework for USVs, based on the concepts of Artiﬁcial Potential Field (APF) and avoidance functions, that

aims to reduce the minimum safe distance that vehicles need to keep from obstacles by explicitly consider-

ing their shape, relative position, and relative orientation. The proposed control framework is theoretically

demonstrated and validated through simulations to ensure collision avoidance at all times and to facilitate the

travel of vehicles in obstacle-dense environments.

1 INTRODUCTION

Collision avoidance is arguably one of the most crit-

ical challenges when operating autonomous USVs.

Not only does the USV need to compensate for dis-

turbances such as currents, waves, and wind, but it is

typically subject to underactuation, which restricts the

vehicle’s maneuverability (Er et al., 2023). Further-

more, the environment in which these vehicles oper-

ate is often unknown and dynamic, requiring the im-

plementation of reactive avoidance control strategies.

Several reactive collision avoidance methods for

USVs have been proposed and studied (refer to (Va-

gale et al., 2021; Lyu et al., 2023) for reviews). One

particular approach of interest due to their relative

ease of analysis and implementation is the use of

APF functions. APF-based methods use repulsive

forces around obstacles to maneuver away from a col-

lision (Xue et al., 2009). These forces can then be

shown, via Lyapunov-based analysis, to guarantee the

safety of a large number of vehicles (Stipanovi

c et al.,

2007). Examples in the literature for USVs vary based

on the vehicle’s maneuverability and the compliance

with other restrictions and regulations (Li et al., 2021;

Zhang et al., 2022; Li et al., 2025). Yet a common

drawback of these APF-based strategies is the treat-

ment of vehicles and obstacles as points or objects of

https://orcid.org/0000-0003-1108-4329

circular shape. This assumption simpliﬁes the analy-

sis and implementation of control algorithms, but ar-

tiﬁcially increases the minimum distance that agents

need to keep from each other by assuming a worst-

case scenario. One solution to reduce this conser-

vatism is the modeling of obstacles and vehicles as

a set of multiple smaller spheres, hence reducing the

agent’s footprint at the expense of increasing the num-

ber of obstacles and artiﬁcial potential ﬁeld functions.

Alternatively, one can wrap the vehicles and ob-

stacles with a convex envelope that considers not only

their shape but also their relative position and orien-

tation. For instance, the work in (Rodr

ıguez-Seda,

2024b; Rodr

ıguez-Seda, 2024a) deﬁnes the repulsive

potential ﬁeld as a function of the vehicles and obsta-

cles’ relative position, orientation, and shape. In con-

trast to the use of a constant distance, as in the case

of agents of circular shape, the work in (Rodr

ıguez-

Seda, 2024b; Rodr

ıguez-Seda, 2024a) uses a contin-

uous, differentiable, non-constant distance function

that is typically smaller than the radius of the mini-

mum enclosing circle. Such an approach is shown to

safely allow the travel of multiple nonholonomic, un-

deractuated ground vehicles through narrow passages

and highly occluded spaces.

In this paper, we apply the avoidance con-

trol concept developed in (Rodr

ıguez-Seda, 2024b;

Rodr

ıguez-Seda, 2024a) for ground vehicles with no-

Rodríguez-Seda, E. J.

Towards Guaranteed Collision Avoidance for Multiple Autonomous Underactuated Unmanned Surface Vehicles in Restricted Waters.

DOI: 10.5220/0013678700003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 53-59

ISBN: 978-989-758-770-2; ISSN: 2184-2809

slip constraints to underactuated USVs subject to

sway and surge motion. We propose a distributed con-

trol law for an arbitrary number of vehicles and static

obstacles and show, via Lyapunov-based analysis, that

if the vehicles start from a safe state and their veloci-

ties are non-zero while they try to resolve the conﬂict,

the vehicles are guaranteed to avoid collisions. A sim-

ulation example with four USVs traveling through a

narrow passage illustrates the beneﬁts of the proposed

approach.

2 PROBLEM FORMULATION

We consider the task of safely coordinating the mo-

tion of N heterogeneous, underactuated USVs. Let

(t) and y

(t) represent the position coordinates of

the center of mass and ψ

(t) be the orientation in the

Earth-ﬁxed frame for the ith vehicle (refer to Fig-

ure 1). Assume that the vehicle is neutrally buoyant.

Then, the nonlinear kinematic and dynamic equations

of motion of the ith USV in still water are given by

˙x

(t) =u

(t)cos ψ

(t) − v

(t)sin ψ

(t) (1a)

˙y

(t) =u

(t)sin ψ

(t) + v

(t)cos ψ

(t) (1b)

(t) =ω

(t) (1c)

˙u

(t) =

(t)ω

(t) −

(t) +

(t)

(1d)

˙v

(t) = −

(t)ω

(t) −

(t) (1e)

(t) =

− m

(t)v

(t) −

(t) +

(t)

(1f)

where u

(t) and v

(t) are the surge and sway speeds,

(t) is the yaw rate, f

(t) and τ

(t) are the control

force and torque inputs, and m

> 0 and d

> 0 are

the mass and damping terms for j ∈ {1, 2,3} (Rey-

hanoglu, 1996; Fossen, 2021). The control objective

is to design

and τ

such that the ith vehicle is sta-

bilized at a desired conﬁguration while avoiding col-

lisions with other USVs and obstacles.

It is well known that the position and orientation

of (1) cannot be simultaneously stabilized at a desired

value using a continuous (Brockett, 1983) or, even,

a discontinuous (Pettersen and Egeland, 1996) state

feedback control law. Therefore, this paper proposes

the use of input-output feedback linearization control

law, where the objective is to regulate the position of

a reference point in front of (x

) given by

+ L

cosψ

, z

+ L

sinψ

(2)

In what follows, we will omit the time argument of

signals unless deemed necessary.

where L

> 0 is a constant parameter and z

]

are the Cartesian coordinates of the ref-

erence point (Rodr

ıguez-Seda et al., 2014; Paliotta

et al., 2018). Now, differentiating twice equation (2)

and applying the following control force and torque









cosψ

sinψ

−m

sinψ

cosψ







− F

− G



(3)

=−

+ d

cosψ

+ m

sinψ

− m

+ d

sinψ

− u

sinψ

+ v

cosψ

− L

cosψ

−

+ d

sinψ

−

+ m

cosψ

−

− m

+ d

cosψ

+ u

cosψ

− v

sinψ

− L

sinψ

one can show that (1) reduces to

(4a)

[−sin ψ

cosψ

]

−

(4b)

where w

= [w

]

is the new control input for the

linearized system. While the internal dynamics (4b)

can only be shown to be Lagrange stable, the linear

dynamics of the reference point (4a) are controllable.

That is, for a any desired position z

∈ R

, one can

design a state feedback control law w

such that z

→

as t → ∞.

To formulate the collision avoidance objective,

consider the interaction of a pair of vehicles as illus-

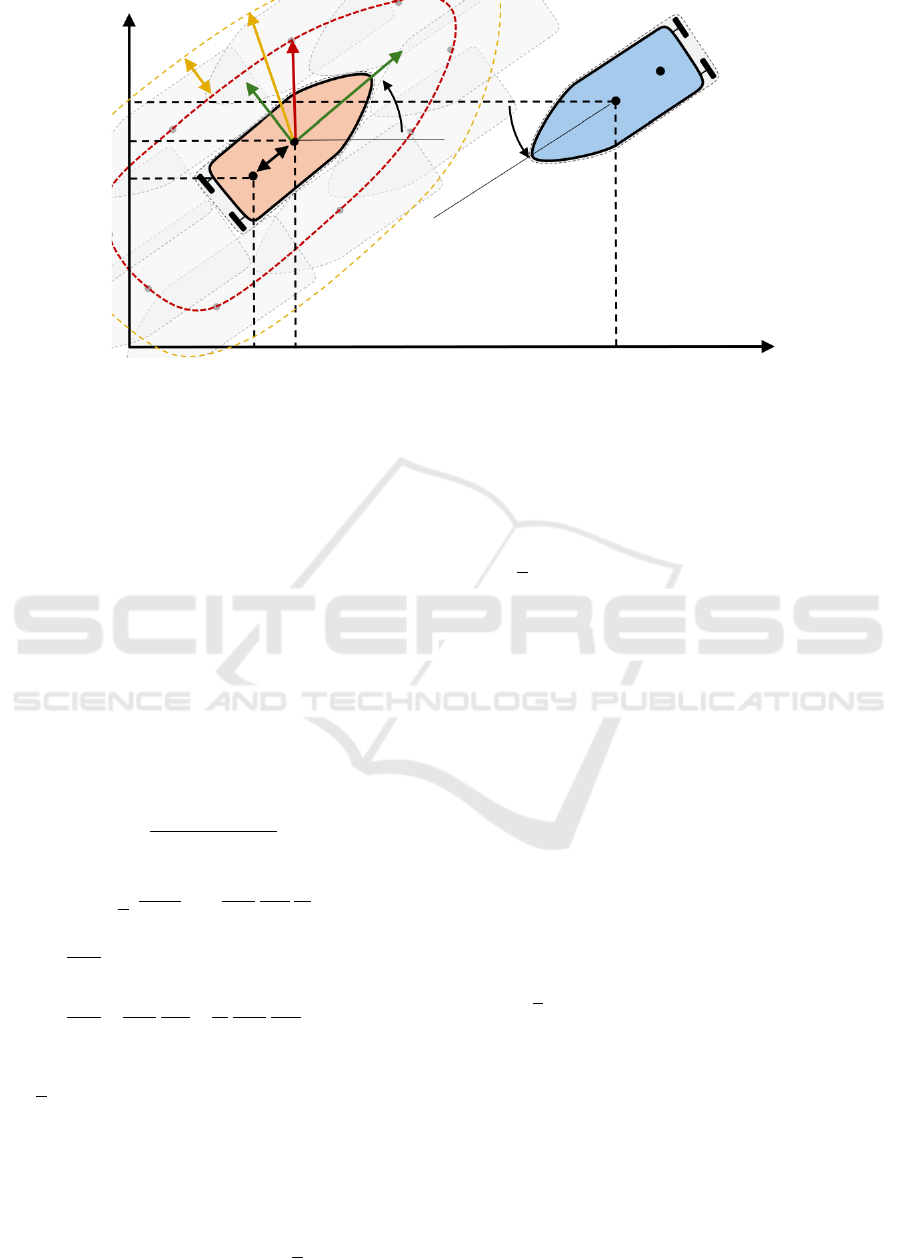
trated in Figure 1. Note that the minimum safe dis-

tance (or envelope) between both vehicles, denoted

as r

i j

, is a function of their relative position and ori-

entations

i j

:= r

i j

,ψ

) = r

,ψ

). (5)

That is, r

i j

depends on the shape of the vehicles and

on how the jth USV or obstacle is positioned and ori-

ented with respect to the ith vehicle. A collision is

said to take place if



− z



≤ r

i j

for some time

t ≥ 0. It is assumed that one can ﬁnd an envelop

function r

i j

that is continuously differentiable with

bounded derivative and that the USVs can detect, ei-

ther via communication or onboard sensors, the rel-

ative position and orientation of other agents within

a bounded detection radius R > sup

i, j̸=i

i j

+ ∆

where ∆

> 0 denotes the reaction gap distance. The

reaction distance, R

i j

= R

= r

i j

+∆

, deﬁnes the dis-

tance at which the vehicles start avoiding each other

(see Figure 1).

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

∆

1 j

2 j

i j

−ψ

i j

Figure 1: Minimum safe distance between two USVs considering their shape, relative positions, and relative orientations.

Having deﬁned the minimum safe distance, one

can formulate the control objective as follows. Design

a control strategy w

such that z

→ z

as t → ∞ and



− z



> r

i j

∀ i, j ̸= i,t ≥ 0, where z

is the desired

position.

3 CONTROL FRAMEWORK

To achieve the control objective, we propose a decen-

tralized control law based on the concept of avoidance

control (Leitmann and Skowronski, 1977)

= K

− z

) − D

+ p

−

∑

j∈N

i j

(6a)

= { j ̸= i |



− z



≤ R

i j

} (6b)

i j

min

(



− z



− R

i j



− z



− r

i j

(6c)

= max

(

∥

∑

j∈N

∂A

i j

∂r

i j

∂r

i j

∂ψ

)

(6d)

∥

[−˙z

˙z

]

, if N

̸=

0 (6e)

i j

∂A

i j

∂z

∂A

i j

∂r

i j

∂r

i j

∂z

∂A

i j

∂r

i j

∂r

i j

∂ψ



−sin ψ

cosψ



(6f)

where K

is a positive deﬁnite constant matrix, µ

̸= 0

and d > 0 are constants, N

is the set of agents within

the ith USV’s reaction distance, and A

i j

is the avoid-

ance function (Stipanovi

c et al., 2007; Rodr

ıguez-

Seda, 2024b). The ﬁrst two terms in (6) represent

the proportional derivative action aimed at stabiliz-

ing the system at the desired conﬁguration, where

, the damping coefﬁcient, is assumed to be a time-

varying function lower-bounded by d. The last term,

∑

j∈N

i j

, is the collision avoidance control, while p

is a perturbation to incentivize a non-zero velocity of

the reference point while the avoidance control is ac-

tive and to facilitate the avoidance of deadlocks. Note

that, when there are no obstacles or other vehicles

within the USV’s reaction distance, a

i j

= p

= 0 and

= d.

Assumption 1. The velocity of the ith vehicle’s refer-

ence point is non-zero when the avoidance control is

active. That is,

∥

̸= 0 if A

i j

> 0 for some j.

Assumption 1 may not be satisﬁed in some spe-

cial cases, such as in environments with dead-ends or

traps. To avoid such cases, the proposed framework

incorporates a control perturbation (6e) that aims to

keep the vessel in motion by making it rotate when

the vehicle is almost stationary.

Theorem 1 (Collision Avoidance). Consider the sys-

tem in (1) with control law (3) and (6). Assume that

is constant, that



(0) − z

(0)



> r

i j

∀ i, j ̸= i,

and that Assumption 1 holds. Then,



(t) − z

(t)



i j

∀ t ≥ 0.

Proof. Consider the following Lyapunov function

V =

∑

i=1

∥

− z

∥

∑

j∈N

i j

(7)

Towards Guaranteed Collision Avoidance for Multiple Autonomous Underactuated Unmanned Surface Vehicles in Restricted Waters

Taking its time derivative yields

V =

∑

i=1



− z

)



∑

i=1

∑

j∈N



∂A

i j

∂z

∂A

i j

∂r

i j

∂r

i j

∂z

∂A

i j

∂r

i j

∂r

i j

∂ψ



| {z }

∑

i=1

∑

j∈N



∂A

i j

∂z

∂A

i j

∂r

i j

∂r

i j

∂z

∂A

i j

∂r

i j

∂r

i j

∂ψ



∑

i=1

∑

j∈N



∂A

i j

∂z

∂A

i j

∂r

i j

∂r

i j

∂z

∂A

i j

∂r

i j

∂r

i j

∂ψ



Now, substituting (6) and (4b) into the above equation

and canceling all applicable terms yields

V =

∑

i=1

−D

∥

∑

j∈N

∂A

i j

∂r

i j

∂r

i j

∂ψ

≤ 0

where we used Assumption 1 and (6d). Since

V ≤ 0,

we have that V is non-increasing and bounded by

V (0) for all t ≥ 0. Now, suppose that for for a pair

of agents



(t) − z

(t)



→ r

i j

for some t. The lat-

ter would imply that A

i j

→ ∞ ⇒ V → ∞, which is a

contradiction. Since the solutions of equation (4a) are

continuous, one has that



(t) − z

(t)



> r

i j

for all

t ≥ 0 and the proof is complete.

Theorem 1 guarantees the safe transit of an arbi-

trary large number of USVs assuming they all start

from a safe state and that they remain in motion while

resolving a conﬂict.

Theorem 2 (Position Stabilization). Assume ∃T

≥ 0

such that A

i j

= 0 ∀ t ≥ T

, j ∈ {1,· ·· , N}/i. Then,

(t) → z

z(t) → 0, and

(t) → 0.

Proof. Deﬁne the error signals as e

= z

− z

and

consider the Lyapunov candidate function

W = K

∥

Taking its time derivative and noting that D

= d and

i j

= p

= 0 for all j ∈ {1,·· · ,N} and t ≥ T

, one can

show that

W = − K

∥

− d

∥

, ∀t ≥ T

which implies that z

− z

and

z converge exponen-

tially to zero as t → 0. Then, manipulating (1) and

(4), one can obtain that u

= [cos ψ

sinψ

]

, which,

in turns, implies that u

→ 0 exponentially as t → 0.

Similarly, substituting (4b) into (1e) yields that

˙v

[sinψ

− cos ψ

]

−

. (8)

Now, since u

→ 0 exponentially, ∃

≥ T

such that

| < u

= d

∀t ≥

. Returning to (8) one

obtains that

˙v

[sinψ

− cos ψ

]

−



−



(9)

for all t ≥

. Now, consider the following Lyapunov

function W =

. Differentiating with respect to

time yields

W =

[sinψ

− cos ψ

]

−



−



≤

∥

| −



−



≤ − κv

, ∀ |v

| ≥

(1 − κ)

∥

where κ ∈ (0,1). Treating

as the input to (9), one

can conclude that (9) is input-to-state stable (Khalil,

2002). Therefore, if

→ 0, so does v

→ 0, which in

turns implies that

→ 0 and the proof is complete.

Theorem 2 establishes that, under no collision

threat, the proposed control law is able to stabilize

the reference point at a desired location in a ﬁxed ori-

entation. In general, we are more interested in the

problem of driving the USV along a desired path or

to visit a sequence of waypoints. For example, let

{χ

i,1

,χ

i,2

,· ·· , χ

i,m

} be an ordered sequence of m way-

points for the ith vehicle and let

M > 0 be the switch-

ing distance threshold. Then, the desired conﬁgura-

tion can be updated as z

(t) = χ

i,k

, ∀t ≥ 0, where

k = 1 for t = 0 and

k =

(

k, if



(t) − χ

i,k



k + 1, otherwise

for k ∈ [2,m − 1].

4 MINIMUM SAFE DISTANCE

One of the main contributions of the proposed ap-

proach is the use of a tighter minimum safe distance,

i j

, that takes into account not only the shape of the

vehicles and obstacles but also their relative position

and orientation. This is in contrast to conventional

APF-based methods that assume objects are of spher-

ical form, yielding always a conservative, worst-case

scenario, minimum safe distance.

In the control framework (3) we assumed that

a differentiable continuous function r

i j

,ψ

)

can be formulated in closed-form. Following the

work of (Rodr

ıguez-Seda, 2024b; Rodr

ıguez-Seda,

2024a), here we present a closed-form of r

i j

for vehi-

cles and obstacles whose shape can be approximated

by rectangles of different lengths and widths.

Assume the ith and jth vehicles (or obstacles) can

be approximated by rectangles with length ℓ

, ℓ

and

width λ

, λ

. Without loss of generality, let their

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

lengths be aligned with the x-axis and deﬁne the fol-

lowing orientation-dependent functions

i j

ℓ

+ cos

i j

+ sin

i j

ℓ

+ sin

i j

+ cos

i j

where ε > 0 is a small constant chosen for smoothness

and

i j

= ψ

− ψ

is the agents’ relative orientation.

Let θ

i j

= atan2(z

2 j

−z

1 j

−z

) represent the angle

between z

and z

. Then, the minimum safe distance

between both agents can be upper bounded by

i j

= r

−δ

i j

+ ρ

−δ

(10)

where δ ≥ 2 is a constant parameter and

2β

+ η

− 2ε

+ (γ

cos(θ

− ψ

) + β

sin(θ

− ψ

))

+ (γ

cos(θ

− ψ

) − β

sin(θ

− ψ

))

for p, q ∈ {i, j}. It is worth noting that choosing

smaller ε → 0 and larger δ → ∞ yields tighter bounds

on the minimum safe distance at the expense of larger

changes in the r

i j

, i.e., larger ∂r

i j

/∂z

and ∂r

i j

/∂ψ

terms.

5 SIMULATIONS

We now present simulation results with the conven-

tional APF approach of assuming obstacles of circular

shape and the proposed avoidance control framework.

We consider four USVs modeled according to (1)

with parameters given as m

= 200 kg, m

= 250 kg,

= 80 kg · m

, d

= 70 kg/s, d

= 100 kg/s,

and d

= 50 kg · m

/s (Reyhanoglu, 1996) for i ∈

{1,2, 3,4}. The vehicles are assumed to have length

ℓ

= 4 m and width λ

= 0.5 m, with the center of

rotation located at 0.33 m from the vehicle’s geomet-

ric center. The workspace, illustrated in the top dia-

gram of Figure 2, consists of a 10 m long, 4 m wide

rectangular passage and a 3 m diameter circular static

obstacle. For the avoidance control, the structure cre-

ating the passage is modeled as a group of 5 m long,

square-shaped obstacles. The vehicles are tasked with

traveling through the passage by following a series of

waypoints denoted by the small open square shapes,

with a switching distance threshold of

M = 1.5 m.

We ﬁrst simulated the case in which vehicles and

obstacles are approximated by circular shapes. In this

scenario, the minimum safe distance is constant, i.e.,

i j

(

ℓ

)

+ (

)

(

ℓ

)

+ (

)

, and the con-

trol law in (3) reduces to

= K

− z

) − d

+ p

−

∑

j∈N

∂A

i j

∂z

where p

has been kept to ease the avoidance of dead-

locks. The control parameters are taken as ∆

= 2 m,

= 1.25I

2×2

, µ

= (−1)

, and d = 6. The geomet-

ric center of the vehicles is chosen as the reference

point, i.e., L = 0.67 m. The simulation results are il-

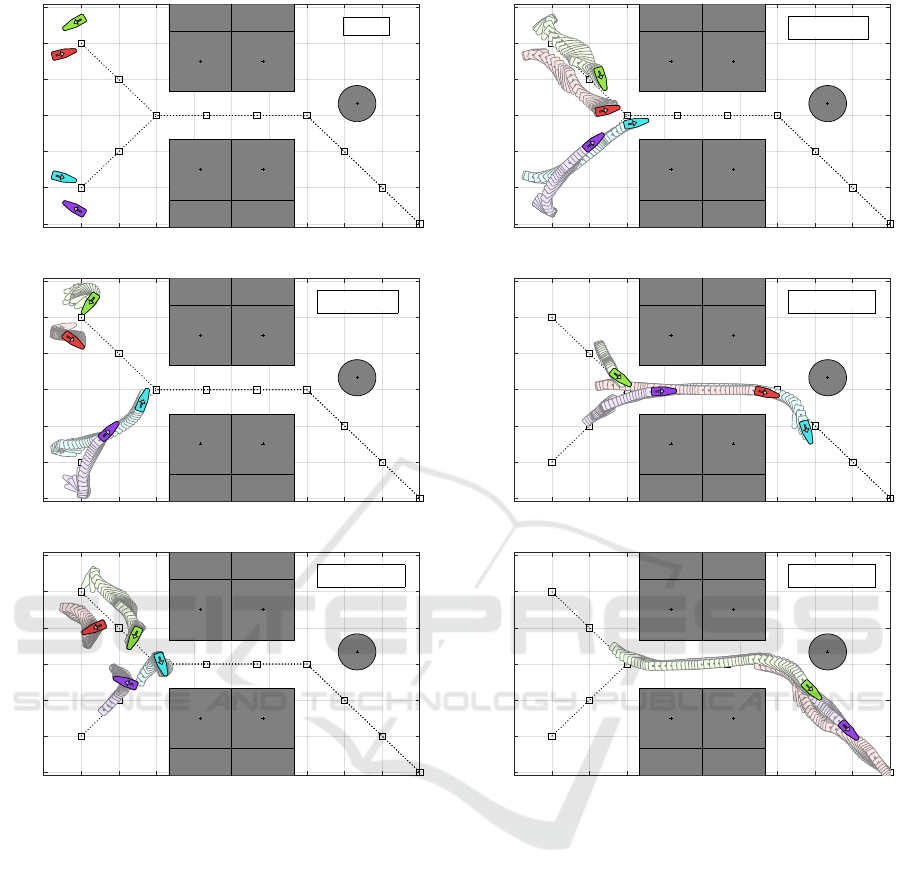
lustrated in Figure 2. Note that the ﬁrst and second

vehicles take nearly 15 s to resolve their ﬁrst conﬂict,

which was converging to the ﬁrst waypoint (refer to

the middle diagram in Figure 2). Eventually, all ve-

hicles move toward the passage, but none of them

is able to travel through. Instead, all four USVs re-

mained in a deadlock.

We then simulated the multi-vehicle system with

the proposed avoidance control (3) keeping same con-

trol parameters with the addition of ε = 0.01 and δ = 6

for the deﬁnition of r

i j

. The results are shown in Fig-

ure 3. The vehicles are in close proximity of each

other and the obstacles within the ﬁrst 15 s. However,

they are able to solve the conﬂicts and one by one is

able to navigate safely through obstacles and the nar-

row passage, avoiding collisions at all times.

6 CONCLUDING REMARKS

This paper proposed a novel distributed, cooperative

collision avoidance control framework for an arbitrar-

ily large group of autonomous, underactuated USVs

in restricted and congested waters. The control frame-

work is built on the concepts of APF and avoidance

functions to guarantee the collision-free transit of ves-

sels under some mild assumptions. The novelty of the

approach relies on the use of a non-constant minimum

safe radius that takes into account the shape and the

relative position and orientation of vehicles and ob-

stacles. The result is a reduction in the minimum safe

distance that vehicles must keep from each other and

other obstacles, allowing them to maneuver in nar-

row and obstacle-dense waters. We mathematically

show that the proposed control framework guarantees

collision avoidance at all times as long as the vehicle

maintains a non-zero velocity while in conﬂict, which

can be enforced by forcing them to rotate. Simulation

results with four vehicles in restricted waters demon-

strated the advantage of the proposed approach over

traditional APF-based methods.

Future research should investigate the ability of

the vehicles to avoid collisions without the assump-

Towards Guaranteed Collision Avoidance for Multiple Autonomous Underactuated Unmanned Surface Vehicles in Restricted Waters

-15 -12 -9 -6 -3 0 3 6 9 12 15

x (m)

-9

-6

-3

y (m)

t = 0 s

-15 -12 -9 -6 -3 0 3 6 9 12 15

x (m)

-9

-6

-3

y (m)

t ∈ [0 s,15 s]

-15 -12 -9 -6 -3 0 3 6 9 12 15

x (m)

-9

-6

-3

y (m)

t ∈ [15 s,60 s]

Figure 2: Sequential motion of the multi-vehicle system un-

der the traditional approach of assuming a constant mini-

mum safe distance. The top diagram illustrates the initial

conﬁguration. The two bottom plots illustrate the motion of

the vehicles from t = 0 s to t = 60 s. Positions and orienta-

tions are superimposed every 0.5 s.

tion of non-zero velocity. In addition, we plan to

formulate the proposed minimum safe distance and

avoidance functions for vehicles and obstacles of

other shapes and to include water disturbances, such

as currents or waves, into the analysis.

REFERENCES

Brockett, R. W. (1983). Asymptotic stability and feedback

stabilization. In Brockett, R. W., Millman, R. S., and

Sussmann, H. J., editors, Differential Geometric Con-

-15 -12 -9 -6 -3 0 3 6 9 12 15

x (m)

-9

-6

-3

y (m)

t ∈ [0 s,15 s]

-15 -12 -9 -6 -3 0 3 6 9 12 15

x (m)

-9

-6

-3

y (m)

t ∈ [15 s,35 s]

-15 -12 -9 -6 -3 0 3 6 9 12 15

x (m)

-9

-6

-3

y (m)

t ∈ [35 s,60 s]

Figure 3: Sequential motion of the multi-vehicle system un-

der the proposed approach, where the minimum safe dis-

tance is a function of their relative position and orientations.

The plots illustrate the motion of the vehicles from t = 0 s to

t = 60 s. Positions and orientations are superimposed every

0.5 s.

trol Theory, pages 181–191. Birkhauser, Boston.

Er, M. J., Ma, C., et al. (2023). Intelligent motion control of

unmanned surface vehicles: A critical review. Ocean

Engineering, 280:114562.

Fossen, T. I. (2021). Handbook of marine craft hydrody-

namics and motion control. John Wiley & Sons, 2nd

edition.

Khalil, H. K. (2002). Nonlinear Systems. Prentice Hall,

New Jersey.

Leitmann, G. and Skowronski, J. (1977). Avoidance con-

trol. J. Optim. Theory Appl., 23(4):581–591.

Li, L., Wu, D., et al. (2021). A path planning strategy uni-

ﬁed with a colregs collision avoidance function based

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

on deep reinforcement learning and artiﬁcial potential

ﬁeld. Applied Ocean Research, 113:102759.

Li, Y., Hou, P., et al. (2025). Research on collision avoid-

ance methods for unmanned surface vehicles based on

boundary potential ﬁeld. Journal of Marine Science

and Engineering, 13(1):88.

Lyu, H., Hao, Z., et al. (2023). Ship autonomous collision-

avoidance strategies—a comprehensive review. Jour-

nal of Marine Science and Engineering, 11(4):830.

Paliotta, C., Lefeber, E., et al. (2018). Trajectory track-

ing and path following for underactuated marine vehi-

cles. IEEE Transactions on Control Systems Technol-

ogy, 27(4):1423–1437.

Pettersen, K. Y. and Egeland, O. (1996). Exponential sta-

bilization of an underactuated surface vessel. In IEEE

Conference on Decision and Control, volume 1, pages

967–972.

Reyhanoglu, M. (1996). Control and stabilization of an un-

deractuated surface vessel. In IEEE Conference on

Decision and Control, volume 3, pages 2371–2376.

Rodr

ıguez-Seda, E. J. (2024a). A decentralized guaran-

teed collision avoidance control framework for multi-

vehicle systems in highly constrained spaces. In Proc.

International Conference on Informatics in Control,

Automation and Robotics, volume 1, pages 229–236.

Rodr

ıguez-Seda, E. J. (2024b). Reactive collision avoid-

ance control for nonholonomic vehicles and obstacles

of arbitrary shape. ASME. Letters Dyn. Sys. Control,

4(3):031005.

Rodr

ıguez-Seda, E. J., Tang, C., et al. (2014). Trajec-

tory tracking with collision avoidance for nonholo-

nomic vehicles with acceleration constraints and lim-

ited sensing. Int. J. Robot. Res., 33(12):1569–1592.

Stipanovi

c, D. M., Hokayem, P. F., et al. (2007). Coopera-

tive avoidance control for multiagent systems. J. Dyn.

Syst. Meas. Control, 129:699–707.

Vagale, A., Oucheikh, R., et al. (2021). Path planning and

collision avoidance for autonomous surface vehicles I:

A review. Journal of Marine Science and Technology,

pages 1–15.

Xue, Y., Lee, B., and Han, D. (2009). Automatic collision

avoidance of ships. Proc. of the Institution of Mechan-

ical Engineers, Part M: Journal of Engineering for the

Maritime Environment, 223(1):33–46.

Zhang, G., Han, J., et al. (2022). Apf-based intelligent navi-

gation approach for usv in presence of mixed potential

directions: Guidance and control design. Ocean En-

gineering, 260:111972.

Towards Guaranteed Collision Avoidance for Multiple Autonomous Underactuated Unmanned Surface Vehicles in Restricted Waters