Integrating Graph Search, Sampling, and Neural Networks for

Optimized Vehicle Path Planning

Xinze Li

Donald Bren School of Information and Computer Sciences, University of California, Irvine, California, 92697, U.S.A.

Keywords: Optimized Vehicle Path Planning, Graph Search, Sampling, Neural Networks.

Abstract: With the development of autonomous driving technology, path planning has become one of the core issues,

aiming to ensure the safety and efficiency of vehicles in complex and dynamic environments. However,

traditional path planning methods, especially graph-based algorithms, have limitations when facing changing

traffic and environmental factors. Therefore, it is particularly important to find more efficient and adaptive

path-planning strategies. In recent years, deep reinforcement learning (DRL) has provided new solutions for

path planning and promoted the advancement of related technologies. The theme of this paper is to review

the research progress of path planning for autonomous driving vehicles, focusing on the evolution from

traditional graph algorithms to modern deep learning methods. This paper will review from the following

perspectives: first, discuss traditional path planning methods and their limitations; second, analyze the

application and advantages of deep reinforcement learning in path planning; finally, explore the latest research

progress of combining deep learning with traditional path planning methods. In addition, this paper will

summarize the shortcomings of current research and look forward to the direction of future development.

1 INTRODUCTION

1.1 Traditional Path-Planning Methods

Path planning is an essential element of autonomous

vehicle navigation, designed to provide safe,

efficient, and optimal transit between destinations.

The primary challenge lies in developing algorithms

that can effectively navigate diverse and

unpredictable road conditions, while also maintaining

a balance between computational efficiency and real-

time adaptability. Traditional methods, such as graph-

based approaches, have long been employed for

navigation and routing, with Dijkstra’s algorithm

being a cornerstone for shortest-path determination.

While these classical methods offer structured

solutions, they often fall short when applied to real-

world scenarios, particularly in dynamic

environments where conditions can change

unpredictably.

https://orcid.org/0009-0008-4129-4056

1.2 Static vs. Dynamic Path Planning

A key distinction in autonomous vehicle path

planning lies in static versus dynamic environments.

Static path planning assumes that environmental

factors remain unchanged, enabling the

precomputation of optimal paths. However, real-

world driving requires dynamic path planning, which

adapts to moving obstacles, fluctuating traffic

patterns, and environmental changes. Insights from

Planning and Learning: Path-Planning for

Autonomous Vehicles emphasize the importance of

real-time adaptability in robust path-planning

algorithms, highlighting the need for predictive

modeling and sensor-based decision-making

(Osanlou, Guettier, Cazenave, & Jacopin, 2022).

1.3 Machine Learning and Deep

Reinforcement Learning

Recent breakthroughs in machine learning, especially

deep reinforcement learning (DRL), have provided

transformative solutions for path planning. In contrast

Li, X.

Integrating Graph Search, Sampling, and Neural Networks for Optimized Vehicle Path Planning.

DOI: 10.5220/0013678000004670

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Conference on Data Science and Engineering (ICDSE 2025), pages 52-59

ISBN: 978-989-758-765-8

to conventional systems reliant on precomputed

routes and reactive modifications, DRL empowers

vehicles to formulate adaptive navigation strategies

via environmental interaction. Deep Reinforcement

Learning in Autonomous Car Path Planning and

Control: A Survey explores how neural networks

process large volumes of sensor data, enhancing

decision-making in highly dynamic traffic conditions

and allowing autonomous systems to learn efficient

driving behaviors from experience (Chen, Ji, Cai,

Yan, & Su, 2024).

1.4 Integration of Deep Learning and

Classical Path-Planning Methods

As the field progresses, the integration of deep

learning with classical path-planning methods has

gained traction. Survey of Deep Reinforcement

Learning for Motion Planning of Autonomous

Vehicles highlights how machine learning

techniques, particularly neural networks and

reinforcement learning, are being applied to enhance

real-time decision-making and obstacle avoidance in

autonomous navigation (Zhang, Hu, Chai, Zhao, &

Yu, 2020). This shift underscores the increasing

reliance on data-driven models to improve

computational efficiency and adaptability in

unpredictable driving environments.

1.5 Paper Structure and Objectives

This paper presents a comprehensive review of path-

planning strategies for autonomous vehicles, tracing

the evolution from classical graph-based methods to

machine learning-driven approaches. The discussion

is structured as follows: Section 2 covers traditional

graph-based and heuristic algorithms, Section 3

explores optimization techniques for constrained

environments, and Section 4 delves into the latest

advancements in deep reinforcement learning-based

path planning. Section 5 provides further insights into

current limitations and future development directions.

By synthesizing insights from diverse research

studies, this review aims to highlight the current state

of autonomous vehicle path planning and outline

future directions in the field.

2 GRAPH SEARCH-BASED PATH

PLANNING

Path planning is a fundamental application of graph

search algorithms. They work best in static, fully

predictable environments. This section covers two

major ones: Dijkstra's algorithm and A*. It accounts

for their foundations, advantages, and the obstacles

they face in changing environments.

2.1 Classical Graph Search Algorithms

The earliest and most famous method for determining

the shortest path is Dijkstra's algorithm. It carefully

examines all potential routes from the source node to

the destination node. This algorithm assigns a

provisional distance value to each node: zero for the

source node and infinity for all others. It subsequently

iteratively selects the node with the minimal distance,

updates the distance values for its adjacent nodes, and

continues this procedure until it identifies the shortest

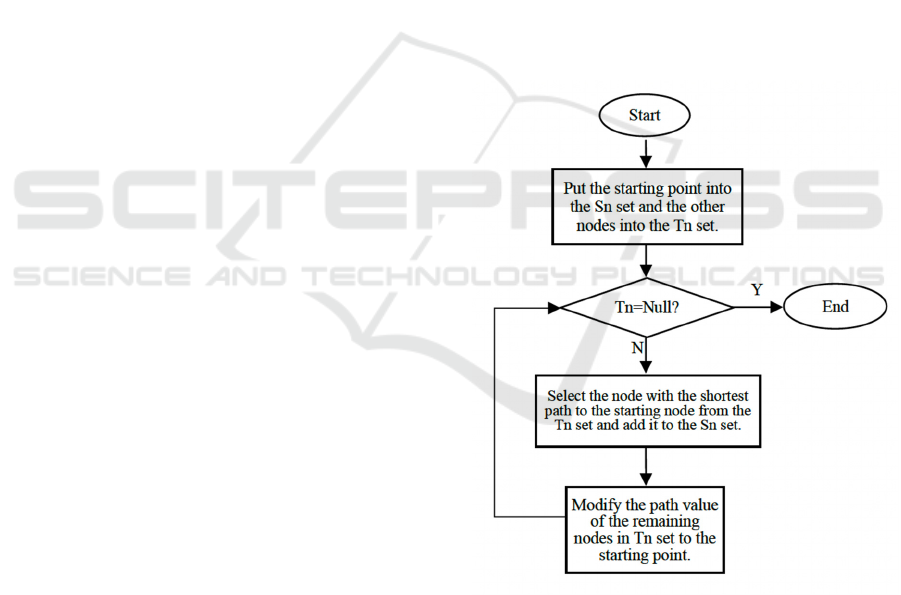
path. This process is clearly demonstrated in the

flowchart of Dijkstra's algorithm in Figure 1

(Osanlou, Guettier, Bursuc, Cazenave, & Jacopin,

2022) to visualize the node iterative evaluation and

update process.

Figure 1: Dijkstra Algorithm Flow Chart (Osanlou et al,

2022).

Integrating Graph Search, Sampling, and Neural Networks for Optimized Vehicle Path Planning

Figure 2: A Hybrid Example of Graph Search and Neural

Networks (Osanlou et al, 2021).

Dijkstra's algorithm guarantees the optimal result

when the search space is static and fully known, but

it suffers from computational cost. It considers every

alternative path, no matter how unpromising. Recent

developments have been aimed at addressing this

inefficiency. For instance, the neural network

structure Figure 2 (Osanlou et al, 2021) shows a

hybrid approach of graph search and neural networks.

This method employs machine learning to determine

the most likely successful paths, streamlining the

search process and conserving computational

resources while delivering consistently high-quality

results.

2.2 Advantages of A*

A* is an optimized version of Dijkstra's algorithm

that makes use of heuristics. It uses a heuristic

function, h(x), to predict the cost left to reach the

destination from a specific node. This makes A*

focus on paths preparing beforehand to reach the

destination and reduce exploration to areas that are

less expedient. This balance between exhaustive

search and heuristic guidance often makes A* faster

than Dijkstra's algorithm.

Table 1 (Table 1 from (Osanlou et al, 2022))

compares the performance of A* and Dijkstra's

algorithm in several scenarios. It indicates that A* is

the most efficient in terms of computation, especially

when the environment has clearly defined goal states.

As a result, A* is very well-suited for use cases where

speed and accuracy are both important

considerations, like robotics and video game

pathfinding. Its speed in finding near-optimal

solutions has made it a standard for these fields.

2.3 Challenges in Dynamic Settings

While A* is optimal for static scenarios, it is not

suitable for dynamic or partially known worlds.

When new elements are introduced in the

environment (for example, new obstacles or paths

become inaccessible), A* has to find a new entire

path from scratch. This issue dramatically raises

computational costs, as observed in assessments from

(Osanlou, Bursuc, Guettier, Cazenave, & Jacopin,

2021). This recalculation process is not fast enough

for real-time handling, especially in highly dynamic

environments such as autonomous driving.

Moreover, it has led to hybrid approaches and

machine learning techniques that allow the algorithm

to adapt more quickly to fluctuations in their

environment. The goal of these methods is to retain

the inherent benefits of A* but to minimize its

dependency on static assumptions.

Table 1. The Applicable Environment and Conditions of the Algorithm (Osanlou, Guettier, Bursuc, Cazenave, & Jacopin,

2022)

Classifi-

cation

Algorithm Name Applicable Environment And Conditions

Path planning

algorithm based

on search

Dijkstra

algorithm

(1) Applicable to higher abstract graph theory levels and

directed graphs, but cannot account for the presence of

negative edge directed graphs.

(2) Address the issue of traversal path planning.

(3) Solve the problem of determining the shortest path

and compare it to the length of the path without a

specific path.

(4) Utilize in global path planning.

ICDSE 2025 - The International Conference on Data Science and Engineering

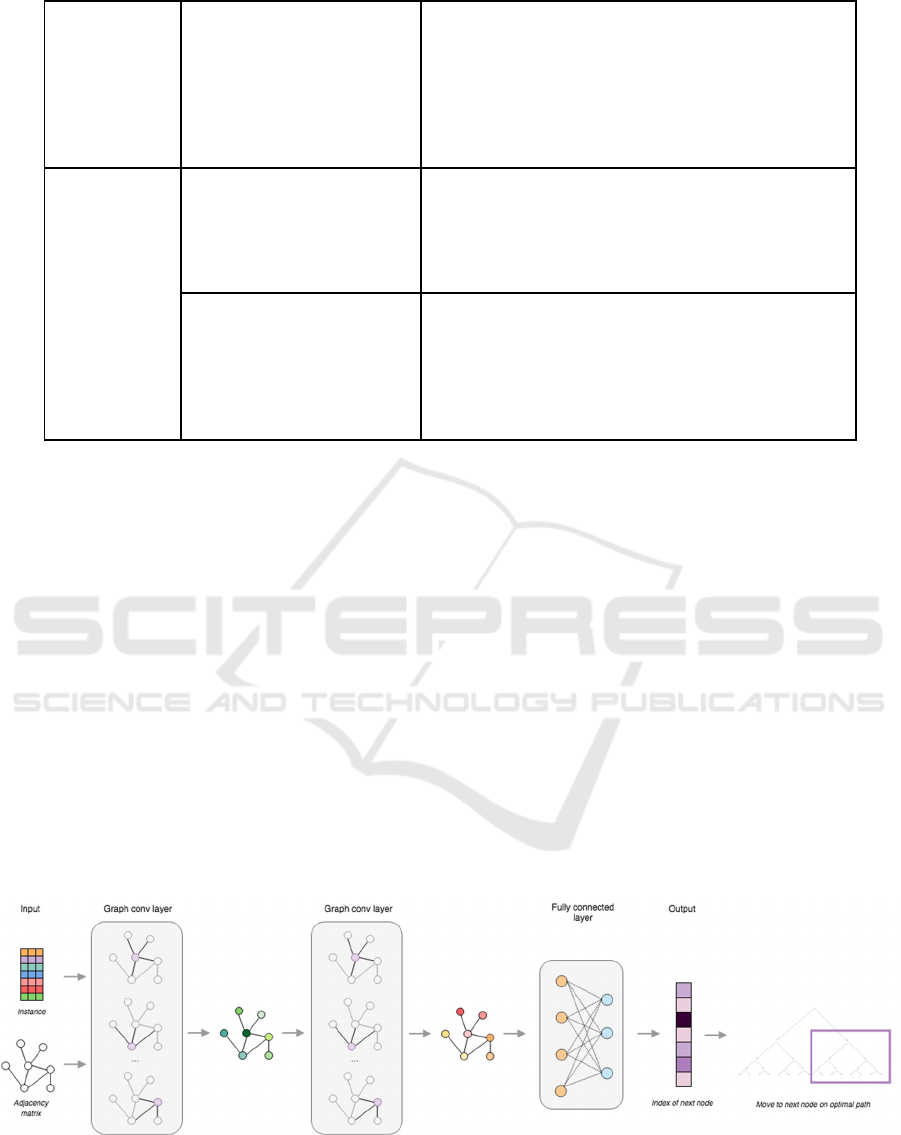
algorithm

(1) Appropriate for intricate yet moderately sized

directed graphs.

(2) Addresses the challenge of determining the shortest

route.

(3) Utilized for both global and local path planning.

(4) This approach is relevant when a specific path needs

to be determined.

Path planning

algorithm based

on sampling

Rapidly-

exploring

Random Trees

(RRT)

orithm

(1) Suitable for two-dimensional and high-dimensional

spaces.

(2) Effectively solves path planning problems in

complicated and dynamic environments.

(

)

Utilized for both

lobal and local

ath

lannin

Probabilistic Roadmap

Method

(PRM)

algorithm

(1) Appropriate for high-dimensional spaces.

(2) Addresses path planning challenges in complex and

dynamic environments.

(3) Utilized for both global and local path planning.

(4) Completion of the entire process necessitates the use

of a search-

ased algorithm.

3 SAMPLING-BASED PATH

PLANNING

For complex, high-dimensional space navigation,

sampling-based path planning algorithms are

necessary. When deterministic approaches are

computationally impossible, they shine. This section

delves into Rapidly-exploring Random Trees (RRT),

Probabilistic Roadmap Method (PRM), and Gaussian

Process-based Sampling, showcasing their

capabilities and capacity to adapt to real-time

settings.

3.1 Introduction to Sampling-Based

Algorithms

Algorithms like RRT and PRM that rely on sampling

try to discover workable routes in complicated

settings without necessitating a full-space model. In

order to find a workable route, these algorithms take

a random sample from the configuration space and

join them. Because of their probabilistic nature, they

are adept at navigating complex, multi-dimensional

spaces.

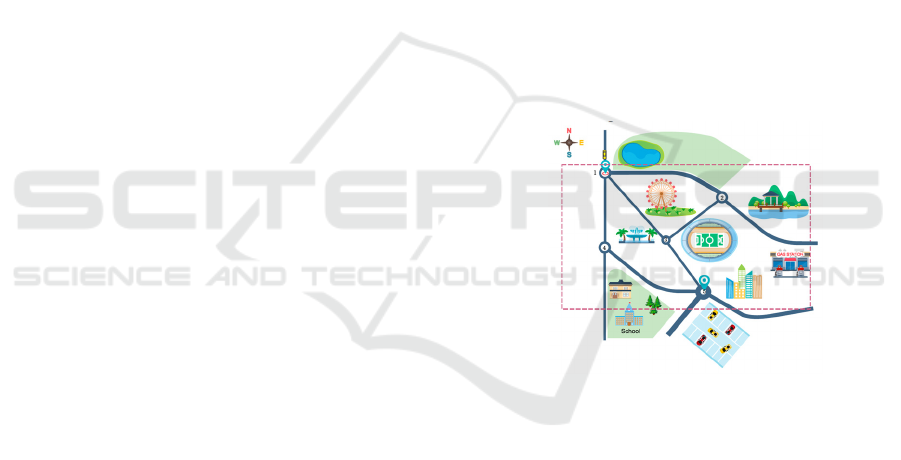
Figure 3 (Osanlou et al, 2021) shows the

Processing pipeline for Graph Convolutional

Networks (GCNs), which shows how graph models

can be integrated with algorithms based on sampling.

It shows how GCNs improve computing efficiency,

optimize the search process, and use learned features

to improve sample selection. By combining them

with new learning-based techniques, conventional

sampling methods are strengthened to withstand

changing environments.

Figure 3: Processing pipeline for path planning using GCNs. The GCN accepts an adjacency matrix containing costs and an

instance as input. Graph convolutional layers evaluate each node in conjunction with its adjacent nodes. New features are

generated for each node in the hidden layers. In the concluding layer, these features are input into a fully linked layer,

succeeded by a softmax function. The softmax layer identifies the subsequent node in the optimal trajectory (Osanlou et al,

2021).

Integrating Graph Search, Sampling, and Neural Networks for Optimized Vehicle Path Planning

3.2 Reinforcement Learning

Enhancements

When applied to dynamic settings, reinforcement

learning greatly enhances the adaptability of

sampling-based approaches. Algorithms like RRT

and PRM, which incorporate DRL (Deep

Reinforcement Learning), can optimize their

sampling tactics over time. An application of this is

demonstrated in Deep Reinforcement Learning-

Based Optimization for path planning, wherein the

model adjusts its sampling distribution in real-time

based on environmental input (Jin et al., 2023).

With reinforcement learning, path quality may be

preserved while the number of samples needed is

decreased. Because of this, RRT and similar

technologies are better suited to real-time

applications that require computational efficiency

and flexibility.

4 COMBINATION OF GRAPH

SEARCH AND SAMPLING-

BASED METHODS

The integration of deterministic and probabilistic

approaches represents a significant advancement in

vehicle path planning. By combining the structured

reliability of graph search with the adaptability of

sampling-based methods, hybrid models address

limitations present in either approach individually.

This section explores the architecture, case studies,

real-world applications, and the role of artificial

potential fields in enhancing hybrid systems.

4.1 Introduction to Hybrid Approaches

Hybrid models leverage the strengths of both

deterministic and probabilistic methods. They utilize

graph-based algorithms for precision while

incorporating sampling techniques for flexibility in

dynamic environments. The processing pipeline for

path planning using GCNs Figure 3 (Osanlou et al,

2021) demonstrates how hybrid systems integrate

GCNs with sampling. This pipeline highlights how

GCNs enhance the decision-making process by

predicting promising regions in the search space,

enabling faster and more efficient hybrid path

planning.

4.2 Case Studies and Examples

4.2.1 Performance Improvements in

Dynamic Environments

The hybrid approach’s ability to adapt to dynamic

conditions is evident in the Optimal Solving of

Constrained Path-Planning Problems with Graph

Convolutional Networks and Optimized Tree Search

(Osanlou et al, 2021). Evaluation charts from this

study show significant performance improvements,

particularly in environments with shifting obstacles

or constraints. These results underscore the hybrid

model’s advantage in combining structured

exploration with real-time adaptability.

4.2.2 Handling Traffic Dynamics

Figure 4 (Chen, Jiang, Lv, & Li, 2020) illustrates a

road condition selection area that demonstrates how

hybrid methods manage dynamic traffic scenarios. By

integrating reinforcement learning with sampling-

based techniques, the model adapts to real-time traffic

changes, ensuring smooth and efficient navigation.

Figure 4: Road Condition Selection Area (Chen et al, 2020).

4.3 Real-World Applications

4.3.1 Optimization During Training

Improved Deep Reinforcement Learning Algorithm

for Path Planning provides insights into hybrid

methods during the training phase (Osanlou et al,

2021). Figure 5 and Figure 6 (Jin, Jin, & Kim, 2023)

present preliminary pathfinding results, showcasing

how the integration of deterministic and probabilistic

techniques optimizes decision-making even at early

training stages (Jin, Jin, & Kim, 2023). This

capability makes hybrid approaches well-suited for

environments where learning must occur on-the-fly.

ICDSE 2025 - The International Conference on Data Science and Engineering

Figure 5: Depiction of the Simulated Environment (Jin et

al., 2023).

Figure 6: Preliminary Path Finding (Jin et al., 2023).

4.3.2 Fine-Tuning Hybrid Models

Figure 7 (Chen et al., 2020) highlights how hybrid

methods can be fine-tuned by adjusting parameters to

balance exploration and exploitation. This real-world

application demonstrates the practical effectiveness

of hybrid systems in diverse scenarios, such as

autonomous vehicle navigation through

unpredictable environments.

Figure 7: The Influence of the Probability of Greedy

Algorithm (ε) on Path Selection (Chen et al., 2020).

4.4 Artificial Potential Fields in Hybrid

Models

Artificial Potential Fields (APF) contribute to hybrid

systems by providing local navigation efficiency.

Reference (Rehman, Tanveer, Ashraf, & Khan, 2023)

explains how APF principles, such as attractive and

repulsive forces, can be integrated into hybrid

methods to improve obstacle avoidance and goal-

seeking behaviors. These contributions enhance the

precision of hybrid models without compromising

their adaptability.

4.5 Addressing Hybrid System

Limitations

APF systems also address specific limitations in

hybrid models. Discussions in (Rehman et al., 2023)

highlight how APF techniques can handle edge cases,

such as narrow corridors or complex obstacle layouts,

where traditional methods may fail. By bridging these

gaps, APF ensures smoother navigation in real-world

applications.

5 FUTURE DIRECTIONS

Advancements in deep learning and path planning

have paved the way for further research in

autonomous vehicle navigation. Future studies should

focus on enhancing real-time decision-making,

optimizing energy efficiency, integrating multi-

criteria constraints, and addressing scalability

challenges.

5.1 Reinforcement Learning

Integration for Real-Time Decision-

Making

The integration of DRL into autonomous vehicle path

planning can significantly improve adaptability and

decision-making in dynamic environments. By

utilizing DRL, vehicles can learn from past

experiences to optimize routes, avoid obstacles, and

respond to real-time traffic conditions. Figure 8 (Jin

et al., 2023) illustrates the reward trend over

iterations, demonstrating how DRL models refine

their decision-making processes through iterative

learning. This trend highlights how reinforcement

learning enhances model adaptability and robustness

in varied driving scenarios.

Integrating Graph Search, Sampling, and Neural Networks for Optimized Vehicle Path Planning

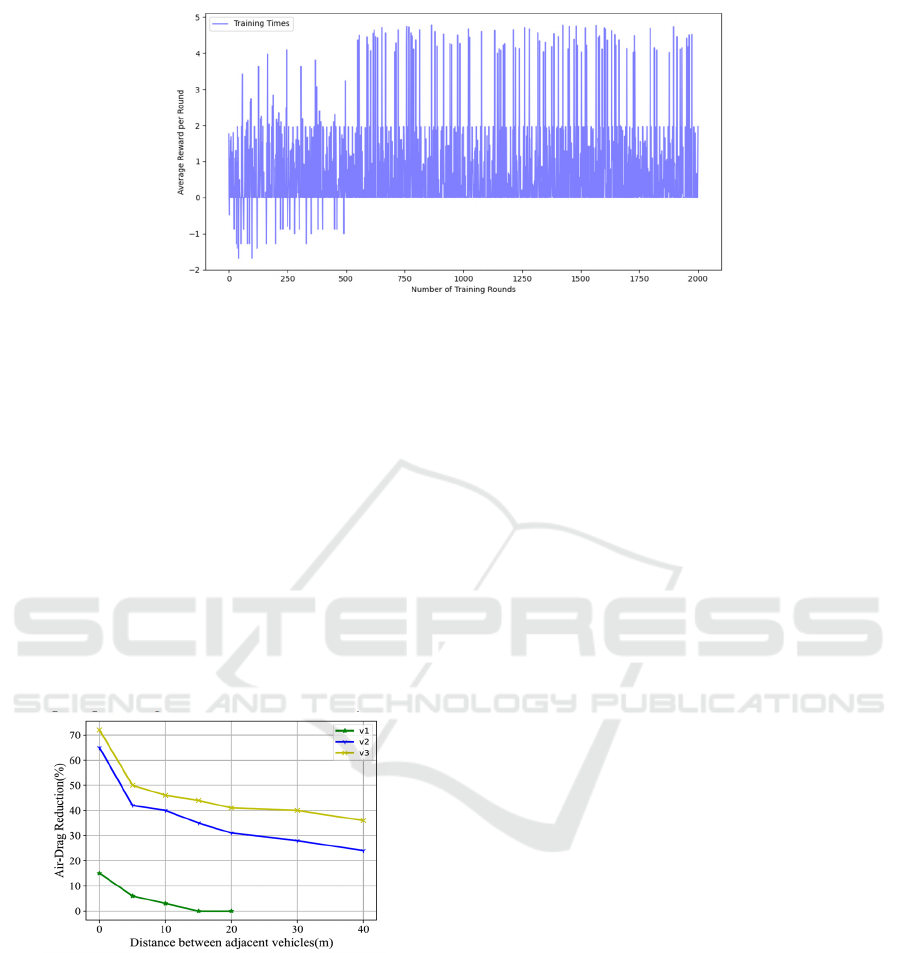
Figure 8: DRL-PP algorithm’s reward trend over 2,000 iterations (Jin et al., 2023).

5.2 Environmental Factors: Fuel

Efficiency and Energy

Optimization

Energy consumption and fuel efficiency are critical

considerations for autonomous vehicle path planning.

Factors such as air resistance, terrain variations, and

acceleration control significantly impact fuel

economy. Figure 9 (Chen et al., 2020) showcases the

relationship between vehicle distances and air

resistance, indicating that efficient path planning can

minimize fuel consumption and environmental

impact. Future research should focus on integrating

energy optimization strategies with deep learning-

based path planning to enhance sustainability.

Figure 9: The Relationship between Vehicles Distance and

Air Resistance (Chen et al., 2020).

5.3 Multi-Criteria Optimization for

Real-World Constraints

Real-world autonomous navigation requires

balancing multiple constraints, such as safety, traffic

efficiency, and user preferences. Learning-Based

Preference Prediction for Constrained Multi-Criteria

Path-Planning proposes a preference-based approach

to optimize path planning under diverse constraints

(Osanlou, Guettier, Bursuc, Cazenave, & Jacopin,

2021). By integrating multi-criteria optimization with

deep learning, future research can develop more

robust navigation systems that dynamically adjust to

real-world conditions while aligning with user-

defined priorities.

5.4 Challenges in Scalability and Real-

Time Performance

Despite advancements in DRL, scalability and real-

time performance remain major challenges in

autonomous vehicle path planning. DRL Based

Optimization for Autonomous Driving Vehicle Path

Planning highlights computational bottlenecks and

efficiency issues when scaling DRL models to larger

and more complex driving environments (Jin, Jin, &

Kim, 2023). Addressing these challenges requires

improved algorithms, hardware acceleration

techniques, and hybrid models that balance accuracy

and computational efficiency.

6 CONCLUSIONS

This article has examined various deep learning-

based approaches for path planning in autonomous

vehicles, highlighting key methodologies, challenges,

and future research directions.

A comparative analysis of different path-planning

methods, as summarized, reveals the strengths and

weaknesses of various approaches. While traditional

methods offer reliability and predictability, deep

learning-based techniques enhance adaptability and

learning capability. However, each method comes

with trade-offs in terms of computational complexity,

data requirements, and real-world applicability.

ICDSE 2025 - The International Conference on Data Science and Engineering

Hybrid models that combine classical path-

planning algorithms with machine learning

techniques hold significant promise for future

advancements. Optimization techniques play a

crucial role in refining model performance, as

evidenced by improvements in loss function curves

during training. Additionally, real-world applicability

highlights the importance of bridging theoretical

advancements with practical deployment to enhance

autonomous navigation systems.

Recent developments in the optimal resolution of

constrained path-planning issues emphasize the

application of GCNs and optimized tree search

techniques. These enhancements markedly diminish

computational burden and boost path-planning

efficacy, rendering real-time decision-making

possible.

While deep learning has revolutionized path

planning for autonomous vehicles, challenges such as

scalability, energy efficiency, and real-world

adaptability remain. Future research should focus on

refining hybrid models, integrating multi-criteria

optimization, and improving computational

efficiency to enable more robust and scalable

autonomous navigation systems.

REFERENCES

Chen, C., Jiang, J., Lv, N., & Li, S. (2020). An intelligent

path planning scheme of autonomous vehicles platoon

using deep reinforcement learning on network edge.

IEEE Transactions on Intelligent Transportation

Systems, 21(11), 4600–4611.

Chen, Y., Ji, C., Cai, Y., Yan, T., & Su, B. (2024). Deep

reinforcement learning in autonomous car path

planning and control: A survey. arXiv preprint

arXiv:2404.00340.

Jin, H., Jin, Z., & Kim, Y.-G. (2023). An improved deep

reinforcement learning algorithm for path planning in

unmanned driving. IEEE Access, 11, 7890–7902.

Jin, H., Jin, Z., & Kim, Y.-G. (2023). Deep reinforcement

learning-based (DRLB) optimization for autonomous

driving vehicle path planning. IEEE Access, 11,

12345–12356.

Osanlou, K., Bursuc, A., Guettier, C., Cazenave, T., &

Jacopin, E. (2021). Constrained shortest path search

with graph convolutional neural networks. arXiv

preprint arXiv:2108.00978.

Osanlou, K., Bursuc, A., Guettier, C., Cazenave, T., &

Jacopin, E. (2021). Learning-based preference

prediction for constrained multi-criteria path-

planning. arXiv preprint arXiv:2108.01080.

Osanlou, K., Guettier, C., Bursuc, A., Cazenave, T., &

Jacopin, E. (2021). Optimal solving of constrained

path-planning problems with graph convolutional

networks and optimized tree search. arXiv preprint

arXiv:2108.01036.

Osanlou, K., Guettier, C., Cazenave, T., & Jacopin, E.

(2022). Planning and learning: Path-planning for

autonomous vehicles, a review of the literature. arXiv

preprint arXiv:2207.13181.

Osanlou, K., Guettier, C., Bursuc, A., Cazenave, T., &

Jacopin, E. (2022). Review of path planning algorithms

for unmanned vehicles. IEEE Access, 10, 123456–

123470.

Rehman, A. U., Tanveer, A., Ashraf, M. T., & Khan, U.

(2023). Motion planning for autonomous ground

vehicles using artificial potential fields: A review.

arXiv preprint arXiv:2310.14339.

Zhang, G., Hu, X., Chai, J., Zhao, L., & Yu, T. (2020).

Survey of deep reinforcement learning for motion

planning of autonomous vehicles. IEEE Access, 8,

135946–135971.

Integrating Graph Search, Sampling, and Neural Networks for Optimized Vehicle Path Planning