On the Asymmetrical Nature of Entity Matching Using Pre-Trained

Transformers

Andrei Olar

Faculty of Mathematics and Computer Science, Babes¸-Bolyai University, Romania

Keywords:

End-to-End Entity Resolution, Asymmetrical Matching, Clustering, Directed Reference Graph.

Abstract:

Entity resolution (ER) is a foundational task in data integration and knowledge discovery, aimed at identify-

ing which information refer to the same real-world entity. While ER pipelines traditionally rely on matcher

symmetry (if a matches b then b matches a) this assumption is challenged by modern matchers based on pre-

trained transformers, which are inherently sensitive to input order. In this paper, we investigate the asymmetric

behavior of transformer-based matchers with respect to input order and its implications for end-to-end (E2E)

ER. We introduce a strong asymmetric matcher that outperforms prior baselines, demonstrate how to integrate

such matchers into E2E pipelines via directed reference graphs, and evaluate clustering performance across

multiple benchmark datasets. Our results reveal that asymmetry is not only measurable but also materially

impacts clustering quality, highlighting the need to revisit core assumptions in ER system design.

1 INTRODUCTION

One of the key processes in knowledge discovery and

data integration responsible for determining which

data refer to the same real-world object is called en-

tity resolution (ER). It has many applications such

as eliminating potential duplicates in large datasets

to improve integration quality and reliability. More-

over, inferring links between records that refer to the

same real-world object from existing data is central to

knowledge discovery.

Most ER approaches rely on two core tasks match-

ing and clustering (Christophides et al., 2020; Binette

and Steorts, 2022). Matching determines the relative

pairwise similarity of data while clustering groups

data together based on their similarity. Some ER so-

lutions focus on matching (Mudgal et al., 2018; Li

et al., 2020) and others focus on clustering (Linacre

et al., 2022; Zeakis et al., 2023). More complete end-

to-end (E2E) ER solutions (Papadakis et al., 2018;

Saeedi et al., 2018) combine the two core compo-

nents into a single pipeline. Pipelining matching and

clustering introduces complexity. Graphs constructed

using the compared items as nodes, with the match-

ing items connected through edges weighted by a

similarity score offer the foundation needed to per-

form clustering based on matching output. They are

https://orcid.org/0009-0006-7913-9276

commonly referred to as similarity graphs (Papadakis

et al., 2018) or reference graphs (Bhattacharya and

Getoor, 2004). The latter term harkens back to the

notion of entity references denoting the items being

compared during matching.

Increasingly, deep learning is used for matching.

Systems like DeepMatcher (Mudgal et al., 2018) and

DeepER (Ebraheem et al., 2018), embed each individ-

ual entity reference independently before determin-

ing the relative similarity. In contrast, models like

Ditto (Li et al., 2020) take a more integrated approach

by encoding entire reference pairs using pre-trained

transformers to compute embeddings before classify-

ing the output as a match or non-match. The latter ap-

proach ﬁxes the order in which entity references are

presented to the model during training, whereas the

former typically allows the model to learn representa-

tions that are invariant to the input order.

Most pairwise ER models assume that matching

is symmetric: if entity reference a matches b, then b

matches a (Fellegi and Sunter, 1969; Talburt et al.,

2007; Benjelloun et al., 2009). In our opinion this

symmetry holds post hoc: when a and b truly refer

to the same real-world entity, the relation is naturally

bidirectional. During ER, matching only estimates

such relations based on similarity, while the matcher

itself may be asymmetric. Asymmetry then becomes

a form of error—potentially informative in diagnos-

ing matcher behavior. This paper focuses on observ-

208

Olar, A.

On the Asymmetrical Nature of Entity Matching Using Pre-Trained Transformers.

DOI: 10.5220/0013672900004000

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2025) - Volume 1: KDIR, pages 208-215

ing the ramiﬁcations of using an asymmetric matcher,

deferring answering the question of how an asymmet-

ric matcher ﬁts existing ER models to future work.

The topic is broached as a phenomenon that is intro-

duced by the sequence-aware nature of transformer-

based models. The exploration begins with an ER

matcher, closely modeled after Ditto, that learns la-

tent representations sensitive to training input order.

We then examine the design changes required for per-

forming clustering and simulate an E2E ER pipeline

with asymmetric matching.

Lastly, we evaluate the resulting system across

standard benchmarks for clustering quality. To study

how matcher asymmetry affects clustering, we build

our evaluation on the algebraic model of ER (Talburt

et al., 2007). This model treats ER as an equivalence

relation, which aligns with how many ER datasets de-

ﬁne ground truth (i.e., ideal matchings). We use the

partitions induced by the ER equivalence relation to

evaluate ER clustering quality and establish baselines

under asymmetric conditions with respect to matcher

input order. A possible critique of this approach is that

it relies on symmetric ground truths while studying

asymmetric matchers. However, this does not pose a

problem in practice: the ground truth is deﬁned inde-

pendently of any particular matcher and reﬂects the

symmetric notion of identity detailed in the previous

paragraph.

The next section presents backround information

and related work with an emphasis on terminology

and reference graphs. Next, the matcher is presented

followed by an experiment highlighting the practical

implications of asymmetric matchers over ER clus-

tering. A discussion of the ﬁndings precedes conclu-

sions and proposed future work.

2 BACKGROUND AND RELATED

WORK

This paper adheres to a design idiom that places

matching and clustering at the core of an ER

pipeline, as shown in both literature and in prac-

tice (Christophides et al., 2020; Binette and Steorts,

2022; Papadakis et al., 2018; Saeedi et al., 2018).

It departs from prior work by performing clustering

on directed reference graphs. Clustering started to

gain more interest in the early 2000s. Several re-

views thoroughly cover clustering algorithms for ER

on undirected similarity graphs (Hassanzadeh et al.,

2009; Saeedi et al., 2017; Papadakis et al., 2023). We

identify and evaluate a key design adaptation needed

to support clustering with asymmetric similarity: us-

ing directed reference graphs and algorithms capable

of handling directionality. To our knowledge, this is

among the ﬁrst empirical baselines for ER clustering

that explicitly accounts for matcher asymmetry.

The use of pairwise similarity to construct graphs

in ER has deep roots. As early as (Fellegi and Sunter,

1969), record linkage was conceptualized in terms of

pairwise decisions that naturally map to edges in a

graph. The work of (Bhattacharya and Getoor, 2004)

was another turning point, transitioning from describ-

ing links among records to formalizing the reference

graph concept: undirected graphs in which nodes rep-

resent records and edges encode pairwise similari-

ties (Bhattacharya and Getoor, 2007). Since then, the

term similarity graph has become prevalent in both

scholarly works (Gruenheid et al., 2014) and broader

ER literature (Christen, 2012) to refer to the same

concept. Because similarity is conceptually linked

with symmetry and this paper addresses an asymmet-

rical setting, we revert to the term reference graph to

emphasize potential directionality.

ER clustering is sometimes evaluated using pre-

cision, recall, and F

score. These metrics are only

comparable when true/false positives and negatives

are deﬁned consistently—which, in the literature we

examined, is not necessarily the case. While some

works (Draisbach et al., 2019) seem to rely on pair-

wise metrics (Menestrina et al., 2010) without an

explicit reference, others produce entirely custom

metrics (Hassanzadeh et al., 2009; Papadakis et al.,

2023) while referring to them using established met-

ric names in ER evaluation such as precision, recall

or F

. In preparing this paper, we encountered a di-

rectly comparable metric when the generalized merge

distance (Menestrina et al., 2010) was used for evalu-

ating multi-source clustering performance (Draisbach

et al., 2019). Similarly, to improve the comparability

with other studies performed on the same benchmark

datasets we use the aforementioned pairwise metrics.

Additionally, we use cluster metrics (Huang et al.,

2006), the adjusted Rand index (Yeung and Ruzzo,

2001) or the Talburt-Wang index (Talburt et al., 2007)

for evaluating ER clustering performance. These met-

rics are implemented and documented in supporting

libraries (Olar and Dios¸an, 2024).

On the Asymmetrical Nature of Entity Matching Using Pre-Trained Transformers

209

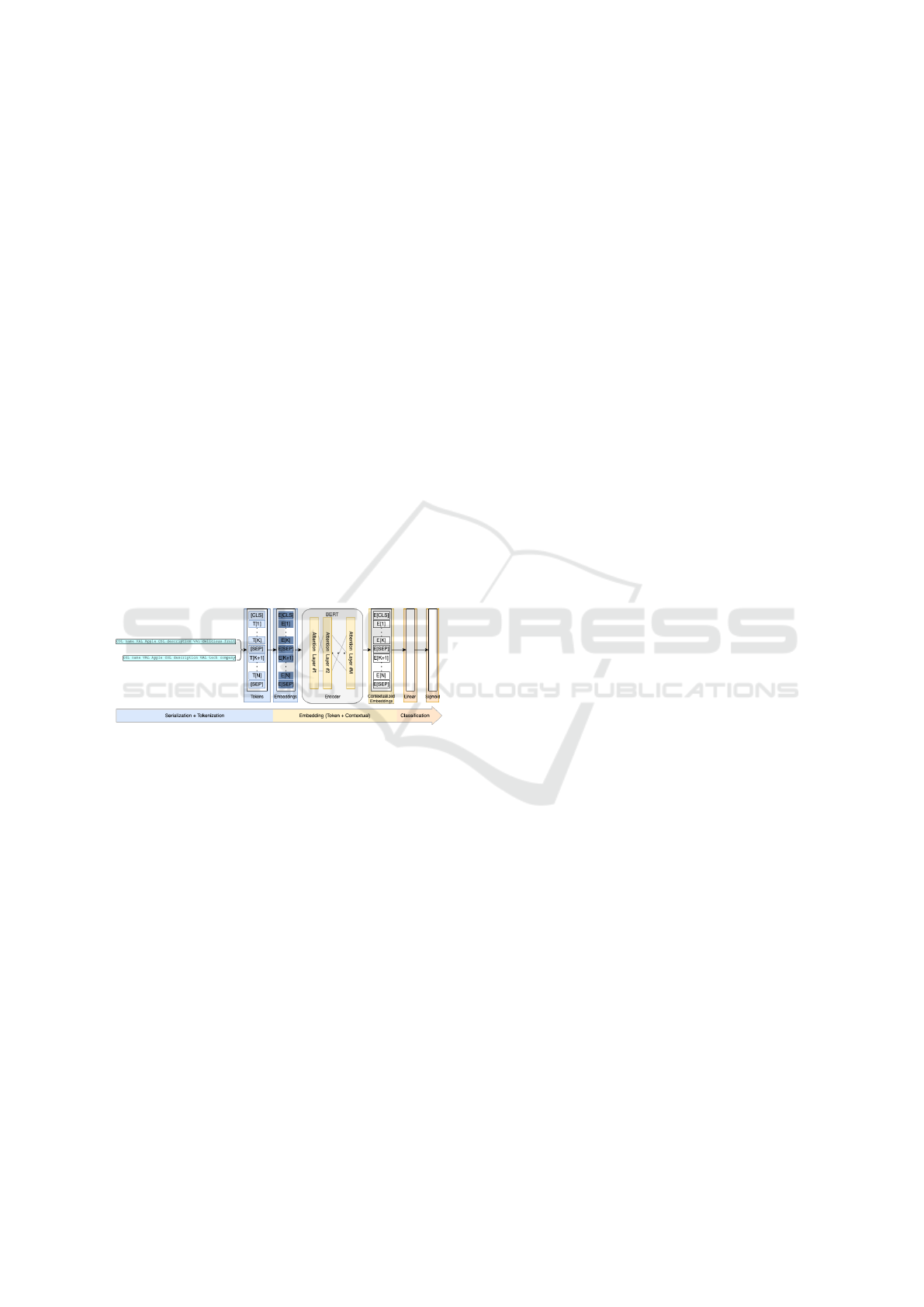
3 E2E ER WITH

TRANSFORMERS

3.1 Matching Using Pre-Trained

Transformers

The ﬁrst core operation of most E2E ER pipelines is

matching, which pairs similar entity references. The

input of the matcher is often formalised as a pair of

entity references. We refer to the totality of input pairs

passed to the matching engine throughout a single

ER pass as the comparison space. Our pipeline uses

a neural matcher architecture based on pre-trained

transformers, following the design of the Ditto (Li

et al., 2020) entity matcher. Figure 1 shows that the

architecture of the matching engine is almost identical

to the one used by Ditto. Our matcher similarly uses

BERT (Devlin et al., 2019) to encode a pair of entity

references instead of each entity reference individu-

ally. The main difference is the use of a single neu-

ron linear output layer with sigmoid activation, rather

than a two neuron softmax output layer. This simpli-

ﬁes binary classiﬁcation and reduces computational

overhead during training.

Figure 1: Architecture of the matching engine which trans-

forms an input of two entity references (formatted as

strings) into a value ranged between 0 and 1 representing

the similarity between the two references.

Because the matcher encodes both entity refer-

ences as a single input, it learns an order-sensitive

representation during training and may produce

different results for the same data if the input order

changes at runtime. For example, ‘ COL name

VAL sony pink cyber-shot 7.2 megapixel

digital camera dscw120p ’ and ‘ COL name

VAL olympus fe-360 digital camera pink

226540 ’ are entity references from (Li et al.,

2020). Since the matcher encodes their concatena-

tion during training, its output becomes sensitive

to the order in which inputs are presented. If we

let R be the set of all entity references and τ a

threshold above which the similarity score produced

by a matcher is considered to be a match then

∃ a, b ∈ R such that matcher(a, b) ̸= matcher(b, a)

because matcher(a, b) ≥ τ and matcher(b, a) < τ. Yet

such a construct still aligns with generic deﬁnitions

of a match function (Benjelloun et al., 2009): it

operates on a pair of records, the output depends

solely on the input records and it outputs a boolean

match/non-match decision.

While matcher asymmetry may be addressed in

various ways (e.g., using symmetric similarity func-

tions), we focus on the ramiﬁcations of matcher asym-

metry on the clustering step, thus enabling E2E ER

even when matching is asymmetric.

3.2 Clustering Algorithms

The other core operation of an E2E ER pipeline is

clustering and it focuses on the colocation of simi-

lar entity references as determined through matching.

Matchers with asymmetric results inﬂuence cluster-

ing by requiring the use of directed graphs. Given

a reference graph G = (V, E) and a matcher m, each

edge in G is weighted by m. If m is symmetric then

m(u, v) = m(v, u), ∀ u, v ∈ V . In this case, the edge

(u, v) can be replaced with (v, u) and the reference

graph is undirected. If the matcher is asymmetric,

∃ u, v ∈ V | m(u, v) ̸= m(v, u). For those u, v, the edge

(u, v) cannot be replaced with (v, u) and the reference

graph must be directed. Therefore, if the matcher is

symmetric the reference graph is undirected, whereas

if the matcher is asymmetric the reference graph is

directed. In short, a directed reference graph is both

necessary and sufﬁcient to represent the output of an

asymmetric matcher.

The E2E ER solution proposed in this paper uses

clustering algorithms that must meet certain criteria.

They must handle directed graphs natively, operate in-

dependently of the number of ER data sources and

require no upfront conﬁgurations with respect to the

number of output clusters. Existing work on incre-

mental record linkage (Gruenheid et al., 2014), bi-

partite graphs (Papadakis et al., 2023) and transform-

ing pairwise duplicates to clusters (Draisbach et al.,

2019) should be consulted for clustering approaches

designed for undirected reference graphs. The efﬁ-

cient computation of the transitive closure on a di-

rected graph is covered elsewhere as well (Nuutila,

1995). Next, we cover the clustering algorithms used

later in our experiment.

Ground Truth – Equivalence Class Partitioning.

To evaluate clustering, we convert the pairwise

ground truth—a subset containing the ideal match-

ings from the comparison space—into a clustered

ground truth by interpreting it as an equivalence re-

lation. As a reﬂexive, symmetric, and transitive re-

lation, it induces a unique partition over the entity

references (Talburt et al., 2007), enabling the use of

KDIR 2025 - 17th International Conference on Knowledge Discovery and Information Retrieval

210

standard partition similarity metrics for evaluation.

Singleton entities—those absent from the pairwise

ground truth—are included as degenerate equivalence

classes to complete the partition. Following the alge-

braic model of ER, the equivalence classes induced

by ER correspond to sets of references identifying

the same real-world entity. The pairwise-to-clustered

ground truth transformation is performed using the

union-ﬁnd data structure (Tarjan, 1979). The efﬁ-

ciency of this method, coupled with optimizations

like rank heuristics and path compression guarantee

near-constant amortized time per operation.

Weakly Connected Components. The connected

components (CC) algorithm (Tarjan, 1971) is a stan-

dard clustering method for undirected graphs and is

a widely adopted baseline in ER pipelines that rely

on undirected reference graphs (Saeedi et al., 2017;

Papadakis et al., 2023). Weakly connected compo-

nents (WCC) is an almost identical algorithm target-

ing directed graphs (Graham et al., 1972). Both al-

gorithms form clusters by grouping nodes connected

by a path—CC in undirected graphs, and WCC in di-

rected graphs by ignoring edge direction. They use

graph traversal to assign all reachable nodes from

each unvisited node to the same cluster. These al-

gorithms are deterministic, non-parametric, and scale

linearly with the number of nodes and edges, mak-

ing them suitable for large-scale ER applications. Be-

cause they treat all edges as symmetric (CC explicitly,

and WCC by disregarding direction), they are unable

to exploit directional signals that may emerge from

asymmetric matchers. Both algorithms are readily

available in the networkx (Hagberg et al., 2008) li-

brary, which we use in our implementation.

CENTER Clustering. The CENTER algo-

rithm (Haveliwala et al., 2000), based on C-

LINK (Hochbaum and Shmoys, 1985), is designed

for large-scale ER on web data modeled as directed

graphs, where directional similarity scores are

preserved and used in clustering. The algorithm

treats each similar pair as a directed edge and forms

clusters by designating the ﬁrst node to appear in

a scan over the edge list as a cluster center. All

other nodes appearing in outgoing edges from this

center are assigned to its cluster, ensuring all cluster

nodes are directly reachable in the graph from the

center via a similarity edge. CENTER is efﬁcient

and deterministic, requiring only a single pass over

the edge list and producing compact, star-shaped

clusters. Its reliance on edge direction makes it espe-

cially suitable in cases where asymmetric similarity

measures are meaningful. Our implementation of

this algorithm, called Parent CENTER (PC), uses a

path-compression technique to assign nodes to their

most similar reachable predecessor in an iterative

manner. The algorithm is implemented using the

networkx library (Hagberg et al., 2008) library and

available on GitHub

Markov Clustering. The Markov clustering (MCL)

algorithm (Van Dongen, 2008) is a graph cluster-

ing technique that simulates random walks to iden-

tify regions of dense connectivity. It has been ap-

plied across various domains to cluster similar en-

tity references based on probabilistic ﬂow patterns.

MCL operates on the graph’s transition matrix, apply-

ing two key operations iteratively: expansion, which

models the spread of ﬂow over multiple steps, and

inﬂation, which sharpens the clustering signal by

strengthening high-probability transitions and sup-

pressing weaker ones. This process continues until

convergence, yielding a block structure in the matrix

that corresponds to the ﬁnal clusters. The algorithm is

deterministic, highly scalable, and ﬂexible through its

inﬂation parameter, which controls cluster granular-

ity. Although commonly used with undirected graphs,

MCL naturally supports directed graphs, since ﬂow

inherently respects edge direction. In our evaluation,

we apply MCL to directed reference graphs using the

implementation provided by the markov clustering

library (Allard, 2025). We use the default parameter

settings of the library for our experiments.

4 EXPERIMENTS

The primary goal of our experiment is to empirically

evaluate matcher asymmetry-speciﬁcally, asymmetry

related to the order in which inputs are presented at

runtime. While asymmetry can arise from various

factors (e.g., input data type or record attribute pro-

cessing order), we focus on the runtime input order

versus training input order due to the textual nature

of the data: the matcher accepts free text inputs al-

though it was trained as described in Section 3.1. As

described there, the comparison space consists of se-

quential pairs of entity references fed to the matcher

individually. This space results from preprocessing

steps such as entity extraction, blocking, and ﬁltering,

as established in prior work (Papadakis et al., 2020).

The benchmark datasets we use deﬁne a ﬁxed com-

parison space, simplifying reproducibility. We refer

to the original order of entity pairs in this space as the

normal pair order. By reversing the order within each

pair, we construct a reversed pair order. To evaluate

input order asymmetry, we apply the matcher and the

earlier-described clustering algorithms to both orders

https://github.com/matchescu/clustering/

On the Asymmetrical Nature of Entity Matching Using Pre-Trained Transformers

211

and compare the outcomes.

The secondary objective of the experiment is to

explore how input order affects E2E ER, particularly

clustering quality. To that end, the normal and re-

versed directed reference graphs are derived from

each pair order, respectively. Baseline ﬁgures us-

ing our selection of clustering algorithms are com-

puted on both graphs. We retain the results from con-

nected components on an undirected graph (derived

from normal pair order) as a baseline for comparison

with work on undirected graphs.

4.1 Datasets

We selected benchmark datasets that were previously

used in the evaluation of Ditto (Li et al., 2020) and

DeepMatcher (Mudgal et al., 2018) for our exper-

iment. They are available in a GitHub repository

and their characteristics are summarized in Table 1.

To keep the experimental scope focused and man-

ageable, we restrict our selection to Clean-Clean ER

datasets, where duplicates occur only across data

sources (Christophides et al., 2020).

Table 1: L and R represent the left and right tables (e.g.,

‘Abt’ and ‘Buy’). A

and A

are their corresponding at-

tribute sets. C S represents the comparison space (i.e., all

evaluated entity reference pairs). T represents the pairwise

ground truth (i.e all matching entity reference pairs from the

comparison space). | · | represents the cardinality of the en-

closed item.

Name Domain |L| |A

| |R| |A

| |L × R| |CS | |T |

Abt-Buy e-commerce 1081 4 1092 4 1180452 9575 1028

Amazon-Google software 1363 4 3226 4 4397038 11460 1167

Beer beer 4345 5 3000 5 13035000 450 68

DBLP-ACM academic 2616 5 2294 5 6001104 12363 2220

DBLP-Scholar academic 2616 5 64263 5 168112008 28707 5347

Fodors-Zagat hospitality 533 7 331 7 176423 946 110

iTunes-Amazon music 6907 9 55923 9 386260161 539 132

Walmart-Amazon electronics 2554 6 22074 6 56376996 10242 962

Our choice of datasets is motivated primarily by

their accessibility and widespread adoption in the ER

community. Each dataset provides three standard

splits: training, validation, and test which consist of

entity reference pairs annotated with binary labels

with match/non-match semantics. We use the training

and validation splits for training the matcher, whereas

clustering evaluation is performed on the full dataset.

4.2 Metrics

We evaluate matcher asymmetry and clustering qual-

ity using the pyresolvemetrics library (Olar and

Dios¸an, 2024). Matcher asymmetry is assessed using

two indicators: raw scores produced by the matcher

and F

scores computed over the comparison space of

each benchmark dataset for both input orders. Clus-

tering quality is evaluated using four representative

metrics: the pair comparison measure, the cluster

comparison measure, the adjusted Rand index, and

the Talburt-Wang index. The pair comparison mea-

sure and adjusted Rand index capture similarity at

the level of pairwise cluster composition, while the

cluster comparison measure and Talburt–Wang index

(TWI) gauge the alignment of entire clusters. TWI,

in particular, is tailored for partition-based evalua-

tion (Talburt et al., 2007), reinforcing the importance

of expressing clustering outputs as proper partitions.

4.3 Training the Matcher

We use the original training, validation and test splits

from each selected dataset without modiﬁcation or

data augmentation. The matcher is trained using the

procedure outlined in (Li et al., 2020), in normal input

order only. Table 2 lists the training parameters and

corresponding validation scores for easier comparison

with Ditto.

Table 2: Matcher training parameters and results. α is the

initial learning rate because decay is employed. The match

threshold τ ∈ [0, 1] is optimised on the validation split.

Ditto

baseline

scores were taken from (Li et al., 2020). F

column contains our matcher’s scores. Both F

scores were

reported on the ‘validation’ split.

Name Batch Size Epochs α τ Ditto

baseline

Abt-Buy 64 15 3e-5 0.45 0.8174 0.9894

Amazon-Google 64 15 3e-5 0.5 0.7004 0.9684

Beer 32 40 3e-5 0.1 0.7344 1.0

DBLP-ACM 64 15 3e-5 0.4 0.9865 0.9966

DBLP-Scholar 64 15 3e-5 0.4 0.9467 0.9981

Fodors-Zagat 32 40 3e-5 0.4 0.9676 1.0

iTunes-Amazon 32 40 1e-6 0.3 0.9138 1.0

Walmart-Amazon 64 15 3e-5 0.35 0.7695 0.9974

Our matcher is implemented using Py-

Torch (Paszke et al., 2017) and the Huggingface

Transformers library (Wolf et al., 2020). We also

use the same pre-trained roberta-base (Liu et al.,

2019) transformer model used by Ditto. As shown in

Table 2 our matcher outperforms the Ditto baseline

on nearly all datasets, in some cases exceeding even

Ditto’s results with data augmentation.

4.4 Matcher Asymmetry

To quantify matcher asymmetry, recall from Sec-

tion 3.1 that a matcher m assigns a score in [0, 1] to

each entity pair (x, y) in a comparison space. We de-

ﬁne ∆ = m(x, y) − m(y, x) as the asymmetry measure

for each pair. Since symmetric matchers yield ∆ = 0

KDIR 2025 - 17th International Conference on Knowledge Discovery and Information Retrieval

212

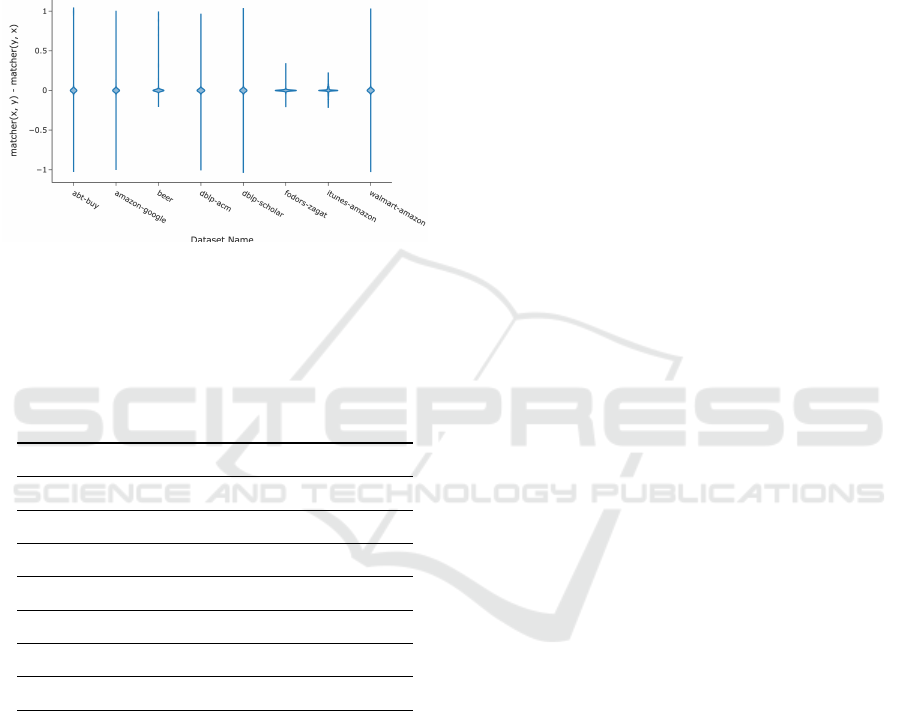
for all pairs, the distribution of ∆ values is an indi-

cator of asymmetry. Figure 2 shows such a distribu-

tion of ∆ values, including numerous outliers. This

raises a follow-up question: how does asymmetry af-

fect the F

score achieved by the matcher under dif-

ferent pair orders? Table 3 addresses this by reporting

our matcher’s F

scores obtained for both the normal

and reversed pair orders.

Figure 2: Distribution of values of the ∆ described in Sub-

section 4.4. For symmetric operations, ∆ would always be

0. The spread and number of outliers indicate a highly

asymmetric matcher.

Table 3: F

scores obtained by the matcher on each dataset,

comparing normal and reversed pair order at runtime.

Name Normal F

Reversed F

Abt-Buy 0.8872 0.5014

Amazon-Google 0.8517 0.7922

Beer 0.9130 0.8333

DBLP-ACM 0.9917 0.9903

DBLP-Scholar 0.9795 0.9671

Fodors-Zagat 0.9910 0.9955

iTunes-Amazon 0.8418 0.8383

Walmart-Amazon 0.9122 0.8819

The higher scores generally obtained for normal

pair order are expected because the pair order used at

runtime coincides with the pair order used in train-

ing. Changing the training pair order results in simi-

lar observations at runtime. The largest F

score dif-

ference, obtained on ‘Abt-Buy’, is explicable through

the larger size of the dataset and the richer textual de-

scriptions available in it. These characteristics allow

the matcher to learn more expressive representations,

making it more sensitive to input order in the absence

of symmetry enforcement. This line of thought is sup-

ported by observations on a smaller dataset with less

descriptive text (Fodors-Zagat), where a marginally

higher F

score is observed in reverse pair order.

4.5 Clustering Evaluation

Clustering performance is measured against the clus-

tered ground truth. We use CC, WCC, and PC with

default settings, and MCL with standard inﬂation and

expansion values (2.0). Figure 3 displays the results

for both normal and reversed reference graphs. Fol-

lowing prior work (Papadakis et al., 2023), CC is ap-

plied to an undirected graph derived from the nor-

mal pair order. WCC matches CC for the normal in-

put order-conﬁrming expectations-while more direc-

tionally sensitive algorithms such as PC and MCL

slightly outperform on average WCC and CC. The

outcomes are not uniform across datasets, with di-

rectionally sensitive algorithms performing better on

some datasets (‘Amazon-Google’) and worse on oth-

ers (‘DBLP-Scholar’). To enable comparison, the ref-

erence CC values from the normal graph are kept

when reversing input order. PC and MCL perform

worse than CC, even when the matcher’s performance

is similar (e.g., ‘DBLP-Scholar’). Conversely, WCC

performs comparably to CC on all but one dataset

(‘Abt-Buy’). This holds even when the matching F

score was signiﬁcantly lower than under normal pair

order (e.g., ‘Amazon-Google’, ‘Beer’). This high-

lights that the effects of matcher asymmetry on E2E

ER can be reduced by the choice of clustering al-

gorithm. Figure 4 shows average clustering perfor-

mance, revealing a slight advantage in favour of direc-

tionally sensitive algorithms (PC, MCL) under nor-

mal pair order. Under reversed pair order, PC and

MCL show a notable drop in performance relative to

WCC and CC. This suggests that matcher asymmetry,

induced by input order at runtime, has a substantial

impact on clustering quality.

We refrain from making deﬁnitive claims about

clustering algorithm performance, as PC and MCL

show inconsistent results across datasets. Neverthe-

less, input order introduces a new, previously under-

explored dimension when using the matcher architec-

ture described in this paper. Future work may explore

other forms of asymmetry or investigate how direc-

tionality can be leveraged to improve clustering (for

example, to address the bad triplet problem (Ailon

et al., 2005)).

5 CONCLUSIONS

This paper examined the implications of using trans-

former matchers in end-to-end (E2E) entity resolu-

tion (ER). Because transformers are sequence-aware,

the similarity score they output depends on the or-

der of input entity references. We visualized the

On the Asymmetrical Nature of Entity Matching Using Pre-Trained Transformers

213

Figure 3: Clustering metric scores across datasets using normal (top row) and reversed (bottom row) pair order.

asymmetry and showed that it entails represent-

ing similarity relations in directed reference graphs,

which can be integrated into existing pipelines by

using specialized clustering algorithms. We also

revealed that clustering performance varies signiﬁ-

cantly with respect to matcher asymmetry and in-

put order. While weakly connected components per-

formed comparably to undirected baselines, more di-

rectionally sensitive algorithms exposed clear differ-

ences—suggesting a trade-off between directional ﬁ-

delity and aggregate clustering quality. These ﬁnd-

ings emphasize the need to reconsider long-held as-

sumptions in ER system design. In particular, they in-

vite further exploration into matcher-clustering com-

patibility and the role of directionality as a tunable

dimension in overall system behavior.

REFERENCES

Ailon, N. et al. (2005). Aggregating inconsistent informa-

tion: ranking and clustering. In Proceedings of the

Thirty-Seventh Annual ACM Symposium on Theory of

Computing: 684-693. ACM.

Allard, G. (2025). markov clustering. GitHub repository.

Accessed: 2025-03-31.

Benjelloun, O. et al. (2009). Swoosh: a generic approach to

entity resolution. The VLDB Journal, 18(1):255–276.

Bhattacharya, I. and Getoor, L. (2004). Deduplication and

group detection using links. In KDD workshop on link

analysis and group detection.

Bhattacharya, I. and Getoor, L. (2007). Collective entity

resolution in relational data. ACM Trans. Knowl. Dis-

cov. Data, 1(1):5–es.

Binette, O. and Steorts, R. C. (2022). (almost) all of entity

resolution. Science Advances, 8(12).

Christen, P. (2012). Data matching systems. Data Match-

ing: Concepts and Techniques for Record Linkage,

Entity Resolution, and Duplicate Detection: 229–242.

Figure 4: Average clustering metric scores across datasets

for normal and reversed pair order.

Christophides, V. et al. (2020). An overview of end-to-end

entity resolution for big data. ACM Comput. Surv.,

53(6).

Devlin, J. et al. (2019). BERT: Pre-training of deep bidi-

rectional transformers for language understanding. In

Proceedings of the 2019 Conference of the North

American Chapter of the Association for Computa-

tional Linguistics: Human Language Technologies,

Volume 1 (Long and Short Papers): 4171–4186. ACL.

Draisbach, U. et al. (2019). Transforming pairwise dupli-

cates to entity clusters for high-quality duplicate de-

tection. J. Data and Information Quality, 12(1).

Ebraheem, M. et al. (2018). Distributed representations of

tuples for entity resolution. Proceedings of the VLDB

Endowment, 11(11):1454–1467.

Fellegi, I. P. and Sunter, A. B. (1969). A theory for record

KDIR 2025 - 17th International Conference on Knowledge Discovery and Information Retrieval

214

linkage. Journal of the American Statistical Associa-

tion, 64(328):1183–1210.

Graham, R. et al. (1972). Complements and transitive clo-

sures. Discrete Mathematics, 2(1):17–29.

Gruenheid, A. et al. (2014). Incremental record linkage.

Proc. VLDB Endow., 7(9):697–708.

Hagberg, A. A. et al. (2008). Exploring network structure,

dynamics, and function using networkx. In Proceed-

ings of the 7th Python in Science Conference:11–15.

Hassanzadeh, O. et al. (2009). Framework for evaluating

clustering algorithms in duplicate detection. Proc.

VLDB Endow., 2(1):1282–1293.

Haveliwala, T. et al. (2000). Scalable techniques for cluster-

ing the web (extended abstract). In Third International

Workshop on the Web and Databases (WebDB 2000).

Hochbaum, D. S. and Shmoys, D. B. (1985). A best possi-

ble heuristic for the k-center problem. Mathematics of

Operations Research, 10(2):180–184.

Huang, J. et al. (2006). Efﬁcient name disambiguation for

large-scale databases. In F

urnkranz, J., Scheffer, T.,

and Spiliopoulou, M., editors, Knowledge Discovery

in Databases: PKDD 2006:536–544.

Li, Y. et al. (2020). Deep entity matching with pre-trained

language models. Proc. VLDB Endow., 14(1):50–60.

Linacre, R. et al. (2022). Splink: Free software for proba-

bilistic record linkage at scale. International Journal

of Population Data Science, 7(3).

Liu, Y. et al. (2019). Roberta: A robustly opti-

mized bert pretraining approach. arXiv preprint

arXiv:1907.11692.

Menestrina, D. et al. (2010). Evaluating entity resolution

results. Proc. VLDB Endow., 3(1-2):208–219.

Mudgal, S. et al. (2018). Deep learning for entity match-

ing: A design space exploration. In Proceedings of

the 2018 International Conference on Management of

Data: 19–34. ACL.

Nuutila, E. (1995). Efﬁcient transitive closure computation

in large digraphs. PhD thesis, Finnish Academy of

Technology, Espoo.

Olar, A. and Dios¸an, L. (2024). Pyresolvemetrics: A

standards-compliant and efﬁcient approach to entity

resolution metrics. In CSEDU(1): 257–263.

Papadakis, G. et al. (2023). An analysis of one-to-one

matching algorithms for entity resolution. The VLDB

Journal, 32(6):1369–1400.

Papadakis, G. et al. (2020). Blocking and ﬁltering tech-

niques for entity resolution: A survey. ACM Comput.

Surv., 53(2).

Papadakis, G. et al. (2018). The return of jedai: end-to-end

entity resolution for structured and semi-structured

data. Proc. VLDB Endow., 11(12):1950–1953.

Paszke, A. et al. (2017). Automatic differentiation in py-

torch.

Saeedi, A. et al. (2017). Comparative Evaluation of Dis-

tributed Clustering Schemes for Multi-source Entity

Resolution. Advances in Databases and Information

Systems:278–293. Cham, Springer.

Saeedi, A. et al. (2018). Scalable matching and clustering

of entities with famer. Complex Systems Informatics

and Modeling Quarterly(16):61–83.

Talburt, J. et al. (2007). An algebraic approach to data qual-

ity metrics for entity resolution over large datasets. In-

formation Quality Management: Theory and Applica-

tions: 1–22. IGI Global.

Tarjan, R. (1971). Depth-ﬁrst search and linear graph algo-

rithms. In 12th Annual Symposium on Switching and

Automata Theory (swat 1971):114–121.

Tarjan, R. (1979). A class of algorithms which require non-

linear time to maintain disjoint sets. Journal of Com-

puter and System Sciences, 18(2):110–127.

Van Dongen, S. (2008). Graph clustering via a discrete un-

coupling process. SIAM Journal on Matrix Analysis

and Applications, 30(1):121–141.

Wolf, T. et al. (2020). Transformers: State-of-the-art natu-

ral language processing. In Proceedings of the 2020

Conference on Empirical Methods in Natural Lan-

guage Processing: System Demonstrations, pages 38–

45, Online. ACL.

Yeung, K. Y. and Ruzzo, W. L. (2001). Details of the

adjusted rand index and clustering algorithms sup-

plement to the paper “an empirical study on princi-

pal component analysis for clustering gene expression

data” ( to appear in bioinformatics ). volume 17:763–

774. Citeseer.

Zeakis A. et al. (2023). Pre-trained embeddings for entity

resolution: An experimental analysis. Proc. VLDB

Endow., 16(9):2225–2238.

On the Asymmetrical Nature of Entity Matching Using Pre-Trained Transformers

215