An Efﬁcient and Scalable Hyperdimensional Computing Framework for

Anomaly Classiﬁcation in Industrial Systems

ıctor Ortega

, Soledad Escolar

, Fernando Rinc

, Jes

us Barba

, Juli

an Caba

and Juan Carlos L

opez

School of Computer Science, University of Castilla-La Mancha, Ciudad Real, Spain

Keywords:

Hyperdimensional Computing, Industrial Systems, Anomaly Detection, Predictive Maintenance, Machine

Learning.

Abstract:

This paper presents a hyperdimensional computing (HDC)-based framework for anomaly classiﬁcation, de-

signed to meet the speciﬁc demands of industrial systems. Inspired by cognitive processes, HDC employs

high-dimensional representations to enable robust, low-complexity, and hardware-efﬁcient computation. The

proposed framework encompasses the entire processing pipeline, from data encoding to anomaly classiﬁcation,

and is optimized for efﬁcient execution on both conventional computing platforms and resource-constrained

devices. To assess its effectiveness, we conduct a case study based on a real-world scenario involving 118

emergency lighting devices that collect and transmit operational data to a central sink capable of detecting

anomalous behavior. Experimental results demonstrate that the proposed approach achieves high classiﬁcation

accuracy and conﬁrm its suitability for deployment in integrated industrial systems with limited computational

resources.

1 INTRODUCTION

Fault detection and mitigation is an ongoing challenge

that has become critically important in modern indus-

trial environments, where intelligent systems and in-

terconnected devices are increasingly integrated into

complex production and monitoring infrastructures

across a wide range of applications. A random, non-

compliant, unexpected behavior in a system, which

may even be malicious is called an anomaly (Bad-

dar et al., 2014). The root cause of such deviating

behavior can vary widely, e.g. component failures,

software errors and environmental factors. Regard-

less the root cause, the consequences of not having

a proper anomaly detection strategy can be serious,

making timely and effective mitigation essential.

Anomaly detection aims to identify patterns in

events that deviate signiﬁcantly from expected or nor-

mal behavior. Typically, each event is represented by

https://orcid.org/0009-0003-1548-3260

https://orcid.org/0000-0002-8019-9640

https://orcid.org/0000-0003-4688-8650

https://orcid.org/0000-0003-1931-3245

https://orcid.org/0000-0002-7641-4643

https://orcid.org/0000-0002-7372-1568

a data instance composed of a set of descriptive fea-

tures, which are not necessarily all equally informa-

tive (Bhuyan et al., 2014). The problem may be for-

mulated as a classiﬁcation problem in which anoma-

lous behaviors need to be distinguished from nor-

mal behaviors (Baddar et al., 2014). The literature

on anomaly detection in industrial systems encom-

passes a broad spectrum of approaches across var-

ious research areas (Chandola et al., 2009; Baddar

et al., 2014), such as: statistics, Machine Learning

(ML), data mining, information theory, and spectral

theory. Among these approaches, those based on ML

have received increased attention for their ability to

learn from data and effectively classify or group ab-

normal and previously unseen behaviors (Nassif et al.,

2021). However, as noted in (Hern

andez-Cano et al.,

2021), several limitations remain, primarily concern-

ing the efﬁciency, power consumption, and robust-

ness of the algorithms. Speciﬁcally, ML-based so-

lutions are highly computationally intensive, making

them impractical for edge devices, which often op-

erate online and under strict constraints in memory,

processing power, and energy consumption. Further-

more, ML algorithms often exhibit high sensitivity

to noise and hardware failures and struggle to es-

tablish causality, meaning that they cannot directly

Ortega, V., Escolar, S., Rincón, F., Barba, J. and Caba, J.

An Efﬁcient and Scalable Hyperdimensional Computing Framework for Anomaly Classiﬁcation in Industrial Systems.

DOI: 10.5220/0013669700003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 429-436

ISBN: 978-989-758-770-2; ISSN: 2184-2809

429

determine whether one variable inﬂuences changes

in another. This limitation is particularly critical in

anomaly detection, where the goal is not only to iden-

tify anomalous behaviors but also to understand their

root causes and provide meaningful justiﬁcations for

effective remediation. The work presented in (Nassif

et al., 2021) offers a systematic literature review of

ML-based techniques to anomaly detection in Internet

of Things (IoT) environments, categorizing them into

supervised, semi-supervised, and unsupervised meth-

ods.

Hyperdimensional Computing (HDC) is a brain-

inspired computational paradigm designed to address

classiﬁcation problems by mimicking aspects of cog-

nitive processing. HDC operates on high-dimensional

vectors, also known as hypervectors, which are capa-

ble of encoding, storing, and manipulating informa-

tion in a manner analogous to distributed representa-

tions in the human brain. The efﬁciency of the tech-

nique lies in the fact that vector operations are highly

parallelizable using, for example, GPUs (Grid Pro-

cessing Units) or accelerators, and can be executed

in real time on a very large data set. These charac-

teristics make it particularly attractive for resource-

constrained environments such as edge devices in IoT

applications.

The main contribution of this work is twofold: 1)

the theoretical foundation of an HDC system imple-

menting a complete processing pipeline for anomaly

classiﬁcation, speciﬁcally adapted to the diverse op-

erational scenarios encountered in industrial comput-

ing; and 2) the validation of a case study focused on

anomaly detection in the behavior of emergency light-

ing devices. The paper is organized as follows: in the

next Section we review the related works, then in Sec-

tion 3 we present the system model for anomaly de-

tection based on HDC. Section 4 describes the real-

world dataset used in our experiments and in Sec-

tion 5 we present the results of the evaluation per-

formed of the proposed HDC system. Finally, in Sec-

tion 6 we draw the main conclusions and suggestions

for future research.

2 RELATED WORKS

Hyperdimensional Computing (HDC) (Kanerva,

2009) is a computational paradigm inspired by

the way the human brain represents and processes

information. It relies on high-dimensional math-

ematical structures known as hypervectors, which

typically consist of thousands of components. These

hypervectors act as the core units for encoding

knowledge and relationships between concepts. By

means of vectorial operations, such as binding (⊗),

bundling (⊕), and permutation (

∏

) (Yu et al., 2022)

(also referred as MAP, multiplication, adding, and

permutation), hypervectors can be combined and

transformed to represent complex data structures and

abstractions.

The processing pipeline of an HDC-based classi-

ﬁcation system usually consists of three main stages:

encoding, training, and classiﬁcation (Chang et al.,

2023; Morris et al., 2019). In the ﬁrst stage, the input

data space is projected into a high-dimensional space

using a suitable encoding method. This encoding pro-

cess is highly dependent on the nature of the input

data and plays a critical role in determining the over-

all classiﬁcation accuracy (Aygun et al., 2023). The

training step aggregates all hypervectors associated to

the samples in some category into a single represen-

tative hypervector, known as the class or prototypical

hypervector, which will be further used in the clas-

siﬁcation process. Training may be done in a single-

step, which means that each hypervector is learnt only

one time or using iterative training, also called retrain-

ing (Shahhosseini et al., 2022). In the ﬁnal step, clas-

siﬁcation (or inference), a test sample is encoded into

a hypervector using the same encoding function and

then compared against all class hypervectors to iden-

tify the class with the highest similarity.

HDC has already demonstrated its potential for

anomaly detection. For instance, the work pre-

sented in (Wang et al., 2022) introduces the ODHD

framework, which adopts a Positive-Unlabeled (P-

U) learning strategy. In this approach, the model is

trained exclusively on inlier samples, while the test-

ing phase involves a dataset that may contain both

inliers and outliers, with no label information pro-

vided. The methodology closely aligns with the

approach followed in this paper. Experimental re-

sults indicate that ODHD outperforms three base-

line methods (OCSVM, Isolation Forest, and Autoen-

coder) across six datasets and three performance met-

rics: accuracy, F1-score, and ROC-AUC. HDC is em-

ployed in (Arliss et al., 2024) for anomaly detec-

tion based on variations in network topology. The

topology is initially represented as a time-ordered se-

quence of graphs, where each graph is directed and

count-weighted. Subsequently, both nodes and edges

are encoded as hypervectors. To identify anoma-

lies, the method ﬁrst calculates a primitive anomaly

score, followed by an anomaly conﬁdence measure

obtained by referencing the score against a histor-

ical distribution of past scores. Experimental re-

sults demonstrate that this approach achieves high

accuracy and efﬁciency on both synthetic and real-

world datasets. The work presented in (Wang et al.,

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

430

2021) proposes HDAD, which leverages HDC to val-

idate sensor readings collected by autonomous vehi-

cles prior to their use in downstream decision-making.

In this approach, sensor data is ﬁrst encoded into an

intermediate hypervector, which is then decoded into

a reconstructed feature vector. The system compares

the reconstructed vector with the original test sam-

ple to assess its validity. The authors report achiev-

ing 100% detection accuracy on a real-world dataset

of vehicle sensor readings. In the IoT scope, HDC

has been used for the detection of network attacks

and evaluated on the NSL-KDD dataset in (Ghajari

et al., 2025). The model achieved an accuracy of

91.55% on the KDDTrain+ subset, outperforming tra-

ditional approaches. The work presented in (Shahhos-

seini et al., 2022) introduces a method based on Hy-

perdimensional Computing (HDC) for learning end-

user physiological and behavioral patterns, speciﬁ-

cally targeting health-related applications on wear-

able devices. The proposed approach employs iter-

ative learning to reﬁne the model over time, achiev-

ing up to 35.8× faster training performance compared

to state-of-the-art deep neural network (DNN) algo-

rithms, while maintaining comparable accuracy.

3 SYSTEM MODEL

We consider a set of n devices d

,... ,d

tailored

to monitor a wide variety of physical and environ-

mental phenomena of interest, including, for instance,

motion, vibration, or gas concentration. In order to

perform this task, such devices are carefully designed

and equipped with custom hardware (e.g. MCU, ad-

vanced sensors, battery) and are provided with com-

munication capabilities to transmit periodically data

of interest, as well as their status and self-diagnostic

information, towards a concentrator node d

, also

known as the sink, which stores the data and subse-

quently forwards it to an external network. Along the

path from the transmitting device towards the sink,

each device selects the next neighbor for data com-

munication by considering several criteria, e.g. the

quality of the link, thus creating a dynamic multi-hop

mesh network with the sink as the ﬁnal destination

within the local network.

During each transmission period, every device

,1 ≤ i ≤ n generates a text message by aggregat-

ing the values of a set of k characteristics, that is,

the variables of interest. These features provide in-

formation about the device’s identity, status (e.g., bat-

tery level), or network diagnostics (e.g., next hop, trip

time, link quality), among others. Most of the fea-

tures collected by the devices are non-deterministic,

which means that their values can ﬂuctuate within a

broad range that may still be considered normal for a

given device. However, device failures can still occur,

which may result in the transmission of outliers that

may take one or more features and that signiﬁcantly

differ from the values that are considered normal.

In practice, data transmitted over time by devices

are aggregated into a ﬁle of features or dataset. Let R

be the data space composed of all data transmitted by

the n devices during a period of time and let R

and

i, j

be the subsets of R that contain all values for de-

vice d

and all values that take the feature j of device

, respectively, with 1 ≤ j ≤ k and 1 ≤ i ≤ n. Given a

set of samples R

i, j

corresponding to device d

and fea-

ture j, we deﬁne its training set R

↑

i, j

as the ascendingly

sorted set of samples, i.e. R

↑

i, j

= {r

min

i, j

,. .. ,r

max

i, j

}. A

single data point r

i, j

∈ R

↑

i, j

represents the x

sam-

ple taken by feature j of device d

. The sequence

of the x

data points of all features j is denoted as

= {r

i,0

i,1

,. .. ,r

i,k−1

}. We denote as r

min

i, j

and r

max

i, j

to the minimum and maximum value, respectively, in

the subset R

↑

i, j

, with r

max

i, j

− r

min

i, j

> 0.

3.1 Encoding

We deﬁne an encoding function ϕ : R → H that maps

each data point r

i, j

in R into a hypervector h ∈ H ,

with h = {−1, 1}

and D is the dimension of the hy-

pervectors (generally, greather or equal than 10,000).

The encoding function ϕ must be carefully designed

to generate hypervectors that preserve the correla-

tion structure of the input data. In this work, ϕ is

based on a quantization-based approach as described

in (Basaklar et al., 2021), that discretizes the input

space to enable consistent and meaningful hypervec-

tor representations.

Let M be the number of quantization levels and

let Q be the set of level hypervectors, i.e. Q =

,. .. ,q

M−1

}, where q

is the m

level hy-

pervector. The ﬁrst level hypervector q

is initial-

ized randomly; the rest of level hypervectors, i.e.,

,. .. ,q

M−1

}, are generated incrementally from the

previous one, speciﬁcally, q

i+1

differs from its prede-

cessor q

by ﬂipping exactly b =

2(M−1)

components,

which ensures a uniform and gradual increase in dis-

similarity across levels. Note that, in doing so, we

produce a matrix of M × D and a three-dimensional

tensor of k × M level hypervectors to represent the

level hypervectors of each d

Let us deﬁne the function L : R → Q that returns

the level hypervector corresponding to a single data

point, that is deﬁned as follows:

An Efﬁcient and Scalable Hyperdimensional Computing Framework for Anomaly Classiﬁcation in Industrial Systems

431

L(r

i, j

) =











x = min

min+σm ≤ x ≤ min +σ(m + 1),

∀x ∈ (min, max),m ∈ [0,M − 1)

M−1

x = max

where σ is deﬁned as the number of items per level,

i.e., σ = r

max

i, j

− r

min

i, j

/M. For each sequence of

samples r

in the data set, the encoding function ϕ

produces its corresponding hypervector, denoted as

, by adding up their level hypervectors:

= L(r

i,0

) ⊕ L(r

i,1

) ⊕ . .. ⊕L(r

i,(k−1)

) (1)

The sum operation corresponds to the bundling func-

tion ⊕, which ensures that the resulting hypervector

is maximally similar to their operands, i.e. it acts by

aggregating the hypervectors taken as input.

3.2 Training

During the training phase, the input data space is used

to generate a class hypervector, also known as the pro-

totypical hypervector, for each device d

, denoted as

H V

, which is computed as:

H V

∀x ∈ R

(2)

H V

is constructed by applying the bundling oper-

ation to the hypervectors of all samples in the data

space associated with device d

. This process encodes

the device’s normal operating behavior into a refer-

ence hypervector, which is later used in the classiﬁca-

tion stage to detect deviations indicative of anomalies.

3.3 Classiﬁcation

Let {H V

,H V

,. .. ,H V

} be the set of class hy-

pervectors for n devices. Let t

be a sequence of sam-

ples t

= {t

i,0

i,1

,. .. ,t

i,(k−1)

} to be tested. We classify

the sequence t

as an outlier of d

iff the cosine similar-

ity function between its hypervector h

and the class

hypervector H V

, computed as:

cos(h

,H V

) =

× H V

||h

|| × ||H V

(3)

is below a certain threshold S

. It is worth noting

that the smaller the difference between h

and H V

the higher the resulting cosine similarity. Addition-

ally, the choice of the threshold value S

is critical to

system performance, as it directly inﬂuences classiﬁ-

cation precision.

4 REAL-WORLD DATASET

DESCRIPTION

The HDC system proposed has been evaluated using

a case study focused on anomaly detection in emer-

gency lighting devices. To this purpose, we consider a

system of n emergency lighting devices distributed in

one or several nearby buildings. These devices are in-

tended to activate automatically when the main power

supply fails (e.g. during outages or blackouts), ensure

visibility and safety in enclosed spaces by provid-

ing essential lighting, evacuation routes, and access

to emergency exits. To ensure that devices function

properly, hyperdimensional computation was used to

learn from the behavior that these devices have and,

with this information, to detect anomalies that may

occur, thus indicating the malfunction of one or sev-

eral emergency lighting devices.

The emergency lighting devices send two types of

messages at different frequencies: 1) status, which

contains the data related to the device state and 2) di-

agnosis, which contains the device diagnostic data.

During two periods of 6 and 24 days respectively,

from December 7th to December 12th and from De-

cember 24th to January 16th, we collect both types of

data (status and diagnosis) from the n devices, which

were merged into one single dataset, where a sample

is formed by the combination of one sample from the

status data and one other sample from the diagnostic

data for a single device. The total number of samples

collected thus is 1820172, each with 117 variables,

resulting in a dataset of size 4.7GB. Since the num-

ber of total variables in each sample was very high,

we implemented an algorithm to discard those vari-

ables whose values were poorly correlated with other

variables and variables providing a low value. After

applying this ﬁltering, we obtained a ﬁnal real-world

dataset with the characteristics described in Table 1.

Figure 1 shows the correlation matrix of k × k vari-

ables and for an emergency lighting device, where red

and blue indicate proportional and inversely propor-

tional correlation, respectively, while gray indicates

that the variables are not related.

Table 1: Real-world dataset parameters.

Param. Description Value

S Number of samples in the dataset 1820172

V Number of variables discarded 81

W Size of the real-world dataset 257 MB

p % of samples used for training 80

1 − p % of samples used for testing 20

4.1 Threshold Selection

The resulting dataset was subsequently divided into

two different subsets. The ﬁrst subset, comprising

p=80% of the total samples, was used to train and

encode the prototypical hypervectors that character-

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

432

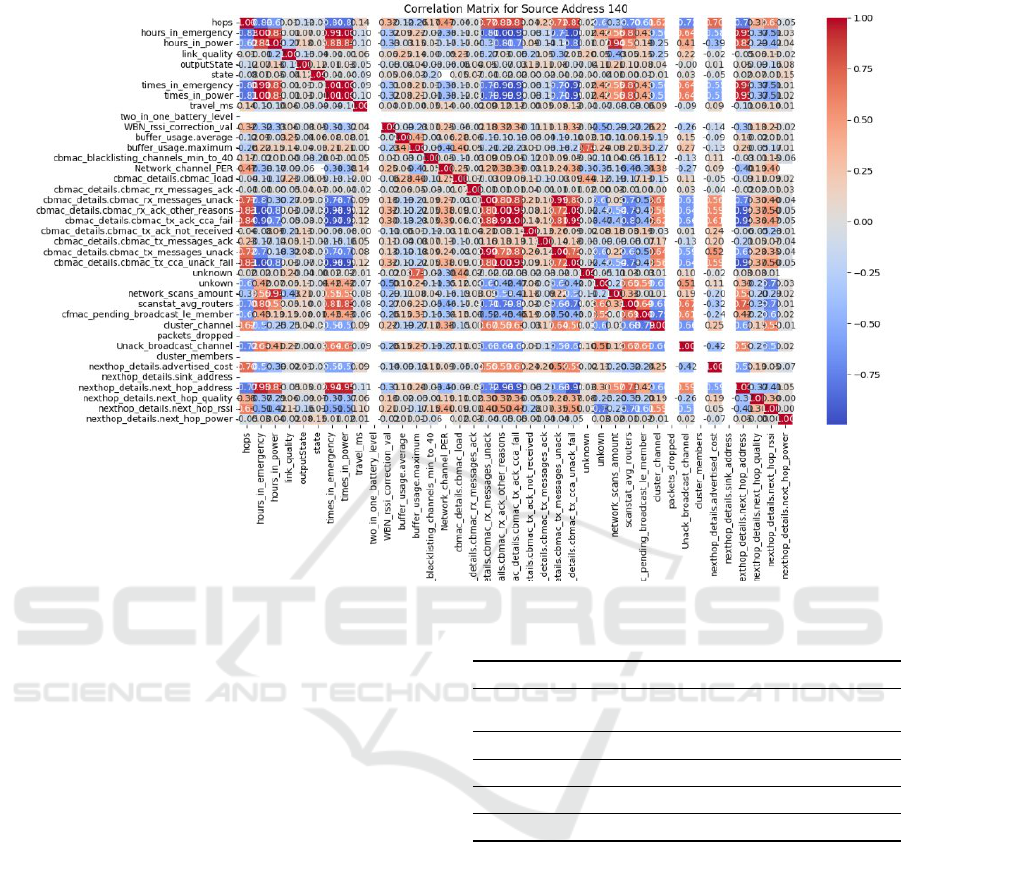
Figure 1: Correlation matrix obtained for an emergency lighting device.

ize the normal behavior of the devices, as described

in Section 3. The second subset, comprising 1 − p of

the total samples, was used to test the HDC model.

We assume that each sample in the training dataset is

considered a normal behavior of an emergency light-

ing device so, consequently, the deﬁnition of anomaly

is based on the similarity between the hipervector of

the test sample and the prototypical hypervector by

using the similarity cosine function, as formulated in

Eq 3. For the sake of simplicity we have deﬁned the

same thresholds for all emergency devices with the

next values: S

= {0.8,0.85,0.9,0.95}.

5 EXPERIMENTATION

We have fully implemented the HDC model explained

in Section 3 using the TorchHD Python library (Hed-

des et al., 2023), and we have executed it on a laptop

with an 11th Gen Intel(R) Core(TM) i5-11400H @

2.70GHz CPU and 16 GB RAM, and a NVIDIA RTX

3050 4GB GDDR6.

Table 2 summarizes the parameters used in the im-

plementation. In Listing 1 we show the Python code

to generate M level hypervectors for a single feature,

based on the quantization-based approach, as detailed

Table 2: Summary of parameters used in the experiments.

Param. Description Value

n Number of devices 118

Number of hypervector classes

k Number of variables 36

D Dimension of the hypervectors 10000

M Number of level hypervectors (LH) [1,3336]

b Changes between consecutive LH [1,2500]

in Section 3.1. This code was parallelized on a GPU

to optimize its performance.

In line 3, the ﬁrst level hypervector is randomly

generated. Line 6 computes the number of changes b

between consecutive level hypervectors as a function

of D and M. In lines from 14 to 20 a set of indices

is created in order to avoid repetitions of components

ﬂipped from one hypervector to another. In line 21 we

ﬂip the selected components from the previous level

hypervector. In line 22 the new hypervector is saved

so it can be used in the following iteration. This pro-

cedure will be performed M times resulting in a ma-

trix of M × D.

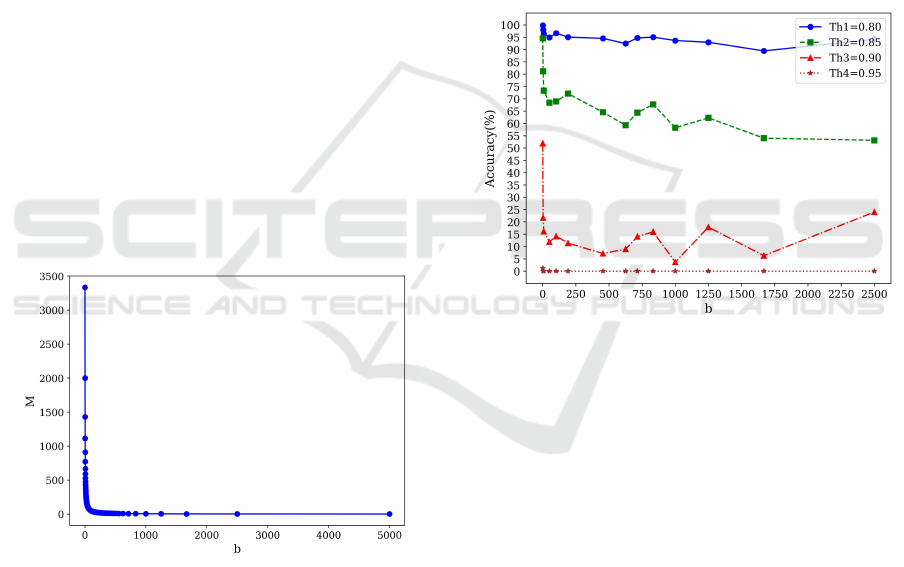
We have evaluated the model using different M

numbers of level hypervectors, which are calculated

by varying the range of items that ﬂip between two

consecutive hypervectors b from 1 to 2500. Note that

An Efﬁcient and Scalable Hyperdimensional Computing Framework for Anomaly Classiﬁcation in Industrial Systems

433

1 def range_hdv_levels(D, M):

2 matrix = []

3 fst_hdv = torchhd.random(1, D,

4 "MAP", dtype=torch.int8)

5 matrix.append(fst_hdv[0])

6 b = round(D / (2 * (M - 1)))

7 if b == 0: b = 1

8 idx = set()

9 for i in range(M):

10 if i == 0:

11 prev_tsr = matrix[0].clone()

12 else:

13 prev_tsr = matrix[i-1].clone()

14 idx_av = list(set(range(D)) - idx)

15 if len(idx_av) < b:

16 idx = set()

17 idx_av = list(range(D))

18 selected = random.sample(idx_av, b)

19 idx.update(selected)

20 indices = torch.tensor(selected)

21 prev_tsr[indices] *= -1

22 matrix[i] = prev_tsr

23 return matrix

Listing 1: Generation of a matrix of correlated hypervec-

tors.

the number of level hypervectors is an important met-

ric to consider, as it poses an interesting tradeoff be-

tween model accuracy and resources employed. We

have computed M as as function of b, and the results

can be seen in Figure 2.

Figure 2: Number of M for each b.

5.1 Accuracy

The objective of the system is to determine whether

the similarity between two hypervectors, one repre-

senting the x

sample and other a hypervector of ref-

erence of the device that represents its normality, is

lower than a certain threshold such that x

is clas-

siﬁed as an anomaly. Speciﬁcally, we are interested

in evaluating the accuracy of our HDC model, by ac-

counting the number of samples correctly classiﬁed

with respect to the total number of samples.

The ﬁrst test was conducted using the testing

dataset, where each sample is assumed to represent

normal behavior. Figure 3 illustrates the accuracy of

the HDC model across different threshold values for

and for different values of b. As expected, increas-

ing the threshold results in decreased accuracy. This

behavior arises because achieving a high cosine sim-

ilarity value requires the test sample to closely match

the reference. Consequently, the best results were ob-

tained with a threshold of 0.8. In contrast, when the

threshold was increased to 0.95, the model’s accuracy

dropped to nearly zero, which means that the majority

of test samples fail to meet the stricter threshold. On

the other hand, the highest accuracy is obtained with

b = 1; note that, however, for small values of b, the

accuracy of the system remains similar to the results

obtained with b = 1.

Figure 3: Accuracy of the model for different values of b.

In order to evaluate how the HDC model behaves

with samples whose values differ signiﬁcantly from

the values in the dataset that, as explained, represent

the normal behavior of the device, we had to gener-

ate synthetic data. The synthetic data was generated

by repeatedly selecting the ﬁrst 100 samples from the

dataset and applying two different deviation values:

0.5 and 0.9. For each case, the same set of 100 en-

tries was used: ﬁrst, the deviation was applied to a

single characteristic; then, to two characteristics; and

progressively to more, until all characteristics were

included. This procedure resulted in the generation

of two more datasets that were used to test the per-

formance of the system anomaly detection. Both

datasets have a total of 3400 samples each and a total

size of 3.9MB. The results of testing the HDC system

with the synthetic data may be observed in Figure 4.

The left side of the ﬁgure shows the accuracy for a

deviation of 0.5, while the right side corresponds to a

deviation of 0.9. As observed, when the threshold is

set to 0.95 or 0.9, the accuracy remains close to 100%

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

434

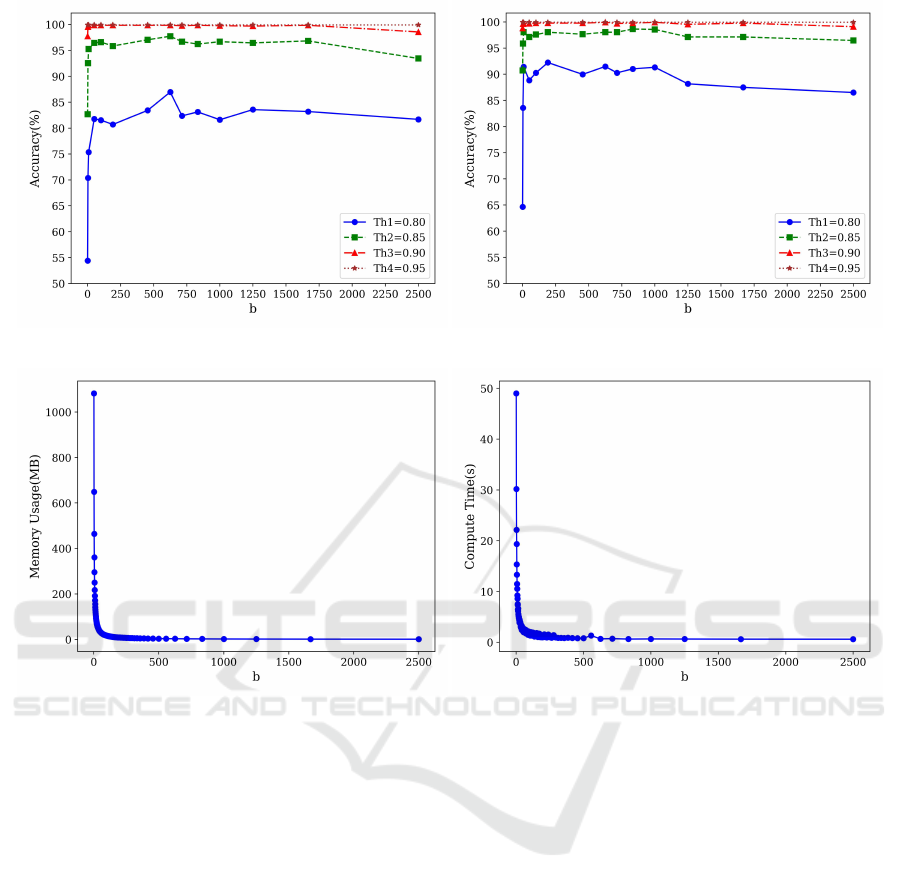
Figure 4: Accuracy of the model with deviations on the synthetic data of 0.5 (left) and 0.9 (right) for different thresholds.

Figure 5: Memory RAM consumption (left) and execution time (right) for different values of b.

across all values of b. In contrast, lower threshold val-

ues result in a noticeable decrease in model accuracy.

These results are due to the fact that these synthetic

data samples are expected to be classiﬁed as anoma-

lies. Therefore, with a higher threshold, it is more

likely that the cosine similarity of a given sample does

not reach the threshold, resulting in its classiﬁcation

as an anomaly and, consequently, in high accuracy. In

contrast, with a lower threshold, it is more likely that

samples reach the threshold, leading to misclassiﬁca-

tions and, therefore, lower accuracy.

5.2 Memory Usage and Execution

Times

HDC systems are inﬂuenced by several key param-

eters that critically affect the resource-performance

tradeoff, as outlined in Table 2. Speciﬁcally, the hy-

pervector dimensionality (D), the number of input

features (k), and the total number of level hypervec-

tors (M) have a substantial impact on RAM consump-

tion, with the storage cost scaling as O(k ×M ×D). In

addition, the size of the dataset used for training and

testing plays a critical role in system design and eval-

uation. Although larger datasets can improve model

accuracy, they also impose greater demands on mem-

ory, computational power, and processing time, which

could limit the feasibility of implementing the HDC

system in an embedded system.

To illustrate this, we have computed the require-

ments of RAM for different values of b of our HDC

system, which will store a different number of level

hypervectors M for different values of b, thus affect-

ing the RAM consumption. In Figure 5 on the left side

is shown how RAM decreases when b increases, since

the HDC system will require less number of level hy-

pervectors. Figure 5 on the right side shows the im-

pact of varying b on the time invested in computing

the level hypervectors. Recall that the procedure of

computing the level hypervectors was parallelized on

a GPU. As observed, in the worst-case scenario with

the lowest value of b, computing the corresponding

M = 3336 level hypervectors takes approximately 50

seconds. However, as illustrated in Figure 3, reducing

An Efﬁcient and Scalable Hyperdimensional Computing Framework for Anomaly Classiﬁcation in Industrial Systems

435

the number of level hypervectors (M) still yields ac-

curacy results comparable to those obtained with the

maximum M. This reduction signiﬁcantly enhances

the feasibility of implementing the HDC system on

embedded platforms.

6 CONCLUSIONS

We have proposed an efﬁcient and scalable HDC sys-

tem for anomaly classiﬁcation in industrial environ-

ments. The system was evaluated in a real-world

scenario involving 118 devices periodically transmit-

ting status information. Our HDC system operates

autonomously, without requiring prior knowledge of

what constitutes an anomaly or labeled training data.

As a result, the system behaves in an unsupervised

manner, continuously learning normal patterns of be-

havior and identifying deviations that may indicate

faults or abnormal conditions, making it particularly

suitable for dynamic and data-scarce industrial set-

tings. As future work, we propose the implementa-

tion of our HDC system on customized accelerators

for the optimization of vector instructions.

ACKNOWLEDGEMENTS

This paper is partially supported by the

Spanish Ministry of Science and Innovation

MCIN/AEI/10.13039/501100011033 under Grant

TALENT-BELIEF (PID2020-116417RB-C44), the

project OASIS (PID2023-148285OB-C41) and the

Project MIRATAR TED2021-132149B-C41 funded

by MCIN/AEI/10.13039/501100011033 and by

European Union NextGenerationEU/PRTR.

REFERENCES

Arliss, W., Godbehere, A. B., and Mueller, G. (2024). Using

hypervectors for efﬁcient anomaly detection in graph

streams. In 2024 IEEE 11th International Conference

on Data Science and Advanced Analytics (DSAA),

pages 1–10.

Aygun, S., Shoushtari Moghadam, M., Najaﬁ, M. H., and

Imani, M. (2023). Learning from hypervectors: A sur-

vey on hypervector encoding.

Baddar, S. W. A.-H., Merlo, A., and Migliardi, M. (2014).

Anomaly detection in computer networks: A state-of-

the-art review. J. Wirel. Mob. Networks Ubiquitous

Comput. Dependable Appl., 5:29–64.

Basaklar, T., Tuncel, Y., Narayana, S. Y., Gumussoy, S., and

Ogras, U. Y. (2021). Hypervector design for efﬁcient

hyperdimensional computing on edge devices.

Bhuyan, M. H., Bhattacharyya, D. K., and Kalita, J. K.

(2014). Network anomaly detection: Methods, sys-

tems and tools. IEEE Communications Surveys & Tu-

torials, 16(1):303–336.

Chandola, V., Banerjee, A., and Kumar, V. (2009).

Anomaly detection: A survey. ACM Comput. Surv.,

41(3).

Chang, C.-Y., Chuang, Y.-C., Huang, C.-T., and Wu, A.-

Y. (2023). Recent progress and development of hy-

perdimensional computing (hdc) for edge intelligence.

IEEE Journal on Emerging and Selected Topics in

Circuits and Systems, 13(1):119–136.

Ghajari, G., Ghimire, A., Ghajari, E., and Amsaad, F.

(2025). Network anomaly detection for iot using hy-

perdimensional computing on nsl-kdd.

Heddes, M., Nunes, I., Verg

es, P., Kleyko, D., Abraham, D.,

Givargis, T., Nicolau, A., and Veidenbaum, A. (2023).

Torchhd: an open source python library to support

research on hyperdimensional computing and vector

symbolic architectures. J. Mach. Learn. Res., 24(1).

Hern

andez-Cano, A., Matsumoto, N., Ping, E., and Imani,

M. (2021). Onlinehd: Robust, efﬁcient, and single-

pass online learning using hyperdimensional system.

In 2021 Design, Automation & Test in Europe Confer-

ence & Exhibition (DATE), pages 56–61.

Kanerva, P. (2009). Hyperdimensional computing: An

introduction to computing in distributed representa-

tion with high-dimensional random vectors. Cognitive

Computation, 1:139–159.

Morris, J., Imani, M., Bosch, S., Thomas, A., Shu, H., and

Rosing, T. (2019). Comphd: Efﬁcient hyperdimen-

sional computing using model compression. In 2019

IEEE/ACM International Symposium on Low Power

Electronics and Design (ISLPED), pages 1–6.

Nassif, A. B., Talib, M. A., Nasir, Q., and Dakalbab, F. M.

(2021). Machine learning for anomaly detection: A

systematic review. IEEE Access, 9:78658–78700.

Shahhosseini, S., Ni, Y., Kasaeyan Naeini, E., Imani, M.,

Rahmani, A. M., and Dutt, N. (2022). Flexible and

personalized learning for wearable health applications

using hyperdimensional computing. In Proceedings of

the Great Lakes Symposium on VLSI 2022, GLSVLSI

’22, page 357–360, New York, NY, USA. Association

for Computing Machinery.

Wang, R., Jiao, X., and Hu, X. S. (2022). Odhd:

one-class brain-inspired hyperdimensional computing

for outlier detection. In Proceedings of the 59th

ACM/IEEE Design Automation Conference, DAC ’22,

page 43–48, New York, NY, USA. Association for

Computing Machinery.

Wang, R., Kong, F., Sudler, H., and Jiao, X. (2021). Brief

industry paper: Hdad: Hyperdimensional computing-

based anomaly detection for automotive sensor at-

tacks. In 2021 IEEE 27th Real-Time and Embed-

ded Technology and Applications Symposium (RTAS),

pages 461–464.

Yu, T., Zhang, Y., Zhang, Z., and Sa, C. D. (2022). Un-

derstanding hyperdimensional computing for parallel

single-pass learning. In Oh, A. H., Agarwal, A., Bel-

grave, D., and Cho, K., editors, Advances in Neural

Information Processing Systems.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

436