Sensorless Admittance Control of a Manipulator Arm Using a Nonlinear

Observer for Force and Velocity Estimation

Brahim Brahmi

1,2 a

Department of Electrical Engineering, King Fahd University of Petroleum & Minerals, Dhahran, Saudi Arabia

Center for of nterdisciplinary Research Center on Intelligent Manufacturing and Robotics, King Fahd University of

Petroleum & Minerals, Dhahran, Saudi Arabia

Keywords:

Nonlinear Observer, Admittance Control, Human-Robot Interaction, Force Estimation, Rehabilitation

Robotics.

Abstract:

This paper presents a nonlinear observer-based approach for estimating force and velocity in a joint-space

admittance-controlled exoskeleton, designed to support safe and compliant physical human–robot interaction.

The observer estimates external interaction forces and joint velocities using only joint position measurements,

eliminating the need for external force or velocity sensors. Integrated into the ETS-MARSE upper-limb reha-

bilitation exoskeleton, the system generates compliant motion trajectories in response to user-applied forces.

An experiment involving a human subject was conducted to validate the observer’s accuracy. The estimated

forces and velocities were compared with reference sensor measurements. Results demonstrate that the ob-

server provides reliable state estimates, enabling accurate tracking of motion and interaction forces with low

error and high responsiveness. The system maintains compliant behavior, supporting natural, user-driven

movement without compromising stability. This work highlights the potential of sensorless estimation in

robotic rehabilitation and interaction-intensive control applications.

1 INTRODUCTION

The emergence of advanced technologies—including

collaborative robotic arms, versatile robotic hands,

and wearable rehabilitation robots—has led to their

growing application in physically interactive tasks

across various settings (Ibarguren et al., 2020; Qin

et al., 2021; Li et al., 2022b). Performing complex

tasks such as rehabilitation, adaptive object handling,

and human engagement often requires precise control

and stabilization of contact forces (Chen et al., 2020).

Unlike soft robots, which rely on material ﬂexibility

to absorb impacts, robotic manipulators depend on

rigid structures to achieve operational precision (Si-

ciliano and Villani, 2000). However, this reliance on

rigidity can pose challenges in sensitive operations

such as grinding or machining, where maintaining

a speciﬁc trajectory while applying precise forces is

critical (Jaroonsorn et al., 2020).

In human–robot collaboration, a central challenge

lies in enabling the robot to interpret the human

partner’s movement intentions, allowing it to engage

in proactive cooperation. Simply programming the

https://orcid.org/0000-0002-4486-0710

robot to follow predeﬁned trajectories is ineffective

in such dynamic interactions. While force control

can regulate interaction forces, its effectiveness is

often limited by poor robustness (Newman, 1992).

Impedance control—originally introduced in (Hogan,

1985) and later reﬁned in numerous studies (Jung and

Hsia, 2000; Lynch et al., 2002)—has emerged as a

widely accepted method for managing interaction dy-

namics. This approach allows the robot to exhibit

compliant behavior in response to external forces ap-

plied by the human partner, enabling smooth collab-

oration by adapting to human-driven motions. How-

ever, since impedance control adjusts the robot’s re-

sponse based on external forces, it inherently resists

sudden motion changes initiated by the user, effec-

tively behaving as an additional inertial load (Iqbal

and Zheng, 1999). Moreover, in human–robot contact

scenarios where physical properties such as stiffness

or position are not precisely known, unpredictable in-

teractions can lead to excessive stress on joint actua-

tors or even cause damage to contact interfaces (Xue

et al., 2020). To mitigate such risks, it is essential

for the system to maintain compliance or dynamically

adapt its impedance characteristics throughout the in-

Brahmi, B.

Sensorless Admittance Control of a Manipulator Arm Using a Nonlinear Observer for Force and Velocity Estimation.

DOI: 10.5220/0013669200003982

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 22nd International Conference on Informatics in Control, Automation and Robotics (ICINCO 2025) - Volume 2, pages 15-23

ISBN: 978-989-758-770-2; ISSN: 2184-2809

teraction. This adaptability enables better regulation

of contact forces, preventing the aforementioned me-

chanical issues (Hongli, 2022). Additionally, estimat-

ing the human partner’s movement intention and inte-

grating this estimation into the robot’s control strategy

is critical to overcoming such limitations.

Admittance control has become a key strategy in

rehabilitation robotics, enabling active user partic-

ipation, task repeatability, and outcome quantiﬁca-

tion (e.g., improvement, effort) (Ozkul and Barkana,

2013). Despite its advantages, certain limitations per-

sist—such as restricted degrees of freedom or ex-

clusive implementation in end-effector-based systems

(Culmer et al., 2010). Various human–robot inter-

action modalities have evolved over time, ranging

from joysticks to advanced biosignals such as EMG

(Karimi and Ahmadi, 2025) and EEG (Hsu et al.,

2025). Among them, force sensors remain widely

used (Zarrin et al., 2024), particularly in support-

ing compliant control through impedance or admit-

tance schemes (Otten et al., 2015). Numerous reha-

bilitation and robotic systems incorporate force sen-

sors to enable compliant interaction. For example,

the iPAM system integrates dual 6-DOF force sen-

sors for bilateral control (Zarrin et al., 2024); Re-

habRoby uses one-axis sensors at the elbow and

shoulder joints (Ozkul and Barkana, 2013); and the

EXO-UL7 includes four 6-axis sensors at key attach-

ment points (Miller and Rosen, 2010). Similarly, the

ETS-MARSE platform features a 6-DOF force sen-

sor to support compliant control strategies (Brahmi

and Saad, 2023). Although these sensors enhance

safety and control precision, they present notable

drawbacks—they are costly, susceptible to thermal

drift and noise, and mechanically fragile, all of which

may compromise performance and safety in physical

human–robot interaction (Katsura et al., 2007).

To address these limitations, nonlinear observer-

based approaches have been explored in industrial

settings as sensorless alternatives for force estima-

tion (Alcocer et al., 2003; Chen et al., 2000). Their

use in rehabilitation robotics has also gained inter-

est. For instance, a nonlinear disturbance observer

was implemented in (Gupta and O’Malley, 2011) to

regulate external forces in a single-DOF rehabilita-

tion setup. In a more complex scenario, (Popescu

et al., 2013) utilized a combination of three nonlinear

observers—a force observer, a velocity observer, and

a force-disturbance observer—to control a hand ex-

oskeleton, enhancing performance without relying on

physical force sensors. Recent trends also explore re-

inforcement learning combined with impedance con-

trol to adapt impedance gains for improved accuracy

and efﬁciency (Li et al., 2022a; Zhang, 2021). How-

ever, these methods face challenges including lim-

ited interpretability, safety concerns due to extensive

physical interaction, and lack of guaranteed conver-

gence or robustness against overﬁtting.

In this paper, we propose a nonlinear observer for

the ETS-MARSE rehabilitation robot to estimate ex-

ternal interaction forces without relying on force or

velocity sensors. Using only joint position measure-

ments, the proposed observer reduces computational

complexity while maintaining performance. The esti-

mated forces are used to infer the user’s movement in-

tention and to implement a compliant control strategy,

facilitating natural human–robot interaction. This ap-

proach simpliﬁes the traditional admittance control

framework by removing the need for Cartesian-to-

joint space transformations via Jacobian inversion, as

joint torques can be directly estimated through the ob-

server. The robot’s impedance behavior is tuned to

support isokinetic-type exercises, ensuring an appro-

priate dynamic response. To further improve estima-

tion accuracy, the observer is augmented with feed-

back from the controller’s internal model, enabling it

to distinguish between user-generated forces and in-

ternal disturbances such as friction or unmodeled dy-

namics. This enhances both reliability and control

performance in assistive rehabilitation tasks.

The structure of the paper is as follows: Section

2 introduces the core problem, detailing the adopted

nonlinear control strategy, the dynamic model of the

rehabilitation robot, its key properties and assump-

tions, and the formulation of the admittance-based

control law. Section 3 focuses on the design of the

nonlinear observer and presents a rigorous stability

analysis. Section 4 outlines the system’s hardware

architecture, experimental setup, and results. Finally,

Section 5 concludes the paper and discusses future re-

search directions.

2 PROBLEM FORMULATION

In this work, we employ the Modiﬁed Function

Approximation Technique (MFAT) (Brahmi et al.,

2024),(Brahmi et al., 2019) to ensure stable and ef-

fective motion control of the ETS-MARSE rehabil-

itation robot. MFAT has previously demonstrated

strong performance, particularly for high degree-of-

freedom systems like ETS-MARSE (7DOF), by ap-

proximating the robot’s dynamic parameters using a

ﬁnite set of orthonormal basis functions. This method

offers several advantages: it eliminates the need for

joint acceleration measurements, contact force deriva-

tives, and matrix inversions, making it computation-

ally efﬁcient and robust. Additionally, MFAT dynam-

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

ically adapts to variations in the robot-human system,

accommodating differences in patient biomechanics

and physiology. However, its performance is sensi-

tive to the selection and number of basis functions,

which can impact both parameter estimation accu-

racy and real-time computational demands. Given

its adaptability and efﬁciency, MFAT was chosen as

the control strategy for this study. This section pro-

vides an overview of the ETS-MARSE robot’s kine-

matic structure to support the reader’s understand-

ing of the system. The full implementation details

of MFAT in ETS-MARSE can be found in previ-

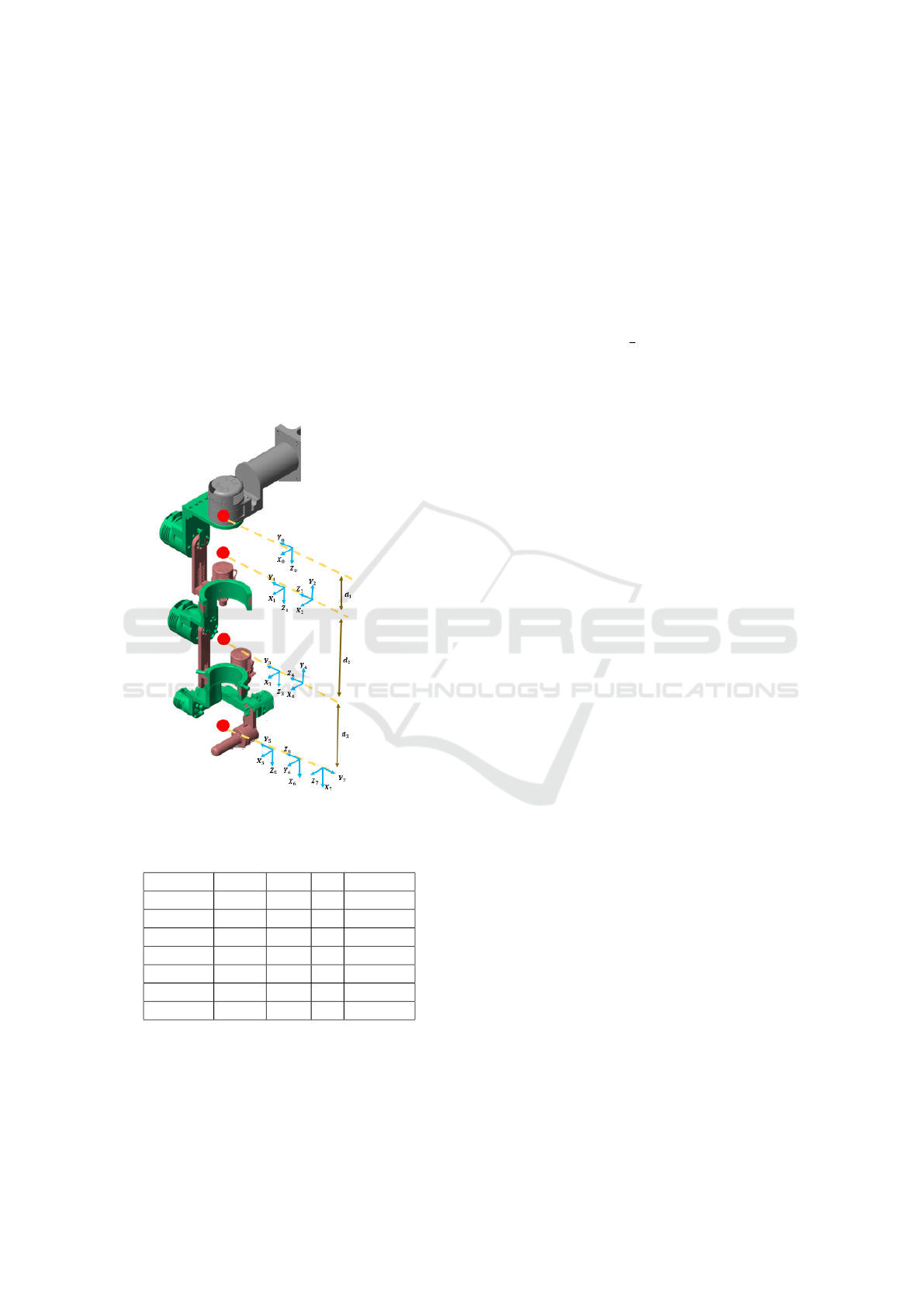
ous works (Brahmi et al., 2024). Fig. 1 illustrates

the frame assignments of the robot, and the modiﬁed

Denavit-Hartenberg parameters are listed in Table 1.

Figure 1: ETS-MARSE exoskeleton robot.

Table 1: ETS-MARSE Denavit-Hartenberg Modiﬁed Pa-

rameters.

Joint (i) α

i−1

1 0

◦

0 d

2 −90

◦

0 0 q

3 90

◦

0 d

4 −90

◦

0 0 q

5 90

◦

0 d

6 −90

◦

0 0 q

− 90

◦

7 −90

◦

0 0 q

The dynamic model of the serial robot manipula-

tor is developed using the Lagrange-Euler approach

as detailed below:

M(q) ¨q +C(q, ˙q) ˙q + G(q) = U − J

(1)

In this context, M(q) ∈ R

n×n

denotes the inertia ma-

trix, while C(q, ˙q) ∈ R

n×n

and G(q) ∈ R

signify the

Coriolis and centrifugal forces, as well as the gravita-

tional vector, respectively. Furthermore, U ∈ R

rep-

resents the control input torque, J

∈ R

n×n

pertains to

the end-effector Jacobian matrix, and F

indicates the

interaction force at the end-effector of the robot. The

dynamic characteristics of the robot (1) are deﬁned by

the following properties:

Property 1. (Siciliano and Khatib, 2016) ∀ q, ˙q, x ∈

, it follows that x

(

M(q) − C(q, ˙q))x = 0, and

equivalently, we have

M(q) − 2C(q, ˙q) = 0.

Property 2. (Siciliano and Khatib, 2016) ∀ q, x, y ∈

we have:

C(q, x)y = C(q, y)x (2)

Property 3. (Siciliano and Khatib, 2016) For robots

that are equipped only with revolute joints, there ex-

ists a constant K

> 0 that fulﬁlls the following in-

equality:

∥C(q, ˙q)∥ ≤ K

∥ ˙q∥ (3)

∀ q, ˙q ∈ R

Assumption 1. For Observer design, we support that

∥ ˙q∥ ≤ K

for any t ≥ 0 when K

> 0

2.1 Admittance-Based Control

To enable the robot to respond to forces exerted by the

user, an admittance control strategy is employed. This

approach interprets external forces as motion com-

mands, allowing for intuitive and compliant interac-

tion between the user and the robotic system. Con-

ceptually, the admittance function serves as a dynamic

mapping from force input to motion output and is

mathematically represented as:

= q + K

−1

(4)

In this formulation, q

∈ R

denotes the updated de-

sired joint trajectory generated by the admittance con-

troller. The term K

∈ R

7×7

is a positive-deﬁnite gain

matrix that acts as a virtual stiffness, analogous to a

spring constant in mechanical systems. The vector

∈ R

represents the estimated external force ap-

plied by the user, and J

is the transpose of the Ja-

cobian matrix, projecting the external force into the

joint space. This control law effectively models a

virtual spring-damper system: when the user applies

a force, the robot responds by adjusting its position

proportionally. Conversely, when the user ceases to

exert force (i.e.,

→ 0), the inﬂuence of the admit-

tance term diminishes, causing q

→ q and the robot

Sensorless Admittance Control of a Manipulator Arm Using a Nonlinear Observer for Force and Velocity Estimation

to stabilize at its last position. This mechanism guar-

antees that the robot effectively follows the user’s in-

tended movements with compliance, while the under-

lying trajectory control manages tasks such as grav-

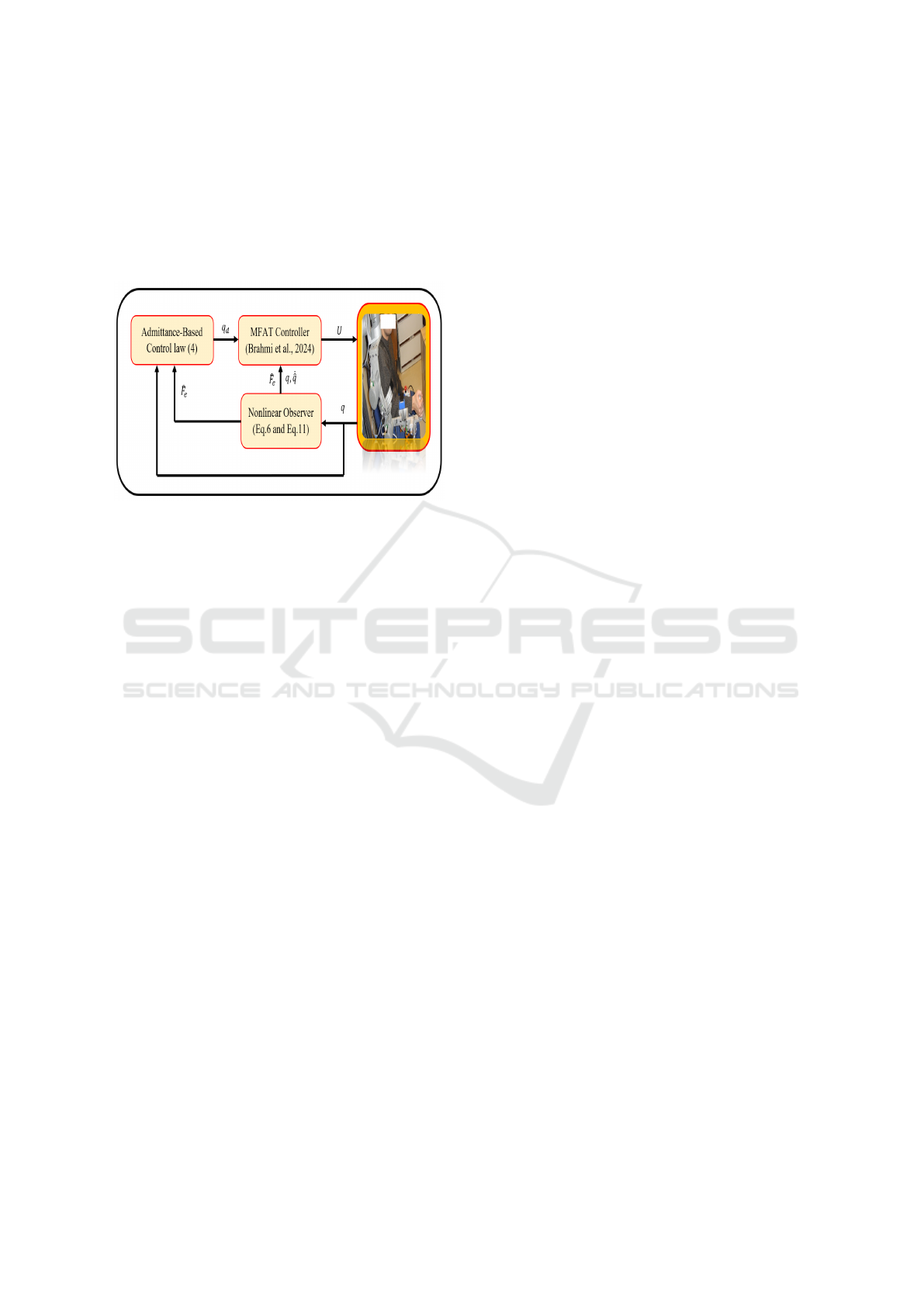
ity compensation. The block diagram of the proposed

control scheme is shown in Fig. 2. The estimation

method

will be elaborated upon in the next section.

Figure 2: Block diagram of the admittance-based control.

3 NONLINEAR OBSERVER

DESIGN

The state representation of the dynamic model (1) is

established by deﬁning the states as: ξ

= q, and ξ

˙q, leading to the following state representation:

(

= ξ

= M

−1

(ξ

)

U −J

(ξ

−C(ξ

)

− G(ξ

)

(5)

From this representation (5), we can develop the

nonlinear observer without the need for the force vec-

tor, as outlined below:











+ K

= M

−1

(ξ

)

U −C(ξ

)

− G(ξ

) + K

= ξ

−

= ξ

− q

(6)

where K

and K

represent diagonal positive deﬁnite

gain matrices. Based on ( (6)), the estimation error

can be expressed in the following state representation:











− K

= M

−1

(ξ

)

− J

(ξ

−C(ξ

)

−C(ξ

)

− K

(7)

By differentiating

and substituting

from

Eq. (7), the dynamics of

is given by:

− K

= M

−1

(ξ

)

− J

(ξ

−C(ξ

)

−C(ξ

)

− K

(8)

The external torque applied to the robot model (1)

can be estimated by:

(ξ

= − M(ξ

)

−

C(ξ

) +C(ξ

)

− M(ξ1)K

− K

(9)

To reduce the computational burden associated

with (9), earlier research (Alcocer et al., 2003) has

shown that a close approximation of the external force

can be achieved by concentrating solely on its ﬁnal

right-hand term. Assuming that environmental forces

change gradually, we can express the estimated value

as:

(ξ

)

= −K

(10)

By multiplying both sides of (10) by J

−T

(ξ

) and tak-

ing K

= K

into account, we derive the following

result:

= −J

−1

(ξ

(11)

3.1 Stability Analysis

The differentiation of the ﬁrst equation of (6) leads to:

+ K

(12)

By substituting

by its value from (6) the dynamic

is given by the following state representation:

= M

−1

(ξ

)

U −C(ξ

)

− G(ξ

) + K

+ K

(13)

Multiplying both side of (13) by M(ξ

) we get:

M(ξ

)

U −C(ξ

)

− G(ξ

) + K

+ K

M(ξ

)

(14)

Then:

M(ξ

)

+C(ξ

)

+ G(ξ

) = U +K

+ K

M(ξ

)

(15)

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

The error dynamics is obtained by subtracting (15)

from (1)

M(ξ

)(

−

) +C(ξ

)

−C(ξ

)

= −J

−K

− K

M(ξ

)

M(ξ

)

+C(ξ

)

−C(ξ

)

= −J

−K

− K

M(ξ

)

(16)

Based on (2) and utilizing the last equation of (6),

we can conclude:

C(ξ

)

−C(ξ

)

= C(ξ

)

+C(ξ

)

(17)

By substituting (17) into (16) we obtain:

M(ξ

)

+C(ξ

)

= −J

− K

−K

M(ξ

)

−C(ξ

)

(18)

Theorem 1. According to Assumption (1), if:

then the equilibrium point

for (16) is asymptoti-

cally stable. The region of attraction is deﬁned by



∈ R

: ∥

∥ <

min

max



− K



(19)

In this framework, M

min

, M

max

denotes the small-

est and largest eigenvalues of M, respectively.

Proof: Next, we will analyze the following Lya-

punov function:

V =

M(ξ

)

(20)

The time derivative of (20) yields the following:

V =

M(ξ

)

M(ξ

)

(21)

By substituting M(ξ

)

from (18) into (21), we

obtain:

V =



− J

− K

M(ξ

)

−C(ξ

)

−C(ξ

)



M(ξ

)



− J

− K

M(ξ

)

−C(ξ

)





M(ξ

)

−C(ξ

)



(22)

By applying Property (1), we can then derive:

V = −

+ K

) −

M(ξ

)

−

C(ξ

)

(23)

Considering the properties described in (2) and

(3), along with the premise presented in Assumption

(1):



C(ξ,

ξ)



−

C(ξ,

ξ)

ξ +

C(ξ,

ξ)



≤ ∥

ξ∥



∥

ξ∥ + K



(24)

From (10), we obtain J

= −K

. As a result,

(23) is transformed as :

V ≤ −∥

ξ∥

M(ξ

) − K



∥

ξ∥ + K

i

(25)

Hence, if

∥

ξ∥ <

− K

(26)

where M(ξ

) = M Then ,

V ≤ −κ∥

ξ∥

(27)

where κ > 0, the right side of (26) is positive by hy-

pothesis. Furthermore,

min

∥

ξ∥

≤ V (

ξ) ≤

max

∥

ξ∥

(28)

It is clear that V (

ξ) is a positive deﬁnite and de-

creasing function deﬁned on (28). Since

V (

ξ) ≤ 0, ∀

satisﬁes the conditions outlined in (26), we can infer

that the equilibrium point

ξ = 0 is uniformly stable,

as shown in (Hahn et al., 1967).

To illustrate this attractive feature, by

∥

ξ(0)∥ <

min

max



− K



(29)

Then,







V (

ξ) ≤ V (

ξ(0))

V (

ξ) ≤ −κ∥

ξ∥

(30)

The inequality (30) ensures that

ξ remains

bounded. Since

ξ and

ξ are conﬁrmed to be bounded

Sensorless Admittance Control of a Manipulator Arm Using a Nonlinear Observer for Force and Velocity Estimation

in (16) it follows that

ξ is uniformly continuous. Ad-

ditionally, from (30), we conclude:

∞

∥

ξ∥

dt ≤ −

∞

V (t)dt = V (0) −V (∞) < ∞

(31)

and therefore:

lim

t→∞

∥

ξ∥ = 0 (32)

which, when substituted into (16) yields:

lim

t→∞

∥

ξ∥ = 0 (33)

Discussion: The convergence of the observer

is guaranteed provided that the joint velocities are

bounded and the initial estimation error lies within

an appropriate region of attraction. However, this re-

quirement on velocity bounds becomes unnecessary

when the observer is integrated with a (MFAT) con-

trol law. The extent of the region of attraction can

be increased by tuning the observer gain constant K

Since the joint positions are assumed to be measur-

able, the observer can be initialized with

ξ(0) = ξ(0),

ensuring that only the initial error in the velocity esti-

mate,

ξ(0), needs to satisfy condition (19).

4 EXPERIMENTAL VALIDATION

The proposed approach is experimentally validated

using the ETS-MARSE system, which is set up with

a National Instruments NI PXI-1031 chassis. This

hardware conﬁguration consists of two key compo-

nents: an FPGA card (NI PXI-7813R) and a dual-

core controller card (NI PXI-8108). The Intel Core

2 Duo-based controller operates at 200 Hz, execut-

ing the outer loop of the proposed algorithm while

concurrently processing joint position feedback from

Hall-effect sensors. Meanwhile, the FPGA card op-

erates at a signiﬁcantly higher frequency of 20 kHz

to ensure accurate real-time execution of the inner-

loop PI current control. The torque commands sent to

the exoskeleton arm are generated via LabVIEW soft-

ware running on a connected host computer (Brahmi

et al., 2024; Brahmi et al., 2019). The chosen val-

ues for the designed observer gains are provided in

Table 2.

In this test, the subject wears the robotic device

and moves it away from the initial position with the

elbow ﬂexed at 90

◦

. The desired trajectory is gener-

ated using the admittance control law (4). Through-

out the experiment, the force applied by the subject is

recorded by the force sensor and compared with the

estimated force derived from (11). This section aims

to evaluate the effectiveness of the proposed nonlin-

ear observer in delivering precise force and velocity

estimates for admittance-based control. The experi-

mental ﬁndings are summarized in Figs. 3–7.

Table 2: Proposed observer gains.

Gains Value

diag[15, 15, 15, 15, 15, 15, 15]

diag[50, 50, 50, 50, 50, 50, 50]

diag[1.1, 1.1, 1.1, 1.1, 1.1, 1.1, 1.1]

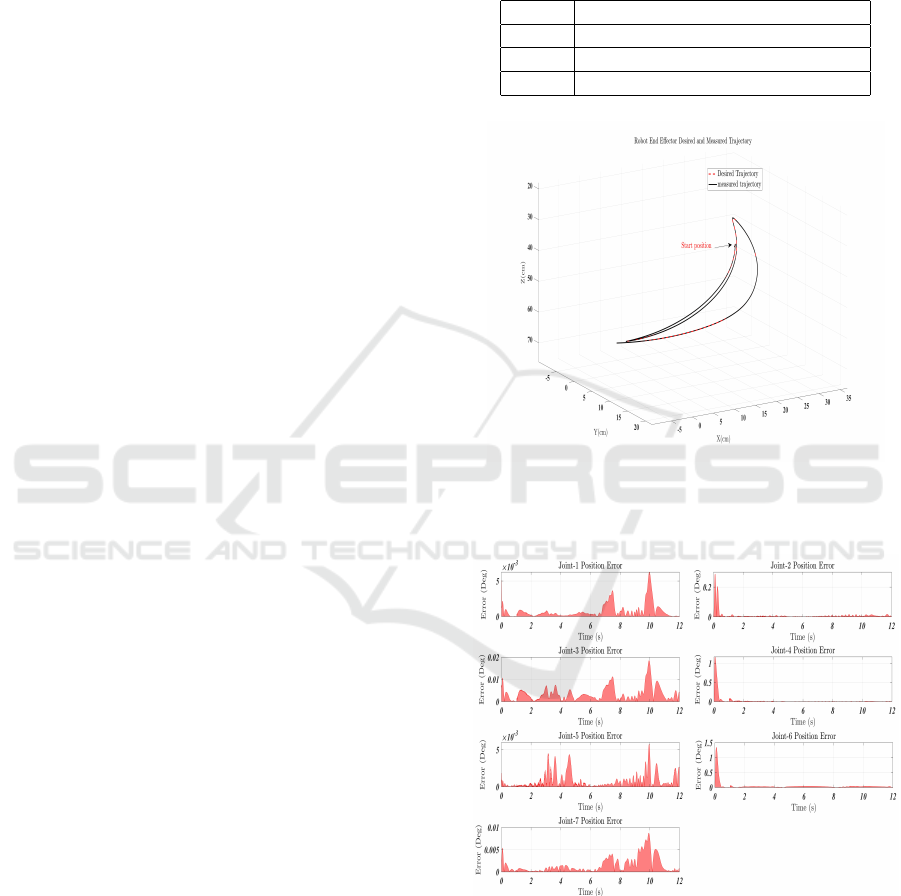
Figure 3: The Cartesian performance of ETS-MARSE in

3D space: the desired trajectory (black line ) and the mea-

sured trajectory (dashed red line).

Figure 4: Joint position Tracking Error Over Time.

Fig. 3 illustrates the 3D Cartesian performance of

the ETS-MARSE system. The measured trajectory,

shown as a dashed red line, closely follows the desired

trajectory represented by the solid black line. This

indicates that the admittance controller, driven by

observer-estimated forces, effectively translates user-

applied inputs into compliant spatial motion. Further-

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

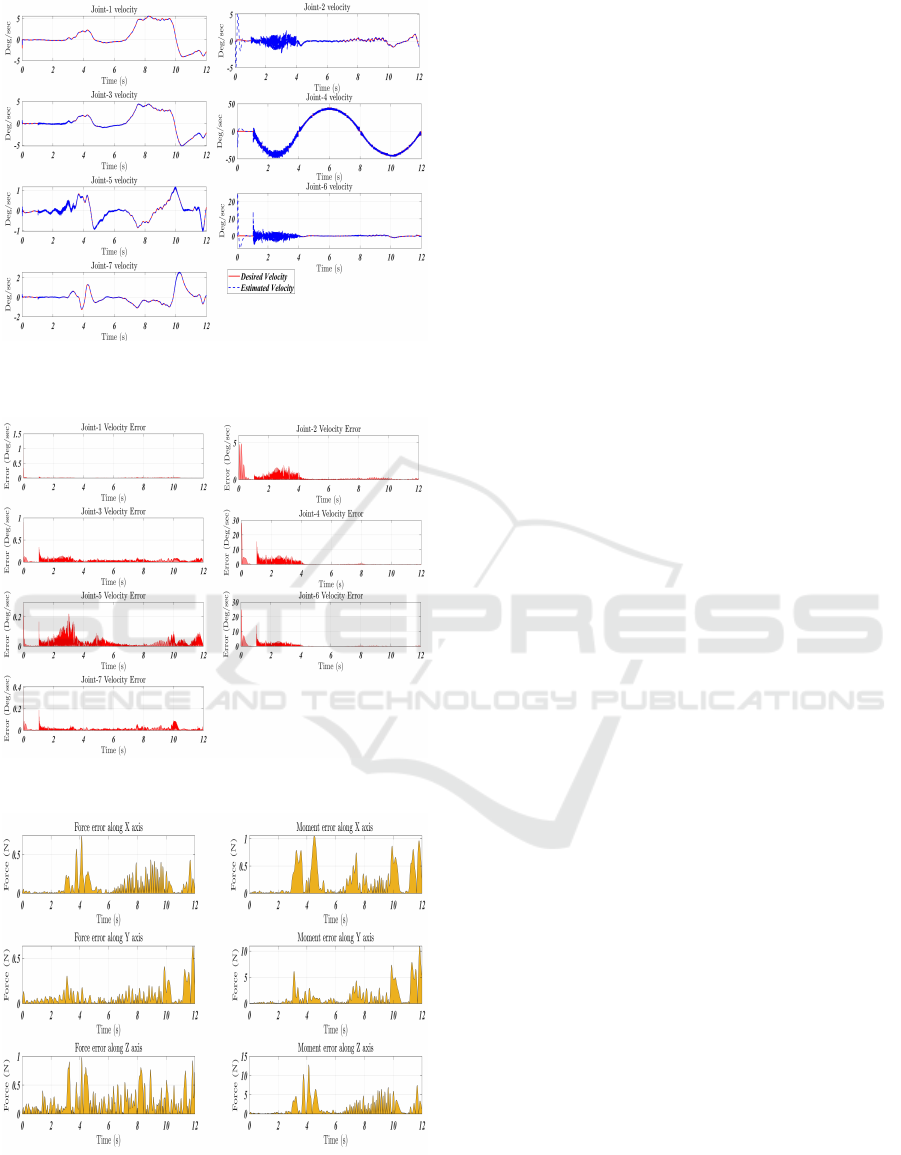
Figure 5: Joint velocity tracking: the desired trajectory (red

solid line ) and the estimated velocity (dashed blue line).

Figure 6: Joint Velocity Tracking Error Over Time.

Figure 7: Tracking error between estimated force and mea-

sured force provided sensor.

more, the robot’s high performance is attributed to

the robust adaptive control implemented in this study

(Brahmi et al., 2024), which effectively accommo-

dates dynamic variations and uncertainties in human-

robot interactions. Fig. 4 presents the joint position

tracking error over time, where errors remain minimal

and stable across all joints. The stability and accuracy

of the admittance control loop further reinforce the re-

liability of the observer in consistently providing state

information necessary for position regulation. Fig. 5

compares the estimated joint velocities (dashed blue

line) with the desired velocity proﬁle (solid red line).

The close correspondence between these two curves

reﬂects the observer’s capability to reconstruct joint

velocities without requiring direct velocity sensing,

even during dynamic transitions. Fig. 6 quantiﬁes the

joint velocity estimation error, which remains small

and bounded throughout the task duration. This out-

come supports the observer’s applicability for real-

time control applications where velocity feedback is

typically absent or unreliable. Fig. 7 compares the

estimated interaction force against the ground-truth

measurements from the force sensor. The estimated

force closely follows the measured values, exhibit-

ing only minor discrepancies during high-dynamic

phases.

5 CONCLUSIONS

This paper introduces a nonlinear observer-based

technique for estimating force and velocity in a joint-

space admittance-controlled exoskeleton. The system

aims to promote safe and compliant interactions be-

tween humans and robots. A thorough stability anal-

ysis is performed using Lyapunov theory to conﬁrm

the asymptotic stability of the estimated states. The

proposed nonlinear observer effectively estimates ex-

ternal forces and joint velocities by relying solely on

joint position feedback. This ability facilitates sensor-

less admittance control in the ETS-MARSE exoskele-

ton. Experimental results validate the accuracy and

robustness of the method, revealing low tracking er-

rors and high compliance with human-intended move-

ments. Consequently, this approach eliminates the

need for delicate and costly force sensors while en-

suring safe and transparent interactions. Future work

will focus on testing with a broader population to as-

sess generalizability across different biomechanical

proﬁles. Additionally, we will investigate adaptive

observer tuning and the integration of biosignal inter-

faces (such as EMG) to enhance responsiveness. Our

efforts will also prioritize real-world deployment sce-

narios, including autonomous rehabilitation sessions

Sensorless Admittance Control of a Manipulator Arm Using a Nonlinear Observer for Force and Velocity Estimation

and tele-operated assistive systems.

ACKNOWLEDGEMENTS

This work was supported by the Center for Interdis-

ciplinary Research on Intelligent Manufacturing and

Robotics at King Fahd University of Petroleum &

Minerals, Dhahran, Saudi Arabia, under the research

grant INMR2508, titled ”Adaptive Learning Control

Design for Safe and Efﬁcient Human-Robot Collabo-

ration in Dynamic Industrial Environments”.

REFERENCES

Alcocer, A., Robertsson, A., Valera, A., and Johansson, R.

(2003). Force estimation and control in robot ma-

nipulators. In Robot Control 2003 (SYROCO’03): A

Proceedings Volume from the 7th IFAC Symposium,

page 55, Wrocław, Poland.

Brahmi, B., Dahani, H., Bououden, S., Fareh, R., and Rah-

man, M. H. (2024). Adaptive-robust controller for

smart exoskeleton robot. Sensors, 24(2):489.

Brahmi, B., Laraki, M. H., Saad, M., Rahman, M. H.,

Ochoa-Luna, C., and Brahmi, A. (2019). Compli-

ant adaptive control of human upper-limb exoskeleton

robot with unknown dynamics based on a modiﬁed

function approximation technique (mfat). Robotics

and Autonomous Systems, 117:92–102.

Brahmi, B. and Saad, M. (2023). Adaptive control of an

electrically driven exoskeleton robot (theory and ex-

periments). Journal of Vibration Engineering & Tech-

nologies, 11(7):3399–3412.

Chen, W.-H., Ballance, D. J., Gawthrop, P. J., and O’Reilly,

J. (2000). A nonlinear disturbance observer for robotic

manipulators. IEEE Transactions on Industrial Elec-

tronics, 47:932–938.

Chen, X., Wang, N., Cheng, H., and Yang, C. (2020). Neu-

ral learning enhanced variable admittance control for

human–robot collaboration. IEEE Access, 8:25727–

25737.

Culmer, P. R., Jackson, A. E., Makower, S., et al. (2010). A

control strategy for upper limb robotic rehabilitation

with a dual robot system. IEEE/ASME Transactions

on Mechatronics, 15:575–585.

Gupta, A. and O’Malley, M. K. (2011). Disturbance-

observer-based force estimation for haptic feedback.

Journal of Dynamic Systems, Measurement, and Con-

trol, 133:014505.

Hahn, W. et al. (1967). Stability of motion, volume 138.

Springer.

Hogan, N. (1985). Impedance control: An approach to ma-

nipulation—part i: Theory; part ii: Implementation;

part iii: Applications. ASME Journal of Dynamic Sys-

tems, Measurement, and Control, 107(1):1–24.

Hongli, C. (2022). Design of a fuzzy fractional order adap-

tive impedance controller with integer order approxi-

mation for stable robotic contact force tracking in un-

certain environment. Acta Mechanica et Automatica,

16(1):16–26.

Hsu, H.-H., Lee, W.-K., and Lee, P.-L. (2025). Designing

an eeg signal-driven dual-path fuzzy neural network-

controlled pneumatic exoskeleton for upper limb re-

habilitation. International Journal of Fuzzy Systems,

pages 1–19.

Ibarguren, A., Daelman, P., and Prada, M. (2020). Con-

trol strategies for dual arm co-manipulation of ﬂexi-

ble objects in industrial environments. In Proc. IEEE

Conf. Ind. Cyberphysical Syst., pages 514–519, Tam-

pere, Finland.

Iqbal, K. and Zheng, Y. F. (1999). Arm-manipulator coor-

dination for load sharing using predictive control. In

Proceedings of the IEEE International Conference on

Robotics and Automation (ICRA), pages 2539–2544.

Jaroonsorn, P. et al. (2020). Robot-assisted transcranial

magnetic stimulation using hybrid position/force con-

trol. Advanced Robotics, 34(24):1559–1570.

Jung, S. and Hsia, T. C. (2000). Robust neural force control

scheme under uncertainties in robot dynamics and un-

known environment. IEEE Transactions on Industrial

Electronics, 47(2):403–412.

Karimi, M. and Ahmadi, M. (2025). ilead: An emg-based

adaptive shared control framework for exoskeleton as-

sistance via deep reinforcement learning. IEEE Trans-

actions on Artiﬁcial Intelligence.

Katsura, S., Matsumoto, Y., and Ohnishi, K. (2007). Mod-

eling of force sensing and validation of disturbance

observer for force control. IEEE Transactions on In-

dustrial Electronics, 54(1):530–538.

Li, M., Wen, Y., Gao, X., Si, J., and Huang, H. (2022a). To-

ward expedited impedance tuning of a robotic prosthe-

sis for personalized gait assistance by reinforcement

learning control. IEEE Transactions on Robotics,

38(1):407–420.

Li, Z., Li, X., Li, Q., Su, H., Kan, Z., and He, W.

(2022b). Human-in-the-loop control of soft exosuits

using impedance learning on different terrains. IEEE

Transactions on Robotics, 38(5):2979–2993.

Lynch, K. M., Liu, C., Sorensen, A., Kim, S., Peshkin, M.,

Colgate, J. E., Tickel, T., Hannon, D., and Shiels, K.

(2002). Motion guides for assisted manipulation. In-

ternational Journal of Robotics Research, 21(1):27–

43.

Miller, L. M. and Rosen, J. (2010). Comparison of multi-

sensor admittance control in joint space and task space

for a seven degree of freedom upper limb exoskeleton.

In 2010 3rd IEEE RAS and EMBS International Con-

ference on Biomedical Robotics and Biomechatronics

(BioRob), pages 70–75, Tokyo, Japan.

Newman, W. S. (1992). Stability and performance limits

of interaction controllers. ASME Journal of Dynamic

Systems, Measurement, and Control, 114:563–570.

Otten, A., Voort, C., Stienen, A., Aarts, R., van Asseldonk,

E., and van der Kooij, H. (2015). Limpact: A hydrauli-

cally powered self-aligning upper limb exoskeleton.

ICINCO 2025 - 22nd International Conference on Informatics in Control, Automation and Robotics

IEEE/ASME Transactions on Mechatronics, 20:2285–

2298.

Ozkul, F. and Barkana, D. E. (2013). Upper-extremity reha-

bilitation robot rehabroby: Methodology, design, us-

ability and validation. International Journal of Ad-

vanced Robotic Systems, 10:1–13.

Popescu, N., Popescu, D., Ivanescu, M., Popescu, D.,

Vladu, C., and Vladu, I. (2013). Force observer-based

control for a rehabilitation hand exoskeleton system.

In 2013 9th Asian Control Conference (ASCC), pages

1–6.

Qin, X. et al. (2021). The adaptive neural network sliding

mode control for angle/force tracking of the dexterous

hand. Advances in Mechanical Engineering, 13.

Siciliano, B. and Khatib, O. (2016). Robotics and the hand-

book. In Springer Handbook of Robotics, pages 1–6.

Springer.

Siciliano, B. and Villani, L. (2000). Robot Force Control.

Springer, Berlin, Germany.

Xue, T., Wang, W., Ma, J., Liu, W., Pan, Z., and Han, M.

(2020). Progress and prospects of multimodal fusion

methods in physical human–robot interaction: A re-

view. IEEE Sensors Journal, 20(18):10355–10370.

Zarrin, R. S., Zeiaee, A., and Langari, R. (2024).

A variable-admittance assist-as-needed controller

for upper-limb rehabilitation exoskeletons. IEEE

Robotics and Automation Letters.

Zhang, Z. (2021). A computational framework for robot

hand design via reinforcement learning. In Proceed-

ings of the IEEE/RSJ International Conference on

Intelligent Robots and Systems (IROS), pages 7216–

7222, Prague, Czech Republic.

Sensorless Admittance Control of a Manipulator Arm Using a Nonlinear Observer for Force and Velocity Estimation