AMAKAN: Fully Interpretable Adaptive Multiscale Attention Through
Kolmogorov-Arnold Networks
Felice Franchini
a
and Stefano Galantucci
b
University of Bari Aldo Moro, 70125, Bari, Italy
Keywords:
Adaptive Multiscale Attention, Interpretability, Kolmogorov–Arnold Networks, Tabular Data.
Abstract:
This paper introduces AMAKAN, a novel method for tabular data classification combining the Adaptive Multi-
scale Deep Neural Network with Kolmogorov–Arnold Network to ensure full interpretability without sacrific-
ing predictive performance. The Adaptive Multiscale Deep Neural Network dynamically focuses on relevant
features at different scales by using learned attention mechanisms. These multiscale features are then refined
by Kolmogorov–Arnold Network layers, which replace typical dense layers with learnable univariate func-
tions on network edges, providing transparency by allowing practitioners to visually see and inspect feature
transformations directly. Experimental results on a variety of real-world datasets demonstrate that AMAKAN
achieves performance equivalent to or better than state-of-the-art baselines while providing transparent and
actionable explanations for its predictions. By the seamless combination of interpretable attention mecha-
nisms with Kolmogorov–Arnold Network layers, the paper presents an explainable and efficient deep learning
method for tabular data across a vast spectrum of application domains.
1 INTRODUCTION
Machine learning research has progressively focused
on creating advanced deep learning models capable
of processing various data modalities, such as text,
images, and time series signals. Despite these suc-
cesses, applying deep learning to tabular data, per-
haps one of the most prevalent data structures in nu-
merous industries, remains an open challenge. Con-
ventional multilayer neural networks tend to struggle
with maintaining high accuracy without compromis-
ing interpretability, a concern that is particularly im-
portant in areas where model transparency is the foun-
dation of trust and accountability.
Recent work has demonstrated that specialized ar-
chitectures can benefit performance and explainabil-
ity for tabular data classification. In particular, the
Adaptive Multiscale Deep Neural Network (Denta-
maro et al., 2024) was developed to provide better
feature weighting with design-time interpretability.
This is achieved using parallel Excitation Layers of
differing compression levels and a Trainable Atten-
tion Mechanism, which programmatically selects the
learned feature dynamically. Although these mecha-
a
https://orcid.org/0009-0000-8887-800X
b
https://orcid.org/0000-0002-3955-0478
nisms partly unlock the internal decision process of
the model, further fine-tuning of its ultimate layers
needs to be conducted to render it a wholly inter-
pretable system.
Kolmogorov-Arnold Networks (KANs) (Liu
et al., 2024) are another powerful recent option for
representing complicated relationships among neural
networks without relying on pre-defined activation
functions in the nodes. Instead, they place learnable
univariate functions on the edges.
In doing so, they automatically offer a path to-
wards transparency and interpretability: any edge in a
KAN may be viewed and analyzed to reveal the evolu-
tion of the input signals. Above all, there are rigorous
theoretical foundations for Kolmogorov-Arnold Net-
works, in the form of the Kolmogorov-Arnold rep-
resentation theorem (Schmidt-Hieber, 2021), to sup-
port their ability to approximate multivariate func-
tions with versatility.
This paper incorporates Kolmogorov-Arnold Net-
works into the latter sections of the Adaptive Mul-
tiscale Deep Neural Network to obtain end-to-end in-
terpretability. That is, the final two dense layers of the
Adaptive Multiscale Deep Neural Network are sub-
stituted with Kolmogorov-Arnold Network layers, al-
lowing explicit insight into feature transformations.
Experimental findings show that such changes consis-
800
Franchini, F., Galantucci and S.
AMAKAN: Fully Interpretable Adaptive Multiscale Attention Through Kolmogorov-Arnold Networks.
DOI: 10.5220/0013654200003967
In Proceedings of the 14th International Conference on Data Science, Technology and Applications (DATA 2025), pages 800-808
ISBN: 978-989-758-758-0; ISSN: 2184-285X
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)

tently result in improved performance while granting
the full transparency required for high-stakes applica-
tions.
The remainder of this paper is organized as fol-
lows. Section 2 discusses recent research on in-
terpretable deep learning methods for tabular data,
including other architectures employing attention
mechanisms and tree-based ensembles. Section 3 in-
troduces the initial Adaptive Multiscale Deep Neural
Network architecture and outlines how Kolmogorov-
Arnold Networks are incorporated into its architec-
ture. Section 4 discusses the experimental setup and
datasets considered, and Section 5 presents results
on classification performance and interpretability im-
pact. Section 6 concludes and gives future work di-
rections for how this improved architecture can serve
as a faithful, fully interpretable deep learning solution
for tabular data.
2 RELATED WORK
2.1 Adaptive Multiscale Deep Neural
Network
The Adaptive Multiscale Deep Neural Network, pre-
sented by Dentamaro et al. (Dentamaro et al., 2024),
has been particularly engineered to improve feature
weighting in tabular data classification, with a high
level of interpretability. Through the integration of
multiple Excitation Layers operating at different lev-
els of compression, the model enables a dynamic
evaluation of input feature relevance. These repre-
sentations are then combined within a Merge Layer
through operations like addition, averaging, concate-
nation, or the Hadamard product, thus enabling the
combination of multi-scale feature representations.
Finally, a Trainable Attention Mechanism further op-
timizes the determined feature importance by adjust-
ing weight parameters during training. This method
yields considerably enhanced classification perfor-
mance, thanks to the ability of the model to ana-
lyze input data at a multi-resolution level, while inter-
pretability is also improved through attention-based
feature weighting.
This model aligns with other explainable deep
learning approaches developed for tabular data. Neu-
ral Oblivious Decision Tree Ensembles (NODE)
(Popov et al., 2019) offers differentiable decision
trees that support gradient-based learning, thus al-
lowing a balance between interpretability and perfor-
mance, similarly to other decision-tree-based method-
ologies (Luo et al., 2021; Dentamaro et al., 2018). As
opposed to typical tree-based algorithms, NODE sup-
ports end-to-end training while also ensuring trans-
parency at the feature level. Similarly, the Soft Deci-
sion Tree Regressor (SDTR) (Luo et al., 2021) blends
decision tree approaches with deep learning, leverag-
ing hierarchical representations to both improve pre-
dictive ability and model explainability.
Besides hybrid tree-based models, there have been
various novel deep learning architectures proposed
for tabular data analysis. TabNet (Arik and Pfis-
ter, 2021) leverages an interpretable sequential at-
tention mechanism that selectively extracts relevant
features step by step, thus improving feature selec-
tion and interpretability. However, it requires large
datasets for the best training outcomes. Also, Cat-
Boost (Prokhorenkova et al., 2018), a gradient boost-
ing system that was particularly tailored for efficient
categorical feature management, combines ordered
boosting and fast categorical variable processing to
maintain high prediction quality with improved inter-
pretability. Aversano et al. (Aversano et al., 2023) fur-
ther contributed to the field by proposing a data-aware
explainable deep learning approach that demonstrates
how interpretability can be integrated into predictive
systems, particularly in process-aware applications.
2.2 Kolmogorov-Arnold Networks
(KANs)
Kolmogorov-Arnold Networks (KANs) (Liu et al.,
2024) leverage the Kolmogorov-Arnold represen-
tation theorem (Schmidt-Hieber, 2021), which
states that every multivariate continuous function
f : [0, 1]
n
→ R can be represented as a superposition
of continuous single-variable functions:
f (x
1
, x
2
, ..., x
n
) =
2n+1
∑
q=1
Φ
q
n
∑
p=1
φ
p,q
(x
p
)
!
where Φ
q
and φ
p,q
are learnable functions.
In contrast to Multi-Layer Perceptrons (MLPs)
that apply fixed activation at neurons, KANs apply
learnable functions to the edges, which increases flex-
ibility and expressiveness.
Some of the most significant distinctions between
KANs and MLPs are as follows:
• Learnable vs. Fixed Activations: KANs make
use of learnable function compositions instead of
fixed activations, thus showing improved data pat-
tern adaptability.
• Weight Multiplication vs. Function Approx-
imation: KANs allow for dynamic transforma-
tions, unlike traditional static weighted sums, by
supporting the learning of functions.
AMAKAN: Fully Interpretable Adaptive Multiscale Attention Through Kolmogorov-Arnold Networks
801

• Shallower yet More Expressive: KANs achieve
strong function approximation using fewer layers,
thus reducing the need for large architectures.
KANs are highly interpretable due to their explicit
modeling of feature transformation. Their learned
functions can be visualized, thus offering important
insights into how features influence predictions. In
addition, their unique architecture makes them im-
mune to catastrophic forgetting, thus ensuring robust-
ness in sequential learning tasks.
Several research works have enabled the devel-
opment of the interpretability of Kolmogorov-Arnold
Networks. Xu et al. (Xu et al., 2024) have incor-
porated symbolic regression into KANs, as shown
by their implementations in Temporal KAN (T-KAN)
and Multi-Task KAN (MT-KAN), and improved
transparency in time-series tasks. Galitsky (Galit-
sky, 2024) has utilized KANs in natural language
processing (NLP) by using inductive logic program-
ming to give word-level explanations. A similar strat-
egy of combining explainability with advanced mod-
eling has also been applied in biomedical contexts,
such as AI-assisted spectroscopy for cancer assess-
ment (Esposito et al., 2023; Gattulli et al., 2023b;
Dentamaro et al., 2021; Gattulli et al., 2023a). De
Carlo et al. (De Carlo et al., 2024) and Sun (Sun,
2024) have explored using KANs in graph neural net-
works and scientific discovery, where inherent com-
plexity presents interpretability challenges. Bozor-
gasl and Chen (Bozorgasl and Chen, ) have pro-
posed Wav-KAN, which incorporates wavelets for en-
hanced transparency. Thanks to these advancements,
KANs have demonstrated their capability to add inter-
pretability in different architectural frameworks. For
this reason, this paper integrates them into the Adap-
tive Multiscale Deep Neural Network to replace its
black-box components and achieve full interpretabil-
ity.
3 REVISED ARCHITECTURE
3.1 Original Network Structure
Adaptive Multiscale Deep Neural Network is pro-
posed to boost feature weighting and attention mecha-
nisms for tabular data classification. The model archi-
tecture consists of multiple parallel Excitation Layers
with different levels of compression to capture and
emphasize relevant features dynamically. The Exci-
tation Layers perform a dense transformation and an
Exponential Linear Unit (ELU) activation function to
enhance the gradient flow, and a second dense trans-
formation and sigmoid activation function to normal-
ize attention weights to [0,1]. The number of exci-
tation layers is defined proportionally to the number
of input features to achieve adaptability to different
datasets.
Excitation Layers’ outputs are merged through a
Merge Layer that carries out one of four operations:
Addition, Averaging, Concatenation, or Hadamard
Product. Through this operation, multi-scale feature
representations are effectively merged before further
processing. To normalize feature representations, the
network carries out Layer Normalization, followed by
a Hadamard Product between the normalized output
and original input features. This operation enhances
feature weighting without losing raw data properties.
A Trainable Attention Mechanism updates feature
importance dynamically using a trainable weight ma-
trix. The matrix, which is set to an identity ma-
trix with a small scaling factor at initialization, is
trained to learn the best feature weighting. With an
explicit model of feature contribution to the classifica-
tion task, this mechanism improves both performance
and interpretability.
The interpretability of the Adaptive Multiscale At-
tention Block is realized through an extensive analy-
sis of features at multiple scales. First, the Excita-
tion Layers present an immediate view of the most
important features relevant for classification by com-
puting attention weights at various levels of granular-
ity. These attention weights enable the investigation
of local feature importance, thereby indicating which
features are emphasized in different parts of the net-
work. Second, the overall importance of each input
variable is determined by summing attention scores
over all instances, providing a high level of under-
standing of feature relevance. Further, the model ex-
plores the variation of feature importance across dif-
ferent classes, allowing an analysis of class-specific
feature dynamics. Finally, the network gains insights
into nonlinear interactions between features, reveal-
ing complex dependencies that are not addressed in
conventional models.
With these mechanisms for interpretability built
into its design, the Adaptive Multiscale Deep Neural
Network is not based on post hoc explainability tech-
niques but is instead inherently transparent regarding
its choices. Having the ability to visualize attention
distributions and examine feature interactions makes
it particularly well-suited to transparency-requiring
applications such as medical diagnosis and financial
modeling.
In order to improve the interpretability of the
model, the final two dense layers have been replaced
by two dense layers obtained from the Kolmogorov-
Arnold Network, as depicted in Figure 1. To main-
DMDH 2025 - Special Session on Data-Driven Models for Digital Health Transformation
802

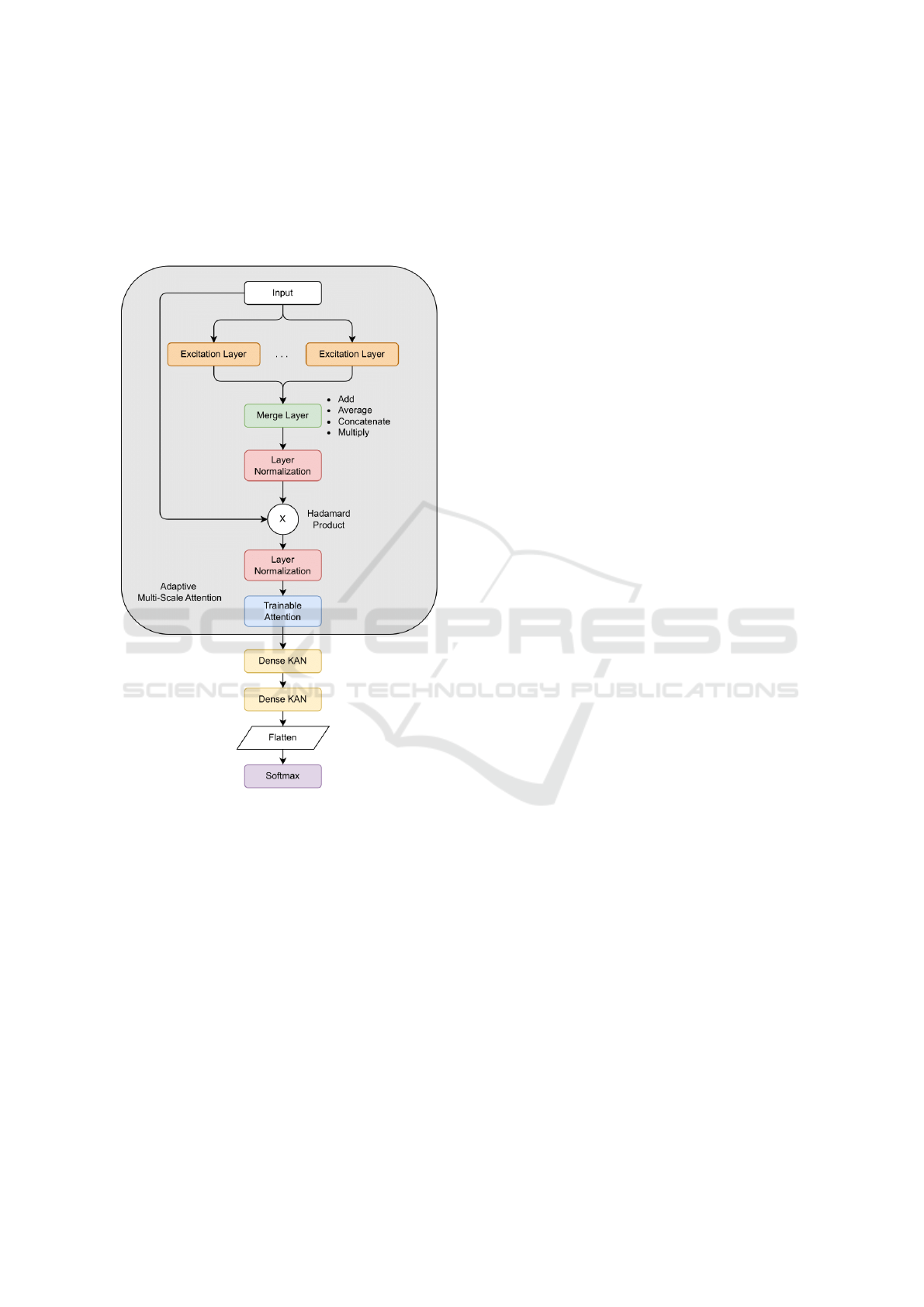
tain consistency with the previous architecture, the
first layer of the Kolmogorov-Arnold Network is set
to have a number of units equal to the number of in-
put features, while the second layer is set to have a
number of units equal to the number of total output
classes.
Figure 1: Adaptive Multiscale Attention Network KAN Ar-
chitecture.
In contrast with the conventional dense layers that
depend on linear transformations followed by pre-set
activation functions, Kolmogorov-Arnold Network
layers inherently use complicated nonlinear transfor-
mations using adjustable function compositions. This
inherent non-linearity obviates the necessity for the
ELU activation function that was used in the dense
layers of the original network. The flexibility of the
Kolmogorov-Arnold Network layers ensures that the
feature transformations are data-dependent, and the
model can adaptively learn the most significant rep-
resentations without pre-defined activation functions.
Every layer in the Kolmogorov-Arnold Network is
implemented using a grid size of 5 and a spline order
of 3, in line with Liu et al.(Liu et al., 2024)’s method-
ology in their original research on Kolmogorov-
Arnold Networks. Such dimensions achieve the best
possible trade-off between computational efficiency
and function approximation capacity and thus ensure
that the network enjoys a considerable amount of ex-
pressiveness while remaining interpretable.
4 EXPERIMENTAL SETUP
The datasets for evaluation are identical to those in
(Dentamaro et al., 2024). An overview of the datasets
is presented in table 1, including the number of in-
stances, features, and their balancing properties.
The datasets were chosen to provide an overall as-
sessment of the suggested architecture. The UCI Ar-
rhythmia dataset was chosen because it has a very
high number of features, and hence it is a suitable
benchmark for testing models that deal with intri-
cate feature interactions. In addition, the collection of
datasets includes imbalanced and balanced datasets so
that the model’s performance is evaluated under vary-
ing class distributions. The inclusion of the Higgs Bo-
son dataset with more than 11 million samples gives
a large-scale benchmark for the scalability of the new
approach. Likewise, the Click-Through Rate dataset
also gives a large yet structured classification problem
with a reasonable feature space. Including the smaller
datasets also tests the model’s ability to handle low
data situations.
To compare and evaluate the suggested architec-
ture against its predecessor version, all experimental
approaches were performed using the same model pa-
rameters defined in (Dentamaro et al., 2024). In ad-
dition, a new baseline experiment was added, where
a Kolmogorov-Arnold Network with a single hidden
layer was used. The number of units in this layer was
set to f × 0.8, where f is the number of features in the
dataset, to provide consistency with the MLP setup
described in (Dentamaro et al., 2024).
According to (Dentamaro et al., 2024), a base-
line Kolmogorov-Arnold Network was trained for a
maximum of 150 epochs with data standardization (Z-
score normalization) being applied before the training
phase was initiated. This approach enables fair com-
parisons by ensuring that all models operate under the
same preprocessing settings.
In order to create a general comparative frame-
work, the methodologies being considered can be
classified as follows:
• Tree-based approaches
– Decision Tree
– Random Forests (Breiman, 2001)
AMAKAN: Fully Interpretable Adaptive Multiscale Attention Through Kolmogorov-Arnold Networks
803

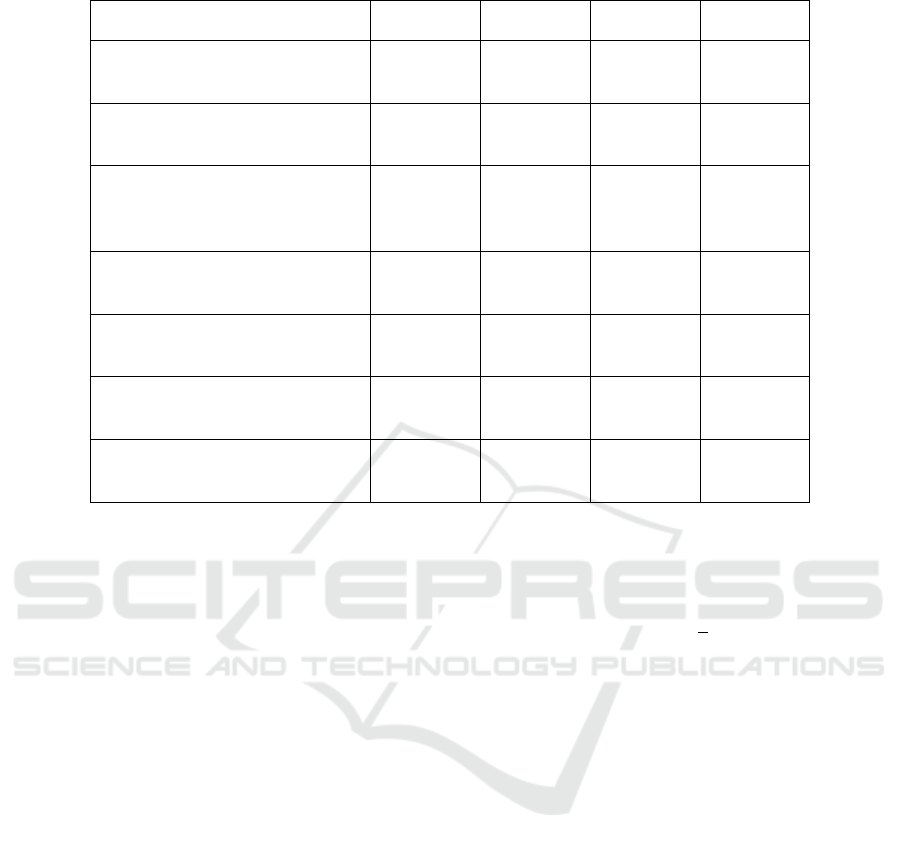
Table 1: Summary of Datasets Used.
Dataset Instances Features Size Balancing
UCI Arrhythmia (Guvenir and
Quinlan, 1997)
452 279 Small Imbalanced
UCI Wisconsin Breast Cancer
(Wolberg and Street, 1993)
569 32 Small Balanced
UCI Cervical Cancer
(Fernandes and Fernandes,
2017)
72 19 Small Imbalanced
UCI Diabetic Retinopathy
(Antal and Hajdu, 2014)
1,151 20 Small Balanced
UCI Heart Disease (Janosi and
Detrano, 1989)
303 14 Small Imbalanced
Click-Through Rate (Aden and
Wang, 2012)
1,000,000 12 Large Balanced
Higgs Boson (Baldi et al.,
2014)
11,000,000 28 Very
Large
Balanced
– XGBoost (Chen and Guestrin, 2016)
– CatBoost (Prokhorenkova et al., 2018)
• Non-tree-based approaches
– TabNet (Arik and Pfister, 2021)
– Multi-Layer Perceptron (MLP)
– Support Vector Machine (SVM) with RBF ker-
nel
– Kolmogorov–Arnold Network (KAN) (Liu
et al., 2024)
– Original Adaptive Multiscale Attention Net-
work (Dentamaro et al., 2024)
With regard to the architecture suggested in this
paper, all experimental protocols were carried out un-
der consistent conditions as outlined in (Dentamaro
et al., 2024). For every dataset, four different model
configurations were tested, differing in the type of
merge layer used. Let s
i
be the output of the i-th Ex-
citation Layer, where n is the number of Excitation
Layers. The merge layer integration was performed
using one of the following four methodologies:
• Addition: The outputs produced by every Exci-
tation Layer are combined through element-wise
addition to create the composite representation:
W
l
=
n
∑
i=1
s
i
(1)
where W
l
is the resulting weighted feature repre-
sentation.
• Averaging: The outcomes obtained from the Ex-
citation Layers undergo averaging to allow for an
equitable aggregation:
W
l
=
1
n
n
∑
i=1
s
i
(2)
where each s
i
preserves a fair contribution to the
final merged representation.
• Hadamard Product: The output resulting from
the Excitation Layers is element-wise multiplied:
W
l
=
n
∏
i=2
s
i−1
· s
i
(3)
• Concatenation: The outputs of the Excitation
Layers are concatenated along the feature dimen-
sion:
W
l
= [s
1
⊕ s
2
⊕ · · · ⊕ s
n
] (4)
where ⊕ represents the concatenation operator,
thus increasing the feature space dimensionality.
The four setups enable a thorough evaluation of
the impact that different merging methods have on the
performance of the model, thus providing insightful
information on their respective contributions to inter-
pretability and accuracy.
5 RESULTS AND DISCUSSION
In this section, an empirical comparison is made
among the proposed architecture and the earlier
DMDH 2025 - Special Session on Data-Driven Models for Digital Health Transformation
804

Adaptive Multiscale Deep Neural Network (Denta-
maro et al., 2024) and the baseline models. The com-
parison is done across various datasets and is mea-
sured in terms of classification accuracy using the F1-
weighted score, which is a balanced measure in case
of class imbalance. The motivation behind the com-
parison is to analyze if the addition of Kolmogorov-
Arnold Network layers can enhance the performance
of classification along with interpretability.
5.1 Performance Evaluation
The results presented in Table 2 demonstrate that
the suggested Adaptive Multiscale Deep Neural Net-
work, equipped with Kolmogorov-Arnold Network
layers, performs better than the baseline architecture
on nearly all datasets, the sole exceptions being Heart
Disease and Higgs Boson. This is seen consistently
across merging strategies, indicating that the substitu-
tion of the last dense layers with Kolmogorov-Arnold
Network layers significantly improves the model’s ca-
pacity to comprehend intricate feature relationships
without sacrificing accuracy.
As per the initial Adaptive Multiscale Deep Neu-
ral Network (Dentamaro et al., 2024), the best con-
figurations in the new architecture include the use of
either the Hadamard Product or Concatenation within
the merge layer. Both methods appear to maximize
the use of multi-scale feature representations, thus im-
proving classification performance. However, such
high performance levels are also maintained using
other merging layers, such as Addition and Averag-
ing, thereby highlighting the resilience of the new ar-
chitecture with different configurations.
Despite these general improvements, the sug-
gested architecture failed to surpass the baseline
model’s performance on the Heart Disease and Higgs
Boson datasets.
• Heart Disease Dataset: As a result of the intrin-
sic complexity of Kolmogorov-Arnold Networks,
the relatively low number of instances must have
impacted the model’s ability to generalize well.
• Higgs Boson Dataset: The performance of the
new architecture is the same as that of the old ar-
chitecture. New and old architecture scores are
still competitive but still fail to beat tree-based
models such as XGBoost and CatBoost.
The results show that the suggested changes sig-
nificantly improve the performance of the Adaptive
Multiscale Deep Neural Network on most datasets,
while at the same time retaining its interpretability
benefits. The slight underperformance on the Heart
Disease and Higgs Boson datasets is likely due to
problem-specific difficulties, as opposed to funda-
mental limitations of the new proposed architecture.
5.2 Impact of Interpretability
Kolmogorov–Arnold Networks (KANs) have a clear
interpretability advantage compared to standard dense
layers. As shown in (Liu et al., 2024), every connec-
tion in the network corresponds to a learnable univari-
ate function, enabling the visualization and investiga-
tion of the routes that input signals take through dif-
ferent layers. Spline-based functions naturally enable
investigation and can be optimized, where necessary,
with techniques like pruning or symbolic fitting.
The Adaptive Multi-Scale Attention Block out-
lined in (Dentamaro et al., 2024) always preserves the
integrity of the original feature set. Specifically, the
recurrent processing of the input before the trainable
attention layer ensures that the subsequent transfor-
mations preserve information relevant to the original
features. Therefore, inspection of the last two dense
layers is instrumental for obtaining a complete under-
standing of the influence that these original features
have on the classification.
A representative case is demonstrated by the ex-
amination of the second KAN layer of the model
learned on the Click dataset. This dataset has 11 in-
put features and a single binary target. Figure 2 shows
the layer after initialization, with each branch having
uniform intensity. While the functions might look su-
perficially equivalent, they contain differences due to
small random fluctuations, which result from the ran-
dom initialization process outlined in the initial paper
regarding Kolmogorov–Arnold networks.
Figure 2: 2nd KAN layer plot after the initialization on
Click-Through Rate (Aden and Wang, 2012).
When the second layer is trained on the Click
dataset, it undergoes a significant change, as can be
seen in Figure 3. Each of the functions has been
adapted to fit the distribution of the data, a fact well
represented by the difference in intensity between the
branches, which represent how much each of the fea-
tures affects the classification. It can be seen that the
seventh feature seems to have the greatest impact, as
represented by the darker branch leading from it to
the output of the layer. This representation well illus-
AMAKAN: Fully Interpretable Adaptive Multiscale Attention Through Kolmogorov-Arnold Networks
805

Table 2: F1-weighted average scores (± standard deviation) on various datasets.
Method Arrhythmia Wisconsin
Breast
Cancer
Cervical
Cancer
Diabetic
Retinopa-
thy
Heart
Disease
Click
Through
Rate
Higgs
Boson
Support Vector
Machines with
RBF
0.486 ±
0.090
0.970 ±
0.010
0.991 ±
0.010
0.704 ±
0.020
0.521 ±
0.060
0.521 ±
0.060
0.764 ±
0.001
Decision Tree 0.646 ±
0.060
0.902 ±
0.030
0.994 ±
0.004
0.611 ±
0.020
0.490 ±
0.050
0.500 ±
0.030
0.716 ±
0.001
Multi Layer
Perceptron
0.634 ±
0.060
0.971 ±
0.010
0.989 ±
0.008
0.706 ±
0.020
0.503 ±
0.070
0.487 ±
0.050
0.761 ±
0.001
Kolmogorov
Arnold Network
0.673 ±
0.070
0.973 ±
0.010
0.992 ±
0.008
0.712 ±
0.020
0.510 ±
0.050
0.533 ±
0.020
0.758 ±
0.002
Random Forest 0.665 ±
0.030
0.948 ±
0.020
0.987 ±
0.010
0.685 ±
0.030
0.525 ±
0.080
0.536 ±
0.060
0.741 ±
0.001
XGBoost 0.675 ±
0.030
0.970 ±
0.008
0.991 ±
0.010
0.694 ±
0.001
0.507 ±
0.050
0.507 ±
0.050
0.774 ±
0.001
TabNet 0.392 ±
0.090
0.935 ±
0.050
0.990 ±
0.010
0.617 ±
0.050
0.464 ±
0.050
0.464 ±
0.050
0.763 ±
0.001
CatBoost 0.664 ±
0.050
0.970 ±
0.020
0.987 ±
0.009
0.682 ±
0.020
0.539 ±
0.050
0.539 ±
0.050
0.769 ±
0.001
Adaptive
Multiscale
Attention - Add
0.679 ±
0.040
0.970 ±
0.004
0.996 ±
0.004
0.740 ±
0.020
0.533 ±
0.050
0.550 ±
0.050
0.769 ±
0.001
Adaptive
Multiscale
Attention - Avg
0.619 ±
0.030
0.970 ±
0.010
0.995 ±
0.005
0.744 ±
0.010
0.535 ±
0.050
0.551 ±
0.050
0.765 ±
0.001
Adaptive
Multiscale
Attention - Mul
0.648 ±
0.004
0.969 ±
0.010
0.995 ±
0.005
0.724 ±
0.010
0.585 ±
0.050
0.609 ±
0.040
0.775 ±
0.001
Adaptive
Multiscale
Attention - Conc
0.630 ±
0.040
0.967 ±
0.010
0.995 ±
0.005
0.723 ±
0.020
0.497 ±
0.050
0.558 ±
0.050
0.766 ±
0.001
Adaptive
Multiscale
Attention With
KANs - Add
0.667 ±
0.083
0.986 ±
0.017
0.996 ±
0.008
0.739 ±
0.027
0.548 ±
0.121
0.582 ±
0.001
0.767 ±
0.003
Adaptive
Multiscale
Attention With
KANs - Avg
0.661 ±
0.077
0.988 ±
0.018
0.996 ±
0.008
0.740 ±
0.027
0.576 ±
0.083
0.591 ±
0.001
0.773 ±
0.002
Adaptive
Multiscale
Attention With
KANs - Mul
0.682 ±
0.077
0.979 ±
0.017
0.997 ±
0.008
0.706 ±
0.029
0.558 ±
0.056
0.615 ±
0.001
0.761 ±
0.002
Adaptive
Multiscale
Attention With
KANs - Conc
0.699 ±
0.075
0.984 ±
0.018
0.993 ±
0.009
0.753 ±
0.032
0.562 ±
0.085
0.589 ±
0.001
0.766 ±
0.002
trates how the spline-based functions are optimized
for the problem at hand, as well as providing an in-
stantaneous way of determining the most relevant in-
puts for the final prediction.
DMDH 2025 - Special Session on Data-Driven Models for Digital Health Transformation
806

Figure 3: 2nd KAN layer plot after the training on Click-
Through Rate (Aden and Wang, 2012).
6 CONCLUSION AND FUTURE
WORK
This paper presents AMAKAN, a fully interpretable
version of the Adaptive Multiscale Deep Neural Net-
work architecture for tabular data classification, re-
placing the last two dense layers of the original model
with Kolmogorov–Arnold Network layers. This en-
hancement takes advantage of the inherent flexibil-
ity of Kolmogorov–Arnold Networks, which replace
fixed activations with spline-based, learnable func-
tions, thereby offering explicit insight into feature
transformations at every stage of the network.
Empirical evaluations conducted over several
datasets demonstrate that the proposed modified ar-
chitecture performs better than the original Adaptive
Multiscale Deep Neural Network in the majority of
the test cases with higher F1-weighted scores. The
rationale behind such improvement is the fact that
the Kolmogorov–Arnold Network layers are adaptive
and thus efficiently learn complicated nonlinear map-
pings of the input data, thus offering a better and more
precise feature representation compared to standard
dense layers.
One of the most important advantages of Kol-
mogorov–Arnold Networks is the increased inter-
pretability. In contrast to dense layers founded on
linear transformations followed by fixed activation
functions, Kolmogorov–Arnold Networks allow one
to utilize visualizable and learnable spline functions,
which are explicit descriptions of complicated non-
linear transformations. This allows to clearly see the
contribution of every feature to predictions with con-
siderably greater transparency.
Looking into the future, several promising direc-
tions for future work have appeared. One direction is
the extension of this hybrid architecture to regression
problems, which may further cement the general use-
fulness and applicability of the method beyond clas-
sification problems. Another direction is the appli-
cation of other interpretability techniques instead of
Kolmogorov–Arnold Networks for the final two lay-
ers, which may yield novel insights and tools, and po-
tentially give a deeper insight into feature relations
and interactions in the data.
Overall, the integration of Adaptive Multiscale
Attention mechanisms with Kolmogorov–Arnold
Networks represents a significant advance towards
fully interpretable, efficient, and effective deep learn-
ing models for the specific needs of tabular data anal-
ysis. The hybrid solution is an attractive direction
of future research that addresses the essential trade-
off between model interpretability and performance
in real-world machine learning applications.
REFERENCES
Aden and Wang, Y. (2012). Kdd cup 2012, track 2. https:
//kaggle.com/competitions/kddcup2012-track2.
Antal, B. and Hajdu, A. (2014). Diabetic Retinopathy De-
brecen. UCI Machine Learning Repository. DOI:
https://doi.org/10.24432/C5XP4P.
Arik, S.
¨
O. and Pfister, T. (2021). Tabnet: Attentive inter-
pretable tabular learning. In Proceedings of the AAAI
conference on artificial intelligence, volume 35, pages
6679–6687.
Aversano, L., Bernardi, M. L., Cimitile, M., Iammarino,
M., and Verdone, C. (2023). A data-aware explain-
able deep learning approach for next activity predic-
tion. Engineering Applications of Artificial Intelli-
gence, 126. Cited by: 7.
Baldi, P., Sadowski, P., and Whiteson, D. (2014). Searching
for Exotic Particles in High-Energy Physics with Deep
Learning. Nature Commun., 5:4308.
Bozorgasl, Z. and Chen, H. Wav-kan: Wavelet
kolmogorov-arnold networks, 2024. arXiv preprint
arXiv:2405.12832.
Breiman, L. (2001). Random forests. Machine learning,
45:5–32.
Chen, T. and Guestrin, C. (2016). Xgboost: A scalable
tree boosting system. In Proceedings of the 22nd acm
sigkdd international conference on knowledge discov-
ery and data mining, pages 785–794.
De Carlo, G., Mastropietro, A., and Anagnostopoulos, A.
(2024). Kolmogorov-arnold graph neural networks.
arXiv preprint arXiv:2406.18354.
Dentamaro, V., Giglio, P., Impedovo, D., Pirlo, G., and
Ciano, M. D. (2024). An interpretable adaptive mul-
tiscale attention deep neural network for tabular data.
IEEE Transactions on Neural Networks and Learning
Systems, pages 1–15.
Dentamaro, V., Impedovo, D., and Pirlo, G. (2018). Licic:
less important components for imbalanced multiclass
classification. Information, 9(12):317.
Dentamaro, V., Impedovo, D., and Pirlo, G. (2021). An
analysis of tasks and features for neuro-degenerative
disease assessment by handwriting. In International
Conference on Pattern Recognition, pages 536–545.
Springer.
AMAKAN: Fully Interpretable Adaptive Multiscale Attention Through Kolmogorov-Arnold Networks
807

Esposito, C., Janneh, M., Spaziani, S., Calcagno, V.,
Bernardi, M. L., Iammarino, M., Verdone, C., Taglia-
monte, M., Buonaguro, L., Pisco, M., Aversano, L.,
and Cusano, A. (2023). Assessment of primary human
liver cancer cells by artificial intelligence-assisted ra-
man spectroscopy. Cells, 12(22). Cited by: 8; All
Open Access, Gold Open Access, Green Open Ac-
cess.
Fernandes, Kelwin, C. J. and Fernandes, J. (2017). Cer-
vical Cancer (Risk Factors). UCI Machine Learning
Repository. DOI: https://doi.org/10.24432/C5Z310.
Galitsky, B. A. (2024). Kolmogorov-arnold network for
word-level explainable meaning representation.
Gattulli, V., Impedovo, D., Pirlo, G., and Semeraro,
G. (2023a). Handwriting task-selection based on
the analysis of patterns in classification results on
alzheimer dataset. In DSTNDS, pages 18–29.
Gattulli, V., Impedovo, D., Pirlo, G., and Volpe, F. (2023b).
Touch events and human activities for continuous
authentication via smartphone. Scientific Reports,
13(1):10515.
Guvenir, H., A. B. M. H. and Quinlan, R. (1997). Ar-
rhythmia. UCI Machine Learning Repository. DOI:
https://doi.org/10.24432/C5BS32.
Janosi, Andras, S. W. P. M. and Detrano, R. (1989). Heart
Disease. UCI Machine Learning Repository. DOI:
https://doi.org/10.24432/C52P4X.
Liu, Z., Wang, Y., Vaidya, S., Ruehle, F., Halverson, J.,
Solja
ˇ
ci
´
c, M., Hou, T. Y., and Tegmark, M. (2024).
Kan: Kolmogorov-arnold networks. arXiv preprint
arXiv:2404.19756.
Luo, H., Cheng, F., Yu, H., and Yi, Y. (2021). Sdtr: Soft
decision tree regressor for tabular data. IEEE Access,
9:55999–56011.
Popov, S., Morozov, S., and Babenko, A. (2019). Neural
oblivious decision ensembles for deep learning on tab-
ular data. arXiv preprint arXiv:1909.06312.
Prokhorenkova, L., Gusev, G., Vorobev, A., Dorogush,
A. V., and Gulin, A. (2018). Catboost: unbiased boost-
ing with categorical features. Advances in neural in-
formation processing systems, 31.
Schmidt-Hieber, J. (2021). The kolmogorov–arnold rep-
resentation theorem revisited. Neural networks,
137:119–126.
Sun, J. Q. (2024). Evaluating kolmogorov–arnold networks
for scientific discovery: A simple yet effective ap-
proach.
Wolberg, William, M. O. S. N. and Street, W.
(1993). Breast Cancer Wisconsin (Diagnos-
tic). UCI Machine Learning Repository. DOI:
https://doi.org/10.24432/C5DW2B.
Xu, K., Chen, L., and Wang, S. (2024). Kolmogorov-arnold
networks for time series: Bridging predictive power
and interpretability. arXiv preprint arXiv:2406.02496.
DMDH 2025 - Special Session on Data-Driven Models for Digital Health Transformation
808