Optimizing Social Consensus: The Impact of Agent Selection and Topic

Strategy on Time to Reach Agreement

Johannes S Vorster

1 a

and Louise Leenen

1,2 b

Department of Computer Science, University of Western Cape, South Africa

CAIR, South Africa

Keywords:

Consensus, Consensus Simulation, Stochastic Simulation, Synchronization, Multi-Agent Simulation.

Abstract:

In the rapidly evolving landscape of organizational structures and project management, achieving timely con-

sensus among team members is crucial for maintaining agility and responsiveness. During the consensus

formation process, team members has the choice of who to talk to in an attempt to consolidate views on a

topic. In this paper we ask the question, to what extent do strategies for selecting team members affect the

speed of consensus formation? Similarly, once two team members engage in conversations on a speciﬁc set

of topics, the question we ask is, to what extent do different strategies for selecting the topics for discussion

affect the time to reach consensus within multi-agent systems. By simulating various strategies, we identify

methods that optimize consensus speed, speciﬁcally highlighting the beneﬁts of prioritizing unaligned agents

and addressing contentious topics early in the process. Our ﬁndings reveal that these strategies signiﬁcantly

enhance consensus efﬁciency, while approaches focusing on aligning with similar views tend to prolong the

process. Additionally, we observe that the initial distribution of agent views, provided the standard deviation

is constant, has negligible effects on consensus time, suggesting that diversity of opinion is more critical than

speciﬁc distribution patterns. These insights offer practical implications for improving decision-making pro-

cesses in organizational and project contexts.

1 INTRODUCTION

1.1 Organizational Context

As technological innovation accelerates, businesses

must adapt their organizational structures and project

delivery methods to remain agile and responsive in

a constantly changing environment. Over the past

two decades, the evolution of organizational struc-

tures and project strategies has become a major topic

in both academia and industry. This discussion is

largely driven by technology companies navigating

the complex interplay of rapid technological advance-

ments, shifting competitive landscapes, and evolv-

ing customer expectations (Reagans et al., 2016;

Keupp et al., 2012; Chang and Harrington, 2000).

Evidence suggests that lateral structures and well-

connected networks offer greater economic value, re-

ﬂected in faster project delivery and reduced resource

use, leading to better investment returns (Will et al.,

https://orcid.org/0000-0001-6452-4186

https://orcid.org/0000-0002-9212-550X

2019). However, project complexity often hampers

consensus-building among team members, causing

delays and failures (Al-Ahmad et al., 2009; Whitney

and Daniels, 2013; Kian et al., 2016; Waheeb and An-

dersen, 2022).

1.2 Consensus Models

Consensus formation in Multi-Agent Systems (MAS)

is a multifaceted challenge, intersecting ﬁelds such as

social sciences, economics, and computational mod-

eling. Traditional methods like the Delphi process

have been complemented by computational models

that simulate consensus dynamics (Yan et al., 2017).

These models draw from social science research on

crowd behavior and voter dynamics (Dunbar, 1998;

Stocker et al., 2001; Leishman et al., 2009). In MAS,

algorithms are designed for high-speed applications,

reﬂecting the need for rapid consensus in dynamic en-

vironments (Amirkhani and Barshooi, 2022).

Vorster, J. S. and Leenen, L.

Optimizing Social Consensus: The Impact of Agent Selection and Topic Strategy on Time to Reach Agreement.

DOI: 10.5220/0013650900003970

In Proceedings of the 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2025), pages 135-144

ISBN: 978-989-758-759-7; ISSN: 2184-2841

135

1.3 Social Settings

The topology and connectivity of social networks sig-

niﬁcantly inﬂuence opinion dynamics and consen-

sus formation. Models such as Erd

os-R

enyi, Watts-

Strogatz, and Barab

asi-Albert provide insights into

how network structures affect the speed and nature

of consensus formation (Erd

os et al., 1960; Watts and

Strogatz, 1998; Barab

asi et al., 2000). These mod-

els highlight the importance of network design in fa-

cilitating or hindering consensus, with complete net-

works often leading to the fastest agreement (Michal-

ski et al., 2022).

1.4 Subversive Agents

The role of subversive agents in consensus processes

has been explored across various domains, reveal-

ing that even a small committed minority can signif-

icantly inﬂuence group dynamics (Xie et al., 2011;

Iacopini et al., 2022). In project teams, subversive

agents can delay consensus by introducing conﬂict-

ing views, underscoring the need for effective man-

agement of dissent and conﬂict (Vorster and Leenen,

2023b).

1.5 Organizational Structure

Organizational structure plays a critical role in con-

sensus formation. Polyarchies, characterized by fully

connected networks, facilitate quicker consensus

compared to hierarchical or hybrid structures (Will

et al., 2019; Vorster and Leenen, 2024a). The choice

of structure impacts not only the speed of decision-

making but also the quality of outcomes, particularly

in innovation and project selection (S

aenz-Royo and

Lozano-Rojo, 2023).

1.6 Our Earlier Work and Motivation

for this Paper

Our previous research has extensively explored the

dynamics of consensus formation within organiza-

tional settings, focusing on various factors that inﬂu-

ence these processes. In Vorster and Leenen (2023a),

we introduced a simulator designed to investigate

consensus within organizations, emphasizing the role

of organizational structure, team dynamics, and arte-

facts. That study highlighted that for a ﬁxed problem

size, consensus could be achieved within a maximum

time frame, independent of the number of agents in-

volved.

Building on that, Vorster and Leenen (2023b) ex-

amined the impact of subversive agents on consensus-

seeking processes. That work revealed how subver-

sive agents, whether engaging in industrial espionage

or acting as disgruntled employees, could subtly de-

lay consensus by inﬂuencing team dynamics without

raising suspicions.

Furthering this exploration, Vorster and Leenen

(2024b) delved into the inﬂuence of subversive agents

on project teams, demonstrating that even a small mi-

nority of such agents could signiﬁcantly extend the

time to reach consensus. This study underscored the

potent inﬂuence of subversive agents in shaping deci-

sion outcomes.

In Vorster and Leenen (2024c), we investigated

the determinants of consensus processes, such as

group size and the role of artefacts. The study found

that artefacts signiﬁcantly reduce consensus time, em-

phasizing their importance in streamlining communi-

cation and collaboration within teams.

Additionally, Vorster and Leenen (2024a) ex-

plored the effectiveness of artefacts and documenta-

tion in facilitating consensus. That research high-

lighted that while polyarchies are efﬁcient at con-

sensus formation, smaller teams with well-structured

artefacts can achieve similar efﬁciency, particularly in

larger organizations where intra-team communication

may cause delays.

These studies collectively contribute to a nuanced

understanding of the factors affecting consensus for-

mation, providing valuable insights for optimizing

decision-making processes in organizational contexts.

This paper investigates the impact of agent se-

lection strategies and topic prioritization on time

to reach consensus. By examining different strate-

gies for selecting discussion topics and agent align-

ment, we aim to identify methods that optimize con-

sensus speed. Our ﬁndings suggest that prioritiz-

ing unaligned agents and discussing topics with the

most differences in views ﬁrst signiﬁcantly improves

consensus efﬁciency. This research contributes to

the broader understanding of consensus dynamics in

organizational and computational contexts, offering

practical insights for enhancing decision-making pro-

cesses.

1.7 This Work: Agent and Topic

Selection Strategies

In this paper we want to investigate two aspects and

the interaction between them; agent selection and

topic selection.

In initial studies mentioned above, agents interact

with other agents at random and do not have a strat-

egy for how to select other agents. In this paper we

investigate two main strategies (a) prioritize selecting

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

136

Topic selection Strategies

(a)

(b)(c) (d)

Frequency [%]

Figure 1: Topic selection strategies: (a) closest same side,

(b) furthest, same side, (c) closest, opposite side, and (d)

furthest, opposite side.

agents that have closely aligned views, and (b) priori-

tize selecting agents with conﬂicting views.

It can be argued that following the ﬁrst strategy is

similar to ﬁrst building a core of support, establish-

ing a large group of agents with a particular view to

portray that view to other agents.

On the other hand, the second strategy, to priori-

tize agents with the furthest views are more aligned

with a philosophy of trying to contain opposing views

and thus restrict the spread of these opposing views as

quickly as possible.

We are interested to see, using our simulation ap-

proach, what the effect of these two strategies are on

the time to reach consensus in a large group where it

is critical that consensus is reached, such as in project

execution (as opposed to social constructs such as

voter views).

An orthogonal aspect of investigation is topic se-

lection; is it better to (a) focus on similar topic, elim-

inating differences quickly and establishing a core of

mutual topics, or (b) focus on trying to address the

topics with highest difference in views ﬁrst.

A second way to look at this variable is for an

agent to select topics based on the relative position

to the group view. Lets say agent i has a view to the

left (or right) of the group’s view on topic k. Would

it be better to ﬁrst select topics where agent j is on

the same side of the issue or is it better to discuss op-

posing topics ﬁrst? Here we identify and investigate

four strategies: (a) prioritise topics on the same side

of the issue and topics closest to the agents views ﬁrst

(Close, same side topics); (b) prioritize topics on the

same side of the issue but with the biggest difference

in views ﬁrst (Furthest, same side topics); (c) opposite

side but closest to the agents own view (Closest, op-

posite view); and (d) opposite view and furthest away

(Furthest, opposite view), see Figure 1 where agent i

has a view close to that of (a).

Here, option (c) aims to pull agents with oppos-

ing views but close to the median view over the line

to ’our side’. Strategy (b) tries to prevent this from

happening to agents on ’our team’. Strategy (d) aims

to address the ’radicals’ on the opposite side ﬁrst and

strategy (a) aims to consolidate and build out the core

of support.

Our approach is to set up two sets; one with nine

experiments (three options on each axis of a two-

variable matrix). Axis one is the agent selection strat-

egy: Random strategy, agents with highest difference

in views ﬁrst, and agents with lowest difference in

views ﬁrst. On the second axis is the topic selection

strategy, with similar three options. And the other set

with twelve experiments, where the second axis cov-

ers the four options mentioned above.

2 METHODOLOGY AND

TERMINOLOGY

This section outlines the methodology and terminol-

ogy used in our study, focusing on the simulation

setup, agent interactions, and consensus measure-

ment. A detailed discussion of topics related to the

simulation and simulator can be found in Vorster and

Leenen (2023a).

2.1 Teams and Topics

The simulation involves two teams: the speciﬁcation

team (team a) and the implementation team (team b).

Team a consists of

N agents, and team b consists of

N agents, with

N ≪

N. Each agent tracks a num-

ber of topics, with team a considering

max

topics

and team b considering

max

topics. The ﬁrst

max

topics are common to both teams, requiring consensus

between both teams.

2.2 Artefacts

Topics are encoded in speciﬁcation artefacts, which

map one-to-one with the topics tracked by team a.

The speciﬁcation contains

max

topics. If an arte-

fact contains fewer topics than discussed by agents

(

max

), the ﬁrst

max

topics coincide with

the artefact’s topics, allowing for the modelling of in-

complete artefacts.

2.3 Agent Connectivity and Meetings

Agents interact based on a connectivity graph mod-

elled as a directed graph. Each agent can only meet

with directly connected agents. Meetings last 30 min-

utes, allowing up to 16 meetings per day. The number

of topics discussed per meeting is determined stochas-

tically, ranging from one to ten. Outcomes for each

Optimizing Social Consensus: The Impact of Agent Selection and Topic Strategy on Time to Reach Agreement

137

topic include compromise consensus, one agent con-

vincing the other, or vice versa. The pseudo-Python

code for meetings between agents i and j is:

random.shuffle(topics)

issuesToDiscuss=randint(1,11)

for k in topics:

if agent[i].view[k]==agent[j].view[k]:

continue

rnd = randint(0,3)

if (rnd==0):

val = int((agent[i].view[k]

+ agent[j].view[k]))/2.0)

agent[i].view[k]=agent[j].view[k]=val

if (rnd==1):

agent[j].view[k] = agent[i].view[k]

if (rnd==2):

agent[i].view[k] = agent[j].view[k]

issuesToDiscuss-=1#

if issuesToDiscuss<=0:

break

2.4 Working on Artefacts

Agents can interact with artefacts within a 30-minute

time-slot, selecting a random number of topics, from

one to ten, where disagreement exists between agent’s

views and the artefacts position. Outcomes include

partial or full internalization of the artefact’s view or

modifying the artefact to reﬂect the agent’s view.

2.5 Measuring Consensus

Consensus is measured using absolute differences be-

tween views (b) on topics (k). For agents i and j, and

artefacts p, the consensus measure for a speciﬁc topic

(k) is:

i j

= δ

i j

− b

= δ

− c

where δ

i j

is a coefﬁcient of understanding each other,

and is taken as δ

i j

= 1 here. The overall consensus for

an agent i over all agents (I

) and all artefacts (I

) for

a speciﬁc topic k is:

∑

j∈I

i j

− b

| +

∑

p∈I

− c

The total difference in views between two agents

on all topics is given by

i j

max

∑

k=1

i j

− b

| (1)

The total consensus across all agents and artefacts

is:

u =

∑

i∈I

∑

j∈I

max

∑

k=1

i j

− b

| +

∑

i∈I

∑

p∈I

max

∑

k=1

− c

This measure (u) and its log is what will be used

to measure the level and extent to which a group has

reached consensus.

2.6 Time and Effort to Reach

Consensus

Agents record their actions in a diary. The effort e

max

to reach consensus is the sum of all actions taken:

max

∑

t=1

∑

i=1

busy(d

)

where busy(d

) = 1 if an action is taken, and 0 oth-

erwise. The simulation stops, after t

max

steps, when

no further actions are taken. We are interested in t

max

(averaged over may simulations) for the various sce-

narios under investigation.

2.7 Meeting Efﬁciency

Meeting efﬁciency is measured by the average num-

ber of topics discussed per meeting. If ¯z(t) is the ob-

served average and ¯z

max

is the maximum expected, ef-

ﬁciency at time t is:

e(t) =

¯z(t)

¯z

max

2.8 Strategy Notation

There are two dimensions to the strategy that an agent

(i) can follow. Firstly the selection of agents to meet

with, which we can denote as Strategy (Agents=far)

for the the strategy of prioritizing agents with over-

all views that are far from the current agent’s views,

that is, agents ( j) where the consensus measure (u

i j

eq. (1)) is relatively large. Three strategies are

considered namely Strategy (Agents=far), Strategy

(Agents=near), and Strategy (Agents=random).

Similarly and independently from the agent selec-

tion strategy an agent can also have a strategy for the

topics that will be discussed in a meeting. Such strate-

gies can be denoted with Strategy (topics=random),

Strategy (topics=Far), and Strategy (topics=Near) for

the three strategies we are considering, where top-

ics=Far denotes a strategy where agents will priori-

tize topics k where |b

− b

| is large relative to other

topics.

An agent’s overall strategy will consist of having

a strategy for agent selection and a strategy for topic

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

138

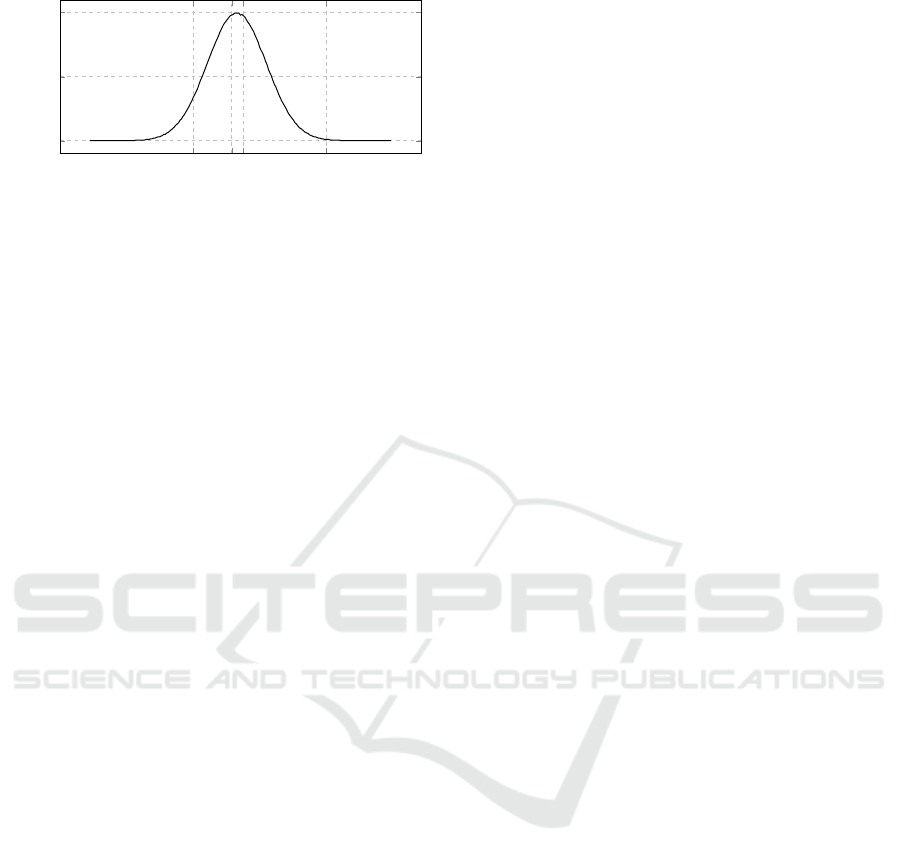
Initial View Histogram

µ − σ

µ + σ

Frequency [%]

Normal

Uniform

Dual-Uniform

Asymetric-Uniform

Figure 2: The distributions used for initial views are: Nor-

mal, Uniform, Dual-Uniform, and Asymetric-Uniform as

shown in the ﬁgure. Each distribution is carefully selected

so that σ=constant=100, for all distributions.

selection, and the combination can therefore be indi-

cated using the same notation, for example Strategy

(agents=random, topics=random).

Next, we move on to the topic of strategies for

agent selection and topic selection. Equation (1) pro-

vide a mechanism for an agent to calculate a consen-

sus measure between it and another agent, and thus an

agent can select the agent with the smallest or largest

such value in order to implement the two strategies (a)

best aligned agent ﬁrst, and (b) furthest aligned agent

ﬁrst.

Similarly agent i can ﬁnd a topic k, such that |b

−

| is the smallest (non-zero) value among the topics

m ∈ {1 to B

max

} for which they are not in agreement.

2.9 Mathematical Model Summary

Key concepts include:

• b

: The view that agent i has on a speciﬁc topic k.

• u

: Consensus on a speciﬁc topic k for agent i.

• u

i j

: Consensus between two agents i and j on all

topics.

• u: Overall consensus measure.

• t

max

: Time to reach consensus.

• e

max

: Effort to reach consensus.

• Strategy (agents=X, topics=Y): A strategy that

prioritizes agents using an agent selection strat-

egy X based on the consensus measure u

i j

, and

a strategy Y for selecting topics to discuss within

meetings based on the measure |b

− b

This methodology provides a framework for

analysing consensus dynamics in multi-agent

systems.

3 SCENARIO CONFIGURATIONS

Agents are initialized with random views on each

of the topics using a speciﬁc distribution. Currently

Normal, Uniform, Dual-Uniform, and Asymmetric-

Uniform are supported, see Figure 2.

A simulation consists of agents meeting in 30

minute sessions where they discuss topics according

the the rules explained above. This continue until all

agents are satisﬁed that they have reached consensus

on all topics with all other agents in their connectiv-

ity network. The number of time-steps that it takes

to reach this state is noted. The exponential decrease

in the consensus measure (u) can be seen as one of

the grey plots in Figure 3. Over many such iterations

averages and standard deviations can be computed, as

shown in the ﬁgure.

Although not the primary focus of this study,

Vorster and Leenen (2023a), pointed out that the con-

sensus process may be dependent on the distribution

of initial views and in that work the mathematical

model was worked out based on a Normal distribution

of initial views. However, the question remained open

and in the ﬁrst part of this work we want to address it

by modelling various initial distributions, see Figure

2. Through that work, it was assumed that the consen-

sus process, in particular how long it takes, is depen-

dent on the standard deviation of the distribution in

the absense of other information. Here we measure

the time to reach consensus for Normal, Uniform,

Dual-Uniform, and Asymmetric-Uniform as shown in

the future. In all these distributions we take care to use

the same mean and sigma in the initial view distribu-

tions.

For example to correctly compute the distribution

of the Asymmetric-Uniform distribution, we selected

the distribution width of the left portion (50 in this

case) and compute what the right-hand portion should

be to give the correct sigma (σ = 100). To ensure

we have not made mistakes in the mathematical cal-

culations or in the Python implementation we simu-

lated stochastically two million distribution calcula-

tions to ensure correctness, with results Normal (σ =

100.05, n=2M), Uniform (σ = 100.00, n=2M), Dual-

Uniform (σ = 99.98, n=2M), Asymmetric-Uniform

(σ = 100.03, n=2M).

The outcome of these simulations are shown in

Figure 4. The effect of initial views are negligible

as can be seen from the (bottom) graphs showing the

difference between the outcome of these distributions

relative to the Normal distribution. This is somewhat

of a surprising results since it then implies that the

time to reach consensus is independent of the dis-

tribution of initial views, but only dependent on the

Optimizing Social Consensus: The Impact of Agent Selection and Topic Strategy on Time to Reach Agreement

139

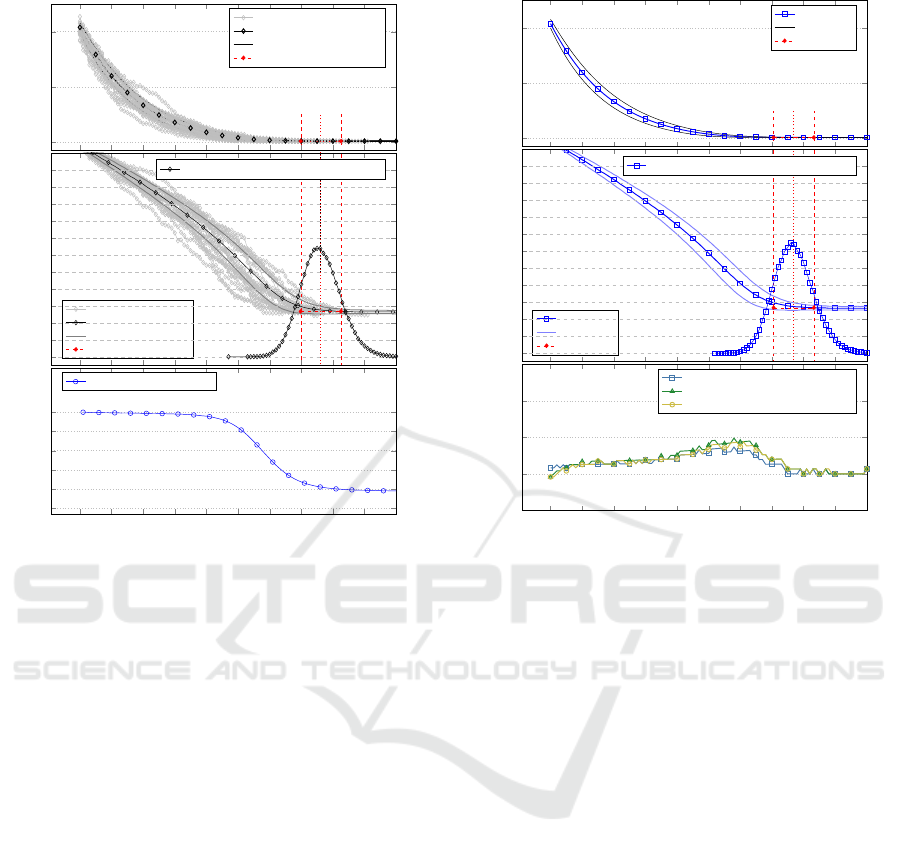
Consensus-reaching processes

·10

Consensus (u)

Consensus for 20 simulations

Averaged Consensus

1σ

max

1σ

Consensus (logu)

logu for 20 simulations

logu averaged

1σ

max

1σ

Histogram [%]

Histogram of t

max

(IV=Normal) N (76.2, 6.36)

0 10 20 30 40

50 60

70 80 90 100

100

Time (t

max

)

Meeting efﬁciency [%]

Topics discussed per meeting

Figure 3: (Top) Various simulations of the 10-group show-

ing the consensus measure (u) over time. (Middle) The same

data as in top graph, but now using log

(consensus). His-

togram of the time it takes to reach consensus over many

such runs (µ = 76.2, σ = 6.36, n=200000). (Bottom) Meet-

ing effectiveness graphs for the two groups.

standard-deviation of views, rather than the type of

distribution, at least for the set of distributions we

have used. This was not predicted in the construction

of the initial mathematical model published in Vorster

and Leenen (2023a) and in future work it would be

worth re-visiting that model and simplifying it using

the ﬁndings from this study.

The simulator is written in Python, and the general

architecture is such that a scenario consisting of a set

of parameters is registered with the simulation class

which manages the execution of scenarios. Many sce-

narios can be registered in sequence before the simu-

lations start.

The scenario parameters include the number of

agents involved, artefacts involved, team structure and

communications channels between agents, the num-

ber of topics under discussion, the distributions used

for initial views of agents, and the agent and topic se-

lection strategies that will be used. Finally, the total

number of simulations that will be executed per sce-

nario parameter is speciﬁed (n=20000 in this case).

The simulator is multi-threaded, each threat ex-

ecutes a speciﬁc scenarios repeatedly for a set time

Effect of Distributionss

·10

Consensus (u)

IV=Uniform

1σ

max

1σ

Consensus (logu)

IV=Uniform

1σ

max

1σ

Histogram [%]

Histogram of t

max

(IV=Uniform) N (76.9, 6.37)

0 10 20 30 40

50 60

70 80 90 100

−1

Time (t

max

)

Log(u) difference [%]

Uniform vs Normal (diff.%)

Dual-Uniform vs Normal (diff.%)

Asymetric-Uniform vs Normal (diff.%)

Figure 4: (Top) Various simulations of the 10-group show-

ing the consensus measure over time when the initial dis-

tribution of views are Uniform. (Middle) The same data as

in top graph, but now using log

(consensus). Histogram of

the time it takes to reach consensus over many such runs

(µ = 76.9, σ = 6.37, n=200000). (Bottom) A difference plot

to highlight the impact of initial view on the consensus pro-

ﬁle.

(usually 60 seconds) and once that time is reached the

thread terminates after the current scenario has ﬁn-

ished execution. Results are appended to various logs.

Every few minutes (30 in the default conﬁguration)

the logs are processed and statistics are calculated for

the results ﬁles. The results ﬁles are such that they

can be directly processed in this L

Xdocument.

Various progress ﬁles are kept up to date so that

simulations can be stopped at any time and re-started

later without the loss of data and very importantly

time.

4 RESULTS

Figure 5 shows the results from the simulations. The

top left plot shows that scenario where agent and topic

selection is completely random and this scenario also

acts as the baseline to compare the other scenarios

against. For this scenario it takes on average 498.32

(σ = 59.80, n = 400000) time steps to reach consen-

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

140

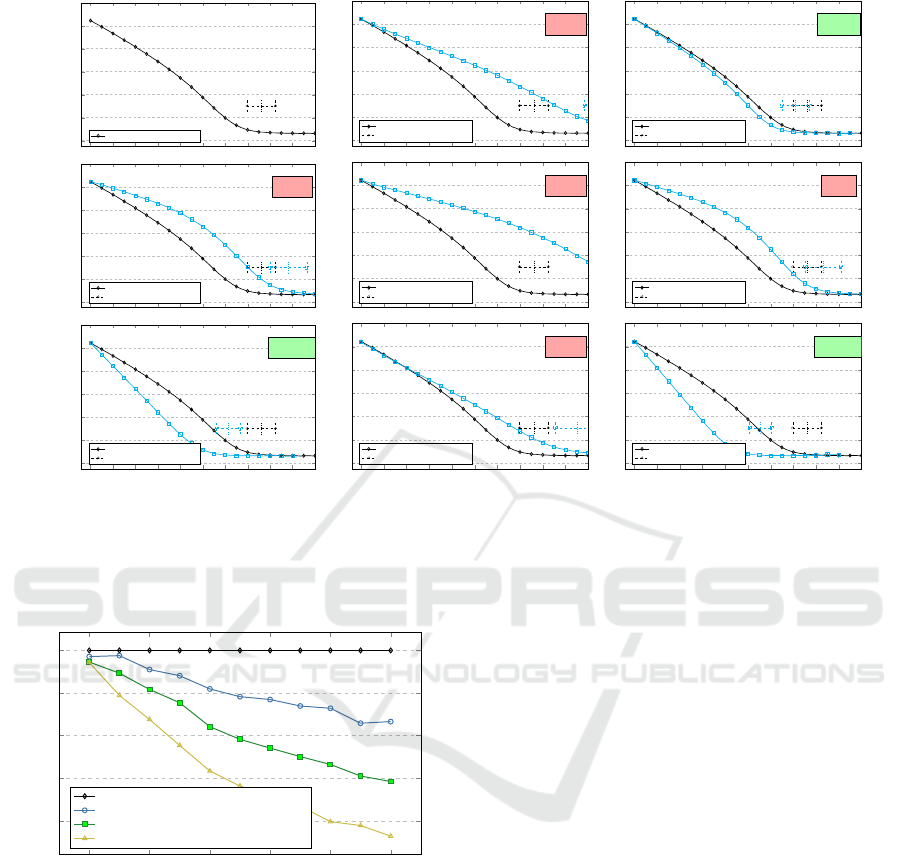
Strategy (agents=random) Strategy (agents=near) Strategy (agents=far)

(topics=random)

Consensus (logu)

agents=random, topics=random

44,5%

agents=random, topics=random

agents=near, topics=random

−6,7%

agents=random, topics=random

agents=far, topics=random

(topics=near)

15,9%

Consensus (logu)

agents=random, topics=random

agents=random, topics=near

62,9%

agents=random, topics=random

agents=near, topics=near

9,2%

agents=random, topics=random

agents=far, topics=near

(topics=far)

−19,3%

Consensus (logu)

agents=random, topics=random

agents=random, topics=far

25,1%

agents=random, topics=random

agents=near, topics=far

−27,1%

agents=random, topics=random

agents=far, topics=far

Figure 5: Agent selection strategies are presented on the horizontal axis and topic selection strategies on the vertical axis. The

black (diamond) plots are the baseline (random agent selection and random topic selection) against which the other strategies

are measured. Each strategy combination also shows the percentage improvement as measured against this baseline. Green

(negative percentage) indicate faster time to reach consensus and a red (positive percentage) indicate longer time to reach

consensus.

% of agents following strategy

0 20 40

80 100

−40

−30

−20

−10

Time to reach Consensus

Strategy: random agents, random topics

Strategy unaligned agents, random topics

Strategy random agents, opposing views ﬁrst

Strategy unaligned agents, opposing views ﬁrst

Figure 6: The effect of number of agents in the group on

the time to reach consensus relative to the random agents,

random topics strategy.

sus. The speciﬁc number of time-steps are not rele-

vant, but the relative difference as shown in the graphs

are the measure we employ for comparison.

First let us discuss the strategies where agents opt

to ﬁrst align with agents that are already close in terms

of their views, Strategy (agents=near), middle col-

umn of Figure 5). All these strategies show a sig-

niﬁcant increase in time to reach consensus Strategy

(topics=random) +44,5%, (topics=near) +62,9 %, and

(topics=far) +25,1%.

Similarly, Strategies (topics=near), middle row

in ﬁgure Figure 5, show increases in time to reach

consensus of +15,9 %, +62,9%, and +9,2 % for

(agents=random), (agents=near), and (agents=far) re-

spectively.

The strategies that lead to improvements in time

to reach consensus are to prioritize unaligned agent

(agents=far), opposing views (topics=far), or both,

with 6,7%, 19,3%, and 27,1 % improvements respec-

tively.

To understand how these results change with the

percentage of agents following the strategy (as op-

posed to random), we ran a large number of exper-

iments (n=400000 per point) with 100 agents in the

group, and varying the number of agents that follow a

speciﬁc strategy. We report here only on the strategies

that improve time to reach consensus.

There results are shown in Figure 6 and from in-

spection of these graphs, are only approximately lin-

ear. It shows that the more agents follow the strategy

the bigger the results, as expected.

Finally, we want to further explore the topic selec-

tion strategy and in particular if there is a difference

in prioritizing members on the same side of an issue

ﬁrst versus the above strategy of far and near classi-

ﬁcations. To do this we deﬁne four topic-selection

strategies based on if the two agents are one the ’same

side’ of an issue versus on the opposite side and if

their views are near or far from each other.

Optimizing Social Consensus: The Impact of Agent Selection and Topic Strategy on Time to Reach Agreement

141

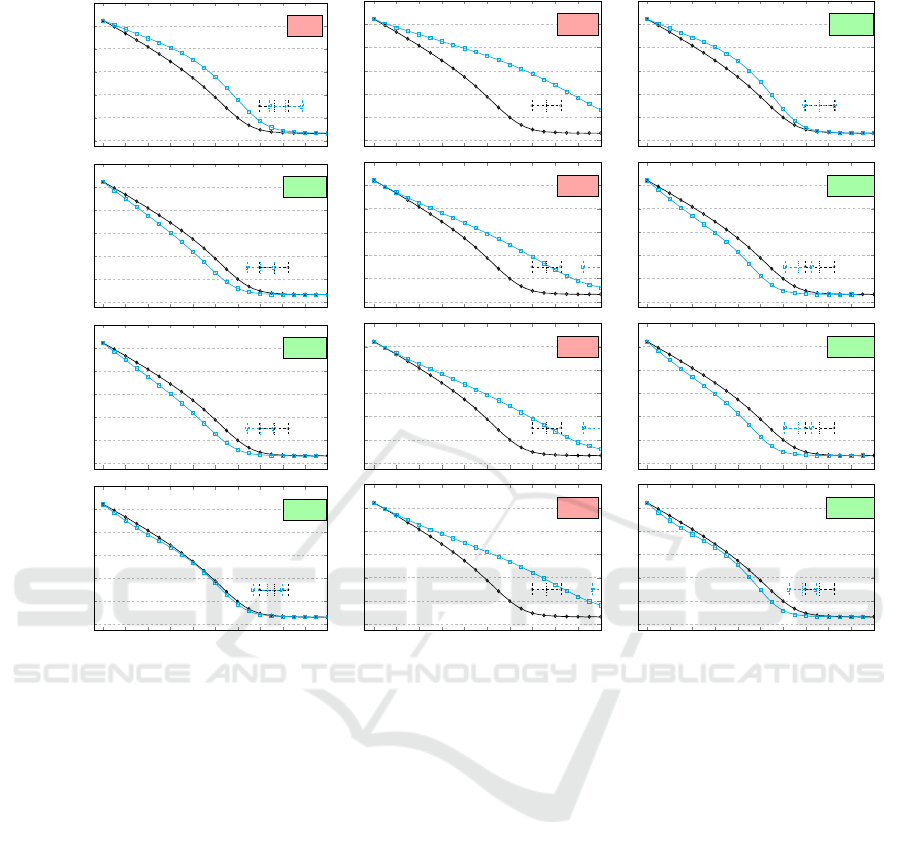
Strategy (agents=random) Strategy (agents=near) Strategy (agents=far)

topics=near,

same side

7,0%

Consensus (logu)

53,7%

−0,1%

topics=far,

opposite side

−7,8%

Consensus (logu)

35,3%

−12,5%

topics=far,

same side

−7,9%

Consensus (logu)

35,3%

−12,6%

topics=near,

opposite side

−3,8%

Consensus (logu)

41,9%

−1 0,0 %

Figure 7: Agent selection strategies are presented on the horizontal axis and topic selection strategies on the vertical axis. The

black (diamond) plots are the baseline (random agent selection and random topic selection) against which the other strategies

are measured. Each strategy combination also shows the percentage improvement as measured against this baseline. Green

(negative percentage) indicate faster time to reach consensus and a red (positive percentage) indicate longer time to reach

consensus.

The results are shown in Figure 7 and indicate that

(agents=far) Strategies dominate any other agent se-

lection strategy.

However, the interesting part is comparing the re-

sults from Figure 7 to that of Figure 5. In particular it

seem that broadly prioritizing far agents irrespective

of perceptions of ’side’ (topics=far, agents=random,

−19,3% in Figure 5) is better than selecting agents

based on perceptions of side (topics=far opposite side,

−7,8%, and topics=far same side, −7,9% in Figure

7).

5 DISCUSSION

5.1 Interpretation of Results

Our ﬁndings indicate that strategies prioritizing un-

aligned agents and opposing views signiﬁcantly en-

hance consensus efﬁciency. Speciﬁcally, the strategy

of selecting agents with the most divergent views and

discussing topics with the greatest differences ﬁrst re-

sulted in the most improvement in time to reach con-

sensus compared to random strategies. This suggests

that addressing the most contentious issues early can

streamline the consensus process by preventing the

entrenchment of opposing views and is a superiour

strategy to ﬁrst building a core of support. Strategies

that focused on aligning with agents already close

in views or discussing similar topics ﬁrst led to in-

creased time to reach consensus. This outcome high-

lights the potential inefﬁciency of reinforcing existing

agreements without addressing underlying conﬂicts.

It is important to address issues that have a high

difference in views early irrespective of perceptions

of ’side’. The results clearly show that ignoring far

from the norm views within perceived ’same’ side

team members can still extend the time to reach con-

sensus and a better strategy is to address issues irre-

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

142

spective of perceived membership sides.

5.2 Implications for Organizational

Practice

These results have practical implications for project

management and organizational decision-making. In

environments where rapid consensus is critical, such

as in project execution, prioritizing engagement with

dissenting opinions and contentious topics can expe-

dite decision-making processes. This approach may

also foster a more inclusive environment by ensur-

ing that diverse perspectives are considered and in-

tegrated early in the decision-making process.

5.3 The Role of Initial View

Distributions

Interestingly, our study found that the initial distribu-

tion of agent views (whether normal, uniform, dual-

uniform, or asymmetric-uniform) had negligible ef-

fects on the time to reach consensus, provided the

standard deviation was constant. This suggests that

the diversity of initial opinions, rather than their spe-

ciﬁc distribution, is a more critical factor in consen-

sus dynamics. This ﬁnding challenges traditional as-

sumptions and suggests new avenues for simplifying

mathematical models of consensus processes.

5.4 Limitations and Future Research

While our study provides valuable insights, it is not

without limitations. The simulations were conducted

in a controlled environment with speciﬁc assump-

tions about agent behaviour and interaction. Future

research could explore more complex models incor-

porating factors such as dynamic network topologies,

varying levels of agent inﬂuence, and real-world con-

straints.

Additionally, the impact of subversive agents on

consensus processes warrants further investigation.

Understanding how these agents can be managed or

mitigated could provide further improvements in con-

sensus efﬁciency.

6 CONCLUSION AND FUTURE

WORK

Earlier research on the causes of project failures, de-

lays, and cost overruns have identiﬁed lack of con-

sensus as one of the key contributing factors. The

consensus formation process is time-consuming, and

often left out of project planning or its effort is under-

estimated.

In this study, we explored the impact of agent se-

lection and topic prioritization strategies on the ef-

ﬁciency of consensus formation within multi-agent

systems. Our ﬁndings indicate that strategies prior-

itizing unaligned agents and contentious topics en-

hance the speed of reaching consensus. Speciﬁcally,

engaging with agents holding divergent views and ad-

dressing the most contentious issues early in the pro-

cess can streamline consensus-building by prevent-

ing the entrenchment of opposing views. Conversely,

strategies focusing on aligning with agents already

close in views or discussing similar topics ﬁrst tend

to prolong the consensus process and is a less efﬁcient

strategy.

These insights have practical implications for or-

ganizational decision-making and project manage-

ment. By prioritizing engagement with dissenting

opinions and contentious topics, organizations can ex-

pedite decision-making processes and foster a more

inclusive environment that integrates diverse perspec-

tives early on. Furthermore, our study reveals that the

initial distribution of agent views, provided the stan-

dard deviation remains constant, has negligible effects

on the time to reach consensus. This suggests that the

diversity of initial opinions is more critical than their

speciﬁc distribution, challenging traditional assump-

tions and offering new avenues for simplifying math-

ematical models of consensus processes.

Despite the valuable insights gained, this study is

not without limitations. The simulations were con-

ducted in a controlled environment with speciﬁc as-

sumptions about agent behavior and interaction. Fu-

ture research could explore more complex models in-

corporating dynamic network topologies, varying lev-

els of agent inﬂuence, and real-world constraints. Ad-

ditionally, the role of subversive agents in consensus

processes warrants further investigation. Understand-

ing how these agents can be managed or mitigated

could provide further improvements in consensus ef-

ﬁciency.

Future work could also focus on developing adap-

tive strategies that dynamically adjust agent and topic

selection based on real-time feedback from the con-

sensus process. Exploring the integration of machine

learning techniques to predict and optimize consensus

pathways could offer signiﬁcant advancements in the

ﬁeld.

Optimizing Social Consensus: The Impact of Agent Selection and Topic Strategy on Time to Reach Agreement

143

REFERENCES

Al-Ahmad, W., Al-Fagih, K., Khanfar, K., Alsamara, K.,

Abuleil, S., and Abu-Salem, H. (2009). A taxonomy

of an it project failure: root causes. International

Management Review, 5(1):93.

Amirkhani, A. and Barshooi, A. H. (2022). Consensus in

multi-agent systems: a review. Artiﬁcial Intelligence

Review, 55(5):3897–3935.

Barab

asi, A.-L., Albert, R., and Jeong, H. (2000). Scale-

free characteristics of random networks: the topology

of the world-wide web. Physica A: statistical mechan-

ics and its applications, 281(1-4):69–77.

Chang, M.-H. and Harrington, J. E. (2000). Centralization

vs. decentralization in a multi-unit organization: A

computational model of a retail chain as a multi-agent

adaptive system. Management Science, 46(11):1427–

1440.

Dunbar, R. I. (1998). The social brain hypothesis. Evo-

lutionary Anthropology: Issues, News, and Reviews:

Issues, News, and Reviews, 6(5):178–190.

Erd

os, P., R

enyi, A., et al. (1960). On the evolution of

random graphs. Publ. Math. Inst. Hung. Acad. Sci,

5(1):17–60.

Iacopini, I., Petri, G., Baronchelli, A., and Barrat, A.

(2022). Group interactions modulate critical mass

dynamics in social convention. Communications

Physics, 5(1):64.

Keupp, M. M., Palmi

e, M., and Gassmann, O. (2012). The

strategic management of innovation: A systematic re-

view and paths for future research. International jour-

nal of management reviews, 14(4):367–390.

Kian, M. E., Sun, M., and Bosch

e, F. (2016). A consistency-

checking consensus-building method to assess com-

plexity of energy megaprojects. Procedia-social and

behavioral sciences, 226:43–50.

Leishman, T. G., Green, D. G., and Driver, S. (2009).

Self-organization in simulated social networks. In

Computer-Mediated Social Networking: First Inter-

national Conference, ICCMSN 2008, Dunedin, New

Zealand, June 11-13, 2008, Revised Selected Papers,

pages 150–156. Springer.

Michalski, R., Serwata, D., Nurek, M., Szymanski, B. K.,

Kazienko, P., and Jia, T. (2022). Temporal network

epistemology: On reaching consensus in a real-world

setting. Chaos: An Interdisciplinary Journal of Non-

linear Science, 32(6).

Reagans, R., Miron-Spektor, E., and Argote, L. (2016).

Knowledge utilization, coordination, and team perfor-

mance. Organization Science, 27(5):1108–1124.

aenz-Royo, C. and Lozano-Rojo, A. (2023). Authoritar-

ianism versus participation in innovation decisions.

Technovation, 124:102741.

Stocker, R., Green, D. G., and Newth, D. (2001). Consensus

and cohesion in simulated social networks. Journal of

Artiﬁcial Societies and Social Simulation, 4(4).

Vorster, J. and Leenen, L. (2023a). Consensus simulator for

organisational structures. In Proceedings of the 13th

International Conference on Simulation and Modeling

Methodologies, Technologies and Applications, pages

15–26.

Vorster, J. and Leenen, L. (2023b). Exploring the effects of

subversive agents on consensus-seeking processes us-

ing a multi-agent simulator. In Proceedings of the 13th

International Conference on Simulation and Modeling

Methodologies, Technologies and Applications, pages

104–114.

Vorster, J. and Leenen, L. (2024a). The unreasonable ef-

fectiveness of artefacts and documentation: An explo-

ration of consensus using multi-agent simulations in

a two-team conﬁguration. In Proceedings of the 14th

International Conference on Simulation and Model-

ing Methodologies, Technologies and Applications –

SIMULTECH, pages 313–323.

Vorster, J. S. and Leenen, L. (2024b). Exploring the im-

pact of subversive agents on consensus processes in

project teams: Multi-agent simulations. In Wagner,

G., Werner, F., and De Rango, F., editors, Simula-

tion and Modeling Methodologies, Technologies and

Applications, pages 29–60, Cham. Springer Nature

Switzerland.

Vorster, J. S. and Leenen, L. (2024c). Stochastic consen-

sus simulation fororganizational cooperation. In Wag-

ner, G., Werner, F., and De Rango, F., editors, Simula-

tion and Modeling Methodologies, Technologies and

Applications, pages 139–173, Cham. Springer Nature

Switzerland.

Waheeb, R. A. and Andersen, B. S. (2022). Causes of prob-

lems in post-disaster emergency re-construction pro-

jectsiraq as a case study. Public Works Management

& Policy, 27(1):61–97.

Watts, D. J. and Strogatz, S. H. (1998). Collective dynamics

of small-world networks. Nature.

Whitney, K. M. and Daniels, C. B. (2013). The root cause

of failure in complex it projects: Complexity itself.

Procedia Computer Science, 20:325–330.

Will, M. G., Al-Kfairy, M., and Mellor, R. B. (2019). How

organizational structure transforms risky innovations

into performance–a computer simulation. Simulation

Modelling Practice and Theory, 94:264–285.

Xie, J., Sreenivasan, S., Korniss, G., Zhang, W., Lim,

C., and Szymanski, B. K. (2011). Social consensus

through the inﬂuence of committed minorities. Phys-

ical Review E, 84(1):011130.

Yan, H.-B., Ma, T., and Huynh, V.-N. (2017). On qualitative

multi-attribute group decision making and its consen-

sus measure: A probability based perspective. Omega,

70:94–117.

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

144