Fuzzy Requirements Veriﬁcation in SysML v2: Direct Modeling and

Scenario-Based Analysis for Cyber-Physical Systems

Adel Khelifati

1 a

, Malika Boukala-Ioualalen

1 b

and Ahmed Hammad

2 c

Faculty of Computer Science, USTHB University, Algiers, Algeria

FEMTO-ST Institute, UMR CNRS 6174, Besanc¸on, France

Keywords:

SysML v2, Fuzzy Logic, Soft Requirements.

Abstract:

Cyber-physical systems (CPS) often involve vague or qualitative requirements such as comfort or energy efﬁ-

ciency, which are difﬁcult to verify using the crisp Boolean logic traditionally employed in Systems Modeling

Language v2 (SysML v2). This paper introduces an approach for modeling and verifying fuzzy requirements

directly within SysML v2 without modifying its metamodel or relying on external tools. Fuzzy semantics are

encoded using native constructs such as calculation deﬁnitions, requirements, and constraints, with satisfac-

tion degrees computed via trapezoidal membership functions and evaluated using the native expression evalu-

ation mechanism provided by the modeling environment. We illustrate the effectiveness and feasibility of our

expression-based fuzzy veriﬁcation approach using a smart building Heating, Ventilation, and Air Condition-

ing (HVAC) system example and clearly show how the modeling is achieved in standard SysML v2 notation.

Furthermore, to extend veriﬁcation capability under variability and uncertainty, we introduce a complemen-

tary external transformation of expression-based model elements into Python scripts to perform scenario-based

evaluation. A batch-based exploration method is then presented to systematically analyze fuzzy requirement

satisfaction under different runtime conditions, offering insights into system robustness and design-space anal-

ysis.

1 INTRODUCTION

Cyber-physical systems (CPS) are increasingly preva-

lent in modern engineering, encompassing systems

that tightly couple software components with physi-

cal processes. They are critical in intelligent trans-

portation, energy management, aerospace, industrial

automation, and smart buildings. These systems

must satisfy a broad spectrum of functional and

non-functional requirements, including safety, perfor-

mance, reliability, and more qualitative aspects such

as comfort, usability, or energy efﬁciency. Many of

these requirements are inherently imprecise, context-

dependent, or subjective. For instance, a ”comfort-

able temperature” or ”low power usage” is not strictly

deﬁned but varies across users, contexts, and opera-

tional conditions.

Model-Based Systems Engineering (MBSE) pro-

vides a framework to manage the complexity of CPS

https://orcid.org/0009-0006-4522-8123

https://orcid.org/0000-0002-8713-4997

https://orcid.org/0000-0003-3739-1650

by enabling formalized system speciﬁcation, trace-

ability, and early-stage analysis. Within MBSE,

the Systems Modeling Language (SysML) (Object

Management Group (OMG), 2012), maintained by

the Object Management Group (OMG), has become

a widely adopted standard. The recent evolution

to SysML v2 (Object Management Group (OMG),

2024) introduces signiﬁcant improvements in seman-

tic precision, modularity, and expressiveness, along

with a formal textual syntax that supports native ex-

pression evaluation and analysis.

However, despite these advancements, exist-

ing veriﬁcation mechanisms in SysML v2 remain

grounded in classical Boolean logic. Requirements

are typically evaluated as either completely satisﬁed

or entirely violated. This binary interpretation is in-

sufﬁcient when dealing with soft requirements, where

partial compliance is expected and acceptable. Con-

sequently, system engineers are limited in their ability

to express and evaluate degrees of satisfaction, lead-

ing to a potential mismatch between stakeholder ex-

pectations and formal system veriﬁcation.

To address this limitation, we propose an ap-

422

Khelifati, A., Boukala-Ioualalen, M. and Hammad, A.

Fuzzy Requirements Veriﬁcation in SysML v2: Direct Modeling and Scenario-Based Analysis for Cyber-Physical Systems.

DOI: 10.5220/0013648400003964

In Proceedings of the 20th International Conference on Software Technologies (ICSOFT 2025), pages 422-429

ISBN: 978-989-758-757-3; ISSN: 2184-2833

proach that integrates fuzzy logic (Zadeh, 1965) into

SysML v2 models for the expression-based speciﬁ-

cation and evaluation of fuzzy requirements. Our

method leverages only native elements of SysML v2,

such as calc def, requirement, attribute, and

constraint to deﬁne fuzzy semantics, without mod-

ifying the metamodel. Using trapezoidal membership

functions, we compute satisfaction degrees as real

values in the range [0, 1], enabling ﬁne-grained veriﬁ-

cation of vague or context-sensitive requirements di-

rectly within the model. Standard constraint mecha-

nisms can assert these satisfaction degrees, providing

partial, traceable, and explainable veriﬁcation.

In addition to in-model veriﬁcation, we extend our

approach with a complementary batch-based analysis

mechanism. This extension allows engineers to ex-

plore how fuzzy requirement satisfaction evolves un-

der varying operational scenarios, such as changes in

environmental conditions or system usage patterns.

While our core method operates entirely within the

SysML v2 environment, the batch extension exports

model elements involving expressions to an exter-

nal Python script that simulates multiple conﬁgura-

tions and assesses robustness through statistical anal-

ysis. This two-tiered process combines the rigor of

expression-based modeling with the ﬂexibility of sce-

nario exploration.

The main contributions of this paper are as fol-

lows:

• We propose an approach to model and verify

fuzzy requirements in SysML v2 using only na-

tive constructs and expression evaluation capabil-

ities.

• We validate the method through a case study in-

volving a smart building HVAC system, where

comfort and energy-related requirements are eval-

uated under uncertainty.

• We propose a batch-based extension to simu-

late scenario variability and assess the robustness

of fuzzy requirement satisfaction across multiple

conﬁgurations.

The remainder of the paper is organized as follows:

Section 2 introduces key concepts from SysML v2

and fuzzy logic. Section 3 presents related work

on fuzzy modeling and veriﬁcation in system de-

sign. Section 4 describes our modeling and veriﬁca-

tion method in detail and illustrates it through a case

study. Section 5 details the batch-based scenario ex-

ploration. Finally, Section 6 concludes the paper and

outlines directions for future research.

2 BACKGROUND

This section introduces the fundamentals of

SysML v2 and fuzzy logic relevant to our approach.

2.1 SysML v2 and Constraint

Evaluation

SysML v2 (Object Management Group (OMG),

2024) provides standardized constructs for the speci-

ﬁcation, structuring, and symbolic evaluation of com-

plex system models. Our approach utilizes core

constructs including part def, part, requirement,

calc def, constraint, and satisfy relationships.

Part Deﬁnitions and Usages. System components

are deﬁned using the part def construct, which

speciﬁes structural attributes such as physical prop-

erties or system parameters (Listing 1). Concrete in-

stances of these components are created using part,

with attribute values deﬁned by the keyword ref

(Listing 2).

Listing 1: Example of part def.

part def A {

attribute x: Real;}

Listing 2: Example of part usage.

part a: A {

ref x = 5.0; }

Requirements. Requirements are declared using the

requirement construct, which may include a tex-

tual description (doc), attributes, and embedded con-

straints (Listing 3).

Listing 3: Example of a requirement.

requirement r1 {

doc /

The value of x shall

remain below a fixed limit

attribute limi t : Real = 10.0;

constraint { a . x < li mit }}

Calculation Deﬁnitions. Reusable computational

functions are deﬁned using calc def (Listing 4) and

invoked throughout the model (Listing 5).

Listing 4: Calculation deﬁnition (calc def).

calc def add {

in a: Real;

in b: Real;

return r: Real;

a + b }

Listing 5: Calling a deﬁned calculation.

attribute sum : Real = add (3.0 , 2.0 ) ;

Fuzzy Requirements Veriﬁcation in SysML v2: Direct Modeling and Scenario-Based Analysis for Cyber-Physical Systems

423

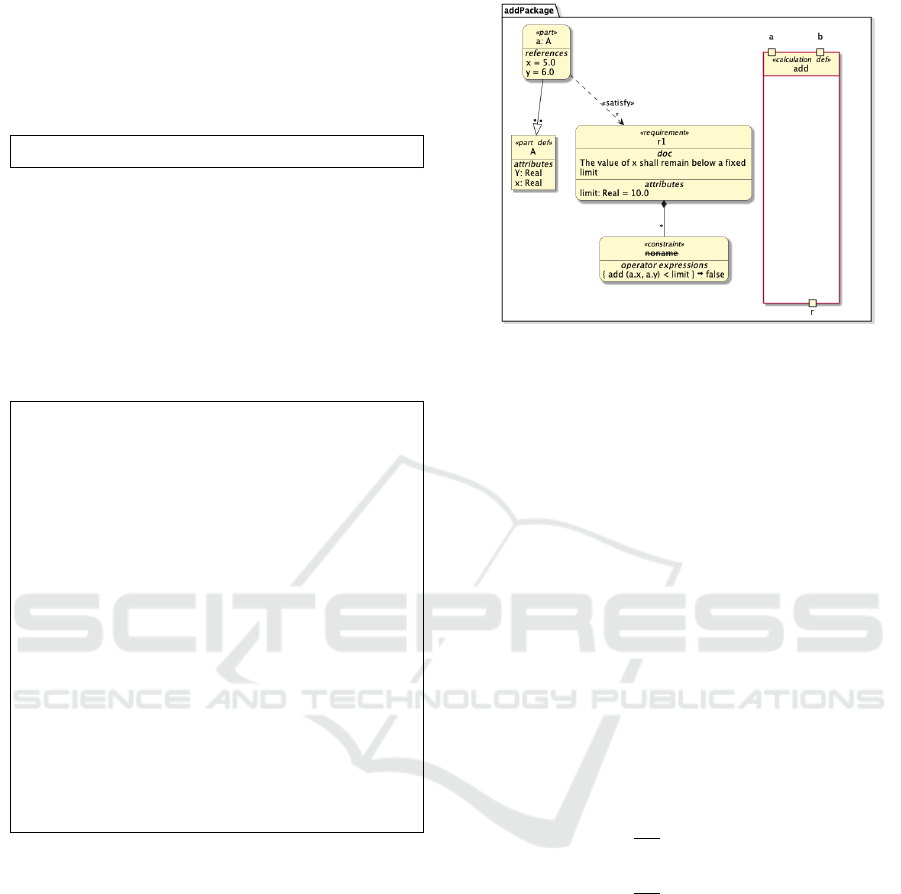
Satisfaction Links (satisfy). The satisfy rela-

tionship explicitly links system components (part) to

their corresponding requirements, ensuring traceabil-

ity and veriﬁcation (Listing 6).

Listing 6: Linking a part to a requirement.

satisfy r1 by a;

Constraints and Their Evaluation. Constraints for-

mally specify conditions that must be fulﬁlled by the

model elements. Constraints can be deﬁned globally

or locally within elements.

Consider the example in Listing 7, where a con-

straint evaluates whether the sum of two attributes re-

mains below a certain threshold using a calculation

deﬁnition.

Listing 7: Complete constraint evaluation example.

package ad d P ack a ge {

private import Sca l a rVa l u es :: *;

calc def add {

in a: Real;

in b: Real;

return r: Real;

a + b }

part def A {

attribute x: Real;

attribute y: Real; }

part a: A {

ref x = 5.0 ;

ref y = 6.0 ; }

requirement r1 {

doc /

The sum of x and y shall

remain below a fixed limit

attribute limi t : Real = 10.0;

constraint { add ( a . x , a. y ) <

li mi t } }

}

Initially, with attributes set to x = 5.0 and y = 6.0,

the evaluation proceeds as:

add(5.0, 6.0) = 11.0 ⇒ 11.0 < 10.0 (false)

This evaluation step is illustrated in Figure 1 (af-

ter evaluation), conﬁrming that the constraint is not

satisﬁed due to the sum exceeding the threshold.

These SysML v2 constructs provide a robust and

structured foundation for specifying and evaluating

requirements in complex systems, facilitating subse-

quent integration with fuzzy logic in our proposed ap-

proach.

2.2 Fuzzy Logic

Fuzzy logic, introduced by Zadeh in 1965 (Zadeh,

1965), extends classical logic by allowing truth values

Figure 1: SysML v2 constraint evaluated to false, since

5.0 + 6.0 ≥ 10.0.

to range continuously between 0 and 1. It is particu-

larly well-suited for representing qualitative, vague,

or imprecise requirements, such as “low energy con-

sumption” or “comfortable temperature,” which can-

not be captured effectively by crisp Boolean logic.

Fuzzy reasoning relies on membership functions

to determine the degree to which a given input sat-

isﬁes a fuzzy concept. Several types of member-

ship functions exist, including triangular, trapezoidal,

Gaussian, and sigmoid functions, each offering differ-

ent modeling ﬂexibility and complexity.

In this paper, we focus on the trapezoidal mem-

bership function due to its simplicity and widespread

use in engineering applications. This function is de-

ﬁned by four parameters (a, b, c, d) and evaluated at a

speciﬁc input value x, returning a satisfaction degree

µ(x) between 0 and 1, as presented in Equation 1.

µ(x) =











0 if x ≤ a or x ≥ d

x−a

b−a

if a < x < b

1 if b ≤ x ≤ c

d−x

d−c

if c < x < d

(1)

3 RELATED WORK

Fuzzy requirements modeling was ﬁrst explored by

Bubenko et al. (Bubenko et al., 1994) and Liu and

Yen (Liu, 1998), who emphasized the use of fuzzy

sets to represent qualitative and imprecise stakeholder

requirements. Their work focused on capturing vague

notions such as “low cost” or “easy to use,” and

formalizing them through membership functions and

trade-off analysis. These early contributions aimed

to support requirements elicitation and reﬁnement but

did not offer executable or veriﬁable models.

Building on this foundation, Baresi et al. (Baresi

ICSOFT 2025 - 20th International Conference on Software Technologies

424

et al., 2010) introduced FLAGS, an extension of the

KAOS goal modeling framework that incorporates

fuzzy and adaptive goals to support runtime require-

ment satisfaction and dynamic adaptation. While

FLAGS enables partial satisfaction tracking and goal

reconﬁguration, it primarily addresses high-level goal

modeling and lacks support for direct veriﬁcation

within design models.

Fuzzy logic has also been applied in extensions

of the Uniﬁed Modeling Language (UML). Ma et

al. (Ma et al., 2012) proposed fuzzy class diagrams by

introducing fuzzy classes, attributes, and relationships

to handle uncertainty in data models. Their approach

facilitates conceptual modeling under imprecision but

does not target operational constraints or veriﬁcation.

Similarly, Han et al. (Han et al., 2014; Han et al.,

2016) proposed the FAME UML proﬁle for model-

ing fuzzy self-adaptive systems using stereotypes and

views for fuzzy control loops. However, FAME fo-

cuses on adaptation logic rather than integrating fuzzy

veriﬁcation directly into design models.

Recent frameworks such as PERSA (Dioni-

sioParaiba and Martins, ), which combines fuzzy

logic with the NFR-Framework, and the conceptual

model proposed by Egesoy and G

uzel (Egesoy and

uzel, 2021) demonstrate the relevance of fuzzy tech-

niques for managing soft and adaptive requirements.

Nonetheless, both approaches remain conceptual or

external to standard modeling environments, offer-

ing little to no integration with modeling tools like

SysML or UML.

In the context of Product Lifecycle Management

(PLM), Taratoukhine and Yadgarova (Taratuknin

and Yadgarova, 2015) applied fuzzy logic to syn-

thesize product conﬁgurations from imprecise cus-

tomer needs. Although effective in its domain, this

work remains domain-speciﬁc and disconnected from

general-purpose system modeling languages.

Within Model-Based Systems Engineering

(MBSE), fuzzy logic has been used to support

architectural evaluations under uncertainty. Dagli et

al. (Dagli et al., 2009) introduced a fuzzy reasoning

approach to explore architectural alternatives by com-

bining fuzzy associative memories with evolutionary

algorithms. While this approach is powerful for early

design exploration, it does not focus on requirements

veriﬁcation nor leverage modeling standards such as

SysML.

Yoo and Lee (Yoo and Lee, 2019) proposed inte-

grating SysML parametric diagrams with MATLAB

and the Analytic Hierarchy Process (AHP) to assess

maintainability using fuzzy values. Their approach

highlights the beneﬁt of combining modeling and

fuzzy analysis but requires tool coupling and exter-

nal processing, limiting the cohesion and reusability

of the model.

In addition to in-model evaluation, some ap-

proaches rely on external tools for scenario simula-

tion or robustness analysis. For example, Yoo and

Lee (Yoo and Lee, 2019) use MATLAB to simulate

different maintainability scenarios. Other approaches

may rely on co-simulation frameworks or script-based

tools to evaluate system behavior under uncertainty.

However, these techniques often involve heavy inte-

gration effort or custom toolchains.

In summary, existing approaches for modeling

and verifying fuzzy requirements generally fall into

one of the following categories: conceptual meth-

ods without execution support, metamodel extensions

in UML, external fuzzy reasoning tools, or hybrid

frameworks requiring tool integration. Very few so-

lutions enable traceable veriﬁcation of fuzzy require-

ments directly within a standard system modeling lan-

guage.

In response to these limitations, we propose an ap-

proach that supports the direct modeling and evalu-

ation of fuzzy requirements within SysML v2. Our

method avoids metamodel extensions, relies solely

on native language constructs, and provides quanti-

tative and traceable veriﬁcation through expression-

based evaluation within the modeling environment.

To further enhance the analysis capabilities under

variability and uncertainty, we also propose an ex-

ternal lightweight extension for scenario-based explo-

ration.

4 DIRECT VERIFICATION OF

FUZZY REQUIREMENTS IN

SysML v2

In this section, we present our approach for modeling

and verifying fuzzy requirements directly within the

SysML v2 modeling environment using only native

constructs. To demonstrate the feasibility and effec-

tiveness of our method, we apply it to a representative

case study involving a smart building HVAC (Heat-

ing, Ventilation, and Air Conditioning) system.

4.1 Modeling Fuzzy Requirements with

Native SysML v2 Constructs

Our approach leverages core SysML v2 constructs,

including calculation deﬁnitions (calc def), require-

ments, attributes, and constraints. This ensures full

compliance with the SysML v2 metamodel, while en-

abling expression-based evaluation of fuzzy seman-

Fuzzy Requirements Veriﬁcation in SysML v2: Direct Modeling and Scenario-Based Analysis for Cyber-Physical Systems

425

tics within the model. Satisfaction degrees are com-

puted using trapezoidal membership functions ex-

pressed through standard calculation logic.

4.1.1 Trapezoidal Membership Function

Implementation

We implement the fuzzy semantics using a trape-

zoidal membership function, chosen for its simplicity

and interpretability in engineering applications. The

function is encoded as a reusable calc def, shown in

Listing 8.

Listing 8: Trapezoidal Membership Function.

calc def tr a pez o id {

in x: Real;

in a: Real;

in b: Real;

in c: Real;

in d: Real;

return r: Real;

if x < a or x > d ? 0

if x > a and x < b ? (( x - a ) / (

b - a ) )

if x >= b and x <= c ? 1

if x > c and x < d ? (( d - x ) / (

d - c ) )

if x >= d ? 0 }

This deﬁnition can be reused to deﬁne fuzzy

satisfaction degrees for various attributes across the

model.

4.1.2 Generic Fuzzy Requirement Speciﬁcation

Fuzzy requirements are modeled using standard

requirement blocks, enhanced with attributes that

compute satisfaction degrees using the trapezoidal

function. Constraints are then applied to evaluate

whether the degree meets a minimum acceptable

threshold, as shown in Listings 9, 10, and 11.

Listing 9: Generic Fuzzy Requirement.

requirement si m ple R eq {

doc /

The value shall be

approximately between 6 and

attribute val : Real = 7. 5;

attribute mu : Real = t rap e zoi d (

val , 5.0 , 6.0 , 8.0 , 9.0) ;

assert constraint {

mu > 0.6 } }

Listing 10: System Element Deﬁnition.

part def Sys t e mEl e m e nt {

attribute inpu t : Real; }

part p: Sy s t emE l e m ent {

ref inpu t = 7 .5 ; }

Listing 11: Linking Requirement and Part.

satisfy si m ple R eq by p;

This modeling pattern is fully evaluatable within

SysML v2, relying exclusively on expression evalua-

tion through native constraint logic.

4.2 HVAC System Case Study

To demonstrate our approach, we model a smart

building HVAC (Heating, Ventilation, and Air Con-

ditioning) system tasked with ensuring both thermal

comfort and energy efﬁciency. These are two inher-

ently vague and context-sensitive requirements. The

HVAC system must maintain an indoor temperature

that is perceived as comfortable by occupants, while

minimizing energy consumption. These objectives

are naturally formulated as fuzzy requirements, re-

ﬂecting user preferences and operational tolerances.

4.2.1 SysML v2 Model of HVAC System

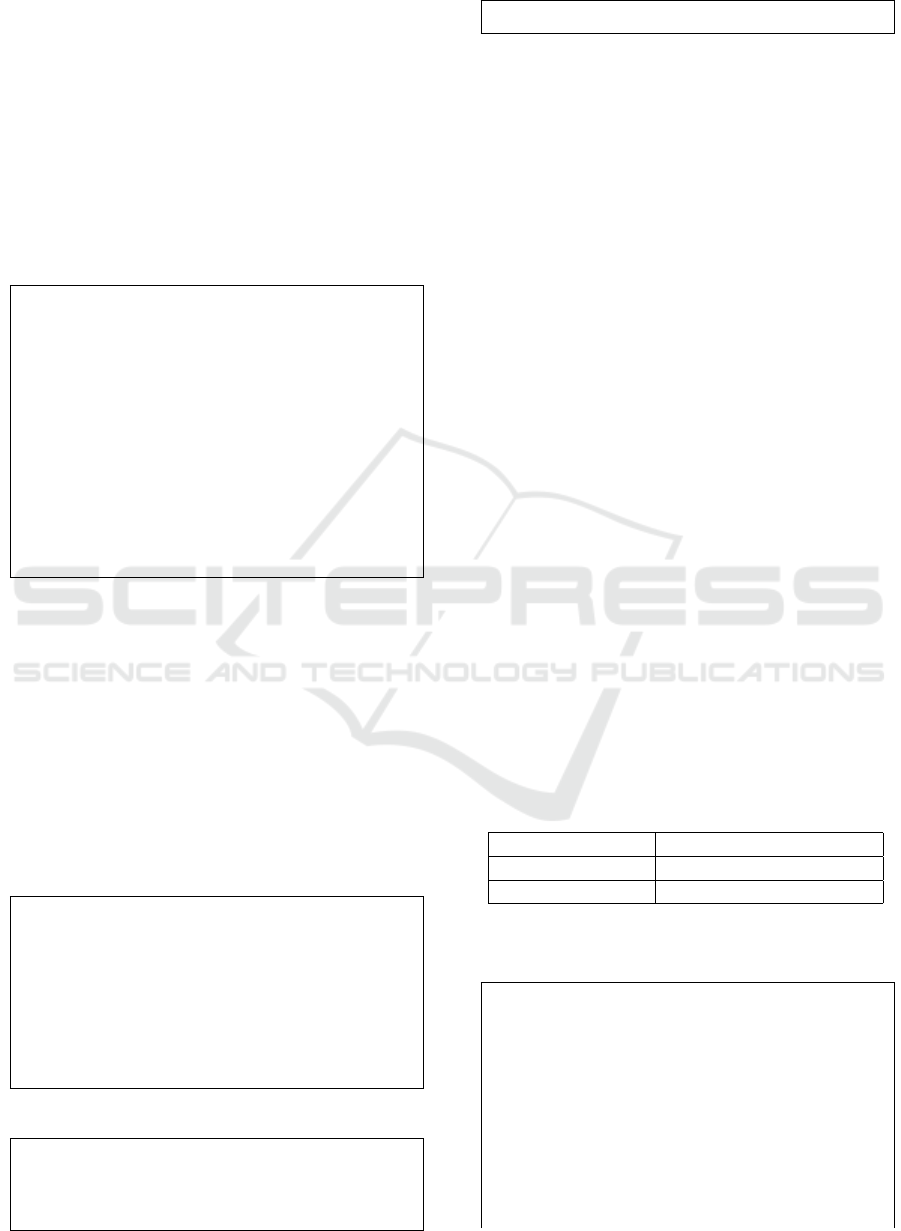
The system is modeled in SysML v2 using the follow-

ing structure:

• A part def block deﬁnes the HVAC system with

attributes for temperature and power.

• Two fuzzy requirements are created: one for com-

fort, and one for power efﬁciency.

• Satisfaction degrees are computed using trape-

zoidal membership functions, with thresholds

speciﬁed via constraints.

The parameters used for the trapezoidal functions are

summarized in Table 1.

Table 1: Trapezoidal Parameters for HVAC Fuzzy Require-

ments.

Requirement Trapezoidal parameters

Thermal Comfort (18, 22,24, 29) °C

Energy Efﬁciency (0, 100, 200, 300) Watts

Listing 12 shows the full model deﬁnition.

Listing 12: HVAC SysML v2 Model.

part def Hv a c Sys t em {

attribute te m p era t u re : Real;

attribute powe r : Real; }

part h va c : H v a cSy s tem {

ref tem p era t u re = 27. 0;

ref powe r = 227 . 5;}

requirement co m f ort R eq {

doc /

The ambient temperature

shall be comfortable.

attribute mu _ c omf o rt : Real =

tr a pez o id ( hv ac . tem pe rat ur e ,

18.0 , 22.0 , 24.0 , 29.0 ) ;

ICSOFT 2025 - 20th International Conference on Software Technologies

426

assert constraint

Com f o r t Con s t r a int {

mu _ c omf o rt > 0 .6 } }

requirement po w erR eq {

doc /

The power usage shall

remain reasonably low.

attribute mu _ pow er : Real =

tr a pez o id ( hv ac . power , 0.0 ,

100 .0 , 200.0 , 3 00. 0) ;

assert constraint Pow e r C onst r a i nt

{ mu _po w er > 0.6 } }

satisfy co m f ort R eq by h va c ;

satisfy po w erR eq by h va c ;

Figures 2 present the model after expression eval-

uation.

4.2.2 Evaluation and Discussion

Following the expression-based evaluation in

SysML v2, the computed satisfaction degrees for the

HVAC system are as follows:

• Comfort satisfaction degree: µ

comfort

= 0.4 (re-

quirement not satisﬁed).

• Energy satisfaction degree: µ

power

= 0.725 (re-

quirement satisﬁed).

These results indicate that the current temperature

lies outside the deﬁned fuzzy comfort zone, whereas

energy consumption remains within the acceptable

fuzzy interval. This kind of partial satisfaction feed-

back, where some requirements are met to a certain

degree, and others are not, is particularly valuable

during the early design stages. It enables engineers

to reason about soft requirements with a ﬁner granu-

larity than binary logic allows and to iteratively reﬁne

system parameters or membership thresholds.

More broadly, this case study illustrates that

SysML v2 can be effectively used to model and verify

fuzzy requirements using only native constructs. Our

approach requires no metamodel extensions or exter-

nal engines. Instead, it relies on the language’s built-

in expression evaluation capabilities to provide a fully

integrated and interpretable veriﬁcation process.

Using fuzzy satisfaction degrees within SysML v2

offers practical beneﬁts, including early detection of

requirement mismatches, enhanced traceability and

explainability through quantitative insights, and im-

proved maintainability via modular updates. Over-

all, our approach enriches SysML v2’s expressive-

ness, enabling quantitative reasoning over soft re-

quirements without deviating from the standard lan-

guage speciﬁcation.

5 BATCH-BASED SCENARIO

EXPLORATION

While our proposed approach enables the evalua-

tion of fuzzy constraints directly within a SysML v2

model using expression-based constructs, Cyber-

Physical Systems (CPS) often operate in inherently

dynamic and uncertain environments. For example,

temperature and energy usage in a smart building may

vary due to changes in weather, occupancy, or user

behavior. Verifying a single conﬁguration, although

valuable, remains insufﬁcient to assess how the sys-

tem performs across a spectrum of real-world situa-

tions.

To address this limitation, we introduce a

lightweight batch-based extension that supports the

evaluation of fuzzy requirement satisfaction under

multiple runtime conditions. This allows engineers to

observe how the system responds to input ﬂuctuations

and to reason about robustness and sensitivity during

early-stage design.

Although SysML v2 provides powerful

expression-based modeling capabilities, it does

not natively support scenario generation or statistical

analysis. However, its precise structure and reusable

expressions can be exported to an executable lan-

guage. In our case, we transform the trapezoidal

membership function and requirement logic into

Python code. This transformation is non-intrusive

and preserves the semantics of the original model.

5.1 Scenario Generation in Python

We deﬁne three scenarios reﬂecting environmental

variability: S1 (mild and stable conditions), S2 (same

average as S1, higher variability), and S3 (stressful

conditions with elevated temperature and energy us-

age).

Each scenario generates a set of temperature

and power consumption values by sampling from

a normal (Gaussian) distribution using the function

np.random.normal(mean, std, size), producing

size samples (10 in our case) with an approximate

mean of mean and variability controlled by std.

A small standard deviation (e.g., 1) simulates sta-

ble or predictable environmental conditions, while a

larger standard deviation (e.g., 3) represents scenar-

ios with greater variability or uncertainty. Listing 13

presents the complete Python script used for generat-

ing and evaluating these scenarios.

Fuzzy Requirements Veriﬁcation in SysML v2: Direct Modeling and Scenario-Based Analysis for Cyber-Physical Systems

427

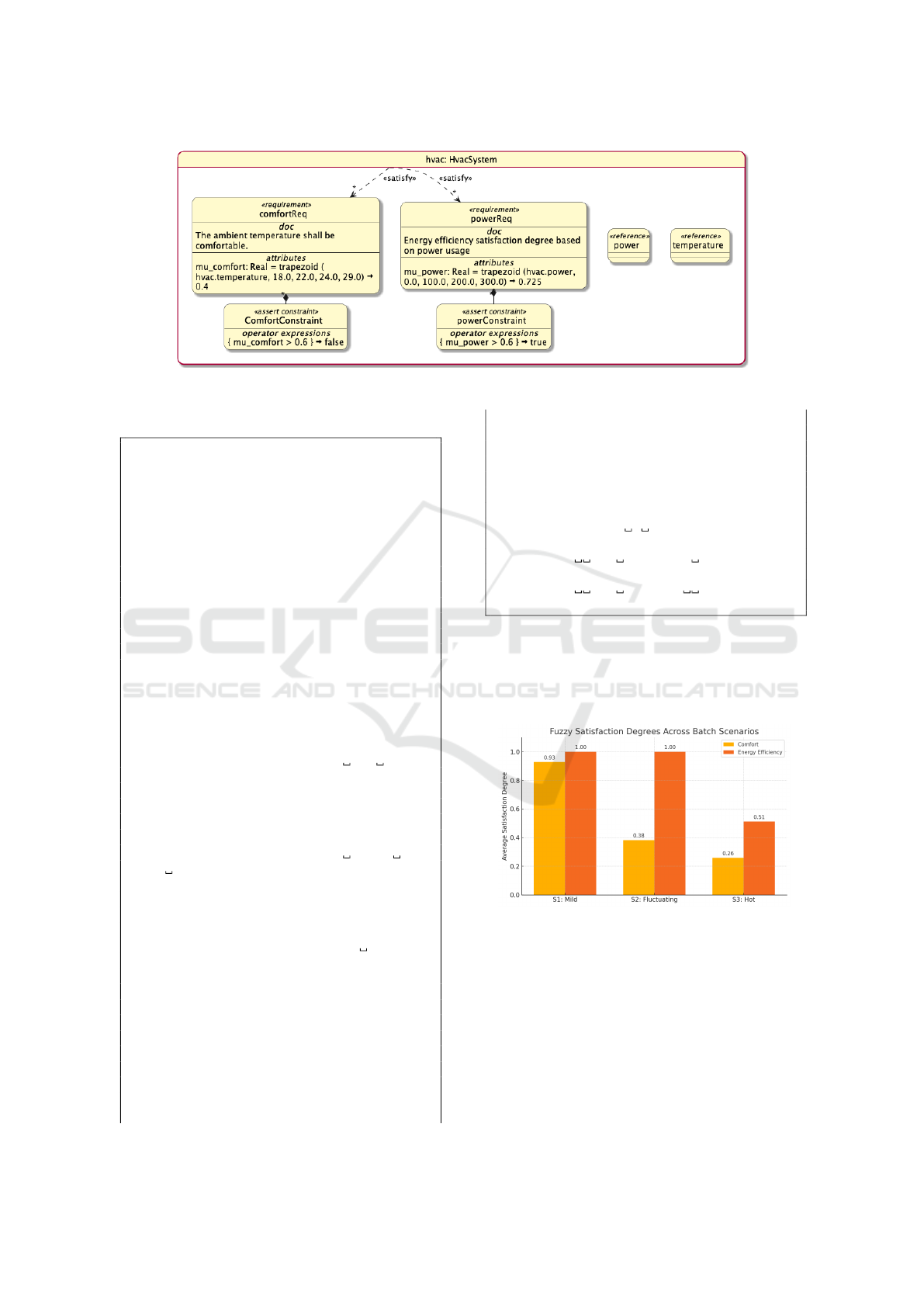
Figure 2: SysML v2 Model After Evaluation (Computed Satisfaction Degrees).

Listing 13: Python script for evaluating fuzzy requirements

across multiple scenarios.

import nump y as np

# Trapezoidal membership function

def tr a pez o id (a , b , c , d , x) :

if x <= a or x >= d: return 0.0

elif a < x < b :

return (x - a ) / (b - a )

elif b <= x <= c: return 1.0

elif c < x < d :

return (d - x ) / (d - c )

else: return 0.0

# Membership functions for fuzzy

requirements

def comf o r t _ memb e r s h ip ( temp ) :

return tr a pez o id (18 , 22 , 24 , 28 ,

temp )

def ener g y _ m emb e r s h ip ( p ow er ) :

return tr a pez o id (0 ,100 ,200 ,300 ,

po we r )

# Scenario definitions

sc e nar i os = {

" S1 ":{ " de s c rip t i on ": " Mil d and sta ble

" ,

" t em p ": np . rand om . nor m al (23 ,

1, 10) ,

" power ": np . r an d om . nor mal

(120 , 10 , 10) , } ,

" S2 ":{ " de s c rip t i on ": " Sam e mean , mor e

va r ian ce ",

" t em p ": np . rand om . nor m al (23 ,

3, 10) ,

" power ": np . r an d om . nor mal

(120 , 30 , 10) , } ,

" S3 ":{ " de s c rip t i on ": " St re ss

co n dit i on ",

" t em p ": np . rand om . nor m al (27 ,

1, 10) ,

" power ": np . r an d om . nor mal

(250 , 15 , 10) , } ,}

# Evaluate satisfaction degrees

for name , sce n ari o in sce n ari o s . i te ms

() :

mu _ c omf o rt = [ co m f ort_ m e m b ersh i p (

t) for t in sc e na r io [" tem p "]]

mu _ ene r gy = [ en e r gy_m e m b e rsh i p ( p )

for p in sc e na r io [" power "]]

sc e nar io [" av g _ com f o rt "] = np . mea n

( mu_c o m for t )

sc e nar io [" av g _ ene r gy "] = np . mea n (

mu _ ene r gy )

# Output results

for name , s in s c ena r ios . ite ms () :

print(f " { name } - { s [ ’ de s cri p t io n ’]}

print(f " Avg Comf ort : { s [ ’

av g _ com f o rt ’]:.3 f} ")

print(f " Avg Ene r gy : { s [ ’

av g _ ene r gy ’]:.3 f} " )

5.2 Results and Interpretation

Figure 3 illustrates the average satisfaction degrees

computed for each scenario.

Figure 3: Average fuzzy satisfaction degrees across batch-

generated scenarios.

The results reveal that under S1 (stable condi-

tions), both requirements are well satisﬁed, indicating

robustness. In S2, increased variability leads to lower

satisfaction, especially for comfort. Under S3 (stress-

ful conditions), satisfaction levels drop signiﬁcantly,

showing the system’s limits in extreme scenarios.

This analysis reveals behavioral trends that cannot

be captured by static Boolean veriﬁcation. Design-

ers can detect system limitations, improve parameter

ICSOFT 2025 - 20th International Conference on Software Technologies

428

ranges, or tune satisfaction thresholds accordingly.

5.3 Discussion

The batch-based evaluation enhances SysML v2 with

variability-aware analysis, allowing robustness as-

sessment under uncertainty, sensitivity exploration to

identify critical inputs, and ﬂexible design-space ex-

ploration without modifying the core model. Al-

though the scenario evaluation is performed exter-

nally, the transformation is lightweight and preserves

model semantics. This hybrid architecture bridges

the gap between structural modeling and dynamic

runtime reasoning, offering a scalable and practical

method for validating fuzzy requirements across di-

verse CPS environments.

6 CONCLUSION

This paper introduced a model-based veriﬁcation ap-

proach for Cyber-Physical Systems (CPS) that sup-

ports specifying and evaluating vague or imprecise

requirements such as comfort or energy efﬁciency us-

ing fuzzy logic directly within the standard SysML v2

language. Unlike existing approaches that rely on

metamodel extensions or external reasoning tools, our

method leverages native SysML v2 constructs, in-

cluding calculation deﬁnitions, attributes, constraints,

and requirements, to encode fuzzy semantics in a

lightweight and compliant manner.

We demonstrated the feasibility of our approach

through a case study of a smart building HVAC sys-

tem, where fuzzy satisfaction degrees were evaluated

using trapezoidal membership functions and standard

constraint mechanisms. This allows for continuous,

explainable, and traceable veriﬁcation of soft require-

ments, moving beyond the limitations of Boolean

logic. Our method thus supports early-stage analysis,

enabling engineers to reason about partial compliance

and explore trade-offs under uncertainty.

To complement the in-model evaluation, we pro-

posed a batch-based scenario analysis that exports key

model logic to Python. This external extension allows

system evaluation under diverse operating conditions

using randomized scenarios, offering insights into

system robustness, variability sensitivity, and perfor-

mance boundaries.

In future work, we plan to extend the method to

support composite fuzzy constraints involving mul-

tiple interacting variables and apply the approach to

larger, more complex CPS domains to evaluate its

scalability and applicability across diverse engineer-

ing contexts.

REFERENCES

Baresi, L., Pasquale, L., and Spoletini, P. (2010). Fuzzy

goals for requirements-driven adaptation. In 2010

18th IEEE international requirements engineering

conference, pages 125–134. IEEE.

Bubenko, J., Rolland, C., Loucopoulos, P., and DeAn-

tonellis, V. (1994). Facilitating” fuzzy to formal” re-

quirements modelling. In Proceedings of IEEE In-

ternational Conference on Requirements Engineering,

pages 154–157. IEEE.

Dagli, C. H., Singh, A., DAUBY, J. P., and Wang, R.

(2009). Smart systems architecting: computational in-

telligence applied to trade space exploration and sys-

tem design. In Systems Research Forum, volume 3,

pages 101–119. World Scientiﬁc.

DionisioParaiba, J. and Martins, L. E. G. A proposal of re-

quirements speciﬁcation process for adaptive systems

based on fuzzy logic and nfr-framework.

Egesoy, A. and G

uzel, A. (2021). Fuzzy logic support for

requirements engineering. International Journal of

Innovative Research in Computer Science & Technol-

ogy, 9(2):14–21.

Han, D., Yang, Q., and Xing, J. (2014). Extending uml for

the modeling of fuzzy self-adaptive software systems.

In The 26th Chinese Control and Decision Conference

(2014 CCDC), pages 2400–2406. IEEE.

Han, D., Yang, Q., Xing, J., Li, J., and Wang, H. (2016).

Fame: A uml-based framework for modeling fuzzy

self-adaptive software. Information and Software

Technology, 76:118–134.

Liu, X. F. (1998). Fuzzy requirements. IEEE Potentials,

17(2):24–26.

Ma, Z. M., Yan, L., and Zhang, F. (2012). Modeling fuzzy

information in uml class diagrams and object-oriented

database models. Fuzzy Sets and Systems, 186(1):26–

46.

Object Management Group (OMG) (2012). OMG Systems

Modeling Language SysML. Technical report.

Object Management Group (OMG) (2024). Systems

Modeling Language (SysML) v2 Beta 2 Speciﬁ-

cation: Language. www.omg.org/spec/SysML/2.0/

Beta2/Language/PDF. Accessed Mars 2025.

Taratuknin, V. and Yadgarova, Y. (2015). A fuzzy logic

approach for product conﬁguration and requirements

management. In 2015 Annual Conference of the

North American Fuzzy Information Processing Soci-

ety (NAFIPS) held jointly with 2015 5th World Confer-

ence on Soft Computing (WConSC), pages 1–5. IEEE.

Yoo, Y.-Y. and Lee, J.-C. (2019). The improvement of main-

tainability evaluation method at system level using

system component information and fuzzy technique.

Journal of the Korea Academia-Industrial coopera-

tion Society, 20(3):100–109.

Zadeh, L. A. (1965). Fuzzy sets. Information and control,

8(3):338–353.

Fuzzy Requirements Veriﬁcation in SysML v2: Direct Modeling and Scenario-Based Analysis for Cyber-Physical Systems

429