Bitcoin Fraud Detection: A Study with Dimensionality Reduction and

Machine Learning Techniques

Nuno Gomes

and Artur J. Ferreira

1,2 a

ISEL, Instituto Superior de Engenharia de Lisboa, Instituto Polit

ecnico de Lisboa, Portugal

Instituto de Telecomunicac¸

oes, Lisboa, Portugal

Keywords:

Bitcoin, Feature Reduction, Feature Selection, Fraud Detection, Supervised Learning.

Abstract:

The use of cryptocurrencies corresponds to a remarkable moment in global ﬁnancial markets. The nature of

cryptocurrency transactions, done between cryptographic addresses, poses many challenges to identify fraud-

ulent activities, since malicious transactions may appear as legitimate. Using data with these transactions,

one may learn machine learning models targeted to identify the fraudulent ones. The transaction datasets are

typically imbalanced, holding a few illicit examples, which is challenging for machine learning techniques to

identify fraudulent transactions. In this paper, we investigate the use of a machine learning pipeline with di-

mensionality reduction techniques over Bitcoin transaction data. The experimental results show that XGBoost

is the best performing method among a large set of competitors. The dimensionality reduction techniques are

able to identify adequate subsets suitable for explainability purposes on the classiﬁcation decision.

1 INTRODUCTION

Cryptocurrencies such as Bitcoin (BTC) marked a

transformative moment in the global ﬁnancial land-

scape. Based on distributed ledger technology

Blockchain, BTC allows rapid, decentralized, and se-

cure transactions, without intermediaries and facil-

itating global payments with reduced fees. As of

January 2025, the market capitalization of cryptocur-

rency exceeded $3.64 trillion, with BTC accounting

for approximately 55.53% of this value ($2.02 tril-

lion) (Team, 2024). This market presence has at-

tracted both legitimate users and malicious actors,

yielding an urgent need for security measures.

The evolution of cryptocurrencies posed a threat

to the foundations of the ﬁnancial system. The de-

centralised nature of BCT, whilst innovative, presents

unique challenges for security, privacy, and fraud

prevention. The pseudo-anonymous characteris-

tics of transactions have enabled various illicit ac-

tivities, including money laundering and ﬁnancial

fraud. Money laundering impacts between 2% and

5% of global Gross Domestic Product (United Na-

tions Ofﬁce on Drugs and Crime, 2011), prompting

the need for Anti-Money Laundering (AML) frame-

works. These frameworks encompass customer iden-

https://orcid.org/0000-0002-6508-0932

tiﬁcation, transaction monitoring, and suspicious ac-

tivity reporting. However, their effectiveness faces

limitations in cryptocurrency contexts due to trace-

ability challenges and regulatory fragmentation.

The European Union has comprehensive regula-

tion through the Markets in Crypto-Assets (MiCA)

framework. This legislation has rules to enhance

transparency, protect consumers, and prevent ﬁ-

nancial crimes. The framework includes mecha-

nisms for tracking crypto-asset transfers and block-

ing suspicious transactions, strengthening market in-

tegrity. Despite these regulatory advances, detect-

ing fraud in BTC transactions remains challenging

due to the complex nature of cryptocurrency transac-

tions and the evolving sophistication of illicit activi-

ties. Unlike traditional ﬁnancial systems with known

identities, BTC transactions occur between crypto-

graphic addresses without revealing personal infor-

mation (Nakamoto, 2008). This poses challenges in

identifying fraudulent activities, as malicious transac-

tions can appear legitimate while concealing illicit be-

havior (Weber et al., 2019). Consequently, Machine

Learning (ML) approaches become essential to ad-

dress these issues effectively.

In this paper, we devise a ML pipeline with dimen-

sionality reduction over imbalanced Bitcoin transac-

tion data. We resort to supervised ML techniques to

identify fraudulent transactions.

716

Gomes, N., Ferreira and A. J.

Bitcoin Fraud Detection: A Study with Dimensionality Reduction and Machine Learning Techniques.

DOI: 10.5220/0013647400003967

In Proceedings of the 14th International Conference on Data Science, Technology and Applications (DATA 2025), pages 716-723

ISBN: 978-989-758-758-0; ISSN: 2184-285X

The remainder of the paper is organized as fol-

lows. Section 2 reviews the state-of-the-art of cryp-

tocurrency fraud detection techniques. The proposed

approach is described in Section 3. Section 4 reports

the experimental results of our approach and their key

ﬁndings. The paper ends in Section 5 with concluding

remarks and directions for future work.

2 RELATED WORK

This Section reviews related work on the topic ad-

dressed in the paper. First, we review cryptocurrency

fraud detection approaches in Section 2.1. Then,

we address the use of speciﬁc techniques on Bitcoin

transaction data in Section 2.2.

2.1 Cryptocurrency Fraud Detection

Figure 1 outlines key milestones in the development

of cryptocurrency fraud detection methods.

2008

Bitcoin Introduction

2009

Rule-Based Detection

2012

Statistical Methods

2016

Machine Learning (SVM, RF)

2019

Ensemble Methods, DNNs

2021

Graph Neural Networks

2023

Transformer Models

2024

Federated Learning

2025+

XAI, Quantum Resistance

Figure 1: A timeline of cryptocurrency fraud detection

methods.

The proposed approaches have evolved from rule-

based systems to ML techniques. Early methods,

while effective for identifying simple fraud patterns,

struggled with scalability and adaptability.

In the past years, ML approaches have become in-

creasingly applied to this problem. We now brieﬂy

review some of ML techniques employed in this con-

text. Ensemble methods enhance predictive perfor-

mance by combining multiple models, thereby reduc-

ing variance, bias, and the risk of overﬁtting. Tech-

niques such as bagging, boosting, and stacking lever-

age diverse learning algorithms achieving more robust

and generalizable outcomes (Alarab and Prakoon-

wit, 2023a). Deep Neural Networks (DNN) employ

multiple hidden layers to model complex patterns in

high-dimensional data. These networks are trained

through a process called backpropagation, which ad-

justs the weights of the network to minimize the er-

ror in its predictions. Transformer models, based on

self-attention mechanisms, have revolutionized nat-

ural language processing and other sequential tasks

by enabling parallel processing and capturing long-

range dependencies (P

erez-Cano and Jurado, 2024;

Liu et al., 2024). Federated learning improves pri-

vacy and efﬁciency by decentralizing model train-

ing on multiple devices while preserving data local-

ity (Ahmed and Alabi, 2024). An approach based

on Explainable Artiﬁcial Intelligence (XAI) to pro-

viding interpretability and transparency to foster trust

and compliance in critical applications is proposed

by Taher et al. (2024). Recent approaches based on

Quantum Resistance, focused on developing crypto-

graphic algorithms resilient to quantum computing

threats, are proposed by Pushpak (2025); Allende

et al. (2023); Olutimehin (2025).

A survey of proposed approaches, is shown in Ta-

ble 1 with their advantages and shortcomings.

These techniques addressed different fraud detec-

tion challenges, namely scalability, interpretability,

and adversarial fraud techniques.

2.2 Bitcoin Fraud Detection

2.2.1 Early Approaches

Following Bitcoin’s introduction, early fraud detec-

tion approaches relied heavily on rule-based systems

and basic statistical analysis. These methods pri-

marily focused on transaction veriﬁcation via the

blockchain consensus mechanism. Although effec-

tive in identifying basic fraud patterns, these mod-

els lacked adaptability to increasingly sophisticated

fraudulent schemes. Ngai et al. (2011) discuss the ap-

plication of data mining techniques in ﬁnancial fraud

detection.

2.2.2 Machine Learning Approaches

ML techniques have been used to detect fraud within

BTC transactions, by identifying anomalous pat-

terns. We have approaches with supervised, unsuper-

vised, and semi-supervised learning techniques en-

hance fraud detection accuracy and efﬁciency.

Table 1: Advantages and Shortcomings of Proposed Ap-

proaches.

Year Methodology Advantages Shortcomings

2009 Rule-Based Detec-

tion

Simple, easy to implement High false positive rate, lacks

adaptability

2012 Statistical Methods Identiﬁes basic transaction

patterns

Limited scalability, struggles

with new fraud techniques

2016 Machine Learning

(SVM, RF)

More accurate fraud detection Requires labeled data, inter-

pretability issues

2019 Ensemble Meth-

ods,DNN

Improved accuracy, better

feature extraction

Computationally expensive, re-

quires ﬁne-tuning

2021 GNN Captures transaction relation-

ships effectively

Low interpretability, requires

large datasets

2023 Transformer Models Handles sequential transac-

tion data efﬁciently

High resource demand, potential

overﬁtting

2024+ Federated Learning,

XAI

Enhances privacy, improves

transparency

Implementation complexity, reg-

ulatory challenges

Bitcoin Fraud Detection: A Study with Dimensionality Reduction and Machine Learning Techniques

717

The 2016-2019 period marked signiﬁcant ad-

vancements in the application of traditional ML tech-

niques to AML and BTC fraud detection. In the

following, we refer to some relevant approaches.

Monamo et al. (2016) apply unsupervised learning

(Trimmed K-means) to detect fraud in BTC transac-

tions. Pham and Lee (2017) explores anomaly de-

tection in BTC networks using unsupervised learn-

ing methods. They resort to a modiﬁed version of

SVM for unlabelled data, achieving greater consis-

tency in detecting anomalies, with a Dual Evaluation

Metric of 0.14415. Yin and Vatrapu (2017) estimate

the proportion of cybercriminal entities in BTC using

supervised ML. Three clustering methods—co-spend,

intelligence-based, and behaviour-based—were ap-

plied to categorize BTC transactions. The models

revealed that cybercrime-related entities account for

29.81% (Bagging) and 10.95% (Gradient Boosting)

of the total entities. Additionally, Bagging identi-

ﬁed 5.79% of addresses and 10.02% of coins linked

to cybercrime. Harlev et al. (2018) demonstrates de-

anonymization of BTC entity types using supervised

ML. Their main ﬁnding was predicting the type of

a yet-unidentiﬁed entity using the Gradient Boost-

ing algorithm, achieving an accuracy of 77% and F1-

score of approximately 75%. Hu et al. (2019) detects

money laundering on BTC networks with deep walk

and node-to-vector techniques outperforming classi-

ﬁers in binary classiﬁcation task reaching an average

accuracy of 92.29% and an F1-score of 93%. Weber

et al. (2019) experiments with GCN for anti-money

laundering in BTC. Zhang and Trubey (2019) inves-

tigates the use of ML models such as logistic regres-

sion, SVM, and artiﬁcial neural networks for money

laundering detection.

Recent studies have improved the performance of

traditional ML models for transaction classiﬁcation

on blockchain-derived, manually labelled dataset.

These include Na

ıve Bayes, SVM, Logistic Regres-

sion, Gradient Boosting, AdaBoost, Random For-

est (RF) (Chauhan et al., 2024; Taher et al., 2024;

Snigdha et al., 2024; Dutta et al., 2024), as well as

anomaly detection (Hisham et al., 2023), Long Short-

Term Memory (G

urﬁdan, 2024), Federated Learn-

ing (Ahmed and Alabi, 2024) and Recurrent Neural

Networks (RNN) Abdulkadhim et al. (2024).

Md et al. (2023) proposed a classiﬁer for detect-

ing fraudulent transactions on the Ethereum network.

Among individual models, RF achieved the highest

accuracy of 95.47%, followed by Gradient Boosting

at 94.61%. The Stacking classiﬁer, combining Multi-

nomial NB and RF as base learners with Logistic Re-

gression as the meta-learner, attained the highest ac-

curacy of 97.18% with an F1 score of 97.02%

Despite its effectiveness, applying ML to fraud

detection presents challenges due to the immutable

and decentralized nature of blockchain data. The

lack of labeled data limits the effectiveness of super-

vised learning, which requires the use of unsupervised

clustering algorithms, such as K-means (MacQueen,

1967) and DBScan (Ester et al., 1996), to detect sus-

picious transaction clusters. Recent studies have also

explored the use of RNN and CNN to analyze transac-

tion sequences and detect anomalous behaviours. In

this context Di et al. (2022), suggested a framework

for modeling BTC transactions as a random graph to

exploit their structural properties and analyze them

from the Graph Theory perspective.

2.2.3 Deep Learning Approaches

Recently, the use of Deep Learning (DL) techniques

has been addressed. We brieﬂy review some of

these approaches. GNN are employed to analyze

blockchain transaction networks, enabling the de-

tection of anomalous behaviour with high preci-

sion. For instance, GNN have achieved state-of-

the-art performance on Elliptic data, attaining an

accuracy of 98.99% and an F1-score of 91.75%

(Alarab and Prakoonwit, 2023b), by effectively cap-

turing complex relationships between blockchain en-

tities. Transformer-based models, including architec-

tures like BERT and GPT, have been adapted for fraud

detection, signiﬁcantly enhancing anomaly detection

performance. These models excel at handling sequen-

tial transaction data and capturing long-range depen-

dencies, making them particularly effective in iden-

tifying patterns of fraudulent behaviour (Yang et al.,

2023).

3 PROPOSED APPROACH

In this Section, we describe the two phases of

our approach: baseline Exploratory Data Analysis

(EDA) and Dimensionality Reduction and Visualiza-

tion (DRV). Section 3.1 depicts the block diagrams of

these phases. Section 3.2 reports a detailed analysis

of the Elliptic dataset (Weber et al., 2019). The ML

techniques used in the two phases of our approach and

the evaluation metrics are summarized in Section 3.3.

3.1 Block Diagrams

The baseline EDA phase is depicted in Figure 2. From

the Elliptic dataset, we provide an exploratory analy-

sis of the data, organizing the data into two and three

classes. Finally, we evaluate ML models.

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

718

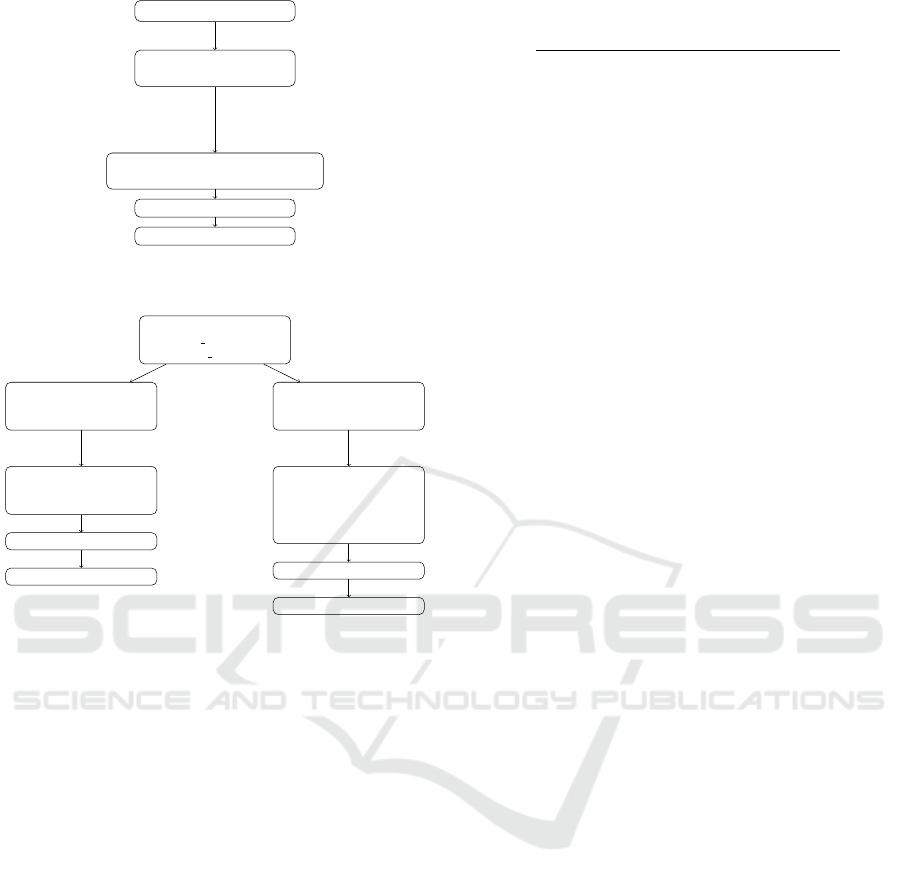
Elliptic Dataset

Graphical Exploratory

Data Analysis

Prepare & Process Dataset for ML

(Split into 2 & 3 Classes)

Learn classiﬁers

Evaluate results

Figure 2: Phase 1 - The baseline Exploratory Data Analysis

(EDA) approach.

Elliptic dataset

(2class version and

3class version)

Dimensionality Reduction

(feature selection)

(ANOVA and XGBoost)

Dimensionality Reduction

(feature reduction)

(PCA and UMAP)

Find Explainability

(identify the most

decisive features)

Find Intrinsic

Dimensionality

(visualize the data

projected into lower

dimensionality space)

Learn classiﬁers

Evaluate

Learn classiﬁers

Evaluate

Figure 3: Phase 2 - The Dimensionality Reduction and Vi-

sualization (DRV) phase approach.

The DR phase is depicted in Figure 3. From

the several versions of the dataset, with two or three

classes, we perform DR with Feature Selection (FS)

and Feature Reduction (FR) techniques. We also ex-

plore combinations of FS and FR methods. The goal

of this phase is to ﬁnd the best performing reduced di-

mensionality for this dataset and to identify the most

decisive features for explainability purposes.

3.2 Elliptic Bitcoin Transaction Dataset

The Elliptic Bitcoin transaction dataset (Weber et al.,

2019), comprises a Bitcoin blockchain transaction

graph where nodes represent individual transactions

(203,769 total) and edges denote Bitcoin ﬂows be-

tween them (234,355 connections). The dataset has

166 attributes per transaction (94 local features and

72 aggregated features), organized across 49 tempo-

ral intervals representing 2-week periods. We have

a signiﬁcant class imbalance, as described in Ta-

ble 2. This poses challenges for supervised learning

approaches as labeled data represents 22.85% of the

dataset (9.76% illicit vs 90.24% licit).

Table 2: Elliptic dataset class distribution.

Class Count Percentage

Illicit (class 1) 4,545 2.2%

Licit (class 2) 42,019 20.6%

Unknown (class 3) 157,205 77.2%

3.3 Machine Learning Techniques

In our experiments we have considered the following

ML methods. For FS, we have considered ANOVA F-

value and XGBoost Feature Importance for Explain-

ability. For FR, we have considered Principal Com-

ponent Analysis (PCA) and Uniform Manifold Ap-

proximation and Projection (UMAP). For the clas-

siﬁcation task, we have assessed many well-known

classiﬁers: Random Forest (RF), Decision Tree (DT),

XGBoost, LightGBM, CatBoost, Support Vector Ma-

chines (SVM), K-Nearest Neighbors (KNN), Multi-

Layer Perceptron (MLP), and Na

ıve Bayes (NB).

We have considered the well-known evaluation

metrics, namely Accuracy, Precision, Recall, and F1-

score. We have also considered the use of the con-

fusion matrix, the area under the Receiver Operat-

ing Characteristic (ROC) curve designated as AUC,

and the Precision-Recall (PR) trade-off, preferred for

class imbalance assessment.

4 EXPERIMENTAL EVALUATION

In this Section, we report the experimental evaluation

of our proposed approach. Section 4.1 describes the

baseline EDA results on the original features, for the

2-class and the 3-class case. Section 4.2 reports the

experimental results of dimensionality reduction with

FS techniques, aiming to achieve explainability. The

experimental evaluation of dimensionality reduction

with FR techniques for visualization purposes and

FS/FR for classiﬁcation is addressed in Section 4.3.

4.1 Baseline Results

4.1.1 Two-Class Dataset

Table 3 shows the results of classiﬁers on the two-

class original dataset (Class 1 and Class 2, in Table 2).

We use 10-fold cross-validation for the assessment.

The model with highest accuracy is XGBoost and

the model with the highest efﬁciency (deﬁned as Ac-

curacy / Training Time) is KNN. Figure 6 depicts an

analysis of XGBoost binary classiﬁcation results re-

garding the confusion matrix, ROC curve, and PR-

curve.

Class 1 shows 8,400 correct predictions and only 4

misclassiﬁcations as Class 0. Class 0 has 846 correct

Bitcoin Fraud Detection: A Study with Dimensionality Reduction and Machine Learning Techniques

719

Figure 6: XGBoost performance on the 2-class dataset: confusion matrix, ROC curve, and PR curve.

predictions, with 63 instances misclassiﬁed as Class

1. The model has nearly perfect Recall for Class

1 (8,400/8,404 = 99.95%) and very high Precision

(8,400/8,463 = 99.26%). The ROC curve shows AUC

of 0.9980. The curve rises almost vertically from the

origin, suggesting the model achieves very high true

positive rates with extremely low false positive rates.

The PR curve analysis shows a perfect performance

with an Average Precision (AP) of 1.00. Precision

remains at 1.0 across nearly the entire range of recall

values, only dropping slightly at the highest recall lev-

els. The model achieves perfect precision even when

recall increases.

The XGBoost model is particularly effective at

identifying Class 1 instances, with almost no false

negatives. Despite the presence of class imbalance,

the model maintains excellent performance across

evaluation metrics. The AUC of 0.9980 and AP of

1.00 suggest a model that would be extremely reliable

in production environments.

4.1.2 Three-Class Dataset

Table 4 shows the summary results of the ML meth-

ods to the 3-class original dataset.

The model with the highest accuracy is XGBoost.

Figure 7 depicts the analysis of the XGBoost classi-

ﬁcation results regarding the confusion matrix, ROC

curve, and PR-curve.

Class 2 shows the best performance with 30,874

correct predictions and relatively few misclassiﬁca-

tions (480 as Class 1 and 87 as Class 0). Class 1

Table 3: Model comparison for 2-class classiﬁcation. The

best accuracy is in boldface.

Model Accuracy Precision Recall F1 Score P. Time (s)

Efﬁciency

(Accuracy/Time)

Naive Bayes 0.6333 0.9198 0.6333 0.7064 4.13 0.1534

KNN 0.9753 0.9748 0.9753 0.975 0.66 1.4706

LinearSVC 0.9726 0.9718 0.9726 0.9718 192.06 0.0051

Decision Tree 0.9798 0.9801 0.9798 0.9799 225.37 0.0043

XGBoost 0.9928 0.9928 0.9928 0.9927 298.1 0.0033

SVM 0.9742 0.9735 0.9742 0.9734 612.54 0.0016

LightGBM 0.9919 0.9919 0.9919 0.9918 969.44 0.001

Random Forest 0.99 0.9901 0.99 0.9898 1040.6 0.001

CatBoost 0.9917 0.9918 0.9917 0.9916 1304.82 0.0008

Logistic Regression 0.9445 0.9403 0.9445 0.9406 1920.06 0.0005

MLP 0.9816 0.9814 0.9816 0.9815 2930.41 0.0003

has good performance with 7,409 correct predictions,

though with some misclassiﬁcations to Class 2 (995).

Class 0 has 750 correct predictions, with misclassiﬁ-

cations primarily to Class 2 (132). All classes show

AUC scores above 0.98, indicating strong discrimi-

native power. Micro average AUC is 0.9960, sug-

gesting excellent overall classiﬁcation performance.

Class 0 has the highest individual AUC (0.9950),

followed by Class 1 (0.9900) and Class 2 (0.9887).

All ROC curves rise steeply at low false positive

rates, indicating the model achieves high true posi-

tive rates while maintaining low false positive rates.

The PR curve analysis shows a curve with strong

performance across all classes. Class 2 shows the

best precision-recall trade-off with Average Precision

(AP) of 0.9964. Class 0 shows degradation in preci-

sion at higher recall values (AP = 0.9222). Class 1

maintains good precision until very high recall val-

ues (AP = 0.9707). The micro-average AP is 0.9924,

conﬁrming excellent overall performance.

The XGBoost model provides adequate perfor-

mance for the 3-class classiﬁcation problem. The

model is particularly effective at identifying Class 2

instances. Despite class imbalance, the model attains

strong performance across all classes with high AUC

and AP scores.

4.2 Feature Selection

We now assess the use of FS techniques over the

dataset. Table 5 compares features selected by dif-

ferent methods for the 2-class dataset.

Table 4: Model comparison for 3-class classiﬁcation. The

best accuracy is in boldface.

Model Accuracy Precision Recall F1 Score P. Time (s)

Efﬁciency

(Accuracy/Time)

Naive Bayes 0.3095 0.8052 0.3095 0.42 6.63 0.0467

Decision Tree 0.923 0.9237 0.923 0.9233 588.92 0.0016

KNN 0.9023 0.8997 0.9023 0.8984 1.28 0.7068

XGBoost 0.9578 0.9573 0.9578 0.9573 925.94 0.001

CatBoost 0.9526 0.9519 0.9526 0.9519 1334.09 0.0007

LinearSVC 0.8509 0.8295 0.8509 0.8281 1602.05 0.0005

Random Forest 0.9523 0.9519 0.9523 0.9512 1730.69 0.0006

LightGBM 0.9507 0.9501 0.9507 0.95 2033.22 0.0005

Logistic Regression 0.8533 0.8306 0.8533 0.8321 3225.23 0.0003

SVM 0.9009 0.8998 0.9009 0.8875 6718.72 0.0001

MLP 0.919 0.9173 0.919 0.917 15742.4 0.0001

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

720

Figure 7: XGBoost performance on the 3-class dataset: confusion matrix, ROC curve, and PR curve.

Table 6 compares features selected by different

methods, for the 3-class dataset.

4.3 Feature Reduction

Figure 8 consists of two complementary plots analyz-

ing PCA results over the 3-class dataset.

Figure 8: PCA Explained variance for the 3-class dataset.

The individual and cumulative explained variance

shows both individual contribution (blue bars) and cu-

mulative explained variance (red step line) for the ﬁrst

10 principal components. The ﬁrst principal compo-

nent captures approximately 10% of the total vari-

ance. Subsequent components contribute progres-

sively less variance, exhibiting a typical elbow pat-

tern and the cumulative explained variance reaches

approximately 45% by the 10th component. This

PCA analysis reveals a dataset with high intrinsic di-

mensionality. No single component or small subset of

components captures the majority of variance. Even

Table 5: Comparison of features selected by different meth-

ods (2-class dataset). Top 10 features selected by each

method showing limited overlap (3 common features).

Selected Features (ANOVA) Selected Features (XGBOOST)

tx ftr 51 tx ftr 30

tx ftr 52 tx ftr 89

tx ftr 53 tx ftr 58

tx ftr 54 tx ftr 79

tx ftr 88 agg ftr 69

tx ftr 89 agg ftr 67

tx ftr 90 tx ftr 54

agg ftr 48 tx ftr 52

agg ftr 56 tx ftr 45

agg ftr 60 tx ftr 4

Table 6: Comparison of features selected by different meth-

ods (3-class dataset). Top 10 features selected by each

method showing limited overlap (3 common features).

Selected Features (ANOVA) Selected Features (XGBOOST)

tx ftr 51 tx ftr 19

tx ftr 52 tx ftr 59

tx ftr 53 tx ftr 84

tx ftr 54 tx ftr 75

tx ftr 58 tx ftr 58

tx ftr 59 tx ftr 33

tx ftr 60 tx ftr 4

tx ftr 64 agg ftr 30

tx ftr 65 tx ftr 52

tx ftr 66 tx ftr 47

with 10 components, less than half of the total vari-

ance is explained. This suggests a complex, high-

dimensional data structure where information is dis-

tributed across many features.

Figure 9 displays a UMAP visualization of the

dataset, reducing high-dimensional data to a 2D rep-

resentation.

Figure 9: UMAP Projection for the 3-class dataset.

The data points are colored by class: gray (2-

Unknown), green (1-Licit) and red (0-Illicit). The

projection shows complex, overlapping clusters with

some visible structure. Class 2 (Unknown, gray) ap-

pears most abundant and widely distributed. Class 1

(Licit, green) shows partial separation in some regions

but considerable overlap with Class 2. Class 0 (Illicit,

red) has fewer points and tends to overlap with both

Bitcoin Fraud Detection: A Study with Dimensionality Reduction and Machine Learning Techniques

721

other classes.

The UMAP visualization shows a signiﬁcant over-

lap between classes. Some regions show higher den-

sity of speciﬁc classes, with partial discriminative

power in the features. The presence of small clus-

ters and substructures suggests potential subgroups

within each class. The manifold structure appears

complex, with multiple connected regions. While

complete class separation is difﬁcult, there exist dis-

tinguishable patterns that ML algorithms might lever-

age. Some outlier points and smaller clusters appear

at the periphery, potentially representing unusual or

anomalous cases.

We now assess the evaluation of classiﬁcation

with reduced dimensionality datasets, using XG-

Boost. Table 7 reports the results for the two-class

version dataset while Table 8 does a similar evalua-

tion for the three class version of the dataset.

Table 7: 2-Class reduced dimensionality with XGBoost.

The best global accuracy is in boldface. The best accuracy

with dimensionality reduction is highlighted in green.

Dataset Accuracy Precision Recall F1 Score P. Time (s) Efﬁciency

2class anova 0.9821 0.9818 0.9821 0.9816 0.37 2.6687

2class anova pca 0.9733 0.9725 0.9733 0.9724 0.35 2.7613

2class anova umap 0.9566 0.9569 0.9586 0.9574 0.22 4.3178

2class original 0.9928 0.9928 0.9928 0.9927 2.93 0.3386

2class original scaled 0.9931 0.9932 0.9931 0.9930 2.81 0.3533

2class pca 0.9715 0.9707 0.9715 0.9706 0.43 2.2647

2class umap 0.9553 0.9536 0.9553 0.9542 0.28 3.4115

2class xgboostfs 0.9839 0.9836 0.9839 0.9836 0.44 2.2515

2class xgboostfs pca 0.9802 0.9798 0.9802 0.9798 0.48 2.0252

2class xgboostfs umap 0.9764 0.9759 0.9764 0.9755 0.23 4.2638

Table 8: 3-Class reduced dimensionality with XGBoost.

The best global accuracy is in boldface. The best accuracy

with dimensionality reduction is highlighted in green.

Dataset Accuracy Precision Recall F1 Score P. Time (s) Efﬁciency

3class anova 0.9071 0.9045 0.9071 0.9036 3.97 0.2286

3class anova pca 0.8871 0.8845 0.8871 0.8789 4.00 0.2216

3class anova umap 0.8739 0.8700 0.8739 0.8615 3.24 0.2698

3class original 0.9578 0.9573 0.9578 0.9573 22.44 0.0427

3class original scaled 0.9576 0.9571 0.9576 0.9571 21.62 0.0443

3class pca 0.8867 0.8830 0.8867 0.8798 4.27 0.2078

3class umap 0.8657 0.8599 0.8657 0.8527 3.04 0.2852

3class

xgboost 0.9259 0.9244 0.9259 0.9238 3.76 0.2464

3class xgboostfs pca 0.8961 0.8939 0.8961 0.8901 3.92 0.2286

3class xgboostfs umap 0.8674 0.8646 0.8674 0.8547 2.92 0.2966

These DR reduction techniques do not improve

the classiﬁcation results, as compared to the use of the

original dimensionality. However, data scaling im-

proves the results of XGBoost, for the 2-class case,

as compared with the ones reported in Table 3.

Among the classiﬁcation models considered XG-

Boost provided the best results, performing better on

the 2-class dataset as compared to the 3-class dataset.

Combining insights from the data visualizations, we

conclude that the dataset exhibits high intrinsic di-

mensionality, as shown by the PCA analysis. The use

of dimensionality reduction techniques needs further

investigation.

5 CONCLUSIONS

The identiﬁcation of fraudulent cryptocurrency trans-

actions has key importance. The transaction data

poses many challenges to machine learning methods.

These datasets have many features and are typically

imbalanced, with a few illicit examples.

In this paper, we have addressed the use of ma-

chine learning techniques over the Elliptic dataset

with Bitcoin transaction data, using dimensionality

reduction and classiﬁcation techniques. Our experi-

mental evaluation has shown that the XGBoost clas-

siﬁer is the best performing method being resilient

to the natural class imbalance. The dimensional-

ity reduction techniques, with selection and reduc-

tion methods, were able to identify adequate and re-

duced subsets suitable for explainability purposes on

the classiﬁcation decision. We have also addressed

the use of explainability techniques to identify the

most decisive features.

As future work, we plan to assess the effect of the

use of instance sampling techniques. We also plan

to explore more supervised dimensionality reduction

techniques to achieve lower dimensionality datasets.

ACKNOWLEDGEMENTS

This research was supported by Instituto

Polit

ecnico de Lisboa (IPL) under Grant

IPL/IDI&CA2024/ML4EP ISEL.

REFERENCES

Abdulkadhim, R., Abdullah, H., and Hadi, M. (2024). Sur-

veying the prediction of risks in cryptocurrency in-

vestments using recurrent neural networks. Open En-

gineering, 14.

Ahmed, A. and Alabi, O. (2024). Secure and scalable

blockchain-based federated learning for cryptocur-

rency fraud detection: A systematic review. IEEE Ac-

cess, 12:102219–102241.

Alarab, I. and Prakoonwit, S. (2023a). Graph-based LSTM

for anti-money laundering: Experimenting temporal

graph convolutional network with bitcoin data. Neural

Processing Letters, 55(1):689–707.

Alarab, I. and Prakoonwit, S. (2023b). Robust recur-

rent graph convolutional network approach based se-

quential prediction of illicit transactions in cryp-

tocurrencies. Multimedia Tools and Applications,

83(20):58449–58464.

Allende, M., Le

on, D., Cer

on, S., Pareja, A., Pacheco, E.,

Leal, A., and Silva, M. (2023). Quantum-resistance in

blockchain networks. Scientiﬁc Reports, 13(1):5664.

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

722

Chauhan, R., Mehtar, K., Kaur, H., and Alankar, B. (2024).

Evaluating cyber-crime using machine learning and

AI approach for environmental sustainability. In Pro-

ceedings of the Sustainable Development through Ma-

chine Learning, AI and IoT, pages 37–49.

Di, Z., Wang, G., Jia, L., and Chen, Z. (2022). Bitcoin

transactions as a graph. IET Blockchain, 2:57–66.

Dutta, S., Sharma, A., and Rajgor, J. (2024). Ethereum

fraud prevention: A supervised learning approach for

fraudulent account recognition. In Proceedings of the

2024 1st International Conference on Trends in Engi-

neering Systems and Technologies.

Ester, M., Kriegel, H., Sander, J., and Xu, X. (1996). A

density-based algorithm for discovering clusters in

large spatial databases with noise. Proceedings of the

Second International Conference on Knowledge Dis-

covery and Data Mining (KDD-96), pages 226–231.

urﬁdan, R. (2024). Suspicious transaction alert and block-

ing system for cryptocurrency exchanges in meta-

verse’s social media universes: Rg-guard. Neural

Computing and Applications, 36:18825–18840.

Harlev, M., Yin, H., Langenheldt, K., Mukkamala, R., and

Vatrapu, R. (2018). Breaking bad: De-anonymising

entity types on the bitcoin blockchain using super-

vised machine learning. In Proceedings of the 51st

Hawaii International Conference on System Sciences.

Hisham, S., Makhtar, M., and Aziz, A. (2023). Anomaly de-

tection in smart contracts based on optimal relevance

hybrid features analysis in the Ethereum blockchain

employing ensemble learning. International Jour-

nal of Advanced Technology and Engineering Explo-

ration, 10(109).

Hu, Y., Seneviratne, S., Thilakarathna, K., Fukuda, K., and

Seneviratne, A. (2019). Characterizing and detecting

money laundering activities on the bitcoin network.

https://arxiv.org/abs/1912.12060.

Liu, T., Wang, Y., Sun, J., Tian, Y., Huang, Y., Xue, T., Li,

P., and Liu, Y. (2024). The role of transformer mod-

els in advancing blockchain technology: A systematic

survey. arXiv.

MacQueen, J. (1967). Some methods for classiﬁcation and

analysis of multivariate observations. Proceedings of

the Fifth Berkeley Symposium on Mathematical Statis-

tics and Probability, 1:281–297.

Md, A., Narayanan, S., Sabireen, H., Sivaraman, A., and

Tee, K. (2023). A novel approach to detect fraud in

ethereum transactions using stacking. Expert Systems,

40(7):e13255.

Monamo, P., Marivate, V., and Twala, B. (2016). Unsu-

pervised learning for robust bitcoin fraud detection.

In 2016 Information Security for South Africa (ISSA),

pages 129–134. IEEE.

Nakamoto, S. (2008). Bitcoin: A peer-to-peer electronic

cash system. Bitcoin.org. https://bitcoin.org/bitcoin.

pdf.

Ngai, E., Hu, Y., Wong, Y., Chen, Y., and Sun, X. (2011).

The application of data mining techniques in ﬁnan-

cial fraud detection: A classiﬁcation framework and

an academic review of literature. Decision Support

Systems, 50(3):559–569.

Olutimehin, A. (2025). The synergistic role of machine

learning, deep learning, and reinforcement learning in

strengthening cyber security measures for crypto cur-

rency platforms. Asian Journal of Research in Com-

puter Science, 18(3):190–212.

Pham, T. and Lee, S. (2017). Anomaly detection in bitcoin

network using unsupervised learning methods. arXiv.

Pushpak, S. (2025). Quantum machine learning technique

for insurance claim fraud detection with quantum fea-

ture selection. Journal of Information Systems Engi-

neering and Management, 10(8s):750–756.

erez-Cano, V. and Jurado, F. (2024). Fraud detec-

tion in cryptocurrency networks—an exploration us-

ing anomaly detection and heterogeneous graph trans-

formers. Future Internet, 17(1):44.

Snigdha, K., Reddy, P., Hema, D., and Gayathri, S. (2024).

Bitpredict: End-to-end context-aware detection of

anomalies in bitcoin transactions using stack model

network. In Proceedings of the 3rd International Con-

ference on Advances in Computing, Communication

and Applied Informatics.

Taher, S., Ameen, S., and Ahmed, J. (2024). Advanced

fraud detection in blockchain transactions: An en-

semble learning and explainable AI approach. En-

gineering, Technology & Applied Science Research,

14:12822–12830.

Team, C. R. (2024). Global cryptocurrency market cap

charts. Available at: https://www.coingecko.com/en/

global-charts (Accessed: 23 April 2025).

United Nations Ofﬁce on Drugs and Crime (2011). Estimat-

ing illicit ﬁnancial ﬂows resulting from drug trafﬁck-

ing and other transnational organized crimes.

Weber, M., Domeniconi, G., Chen, J., Weidele, D. K. I.,

Bellei, C., Robinson, T., and Leiserson, C. E. (2019).

Anti-money laundering in bitcoin: Experimenting

with graph convolutional networks for ﬁnancial foren-

sics. arXiv preprint arXiv:1908.02591. {https://arxiv.

org/abs/1908.02591}.

Yang, X., Zhang, C., Sun, Y., Pang, K., Jing, L., Wa, S., and

Lv, C. (2023). Finchain-bert: A high-accuracy auto-

matic fraud detection model based on nlp methods for

ﬁnancial scenarios. Information, 14(9):499.

Yin, H. and Vatrapu, R. (2017). A ﬁrst estimation of the pro-

portion of cybercriminal entities in the bitcoin ecosys-

tem using supervised machine learning. In 2017 IEEE

International Conference on Big Data (Big Data),

pages 3690–3699. IEEE.

Zhang, Y. and Trubey, P. (2019). Machine learning and

sampling scheme: An empirical study of money

laundering detection. Computational Economics,

54(3):1043–1063.

Bitcoin Fraud Detection: A Study with Dimensionality Reduction and Machine Learning Techniques

723