
Iterative Learning Robust PD-SDRE Control for Active
Transfemoral Prostheses
Anna Bavarsad
a
, Elias August
b
and Magnús Kjartan Gíslason
c
Reykjavik University, Department of Engineering, Menntavegur 1,
102 Reykjavik, Iceland
Keywords: Prosthetic Legs, Sliding Mode Control, Iterative Learning Control, SDRE, Robotics.
Abstract: In this paper, we present a novel control strategy for active prosthetic legs. The approach uses an intelligent
robust Proportional-Derivative State-Dependent Riccati Equation controller to reduce the use of
biomechanical energy, enhance performance and robustness. We include an Iterative Learning Control
algorithm, to minimise control errors and allow the controller gains to adapt over time, and robust Sliding
Mode Control to specifically address potential parametric and non-parametric uncertainties, disturbances, and
noise. We conduct tests to demonstrate that the proposed controller not only maintains stability but also
outperforms existing methods in terms of energy efficiency and tracking. Application of the proposed method
in simulations shows significant improvements when compared to other methods from the literature, with up
to 98.3% reduction in position tracking error and up to 91.9% reduction in control cost. Furthermore, for
angular tracking of the hip and knee, improvements of up to 32.6% and 44.9%, along with torque reductions
of up to 67.5% and 87.5%, are observed. This study represents a step forward in providing an effective
solution for controlling active prosthetic devices.
1 INTRODUCTION
The global incidence of lower limb amputation
continues to rise, with over 200,000 cases reported
annually in the United States alone (McDonald et al.,
2021, Ziegler-Graham et al., 2008), while there is an
urgent need for advanced prosthetic solutions that
restore natural gait and improve the overall quality of
life for amputees. Amputations can occur at various
levels, including transtibial (below the knee),
transfemoral (above the knee), foot amputations, and
hip and knee disarticulations (Kibria and Commuri,
2024). Restoring complete mobility remains
particularly challenging for transfemoral amputees.
Currently, there are three primary types of prosthetic
legs: passive, active (with motor control), and semi-
active ones (control without motors). Passive
prostheses require users to engage their residual hip
joint to move the prosthetic knee, which leads to
increased effort, of up to 60% more biomechanical
energy usage compared to other individuals, and
potential discomfort (Bukowski, 2006 and Chin et al.,
a
https://orcid.org/0000-0002-6444-487X
b
https://orcid.org/0000-0001-9018-5624
c
https://orcid.org/0000-0003-0872-5201
2005). Active prostheses offer some key advantages
over passive ones, such as a reduced energy usage,
improved stability, and more natural movement
(Orendurff et al., 2006, Kaufman et al., 2008,
Camargo et al., 2022). However, they require
complex control systems and are more expensive.
Moreover, ensuring stability, responsiveness, and
energy efficiency is challenging in the presence of
uncertainties and disturbances (Müßig et al., 2019,
Martini et al., 2020). Users of robotic leg prostheses
often struggle with stability and symmetry compared
to healthy individuals, largely due to system
uncertainties and environmental disturbances, such as
unknown mass distribution and complex foot-ground
interactions, respectively, and sensor noise (Ma et al.,
2024).
Designing controllers that provide performance for
different users and environments remains challenging
(Kashiri et al., 2018). In this paper, we propose a
novel control strategy to address the following
multiple control objectives simultaneously: energy
efficiency, accurate trajectory tracking, and
Bavarsad, A., August, E., Gíslason and M. K.
Iterative Learning Robust PD-SDRE Control for Active Transfemoral Prostheses.
DOI: 10.5220/0013645200003970
In Proceedings of the 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2025), pages 117-125
ISBN: 978-989-758-759-7; ISSN: 2184-2841
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)
117

robustness. While recent studies, such as (Saat et al.,
2024), have explored various advancements in
Proportional-Integral-Derivative (PID) and
Proportional-Derivative (PD) control methods, this
work focuses on a novel approach by proposing an
intelligent PD State-Dependent Riccati Equation
(PD-SDRE) control approach, which merges the
effectiveness of a traditional PD controller with the
advanced optimisation capabilities of SDRE control.
SDRE control is designed for systems whose
dynamics explicitly depend on the state. It aims to
minimise a predefined cost function while
maintaining stability. SDRE control does not require
model linearisation, but the dynamic adjustment of
controller gains based on the system’s state, making
it particularly effective for complex nonlinear
systems (Çimen, 2008, Nekoo, 2019). It has been
successfully applied in various fields, especially
robotics (Bavarsad et al., 2020, Bavarsad et al., 2021).
To further improve the controller, we also integrate
an Iterative Learning Control (ILC) algorithm. ILC is
particularly useful in environments that call for
repeated tasks, as it progressively optimises the
control using data from prior iterations. This allows
the system to “learn” from previous errors and to
improve the performance. Given the repetitive nature
of activities such as walking and climbing stairs, ILC
is particularly suitable for improving performance
over time after the PD-SDRE controller provides the
initial input (Ahn et al., 2007, Shen, 2018, Nekoo et
al., 2022, Memon and Shao, 2021).
Our approach also includes the integration of robust
Sliding Mode Control (SMC) for managing
uncertainties. In principle, it drives the system’s state
to “slide” along a predefined surface, known as the
sliding surface, on which the system exhibits
simplified behaviour. Once on this surface, the
dynamics of the system become less sensitive to
model uncertainties and external disturbances,
making SMC particularly useful in unpredictable
environments (Slotine and Li, 1991). This paper
introduces the following key innovations:
1. Application of PD-SDRE with ILC: To our
knowledge, this study is the first one to apply PD-
SDRE in combination with ILC to active
prosthetic legs.
2. Enhanced Robustness through SMC: Our
integration of robust SMC techniques improves
the system’s ability to cope with parametric and
non-parametric uncertainties while maintaining
stability and performance.
3. Simplified Desired Dynamics Calculation in ILC:
We simplify the dynamics calculations required
by the ILC. Instead of computing the Jacobian
matrix, we use desired trajectory values for
position, velocity, and acceleration for the
calculation of the desired dynamics. This reduces
computational complexity and broadens the
controller’s applicability to various robotic
systems, including active prosthetic legs.
Simulations show that this modified ILC
approach effectively learns desired dynamics to
improve trajectory tracking over time.
The structure of the remainder of this paper is the
following. In Section 2, we present the model for an
active transfemoral prosthesis and in Section 3, the
design of the ILC robust PD-SDRE controller.
Section 4 provides simulation results and shows the
effectiveness of our approach. Section 5 discusses the
results and concludes the paper.
2 DYNAMIC MODEL OF AN
ACTIVE TRANSFEMORAL
PROSTHESIS
The three degrees-of-freedom dynamical model for
the active transfemoral prosthesis is given by (Azimi
et al., 2015):
𝑴
𝑷
𝒒
𝑡
𝒒
𝑡
+
𝑪
𝑷
𝒒
𝑡
, 𝒒
𝑡
𝒒
𝑡
+𝑮
𝑷
𝒒
𝑡
+ 𝑹
𝑷
𝒒
𝑡
, 𝒒
𝑡
= 𝒖
𝑡
−𝑻
𝒆
𝒒
𝑡
.
(1)
In (1), 𝑴
𝑷
𝒒
𝑡
is the invertible inertia matrix,
𝑪
𝑷
𝒒
𝑡
, 𝒒
𝑡
represents the Coriolis and centripetal
matrix,
𝑮
𝑷
𝒒
𝑡
denotes the gravity vector, and
𝑹
𝑷
𝒒
𝑡
, 𝒒
𝑡
accounts for the nonlinear damping
vector. Vector
𝒒
=
𝑞
𝑞
𝑞
describes the
displacement of the joints, where
𝑞
corresponds to
the hip vertical displacement,
𝑞
is the thigh angle,
and
𝑞
is the knee angle. 𝒖
𝑡
includes the control
force at the hip and the control torques at thigh and
knee joints. Term
𝑻
𝒆
𝒒
𝑡
captures the combined
effects of the horizontal,
𝐹
, and the vertical, 𝐹
,
components of the ground reaction force (GRF) on
each joint. The complete equations are:
𝑃
= 𝑚
+ 𝑚
+ 𝑚
,
𝑃
= 𝑚
𝑙
+ 𝑚
𝑙
+ 𝑚
𝑐
, 𝑃
= 𝑚
𝑐
,
𝑃
= 𝐼
+ 𝐼
+ 𝑚
𝑐
+ 𝑚
𝑐
+ 𝑚
𝑙
+ 𝑚
𝑙
+
2𝑚
𝑐
𝑙
,
𝑃
= 𝑚
𝑐
𝑙
, 𝑃
= 𝑚
𝑐
+ 𝐼
, 𝑃
= 𝑏, 𝑃
= 𝑓,
𝑴
𝑷
=
𝑃
𝑚
𝑃
𝑐𝑜𝑠
𝑞
+ 𝑞
𝑚
𝑃
+2𝑃
𝑐𝑜𝑠𝑞
𝑃
+ 𝑃
𝑐𝑜𝑠𝑞
𝑃
𝑐𝑜𝑠
𝑞
+ 𝑞
𝑃
+ 𝑃
𝑐𝑜𝑠𝑞
𝑃
,
𝑚
= 𝑃
cos
𝑞
+ 𝑞
+ 𝑃
cos 𝑞
,
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
118
𝑪
𝑷
=
0 𝑐
−𝑞
𝑃
sin 𝑞
𝑐
0 −𝑞
𝑃
sin 𝑞
𝑐
0 𝑞
𝑃
sin 𝑞
0
,
(2)
𝑐
= −𝑞
𝑃
sin
𝑞
+ 𝑞
−𝑞
𝑃
sin
𝑞
+ 𝑞
,
𝑐
= −𝑞
𝑃
sin 𝑞
−𝑞
𝑃
sin 𝑞
,
𝑮
𝑷
= −𝑔
𝑃
𝑃
𝑚
𝑃
𝑐𝑜𝑠
𝑞
+ 𝑞
, 𝑹
𝑷
=
𝑃
𝑡𝑎𝑛ℎ𝑞
𝑃
𝑞
0
,
𝑻
𝒆
𝒒
𝑡
=
𝐹
𝐹
𝑙
cos 𝑞
+ 𝑙
𝑐
−𝐹
𝑙
sin 𝑞
+ 𝑙
𝑠
𝐹
𝑙
𝑐
−𝐹
𝑙
𝑠
,
𝑐
=cos
𝑞
+ 𝑞
, 𝑠
=sin
𝑞
+ 𝑞
𝐿
= 𝑞
+ 𝑙
sin 𝑞
+ 𝑙
𝑠
,
𝐹
=
0 , 𝐿
𝑠
𝑘
|
𝑠
−𝐿
|
, 𝐿
𝑠
, 𝐹
= 𝛽𝐹
.
As in (Azimi et al., 2015), we assume that a treadmill
is used as walking surface and the treadmill belt is
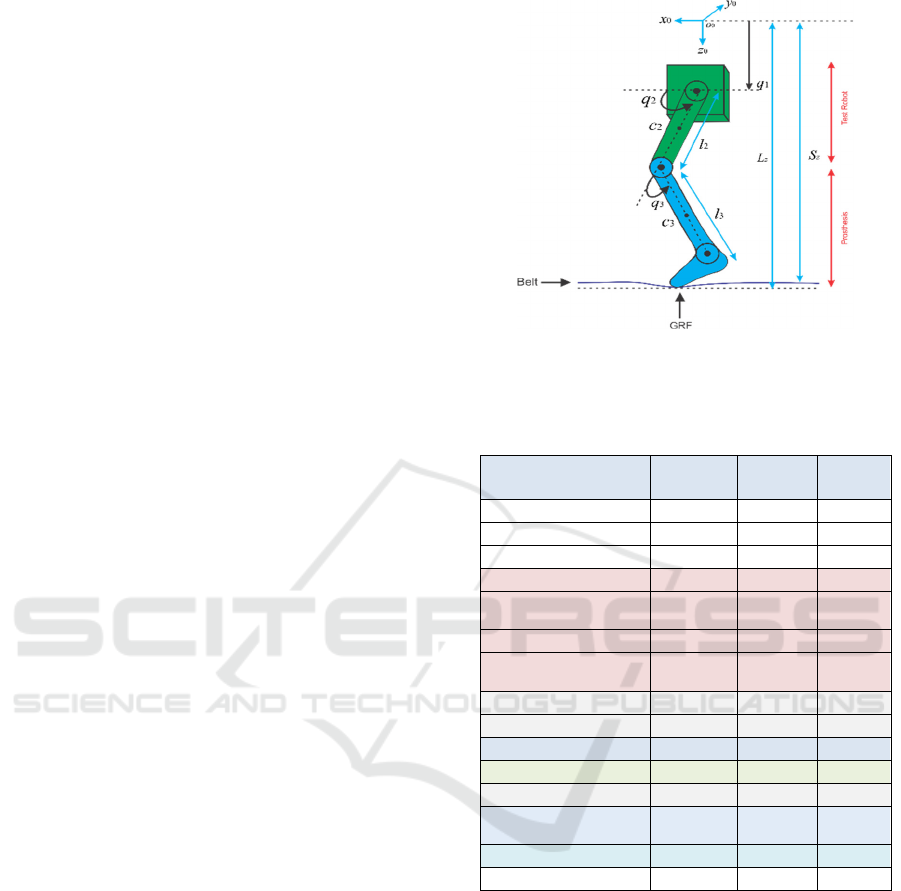
modelled by a mechanical spring. In (2),
𝐿
represents the vertical position of the lower leg in the
belt’s global coordinate system
𝑥
, 𝑦
, 𝑧
(see Figure
1). Description and specific nominal values for the
model and the treadmill parameters are provided in
Table 1.
To allow for a comparison with the results in
(Bavarsad et al., 2020) and (Azimi et al., 2015), we
use parameters from these references. State vector,
input vector, and reference trajectory
are
𝒙
𝑡
=
𝑞
𝑞
𝑞
𝑞
𝑞
𝑞
,
𝒖
𝑡
= 𝐹
𝜏
𝜏
,
𝒓
𝑡
=
𝑟
𝑟
𝑟
𝑟
𝑟
𝑟
𝑟
𝑟
𝑟
.
(3)
For
𝒓
𝑡
, we use walking data from the Motion Study
Laboratory at the Cleveland Department of Veterans
Affairs Medical Center (Azimi et al., 2015). Finally,
the state-space representation of system (1) is given
by
⎣
⎢
⎢
⎢
⎢
⎡
𝑥
𝑥
𝑥
𝑥
𝑥
𝑥
⎦
⎥
⎥
⎥
⎥
⎤
=
⎣
⎢
⎢
⎢
⎢
⎡
𝑥
𝑥
𝑥
𝑣
𝑣
𝑣
⎦
⎥
⎥
⎥
⎥
⎤
,
𝒗𝑡= 𝑴
𝑷
𝒖𝑡−𝑻
𝒆
−𝑪
𝑷
𝒒
−𝑮
𝑷
−𝑹
𝑷
.
(4)
Figure 1: The Prismatic-Revolute-Revolute structure of the
active transfemoral prosthesis (Azimi et al., 2015).
Table 1: Nominal values and specific parameters for
prosthesis model and treadmill.
Description
Parameter
Nominal
value
Unit
Mass of link 1
𝑚
40.5969
kg
Mass of link 2
𝑚
8.5731
kg
Mass of link 3
𝑚
2.29
kg
Thigh length
𝑙
0.425
m
Length from knee joint
to bottom of shoe
𝑙
0.527
m
Center of mass on thigh
𝑐
0.09
m
Center of mass on shank
𝑐
0.32
m
Rotary inertia of link 2
𝐼
0.138
kgm
2
Rotary inertia of like 3
𝐼
0.0618
kgm
2
Sliding friction in link 1
𝑓
83.33
N
Rotary actuator damping
𝑏
9.75
Nms
Acceleration of gravity
𝑔
9.81
m/s
2
Vertical distance from
the origin of belt frame
𝑆
0.905
m
Belt stiffness
𝐾
37000
N/m
Friction coefficient
𝛽
0.2
-
3 LEARNING CONTROL WITH
ROBUST PD - SDRE
3.1 SDRE
Consider the following uncertain nonlinear system,
𝒙
𝑡
=
𝒇
𝒙
𝑡
+ 𝒈
𝒙
𝑡
𝒖
𝑡
.
(5)
In (5),
𝒇
𝒙
𝑡
and
𝒈
𝒙
𝑡
𝒖
𝑡
represent the actual
system dynamics, which include uncertainties due to
unknown but bounded parameter values. Next, we
transform (5) using State Dependent Coefficients
parametrisation matrices, that is, we let
𝒇𝒙
𝑡
=
Iterative Learning Robust PD-SDRE Control for Active Transfemoral Prostheses
119

𝑨𝒙
𝑡
𝒙
𝑡
, 𝑨𝒙
𝑡
: ℝ
→ℝ
×
, and 𝒈𝒙
𝑡
=
𝑩𝒙
𝑡
, 𝑩𝒙
𝑡
: ℝ
→ℝ
×
, and consider the
following nonlinear dynamical system,
𝒙
𝑡
= 𝑨𝒙
𝑡
𝒙
𝑡
+ 𝑩𝒙
𝑡
𝒖
𝑡
,
𝒚
𝑡
= 𝑪𝒙
𝑡
𝒙
𝑡
.
(6)
Note that matrices 𝑨𝒙
𝑡
and 𝑩𝒙
𝑡
are not
unique (Çimen, 2008). In this paper,
𝑨𝒙
𝑡
×
=
0
×
𝐼
×
0
×
−𝑴
×
𝒙
𝑡
𝑪
×
(𝒙
(
𝑡
, 𝒙
(
𝑡
)
,
𝑩𝒙
(
𝑡
)
×
=
0
×
𝑴
×
𝒙
(
𝑡
)
,
𝑪𝒙
(
𝑡
)
×
= 𝐼
×
.
(7)
Definition 1 (Çimen, 2008): (6) is stabilisable
(controllable) if, for every
𝒙∈Ω, the pair
𝑨𝒙
(
𝑡
)
, 𝑩𝒙
(
𝑡
)
is pointwise linear stabilisable
(controllable).
Definition 2 (Çimen, 2008): (6) is detectable
(observable) if, for every
𝒙∈Ω, the pair
𝑨𝒙
(
𝑡
)
, 𝑪𝒙
(
𝑡
)
is pointwise linear detectable
(observable).
If (6) is controllable and observable, then an optimal
controller is obtained by minimising cost function
𝐽
=
1
2
𝒙
(
𝑡
)
𝑪
𝑸𝑪𝒙
(
𝑡
)
+ 𝒖
(
𝑡
)
𝑹𝒖
(
𝑡
)
𝑑𝑡
𝟎
,
(8)
where weighting matrices 𝑸 and 𝑹 are positive
definite. The optimal control law is then given by
𝒖
(
𝑺𝑫𝑹𝑬
)
(
𝑡
)
= −𝑹
𝑩
(
𝒙
)
𝑲
(
𝒙
)
𝒆, 𝒆
,
(9)
where 𝒆= 𝒙−𝒓 , 𝒆
= 𝒙
−𝒓
, and matrix 𝑲𝒙
(
𝑡
)
is
determined by solving the following algebraic SDRE:
𝑨
(
𝒙
)
𝑲
(
𝒙
)
+ 𝑲
(
𝒙
)
𝑨
(
𝒙
)
−
𝑲
(
𝒙
)
𝑩
(
𝒙
)
𝑹
𝟏
𝑩
(
𝒙
)
𝑲
(
𝒙
)
+ 𝑪
𝑸𝑪= 𝟎.
(10)
Note also that we will partition 𝑲
(
𝒙
)
into the
following four-square blocks:
𝑲
(
𝒙
)
=
𝑲
𝟏𝟏
(
𝒙
)
𝑲
𝟏𝟐
(
𝒙
)
𝑲
𝟏𝟐
𝑻
(
𝒙
)
𝑲
𝟐𝟐
(
𝒙
)
.
(11)
Finally, as in (Nekoo, 2019, Bavarsad et al., 2021),
we incorporate unfactored terms into
𝒖
𝒂𝒅𝒅
(
𝑡
)
= 𝑮
𝑷
𝒒
(
𝑡
)
+ 𝑹
𝑷
𝒒
(
𝑡
)
+ 𝑻
𝒆
𝒒
(
𝑡
)
(12)
such that the control law becomes
𝒖
(
𝑡
)
= 𝒖
(
𝑺𝑫𝑹𝑬
)
(
𝑡
)
+ 𝒖
𝒂𝒅𝒅
(
𝑡
)
.
(13)
3.2 PD - SDRE
To include PD control, the control law is modified to:
𝒖
(
𝑷𝑫𝑺𝑫𝑹𝑬
)
(
𝑡
)
= −ℵ
𝟏
(
𝒙
)
𝒆−ℵ
𝟐
(
𝒙
)
𝒆
,
(14)
ℵ
𝟏
(
𝒙
)
= 𝑹
𝟏
𝑴
𝑷
𝟏
𝑲
𝟏𝟐
,
ℵ
𝟐
(
𝒙
)
= 𝑹
𝟏
𝑴
𝑷
𝟏
𝑲
𝟐𝟐
.
(15)
(16)
Note that matrices (15) and (16) are not necessarily
symmetric positive definite. To ensure the stability of
the controller, the gain matrices must be symmetric
positive definite (Nekoo et al., 2022). To address this,
we consider the following transformation,
𝑲
𝑺𝑷
(
𝒙
)
=
𝑲
𝟏𝟐
𝑴
𝑷
𝟏
𝑹
𝟏
𝑴
𝑷
𝟏
𝑲
𝟏𝟐
𝑲
𝟏𝟐
𝑴
𝑷
𝟏
𝟐
,
𝑲
𝑺𝑫
(
𝒙
)
=
𝑲
𝟐𝟐
𝑴
𝑷
𝟏
𝑹
𝟏
𝑴
𝑷
𝟏
𝑲
𝟐𝟐
𝑲
𝟐𝟐
𝑴
𝑷
𝟏
𝟐
,
(17)
(18)
and reformulate control law (14) such that
𝒖
(
𝑷𝑫𝑺𝑫𝑹𝑬
)
(
𝑡
)
= −𝑲
𝑺𝑷
(
𝒙
)
𝒆−𝑲
𝑺𝑫
(
𝒙
)
𝒆
.
(19)
As proving stability for this control law follows a
procedure like the one in (Nekoo et al., 2022), the
details are omitted.
3.3 Robust SMC PD - SDRE
For robustness, we follow the approach presented in
(Slotine and Li, 1991) and define the following first
order sliding surface,
𝒔
(
𝒙, 𝑡
)
= 𝒆
(
𝒙, 𝑡
)
+ 𝜞𝒆
(
𝒙, 𝑡
)
,
(20)
where 𝜞 is a strictly positive constant matrix,
determined by the user. To drive the system towards
the siding surface 𝑠=0, we add the following to the
control,
𝒖
𝑺𝑴𝑪
(
𝑡
)
= −𝑲
𝒅
𝑠𝑔𝑛
(
𝒔
)
, (21)
where 𝑲
𝒅
= 𝑑𝑖𝑎𝑔(𝑘
, 𝑘
, 𝑘
) is a strictly positive
constant matrix. Since SMC suffers from the
chattering phenomenon, which arises from the
discontinuous nature of the sign function, we replace
𝑠𝑔𝑛
(
𝑠
)
by saturation function 𝑠𝑎𝑡
(
𝑠
/𝜑
)
, where
𝑠𝑎𝑡
(
𝑠
/𝜑
)
= 𝑠
/𝜑
if
|
𝑠
/𝜑
|
<1, 𝑠𝑎𝑡
(
𝑠
/𝜑
)
= 𝑠𝑔𝑛
(
𝑠
)
otherwise, and 𝜑
>0 (Slotine and Li, 1991). The
control law is now given by
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
120

𝒖
𝑹𝒐𝒃𝒖𝒔𝒕𝑷𝑫𝑺𝑫𝑹𝑬
(
𝑡
)
= 𝒖
𝑷𝑫𝑺𝑫𝑹𝑬
+ 𝒖
𝑺𝑴𝑪
=
−𝑲
𝑺𝑷
(
𝒙
)
𝒆−𝑲
𝑺𝑫
(
𝒙
)
𝒆
−𝑲
𝒅
𝑠𝑎𝑡
(
𝜱
𝒔
)
, 𝛷
,
=
𝜑
𝑖
, 𝛷
,
=0.
(22)
3.4 Iterative Learning Robust
PD -SDRE Control
To apply ILC, we modify the equation of motion by
adding and subtracting desired dynamics
𝑫
𝒅
(
𝒓
, 𝒓
, 𝒓
)
from (1):
𝑴
𝑷
(
𝒒
)
−𝑴
𝑷
(
𝒓
)
(
𝒒
−𝒓
)
+
𝑪
𝑷
(
𝒒, 𝒒
)
−
𝑪
𝑷
(
𝒓, 𝒓
)
(
𝒒
−𝒓
)
+ 𝑮
𝑷
(
𝒒
)
+ 𝑹
𝑷
(
𝒒, 𝒒
)
+ 𝑻
𝒆
=
𝒖
(
𝑡
)
−𝑫
𝒅
(
𝒓
, 𝒓
, 𝒓
)
,
(23)
Where
𝑫
𝒅
(
𝒓
, 𝒓
, 𝒓
)
= 𝑴
𝑷
(
𝒓
)
𝒓
+ 𝑪
𝑷
(
𝒓, 𝒓
)
𝒓
.
(24)
Since we wish to minimise the sum of tracking errors
over time, the performance index is defined as
follows,
𝐽
=
1
2
𝑯
𝑰𝑳𝑪
(
𝑡
)
−𝑫
𝒅
(
𝑡
)
,
(25)
where 𝑁
is the number of iterations and 𝑫
𝒅
(
𝑡
)
is the
desired dynamics at the 𝑖 -th iteration. We, thus,
express the final control law as
𝒖
𝑭𝒊𝒏𝒂𝒍
(
𝑡
)
= 𝒖
𝑹𝒐𝒃𝒖𝒔𝒕𝑷𝑫𝑺𝑫𝑹𝑬
(
𝑡
)
+ 𝑯
𝑰𝑳𝑪
(
𝑡
)
+ 𝒖
𝒂𝒅𝒅
(
𝑡
)
.
(26)
Applying the gradient descent method to (25) yields
the following training rule updating 𝑯
𝑰𝑳𝑪
(
𝑡
)
:
𝑯
𝑰𝑳𝑪
= 𝑯
𝑰𝑳𝑪
−𝛼×
𝑯
𝑰𝑳𝑪
−𝑫
𝒅
(
𝑡
)
,
0 < 𝛼<1.
(27)
Training rule (27) uses the desired dynamics to update
the control, where learning rate 𝛼 is a constant scalar
(Nekoo et al., 2022).
Note that this paper presents an alternative approach
to (Nekoo et al., 2022). In (Nekoo et al., 2022),
computing the desired dynamics requires, both, the
forward kinematics and the Jacobian matrix.
However, for some systems, the determinant of the
Jacobian matrix can become zero (see (Richter and
Simon, 2015)), which renders the approach
unsuitable for them. We circumvent the need for
above computations by using directly the desired
trajectory values for position, velocity, and
acceleration, given in (24). Figure 2 provides a block
diagram that illustrates the overall system
architecture and highlights the integration and
interaction among the components of the proposed
three-layer control framework.
4 SIMULATION RESULTS
DC motors are responsible for generating the torque
necessary for operating the prosthesis. These motors
have specific speed and torque limitations, which
determine permissible control signal ranges, and are
given by:
𝑢
(
𝑡
)
=
𝑢
,
(
𝑡
)
𝑖𝑓 𝑢
(
𝑡
)
> 𝑢
,
(
𝑡
)
𝑢
(
𝑡
)
𝑖𝑓 𝑢
,
(
𝑡
)
< 𝑢
(
𝑡
)
< 𝑢
,
(
𝑡
)
𝑢
,
(
𝑡
)
𝑖𝑓 𝑢
,
(
𝑡
)
> 𝑢
(
𝑡
)
, 𝑖= 1,2,3.
(28)
To closely align simulation results with reality, we
use the following saturation limits: (−1200 N, 1200
N) for hip displacement force, (−900 Nm, 900 Nm) for
thigh torque, and
(−400 Nm, 400 Nm) for knee torque.
To assess the performance of the proposed control,
we employ two metrics: The Root Mean Square
Error,
𝑅𝑀𝑆𝐸
, for each state and the Root Mean
Square for each control input
𝑅𝑀𝑆𝑈
. These metrics
evaluate the steady-state error and control effort,
providing a measure of controller performance:
𝑅𝑀𝑆𝐸
=
(
𝑥
−𝑟
)
𝑑𝑡
, 𝑖= 1,2,3, (29)
𝑅𝑀𝑆𝑈
=
1
𝑇
𝑢
𝑑𝑡
, 𝑗 = 1,2,3
For comparing the proposed method with those in
references (Bavarsad et al., 2020) and (Azimi et al.,
2015), we use the same initial conditions.
Specifically, the initial state is set t
o 𝒙
𝒊𝒏𝒊𝒕𝒊𝒂𝒍
=
0.019, 1.13, 0.09, 0.09, 0, 1.6
(omitting units).
Weighting matrices
𝑸 and 𝑹, along with the design
parameters for the ILC and SMC, represented by
𝑲
𝒅
,
𝜞, and 𝜱, are specified in Table 2.
Table 2: Controllers’ parameters.
Controllers Design Parameters and Values
PD-SDRE
𝑸= 𝑑𝑖𝑎𝑔[10
,10
,10
,10
,10
,5
×10
]
𝑹= 𝑑𝑖𝑎𝑔[0.1,0.1,0.1]
ILC
𝛼=0.7
Number of iterations = 10
SMC
𝑲
𝒅
= 𝑑𝑖𝑎𝑔
[
50,75,40
]
𝜞= 𝑑𝑖𝑎𝑔
[
51,27,9
]
𝜱= 𝑑𝑖𝑎𝑔
[
2,2,2
]
Iterative Learning Robust PD-SDRE Control for Active Transfemoral Prostheses
121
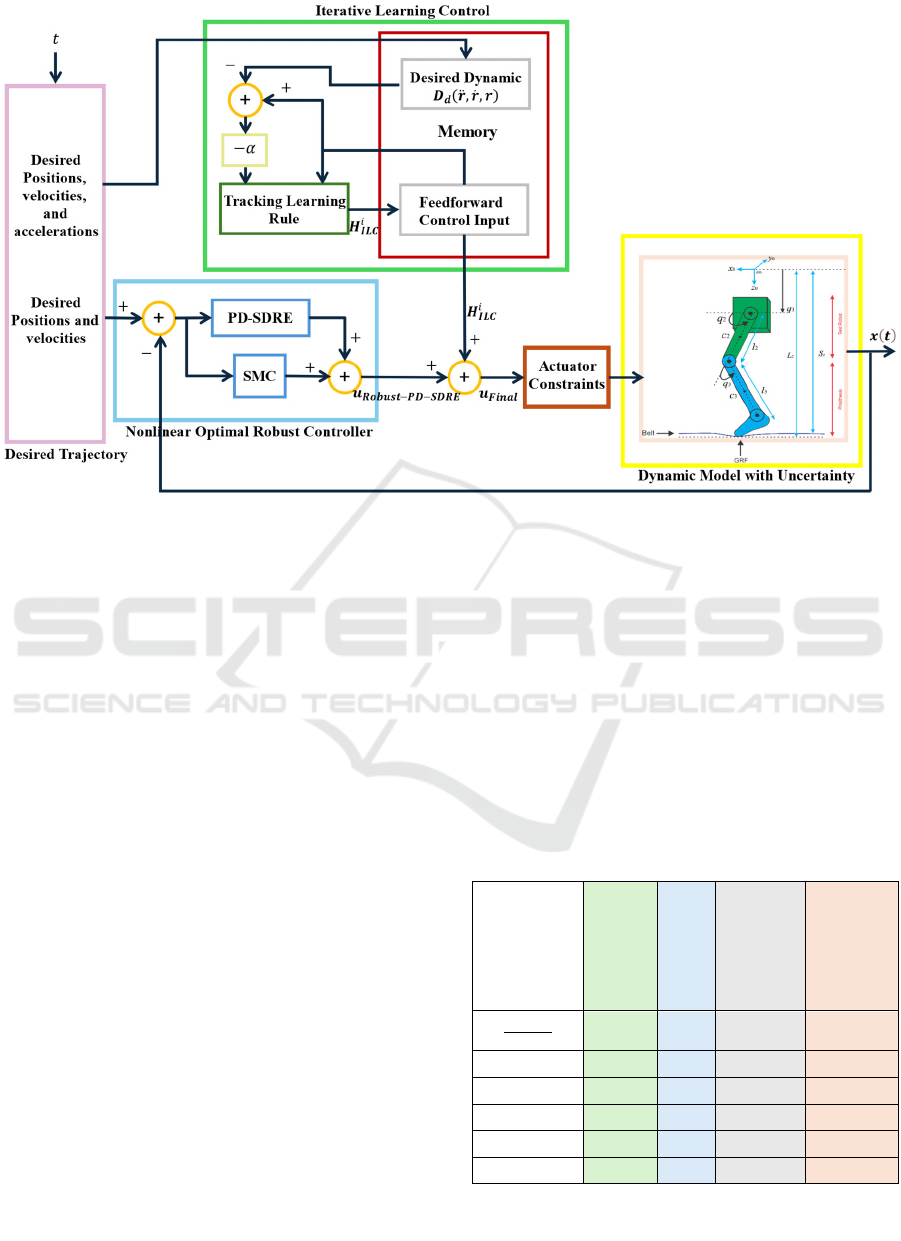
Figure 2: A control system block diagram of proposed approach.
4.1 Nominal Parameter Values
Table 3
provides a detailed comparison of the RMSE
and the RMSU, where, for better comparability, we
“normalised” 𝑅𝑀𝑆𝐸
by dividing it by 0.02 m
(maximal hip displacement). The results show
significant improvements in, both, tracking accuracy
and energy efficiency of the proposed control
approach (ILC + PD-SDRE + SMC) relative to two
other methods: Integral State Control + SDRE + SMC
(Bavarsad et al., 2020) and Robust Adaptive
Impedance Control (Azimi et al., 2015). In position
tracking (𝑅𝑀𝑆𝐸
), our method reduces the error by
95.4% relative to (Bavarsad et al., 2020) and by
98.3% relative to (Azimi et al., 2015). For the first
angular tracking metric 𝑅𝑀𝑆𝐸
, an improvement of
32.6% compared to (Bavarsad et al., 2020) and 28.1%
compared to (Azimi et al., 2015) is achieved, while
the second angular tracking metric 𝑅𝑀𝑆𝐸
shows a
44.9% improvement over (Azimi et al., 2015).
In terms of control cost, the proposed strategy
achieves reductions of 77.8% and 91.9% compared to
(Bavarsad et al., 2020) and (Azimi et al., 2015) in
𝑅𝑀𝑆𝑈
, respectively. The first control torque metric
𝑅𝑀𝑆𝑈
indicates a 67.5% improvement over (Azimi
et al., 2015) but a 35.8% increase over (Bavarsad et
al., 2020). For the second control torque metric
𝑅𝑀𝑆𝑈
, we observe reductions of 87.5% relative to
(Azimi et al., 2015) and an increase of 75.8%
compared to (Bavarsad et al., 2020). While the
proposed approach improves tracking performance
and energy efficiency, we see that they may not
improve simultaneously.
The integration of ILC leads to improvements in
various performance parameters. Notably, the
displacement error improves by 2.36%, while the first
angular parameter shows an 8.13% reduction in error
and the second angular parameter improves by
4.77%. Furthermore, the necessary force is reduced
by 0.72% and the torque by 12.42%. However, there
is a slight increase in knee torque of 3.59%.
Table 3: Comparison with references (Bavarsad et al.,
2020), (Azimi et al., 2015).
ILC +
PD-
SDRE +
SMC
PD-
SDRE
+ SMC
Integral
State
Control +
SDRE +
SMC
(Bavarsad
et al., 2020)
Robust
Adaptive
Impedance
Control
(Azimi et
al., 2015)
𝑅𝑀𝑆𝐸
0.02 m
0.0120 0.0123 0.26 0.715
𝑅𝑀𝑆𝐸
(rad) 0.0032 0.0035 0.0048 0.0045
𝑅𝑀𝑆𝐸
(rad) 0.0030 0.0031 0.0011 0.0054
𝑅𝑀𝑆𝑈
(N) 31.6 31.8 142 388
𝑅𝑀𝑆𝑈
(Nm) 22.1 25.23 16.28 68
𝑅𝑀𝑆𝑈
(Nm) 4.514 4.358 2.568 36
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
122

4.2 Changing Parameter Values
To test the robustness of the proposed approach, first,
we investigate the effect of a ±30% change in the
parameters’ vector. We observe a minor
increase/decrease in tracking error and control cost.
Figure 3 illustrates the horizontal and vertical GRFs.
The resulting forces closely match those observed in
able-bodied individuals. Figure 4 depicts the
performance of the proposed controller in tracking
desired trajectories. Despite non-zero initial errors in
all states, the controlled system quickly converges to
desired values. Moreover, despite a ±30% change in
system parameters, the amplitudes in the graphs
exhibit very minimal variations. This indicates the
reliability of the proposed method.
Figure 3: Horizontal and vertical GRF in nominal mode and
±30% parametric change, considering saturation bounds.
(a)
(b)
(c)
Figure 4: Tracking performance in nominal mode and
±30% parametric change, considering saturation bounds:
a) Hip displacement, b) Thigh angle, c) Knee angle.
Figure 5 shows the control signals. Evidently, a peak
occurs at the start of the motion, which is due to the
difference between the initial state values and the
starting points of the desired trajectories. The good
performance of the proposed controller is
demonstrated also by the fact that the control signals
always remain within saturation limits. Furthermore,
the amplitude of the control signals, when we change
parameters, remains almost identical, indicating the
reliability of the proposed controller.
Fx and Fz (N)
Vertical Hip Displacement (m)
Thigh Angle (rad)Knee Angle (rad)
Iterative Learning Robust PD-SDRE Control for Active Transfemoral Prostheses
123
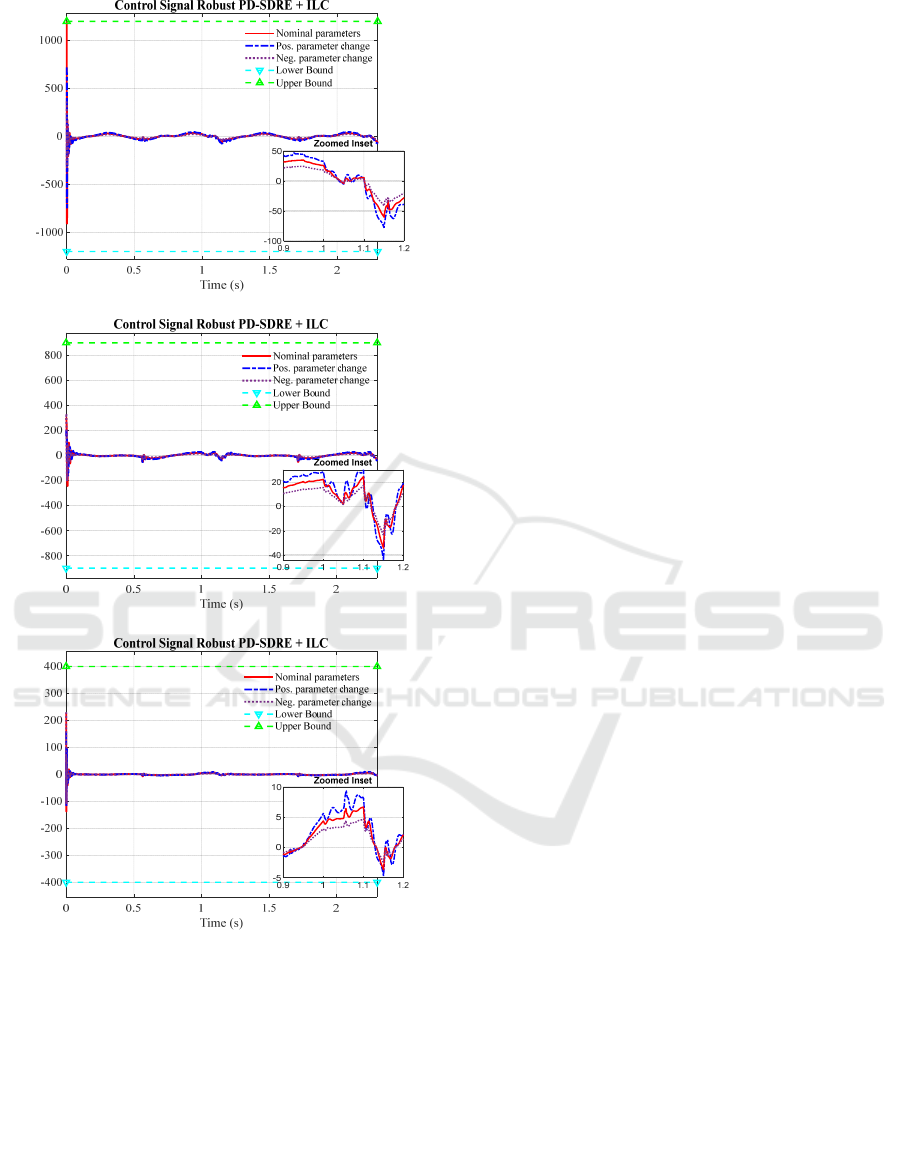
(a)
(b)
(c)
Figure 5: Control signals in nominal mode and ±30%
parametric change with saturation bounds a) Hip force, b)
Thigh torque, c) Knee torque.
Finally, we also apply a ±30% change to each of the
eight parameters 𝑃
individually, modifying only one
parameter at a time, with ILC set to five iterations.
Despite the change, we again observe good
performance, that is, relatively low RMSE values for
both position and angle tracking, and a relatively low
control effort (not shown, for space reasons).
5 CONCLUSIONS
In this paper, we present a novel control strategy for
active prosthetic legs. Our proposed approach, which
combines a PD-SDRE controller with ILC and robust
SMC, considerably reduced biomechanical energy
consumption and improved tracking performance
compared to existing approaches. The integration of
robust SMC aimed at managing disturbances, to
ensure that the system remains resilient under varying
conditions, as indicated by our various scenarios of
parametric change, while the integration of ILC
further improved the control strategy. Our results
clearly advance the field of prosthesis control.
Despite these promising results, the proposed control
strategy has a limitation that should be addressed in
future studies. Specifically, the SDRE controller
requires full state information, which may not always
be directly available in real-world applications.
Obtaining all necessary state variables typically
demands a large number of sensors, while reducing
sensor count remains a significant challenge in
robotic leg design. To overcome this issue, future
work will focus on the design and integration of a
nonlinear state estimator to reduce sensor dependency
and further enhance the performance of the proposed
control framework. An initial investigation into
estimator development has already been reported in
our recent study (Bavarsad and August, 2025). In
addition, practical implementation of the three-layer
controller on a real active prosthetic leg is planned,
with experimental validation under various gait
conditions to assess real-world applicability and
robustness. This promises to bring significant
improvements in prosthetics.
REFERENCES
Ahn, H. S., Chen, Y., & Moore, K. L. (2007). Iterative
learning control: Brief survey and categorization. IEEE
Transactions on Systems, Man, and Cybernetics, Part
C (Applications and Reviews), 37(6), 1099-1121.
Azimi, V., Simon, D., & Richter, H. (2015, October). Stable
robust adaptive impedance control of a prosthetic leg.
In Dynamic Systems and Control Conference (Vol.
57243, p. V001T09A003). American Society of
Mechanical Engineers.
Bavarsad, A., August, E., (2025). Nonlinear Estimator
Based Iterative Learning PD-SDRE Control for Active
Transfemoral Prosthetic Legs. The 13
th
IFAC
Symposium on Nonlinear Control Systems (NOLCOS).
Reykjavik, Iceland.
Bavarsad, A., Fakharian, A., & Menhaj, M. B. (2020).
Optimal sliding mode controller for an active
Hip Force (N)
Thigh Torque (N.m)Knee Torque (N.m)
SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
124

transfemoral prosthesis using state-dependent riccati
equation approach. Arabian Journal for Science and
Engineering, 45(8), 6559-6572.
Bavarsad, A., Fakharian, A., & Menhaj, M. B. (2021). A
nonlinear robust optimal controller for an active
transfemoral prosthesis: an estimator-based state-
dependent riccati equation approach. Proceedings of
the Institution of Mechanical Engineers, Part I: Journal
of Systems and Control Engineering, 235(3), 313-329.
Bukowski, E. L. (2006). Atlas of amputations and limb
deficiencies: Surgical, prosthetic, and rehabilitation
principles, ed 3. Physical Therapy, 86(4), 595-596.
Camargo, J., Bhakta, K., Herrin, K., & Young, A. (2023).
Biomechanical evaluation of stair ambulation using
impedance control on an active prosthesis. Journal of
Biomechanical Engineering, 145(2), 021007.
Chin, T., Sawamura, S., Shiba, R., Oyabu, H., Nagakura,
Y., & Nakagawa, A. (2005). Energy expenditure during
walking in amputees after disarticulation of the hip: a
microprocessor-controlled swing-phase control knee
versus a mechanical-controlled stance-phase control
knee. The Journal of Bone & Joint Surgery British
Volume, 87(1), 117-119.
Çimen, T. (2008). State-dependent Riccati equation
(SDRE) control: a survey. IFAC Proceedings
Volumes, 41(2), 3761-3775.
Kashiri, N., Abate, A., Abram, S. J., Albu-Schaffer, A.,
Clary, P. J., Daley, M., ... & Tsagarakis, N. (2018). An
overview on principles for energy efficient robot
locomotion. Frontiers in Robotics and AI, 5, 129.
Kaufman, K. R., Levine, J. A., Brey, R. H., McCrady, S. K.,
Padgett, D. J., & Joyner, M. J. (2008). Energy
expenditure and activity of transfemoral amputees
using mechanical and microprocessor-controlled
prosthetic knees. Archives of physical medicine and
rehabilitation, 89(7), 1380-1385.
Kibria, Z., & Commuri, S. (2024, June). Intelligent Control
of Prosthetic Leg for Gait Symmetry. In 2024
International Symposium on Medical Robotics
(ISMR) (pp. 1-8). IEEE.
Ma, X., Zhang, X., & Xu, J. (2024). Robotic leg prosthesis:
A survey from dynamic model to adaptive control for
gait coordination. IEEE Transactions on Neural
Systems and Rehabilitation Engineering, 32, 607-624.
Martini, E., Cesini, I., D’Abbraccio, J., Arnetoli, G.,
Doronzio, S., Giffone, A., ... & Crea, S. (2020).
Increased symmetry of lower-limb amputees walking
with concurrent bilateral vibrotactile feedback. IEEE
Transactions on Neural Systems and Rehabilitation
Engineering, 29, 74-84.
McDonald, C. L., Westcott-McCoy, S., Weaver, M. R.,
Haagsma, J., & Kartin, D. (2021). Global prevalence of
traumatic non-fatal limb amputation. Prosthetics and
orthotics international, 45(2), 105-114.
Memon, F., & Shao, C. (2021). Data-driven optimal PID
type ILC for a class of nonlinear batch
process. International Journal of Systems
Science, 52(2), 263-276.
Müßig, J. A., Brauner, T., Kröger, I., Varady, P. A., Brand,
A., Klöpfer-Krämer, I., ... & Augat, P. (2019). Relation
between the amount of daily activity and gait quality in
transfemoral amputees. International Journal of
Rehabilitation Research, 42(2), 139-144.
Nekoo, S. R. (2019). Tutorial and review on the state-
dependent Riccati equation. Journal of Applied
Nonlinear Dynamics, 8(2), 109-166.
Nekoo, S. R., Acosta, J. Á., Heredia, G., & Ollero, A.
(2022). A PD-type state-dependent Riccati equation
with iterative Learning Augmentation for Mechanical
systems. IEEE/CAA Journal of Automatica
Sinica, 9(8), 1499-1511.
Orendurff, M. S., Segal, A. D., Klute, G. K., & McDowell,
M. L. (2006). Gait efficiency using the C-Leg. Journal
of rehabilitation research and development, 43(2), 239.
Richter, H., Simon, D., Smith, W. A., & Samorezov, S.
(2015). Dynamic modeling, parameter estimation and
control of a leg prosthesis test robot. Applied
Mathematical Modelling, 39(2), 559-573.
Saat, S., Ahmad, M. A., & Ghazali, M. R. International
Journal of Cognitive Computing in Engineering.
Shen, D. (2018). Iterative learning control with incomplete
information: A survey. IEEE/CAA Journal of
Automatica Sinica, 5(5), 885-901.
Slotine, J. J. E., & Li, W. (1991). Applied nonlinear
control (Vol. 199, No. 1, p. 705). Englewood Cliffs, NJ:
Prentice hall.
Ziegler-Graham, K., MacKenzie, E. J., Ephraim, P. L.,
Travison, T. G., & Brookmeyer, R. (2008). Estimating
the prevalence of limb loss in the United States: 2005
to 2050. Archives of physical medicine and
rehabilitation, 89(3), 422-429.
Iterative Learning Robust PD-SDRE Control for Active Transfemoral Prostheses
125
