TACO: A Lightweight Tree-Based Approximate Compression Method
for Time Series
Andr
´
e Bauer
Illinois Institute of Technology, Chicago, U.S.A.
Keywords:
Time Series Compression, Evaluation.
Abstract:
The rapid expansion of time series data necessitates efficient compression techniques to mitigate storage and
transmission challenges. Traditional compression methods offer trade-offs between exact reconstruction, com-
pression efficiency, and computational overhead. However, many existing approaches rely on strong statistical
assumptions or require computationally intensive training, limiting their practicality for large-scale applica-
tions. In this work, we introduce TACO, a lightweight tree-based approximate compression method for time
series. TACO eliminates the need for training, operates without restrictive data distribution assumptions, and
enables selective decompression of individual values. We evaluate TACO on five diverse datasets comprising
over 170,000 time series and compare it against two state-of-the-art methods. Experimental results demon-
strate that TACO achieves compression rates of up to 92%, with average compression ratios ranging from 7.55
to 20.86, while maintaining reconstruction errors as low as 10
−6
, outperforming state-of-the-art approaches in
three of the five datasets.
1 INTRODUCTION
By 2028, the global volume of data created, cap-
tured, copied, and consumed is projected to reach
394 zettabytes, according to Statista
1
. A significant
portion of this data consists of time series generated
across diverse domains, including smart grids, IoT
sensors, climate monitoring stations, personal fitness
trackers, and financial markets. These real-valued se-
quences serve as a critical foundation for various ap-
plications such as prediction (Liu and Wang, 2024),
classification (Mohammadi Foumani et al., 2024),
and anomaly detection (Zamanzadeh Darban et al.,
2024). As the volume of time series data continues
to expand, efficient storage and transmission meth-
ods are becoming increasingly essential. A recent
survey (Chiarot and Silvestri, 2023) underscores the
urgent need for effective time series compression, as
the unchecked growth of such data imposes signifi-
cant infrastructural challenges. Without compression,
the relentless accumulation of time series data can
overwhelm storage systems, congest network band-
width, and increase I/O overhead, leading to perfor-
mance bottlenecks and higher operational costs.
To address these challenges, various time se-
1
Statista: https://www.statista.com/statistics/871513/
worldwide-data-created/
ries compression techniques have been developed,
broadly categorized into lossless and lossy methods.
Lossless compression preserves data integrity, mak-
ing it suitable for applications requiring exact recon-
struction, such as financial transactions and medi-
cal records. Common techniques, including delta
encoding and Huffman coding, exploit temporal re-
dundancy to reduce storage without information loss.
In contrast, lossy compression achieves higher com-
pression ratios by allowing controlled inaccuracies,
which is beneficial for applications like sensor moni-
toring and visualization. Recent advancements lever-
age deep learning-based autoencoders to transform or
approximate time series data, enabling efficient stor-
age while preserving essential patterns (Tnani et al.,
2022; Zheng and Zhang, 2023; Liu et al., 2024;
Chiarot et al., 2025). The choice between these ap-
proaches involves a trade-off between compression
efficiency, computational complexity.
Despite these advancements, existing time series
compression methods often struggle with trade-offs
between flexibility, computational efficiency, and ac-
cessibility of compressed data. Many approaches rely
on strong statistical assumptions or require computa-
tionally intensive training, limiting their applicability
across diverse real-world datasets. To overcome these
limitations, we propose TACO, a lightweight Tree-
182
Bauer and A.
TACO: A Lightweight Tree-Based Approximate Compression Method for Time Series.
DOI: 10.5220/0013644600003967
In Proceedings of the 14th International Conference on Data Science, Technology and Applications (DATA 2025), pages 182-190
ISBN: 978-989-758-758-0; ISSN: 2184-285X
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)

based Approximate COmpression method for time se-
ries. TACO is designed to:
1. operate without restrictive assumptions about data
distribution,
2. require no training phase, allowing for immediate
deployment, and
3. enable selective decompression of individual val-
ues without reconstructing the entire series.
To evaluate TACO, we conducted experiments on
five diverse datasets comprising more than 170,000
time series and compared it against two state-of-the-
art methods. The results demonstrate that TACO
achieves a compression rate of up to 92%, with av-
erage compression ratios ranging from 7.55 to 20.86,
while maintaining a low reconstruction error in the
range of 10
−3
to 10
−6
. Notably, TACO consistently
outperformed the competing methods in terms of bal-
ancing compression and accuracy, achieving the best
compression performance in three out of the five
datasets while exhibiting the lowest reconstruction er-
ror in nearly all cases.
The remainder of this paper is structured as fol-
lows: Section 2 provides background information and
reviews related work. Section 3 introduces TACO.
Section 4 presents and discusses the results. Section 5
concludes the paper.
2 BACKGROUND AND RELATED
WORK
In this section, we introduce pairing functions that are
utilized within in TACO, highlight other pairing func-
tions and compression methods and discuss related
work.
2.1 Cantor Pairing Function
The Cantor Pairing Function (CPF), introduced in
1878 (Cantor, 1878), is one of the earliest and most
well-known pairing functions, and serves as a funda-
mental example in elementary set theory (Enderton,
1977). It provides a unique and reversible mapping of
pairs of positive integers (x,y) ∈N to a single positive
integer z ∈ N using
z = π(x,y) =
(x + y)(x + y + 1)
2
+ x.
To retrieve the original pair based on z, we use
x = z −
w(w + 1)
2
and y = w −x,
where
w =

√
8z + 1 −1
2

.
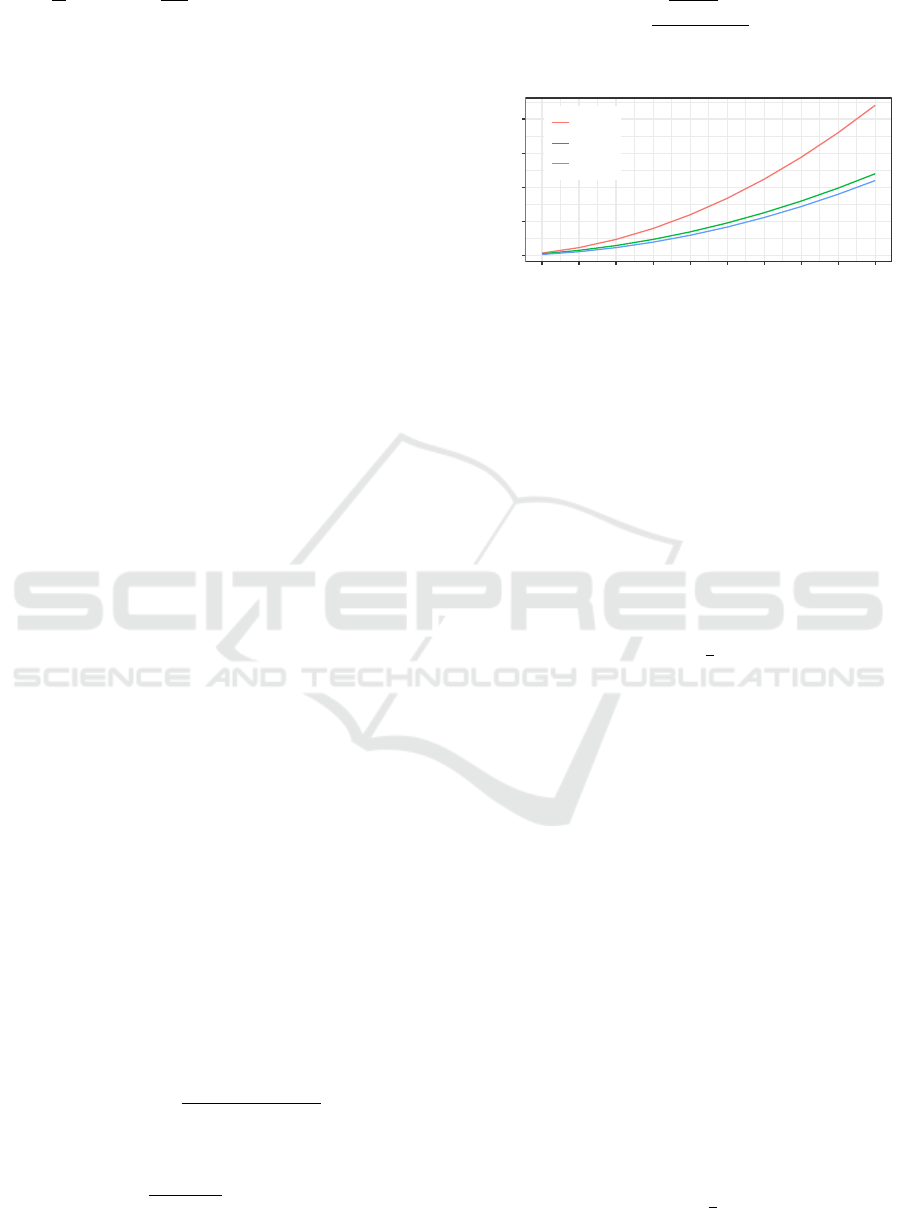
A visualization of CPF pairings is shown in Figure 1.
0
50
100
150
200
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6) (1,7) (1,8) (1,9) (1,10)
Value Pairs
Paired Value
CPF
SPF
RSPF
Figure 1: Visualization of different paring functions.
2.2 Szudzik Pairing
The Szudzik Pairing Function (SPF), introduced in
2006 (Szudzik, 2006), offers a more computationally
efficient alternative to CPF. Like CPF, it uniquely and
reversibly maps pairs of positive integers (x,y) ∈N to
a single positive integer z ∈ N, but is defined as
z = π(x,y) =
(
y
2
+ x if x < y,
x
2
+ x +y otherwise.
To retrieve (x,y), we first compute
w = ⌊
√
z⌋.
If z −w
2
< w, we calculate
x = z −w
2
and y = w.
Otherwise,
x = w and y = z −w
2
−w.
A visualization of SPF pairings is also shown in Fig-
ure 1.
2.3 Rosenberg-Strong Pairing Function
The Rosenberg-Strong Pairing Function (RSPF), in-
troduced in 1972 (Rosenberg and Strong, 1972),
is particularly useful in the context of space-filling
curves and finds applications in computer graphics
and data structures (Szudzik, 2017). Like the other
functions, it maps pairs of positive integers (x,y) ∈ N
to a single positive integer z ∈ N, defined as
z = π(x,y) = max(x,y)
2
+ max(x,y) + x −y.
To obtain (x,y), we first compute
w = ⌊
√
z⌋
TACO: A Lightweight Tree-Based Approximate Compression Method for Time Series
183

If z −w
2
< w, we calculate
x = z −w
2
, and y = w.
Otherwise,
x = w, y = w
2
+ 2w −z.
A visualization of RSPF pairings is also provided in
Figure 1.
2.4 Other Pairing Functions
In addition to the functions discussed above, other
pairing functions such as the Hopcroft-Ullman Pair-
ing Function (Hopcroft et al., 2001) and the G
¨
odel
Pairing Function (G
¨
odel, 1931) exist. However, these
are not considered in TACO because their inverse op-
erations require iterative operations, whereas the three
functions we focus on decompress in constant time
O(1). Specifically, both the G
¨
odel and Hopcroft-
Ullman functions exhibit decompression in O(log z)
time, proportional to the number of bits required to
represent z.
2.5 Other Compression Methods
Several other compression methods exist, each with
its own strengths and weaknesses. One simple
method is delta encoding, which stores the differences
between consecutive values, and decompression is
done via cumulative summation. Another approach is
Huffman coding, which assigns variable-length codes
to data values based on their frequency of occurrence.
However, if the time series lacks repeating values or
patterns, the compressed and decompressed data may
be nearly identical in size and in the case of Huff-
man encoding the decoding has to be saved in the
addition. Similarly, Run-length encoding stores re-
peated values along with the number of consecutive
occurrences, but it can also be inefficient when there
are few repetitions. Other lossless compression meth-
ods like Gzip aim to eliminate redundancy in the data.
These methods are all effective in specific scenarios,
depending on the nature of the data.
2.6 Related Work
A recent survey discusses various approaches to time
series compression (Chiarot and Silvestri, 2023). Our
focus is on value-level compression rather than bit-
level compression, as once a time series is com-
pressed at the value level, further optimizations can
be applied at the bit level.
Several recent methods have emerged, including
TSXor (Bruno et al., 2021), ATSC (Rolo et al., 2024),
and NeaTS (Guerra et al., 2024). TSXor leverages
similarities between consecutive time series values
by maintaining a window of recent values and com-
pressing new ones using XOR differences. ATSC em-
ploys function approximation techniques such as Fast
Fourier Transforms and interpolation, achieving com-
pression by storing only the parameters of the fitted
functions. Similarly, NeaTS enables random access
while maintaining efficient compression by approxi-
mating time series with nonlinear functions and using
a partitioning algorithm to minimize storage.
Another class of approaches is based on Symbolic
Aggregate approXimation (SAX) (Lin et al., 2007),
which transforms time series data into discrete sym-
bols using piecewise aggregate approximation and
predefined Gaussian-based breakpoints. While SAX
provides a form of lossy compression, it assumes a
Gaussian distribution, making it less suitable for non-
Gaussian data. Additionally, its fixed segmentation
approach may fail to capture local trends or variable-
length patterns. More recent work has addressed
some of these limitations (Malinowski et al., 2013;
Chen, 2023).
Autoencoders have also gained attention for time
series compression due to their ability to learn
compact, low-dimensional representations of high-
dimensional data. However, a key drawback of
autoencoder-based compression is the need for model
training, which can be computationally expensive and
time-consuming. Recent examples of work in this
area include (Tnani et al., 2022; Zheng and Zhang,
2023; Liu et al., 2024; Chiarot et al., 2025).
TACO differs from these existing methods in sev-
eral key aspects. Unlike SAX-based approaches, it
does not rely on underlying assumptions such as a
Gaussian distribution, making it more flexible for di-
verse time series data. Additionally, it does not re-
quire model training, as is the case with autoencoder-
based methods, ensuring a lightweight and efficient
on-the-fly compression. Compared to TSXor, ATSC,
and NeaTS, our approach enables the decompression
of individual time series values without the need to
fully decompress the entire series, providing greater
efficiency and flexibility in data retrieval.
3 TACO
In this section, we introduce TACO, a lightweight
Tree-based Approximate COmpression method for
time series. We first describe the compression pro-
cess, followed by the decompression procedure.
DATA 2025 - 14th International Conference on Data Science, Technology and Applications
184

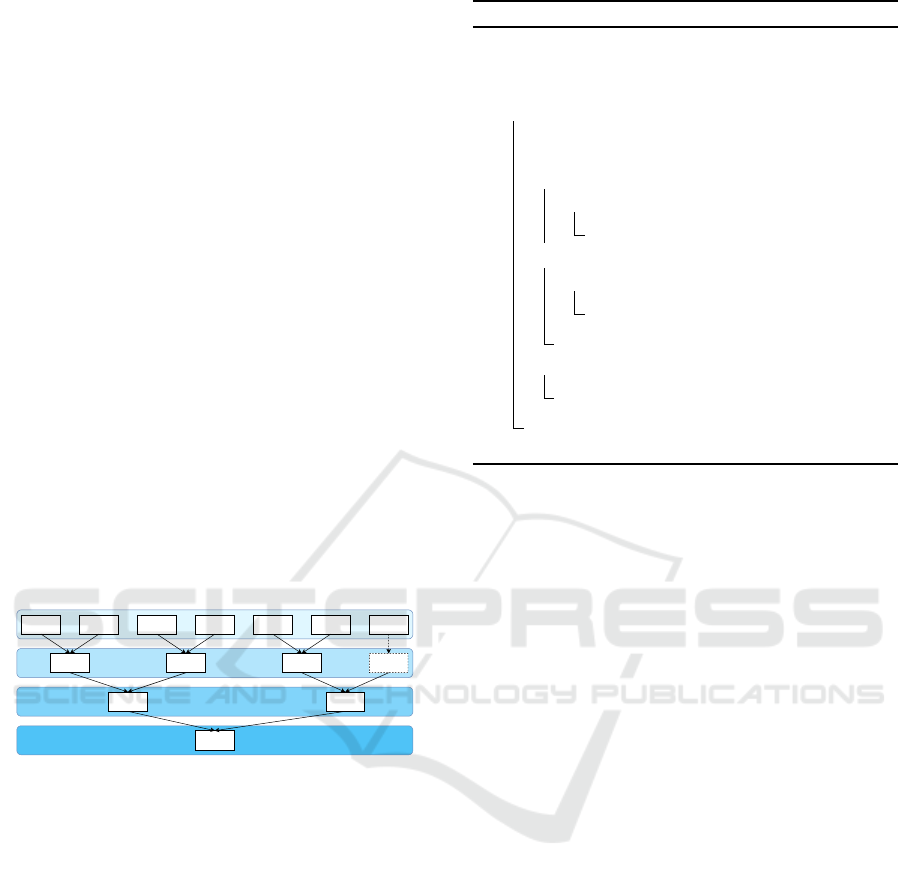
3.1 Compression
TACO is implemented in Python and the core idea be-
hind its compression is illustrated in Figure 2. Each
consecutive pair of values is mapped to a new inte-
ger using a pairing function, resulting in a reduced
time series with approximately half the original num-
ber of values (or half plus one if the series has an
odd length). This process is iteratively applied until,
ideally, the compressed series contains only a single
value. However, since the paired values increase in
size with each iteration, the process stops if the result
of a paired value exceeds a predefined threshold (e.g.,
to prevent an integer overflow). Regardless, each it-
eration approximately halves the length of the time
series. The detailed compression process is outlined
in Algorithm 1. The while-loop (Lines 1–13) repre-
sents the compression steps shown as progressively
darker blue boxes in Figure 2. As long as the time
series length is greater than one and none of the val-
ues exceed the threshold v (Lines 11–12), the series
continues to be compressed iteratively. If the length
is even (Lines 4–6), all the values are paired using a
pairing function. If the length is odd, all values are
paired except the last one (see example in Figure 2),
which is directly appended to the compressed series.
y
1
y2 y3 y4 y5
y'1 y'2
y''1
y'''1
y6 y7
y'3 y'4
y''2
Figure 2: Schematic overview of the compression. Solid
black arrows indicate input to the pairing function, while
dashed arrows and boxes represent virtual copies created at
each iteration to form the complete compressed time series.
For clarity, the pseudo-code omits preprocessing
and metadata storage. Since pairing functions require
positive integers, the time series is shifted by its min-
imum value plus one to ensure all values are ≥ 1. If
the minimum value is already ≥ 1, it is set to 0 for
consistency. Consequently, both the original length
and the minimum value must be stored. Thus, the fi-
nal compressed series takes the form (l,m,y
1
,y
2
,.. .),
where l is the original length and m is the minimum
value.
For time series with real numbers, a different ap-
proach is needed since the pairing function requires
integers. The series is split into two: one contain-
ing integer parts and the other containing fractional
parts. The fractional part is converted into an inte-
ger by multiplying by 10
t
(where t is user-defined)
Algorithm 1: Element-Wise Pairing.
Input: ts: time series, v: maximal value to
avoid overflow, f unc: pairing
function
1 while length(ts) > 1 do
2 b ← [];
3 n ← length(ts);
4 if n is even then
5 for i ← 0 to n −1 step 2 do
6 b.append( f unc(ts[i],ts[i +1]));
7 else
8 for i ← 0 to n −2 step 2 do
9 b.append( f unc(ts[i],ts[i +1]));
10 b.append(ts[n −1]);
11 if any x ∈ b > v then
12 return ts;
13 ts ← b;
14 return ts;
and rounding. In other words, t specifies the num-
ber of digits to be preserved. For example, given
(2.23,3.13,5.01) and t = 2, the transformation re-
sults in integer series (2,3, 5) and (23,13,1). Each re-
sulting integer series is compressed separately, yield-
ing (l,m
1
,y
1,1
,y
1,2
,.. ., −1,m
2
,y
2,1
,y
2,2
,.. .). Since
all values, except for the first two, are greater than
0, the presence of -1 serves as an indicator during
decompression that the original time series contained
real numbers.
3.2 Decompression
The only information we need to decompress the
compressed time series is the original length. If
the compressed series contains a single value, Algo-
rithm 2 recursively reconstructs the original series. If
the original length was one, the function returns the
single compressed value (Lines 1–2). If the length
was two, the inverse pairing function is applied (Lines
3–4). Otherwise, the inverse pairing function is ap-
plied (Line 5), the depth of the tree d is determined
(Line 6), and the left and right branches are recon-
structed recursively (Lines 7–8).
If the compressed series contains multiple values,
Algorithm 3 iteratively decompresses them. When
the series consists of a single value, REP is called di-
rectly. Otherwise, the smallest power of 2 greater than
or equal to the number of compressed elements is cal-
culated (Line 3). This represents the number of leaves
in the full tree hidden within each compressed value.
For example, in Figure 2, the second layer from the
TACO: A Lightweight Tree-Based Approximate Compression Method for Time Series
185

Algorithm 2: Reverse Element Pairing (REP).
Input: c: compressed value, num: length of
original time series, i f unc: inverse of
pairing function
1 if num == 1 then
2 return c;
3 else if num == 2 then
4 return i f unc(c);
5 z ← i f unc(c);
6 d ←⌈log
2
(num)⌉−1;
7 l ← REP(z[0],2
d
,i f unc);
8 r ← REP(z[1], num −2
d
,i f unc);
9 return [l, r];
bottom has f = 4, while the second layer from the
top has f = 2. The algorithm iterates over each com-
pressed value, calling REP for decompression (Line 7)
and adjusting the remaining length (Line 10). For the
last compressed value, we have to check whether the
remaining length equals f (Lines 6–7) or the tree has
fewer leaves (Lines 8–9) as shown in the right branch
in Figure 2.
Algorithm 3: Reverse Pairing.
Input: z: compressed time series, num:
original length of time series, i f unc:
inverse pairing function
1 if length(z) == 1 then
2 return REP(z,num,i f unc);
3 f ← 2
⌈log
2
(⌈num/length(z)⌉)⌉
;
4 seq ← [];
5 for i ← 0 to length(z) −1 do
6 if num ≥ f then
7 seq.append(REP(z[i], f , i f unc));
8 else
9 seq.append(REP(z[i],num,i f unc));
10 num ← num − f ;
11 return seq;
Both algorithms efficiently reconstruct the com-
pression tree, allowing for rapid and memory-efficient
selective decompression of only the necessary portion
of the time series, eliminating the overhead of decom-
pressing the entire time series.
For clarity, the algorithms omit the postprocess-
ing and loading of the metadata. As a final step in
the postprocessing, if the time series was shifted to
ensure the minimum value was ≥ 1, it is shifted back
using the stored value of m. This process ensures loss-
less (de)compression when the original time series
consists solely of integers. However, for time series
with real numbers, the (de)compression can be lossy
if the user-defined parameter t was set too small. To
decompress such a time series, the integer and frac-
tional parts are decompressed separately, with each
part being shifted by their respective minimum val-
ues if needed, and then combined to reconstruct the
original time series.
4 EVALUATION
In this section, we describe the dataset, applied mea-
sures, and competing methods, followed by a compar-
ison of different pairing functions and an evaluation of
TACO against state-of-the-art methods. Partial results
are publicly available through a Code Ocean capsule
2
.
Due to memory and time constraints, we were unable
to provide the full set of results.
4.1 Datasets
To assess compression performance, we used five
diverse time series datasets comprising more than
170,000 time series, detailed in Table 1. The first
dataset is the Libra dataset (Bauer et al., 2021), used
in the Libra benchmark for evaluating forecasting
methods. It contains 400 time series with an aver-
age length of 3,368.7, ranging from 20 to 372,864.
The second and third datasets, M3 (Makridakis and
Hibon, 2000) and M4 (Makridakis et al., 2020), orig-
inate from the Makridakis Forecasting Competitions.
The M3 dataset contains 3,003 time series with an av-
erage length of 78.7, ranging from 20 to 144, while
the M4 dataset consists of 100,000 time series with
an average length of 252.8, ranging from 19 to 9,993.
The fourth dataset, the UCR Time Series Classifica-
tion Archive (Dau et al., 2018) (UCR), is widely used
in the time series data mining community. From the
128 hosted datasets, we extracted 68,204 time series
with an average length of 1,167.7, ranging from 40 to
24,000. The final dataset is the New York City TLC
Trip Record Data (City of New York, 2025) (NYC),
from which we extracted 42 time series from January
2009, with an average length of 4,747,112.6, ranging
from 788,465 to 7,696,027.
Throughout this study, we refer to time series as
univariate sequences without timestamps, represented
as vectors ∈ R
n
, where n is the length of the time se-
ries.
2
Code Ocean capsule: 10.24433/CO.6381492.v1
DATA 2025 - 14th International Conference on Data Science, Technology and Applications
186

Table 1: Length distribution of the datasets.
Dataset Mean Median SD [Min, Max]
Libra (n = 400) 3,368.7 569.5 19,081.4 [20; 372,864]
M3 (n = 3,303) 78.7 69 43.8 [20; 144]
M4 (n = 100,000) 252.8 106 593.4 [19; 9,933]
UCR (n = 68,204) 1,167.7 650 1,763.5 [40; 24,000]
NYC (n = 42) 4.7·10
6
6.4·10
6
2.8·10
6
[0.8·10
6
; 6.8·10
6
]
4.2 Assessment of Compression
To evaluate compression, we measured (i) the length
of time series before and after compression, (ii) the to-
tal dataset size in kilobytes before and after compres-
sion, (iii) the compression ratio, defined as the size of
the original time series divided by the size of the com-
pressed time series, and (iv) the reconstruction error,
measured using mean absolute error (MAE) between
the original and decompressed time series.
TACO preserves metadata such as the original
length and minimum value of the time series. For in-
teger time series, the compressed format includes two
metadata values (length and minimum value) along-
side the compressed values. For example, if a com-
pressed time series has a length of 5, the measure uses
the value 7 (2 + 5). For real-valued time series, three
metadata values are stored (length, minimum integer
value, and minimum floating value) as well as the de-
limiter. For instance, if the compressed integer time
series has length 3 and its fractional counterpart has
length 3, the measure considers the value 12 (2 + 5
+ 1 + 1 + 3). The applied measures takes this into
account.
4.3 Competing Methods
For benchmarking, we applied TACO with three pair-
ing functions: CFP, SFP, and RSFP (see Section 2).
Although TACO is implemented in Python, which
supports arbitrary-precision integers (bignum), we set
the threshold v to 10
128
. To enhance cross-language
applicability, we also evaluated RSFP with v set to the
maximum unsigned long value, denoted as RSFP
∗
.
For competing methods representing the state-of-the-
art, we selected TSXor
3
and ATSC
4
, as they do not
require training, allowing a lightweight compression
as TACO.
4.4 Pairing Function Comparison
To identify the best pairing function, we first evalu-
ated integer compression by rounding all time series
3
TSXor: https://github.com/andybbruno/TSXor
4
ATSC: https://github.com/instaclustr/atsc
values to the next integer. This approach enables di-
rect comparison of compression effectiveness before
assessing the compression for real-valued time series.
We applied CFP, SFP, RSFP, and RSFP
∗
, with results
shown in Table 2. The column Uncomp. reflects char-
acteristics of the uncompressed dataset.
Table 2: Integer compression comparison of the utilized
pairing functions.
Measure Uncomp. CFP SFP RSFP RSFP
∗
Libra
Average Length 3,368.74 121.61 116.78 116.78 816.95
Total Size [KB] 11,605 439 423 423 7,458
Avg. Comp. Ratio - 27.97 29.13 29.13 6.83
M3
Average Length 78.66 4.55 3.25 3.25 20.00
Total Size [KB] 2,210 344 299 299 746
Avg. Comp. Ratio - 6.74 10.33 10.33 3.30
M4
Average Length 252.80 12.82 11.71 11.71 63.33
Total Size [KB] 223,871 17,812 16,916 16,916 61,850
Avg. Comp. Ratio - 12.27 13.70 13.70 3.63
UCR
Average Length 1,167.73 12.52 12.01 11.88 76.40
Total Size [KB] 677,853 12,078 11,810 11,757 49,500
Avg. Comp. Ratio - 61.35 69.17 69.17 15.61
NYC
Average Length 4,74·10
6
0.17·10
6
0.17·10
6
0.17·10
6
0.87·10
6
Total Size [KB] 20.23·10
6
0.74·10
6
0.75·10
6
0.75·10
6
3.73·10
6
Avg. Comp. Ratio - 69.44 69.44 69.44 8.33
For Libra, M4, UCR, and NYC, TACO with each
of the pairing functions consistently achieved a size
reduction of 92%, reducing average time series length
from 3,368.74 to under 122, from 252.8 to under
13, from 1,167.73 to under 13, and from 4,747,112
to 174,112, respectively. The best average compres-
sion ratio (69.44) was observed for NYC. Only for
M3, TACO achieved a slightly lower average com-
pression rate (84.43%–86.47%) and the lowest com-
pression ratio (6.74). TACO using RSFP
∗
yielded av-
erage compression ratios of 6.83, 3.30, 3.63, 15.61,
and 8.33 for the datasets in order. Overall, RSFP (al-
though not visible due to the rounding) provided the
best average compression ratios and was selected for
comparison against the state-of-the-art methods.
4.5 Comparison of Compression
Methods
We investigated TACO using RSFP, alongside TSXor
and ATSC on all time series in their original form.
Table 3 presents compression ratios, while Table 4
reports reconstruction errors. A
†
symbol indicates
dataset-specific issues such as failed compression or
decompression errors.
For Libra, UCR, and NYC, we set t = 4 (preserv-
ing 4 decimal places), while for M3 and M4, we set
t = 1 and t = 2, respectively. TACO achieved an aver-
age compression rate between 7.55 and 20.86 across
TACO: A Lightweight Tree-Based Approximate Compression Method for Time Series
187

Table 3: Comparison of the compression ratio across the
datasets.
Dataset Mean Median SD [Min, Max]
TACO
Libra 12.55 9.66 4.67 [1.41, 23.74]
M3 7.55 5.42 3.38 [1.23, 12.27]
M4 10.33 6.67 4.52 [1.18, 48.13]
UCR 12.06 9.96 4.91 [2.14, 143.78]
NYC 20.86 15.72 86.83 [7.41, 473.12]
TSXor
Libra
†
14.55 11.68 15.31 [2.68, 128.94]
M3
†
2.05 1.95 0.77 [0.80, 4.73]
M4
†
3.05 2.77 1.39 [0.76, 18.99]
UCR
†
5.59 3.22 7.03 [0.57, 65.78]
NYC
†
7.22 2.89 13.11 [0.50, 50.35]
ATSC
Libra 33.84 4.93 50.85 [2.01, 191.06]
M3 4.51 2.58 4.41 [0.60, 22.57]
M4
†
9.51 3.56 13.73 [0.50, 103.21]
UCR
†
4.37 1.38 18.05 [0.55, 225.94]
NYC
†
593.24 47.37 3326.14 [0.52, 21630.39]
Table 4: Comparison of the average reconstruction error.
Dataset Mean Median SD [Min, Max]
TACO
Libra 2.55 ·10
−5
2.50 ·10
−5
1.99 ·10
−6
[0.00, 4.07 ·10
−5
]
M3 2.31 ·10
−2
0.00 1.16 ·10
−2
[0.00, 3.64 ·10
−2
]
M4 2.44 ·10
−3
0.00 1.20 ·10
−3
[0.00, 3.43 ·10
−3
]
UCR 2.52 ·10
−5
2.48 ·10
−5
9.25 ·10
−6
[0.00, 5.00 ·10
−5
]
NYC 2.45 ·10
−5
0.00 1.24 ·10
−5
[0.00, 2.54 ·10
−5
]
TSXor
Libra
†
5.79 ·10
16
0.50 7.79 ·10
17
[0.24, 1.05 ·10
19
]
M3
†
0.17 0.00 0.20 [0.00, 0.68]
M4
†
0.22 0.00 0.24 [0.00, 0.93]
UCR
†
2.89 ·10
18
0.49 6.28 ·10
18
[0.00, 1.84 ·10
19
]
NYC
†
- - - -
ATSC
Libra 808.34 0.51 6.95 ·10
3
[0.00, 1.08 ·10
5
]
M3 3.98 88.71 71.23 [0.00, 1.23 ·10
3
]
M4
†
72.68 47.16 106.53 [0.00, 1.28 ·10
4
]
UCR
†
6.22 0.40 2.88 ·10
1
[0.00, 2.11 ·10
2
]
NYC
†
1.04 ·10
5
0.55 2.21 ·10
5
[0.00, 6.77 ·10
5
]
datasets. The reduction from Table 2 is due to the ad-
ditional separation and handling of integer and frac-
tional parts of real-valued time series. In other words,
the decrease is introduced by the fraction of time se-
ries that are real numbers but were considered be-
forehand as integer. The highest reconstruction error
appeared in M3 (2.31 × 10
−2
) due to t = 1, as the
M3 time series have two-digit precision. Other errors
ranged from 10
−2
to 10
−5
. If integer-only compres-
sion were used, the reconstruction error would be at
most 1, as the reconstruction error solely is introduced
by the fractional part. This way, TACO would yield
here higher results and for almost all datasets still ex-
hibit the lowest error compared to the other methods.
TSXor encountered issues with 0, 3, 12,521,
57,436, and 42 time series across the datasets in or-
der, respectively. For instance, for M4, 2,551 out of
100,000 compressed series failed to decompress, or
for NYC, all 42 decompressed time series had differ-
ent lengths than the original time series, preventing
reconstruction error calculation. TSXor achieved a
higher compression ratio (33.84) compared to TACO
only for Libra but at the cost of significantly higher
reconstruction errors (in the order of 10
3
to 10
24
). In
other words, the higher compression is achieved by
sacrificing accuracy during the decompression. Some
compressed series even exceeded the original size
(i.e., compression ratio < 1).
ATSC encounters problems on 13, 4,032, and 11
time series from M4, UCR, and NYC, respectively,
due to length mismatches of the decompressed time
series. While ATSC achieved higher compression ra-
tios for Libra and NYC—especially with its superior
compression for NYC (50x higher than TACO)—it
exhibited reconstruction errors up to 6.77 ×10
5
. In
some cases, ATSC also produced compressed time se-
ries longer than the original series.
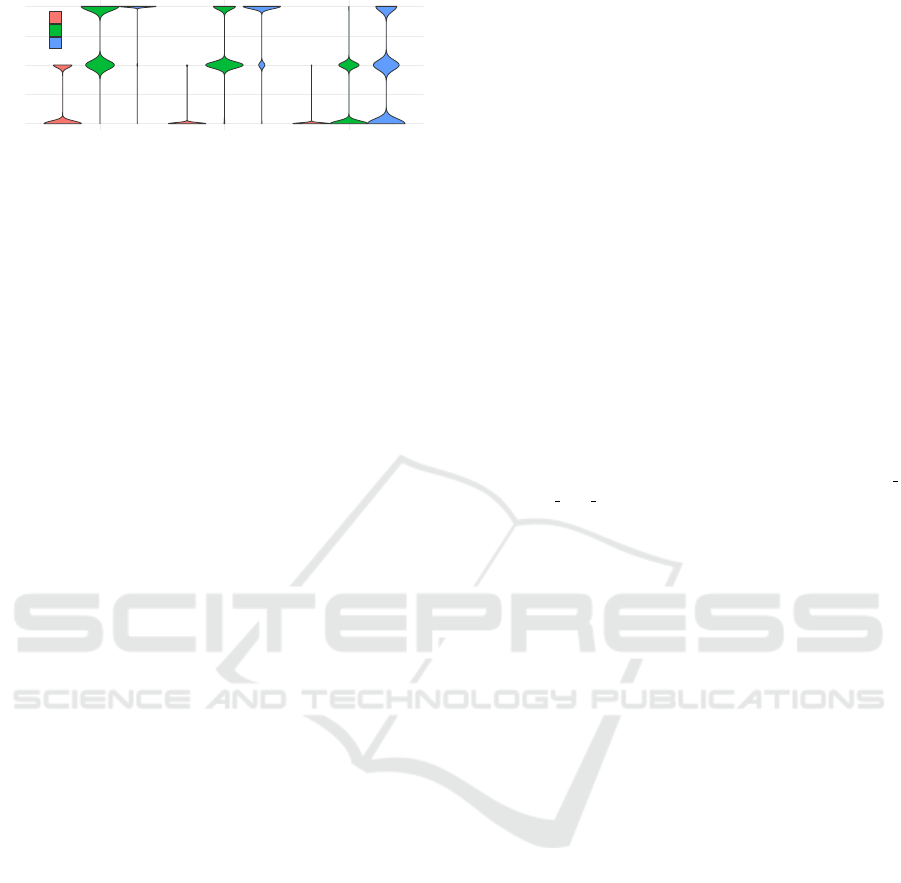
To further analyze the accuracy trade-off, we
ranked methods based on compression ratio and re-
construction error across all time series that were suc-
cessfully processed. Figure 3 visualizes these rank-
ings using violin plots, where the violin width rep-
resents the number of time series. TACO achieved
the best compression for 57.35% of the time se-
ries, ranked second in 30.45%, and third in 12.30%.
Across all rankings, it had for almost all time series
the lowest reconstruction error and never exhibited
the highest error, as reflected by the absence of rank
3 in the error ranking. TSXor ranked first in com-
pression for 6.90%, second for 37.96%, and third for
55.14% of the time series. However, while exhibit-
ing the best compression, it yielded also the highest
reconstruction error in 60% in these cases. ATCS
ranked first, second, and third in compression for
35.81%, 31.66%, and 32.53% of the time series, re-
spectively, but in 98.58% of its top-ranked compres-
sion performance, it resulted in the highest recon-
struction error. Taking the trade-offs between com-
pression ratio and reconstruction accuracy in account,
TACO is demonstrating a good balance.
In summary, across the five datasets, TACO
demonstrated good compression performance,
achieving the highest compression ratios in three
out of five datasets. It achieved compression ratios
ranging from 7.55 to 20.86, all while maintaining
low reconstruction error. Compared to the competing
methods, TACO achieved the best balance between
compression and accuracy, never exhibiting the
highest reconstruction error. TSXor, despite high
DATA 2025 - 14th International Conference on Data Science, Technology and Applications
188

1
2
3
1 2 3
Compression Rank
Error Rank
TACO
TSXor
ATCS
Figure 3: Compression ratio vs. reconstruction error com-
parison.
compression ration in select cases, often resulted
in excessive reconstruction errors, with some com-
pressed series exceeding their original size. ATSC
achieved the highest compression for the remaining
two datasets but introduced significant reconstruction
errors and length mismatches in decompressed time
series.
5 CONCLUSION
The growth of time series data generated necessitates
efficient compression techniques to mitigate storage,
bandwidth, and computational challenges. While ex-
isting methods offer various trade-offs, they often suf-
fer from restrictive assumptions, high computational
costs, or limited flexibility. To address these short-
comings, we introduced TACO, a lightweight, tree-
based approximate compression method that oper-
ates without strong statistical assumptions, requires
no training, and supports selective decompression.
Our experimental evaluation on five diverse datasets
demonstrates that TACO achieves high compression
rates while maintaining low reconstruction errors,
outperforming state-of-the-art approaches three of the
five datasets. These results highlight TACO’s poten-
tial as a practical and efficient solution for real-world
time series compression.
ACKNOWLEDGEMENTS
This work was funded by the Deutsche Forschungs-
gemeinschaft (DFG, German Research Foundation) –
510552229.
REFERENCES
Bauer, A., Z
¨
ufle, M., Eismann, S., Grohmann, J., Herbst,
N., and Kounev, S. (2021). Libra: A benchmark for
time series forecasting methods. In Proceedings of
the ACM/SPEC International Conference on Perfor-
mance Engineering, pages 189–200.
Bruno, A., Nardini, F. M., Pibiri, G. E., Trani, R., and Ven-
turini, R. (2021). Tsxor: A simple time series com-
pression algorithm. In String Processing and Informa-
tion Retrieval: 28th International Symposium, SPIRE
2021, Lille, France, October 4–6, 2021, Proceedings
28, pages 217–223. Springer.
Cantor, G. (1878). Ein beitrag zur mannigfaltigkeitslehre.
Journal f
¨
ur die reine und angewandte Mathematik
(Crelles Journal), 1878(84):242–258.
Chen, X. (2023). Joint symbolic aggregate approximation
of time series. arXiv preprint arXiv:2401.00109.
Chiarot, G. and Silvestri, C. (2023). Time series compres-
sion survey. ACM Computing Surveys, 55(10):1–32.
Chiarot, G., Vascon, S., Silvestri, C., and Ochoa, I. (2025).
Rat-cc: a recurrent autoencoder for time-series com-
pression and classification. IEEE Access.
City of New York (2025). Tlc trip record data. https://www.
nyc.gov/site/tlc/about/tlc-trip-record-data.page.
Dau, H. A., Keogh, E., Kamgar, K., Yeh, C.-C. M., Zhu,
Y., Gharghabi, S., Ratanamahatana, C. A., Yanping,
Hu, B., Begum, N., Bagnall, A., Mueen, A., and
Batista, G. (2018). The ucr time series classifica-
tion archive. https://www.cs.ucr.edu/
∼
eamonn/time
series data 2018/.
Enderton, H. B. (1977). Elements of set theory. Gulf Pro-
fessional Publishing.
G
¨
odel, K. (1931).
¨
Uber formal unentscheidbare s
¨
atze
der principia mathematica und verwandter systeme i.
Monatshefte f
¨
ur mathematik und physik, 38:173–198.
Guerra, A., Vinciguerra, G., Boffa, A., and Ferrag-
ina, P. (2024). Learned compression of nonlin-
ear time series with random access. arXiv preprint
arXiv:2412.16266.
Hopcroft, J. E., Motwani, R., and Ullman, J. D. (2001). In-
troduction to automata theory, languages, and compu-
tation. Acm Sigact News, 32(1):60–65.
Lin, J., Keogh, E., Wei, L., and Lonardi, S. (2007). Ex-
periencing sax: a novel symbolic representation of
time series. Data Mining and knowledge discovery,
15:107–144.
Liu, J., Djukic, P., Kulhandjian, M., and Kantarci, B.
(2024). Deep dict: Deep learning-based lossy time
series compressor for iot data. In ICC 2024-IEEE
International Conference on Communications, pages
4245–4250. IEEE.
Liu, X. and Wang, W. (2024). Deep time series forecast-
ing models: A comprehensive survey. Mathematics,
12(10):1504.
Makridakis, S. and Hibon, M. (2000). The m3-competition:
results, conclusions and implications. International
journal of forecasting, 16(4):451–476.
Makridakis, S., Spiliotis, E., and Assimakopoulos, V.
(2020). The m4 competition: 100,000 time series
and 61 forecasting methods. International Journal of
Forecasting, 36(1):54–74.
Malinowski, S., Guyet, T., Quiniou, R., and Tavenard, R.
(2013). 1d-sax: A novel symbolic representation for
time series. In International Symposium on Intelligent
Data Analysis, pages 273–284. Springer.
TACO: A Lightweight Tree-Based Approximate Compression Method for Time Series
189

Mohammadi Foumani, N., Miller, L., Tan, C. W., Webb,
G. I., Forestier, G., and Salehi, M. (2024). Deep
learning for time series classification and extrinsic re-
gression: A current survey. ACM Computing Surveys,
56(9):1–45.
Rolo, C., Bromhead, B., and Verghese, J. (2024).
Atsc - a novel approach to time-series compres-
sion. https://github.com/instaclustr/atsc/blob/main/
paper/ATCS-AdvancedTimeSeriesCompressor.pdf.
Rosenberg, A. and Strong, H. (1972). Addressing ar-
rays by shells. IBM Technical Disclosure Bulletin,
14(10):3026–3028.
Szudzik, M. (2006). An elegant pairing function. In Wol-
fram Research (ed.) Special NKS 2006 Wolfram Sci-
ence Conference, pages 1–12.
Szudzik, M. P. (2017). The rosenberg-strong pairing func-
tion. arXiv preprint arXiv:1706.04129.
Tnani, M.-A., Subarnaduti, P., and Diepold, K. (2022). Ex-
tract, compress and encode: Litnet an efficient autoen-
coder for noisy time-series data. In 2022 IEEE Inter-
national Conference on Industrial Technology (ICIT),
pages 1–8. IEEE.
Zamanzadeh Darban, Z., Webb, G. I., Pan, S., Aggarwal,
C., and Salehi, M. (2024). Deep learning for time se-
ries anomaly detection: A survey. ACM Computing
Surveys, 57(1):1–42.
Zheng, Z. and Zhang, Z. (2023). A temporal convo-
lutional recurrent autoencoder based framework for
compressing time series data. Applied Soft Comput-
ing, 147:110797.
DATA 2025 - 14th International Conference on Data Science, Technology and Applications
190