Extending Null Embedding for Deep Neural Network (DNN)
Watermarking
Kaan Altınay
1 a
, Devris¸
˙
Is¸ler
2,3 b
and Zekeriya Erkin
1 c
1
Cyber Security Group, Delft University of Technology, Van Mourik Broekmanweg, Delft, The Netherlands
2
IMDEA Networks Institute, Madrid, Spain
3
Universidad Carlos III de Madrid, Madrid, Spain
Keywords:
Watermarking, Ownership, DNN Watermarking.
Abstract:
The rise of Machine Learning (ML) has opened new business opportunities, particularly through Machine
Learning as a Service (MLaaS), where costly models like Deep Neural Networks (DNNs) can be outsourced.
However, this also raises concerns about model piracy. To protect against unauthorized use, watermarking
techniques have been developed. One such method, null embedding by Li et al., disables the model if pirated
but reduces classification accuracy. This paper proposes modifications to the null-embedding technique that
reduce this impact and keep the classification accuracy close to that of a non-watermarked model.
1 INTRODUCTION
The growing popularity of Deep Neural Networks
(DNN), along with the challenges of training and fine-
tuning them, has led to the emergence of a new mar-
ket: Machine Learning as a Service (MLaaS) (Ribeiro
et al., 2016). Due to its economic growth and in-
centives, it has become crucial for ML developers
to protect their models against piracy and infringe-
ment to protect their ownership rights. Watermark-
ing is a well-known technique for protecting owner-
ship upon copying and unauthorized distribution for
various assets such as datasets (
˙
Is¸ler et al., 2024),
databases (Sion et al., 2004), and machine learning
models (Adi et al., 2018). Watermarking consists of
two algorithms: 1) generation (or embedding/inser-
tion); and 2) verification (or extraction/detection). In
the generation algorithm, a watermark is embedded to
the original data by using a high entropy watermark-
ing secret key. Later, an owner computes the verifica-
tion algorithm on suspected data using its watermark-
ing secret key to extract/detect the watermark which
is used as a proof of ownership even if the data is
modified (un)intentionally. Due to the imperceptibil-
ity property of watermarking schemes, watermarking
does not affect the utility/functionality of the original
a
https://orcid.org/0009-0007-6048-8772
b
https://orcid.org/0000-0003-4895-8827
c
https://orcid.org/0000-0001-8932-4703
data (e.g., a watermarked model having a very close
accuracy compared to the original model).
Previous work on DNN watermarking relies on
either white-box or black-box verification (Guo and
Potkonjak, 2018). The white-box method requires
access to the model’s internal parameters, which is
unrealistic when a model owner suspects piracy by
a third party. In contrast, the black-box approach,
where the owner verifies the watermark by query-
ing the model, is more practical and secure. Most
black-box methods use backdoors that trigger a spe-
cific output known only to the owner. However, these
can be vulnerable if attackers discover the trigger be-
havior (Li et al., 2020). To address this, (Li et al.,
2020) introduced null embedding, which ties the wa-
termark to the model’s accuracy—making piracy at-
tempts break the model. While effective, this method
can reduce accuracy by up to 1.5%, which may be
unacceptable for performance-critical applications.
In this preliminary work, we propose a new DNN
watermarking using the null embedding based on the
work by (Li et al., 2020). Our modified approach im-
proves the classification accuracy while maintaining
the robust watermark against piracy attacks. We pro-
pose four new methods for the null embedding using
four filters: 1) random; 2) peripheral; 3) circular; and
4) triangular. We later run extensive experiments to
validate our claims on accuracy improvement using
CIFAR-10 and MNIST datasets and compare our re-
sults with (Li et al., 2020). The results show that the
Altınay, K.,
˙
I¸sler, D. and Erkin, Z.
Extending Null Embedding for Deep Neural Network (DNN) Watermarking.
DOI: 10.5220/0013641200003979
In Proceedings of the 22nd International Conference on Security and Cryptography (SECRYPT 2025), pages 771-776
ISBN: 978-989-758-760-3; ISSN: 2184-7711
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)
771

non-watermarked model yields a validation set clas-
sification accuracy of 82.91 ± 0.19%. The best of
the proposed watermarking methods yields an accu-
racy of 82.79±0.17%, which is an improvement over
82.44 ±0.39% from (Li et al., 2020).
2 RELATED WORK
(Uchida et al., 2017) proposes the first DNN water-
marking, which is a white-box verifiable technique
based on embedding a watermark in the parameters
of the model. Their work is later used as the bench-
mark for requirement definitions such as fidelity and
robustness in the DNN watermarking domain. (Zhang
et al., 2018) proposed a black-box verifiable DNN
watermarking method. Their technique used an idea
from backdoor attacks on DNNs to embed the water-
mark. A train image is embedded with a pattern and
this image has a label that it should not have (e.g., a
watermarked car image results in the label ’plane’).
Most black-box watermarking techniques are
based on the backdoor approach introduced by
(Zhang et al., 2018), where specific inputs trigger
a known output for verification. (Guo and Potkon-
jak, 2018) investigated DNN watermarking in embed-
ded systems and proposed using cryptographic tech-
niques, such as embedding the owner’s signature dur-
ing training, to strengthen ownership verification.
All the aforementioned black-box watermarking
techniques are insecure against piracy as shown by
(Li et al., 2020). To mitigate piracy attacks, the
same paper suggests null embedding, which is a tech-
nique that uses a bit sequence to build a strong depen-
dency between the normal classification accuracy of
the model and the watermark. This makes it impos-
sible for attackers to remove the watermark or insert
their own. This unique resistance against piracy is
why we chose their technique to study further.
Algorithm 1: WMGenerate (sk, h, w, n).
Data: sk, h, w, n
Result: {bits, pos}
1 σ ← Sign(sk, v)
2 {bits, pos} ← Transform (σ, h, w, n)
3 return {bits, pos}
3 PRELIMINARIES
As in (Li et al., 2020), we utilize a collision-resistant
hash function Hash (Katz and Lindell, 2014), a dig-
ital signature (Katz and Lindell, 2014) (Sign and
SignVerify) where a private signing key and public
verification key are denoted by sk and vk, respectively,
and existing DNN training techniques.
3.1 Watermarking with Null
Embedding
As mentioned, we base our watermarking on the null
embedding of a watermark into the training dataset d
of a DNN model M as proposed by (Li et al., 2020).
The training set d consists of data points in a matrix
format with dimensions of h (height) and w (width).
Below, due to page limitations we briefly describe
their watermark generation, embedding, and verifica-
tion algorithms (see their paper for further details).
Generation. The watermark generation algorithm,
see Algorithm 1, receives the following inputs: the
owner’s secret key sk, the height h and width w of the
image to be watermarked, and the length of one side
of the square filter n. First, a signature is generated
using sk to sign v which is the concatenation of a veri-
fier string and a timestamp, v = str||time. Afterwards,
Transform is called. Transform uses hashes of σ and
modulos to determine the tuple of the square’s posi-
tion, and the bit pattern embedded in it {bits, pos}, as
shown in Algorithm 2.
Algorithm 2: Transform (σ, h, w, n).
Data: σ, h, w, n
Result: {bits, pos}
1 bits ←Hash(σ) mod 2
n
2
;
2 pos = (x, y) ← (Hash(σ) mod (h −n),
Hash(σ) mod (w −n));
3 return {bits, pos}
Embedding. Null embedding (Li et al., 2020) consists
of applying a filter f ilter to a matrix-like data format,
which disguises part of the matrix as having extreme
values outside the normal dataset range. This effec-
tively reduces the learning space of the model. For
example, a 32×32 image is null-embedded by a 6 ×6
square filter with pixel color values of either λ = 2000
or −λ = −2000, depending on the bit pattern. Be-
cause both values are far from the normal color range
of [0, 255], these pixels no longer serve a purpose in
the image classification. f ilter is essentially the wa-
termark {bits, pos} and the shape in which it will be
applied. Figure 1c illustrates the square shape.
The embedding algorithm for a square filter is
shown by Algorithm 3 where the input variables in-
clude a (very) large number λ, and side length of the
square filter n. The watermarked subset is then added
back into the training set. If we chose 10% of images
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
772

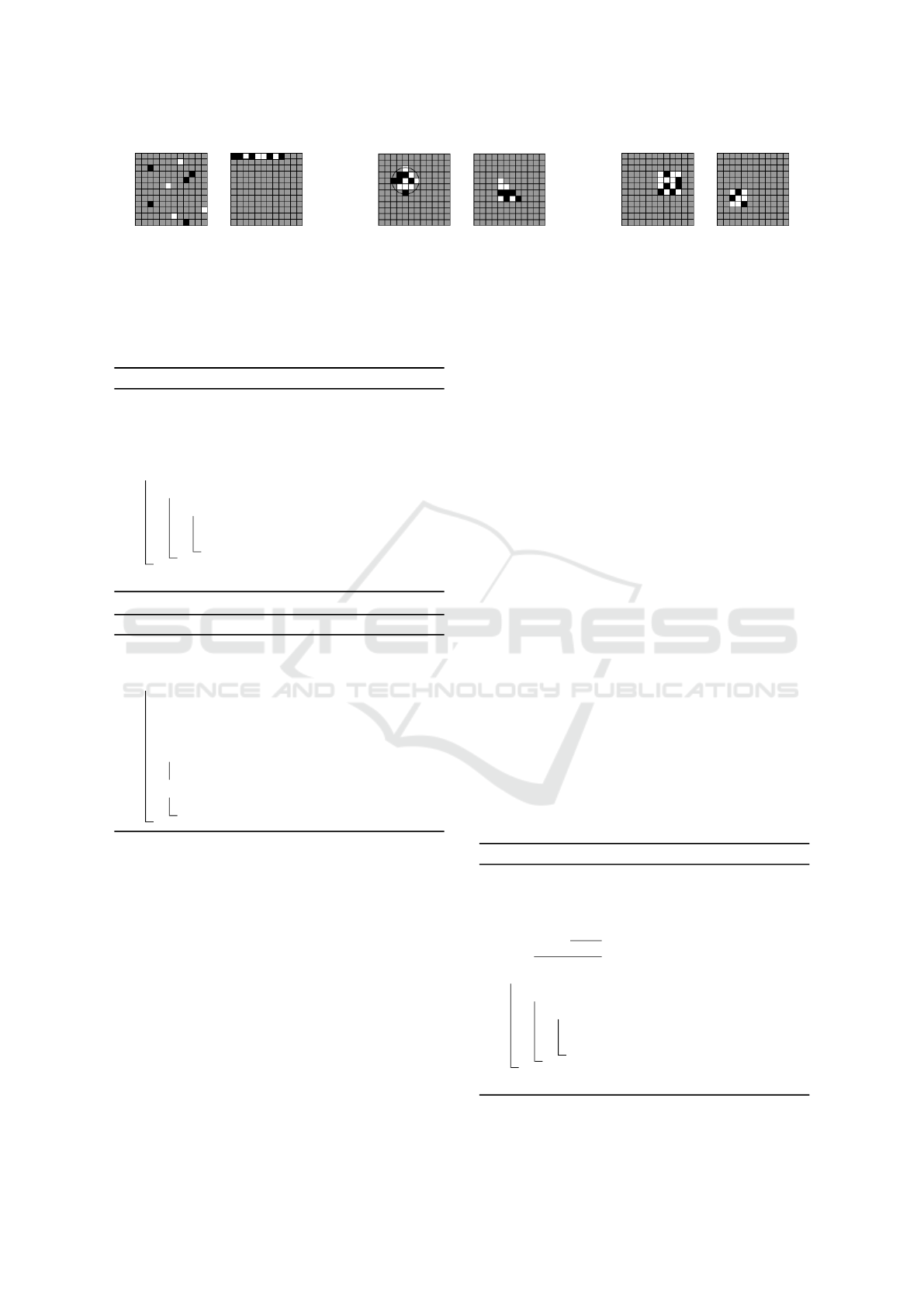
(a) Random and Peripheral patterns (b) Circular and Triangular patterns (c) 4x4 and 3x3 Square patterns
Figure 1: Different embedding patterns on a 12x12 image. White squares are set to λ = 2000, black squares to −λ.
to watermark, the training set size increases by 10%
(since each watermarked image in subset also has its
unmarked counterpart). Finally, we train M on the
augmented dataset.
Algorithm 3: EmbedSquare (d, bits, pos, λ, n)
Data: {d, bits, pos, λ, n}.
Result: Embedded Subset
1 (m = Most Significant Bit of bits)
2 subset ← random sample from d
3 for image ∈subset do
4 for i ∈ [n] do
5 for j ∈ [n] do
6 image[i, j] ← m ·λ −(1 −m)λ
7 bits << 1
8 return subset
Algorithm 4: WMVerify (d, vk, σ, h, w, n, T ).
Data: {d, vk, σ, h, w, n, T }
Result: Verified/ Rejected
1 if SignVerify(vk, σ) then
2 (bits, pos) ←Transform (σ, h, w, n);
3 d
New
← d + EmbedSquare (d, bits,
pos, λ, n);
4 if [Accuracy
M
(d
New
)] ≥ T then
5 return Verified;
6 else
7 return Rejected;
Verification. The verification algorithm, see Algo-
rithm 7, receives the following inputs: the data d, the
owner’s public key vk and signature σ, the height h
and width w of the input images, the length of one
side of the square filter n, and a threshold T . Verifi-
cation of the watermark is achieved by first checking
if the owner’s public key can verify the signature. Af-
terwards, a new set of watermarked data points are
generated. This can be done by anyone who has ac-
cess to Transform described in Algorithm 2. After
generation, the trained model is asked to guess la-
bels for the newly generated data points. The veri-
fication returns Verified if the model returns an ac-
curacy higher than a certain pre-determined threshold
T . Otherwise, verification fails and the algorithm re-
turns Rejected.
4 MODIFICATIONS OF NULL
EMBEDDING
The main idea behind our improved approach is to
change the shape and position of the watermark so
it doesn’t interfere as much with normal model be-
havior, while still working effectively. The original
method (Li et al., 2020) used a square patch placed
randomly, which could block important parts of the
image. Instead, we suggest using other shapes (i.e.,
random, peripheral, circular, or triangular patterns)
that take up the same space but are arranged differ-
ently. These new patterns are less likely to cover key
parts of the image, helping the model stay accurate
while still including a clear watermark.
The original watermark method also introduced
something called “true embedding,” where the reverse
of the watermark was used with wrong labels to test
if a model was truly watermarked. While this adds an
extra layer of proof, our results show it is not needed
and just using the basic watermark is already very re-
liable, with almost no false positives. Adding true em-
bedding makes things more complex and could hurt
accuracy. With the simpler method and smarter water-
mark patterns, we keep strong protection while avoid-
ing extra training or performance problems.
Algorithm 5: EmbedTriangular(d, bits, pos,λ, n).
Data: d, bits, pos, λ, n
Result: Embedded Subset
1 (m = Most Significant Bit of bits)
2 subset ← random sample from d
3 k ←
−1+
√
1+8n
2
2
4 for image ∈subset do
5 for i ∈ [k] do
6 for j ∈ [i] do
7 image[i, j] ← m ·λ −(1 −m)λ
8 bits << 1
9 return subset
Extending Null Embedding for Deep Neural Network (DNN) Watermarking
773

4.1 Types of Filters Considered
For our work, we use the following four filter patterns:
Random, Peripheral, Circular, and Triangular. To
keep the training domain at a similar size to images
embedded with the original square pattern, all filters
below were made to have the same pixel count as the
original pattern (or close if not possible). For a dif-
ferent filter, we have to determine which pixels in the
image belong to the watermark shape. For instance,
for a square or rectangular patch, this is a contiguous
block. For the peripheral filter, it could be the first
few rows/columns (forming an L-shape) covering n
pixels. For a circular filter, all pixels are within a ra-
dius r of the center point.
Random Filter. The random embedding pattern as
illustrated in Figure 1a chooses the same number of
pixels as the square filter (36 in our test) at random
throughout the image. This has the effect of not
blocking any significant features for the human eye,
but is very similar to introducing noisy training sam-
ples into the training dataset. This can cause lower
verifiability of the watermark as it is not perceivable,
and potentially harm the classification accuracy.
Peripheral Filter. This filter as illustrated in Figure 1a
is constructed by selecting the top-most and left-most
pixels possible in the image for pattern embedding.
This pattern was chosen as the extremes of a matrix-
like data structure can be cropped without disturbing
the coherency of the rest of the data. Especially in
image datasets like the ones we used, the peripherals
of the image tend to not have parts of the object being
labeled from the image. This means that the classifi-
cation accuracy is less affected than other methods of
reducing the training domain.
Circular Filter. To embed this filter, a circle is cho-
sen with a center pixel determined similarly to the
filter position determination in Algorithm 2. After-
wards, the radius of a circle with equal surface area
to the square is calculated, and pixels with centers
within this circle are used to embed the bit pattern.
This method was chosen as it will have the effect
of minimizing the perimeter of the watermark shape.
As DNNs use adjacent pixels to learn patterns, it im-
proves to result in better classification accuracies in
comparison to a square filter (see Figure 1b).
Triangular Filter. The triangular filter uses a triangle
with an area less than or equal to that of the square to
embed the bit pattern. Its reason for inclusion is to see
if there are significant classification differences be-
tween using different regular polygon shapes for null
embedding. Data in matrix form does not tend to have
features that can be derived from a diagonal along the
matrix. Therefore, we predict that it is less likely for
a triangle to block a significant feature in compari-
son to a square. The number of rows in the triangular
filter is determined as k =
−1+
√
1+8x
2
. The goal is to
create the largest triangle where the i
th
row has ≤i el-
ements, with the number of pixels not exceeding the
number of pixels in the equivalent square filter. Given
the number of pixels in the square filter as x, we want
to find the largest integer k such that
k(k+1)
2
≤x. Rear-
ranging this inequality gives k
2
+k −2x = 0, and plug-
ging a = 1, b = 1, c = −2x into the quadratic formula
yields k =
−1±
√
1
2
−4·1·(−2x)
2
=
−1+
√
1+8x
2
. Algorithm
5 shows how this equation is used in the embedding.
5 EXPERIMENTAL SETUP AND
ANALYSIS
5.1 Setup
All experiments were conducted on an HP ZBook
Power G7 laptop with an NVIDIA Quadro T1000
GPU, using Python. We used SHA256 for hashing
and RSA PKCS#1 v1.5 for digital signatures. The
CIFAR-10 (60K images) and MNIST (70K images)
datasets, each with 10 class labels, were used for ob-
ject and digit recognition, respectively. Models were
built with TensorFlow 2.16 via the Keras API, run-
ning on Windows Subsystem for Linux (WSL2) to
enable GPU support, as native Windows support was
dropped after TensorFlow 2.10.
Data Split and DNN Structure. CIFAR-10 was split
to have 50K data points in the training set and 10K in
the validation set. MNIST was split to have 60K data
points in the training set and 10K in the validation set.
10% of the training dataset was selected randomly
before each training to be embedded with the water-
mark. With the addition of the watermarked data, the
total training set has a size of 55K for CIFAR-10 and
66K for MNIST. To match the experimental setup from
(Li et al., 2020), the DNN for training on CIFAR-10
was constructed with 6 convolutional and 3 dense lay-
ers. The DNN for training on MNIST was constructed
with 2 convolutional and 2 dense layers.
The model M
CIFAR-10
on CIFAR-10 was trained
for 50 epochs in each round, while the MNIST DNN
M
MNIST
was trained for 20 epochs. This is because
MNIST is a lot simpler, and thus the DNN achieves
higher accuracy fast. For both datasets, the results ob-
tained from 5 rounds of training were averaged out for
each configuration presented in the following section.
Trials.Before experimenting with the aforementioned
filter types in Section 4, the square filter used by (Li
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
774

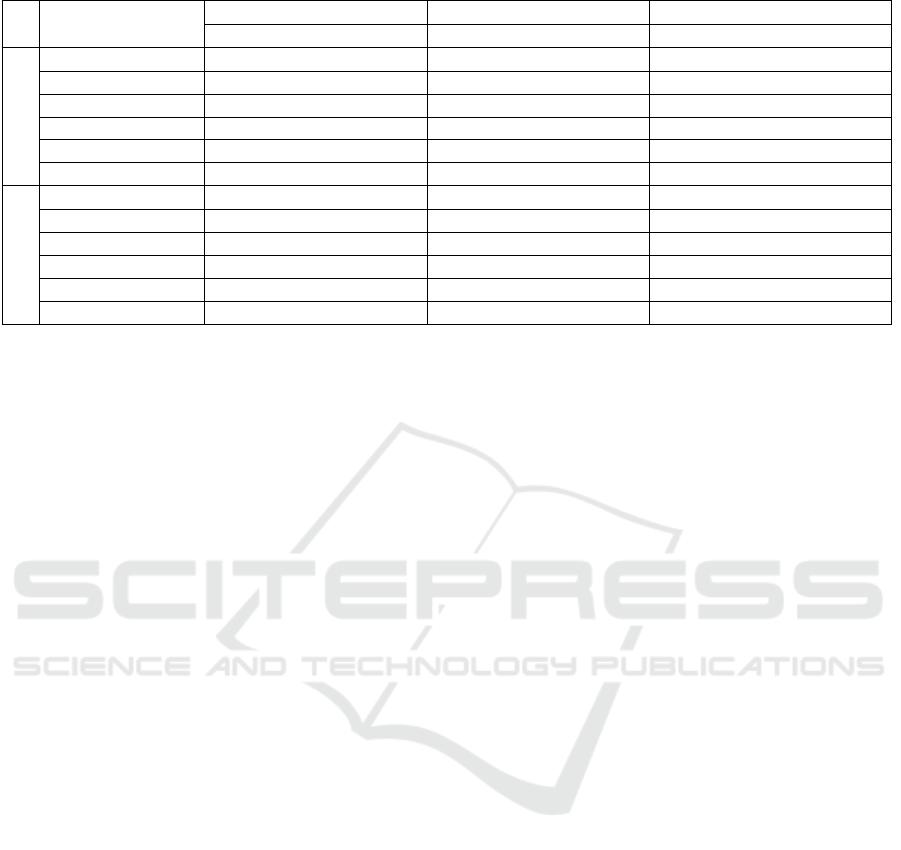
Table 1: Performance Comparison of Watermarking Methods on CIFAR-10 and MNIST. Best accuracy values are bolded.
Method
Training Validation Verification
Accuracy Loss Accuracy Loss Accuracy Loss
CIFAR-10
No Watermark 98.56±0.12 0.04±0.00 82.91±0.19 0.85±0.01 12.14±1.26 73.61±27.75
Square (Li et al.) 98.41±0.39 0.05±0.01 82.44±0.39 0.86±0.05 96.67±1.78 0.11±0.06
Random 98.36±0.23 0.05±0.01 82.61±0.20 0.84±0.02 66.48±5.30 1.55±0.33
Peripheral 98.74±0.15 0.04±0.00 82.60±0.30 0.88±0.02 99.50±0.18 0.02±0.01
Circular 98.56±0.28 0.04±0.01 83.01±0.27 0.83±0.04 95.50±1.17 0.14±0.04
Triangular 98.73±0.08 0.04±0.00 82.79±0.17 0.87±0.02 99.44±0.25 0.02±0.01
MNIST
No Watermark 99.86±0.03 0.00±0.00 99.42±0.03 0.02±0.00 95.15±4.37 0.17±0.17
Square (Li et al.) 99.83±0.07 0.01±0.00 99.43±0.03 0.02±0.00 99.60±0.52 0.01±0.01
Random 99.85±0.03 0.01±0.00 99.44±0.03 0.02±0.00 99.17±0.67 0.03±0.02
Peripheral 99.87±0.01 0.00±0.00 99.41±0.04 0.02±0.00 99.98±0.02 0.00±0.00
Circular 99.83±0.06 0.01±0.00 99.38±0.03 0.02±0.00 99.62±0.32 0.01±0.01
Triangular 99.88±0.02 0.00±0.00 99.43±0.03 0.02±0.00 99.99±0.01 0.00±0.00
et al., 2020) was implemented following the pseu-
docode procedure in their paper. The results obtained
from the DNN watermarked with the square pattern
were then used as the benchmark to compare the per-
formance of our proposed pattern varieties. Addition-
ally, the model was trained with the same parameters
but without a watermark to be able to compare the
loss of accuracy on the validation set.
5.2 Evaluation Metrics
For our experiments, we evaluate our approach on
each aforementioned datasets using two metrics for
each training, validation, and watermark verification:
1) Accuracy; and 2) Loss. Sparse Categorical Cross-
Entropy is used as the loss function. This loss func-
tion was chosen to keep the results comparable with
the experimentation performed in (Li et al., 2020).
After each training round, the epoch after which M
yielded the highest accuracy for the validation set
was used as the representative data for that round.
This epoch was usually between the 40th-50th for
M
CIFAR-10
and the 15th-20th for M
MNIST
. The reason
of later epochs sometimes performing worse is that
the model starts overfitting to the training set after a
certain number of epochs.
Table 1 shows the average values from 5 trials
for each watermarking method. The results from the
models on the training data, validation data, and wa-
termark verifiability are explained below.
Training Data. The accuracy and loss of each embed-
ding method on the training data are shown in Table
1 under Training. For models trained for the same
number of epochs on the same size dataset, these val-
ues are expected to be similar regardless of the em-
bedding method.
Validation Data.Validation results are key for com-
paring the impact of different watermarking methods
on model accuracy. As shown in Table 1 (Validation),
our proposed patterns reduce accuracy loss compared
to the original square filter; hence confirming the ef-
fectiveness of our modifications.
Watermark Verifiability. This metric is important as
it is a hard requirement for any watermarking method
to be verifiable in the models they are embedded in.
If a watermarking method yields high accuracy in the
original classification task but is not verifiable, then
it is not a functioning watermark. The accuracy and
loss of each embedding method in detecting the wa-
termark are shown in Table 1 under Verification.
5.3 Analysis
Before discussing the results as presented in Table
1, it is worth to note that some watermarked mod-
els have a higher accuracy than the non-watermarked
(non-WM) model on the training set. This indicates
that the high number of epochs used for training made
the accuracies of watermarked and non-WM models
indistinguishable. Thus, the training accuracy has es-
sentially saturated, and further training is unlikely to
yield any significant improvement.
The model embedded with a random pattern per-
formed significantly worse than the other water-
marked models in terms of watermark verification.
Therefore, we excluded this randomly watermarked
model when determining the verifiability threshold
for either dataset since it would skew the threshold
due to its poor verification performance.
CIFAR-10 Dataset. Among the models trained on
CIFAR-10, the circular pattern watermark achieved
the highest average validation accuracy, slightly out-
performing the non-watermarked model, though still
within one standard deviation (SD). The triangular
pattern also fell within one SD but showed lower vari-
ability than the circular one, suggesting more consis-
Extending Null Embedding for Deep Neural Network (DNN) Watermarking
775

tent performance. Both circular and triangular pat-
terns had lower SDs than the square pattern, which
also converged more slowly to a validation accuracy
of around 82%. For watermark verification, a thresh-
old of T = 90% proved effective. The peripheral pat-
tern showed the best verification results, closely fol-
lowed by the triangular pattern, making the triangular
pattern the most balanced choice overall.
MNIST Dataset. On MNIST, the classification task
was significantly easier for the trained DNNs (base-
line ∼ 99.4% accuracy). Therefore, the training set
classification accuracy quickly converges to values
higher than 99%. Similarly in the validation set ac-
curacy, all watermarking methods have yielded an ac-
curacy of around 99.4%. The fact that almost all of
the validation accuracies lie within an SD of each
other means that it is difficult to infer much from
these values. Our results show that the Square and
Random watermarked models have performed clos-
est to the non-WM model. Even though the Ran-
dom watermarked model appears to have the most
accurate and reliable validation set, its performance
in verifiability is significantly lower than the other
watermarked models. The Triangular watermarked
model offers the best watermark verifiability among
all methods tested. Combined with its validation ac-
curacy, which closely matches the non-watermarked
model, it proves to be the most effective option. Our
results suggest that a verification threshold of T =
99% is suitable.
Comparison with Li et al. Compared to the re-
sults in (Li et al., 2020), our findings show some no-
table differences. First, our CIFAR-10 models did not
reach the reported 88% normal classification (NC) ac-
curacy, despite closely following the original proce-
dure. Even with 100 training epochs, accuracy stayed
around 84%, likely due to hardware limitations. In
contrast, our MNIST models achieved over 99% NC
accuracy, exceeding the 98.7% reported by (Li et al.,
2020). While they used a 50% embedding rate for
MNIST, we found no benefit in doing so and used a
consistent 10% rate for both datasets. On CIFAR-10,
models using circular or triangular watermark pat-
terns performed about 0.5% better in NC accuracy
than those using the square pattern. This suggests that
non-square shapes are more effective for preserving
model accuracy when using null embedding.
6 FUTURE WORK AND
CONCLUSION
We proposed four new ways to embed a watermark
into a DNN with the null embedding method from (Li
et al., 2020). Experiments on CIFAR-10 showed that
the circular pattern preserves model accuracy best,
improving performance by about 0.5% compared to
the square pattern and matching the accuracy of a
non-watermarked model. Future work includes test-
ing the impact of transfer learning and fine-tuning.
ACKNOWLEDGEMENTS
This paper is supported by the European Union’s
Horizon Europe research and innovation program un-
der grant agreement No. 101094901, the Septon
and 101168490, the Recitals Projects. Devris¸
˙
Is¸ler
was supported by the European Union’s HORIZON
project DataBri-X (101070069).
REFERENCES
Adi, Y., Baum, C., Ciss
´
e, M., Pinkas, B., and Keshet, J.
(2018). Turning your weakness into a strength: Wa-
termarking deep neural networks by backdooring. In
USENIX Security.
Guo, J. and Potkonjak, M. (2018). Watermarking Deep
Neural Networks for Embedded Systems. In 2018
IEEE/ACM ICCAD. ISSN: 1558-2434.
˙
Is¸ler, D., Cabana, E., Garc
´
ıa-Recuero,
´
A., Koutrika, G., and
Laoutaris, N. (2024). Freqywm: Frequency water-
marking for the new data economy. In IEEE ICDE.
Katz, J. and Lindell, Y. (2014). Introduction to Modern
Cryptography, Second Edition. CRC Press.
Li, H., Wenger, E., Shan, S., Zhao, B. Y., and Zheng, H.
(2020). Piracy Resistant Watermarks for Deep Neural
Networks. arXiv:1910.01226 [cs, stat].
Ribeiro, M., Grolinger, K., and Capretz, M. (2016). MLaaS:
Machine learning as a service.
Sion, R., Atallah, M. J., and Prabhakar, S. (2004). wmdb.:
Rights protection for numeric relational data. In IEEE
ICDE.
Uchida, Y., Nagai, Y., Sakazawa, S., and Satoh, S. (2017).
Embedding watermarks into deep neural networks. In
ACM ICMR.
Zhang, J., Gu, Z., Jang, J., Wu, H., Stoecklin, M., Huang,
H., and Molloy, I. (2018). Protecting intellectual prop-
erty of deep neural networks with watermarking. In
ACM AsiaCCS.
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
776