Privacy-Enhancing Federated Time-Series Forecasting: A

Microaggregation-Based Approach

Sargam Gupta

and Vicenc¸ Torra

Department of Computing Science, Ume

a University, Ume

a, Sweden

Keywords:

Time-Series Data, Privacy, Microaggregation, Federated Learning, k-Anonymity.

Abstract:

Time-series forecasting is predicting future values based on historical data. Applications include forecasting

trafﬁc ﬂows, stock market trends, and energy consumption, which signiﬁcantly helps to reduce costs and ef-

ﬁciency. However, the complexity inherent in time-series data makes accurate forecasting challenging. This

article proposes a novel privacy-enhancing k-anonymous federated learning framework for time-series pre-

diction based on microaggregation. This adaptable framework can be customised based on the client-side

processing capabilities. We evaluate the performance of our proposed framework by comparing it with the

centralized one using the standard metrics like Mean Absolute Error on three real-world datasets. Moreover,

we performed a detailed ablation study by experimenting with different values of k in microaggregation and

different client side forecasting models. The results show that our approach gives comparable a good privacy-

utility tradeoff as compared to the centralized benchmark.

1 INTRODUCTION

Time-series forecasting predicts future values based

on historical data, crucial for decisions with appli-

cations in energy, transport, ﬁnance, economics, and

weather. However, the nature of time series is quite

complex which makes forecasting a challenging task

(Petropoulos et al., 2022).

In the beginning, multiple statistical methods

based on averaging have been used.Then, these mod-

els evolved to become approaches like Autoregressive

integrated moving average (Shumway et al., 2017)

and several machine learning approaches like differ-

ent Trees (Ulvila, 1985) and Support Vector Machines

uller et al., 1997) but these were not compatible

with nonlinear data patterns. With more data and

computational power available several deep learning

arcitectures were also used. These included Multi-

layer Perceptrons (Rumelhart et al., 1986), Recur-

rent Neural Networks (Hopﬁeld, 1982), Convolu-

tional Neural Networks (LeCun et al., 1998) and

Graph Neural Networks (Scarselli et al., 2008). There

have been specialised models in literature proposed to

deal with time series data like Long Short-Term Mem-

ory (Hochreiter and Schmidhuber, 1997) and Tempo-

https://orcid.org/0000-0003-0216-4992

https://orcid.org/0000-0002-0368-8037

ral Convolutional Networks (Bai et al., 2018). How-

ever, most of the approaches used were highly cen-

tralized.

Since the real-world time-series data is quite large

and continuously growing, it is not feasible to process

it centrally. Also, collecting data from different lo-

cations or clients and storing it in a server for model

training may lead to privacy threats such as reveal-

ing sensitive information about the individuals whose

data is being collected which is against the privacy

regulations in various nations (Voigt and Von dem

Bussche, 2017; Wilson and Commissioner, 2020).

Hence, to overcome these issues, federated learning

(FL) (McMahan et al., 2017b) can be seen as a po-

tential solution to build global forecasting models for

time series data. However, intuitively FL might seem

privacy-preserving, but, studies have shown that even

just sharing the gradients isn’t safe (Bai et al., 2024;

Wu et al., 2023) as these can be used to infer the train-

ing data. To further strengthen the privacy in feder-

ated settings, there is a need to introduce some sort of

privacy mechanisms.

Most masking methods that have been proposed

are mostly for standard databases or images. Only a

few methods have been proposed to mask the time-

series data which are mainly introduced in the cen-

tralized setting (Nin and Torra, 2006b; Nin and Torra,

2009). We employ miocroaggregation as a technique

Gupta, S. and Torra, V.

Privacy-Enhancing Federated Time-Series Forecasting: A Microaggregation-Based Approach.

DOI: 10.5220/0013641100003979

In Proceedings of the 22nd International Conference on Security and Cr yptography (SECRYPT 2025), pages 765-770

ISBN: 978-989-758-760-3; ISSN: 2184-7711

765

to satisfy k-anonymity (Samarati, 2001) in our ap-

proach. The idea of k-anonymity is about grouping

individual records into clusters of at least k records

based on some similarity metric, and then replacing

the records in each cluster with an aggregated values,

such as the mean or some sort of representative. This

ensures that an individual’s data is indistinguishable

from at least k-1 other individuals, thereby satisfying

the k-anonymity requirement.

In our work, we propose a new framework for

time-series protection in federated settings based on

microaggregation (Domingo-Ferrer and Mateo-Sanz,

2002) which has been validated in the literature to en-

sure good performance on standard numerical data.

We also experiment with different values of the tun-

ing parameter k in microaggregation which ensures

different privacy levels. The framework has been val-

idated for robustness with multiple client-side fore-

casting models to ensure that it performs well even

with light-weight models.

The remaining part of this paper is organized as

follows. Section 2 reviews some basic concepts. Our

proposed prediction mechanism is described in Sec-

tion 3. Section 4 describes the experimental settings.

Section 5 contains a discussion on the results. Section

6 gives the conclusion and future work.

2 BACKGROUND

In this section, we describe the relevant background

topics required to understand our proposed frame-

work.

2.1 Microaggregation

Microaggregation (Domingo-Ferrer and Mateo-Sanz,

2002) is a masking method that comes originally from

statistical disclosure control of numerical microdata.

In simple words, the process of microaggregation is

about building small microclusters within the data and

then replacing the original data in each cluster by its

representative. This succeeds in achieving privacy in

the ﬁnal database as in each cluster which contains a

deﬁned number of records, their exists a cluster repre-

sentative rather than each record in the data. Previous

studies show that this masking method gives a good

trade-off between information loss and disclosure risk

(Mortazavi and Jalili, 2014).

Mathematically, microaggregation can be viewed

as an optimization problem. The main objective is

to ﬁnd the clusters in the data i.e., to make partitions

in data such that it minimized the overall global er-

ror. Each cluster needs to have a minimum number

of records deﬁned by k to satisfy the privacy require-

ment. The objective function minimizes the intraclus-

ter distance such that the distance between the records

and their cluster representatives is minimal. Never-

theless, ﬁnding an optimal solution to this kind of op-

timization problem is an NP problem (Nin and Torra,

2006a). There has been some research on ﬁnding

heuristics to solve this. One of them is the Maximum

Distance Average Vector (MDAV) algorithm.

This is the generic algorithm for MDAV and can

be applied to various distances and averages.

For applying this algorithm to time-series data, we

get inspired by (Nin and Torra, 2006b). We deﬁne a

time series as a pair of temporal variable t

and time-

dependent variable v

i.e., {(v

)} where k = 1,....,

N. Here t

k+1

> t

We have used distance based on the raw values of

the time series of equal length in the current imple-

mentation. For the experiments, we have used the Eu-

clidean distance for computing the distance between

records and the cluster representative to compute the

average. We deﬁne it as follows:

(x,v) =

∑

k=1

− v

)

Here, we assume x and v to be two time-series of

N dimension. Each time series is deﬁned as the pair of

values {(v

)} where k = 1,...., N. We consider the

series to be of equal length and their temporal com-

ponents are the same.

For calculating average on the cluster centers, we

use the component-wise mean. It is deﬁned such as

we have a given set of V = {v

}

j=1,2,...J

with a time

series v

for j = 1,..,J, each one with v

, we deﬁne

it as :

˜v

= (1/J)

∑

j=1

2.2 Federated Learning

Federated Learning (FL) (McMahan et al., 2017b) is

a distributed machine learning paradigm in which the

client’s local data remains on the device itself. In the

centralized machine learning, the data needs to be col-

lected at a central location and then, an overall gen-

eralization of the data can be done. However, FL is

better in this case as the data on different clients per-

form local model updates on their devices and share

only model parameters or gradients, not their original

datasets. The federated approach enhances privacy by

keeping sensitive data on-device and reduces commu-

nication costs by transmitting compact model updates

instead of sharing the whole datasets however, there

are a set of privacy issues that still exist.

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

766

In the simple FL approach, in each communica-

tion round, the server transmits the global model pa-

rameters to the selected clients. These clients perform

the local model training on their dataset and send their

updated parameters to the server which then aggre-

gates the differences to the global model. This com-

munication stops when convergence is achieved or a

speciﬁed number of rounds are completed.

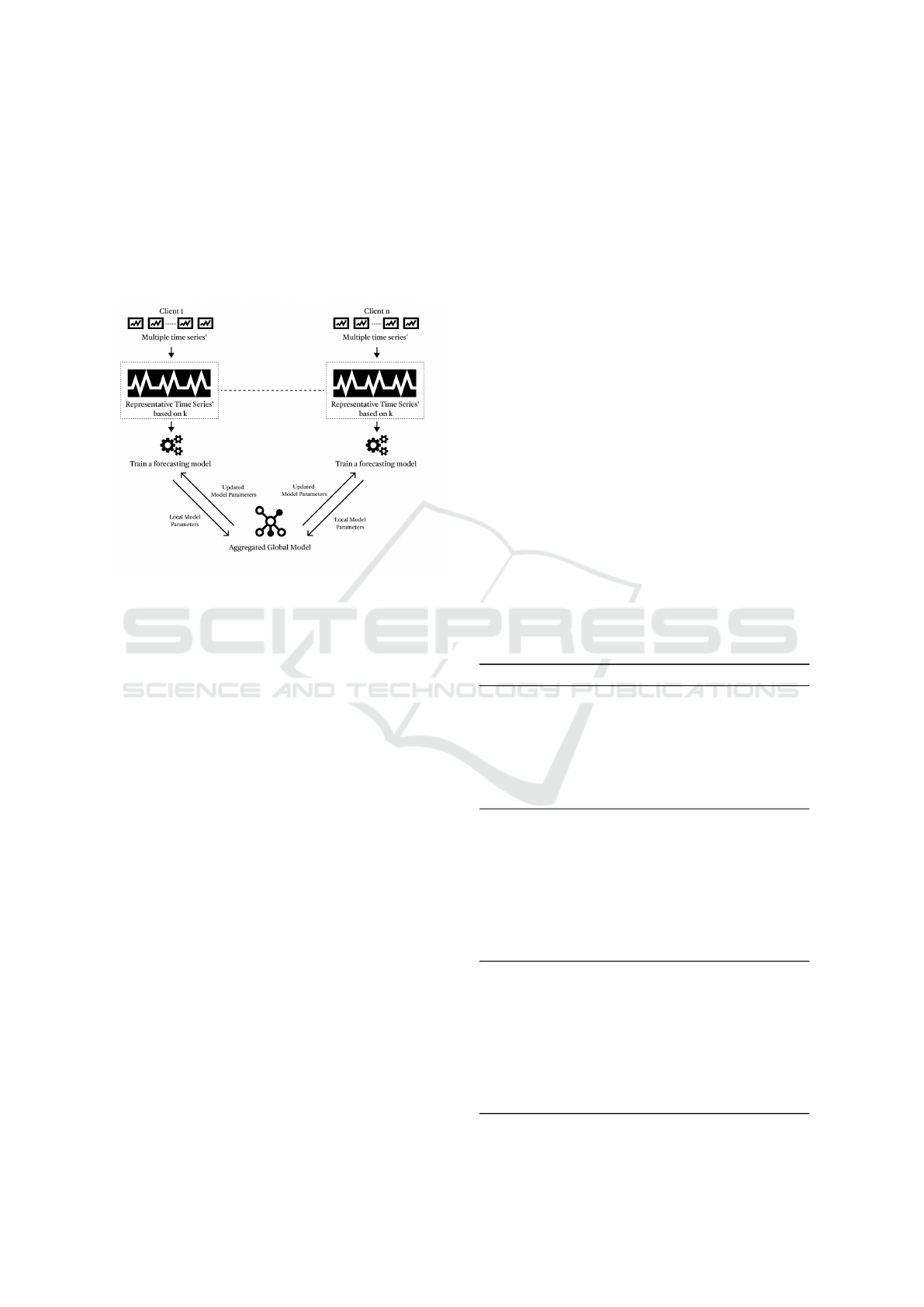
Figure 1: Proposed methodology with an application to en-

ergy consumption prediction.

3 METHODOLOGY

In this section, we propose our new

microaggregation-based federated time-series

prediction framework. Our proposed framework

aims to provide a privacy-preserving solution to

time-series prediction problem in the federated

settings. To validate our framework, we compare our

approach with the centralized framework.

On the client side, each client has multiple time-

series collected. These time-series could be anything

like stock opening values, energy consumption values

in kwh for apartments in a building or the trafﬁc ﬂow

data in a similiar area. The data will have a mandatory

date-time column that is a continuous value.

Before building a model on these time series, to

ensure a privacy layer in the framework, we use mi-

croaggregation. In microaggreagtion, we experiment

with multiple values of k. The signiﬁcance of the

value of k is that this ensures that in clustering there

are atleast k time series in a cluster. The algorithm

used has been described in the previous section in-

spired by (Nin and Torra, 2006b). Then after getting

the representative time series, we build a prediction

model on them on each client. In the literature several

models have been proposed to deal with these types

of data. However, not all models are suitable to work

with the federated settings as the client’s processing

capacity may not be enough. So, we have selected a

few light-weight models that can be used in this set-

tings. These models are described in the 5 section.

We use the FedAVG algorithm (McMahan et al.,

2017a) for parameter aggregation. It is simplest and

formerly proposed aggregation algorithm. Each itera-

tion of FedAvg starts with initializing a global model

to all the participating clients. This could be a subset

of clients selected in each iteration or all the clients

in case of the full-participation. The clients train on

this inialized model with their local datasets and ob-

tain a new updated model. The updates in the model

parameters are then sent to a global server where ag-

gregation takes place. The global server aggregates

these updates by performing a weighted average of

their values forming a new global model. Again, this

updated global model is sent back to the clients for

retraining. This process continues iteratively until

it reaches convergence or the maximum number of

rounds are acheived. Once, the converged model is

achieved, then this model is used to predict on the test

data to evaluate its performance.

4 EXPERIMENTAL SETTINGS

Table 1: Parameter Settings for Models.

Model Parameters Values

GRU/LSTM

hidden dimensions 20

dropout 0

batch size 16

local epochs 10

optimizer kwargs ”lr”: 1e-3

random state 42

training length 96

input chunk length 96

TCN

likelihood QuantileRegression()

kernel size 3

num ﬁlters 4

dropout 0.2

batch size 32

local epochs 10

optimizer kwargs ”lr”: 1e-3

random state 42

input chunk length 96

output chunk length 24

NBeats Model

input chunk length 96

output chunk length 24

num stacks 10

num blocks 1

num layers 4

layer width 512

epochs 10

nr epochs val period 1

batch size 800

random state 42

Privacy-Enhancing Federated Time-Series Forecasting: A Microaggregation-Based Approach

767

Table 1 summarizes the parameter settings for the

models.

For performing the experimental analysis we have

used three different real-world datasets capturing

three different types of time-series mentioned below:

• Electricity Dataset (Trindade, 2015): This dataset

contains the measurements of electric power con-

sumption in households with a 15-minute sam-

pling rate. The data is collected from 370 differ-

ent households in Portugal. This data is available

for 4 years from 2011 to 2016. We have used one

year’s data from 01 January 2012 to 01 January

2013 for performing our experiments.

• PEMS Dataset (http://pems.dot.ca.gov): This

dataset contains the trafﬁc ﬂow information from

the San Francisco Bay area freeways. The data

is collected from 862 different sensors located on

the highway system. The data is available for two

years from 2015 to 2016 with a reading of traf-

ﬁc on roads after every hour. We have used one

year’s data from 01 January 2015 to 01 January

2016 for performing our experiments.

• Huge Stocks Dataset (https://www.kaggle.com/

datasets/borismarjanovic/ price-volume-data-for-

all-us-stocks-etfs): This is a publicly available

dataset that contains the historical daily prices and

volumes of all U.S. stocks and ETFs from 1999 to

2017. Initially, the dataset has ﬁles for different

stocks with columns that have Open, High, Low,

Close, Volume, OpenInt attributes. We have used

only the Open attribute from 2013 to 2015 for our

approach.

To divide the time-series between the clients, in

the Electricity and PEMS datasets, we choose the

time-series’ of sensors in one region as a single client

for simulation. For the stocks dataset we divide the

time-series’ equally among the clients. We consider

the homogenous case in which all the clients have

same timestamps and equal number of time-series’.

We split the data into 80% for training, 10% for val-

idation and 10% for testing for both centralized and

federated settings. We have used the Mean Absolute

Error as the metric to measure the performance of our

approach. For the implementation of various time-

series forecasting models, we use the Darts (Herzen

et al., 2022) Python library. We performed 3 itera-

tions of FedAvg. For centralized approach, we run 40

rounds for each model with the same parameters.

Table 2: Centralized Approach on Electricity Dataset.

Forecasting Model Mean Absolute Error

LSTM 0.0226

GRU 0.0899

NBeats 0.0028

DeepTCN 0.0012

Table 3: Centralized Approach on PEMS Dataset.

Forecasting Model Mean Absolute Error

LSTM 0.0645

GRU 0.0058

NBeats 0.0953

DeepTCN 0.0259

Table 4: Centralized Approach on Huge Stocks Dataset.

Forecasting Model Mean Absolute Error

LSTM 0.2080

GRU 0.2073

DeepTCN 0.2173

5 DISCUSSION

The results of the proposed framework are depicted in

Tables 2,3, 4 and 5. The Tables 2, 3 and 4 contain the

mean absolute error when we considered a centralized

approach using the four different forecasting mod-

els namely LSTM, GRU, NBeats and DeepTCN on

Electricity Dataset, PEMS Dataset and Huge Stocks

Dataset respectively.

The Table 5 contains the results of the feder-

ated approach on the microaggregated data. We

have experimented with ﬁve different values of the

k = 2,4,6,9,12 on the same four forecasting models

based on the stated parameters.

As a generic idea, with the smaller value of k,

there will be more partitions in the data which leads to

more cluster formation and more representation of the

data leading to a higher accuracy. However, from the

results in the Table 5, we can see an opposite trend.

This has been observed in previous research as well

that it is not an absolute case that the performance

of a classiﬁer will worsen with addition of a privacy

mechanism. Authors in (Aggarwal and Yu, 2004;

Sakuma and Osame, 2017) conclude similiar results

where anonymization shows noise reduction effects

and leads to higher performance. With the increasing

value k, in the Energy Consumption and Huge Stocks

Dataset, we ﬁnd that a higher value of k is yielding a

lower MAE value. This could be attributed to the fact

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

768

Table 5: Combined Client Set MAE with different values of k across datasets.

Dataset Model k=2 k=4 k=6 k=9 k=12

Energy Consumption

LSTM 0.1983 0.1896 0.2473 0.1681 0.1543

GRU 0.2866 0.2108 0.1587 0.3547 0.2121

Nbeats 0.1270 0.1170 0.1170 0.1185 0.1067

DeepTCN 0.1828 0.1441 0.1336 0.1204 0.1017

PEMS

LSTM 0.0504 0.0431 0.471 0.0658 0.0702

GRU 0.0566 0.0534 0.0460 0.0881 0.0630

Nbeats 0.0566 0.0533 0.0535 0.0461 0.0365

DeepTCN 0.0638 0.0425 0.0440 0.0458 0.0328

Huge Stocks

LSTM 0.2717 0.2368 0.1749 0.2129 0.2168

GRU 0.2622 0.2420 0.2005 0.2216 0.1968

DeepTCN 0.1931 0.1845 0.1897 0.1872 0.1936

that here based on the nature of the time-series data,

the process of microaggregation is giving a smoothing

effect.

In our federated time-series setup, with a larger

k in microaggregation, each client’s local dataset be-

comes less noisy as microaggregation replaces the in-

dividual series with the cluster representative, leading

to local gradients being more stable, and the global

model converging more smoothly, hence, giving a

better generalization on the test set. Larger k values

here might be reducing variance and eliminating ex-

treme values in the time-series, leading to better per-

formance.

Also, as mentioned in the literature (Kim et al.,

2024), a challenge with time-series data is that it is

dependent on the domain and data frequency which

is evident in our case as the three time-series are very

diverse. It would be intersting to also test and ﬁnd a

threshold k value until which microaggregation may

act as a regularization and then, lead to degraded per-

formance afterwards as a part of our future work.

Another interesting study would be with reference

to (Adewole and Torra, 2024), where authors show

that the aggregated values in the smart grid datasets

are not safe even when published as an aggregated

value. We can also incorporate global differential pri-

vacy (Dwork et al., 2006) at the aggregation level in

future work for the proposed framework. Overall, the

results of our proposed microaggregated federated ap-

proach are comparable to the centralized models and

hence, can be used as a good privacy-enhancing alter-

native for time-series forecasting.

6 CONCLUSION AND FUTURE

WORK

This paper proposes a novel federated learning based

time-series forecasting framework that is forecasting

model agnostic. The proposed federated framework

is privacy-preserving as it not only restricts any data

sharing among the clients because of its federated

nature but also employs microaggregation as an ap-

proach to satisfy k-anonymity. The proposed frame-

work has been validated on three different domain

time-series datasets.

In the future, we would like to investigate more

about the impact of different experiment settings like

highly skewed clients’ databases using the proposed

framework. Moreover, in the literature, studies (Torra

and Navarro-Arribas, 2023) quantify the attribute dis-

closure risk in case of k-anonymous datasets, hence,

it would be interesting to investigate the same for our

proposed federated setting.

ACKNOWLEDGEMENTS

This work has been partially supported by the Wallen-

berg AI, Autonomous Systems and Software Program

(WASP) funded by the Knut and Alice Wallenberg

Foundation. The computations were enabled by the

supercomputing resource Berzelius provided by the

National Supercomputer Centre at Link

oping Univer-

sity and the Knut and Alice Wallenberg Foundation.

Privacy-Enhancing Federated Time-Series Forecasting: A Microaggregation-Based Approach

769

REFERENCES

Adewole, K. S. and Torra, V. (2024). Energy disaggregation

risk resilience through microaggregation and discrete

fourier transform. Information Sciences, 662:120211.

Aggarwal, C. C. and Yu, P. S. (2004). A condensation ap-

proach to privacy preserving data mining. In Inter-

national Conference on Extending Database Technol-

ogy, pages 183–199. Springer.

Bai, L., Hu, H., Ye, Q., Li, H., Wang, L., and Xu, J. (2024).

Membership inference attacks and defenses in feder-

ated learning: A survey. ACM Computing Surveys,

57(4):1–35.

Bai, S., Kolter, J. Z., and Koltun, V. (2018). An em-

pirical evaluation of generic convolutional and recur-

rent networks for sequence modeling. arXiv preprint

arXiv:1803.01271.

Domingo-Ferrer, J. and Mateo-Sanz, J. M. (2002). Practical

data-oriented microaggregation for statistical disclo-

sure control. IEEE Transactions on Knowledge and

data Engineering, 14(1):189–201.

Dwork, C., McSherry, F., Nissim, K., and Smith, A. (2006).

Calibrating noise to sensitivity in private data anal-

ysis. In Halevi, S. and Rabin, T., editors, Theory

of Cryptography, pages 265–284, Berlin, Heidelberg.

Springer Berlin Heidelberg.

Herzen, J., L

assig, F., Piazzetta, S. G., Neuer, T., Tafti,

L., Raille, G., Pottelbergh, T. V., Pasieka, M.,

Skrodzki, A., Huguenin, N., Dumonal, M., Ko

scisz,

J., Bader, D., Gusset, F., Benheddi, M., Williamson,

C., Kosinski, M., Petrik, M., and Grosch, G. (2022).

Darts: User-friendly modern machine learning for

time series. Journal of Machine Learning Research,

23(124):1–6.

Hochreiter, S. and Schmidhuber, J. (1997). Long Short-

Term Memory. Neural Computation, 9(8):1735–1780.

Hopﬁeld, J. J. (1982). Neural networks and physical sys-

tems with emergent collective computational abili-

ties. Proceedings of the national academy of sciences,

79(8):2554–2558.

Kim, J., Kim, H., Kim, H., Lee, D., and Yoon, S. (2024).

A comprehensive survey of time series forecasting:

Architectural diversity and open challenges. arXiv

preprint arXiv:2411.05793.

LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).

Gradient-based learning applied to document recogni-

tion. Proceedings of the IEEE, 86(11):2278–2324.

McMahan, B., Moore, E., Ramage, D., Hampson, S., and

Arcas, B. A. y. (2017a). Communication-Efﬁcient

Learning of Deep Networks from Decentralized Data.

In Singh, A. and Zhu, J., editors, Proceedings of

the 20th International Conference on Artiﬁcial Intelli-

gence and Statistics, volume 54 of Proceedings of Ma-

chine Learning Research, pages 1273–1282. PMLR.

McMahan, B., Moore, E., Ramage, D., Hampson, S., and

y Arcas, B. A. (2017b). Communication-efﬁcient

learning of deep networks from decentralized data. In

Artiﬁcial intelligence and statistics, pages 1273–1282.

PMLR.

Mortazavi, R. and Jalili, S. (2014). Fast data-oriented mi-

croaggregation algorithm for large numerical datasets.

Knowledge-Based Systems, 67:195–205.

uller, K.-R., Smola, A. J., R

atsch, G., Sch

olkopf, B.,

Kohlmorgen, J., and Vapnik, V. (1997). Predicting

time series with support vector machines. In Interna-

tional conference on artiﬁcial neural networks, pages

999–1004. Springer.

Nin, J. and Torra, V. (2006a). Distance based re-

identiﬁcation for time series, analysis of distances.

In Privacy in Statistical Databases: CENEX-SDC

Project International Conference, PSD 2006, Rome,

Italy, December 13-15, 2006. Proceedings, pages

205–216. Springer.

Nin, J. and Torra, V. (2006b). Extending microaggregation

procedures for time series protection. In International

conference on rough sets and current trends in com-

puting, pages 899–908. Springer.

Nin, J. and Torra, V. (2009). Towards the evaluation of

time series protection methods. Information Sciences,

179(11):1663–1677.

Petropoulos, F., Apiletti, D., Assimakopoulos, V., Babai,

M. Z., Barrow, D. K., Taieb, S. B., Bergmeir, C.,

Bessa, R. J., Bijak, J., Boylan, J. E., et al. (2022).

Forecasting: theory and practice. International Jour-

nal of Forecasting, 38(3):705–871.

Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986).

Learning representations by back-propagating errors.

nature, 323(6088):533–536.

Sakuma, J. and Osame, T. (2017). Recommenda-

tion with k-anonymized ratings. arXiv preprint

arXiv:1707.03334.

Samarati, P. (2001). Protecting respondents identities in mi-

crodata release. IEEE transactions on Knowledge and

Data Engineering, 13(6):1010–1027.

Scarselli, F., Gori, M., Tsoi, A. C., Hagenbuchner, M.,

and Monfardini, G. (2008). The graph neural net-

work model. IEEE transactions on neural networks,

20(1):61–80.

Shumway, R. H., Stoffer, D. S., Shumway, R. H., and Stof-

fer, D. S. (2017). Arima models. Time series analysis

and its applications: with R examples, pages 75–163.

Torra, V. and Navarro-Arribas, G. (2023). Attribute dis-

closure risk for k-anonymity: the case of numerical

data. International Journal of Information Security,

22(6):2015–2024.

Trindade, A. (2015). ElectricityLoadDiagrams20112014.

UCI Machine Learning Repository.

Ulvila, J. W. (1985). Decision trees for forecasting. Journal

of Forecasting, 4(4):377–385.

Voigt, P. and Von dem Bussche, A. (2017). The eu gen-

eral data protection regulation (gdpr). A Practical

Guide, 1st Ed., Cham: Springer International Pub-

lishing, 10(3152676):10–5555.

Wilson, C. S. and Commissioner, U. (2020). A deﬁning

moment for privacy: The time is ripe for federal pri-

vacy legislation. In Speech at Future of Privacy Fo-

rum by Commissioner of US Federal Trade Commis-

sion (FTC), volume 6.

Wu, R., Chen, X., Guo, C., and Weinberger, K. Q. (2023).

Learning to invert: Simple adaptive attacks for gradi-

ent inversion in federated learning. In Uncertainty in

Artiﬁcial Intelligence, pages 2293–2303. PMLR.

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

770