
An Enhanced Two-Step CPA Side-Channel Analysis Attack on ML-KEM
Mark Kennaway
a
, Tuan Hoang
b
, Ayesha Khalid
c
, Ciara Rafferty
d
and M
´
aire O’Neill
e
,
The Centre for Secure Information Technologies (CSIT), Queens University Belfast, U.K.
Keywords:
ML-KEM, CRYSTALS-Kyber, Side Channel Attack, Correlation Power Analysis, Quantum Safe
Cryptography, Post Quantum Cryptography, IoT Security, Power Analysis Attacks, Cryptanalysis.
Abstract:
This work presents an enhanced two-step Correlation Power Analysis (CPA) attack targeting the recently
standardised ML-KEM on an ARM Cortex M4. Our enhancement exploits the knowledge of intermittent
variables to identify sample points of interest and develop bespoke attack functions. Step one targets the odd
coefficients of each Secret Key Polynomial Vector ( ˆs), before step two targets the remaining even coefficients
using more elaborate attack functions. After successfully demonstrating key recovery for the first set of ˆs, we
then characterise leakage behaviour, revealing a trend indicating recovery of each coefficient becomes more
efficient with subsequent iterations of the internal doublebasemul operation. By applying our enhanced two-
step attack methodology, we successfully recovered the entire key using only 179 traces, without the need for
elaborate preconditions or ciphertext manipulations. We obtain remarkable results in the initial stage of our
attack, while the second phase achieves performance comparable to other recent studies.
1 INTRODUCTION AND
MOTIVATION
In August 2024, the National Institute of Standards
and Technology (NIST) announced
1
three Federal
Information Processing Standards (FIPS) to protect
against quantum-enabled attacks on contemporary
public key cryptography algorithms. Two of these,
namely FIPS 203, the Module Lattice Key Exchange
Mechanism (ML-KEM) (NIST, 2023a), and FIPS
204, the Module Lattice Digital Signature Algorithm
(ML-DSA) (NIST, 2023b), leverage the security of
module lattices and the module learning-with-errors
(MLWE) problem (Albrecht et al., 2015). Module
Lattices strike a balance between standard lattices,
which are complex and resource-intensive, and ideal
lattices, which are more efficient but may be less
secure due to their structure (Khalid et al., 2019).
ML-KEM employs vectors of polynomials which
are optimised through the Number Theoretic Trans-
form (NTT), enhancing performance while maintain-
a
https://orcid.org/0009-0007-5742-2000
b
https://orcid.org/0009-0005-4915-4769
c
https://orcid.org/0000-0002-4815-6966
d
https://orcid.org/0000-0002-3670-366X
e
https://orcid.org/0000-0002-6865-6212
1
https://csrc.nist.gov/news/2024/postquantum-
cryptography-fips-approved
ing strong security guarantees.
Despite theoretical resistance to quantum and
classical attacks, ML-KEM and ML-DSA remain sus-
ceptible to Side Channel Analysis (SCA) attacks if
naively implemented. SCA (Kocher, 1996) attacks
apply a divide-and-conquer approach to enable sta-
tistical analysis of sensitive data such as the secret
key by isolating independent parts. The large num-
ber of bits of sensitive data, e.g., a 128-bit secret key
with AES or the 512-coefficients of the secret key in
ML-KEM, is broken down into smaller sub-keys or
single coefficients. Next, the correlation (Brier et al.,
2004) between the side-channel information and that
sensitive data in execution is analysed, often reveal-
ing the sensitive data. This risk is especially pro-
nounced in IoT devices, where constrained resources
exacerbate any side-channel vulnerabilities. While
classical cryptosystems like RSA and ECC have been
extensively studied for such weaknesses, LBC’s re-
silience remains relatively under explored. Existing
research often focuses on complex attacks, overlook-
ing simpler, more practical methods that real-world
adversaries might exploit. Given the ongoing adop-
tion of PQC, research that rigorously demonstrates
and quantifies leakage of LBC implementations via
physical side channels is essential to inform devel-
opers and support the deployment of more effective
countermeasures.
Kennaway, M., Hoang, T., Khalid, A., Rafferty, C., O’Neill and M.
An Enhanced Two-Step CPA Side-Channel Analysis Attack on ML-KEM.
DOI: 10.5220/0013638600003979
In Proceedings of the 22nd International Conference on Security and Cryptography (SECRYPT 2025), pages 263-274
ISBN: 978-989-758-760-3; ISSN: 2184-7711
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)
263

In this paper, we present a known ciphertext corre-
lation power analysis attack on ML-KEM. We exploit
the power leakage during the polynomial multiplica-
tion in the decryption step. Concretely, the contribu-
tions of our article can be summarised as follows:
• We propose a non-profiled, known ciphertext
side-channel attack methodology targeting the
polynomial multiplication in the recently stan-
dardised ML-KEM. Our techniques are generic
for various security levels of ML-KEM and can
also be applied to any other lattice-based algo-
rithms which use similar polynomial multiplica-
tions.
• We contribute knowledge from within the imple-
mentation to provide an enhanced two-step attack
model which can reveal all coefficients of the pri-
vate key. Our enhancement uses Pearson Corre-
lation Coefficient (PCC) to prove our bespoke at-
tack functions and pinpoint sample Points of In-
terest (PoI) for revealing areas of leakage. The
two-step attack model reveals all private key co-
efficients, while a single-step attack model can re-
veal the odd coefficients only.
• We practically demonstrate the use of our two-
step attack using real power traces captured dur-
ing the base multiplication of Kyber512 decryp-
tion. Traces are collected using a ChipWhis-
perer (O’Flynn and Chen, 2014) Lite Capture
with CW308 UFO baseboard hosting a CW308T-
STM32F3 Cortex-M4 microcontroller (NewAE
Technology Inc., 2018).
• Our results demonstrate the effectiveness of our
enhanced two-step attack methodology, achieving
full key recovery with only 179 traces while elim-
inating the need for elaborate preconditions or ci-
phertext manipulations, surpassing prior works in
the initial phase and matching state-of-the-art per-
formance in the second phase.
The rest of the paper is organised as follows. Sec-
tion 2 reviews related works, then Section 3 provides
preliminaries, before presenting our attack model and
methodology. Attack results are detailed in Section
4, while Section 5 contains discussion of results and
a limited comparison with other non-profiled attacks.
Section 5 continues with some comments on coun-
termeasures, before reaching a conclusion and a look
forward to future work.
1.1 Notations
The parameters n, q, k, η
1
, η
2
, d
u
and d
v
introduced
in Section 3 are used as described in the Round 3 Ky-
ber submission (Avanzi et al., 2021). We use n to
denote the number of coefficients in each vector and k
to denote the number of vectors. We write u and v to
denote the two equal parts of the same decoded, de-
compressed ciphertext, q represents the divisor in all
modulus operations, while d
u
and d
v
denotes the size
of the set into which the function Compress
q
maps
elements modulo q. We write sk to denote the secret
key as generated by the Kyber CPAPKE.KeyGen() al-
gorithm, while ˆs represents the decoded sk. We write
ˆs
i
j
to refer to the j’th coefficient of the i’th vector, for
example the first four coefficients of the first secret
key polynomial vector is written as { ˆs
0
1
, ˆs
0
2
, ˆs
0
3
, ˆs
0
4
}. In
sections 3 and 4 we write
ˆ
h
i
j
within attack functions
to represent a hypothetical key coefficient, before re-
covery of that same correct key coefficient ˆs
i
j
.
2 RELATED WORKS
Side Channel Analysis Attacks or SCAs have been
broadly classified into two classes: profiling attacks
and non-profiling attacks. In non-profiling attacks,
the adversary relies solely on leakage data collected
from the target device. In contrast, profiling attacks
are more complex and powerful, leveraging a physi-
cal replica of the target device to create precise mod-
els of its behaviour under attack. Classical profil-
ing attacks include Template Attacks (Chari et al.,
2003), the Stochastic Model (Doget et al., 2011), and
Maghrebi et al (Maghrebi et al., 2016) who replaced
the traditional template based attack with a more so-
phisticated Deep Learning (DL) approach to profiling.
The remainder of this section reviews recent examples
of each class from literature with Table 1 containing
a summary, grouped into Non-Profiled and Profiled
(including template and Deep Learning).
2.1 Non-Profiling Attacks on FIPS
203/204
A review of published literature on attacks within
FIPS 203 and FIPS 204 shows a minority of ap-
proaches to be non-profiled. Polynomial Multiplica-
tion is targeted in all the non-profiling approaches re-
viewed, most likely because it is considered low hang-
ing fruit for a basic level attack. Although in some
cases non-profiling attacks take longer to retrieve a se-
cret key, (Chen et al., 2021) showed how acceleration
can be achieved through collecting more measure-
ments, while (Tosun and Savas, 2024) included other
factors like coefficient modulus or machine word half
size, showing the effects of these on leakage and key
recovery, despite masking (Tosun et al., 2024). Mu-
jdei et al (Mujdei et al., 2024) similarly focus on co-
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
264

Table 1: Recent SCAs targeting PQC Federal Information Processing Standards.
Ref PQC Target Implementation Masked Class
This Work FIPS 203 PM/fqmul outputs PQM4 No Non-Profiled
(Tosun et al., 2024) FIPS 203/204 PM PQM4 Yes Non-Profiled
(Mujdei et al., 2024) FIPS 203 PM PQM4 No Non-Profiled
(Chen et al., 2021) FIPS 204 PM/PS/PA Ref C No Non-Profiled
(Tosun and Savas, 2024) FIPS 203/204 PM PQM4 Yes Non-Profiled
(Yang et al., 2023) FIPS 203 PM Ref C/PQM4 No Non-Profiled
(Primas et al., 2017) FIPS 203/204 NTT PQM4 Yes Profiled
(Ulitzsch et al., 2024) FIPS 204 binary unpacking Ref C No Profiled
(Xu et al., 2022) FIPS 203 Inverse NTT/MD Ref C/PQM 4 No Profiled
(Ravi et al., 2022a) FIPS 203 MD/Storage PQM4 Yes Profiled
(Ravi et al., 2020) FIPS 203 MD/Storage PQM4 Both Profiled
(Ravi et al., 2022b) FIPS 203/204 PM/MD PQM4 Yes Profiled
(Mu et al., 2022) FIPS 203 PS/NTT Ref C No Template
(Sim et al., 2022) FIPS 203 MR/MD Ref C/PQM4 Yes MLP
(Kim et al., 2020) FIPS 204 NTT/Sparse PM Ref C Both MLP
(Sim et al., 2020) FIPS 203 ME/MD PQM4 Yes MLP
(Backlund et al., 2022) FIPS 203 ME PQM4 Yes NN
(Dubrova et al., 2023) FIPS 203 ME PQM4 Yes RNN
(Hoang et al., 2024) FIPS 203 PM/fqmul inputs PQM4 No CNN
Acronym Meaning Acronym Meaning
PM Polynomial Multiplication ME Message Encoding
PS Polynomial Substitution MLP Multi-Layer Perceptron
PA Polynomial Addition NN Neural Network
MD Message Decoding RNN Recursive Neural Network
MR Modular Reductions CNN Convolutional Neural Network
efficient modulus, but also which multiplication algo-
rithm is being used, showing Toom-Cook implemen-
tations to be more straightforward to attack. The ref-
erence implementation of Dilithium, which has a very
similar NT T implementation to Kyber, was targeted
by (Chen et al., 2021), improving upon the otherwise
conventional brute force approach over 23-bit secrets
by around 7 times. Finally, the work of Yang et al
(Yang et al., 2023) emphasises how carefully choos-
ing ciphertexts in the attack can significantly reduce
the number of traces needed and therefore run-time
of the attack.
2.2 Profiling Attacks on FIPS 203/204
A majority of approaches reviewed are understood to
take advantage of a profiling phase, as part of a more
complex attack where an adversary has a more ad-
vanced capability through ownership of an identical
device to the one under attack. Naturally, this gives
rise to research which enables targeting other features
of implementation, for example (Primas et al., 2017)
(Xu et al., 2022) (Mu et al., 2022) (Kim et al., 2020)
targeting NTT operations. Another common target
of profiled attacks is message encoding (Sim et al.,
2020) (Backlund et al., 2022) (Dubrova et al., 2023)
which handles the necessary transform of binary data
to polynomial vectors. In a similar vein, the decoding
function (Ulitzsch et al., 2024) (Ravi et al., 2022a)
(Ravi et al., 2020) (Ravi et al., 2022b) (Xu et al.,
2022) performing the reverse action of encoding, has
become a target of many influential works.
The emergence of Deep Learning (DL) in recent
years has become a disruptive technology, and its
use as an enhancement to SCA is a natural exten-
sion to profiled attacks. Bo-Yeon et al in (Sim et al.,
2020) pioneered a DL-SCA by employing cluster-
ing recognition and pattern analysis, attacking Ky-
ber among other schemes. A multi-layer perceptron
model (MLP) was used to recover the secret mes-
sage from unprotected implementations, with attack
points generated using the sum of squared pairwise t-
differences (SOST) values of power traces. Bo-Yeon
et al (Sim et al., 2022) later exploited leakages of
Barrett Reduction in a successful DL-SCA, leverag-
ing the side channel leakage study of Xu et al (Xu
et al., 2022), and incremental storage leakage shown
by (Ravi et al., 2020) and (Ravi et al., 2022a). Back-
lund et al subsequently adapted techniques shown
by (Ngo et al., 2022) to attack a masked and shuf-
fled software implementation of Kyber (Backlund
et al., 2022), before a new recursive Neural Net-
work based method was introduced by Dubrova et al
An Enhanced Two-Step CPA Side-Channel Analysis Attack on ML-KEM
265

(Dubrova et al., 2023). This was used to attack the re-
encryption which occurs during the FO Transform of
a masked Kyber implementation on the ARM Cortex
M4. In summary, DL-SCA represents the most com-
plex class of attacks, involving increased setup and
staging times, often targeting technically advanced
adversaries.
3 ML-KEM
CRYSTALS-Kyber KEM is the first lattice based
PQC algorithm chosen by NIST for standardisation
as ML-KEM. As illustrated in Table 2, the relative
balance between performance and security can be di-
rectly adjusted by tweaking the size of the matrix k;
the choice of k varies to 2, 3, or 4 for security lev-
els 1 (Kyber512), 3 (Kyber768) and 5 (Kyber1024),
respectively. This parameter k is used to limit the di-
mensions of the public-key matrix A, with all matrix
elements residing in the ring Z
q
[x]/(x
n
+ 1). The pa-
rameter n is fixed at 256, and since the second round
submission, the parameter q has been set to 3,329. Pa-
rameters η
1
and η
2
regulate coefficient size, while d
u
and d
v
manage the compression of ciphertext values u
and v respectively, with δ representing the probability
of KEM failure.
Table 2: Parameters of Kyber ML-KEM under three differ-
ent security levels (Avanzi et al., 2021).
n k q η
1
η
2
(d
u
,d
v
) δ Security Level
Kyber512 256 2 3329 3 2 (10,4) 2
−139
1
Kyber768 256 3 3329 2 2 (10,4) 2
−164
3
Kyber1024 256 4 3329 2 2 (11,5) 2
−174
5
The IND-CCA2 secure Kyber KEM sub-
mitted to NIST PQC Round 3 is referred to as
Kyber.CCAKEM. It consists of three main steps:
key generation (Kyber.CCAKEM.KeyGen), key
encapsulation (Kyber.CCAKEM.Enc), and key
decapsulation (Kyber.CCAKEM.Dec). The Ky-
ber.CCAKEM implementation is built on top of
the Kyber.CPAPKE, using the Fujisaki-Okamoto
transform (Fujisaki and Okamoto, 1999). Ky-
ber.CPAPKE comprises three components: key
generation (Kyber.CPAPKE.KeyGen), encryp-
tion (Kyber.CPAPKE.Enc), and decryption (Ky-
ber.CPAPKE.Dec).
A functional description of the decryption opera-
tion now follows, highlighting its vulnerability to at-
tacks due to the risk of exposing data related to the
secret key. This vulnerability is the focal point of our
attack. For more details on other operations contained
in the Round 3 submission, the reader is kindly re-
ferred to (Avanzi et al., 2021).
3.1 Kyber PKE Decryption
The deterministic decryption algorithm
CPAPKE.Dec(sk,c) takes a secret key (sk) and
ciphertext (c) as inputs and generates either a mes-
sage m ∈ M or an indication of rejection. Decryption
involves vector multiplication between sk and c in
the NTT domain, each result corresponding to a
polynomial of degree 255 with integer coefficients
ranging from 0 to 3328 due to q being 3329. Below,
we provide an explanation of Algorithm 1, with line
4 containing our attack point.
• Preamble: The ciphertext c is input along with the
secret key sk.
• Line 1: The first part of c is decoded and decom-
pressed into u.
• Line 2: The second part of c is decoded and de-
compressed into v.
• Line 3: sk is de-serialized as ˆs := Decode
12
(sk).
• Line 4: m is recovered by m := Compress
q
(v −
ˆs
T
u,1).
The Kyber decryption operation is invoked for de-
capsulation, with the input ciphertext always being
multiplied by the secret key, independent of the ci-
phertext’s validity. This provides our opportunity for
SCA, and the adversary can establish a decryption or-
acle in order to conduct a known ciphertext attack.
Algorithm 1: KYBER.CPAPKE.DEC(sk,c).
Require: Secret key sk ∈ B
12·k·n/8
,
Ciphertext c ∈ B
d
u
·k·n/8+d
v
·n/8
Ensure: Message m ∈ B
32
1: u ← Decompress
q
(Decode
d
u
(c),d
u
)
2: v ← Decompress
q
(Decode
d
v
(c +
d
u
· k · n/8),d
v
)
3:
ˆ
s ← Decode
12
(sk)
4: m ← Encode
1
(Compress
q
(v −
NTT
−1
(
ˆ
s
T
◦ NTT(u)),1))
5: return m
3.2 Decryption on ARM Cortex M4
With our implementation of PQM4 (Kannwis-
cher et al., 2018), decryption is handled by the
nine suboperations displayed in Table 3. Note
poly frombytes mul, (&mp, sk) and (&bp, sk),
which correspond to line 4, and ˆs
T
◦ NTT(u) of
the decryption algorithm depicted in Algorithm
1, respectively. During the first occurrence of
poly frombytes mul, the first half of the ciphertext in-
teracts with
ˆ
s
0
. Similarly the second half of the ci-
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
266

Table 3: CPAPKE.Dec Sub Operations in our PQM4 (Kan-
nwischer et al., 2018) Implementation.
No. Sub Operation
1. poly unpackdecompress (&mp, c, 0);
2. poly ntt(&mp);
3. poly frombytes mul(&mp, sk);
4. for(int i = 1; i ¡ KYBER K; i++) {
poly unpackdecompress(&bp, c, i);
poly ntt(&bp);
poly frombytes mul(&bp, sk + i*KYBER POLYBYTES);
poly add(&mp, &mp, &bp); }
5. poly invntt(&mp);
6. poly decompress(v, c+KYBER POLYVECCOMPRESSEDBYTES);
7. poly sub(&mp, v, &mp);
8. poly reduce(&mp);
9. poly tomsg(m, &mp);
phertext interacts with
ˆ
s
1
as part of the latter occur-
rence of poly frombytes mul.
Within poly frombytes mul, the most granular
functions interacting with parts of the secret key and
ciphertext can be identified. As part of this subop-
eration, the assembly-level doublebasemul asm is
specifically designed for this multiplicative purpose.
It consists of two basemul functions, each conduct
pair point-wise multiplications of two 12-bit secret
key inputs with two 12-bit ciphertext inputs. The re-
sults of these multiplications are stored as r
0
and r
1
re-
spectively in the case of the first basemul. For a com-
plete assembly code listing of doublebasemul asm,
the reader is referred to Appendix A.
The following detailed examination of basemul
highlights the points where secret key information
could be exposed and exploited through SCA. The
multiplication process f
qmul
( ˆs
T
, ˆu) for the first ex-
ecution of doublebasemul breaks down into point-
wise multiplication between { ˆs
0
0
, ˆs
0
1
, ˆs
0
2
, ˆs
0
3
} and { ˆu
0
0
,
ˆu
0
1
, ˆu
0
2
, ˆu
0
3
} as described in Fig. 1. Here we can
see each basemul between the ciphertext coefficient
ˆu = NT T (u) and secret key coefficient ˆs
T
consists of
five consecutive f
qmul
executions.
For the first coefficient pairs, we can denote the
input values to the basemul calculation to be s =
{s
0
,s
1
} and u = {u
0
,u
1
}. Next the point-wise mul-
tiplication on Zq is performed, this is denoted by
f
qmul
and for each basemul occurs four times be-
tween s and u and one further time between r0
and zeta. Hence, each basemul consists of five
f
qmul
of f
qmul
(s
1
,u
1
), f
qmul
(r
0
,zeta), f
qmul
(s
0
,u
0
),
Figure 1: The two basemul operations which comprise
doublebasemul.
f
qmul
(s
0
,u
1
) and f
qmul
(s
1
,u
0
), producing outputs r
0
and r
1
.
Coefficient s
0
is exclusively involved in the
f
qmul
(s
0
,u
0
) and f
qmul
(s
0
,u
1
) operations, while sim-
ilarly coefficient s
1
is only related to the f
qmul
(s
1
,u
0
)
and f
qmul
(s
1
,u
1
) operations. The computation of
doublebasemul is the same for every coefficient
pair, simply comprising of two basemul calculations.
Therefore if we are able to retrieve s
0
and s
1
using any
or all five f
qmul
from the first execution of basemul we
would be able to further attack the remaining f
qmul
in
subsequent basemul executions to retrieve all secret
key coefficients.
3.3 Attack Model
The secrecy of a ML-KEM implementation is fully
compromised if the secret key is revealed in its en-
tirety. We hypothesise that this can be achieved by
performing a CPA attack (Brier et al., 2004) which
targets each 12-bit coefficient of the polyvector ˆs in
Algorithm 1 during the decryption process. We use
the Hamming Weight (HW) power model as part of
our attack model for our CPA.
Examination of doublebasemul asm shows sev-
eral intermittent values to be temporarily stored in
registers tmp and tmp2, post montgomery reduc-
tion. Figure 2 contains the assembly code of the first
basemul related to these registers in running order.
sm ul tt tmp , poly0 , poly1
mo n tg ome ry q , qinv , tmp , tm p2
sm ul tb tmp2 , tmp2 , zeta
sm la bb tmp2 , po ly0 , poly1 , t mp2
mo n tg ome ry q , qinv , tmp2 , tmp
sm ua dx tmp2 , po ly0 , p ol y1
mo n tg ome ry q , qinv , tmp2 , t mp3
Figure 2: The assembly code of basemul from PQM4 (Kan-
nwischer et al., 2018).
There are several differences between the instruc-
tions shown in Figure 2, which are crucial to under-
standing potential leakage for our attack model.
• SMULTT
2
is a top-by-top multiplication instruc-
tion, applied to the top 16 bits of poly0 ( ˆs
odd
) and
the top 16 bits of poly1 ( ˆu
odd
), storing the 32-bit
result in tmp. The first montgomery reduction is
then perfomed on the contents of tmp, with the
result being stored in tmp2.
2
https://developer.arm.com/documentation/ddi0597/
2024-12/Base-Instructions/SMULBB–SMULBT–
SMULTB–SMULTT–Signed-Multiply–halfwords–
An Enhanced Two-Step CPA Side-Channel Analysis Attack on ML-KEM
267

• SMLABB is a bottom-by-bottom multiply and ac-
cumulate instruction, applied to the bottom 16
bits of poly0 ( ˆs
even
) with bottom 16 bits of poly1
( ˆu
even
), then within the same instruction the result
is added to the contents of tmp2.
• SMUADX
3
is a dual multiply instruction, which
performs two parallel multiplications of the top
16 bits of poly0 ( ˆs
odd
) with the bottom 16 bits of
poly1 ( ˆu
even
). Simultaneously the bottom 16 bits
of poly0 ( ˆs
even
) is multiplied with the top 16 bits of
poly1 ( ˆu
odd
) and within the same instruction both
products are added and stored into tmp2.
Application of these instructions to our implemen-
tation shows the multiplication part of f
qmul
(s
1
,u
1
) is
calculated and stored separately, while f
qmul
(s
0
,u
0
) is
not; rather, it is calculated and added together with
the output from f
qmul
( f
qmul
(s
1
,u
1
),zeta) within a sin-
gle instruction. In a similar way, the f
qmul
(s
0
,u
1
) and
f
qmul
(s
1
,u
0
) operations use an instruction which com-
bines multiple actions. The key takeaway is the ap-
pearance of a potential opportunity to exploit leakage
by targeting the contents of tmp2 register, after the
first reduction.
We now use this understanding to begin to build
some generalised attack functions. For recovery of all
odd coefficients, we theorise that ( f
qmul
( ˆs
odd
, ˆu
odd
))
can be used to form an attack function, aiming to
correlate with the intermittent variable r
0
stored in
tmp2. This is a unique opportunity, since only
the tmp2 register appears to contain solely the re-
sult of ( f
qmul
( ˆs
odd
, ˆu
odd
)) post reduction, in con-
trast to tmp and tmp3 which are used to store
the results r
0
and r
1
respectively. For recovery
of all even coefficients therefore we theorise that
( f
qmul
( f
qmul
( ˆs
odd
, ˆu
odd
),zeta) + f
qmul
( ˆs
even
, ˆu
even
) can
be used to form a second attack function, aiming to
correlate with the final value r
0
stored in tmp. We
also note that the attack function ( f
qmul
(s
even
,u
odd
))
+ f
qmul
(s
odd
,u
even
) which aims to correlate with r
1
stored in tmp3 exists as an alternative.
3.4 Attack Methodology
Our preprocessing involves use of the Pearson Corre-
lation Coefficient (Kirch, 2008) (PCC) to prove the at-
tack model, identifying Points of Interest (PoI) which
reveal areas of high correlation over time by sample
point, and to enable formation of bespoke attack func-
tions for use in the CPA attack.
3
https://developer.arm.com/documentation/dui0348/c/
Compiler-specific-Features/Instruction-intrinsics/–smuadx-
intrinsic
Our two-step attack uses an incrementally cal-
culated version of PCC (Bottinelli and Bos, 2017),
which creates a new axis on the captured data and pro-
vides a more in-depth perspective for correlation anal-
ysis leading to key recovery. Since traces are added
incrementally and then correlations recalculated, the
new axis created is the number of traces used, hence
it becomes possible to measure the amount of traces
required before a specific hypothetical key stands
out from other hypothetical key correlation levels.
This is known as the minimum number of traces
which allows a Measurement to Disclosure (MtD),
proposed by (Tiri et al., 2005) and used in (Mangard
et al., 2007), we use MtD to determine the minimum
amount of traces required to recover each coefficient
of ˆs.
3.5 Research Environment
Our research environment involved setup of the Chip-
Whisperer (O’Flynn and Chen, 2014) Lite Capture
with CW308 UFO baseboard hosting a CW308T-
STM32F3 Cortex-M4 microcontroller (NewAE Tech-
nology Inc., 2018). The decryption oracle is estab-
lished by implementing the Kyber512 decryption op-
erations of the PQM4 (Kannwischer et al., 2018) li-
brary on the microcontroller. Our ciphertexts are gen-
erated by applying the deterministic CPAPKE.Enc to
randomly generated 32-byte plaintext messages. We
attack doublebasemul asm in assembly code by cap-
turing traces pertaining to these operations only, with
a default sampling rate of 4 ∗ 7.37MHz. We isolate
each coefficient of ˆs, and collect traces during the ex-
ecution of the assembly code in Appendix A. We
collected 500 power traces, along with ˆs and ˆu in-
puts and ˆr results then cross-validated these ˆs, ˆu and
ˆr against corresponding values from a laptop-based
reference implementation. This found that the input
coefficients ˆs and ˆu and the output results ˆr matched
with the corresponding values from the laptop imple-
mentation. This confirmed the laptop implementation
can reliably generate data to use as part of our attack
targeting the Cortex M4 implementation.
3.6 PoI and Attack Function Evaluation
We use the raw f
qmul
outputs extracted from our lap-
top implementation to correlate with our power traces.
The aim of preprocessing is to test our attack theory
through identifying PoI, then finalise our attack func-
tions.
This results in a significant global peak of cor-
relation levels, and the PoI emerged around sam-
ple points 153-164 for f
qmul
(s
1
,u
1
), as illustrated in
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
268
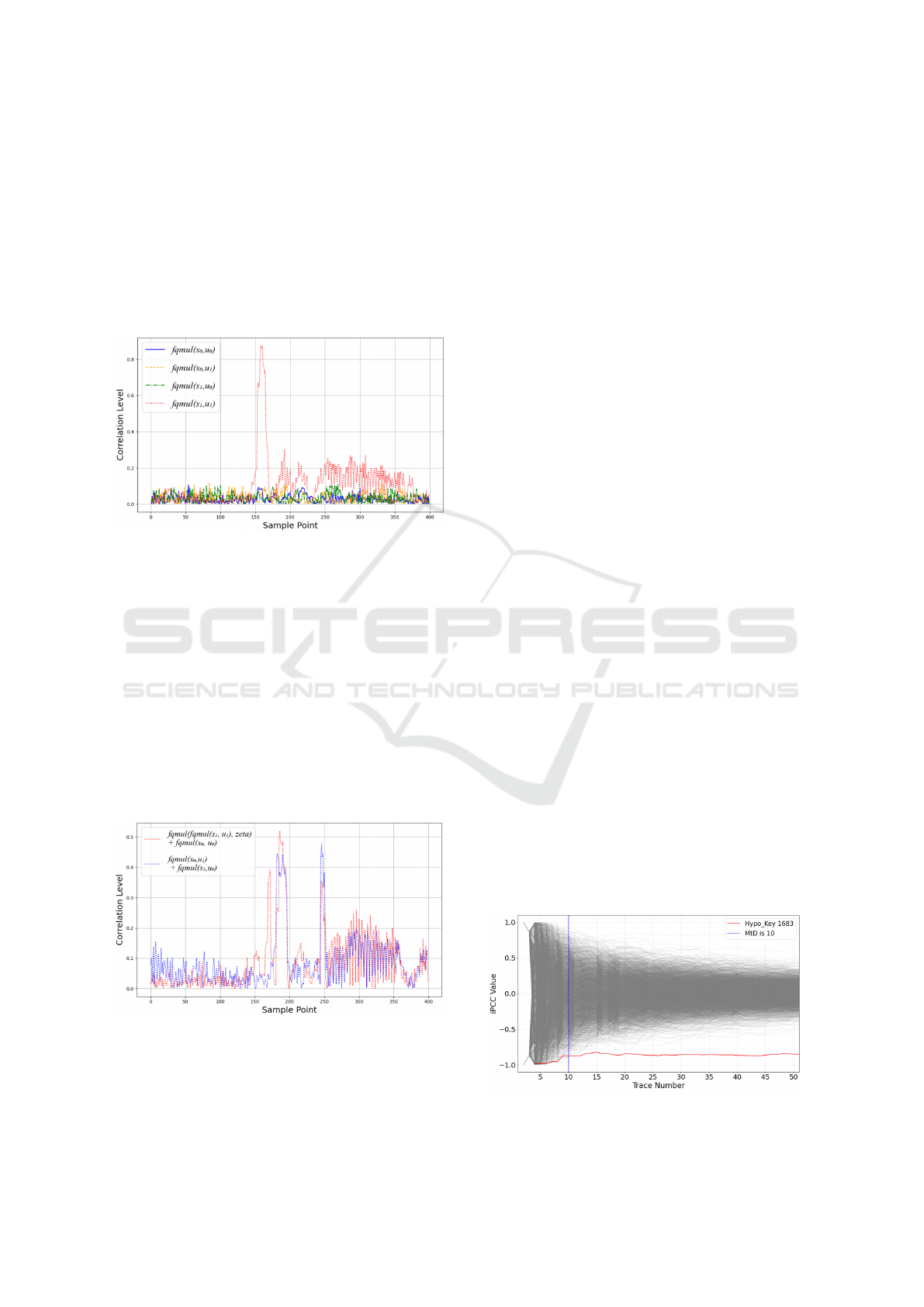
Fig. 3. Since the second basemul is a carbon copy of
these five f
qmul
, involving the next set of coefficients,
it is reasonable to expect a similar global peak to
be present with ( f
qmul
(s
3
,u
3
)). Correlation between
captured traces and ( f
qmul
(s
0
,u
0
)), ( f
qmul
(s
1
,u
0
)) and
( f
qmul
(s
0
,u
1
)) remains consistently low across all
points, indicating that there is no leakage of signifi-
cance for these functions. Consequently, we conclude
that s
0
cannot be directly revealed through a single-
step attack.
Figure 3: PoI Detection for Step One: Correlation of single
f
qmul
functions by sampling point. A global peak presents
around PoI [153-164] for f
qmul
(s
1
,u
1
) only.
The same technique is now applied using r
0
and
r
1
, this time against even coefficients, which results
in global peaks being identified for each and is il-
lustrated in Fig. 4, with the former global peak (r
0
)
marginally higher than the latter (r
1
). Concentrating
on r
0
, shown in Figure 4 as f
qmul
( f
qmul
(s
1
,u
1
),zeta)
+ f
qmul
(s
0
,u
0
), a second interesting area is located
around the sample points 185-190 and indicates a
second attack point to recover the even coefficients,
forming Step Two of our attack. With our attack func-
tions positively evaluated, we now craft more formal
functions for use as part of each attack step.
Figure 4: PoI Detection for Step Two: Correlation of
summed f
qmul
functions by sampling point. Global peaks
present at PoI [185-190] and [245-250].
3.6.1 Step One: Recover Odd Coefficients s
1
, s
3
We hypothesise that coefficients s
1
and s
3
can
be recovered by correlating HW( f
qmul
(h
1
,u
1
)) and
HW ( f
qmul
(h
3
,u
3
)) with our captured power traces,
where h represents our hypothetical key value 0-3328
in the NT T domain.
3.6.2 Step Two: Recover Even Coefficients s
0
, s
2
We further hypothesise that coefficients s
0
and s
2
can now be recovered using the values for s
1
and s
3
discovered in Step One, and then correlat-
ing HW ( f
qmul
( f
qmul
(s
1
,u
1
),zeta) + f
qmul
(h
0
,u
0
)) and
HW ( f
qmul
( f
qmul
(s
3
,u
3
),−zeta) + f
qmul
(h
2
,u
2
)) with
our power traces.
4 ATTACK RESULTS
4.1 Step One
The following attack functions were coded:
HW ( f
qmul
(h
0
1
,u
0
1
)), HW ( f
qmul
(h
1
1
,u
1
1
)) and
HW ( f
qmul
(h
0
3
,u
0
3
)), HW ( f
qmul
(h
1
3
,u
1
3
)) and 3329
hypothesis keys computed for each, using co-
efficients from 500 different ciphertexts. These
were then correlated against the corresponding 500
recorded power traces. The preprocessing provided
PoIs where high correlations of hypothetical key
values h
0
1
, h
1
1
and h
0
3
, h
1
3
can be found, these were
systematically investigated with respect to key space.
With reference to Table 4 and in relation to h
0
1
,
four consecutive sample points from 157 to 160 which
have a stronger level of correlation than the rest, stand
out. Furthermore, all of the top five correlations relate
to the same hypothetical key value, 1683. We can now
say with certainty that s
0
1
, s
1
1
have been revealed as our
highest correlating hypothetical key values, 1683 and
1920 respectively. Furthermore, it can be noted the
same four PoIs show the strongest correlations across
each ˆs, these are identified for further analysis.
Figure 5: The MtD for s
0
1
is 10.
An Enhanced Two-Step CPA Side-Channel Analysis Attack on ML-KEM
269

Table 4: Top correlations for h
0
1
, h
1
1
and h
0
3
, h
1
3
, with absolute values.
Rank h
0
1
PoI Value h
1
1
PoI Value h
0
3
PoI Value h
1
3
PoI Value
1 1683 158 0.86871 1920 158 0.87638 2355 213 0.60609 2336 214 0.55389
2 1683 160 0.867 1920 160 0.87431 2355 214 0.59998 2336 213 0.55244
3 1683 157 0.865 1920 157 0.87166 2355 216 0.56978 2336 215 0.54128
4 1683 159 0.854 1920 159 0.85838 2355 215 0.55751 2336 216 0.51927
5 1683 161 0.809 1409 158 0.84039 1044 382 0.4673988 1044 385 0.47017
Keyspace exploration at these eight sample points
using incremental PCC is conducted next, to discover
which sample point will provide the lowest MtD. In
turn, we now fix the sample point at each PoI [157-
160] and then investigate correlations across the key
space. Fig. 5 contains the MtD displaying hypotheti-
cal key correlation values as the numbers of traces in-
crease, our highest correlating key (1683) is coloured
red to show clear divergence from the rest of the hy-
pothetical keys which begins after the 10th trace. The
MtD for a
0
1
is shown to be 10 traces at PoI 159.
Similarly, for h
0
3
, h
1
3
and with reference to Table 4,
we see significantly higher levels of correlation at four
consecutive sample points from 213 to 216 compared
to the rest. We can say with certainty at this point, se-
cret key coefficients s
0
3
, s
1
3
have been revealed as our
highest correlating hypothetical key values 2355 and
2336 respectively. For h
0
3
, h
1
3
we now fix our attention
at each PoI [213-216] in turn, and then investigate cor-
relations at these sample points across the key space.
Fig. 6 shows h
0
3
, again coloured in red, as it begins
to diverge from other hypothetical keys after the 43rd
trace.
Figure 6: The MtD for s
0
3
is 43.
4.2 Step Two
The following attack functions were coded:
HW ( f
qmul
( f
qmul
(s
0
1
,u
0
1
),zeta) + f
qmul
(h
0
0
,u
0
0
))
HW ( f
qmul
( f
qmul
(s
0
3
,u
0
3
),−zeta) + f
qmul
(h
0
2
,u
0
2
))
HW ( f
qmul
( f
qmul
(s
1
1
,u
1
1
),zeta) + f
qmul
(h
1
0
,u
1
0
))
HW ( f
qmul
( f
qmul
(s
1
3
,u
1
3
),−zeta) + f
qmul
(h
1
2
,u
1
2
))
This enables 3329 hypothesis keys to be computed
across coefficients from 500 different ciphertexts for
each function. In a similar fashion to Step One, the
500 results from the new attack functions were corre-
lated against 500 recorded power traces, Table 5 con-
tains the top five correlations for h
0
0
, h
1
0
and h
0
2
, h
1
2
respectively. This time, the correlation levels are no-
tably lower, likely due to the more elaborate algebraic
structure involved in these functions, and the sample
points where they occur are not necessarily grouped
into four consecutive points. Nevertheless we can still
reliably deduce that 72, 3015 are the values of s
0
0
, s
1
0
and 2841, 780 are the values of s
0
2
, s
1
2
respectively.
Figure 7: The MtD for s
0
0
is 179.
Again we use incremental PCC to attempt to mea-
sure the amount of traces required for key disclosure
by fixing and exploring sample points [185-190] and
[237-242] respectively. Fig. 7 shows h
0
0
, in red as it
begins to diverge from other hypothetical keys after
the 179th trace, while Fig. 8 shows h
0
2
, diverging after
43 traces.
Figure 8: The MtD for s
0
2
is 43.
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
270
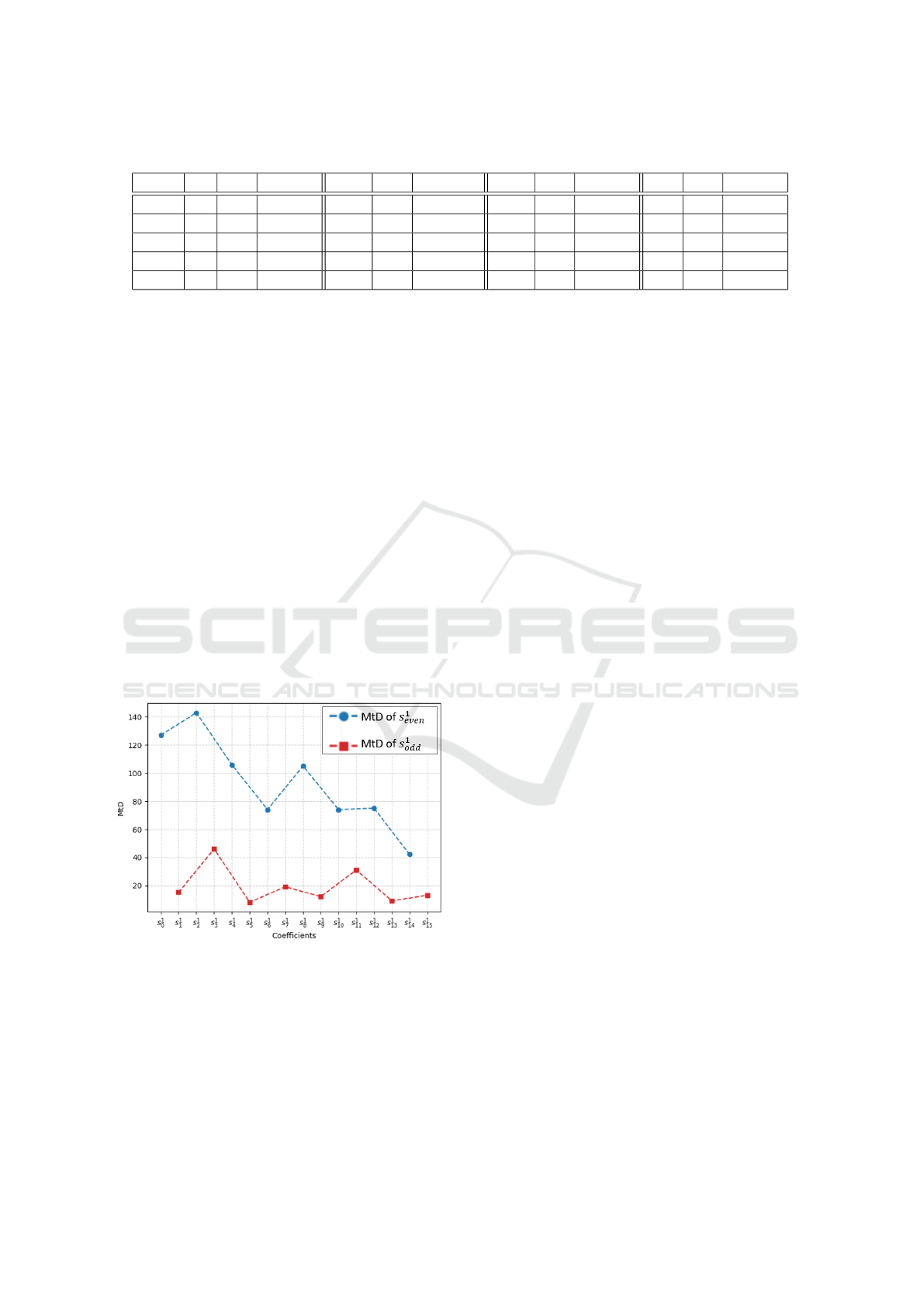
Table 5: Top correlations for h
0
0
, h
1
0
and h
0
2
, h
1
2
, with absolute values.
Rank h
0
0
PoI Value h
1
0
PoI Value h
0
2
PoI Value h
1
2
PoI Value
1 72 186 0.32310 3015 189 0.37602 2841 238 0.40217 780 237 0.36858
2 72 185 0.31498 3015 190 0.36710 2841 240 0.39627 780 237 0.36626
3 72 189 0.31447 3015 185 0.36352 2841 237 0.38969 780 242 0.36562
4 72 188 0.30410 3015 186 0.361761 2841 241 0.36919 780 241 0.36017
5 72 190 0.29981 3015 193 0.342511 2841 242 0.36916 780 239 0.34463
5 DISCUSSION
Each basemul requires the five f
qmul
operations ex-
plained earlier and presented in Fig. 1 and Fig. 2.
The first, ( f
qmul
(s
1
,u
1
)) is unique in that it has its
post reduction result stored for at least one clock cycle
in the tmp2 register, according to Appendix A. This
accounts for the global peak encountered during our
evaluation prior to Step One, as illustrated in Fig. 3.
During the attack four sample points 157-160 stand
out, this is explainable since we are sampling at four
times the clock speed, hence it is likely to show the
clock cycle at which tmp2 resides in register. None
of the other f
qmul
outputs in basemul are stored, rather
they are interpolated with each other or the result of
( f
qmul
( f
qmul
(s
1
,u
1
),±zeta)), as such they offer sev-
eral local peaks only. The same pattern repeats with
the next basemul and can be exploited again to re-
cover s
3
by attacking ( f
qmul
(s
3
,u
3
)), then replicated
for all of the odd coefficients investigated.
Figure 9: MtD for first 16 coefficients of
ˆ
s
1
(s
1
0
− s
1
15
).
Another trend is the decreasing values for MtD as
progression is made through each doublebasemul, il-
lustrated in Fig. 9. This is to be expected since factors
such as noise decrease with device operation, allow-
ing traces to exhibit stronger correlations to data leak-
age. This trend would be expected to continue with
a gradually diminishing MtD, before reaching some
minimum value.
5.1 Results Comparison
The differences in research environments and ap-
proaches of various research groups make an inter-
class comparison of results challenging. In particu-
lar the more advanced Profiled SCA attacks such as
template or DL-SCA attacks, would clearly not allow
for a fair statistical comparison. In Table 6, we limit
a like-for-like comparison using the reported number
of traces used as an indication of attack results from
the non-profiled class only. The approaches listed
employ differing methodologies in an effort to en-
hance their respective CPA. None however, take ad-
vantage of the direct leakage of odd coefficients ex-
plained in our attack model and exploited through our
step one attack functions. The work of (Mujdei et al.,
2024) adopts a generic approach and applied to sev-
eral lattice-based KEMs. For the attack on Kyber,
they recover two coefficients at once, (Tosun et al.,
2024) similarly take this approach which implies a
search over q
2
combinations. The zero-value filtering
method described in the latter suggests that during the
attack, coefficients are isolated by ensuring the value
of u
0
is set to 0 for f
qmul
(s
0
,u
1
) and u
1
is set to zero
for ( f
qmul
(s
1
,u
0
), thus reducing the search to q, how-
ever this will require capture of q traces. With the
method of (Tosun and Savas, 2024), the attack is iden-
tical over the polynomials of
ˆ
s
k
n
, hence recovery for s
1
is repeated for s
2
, and all coefficients in ˆs. It’s diffi-
cult to say if the ciphertext manipulation method laid
out in (Yang et al., 2023) constitutes a more impactful
enhancement that ours, nevertheless it does introduce
an overhead along with increased complexities. This
work does also include assembly code analysis on a
level similar to ours, but does overlook exploiting use
of the smultt instruction to further enhance their at-
tack as do all other attacks in Table 6.
Our methodology, which divides key recovery
into two distinct phases facilitated by our enhance-
ment, yields superior results in the initial stage of the
attack without requiring ciphertext manipulation or
zero-value filtering. The second phase achieves per-
formance comparable to that of peer research groups,
also without reliance on elaborate preconditions.
An Enhanced Two-Step CPA Side-Channel Analysis Attack on ML-KEM
271

Table 6: Comparison with other Non-Profiled Attacks.
Ref Security Level No. Traces
This Work 1: Kyber512 179
(Tosun et al., 2024) 3: Kyber768 250-400
(Mujdei et al., 2024) 3: Kyber768 200
(Tosun and Savas, 2024) 3: Kyber768 160
(Yang et al., 2023) 1: Kyber512 25-500
5.2 Countermeasures
The most effective countermeasure against this type
of SCA is to avoid deploying ML-KEM in a semi-
static key configuration. Increasing the frequency of
key updates not only complicates key recovery for
an attacker but also reduces the potential utility of
a successfully recovered key. This reduction is di-
rectly proportional to the key refresh rate. However,
more frequent key changes inevitably lead to greater
computational overhead, presenting a clear trade-off
between security and performance. The optimal bal-
ance will depend on the specific use case, implemen-
tation details, and other contextual factors. Notably,
our research demonstrates successful key recovery af-
ter only 179 traces, suggesting a practical upper limit
for key reuse in unprotected implementations.
Secondly, although reviewed literature suggests a
limited effect, still techniques such as shuffling and
masking will make attacks more difficult, if employed
carefully.
5.3 Conclusions
This work has introduced an enhanced two-step CPA
attack targeting ML-KEM recently standardised by
NIST in FIPS 203. Our attack demonstrates that ML-
KEM implementations without countermeasures are
vulnerable to CPA SCAs by an adversary. Our en-
hancement reduces the computational effort required
by identifying PoIs for keyspace enumeration, thus
enhancing the efficiency of the CPA. Our enhanced
attack ranks among the top-performing non-profiled
CPA SCAs targeting polynomial multiplication in
ML-KEM, outperforming several other works with-
out introducing elaborate preconditions.
In our future work we will explore use of counter-
measures such as the masking used in (Heinz et al.,
2022) to prevent information leakage from the side
channel while executing ML-KEM. We also intend to
build upon previous DL-SCA research (Hoang et al.,
2024) with a similar enhancement that leverages f
qmul
outputs against both protected and unprotected imple-
mentations of ML-KEM.
ACKNOWLEDGEMENTS
This work is partially funded by the Integrated Quan-
tum Networks (IQN) Research Hub (EP/Z533208/1).
REFERENCES
Albrecht, M. R., Player, R., and Scott, S. (2015). On the
concrete hardness of learning with errors. Journal of
Mathematical Cryptology, 9(3):169–203.
Avanzi, R., Joppe Bos, L. D., Eike Kiltz, T. L.,
Vadim Lyubashevsky, J. M. S., Peter Schwabe, G. S.,
and Stehl
´
e, D. (2021). CRYSTALS-Kyber algorithm
specifications and supporting documentation v3.02.
Backlund, L., Ngo, K., G
¨
artner, J., and Dubrova, E. (2022).
Secret Key Recovery Attacks on Masked and Shuffled
Implementations of CRYSTALS-Kyber and Saber.
Cryptology ePrint Archive, Paper 2022/1692. https:
//eprint.iacr.org/2022/1692.
Bottinelli, P. and Bos, J. W. (2017). Computational as-
pects of correlation power analysis. Journal of Cryp-
tographic Engineering, 7(3):167–181.
Brier, E., Clavier, C., and Olivier, F. (2004). Correla-
tion power analysis with a leakage model. In Cryp-
tographic Hardware and Embedded Systems - CHES
2004: 6th International Workshop Cambridge, MA,
USA, August 11-13, 2004. Proceedings, volume 3156
of Lecture Notes in Computer Science, pages 16–29,
Cambridge, MA, USA. Springer.
Chari, S., Rao, J. R., and Rohatgi, P. (2003). Template
attacks. In Cryptographic Hardware and Embed-
ded Systems-CHES 2002: 4th International Workshop
Redwood Shores, CA, USA, August 13–15, 2002 Re-
vised Papers 4, pages 13–28. Springer.
Chen, Z., Karabulut, E., Aysu, A., Ma, Y., and Jing, J.
(2021). An efficient non-profiled side-channel at-
tack on the crystals-dilithium post-quantum signature.
2021 IEEE 39th International Conference on Com-
puter Design (ICCD 2021), page 583–90.
Doget, J., Prouff, E., Rivain, M., and Standaert, F.-X.
(2011). Univariate side channel attacks and leak-
age modeling. Journal of Cryptographic Engineering,
1:123–144.
Dubrova, E., Ngo, K., G
¨
artner, J., and Wang, R. (2023).
Breaking a Fifth-Order Masked Implementation of
CRYSTALS-Kyber by Copy-Paste. In Proceedings of
the 10th ACM Asia Public-Key Cryptography Work-
shop, APKC ’23, page 10–20, New York, NY, USA.
Association for Computing Machinery.
Fujisaki, E. and Okamoto, T. (1999). Secure integration
of asymmetric and symmetric encryption schemes.
In Annual international cryptology conference, pages
537–554. Springer.
Heinz, D., Kannwischer, M. J., Land, G., P
¨
oppelmann, T.,
Schwabe, P., and Sprenkels, A. (2022). First-order
masked kyber on ARM cortex-m4. Cryptology ePrint
Archive, Paper 2022/058.
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
272

Hoang, A.-T., Kennaway, M., Pham, T., Mai, T., Khalid,
A., Rafferty, C., and O’Neill, M. (2024). Deep learn-
ing enhanced side channel analysis on CRYSTALS-
Kyber. In The 25th International Symposium on
Quality Electronic Design (ISQED’24): Proceedings,
pages 1–8. Institute of Electrical and Electronics En-
gineers Inc.
Kannwischer, M. J., Rijneveld, J., Schwabe, P., and Stof-
felen., K. (2018). Post-quantum cryptography on
ARM Cortex-M4 family of microcontrollers. https:
//github.com/mupq/pqm4.
Khalid, A., McCarthy, S., O’Neill, M., and Liu, W.
(2019). Lattice-based cryptography for iot in a quan-
tum world: Are we ready? In 2019 IEEE 8th Inter-
national Workshop on Advances in Sensors and Inter-
faces (IWASI), pages 194–199, Otranto, Italy. IEEE.
Kim, I.-J., Lee, T.-H., Han, J., Sim, B.-Y., and Han, D.-G.
(2020). Novel Single-Trace ML Profiling Attacks on
NIST 3 Round candidate Dilithium. Cryptology ePrint
Archive, Paper 2020/1383.
Kirch, W., editor (2008). Pearson’s Correlation Coefficient,
pages 1090–1091. Springer Netherlands, Dordrecht.
Kocher, P. C. (1996). Timing attacks on implementations
of Diffie-Hellman, RSA, DSS, and other systems. In
Koblitz, N. I., editor, CRYPTO96, volume 1109 of
LNCS, pages 104–13. Springer, Berlin.
Maghrebi, H., Portigliatti, T., and Prouff, E. (2016). Break-
ing cryptographic implementations using deep learn-
ing techniques. In Security, Privacy, and Applied
Cryptography Engineering: 6th International Confer-
ence, SPACE 2016, Hyderabad, India, December 14-
18, 2016, Proceedings 6, pages 3–26. Springer.
Mangard, S., Oswald, E., and Popp, T. (2007). Power
Analysis Attacks: Revealing the Secrets of Smart
Cards. Advances in Information Security. Springer,
New York.
Mu, J., Zhao, Y., Wang, Z., Ye, J., Fan, J., Chen, S., Li, H.,
Li, X., and Cao, Y. (2022). A Voltage Template Attack
on the Modular Polynomial Subtraction in Kyber. In
2022 27th Asia and South Pacific Design Automation
Conference (ASP-DAC), pages 672–677.
Mujdei, C., Wouters, L., Karmakar, A., Beckers, A.,
Bermudo Mera, J. M., and Verbauwhede, I. (2024).
Side-channel analysis of lattice-based post-quantum
cryptography: Exploiting polynomial multiplication.
ACM Trans. Embed. Comput. Syst., 23(2).
NewAE Technology Inc. (2018). ChipWhisperer Level 1
Starter Kit Product Datasheet. https://media.newae.
com/datasheets/NAE-SCAPACK-L1\ datasheet.pdf.
Ngo, K., Wang, R., Dubrova, E., and Paulsrud, N. (2022).
Side-Channel Attacks on Lattice-Based KEMs Are
Not Prevented by Higher-Order Masking. IACR Cryp-
tol. ePrint Arch., 2022:919.
NIST (2023a). FIPS 203: Module-lattice-based key-
encapsulation mechanism standard. https://nvlpubs.
nist.gov/nistpubs/FIPS/NIST.FIPS.203.ipd.pdf.
NIST (2023b). FIPS 204: Module-lattice-based digital
signature standard. https://nvlpubs.nist.gov/nistpubs/
FIPS/NIST.FIPS.204.ipd.pdf.
O’Flynn, C. and Chen, Z. (2014). Chipwhisperer: An open-
source platform for hardware embedded security re-
search. In ChipWhisperer: An Open-Source Platform
for Hardware Embedded Security Research, volume
8622.
Primas, R., Pessl, P., and Mangard, S. (2017). Single-Trace
Side-Channel Attacks on Masked Lattice-Based En-
cryption. In Cryptographic Hardware and Embed-
ded Systems - CHES 2017 - 19th International Con-
ference, Taipei, Taiwan, September 25-28, 2017, Pro-
ceedings, pages 513–533.
Ravi, P., Bhasin, S., Roy, S. S., and Chattopadhyay, A.
(2022a). On Exploiting Message Leakage in (Few)
NIST PQC Candidates for Practical Message Re-
covery Attacks. IEEE Transactions on Information
Forensics and Security, 17:684–699.
Ravi, P., Chattopadhyay, A., D’Anvers, J. P., and Baksi,
A. (2022b). Side-channel and Fault-injection at-
tacks over Lattice-based Post-quantum Schemes (Ky-
ber, Dilithium): Survey and New Results. Cryptology
ePrint Archive, Paper 2022/737.
Ravi, P. V., Bhasin, S., Roy, S. S., and Chattopadhyay, A.
(2020). Drop by Drop you break the rock - Exploiting
generic vulnerabilities in Lattice-based PKE/KEMs
using EM-based Physical Attacks. IACR Cryptol.
ePrint Arch., 2020:549.
Sim, B.-Y., Kwon, J., Lee, J., Kim, I.-J., Lee, T.-H., Han, J.,
Yoon, H., Cho, J., and Han, D.-G. (2020). Single-trace
attacks on message encoding in lattice-based KEMs.
IEEE Access, 8:183175–183191.
Sim, B.-Y., Park, A., and Han, D.-G. (2022). Chosen-
ciphertext clustering attack on CRYSTALS-Kyber us-
ing the side-channel leakage of Barrett Reduction.
IEEE Internet of Things Journal, 9(21):21382–21397.
Tiri, K., Hwang, D., Hodjat, A., Lai, B.-C., Yang, S., Schau-
mont, P., and Verbauwhede, I. (2005). Prototype ic
with wddl and differential routing – dpa resistance as-
sessment. In Rao, J. R. and Sunar, B., editors, Cryp-
tographic Hardware and Embedded Systems – CHES
2005, pages 354–365, Berlin, Heidelberg. Springer
Berlin Heidelberg.
Tosun, T., Moradi, A., and Savas, E. (2024). Exploiting
the Central Reduction in Lattice-Based Cryptography.
Cryptology ePrint Archive, Paper 2024/066.
Tosun, T. and Savas, E. (2024). Zero-Value Filtering for
Accelerating Non-Profiled Side-Channel Attack on
Incomplete NTT-Based Implementations of Lattice-
Based Cryptography. IEEE Transactions on Informa-
tion Forensics and Security, PP:1–1.
Ulitzsch, V. Q., Marzougui, S., Tibouchi, M., and Seifert, J.-
P. (2024). Profiling side-channel attacks on dilithium.
In Smith, B. and Wu, H., editors, Selected Areas in
Cryptography, pages 3–32, Cham. Springer Interna-
tional Publishing.
Xu, Z., Pemberton, O., Roy, S. S., Oswald, D., Yao, W., and
Zheng, Z. (2022). Magnifying Side-Channel Leakage
of Lattice-Based Cryptosystems With Chosen Cipher-
texts: The Case Study of Kyber. IEEE Transactions
on Computers, 71(9):2163–2176.
Yang, Y., Wang, Z., Ye, J., Fan, J., Chen, S., Li, H., Li,
An Enhanced Two-Step CPA Side-Channel Analysis Attack on ML-KEM
273

X., and Cao, Y. (2023). Chosen ciphertext correlation
power analysis on Kyber. Integration, 91:10–22.
A APPENDIX
A complete assembly code listing of double-
basemul asm, as used in PQM4 (Kannwischer et al.,
2018).
dou ble b as e mul _ as m :
push { r4 - r1 1 , lr }
rptr . req r0
aptr . req r1
bptr . req r2
zeta . req r3
po ly 0 . req r4
po ly 1 . req r6
po ly 2 . req r5
po ly 3 . req r7
q . req r8
qinv . req r8
tmp . req r9
tmp2 . req r1 0
tmp3 . req r1 1
movw q , #332 9
movt qinv , #3 32 7
ldrd po ly 0 , p ol y2 , [ a ptr ] , #8
ldrd po ly 1 , p ol y3 , [ b ptr ] , #8
// b as emul (r - > c oe ff s + 4 * i ,
a - > co ef fs + 4 * i ,
b - > co ef fs + 4 * i ,
ze ta s [6 4 + i ]);
sm ul tt tmp , p ol y0 , p oly1
mo n tg ome ry q , q inv , tmp , tm p2
sm ul tb t mp2 , tmp2 , zeta
sm la bb t mp2 , poly0 , po ly 1 , t mp2
mo n tg ome ry q , q inv , tm p2 , tmp
// r [0] in upper ha lf of t mp
sm ua dx t mp2 , poly0 , po ly 1
mo n tg ome ry q , q inv , tm p2 , tm p3
// r [1] in upper ha lf of tmp3
pk ht b tm p , tmp3 , tm p , asr #16
str tmp , [ rptr ] , #4
neg zeta , zeta
// b as emul (r - > c oe ff s + 4 * i + 2 ,
a - > co ef fs + 4 * i + 2,
b - > co ef fs + 4 * i + 2,
- z etas [64 + i ]);
sm ul tt tmp , p ol y2 , p oly3
mo n tg ome ry q , q inv , tmp , tm p2
sm ul tb t mp2 , tmp2 , zeta
sm la bb t mp2 , poly2 , po ly 3 , t mp2
mo n tg ome ry q , q inv , tm p2 , tmp
// r [0] in upper ha lf of t mp
sm ua dx t mp2 , poly2 , po ly 3
mo n tg ome ry q , q inv , tm p2 , tm p3
// r [1] in upper ha lf of tmp3
pk ht b tm p , tmp3 , tm p , asr #16
str tmp , [ rptr ] , #4
pop { r4 - r 11 , pc }
SECRYPT 2025 - 22nd International Conference on Security and Cryptography
274
