SONNI: Secure Oblivious Neural Network Inference

Luke Sperling and Sandeep S. Kulkarni

Department of Computer Science and Engineering,

Michigan State University, U.S.A.

Keywords:

Fully Homomorphic Encryption, MLaaS, Privacy.

Abstract:

In the standard privacy-preserving Machine learning as-a-service (MLaaS) model, the client encrypts data

using homomorphic encryption and uploads it to a server for computation. The result is then sent back to the

client for decryption. It has become more and more common for the computation to be outsourced to third-

party servers. In this paper we identify a weakness in this protocol that enables a completely undetectable novel

model-stealing attack that we call the Silver Platter attack. This attack works even under multikey encryption

that prevents a simple collusion attack to steal model parameters. We also propose a mitigation that protects

privacy even in the presence of a malicious server and malicious client or model provider (majority dishonest).

When compared to a state-of-the-art but small encrypted model with 32k parameters, we preserve privacy with

a failure chance of 1.51 × 10

−28

while batching capability is reduced by 0.2%.

Our approach uses a novel results-checking protocol that ensures the computation was performed correctly

without violating honest clients’ data privacy. Even with collusion between the client and the server, they are

unable to steal model parameters. Additionally, the model provider cannot learn any client data if maliciously

working with the server.

1 INTRODUCTION

Training large machine learning models is very time

consuming and expensive. One way for a provider

to recuperate the cost of generating machine learning

models is to provide machine learning as-a-service

(MLaaS) where the provider permits a client to com-

pare their data with the model. For example, a hos-

pital could pay to have automated screenings for skin

cancer.

The use of MLaaS generates an issue of privacy

for the client, as the data it is using is private and the

client is concerned about possible leak of this private

data to provider. The issue of privacy is especially im-

portant to client as the data is often one-of-a-kind and

cannot be replaced/regenerated, such as in the case of

medical or biometric data. For this reason, for several

years, MLaaS systems have been designed with client

data privacy in mind.

However, as MLaaS becomes more widespread

and the models become more complex, the provider

lacks the computational power needed to provide

MLaaS on its own. Especially in the context of avail-

ability of third-party servers to provide computational

capability, it is in the interest of the provider to out-

source the MLaaS service to a server that will only

provide the computational capability. Here, in addi-

tion to client privacy, privacy of the provider is criti-

cal. Speciﬁcally, since the development of the model

requires signiﬁcant computational and ﬁnancial in-

vestment, it is critical that the model remain a secret

and not be revealed to anyone.

Our work focuses on using oblivious neural net-

works with mulitikey encryption. The protocol in

(Chen et al., 2019b) provides privacy only for the

honest-but-curious and collusion models. In other

words, if the server, model provider or client is only

going to try to infer from the data it has learned, the

privacy property is satisﬁed. However, if the server

is malicious and violates the protocol even slightly,

it can leak model parameters without being detected.

One way to do this is to encrypt the model parameters

as the return value and send them to the client instead

of sending the actual result of the model. In this case,

the server will not be able to detect this as the data

it sees is encrypted with the client’s key. It follows

that this attack would go completely undetected by

the model provider 100% of the time.

A simple solution would be to have the model

provider check the result before returning it to the

client. However, in this case, the provider learns the

output of the model when applied to the private data.

Sperling, L. and Kulkarni, S. S.

SONNI: Secure Oblivious Neural Network Inference.

DOI: 10.5220/0013638100003979

In Proceedings of the 22nd International Conference on Security and Cryptography (SECRYPT 2025), pages 515-522

ISBN: 978-989-758-760-3; ISSN: 2184-7711

515

Figure 1: Standard Outsourced Oblivious Neural Network

Inference Model.

Moreover, this output can be used to learn the private

data itself (Mai et al., 2018) .

In this paper, we identify a novel attack against

oblivious neural network inference and propose a se-

cure protocol that we call Secure Oblivious Neural

Network Inference, or SONNI, to combat it and en-

sure security in the presence of a dishonest server and

dishonest client/provider (majority dishonest).

Contributions of the Paper. We introduce a novel

attack, called the Silver Platter attack, to enable model

stealing in the oblivious neural network inference set-

ting. We propose a novel protocol for oblivious neural

network inference that mitigates this novel attack and

does not violate the client’s data privacy. We evaluate

our protocol in terms of the level of privacy it provides

and the overhead of providing that privacy.

Organization of the Paper. In Section 2 we provide

background of the encryption schemes employed in

this work. In Section 3 we detail the vulnerability of

the existing outsourced neural network inference pro-

tocol and the novel attack we construct. We propose

a solution and prove its security in Section 4. We pro-

vide related work in Section 5 and closing remarks in

Section 6.

2 BACKGROUND

2.1 Fully Homomorphic Encryption

Traditional encryption schemes require decryption

before any data processing can occur. Homomorphic

encryption (HE) allows arithmetic directly over ci-

phertexts without requiring access to the secret key

needed for decryption, enabling data oblivious proto-

cols. Fully homomorphic encryption (FHE) schemes

support an unlimited number of multiple types of op-

erations. The Cheon-Kim-Kim-Song (CKKS) (Cheon

et al., 2017) cryptosystem supports additions as well

as multiplications of ciphertexts. The message space

of CKKS is vectors of complex numbers.

A small amount of error is injected into each ci-

phertext at the time of encryption to guarantee the

security of the scheme. This error grows each arith-

metic operation performed. Therefore, once a certain

threshold of multiplications are performed the error

grows too large to decrypt correctly. Although the

bootstrap operation reduces this error to allow cir-

cuits of unlimited depth, for the purposes of this work

no such operations are needed. The following opera-

tions are supported: Encode: Given a complex vec-

tor, return an encoded polynomial. Decode: Given a

polynomial, return the encoded complex vector. En-

crypt: Given a plaintext polynomial and public key,

return a ciphertext. Decrypt: Given a ciphertext and

the corresponding secret key, return the underlying

polynomial. Ciphertext Addition: Given two ci-

phertexts, or a ciphertext and a plaintext, return a ci-

phertext containing an approximate element-wise ad-

dition of the underlying vectors. Ciphertext Multi-

plication: Given two ciphertexts, or a ciphertext and

a plaintext, return a ciphertext containing an approx-

imate element-wise multiplication of the underlying

vectors. Relinearization: Performed after every mul-

tiplication to prevent exponential growth of ciphertext

size. This function is assumed to be executed after

every homomorphic multiplication in this work for

simplicity. Ciphertext Rotation: Given a ciphertext,

an integer, and an optionally-generated set of rotation

keys, rotate the underlying vector a speciﬁed number

of times. For instance, Rotate(Enc([1, 2, 3, 4]), 1, k

)

returns Enc([2, 3, 4, 1]).

2.2 Multikey Encryption

Chen et al. (Chen et al., 2019b) extended existing

FHE schemes to operate on multiple sets of secret

key, public key pairs. Consider the case where there

are two key pairs owned by two parties (such as the

Client and Provider). Each party encrypts a value us-

ing their respective public keys. These ciphertexts,

denoted by enc

(X) and enc

(Y ) can be multiplied

together homomorphically, resulting in enc

c, p

(XY ).

Note that this notation means the ciphertext is now

multikey encrypted by the keys of both the Client and

the Provider and that enc

(V ) = enc

(V ). The

following additional operations are supported:

• PartialDec(ciphertext, secret

key) - given a mul-

tikey encrypted ciphertext and one of the secret

keys corresponding to a public key encrypting the

ciphertext, return a partial decryption of the ci-

phertext. This partial decryption does not yield

any additional information.

• Combine(partial decryptions) - given an array of

partial decryptions, return the underlying plain-

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

516

text value. This combine function only works if

there is a partial decryption corresponding to each

public key used in the multikey encryption.

3 PROPOSED MODEL STEALING

ATTACK

In this section, we demonstrate that the existing ap-

proach for using multiparty encryption to provide pri-

vacy in outsourced MLaaS systems suffers from a se-

rious violation of privacy for the provider if the server

behaves maliciously and tries to leak parameters to

the client. We call this attack the Silver Platter attack,

as the adversary is delivered the exact model parame-

ters with little effort. Additionally, this attack will go

unnoticed by the provider.

Typical Execution for the Protocol in (Chen et al.,

2019b): The communication between client,

provider and server is as shown in Figure 1 where

we utilize the oblivious neural network inference pro-

tocol from (Chen et al., 2019b). The client en-

crypts their data using FHE and the provider encrypts

their function parameters using a different public key.

These encryptions (along with the corresponding pub-

lic keys) are sent to the server. The server then com-

putes enc

c, p

( f (x)) which is returned to both the client

and the provider. Partial decryptions are obtained

with each party’s secret key and are combined by the

client to obtain the full decryption of f (x).

The approach in (Chen et al., 2019b) preserves the

privacy of the client as the provider and server only

sees the encrypted version of the data. It also pre-

serves the privacy of provider if the server is honest-

but-curious, as the server only sees the data in en-

crypted format. However, if server is dishonest, it

can collude with client to reveal the model parame-

ters. We discuss such attacks next.

Silver Platter Attack: In step 2 of Figure 1, a ma-

licious server sends an encryption of the parameters

enc

c, p

( f ) instead of the intended result enc

c, p

( f (x)).

enc

c, p

( f ) can be trivially computed from enc

( f )

which is obtained by the server during step 1. This

ciphertext is fully decrypted only by the client dur-

ing step 3, revealing private model parameters. This

attacks appears identical to normal operation to the

provider. In cases where there are multiple ciphertexts

with model parameters, the attack may be repeated to

obtain them all.

The reason we call this the Silver Platter attack

is that this can be repeated ad inﬁnitum without the

provider learning anything about the fact that the

model is being compromised. This paper focuses on

addressing this attack.

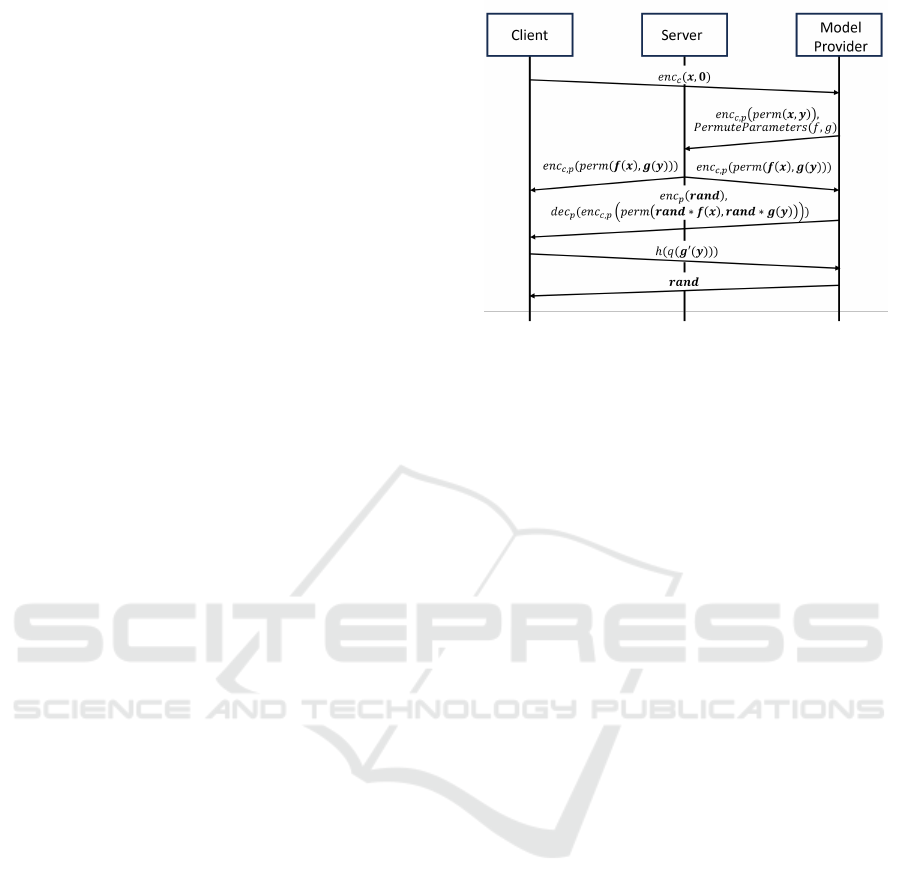
Figure 2: SONNI sequence diagram.

4 ATTACK MITIGATION VIA

OBLIVIOUS RESULTS

CHECKING

In this section, we propose a protocol that mitigates

the Silver Platter attack and we prove its security.

First, in Section 4.1 we introduce the problem for-

mally. Next, in Section 4.2 we describe our approach

at a high level before going into details in Section 4.3.

We then describe the special steps needed to prepare

the ciphertext at the beginning of the computation as

well as the work needed to check that the result was

computed correctly. Lastly, in Section 4.4 we analyze

our protocol and prove its security.

4.1 Problem Statement

In this section, we deﬁne the problem statement for

dealing with Silver Platter attack. Here, a party

(client, server or provider) may be honest or dishon-

est. An honest party follows the prescribed protocol,

while a dishonest party could be byzantine and behave

arbitrarily. We assume that the dishonest party intends

to remain hidden. Therefore, it will send messages of

the required type (such as CKKS ciphertexts). How-

ever, the data inside may be incorrect.

Recall that in the multiparty communication, the

client starts with its own data, x, and desires to obtain

a value f (x) where f is a function known to provider.

The actual computation of f (x) is done by a server.

In the multiparty communication considered in

this paper, we follow a secure with abort approach

where security is guaranteed at all times, i.e., the

provider or server never learns the client data, x or the

computed value f (x) but if dishonest behavior is de-

tected, the computation may be aborted. This remains

true in all cases, i.e., even if the provider and server

SONNI: Secure Oblivious Neural Network Inference

517

send additional messages between them privacy will

not be violated. We also want to ensure that the model

parameters are never revealed to the client even if the

server and client collude and send additional mes-

sages between them. However, if everyone behaves

honestly then the client should receive the value of

f (x). Thus, the privacy requirements are as follows:

Liveness. Upon providing enc

(x) to provider, the

client should eventually learn f (x) if the provider

and server behave honestly.

Provider Privacy The client should not learn the

model parameters even if the server is colluding

with the client.

Client Privacy. The provider should not learn x or

f (x) even if the server is colluding with the

provider.

Oblivious Inference. The server should not learn in-

put x, model parameters, or result f (x).

Secure with Abort. If any party violates the proto-

col then the computation is aborted and the client

does not learn anything.

4.2 Mitigation Approach

In this section, we propose our approach for providing

privacy to provider as well as the client. Speciﬁcally,

the approach in (Chen et al., 2019b) already provides

privacy for the client data. We ensure that the cor-

responding privacy is preserved while permitting the

provider to have control over the data being transmit-

ted to the client so that it can verify that the server is

not trying to leak the provider’s private data (namely

the model parameters) to the client.

Our approach is based on the observation that ma-

chine learning algorithms operate on vectors as op-

posed to scalars, making FHE well-suited to the task.

Ciphertexts in FHE encode and encrypt entire vectors

of real values. We take advantage of this fact for our

mitigation strategy. We dedicate some slots of the

ciphertext (and therefore some indices of the under-

lying vector) to verify the computation is performed

correctly. These slots will not contain f (x) values but

rather randomly-generated values for use in a results

checking step.

The basic idea of the protocol is to have the server

compute f (x) in most slots of the ciphertext and g(y)

in other slots, where g is a function that is of the same

form as f (e.g., if f is a linear/quadratic function then

g is also a linear/quadratic function with different pa-

rameters.). Here, g is a random function generated

at the start of the protocol by the provider and y is

a random secret input vector also generated by the

provider. Upon receiving the answer from the server,

the provider will get the decryption of g(y) by re-

questing it from the client. And, if the value of g(y)

matches then the provider will return the result to the

client. Since g and y are only known to the provider,

if g(y) is computed correctly then it provides a conﬁ-

dence to the provider that the server is likely to have

performed honestly. If g(y) is not computed correctly,

then the provider would realize that either server or

client is being dishonest and can refuse to provide the

partial decryption of the encrypted value of f (x) nec-

essary to learn f (x) (the provider aborts).

4.3 Protocol Details

SONNI is built on top of the existing oblivious neu-

ral network inference protocol with added steps. The

protocol is detailed in Algorithm 1.

First in step 1, the client generates a ciphertext

containing the vector x in the ﬁrst d slots of the ci-

phertext and sends it to the provider. The provider in-

serts the y values in slots d + 1..d + m, where m slots

are used for y. Subsequently, provider permutes this

vector in step 3. It also permutes function f and g

in a similar fashion. As an illustration if the f was

x[1] + 2x[2] and (x[1], x[2]) is permuted to (x[2], x[1])

then f would be changed to 2x[2] + x[1].

Additionally, to permute the computation, the

provider can also change f to be 2x[2]+x[1]+0∗y[1],

where y[1] is one of the values used for the computa-

tion of g(y). Likewise, the computation of g can use

some of the values in the x vector with coefﬁcient 0.

It could use any arithmetic operation that uses y (re-

spectively, x) while computing the value of f (x) (re-

spectively g(y)) in such a way that the ﬁnal answer

will be independent of the y (respectively x) value.

This will prevent the server from performing data-

ﬂow techniques to determine the slots used for f and

Since the server is not aware of the placement of x

and y in the ciphertext and it uses the permuted input,

it computes permuted f (x) and g(y) in step 6. This

value is sent to both the client and the provider.

In step 10, the client uses the mask provided by

the provider to compute enc

c, p

′

(y)), where g

′

(y)

denotes g(y) masked by a random vector known to

the provider (similarly f

′

(x) denotes f (x) masked by

that same random vector). This value and the partial

decryption provided by provider is used to compute

′

(y). If g

′

(y) is computed correctly, then the model

owner is convinced that the entire vector was com-

puted correctly.

Since the computation of g

′

(y) by the client may

have a small error due to the use of FHE whereas

the value computed by the provider is the exact value

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

518

of g

′

(y), we use g

′

(y) to denote the value computed

by the client and g

′

(y) to be value computed by the

provider. Each value is quantized such that q(g

′

(y))

will be equal to q(g

′

(y))

Then, in steps 11-14, the client and provider per-

form a privacy-preserving comparison protocol to en-

sure q(g

′

(y)) was computed correctly. After this

passes, the client and provider jointly decrypt the re-

sult ciphertext containing f (x) and only the client

learns f (x). One of the concerns in this step is a

malicious provider that tries to compromise the pri-

vacy of the client. Speciﬁcally, in this step, if the

provider speciﬁes the incorrect indices such that the

indices correspond to f

′

(x) instead of g

′

(y), then the

provider could learn the value of f (x). To prevent

this, the proof that the client computes the value of

′

(y) correctly is achieved via a zero-knowledge ap-

proach discussed later in this section.

Algorithm 1: Secure Oblivious Neural Network Inference.

1: C sends to P : enc

(x[1], x[2], ...x[d], 0, ...0)

2: P computes enc

c, p

(x[1], x[2], ...x[d], y[1], y[2], y[m])

3: P computes enc

c, p

(perm(x, y))

4: P computes PermuteParameters( f , g) using the same permu-

tation.

5: P sends to S : enc

c, p

(perm(x, y)), PermutaParameters( f , g)

6: S computes and sends to P and C : enc

c, p

(perm( f (x), g(y)))

7: P computes rand = [−1, 1]

d+m

8: P computes enc

c, p

(perm( f

′

(x), g

′

(y))) =

mult(enc

c, p

(perm( f (x), g(y))), rand)

9: P sends to C : dec

(enc

c, p

(perm( f

′

(x), g

′

(y)))), enc

(rand)

10: C computes g

′

(y)

11: C sends to P : hash

= h(q(g

′

(y)))

12: P computes g

′

(y)

13: P computes hash

= h(q(g

′

(y)))

14: If hash

̸= hash

, P aborts

15: P sends to C : rand

16: C computes f (x)

The above protocol has two important stages, ci-

phertext preparation (lines 2-5) and result checking

(11-14). Next, we provide additional details of these

steps. Ciphertext preparation refers to the manipu-

lation done by the provider before it sends the data

to server to compute f (x) and g(y) whereas the re-

sult checking refers the the computation between the

client and provider so that it can verify that g(y) was

computed correctly by the server.

4.3.1 Ciphertext Preparation

The security of our proposed protocol relies on the

client and server not knowing the indices of the y val-

ues. To achieve this, the client appends m zeroes to the

end of their data vector x before encryption. This ci-

phertext is sent to the provider. Then, through a series

of masking multiplications, rotations, and additions,

the ciphertext is shufﬂed. We note that we do not re-

quire arbitrary ciphertext shufﬂing for the security of

our protocol. Our security rests on the server not be-

ing able to guess which slots correspond to x values

and which slots correspond to y values. The vectors of

function parameters are shufﬂed in the same manner

prior to encryption. The provider ﬁnally adds random

y values to the zero indices in the ciphertext.

4.3.2 Result Checking

If the provider does not verify that the ciphertext they

are decrypting does not contain model parameters,

the Silver Platter attack will succeed. However, the

provider should not learn f (x) so it is not permissi-

ble to have the provider decrypt the result, examine

it, and return it to the client. Indeed, if this were al-

lowed, the protocol would be open to an attack where

the provider works with the server to learn x in a sim-

ilar manner. Our idea is to give the client access only

to the computed g(y). If the client is able to correctly

tell the provider the values of g(y), then the provider

will help the client decrypt the ﬁnal result and gain

access to f (x).

The provider generates a random vector rand ∈

d+m

that contains in each index a random nonzero

real value. This vector is sent to the client. Both the

provider and the client compute:

enc

c, p

(perm( f

′

(x), g

′

(y)))

= mult(enc

c, p

(perm( f (x), g(y))), rand)

They also compute a partial decryption of this re-

sultant ciphertext. The provider sends their partial de-

cryption to the client that combines the partial decryp-

tions to recover g

′

(y) = g(y) × rand (and additionally

′

(y) = f (y) × rand).

The provider computes g

′

(y), as they know g, y,

and rand due to having generated each in plaintext at

the start of the computation. Now, the provider needs

to be convinced that they have the same value of g

′

(y)

as the client without revealing these values to each

other. If the client were to send g

′

(y) to the provider,

the provider could take advantage of this by storing

f (x) or x in lieu of g

′

(y) (or an obfuscated version

thereof). Similarly, the provider cannot simply send

′

(y) to the client because the client could simply lie

and state that the values are the same.

A secure two-party computation protocol is

needed to prove to the provider that the values of

′

(y) are the same without revealing those values to

SONNI: Secure Oblivious Neural Network Inference

519

the other. This protocol can work on plaintext val-

ues because g

′

(y) exists in plaintext to both parties at

this point in the protocol (as decryption has already

occurred). Both parties compute h(g

′

(y)) for some

low-collision hash function h. The client sends their

result to the provider and the provider veriﬁes that the

hashes are identical.

Due to the approximate nature of arithmetic un-

der FHE, the value of g

′

(y) decrypted by the client is

likely to be slightly different than the value computed

in plaintext by the provider. To mitigate this, we use

a simple uniform quantization scheme with intervals

large enough that the noise from homomorphic com-

putations will not affect the performance. Therefore,

the client and provider compute h(q(g

′

(y))) instead of

h(g

′

(y)) for a quantization scheme q.

Once the provider is convinced that g

′

(y) was

computed correctly, they share the random vector

rand with the client to for use in recovering f (x).

4.4 Security Analysis

In this subsection, we evaluate the theoretical prob-

abilities of attacks successfully working against the

proposed system. We refer to the probability of break-

ing the homomorphic encryption scheme as ε

and the

probability of breaking the incorporated hash function

as ε

. These values are negligible, given proper selec-

tion of encryption security parameters and hash func-

tion.

Theorem 1. Let d be the dimensionality of the client’s

secret data x and m be the number of ciphertext slots

dedicated to containing y values. The probability

of successfully performing the Silver Platter attack

against SONNI to steal k scalar model parameters is

upper bounded by (

d+m

)

+ ε

Theorem 2. The probability of the provider work-

ing with the server to successfully steal any amount

of client data x or f (x) is upper bounded by ε

+ ε

Due to reasons of space, we provide detailed

proofs in (Sperling and Kulkarni, 2025).

In Figure 3, we analyze Theorem 1 quantitatively.

We assume in this analysis that the attack will be per-

formed in one round, rather than stealing one param-

eter per transaction (as that becomes incredibly costly

from a ﬁnancial perspective when the number of pa-

rameters reaches thousands or millions). In FHE ap-

plications it is a common practice to use 128-1024

size vectors (Jindal et al., 2020). We consider the case

where the ciphertext has 1024 slots, some of which

(d) are allocated to the client and some (m) are allo-

cated to the provider. When m = 1, i.e., only one slot

is allocated to the provider for veriﬁcation of g(y),

Table 1: Probability of successful Silver Platter attack

against SONNI. Vector size of 1024 is used.

m Parameters Stolen P(Success)

10 0.952

128 0.513

256 0.237

512 0.0311

10 0.720

128 0.011

256 6.34 × 10

−5

512 7.07 × 10

−11

512

10 9.25 × 10

−4

128 2.88 × 10

−43

256 1.02 × 10

−96

512 1.23 × 10

−307

the probability of a successful Silver Platter is quite

high. However, even with a few slots for the provider,

the probability of a successful Silver Platter decreases

sharply. Table 1 demonstrates this. With m = 32, i.e.,

32 slots allocated to provider, the probability of steal-

ing 10 parameters is 0.720, the probability of stealing

128 parameters is 0.011, and so on. The probability of

stealing 512 parameters is 7.07 × 10

−11

. We note that

modern machine learning models often include thou-

sands or millions of parameters. The simple projec-

tion matrix model featured in (Sperling et al., 2022)

includes 32768 parameters. Even if the adversary

maximizes their chance of successfully performing

the attack by stealing a single model parameter at a

time over 32768 transactions and if only 2 ciphertext

slots dedicated to veriﬁcation of g(y), the probabil-

ity of stealing all these parameters is 1.51 × 10

−28

Stealing just half of the parameters has a chance of

1.23 × 10

−14

of success. Batching capability is re-

duced by only 0.2% while privacy is maintained with

only a negligible chance of being violated.

In the case where even a small number of model

parameters leaking is undesirable, using an m value of

512 ensures that Silver Platter attacks are extremely

unlikely to be successful. Even stealing 10 in this cir-

cumstance has only a 9.25 × 10

−4

chance of succeed-

ing.

Also, our protocol preserves client privacy. This

is especially important for a client as its data, x or

f (x), is often impossible to replace, as the data cor-

responds to medical information, biometric informa-

tion, etc. By contrast, revealing a very small num-

ber of parameters does not signiﬁcantly affect the

provider. As discussed in Section 3, the Silver Platter

is undetectable for the provider if one uses the exist-

ing approach (Chen et al., 2019b). With the level of

security provided to both the client and provider, we

can provide privacy guarantees to both of them with a

reasonable overhead.

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

520

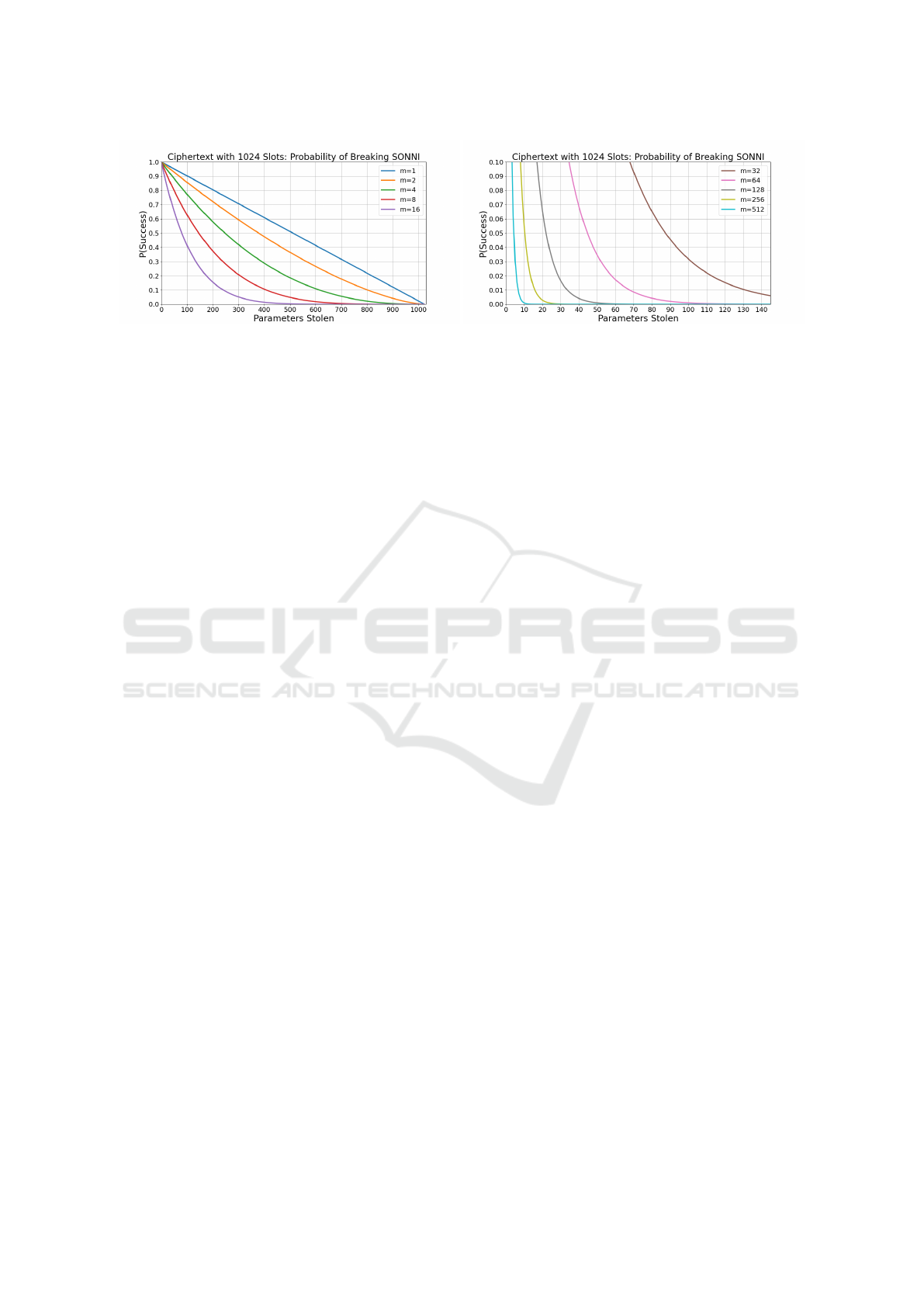
Figure 3: Probability of performing a Silver Platter attack without being detected based on the number of ciphertext slots

dedicated to checked values.

5 RELATED WORK

Oblivious neural network inference aims to evaluate

machine learning models without learning anything

about the data and has seen much attention in recent

years (Mann et al., 2023). XONN achieves this with

a formulation similar to garbled circuits (Riazi et al.,

2019). There is a privacy concern related to outsourc-

ing these computations. Namely, that the model will

be learned by the server. FHE has been used for in-

ference that not only protects sensitive client data, but

also prevents learning the provider’s private data (i.e.

the model) (Chen et al., 2019b). As we discuss thor-

oughly in this work, this approach is open to the un-

detectable Silver Platter attack. Our work protects not

only client data, as is expected in the classical obliv-

ious neural network inference formulation, but also

that of the provider.

Model stealing attacks aim to learn models from

black-box access. Broadly speaking, this either at-

tempts to steal exact model values or general model

behavior. Our work examines the former scenario.

This falls into three categories: stealing training

hyperparameters (Wang and Gong, 2018), stealing

model parameters (Lowd and Meek, 2005; Reith

et al., 2019), and stealing model architecture (Oh

et al., 2019; Yan et al., 2020; Hu et al., 2019), often

using side-channel attacks.

Gentry’s seminal work constructing the ﬁrst FHE

scheme (Gentry, 2009) paved the way for more

privacy-preserving applications on the cloud. Con-

cerns over data privacy led to the development of

multi-key encryption featuring multiple pairs of pub-

lic and private keys. The ﬁrst use of multi-key FHE

was proposed by L

opez et al. (L

opez-Alt et al., 2012).

Work followed suit, improving speed as well as sup-

porting more modern schemes (Chen et al., 2019a;

Ananth et al., 2020). These schemes are developed

for secure cloud computation. Speciﬁc optimizations

have been proposed for federated learning (Ma et al.,

2022). Work in FHE has often assumed the honest-

but-curious threat model. Our work shows that this

opens the way for undetectable and 100% successful

attacks.

6 CONCLUSION

In this paper, we demonstrated that the current ap-

proach to oblivious neural network inference (Chen

et al., 2019b) suffers from a simple attack, namely the

Silver Platter attack. It permits the server to reveal all

model parameters to the client in a way that is com-

pletely undetected by the provider.

We also presented a protocol to deal with the Sil-

ver Platter attack. The protocol relied on the obser-

vation that FHE based techniques utilize vector-based

computation. We used a few slots in this vector to

compute a function g(y) that could be veriﬁed by the

provider so that it can gain conﬁdence that the server

is not trying to steal the model parameters with the

help of the client. Our protocol provided a tradeoff

between the overhead (the number of slots used for

veriﬁcation) and the probability of a successful attack.

We demonstrated that even with a small overhead in

terms of the number of slots used for veriﬁcation, the

probability that a server can steal several parameters

remains very small. Modern machine learning models

often involve billions of parameters. We showed that

the probability of stealing even 1% of the parameters

is very small.

REFERENCES

Ananth, P., Jain, A., Jin, Z., and Malavolta, G. (2020).

Multi-key fully-homomorphic encryption in the plain

model. In Theory of Cryptography: 18th International

Conference, TCC 2020, Durham, NC, USA, Novem-

SONNI: Secure Oblivious Neural Network Inference

521

ber 16–19, 2020, Proceedings, Part I 18, pages 28–57.

Springer.

Chen, H., Chillotti, I., and Song, Y. (2019a). Multi-key

homomorphic encryption from tfhe. In Advances

in Cryptology–ASIACRYPT 2019: 25th International

Conference on the Theory and Application of Cryptol-

ogy and Information Security, Kobe, Japan, December

8–12, 2019, Proceedings, Part II 25, pages 446–472.

Springer.

Chen, H., Dai, W., Kim, M., and Song, Y. (2019b). Efﬁcient

multi-key homomorphic encryption with packed ci-

phertexts with application to oblivious neural network

inference. In Proceedings of the 2019 ACM SIGSAC

Conference on Computer and Communications Secu-

rity, pages 395–412.

Cheon, J. H., Kim, A., Kim, M., and Song, Y. (2017). Ho-

momorphic encryption for arithmetic of approximate

numbers. In Advances in Cryptology–ASIACRYPT

2017: 23rd International Conference on the Theory

and Applications of Cryptology and Information Se-

curity, Hong Kong, China, December 3-7, 2017, Pro-

ceedings, Part I 23, pages 409–437. Springer.

Gentry, C. (2009). Fully homomorphic encryption using

ideal lattices. In Proceedings of the forty-ﬁrst annual

ACM symposium on Theory of computing, pages 169–

178.

Hu, X., Liang, L., Deng, L., Li, S., Xie, X., Ji, Y.,

Ding, Y., Liu, C., Sherwood, T., and Xie, Y. (2019).

Neural network model extraction attacks in edge de-

vices by hearing architectural hints. arXiv preprint

arXiv:1903.03916.

Jindal, A. K., Shaik, I., Vasudha, V., Chalamala, S. R., Ma,

R., and Lodha, S. (2020). Secure and privacy pre-

serving method for biometric template protection us-

ing fully homomorphic encryption. In 2020 IEEE 19th

international conference on trust, security and privacy

in computing and communications (TrustCom), pages

1127–1134. IEEE.

opez-Alt, A., Tromer, E., and Vaikuntanathan, V. (2012).

On-the-ﬂy multiparty computation on the cloud via

multikey fully homomorphic encryption. In Proceed-

ings of the forty-fourth annual ACM symposium on

Theory of computing, pages 1219–1234.

Lowd, D. and Meek, C. (2005). Adversarial learning. In

Proceedings of the eleventh ACM SIGKDD interna-

tional conference on Knowledge discovery in data

mining, pages 641–647.

Ma, J., Naas, S.-A., Sigg, S., and Lyu, X. (2022). Privacy-

preserving federated learning based on multi-key ho-

momorphic encryption. International Journal of In-

telligent Systems, 37(9):5880–5901.

Mai, G., Cao, K., Yuen, P. C., and Jain, A. K. (2018). On

the reconstruction of face images from deep face tem-

plates. IEEE transactions on pattern analysis and ma-

chine intelligence, 41(5):1188–1202.

Mann, Z.

A., Weinert, C., Chabal, D., and Bos, J. W. (2023).

Towards practical secure neural network inference:

the journey so far and the road ahead. ACM Com-

puting Surveys, 56(5):1–37.

Oh, S. J., Schiele, B., and Fritz, M. (2019). Towards

reverse-engineering black-box neural networks. Ex-

plainable AI: interpreting, explaining and visualizing

deep learning, pages 121–144.

Reith, R. N., Schneider, T., and Tkachenko, O. (2019). Ef-

ﬁciently stealing your machine learning models. In

Proceedings of the 18th ACM Workshop on Privacy in

the Electronic Society, pages 198–210.

Riazi, M. S., Samragh, M., Chen, H., Laine, K., Lauter,

K., and Koushanfar, F. (2019). {XONN}:{XNOR-

based} oblivious deep neural network inference. In

28th USENIX Security Symposium (USENIX Security

19), pages 1501–1518.

Sperling, L. and Kulkarni, S. S. (2025). Sonni: Secure

oblivious neural network inference.

Sperling, L., Ratha, N., Ross, A., and Boddeti, V. N. (2022).

Heft: Homomorphically encrypted fusion of biomet-

ric templates. In 2022 IEEE International Joint Con-

ference on Biometrics (IJCB), pages 1–10. IEEE.

Wang, B. and Gong, N. Z. (2018). Stealing hyperparame-

ters in machine learning. In 2018 IEEE symposium on

security and privacy (SP), pages 36–52. IEEE.

Yan, M., Fletcher, C. W., and Torrellas, J. (2020). Cache

telepathy: Leveraging shared resource attacks to learn

{DNN} architectures. In 29th USENIX Security Sym-

posium (USENIX Security 20), pages 2003–2020.

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

522