An Extreme Gradient Boosting (XGBoost) Trees Approach to Detect and

Identify Unlawful Insider Trading (UIT) Transactions

Krishna Neupane

1 a

and Igor Griva

2 b

George Mason University, Department of Computational and Data Science, U.S.A.

George Mason University, Department of Mathematical Science, U.S.A.

Keywords:

Unlawful Insider Trading, Ensemble Methods, Decision Trees, Fraudulent Activities, XGBoost.

Abstract:

Corporate insiders have control of material non-public preferential information (MNPI). Occasionally, the

insiders strategically bypass legal and regulatory safeguards to exploit MNPI in their execution of securities

trading. Due to a large volume of transactions a detection of unlawful insider trading becomes an arduous

task for humans to examine and identify underlying patterns from the insider’s behavior. On the other hand,

innovative machine learning architectures have shown promising results for analyzing large-scale and complex

data with hidden patterns. One such popular technique is eXtreme Gradient Boosting (XGBoost), the state-of-

the-arts supervised classiﬁer. We, hence, resort to and apply XGBoost to alleviate challenges of identiﬁcation

and detection of unlawful activities. The results demonstrate that XGBoost can identify unlawful transactions

with a high accuracy of 97 percent and can provide ranking of the features that play the most important role in

detecting fraudulent activities.

1 INTRODUCTION

Corporate insiders, in their privileged roles, access

material non-public information (MNPI). While the

Securities Exchange Act of 1934, speciﬁcally Sec-

tion 10b-5

, prohibits utilizing this information for

ﬁnancial gain, detecting violations is challenging.

Insiders often employ creative strategies to conceal

their trading activities. These unlawful trades often

mimic routine transactions (Cohen et al., 2012), mak-

ing them opaque and difﬁcult to identify using tradi-

tional, manually-engineered approaches. Therefore,

effectively uncovering hidden patterns of such activ-

ity within voluminous transaction data requires inno-

vative methodologies that have demonstrated effec-

tiveness (Mayo and Hand, 2022), (Varol et al., 2017).

Historically, research on detecting unlawful in-

sider trading (UIT) has often been grounded in eco-

nomic theories and legal analysis. Kyle’s 1985 pa-

per provided the ﬁrst signiﬁcant theoretical formula-

tion for unlawful insider trading (UIT), applying in-

formation asymmetry—the phenomenon of unequal

information causing market disequilibrium—through

a dynamic model that examines how private infor-

https://orcid.org/0000-0003-3911-3988

https://orcid.org/0000-0002-2291-233X

mation affects prices, market liquidity, and its value

(Kyle, 1985). Following this foundational work,

other studies analyzing information asymmetry in in-

sider trading include Seyhun’s 1986 study (Seyhun,

1986), which investigated insider and outsider trad-

ing proﬁts and the determinants of insiders’ predictive

ability using a large transaction dataset, discussing

implications for market efﬁciency. Rozeff and Za-

man’s 1988 paper (Rozeff and Zaman, 1988) exam-

ined whether publicly available insider trading data

allows outsiders to earn abnormal proﬁts, ﬁnding the

anomaly persists but is largely explained by size and

earnings/price effects when considering transaction

costs. Lin and Howe’s 1990 paper (Lin and Howe,

1990) examined insider trading proﬁtability in the

OTC/NASDAQ market, ﬁnding insiders show timing

ability but high transaction costs preclude outside in-

vestors from earning abnormal proﬁts by mimicking

them, and identifying determinants of insider proﬁts.

Huddart, Hughes, and Levine’s 2007 study (Huddart

and Ke, 2007) investigated the relationship between

insiders’ trades and ﬁrms’ information asymmetry,

analyzing whether proxies for information asymme-

try are associated with insider trading patterns as pre-

dicted by informed trading theories. Finally, Arm-

strong, Jagolinzer, and Pagach’s 2012 paper (Arm-

strong et al., 2012) examined the relationship between

Neupane, K., Griva and I.

An Extreme Gradient Boosting (XGBoost) Trees Approach to Detect and Identify Unlawful Insider Trading (UIT) Transactions.

DOI: 10.5220/0013637500003967

In Proceedings of the 14th International Conference on Data Science, Technology and Applications (DATA 2025), pages 171-181

ISBN: 978-989-758-758-0; ISSN: 2184-285X

171

corporate governance and ﬁrms’ information environ-

ments, ﬁnding that state antitakeover laws were as-

sociated with decreased information asymmetry and

increased ﬁnancial statement informativeness.

Complementing studies on information asymme-

try, scholars have also been motivated by the theory

of liquidity preferences to study unlawful insider trad-

ing. Amihud and Mendelson’s 1987 paper examined

how trading mechanisms affect price behavior and

return patterns, highlighting their impact on market

liquidity (Amihud and Mendelson, 1987). Easley et

al.’s 1996 paper investigated how information-based

trading affects spreads for different stocks, ﬁnding it

contributes to observed differences in market liquid-

ity (Easley et al., 1996). Pagano and Steil’s 1996 pa-

per investigated whether greater transparency in trad-

ing systems enhances market liquidity by reducing

trading costs for uninformed participants (Pagano and

R”oell, 1996). More directly linking insider trading

to liquidity, Cao, Chen, and Shen’s 2004 paper tested

the hypothesis that insider trading impairs market liq-

uidity, ﬁnding that signiﬁcant insider trading around

IPO lockup expirations had little negative effect on ef-

fective spreads and improved other liquidity measures

(Cao et al., 2004).

In addition to economic perspectives, legal schol-

ars have debated whether insider trading should be

fully lawful versus unlawful. Bainbridge’s 2022

paper (Bainbridge, 2022) critically examined the

evolving legal standards applied by Delaware courts

to controlling shareholder transactions, contending

that increased skepticism leads to overregulation and

proposing reforms to reduce costs and encourage in-

vestment. Manne’s foundational 1966 work (Manne,

1966) reexamined the debate on insider trading’s role,

arguing that informed trading facilitates the timely

transmission of valuable information to top managers

and large shareholders, thus contributing to market ef-

ﬁciency.

In contrast to the pro-lawful stance, the opposing

camp argues that insider trading impedes and erodes

investor conﬁdence and increases agency costs, with

research supporting the need for regulation. Gan-

gopadhyay et al.’s 2022 study (Gangopadhyay and

Yook, 2022) found that opportunistic insider trading

proﬁts, particularly from purchases, signiﬁcantly de-

creased following the enactment of the Dodd-Frank

Act, suggesting regulation impacts strategic insider

behavior. Cumming et al.’s 2011 paper (Cumming

et al., 2011) examined stock exchange trading rules

concerning market manipulation, insider trading, and

broker-agency conﬂict across countries and over time,

ﬁnding that differences in these rules signiﬁcantly af-

fect market liquidity.

Detection methods derived from these domains

typically rely on explicitly stated functional rela-

tionships and limited sets of covariates (e.g., vol-

ume, prices, returns, book-to-market, inﬂuence, senti-

ment, and so on) (Jacobs and Weber, 2015), (Fishman

and Hagerty, 1995), (John and Narayanan, 1997),

(Leamer, 1978). These traditional approaches strug-

gle to capture the interactiveness and non-linearities

inherent in data, leading to potential model misspec-

iﬁcations and limited discovery of complex empiri-

cal irregularities. Furthermore, techniques often em-

ployed, such as time-series forecasting are known for

their lack of scalability with increasing data volumes

and can be prone to over-generalization when evalu-

ated on single train/test splits (Hand, 2009), (Ander-

son, 2007), (Ge and Smyth, 2000), (Hamilton, 1989),

(Rabiner and Juang, 1986), (Box et al., 1972).

Addressing the limitations of traditional meth-

ods and the need for innovative approaches, ma-

chine learning (ML) techniques, particularly classi-

ﬁers, represent a promising avenue for detecting com-

plex hidden patterns indicative of UIT (Sundarkumar

and Ravi, 2015), (Louzada and Ara, 2012). In the

context of UIT, numerous studies have leveraged var-

ious classiﬁcation methods to identify potential UIT

based on data from events, news, public information

releases, and transaction patterns (Li et al., 2022),

(Rizvi et al., 2022), (Seth and Chaudhary, 2020), (Is-

lam et al., 2018), (Goldberg et al., 2003).

Among the scalable and data-driven ML tech-

niques successfully applied in this domain are en-

semble methods, such as Random Forest (RF) and

XGBoost. These methods are effective because they

learn and discover empirical regularities directly from

data without requiring pre-deﬁned functional relation-

ships. Both RF and XGBoost have demonstrated suc-

cess in detecting, identifying, and characterizing UIT.

Speciﬁc studies illustrate this success. For instance,

Deng et al. (Deng et al., 2021) implemented RF in

the Chinese Securities Market with 26 features, ac-

curately classifying over 75 percent of UIT. Building

upon this, Neupane et al. (Neupane and Griva, 2024)

extended the feature space to 110 features, achieving

over 95 percent accuracy with RF. Related work has

also utilized XGBoost for this purpose, with an effort

by Deng et al. (Deng et al., 2019) reporting 85 percent

accuracy. Drawing on these consistent and promis-

ing results, the current study utilizes XGBoost, lever-

aging its architectural design for parallel computing

and its iterative process of updating parameters to

strengthen weak learners by implicitly engaging ev-

ery feature. This approach fundamentally addresses

the drawbacks of manual feature engineering, such as

mis-speciﬁcations and omitted features, by inherently

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

172

handling inter-dependencies, multi-dimensionalities,

and non-linearities in data (Malhotra, 2021), (Hou

et al., 2020), (Iskhakov et al., 2020), (Camerer, 2019),

(Fudenberg and Liang, 2019).

This study makes several contributions. First, the

feature space for XGBoost-based UIT detection is ex-

tended from 26 to 110 features to assess the impact

on accuracy. Second, the analysis is based on a sig-

niﬁcantly larger number of transactions from the US

Securities market compared to previous work. Third,

a simpliﬁed parameter search technique is employed

for improved efﬁciency over external optimization

methods. Fourth, using two ranking techniques, dis-

tinct features that play prominent roles in identifying

unlawful trading within a mixed set of institutional,

trade, and ﬁnancial features are identiﬁed, with results

compared both with and without removing correlation

between features.

The manuscript is organized as follows. Section 2

describes the methodology, outlining the theory be-

hind various used techniques, hyper-parameter tun-

ing, performance measures and feature selection cri-

teria. Section 3 describes the experimental settings.

Section 4 includes data description, classiﬁcation re-

sults, and feature ranking. Section 5 discusses the

results and provides conclusions and possible future

directions.

2 PROPOSED METHODOLOGY

To detect UIT, the paper implement XGBoost, a

method well-known for its ability to capture complex

nonlinear interactions in the data, which is a basis for

attaining high out-of-sample accuracy. Designed for

speed and efﬁcient memory management, XGBoost

has demonstrated superior performance across di-

verse applications, including credit scoring (Mushava

and Murray, 2022), fraud detection (Zhang et al.,

2020), consumer credit risk evaluation (Wang et al.,

2022a), DNA sequence identiﬁcation (Sang et al.,

2020), and climate science (Wang et al., 2022b).

Moreover, as an ensemble method, it aligns with tech-

niques considered effective for empirical work in eco-

nomics (Athey, 2019). The approach taken in this

study leverages corporate governance, trade, and ﬁ-

nance data for detecting UIT by extending the ap-

plication of XGBoost to this domain. The method-

ology also integrates Principal Component Analysis

with XGBoost for comparative analysis. For compar-

ison, the results are contrasted with previous studies,

speciﬁcally those by (Deng et al., 2021), (Deng et al.,

2019), and (Neupane and Griva, 2024). These repre-

sent the only publicly available comparative studies in

this area.

2.1 eXtreme Gradient Boosting

(XGBoost)

XGBoost was proposed by (Chen and Guestrin,

2016), which is a highly scalable and powerful algo-

rithm belonging to the gradient boosting family. It

implements a distributed gradient tree boosting strat-

egy, training the model by sequentially learning from

multiple weak classiﬁers and iteratively updates them

to correct errors from preceding steps, while also al-

lowing for efﬁcient memory management. This itera-

tive process combines the updated weak learners into

a powerful ensemble. In summary, XGBoost trains its

model through this iterative boosting process: It starts

with an initial base prediction. Then, in each step, it

calculates the errors (residuals), constructs and ﬁts a

new decision tree to predict these residuals, and adds

the tree to the ensemble to minimize loss. Predictions

are updated, new residuals calculated, and this se-

quence is repeated for a set number of iterations. The

ﬁnal prediction combines the outputs from all trees.

Formally, consider a training dataset, D = (x

)

i=1

where n is the number of instances (rows) and each in-

stance (x

∈ R

) is a vector of m features (columns),

∈ R represents the label for the i-th instance (e.g., 1

for unlawful, 0 for lawful). The predicted value, ˆy

for

the i-th instance from an ensemble model comprising

K decision trees is given by the sum of the predictions

from each tree as in Equation 1.

ˆy

∑

k=1

), f

∈ F, (1)

where f

denotes the k-th decision tree and F is

the functional space containing all possible decision

trees. XGBoost aims to minimize a regularized objec-

tive function Ob j to learn the set of trees f

k=1

. This

objective function combines the training loss and a

regularization term to control model complexity. The

loss function ℓ(y

, ˆy

) measures the difference between

the actual label (y

) and the predicted value ( ˆy

) for

a single instance. The total training loss over the

dataset is the sum of individual instance losses given

by Equation 2.

L(y,

y) =

∑

i=1

ℓ(y

, ˆy

), (2)

where y and

y are the vectors of actual and pre-

dicted labels for all n instances, respectively. The loss

function ℓ can be selected based on the task (e.g.log

loss for classiﬁcation). During training, XGBoost it-

eratively adds trees, optimizing the objective function

An Extreme Gradient Boosting (XGBoost) Trees Approach to Detect and Identify Unlawful Insider Trading (UIT) Transactions

173

with respect to the parameters of the new tree being

added at each step. The regularization term Ω( f

)

for the k-th decision tree f

is calculated based on the

tree’s structure and leaf weights given by Equation 3.

Ω( f

) = γT

∑

j=1

k, j

, (3)

where T

is the number of leaf nodes in the k-th

tree, w

k, j

is the prediction weight of the j-th leaf in

the k-th tree (with (w

k, j

) being its square), (γ) is the

L1 regularization term on the number of leaves, and

(λ) is the L2 regularization term on the leaf weights.

These terms control tree pruning and the magnitude

of leaf weights, respectively. The overall regularized

objective function that XGBoost minimizes is deﬁned

as the sum of the total training loss and a regulariza-

tion term Ω that penalizes the complexity of the trees

given by Equation 4.

Ob j =

∑

i=1

ℓ(y

, ˆy

) +

∑

k=1

Ω( f

), (4)

2.2 Parameter Tuning

Tuning hyperparameters is crucial for many ML tech-

niques, and XGBoost is no exception; it is essential

for minimizing the objective function and controlling

overﬁtting. These parameters, which can be catego-

rized into regularization, pruning, and sampling, in-

ﬂuence the overall prediction errors. For Regulariza-

tion, commonly used hyperparameters are Learning

rate (η) and L2 regularization (λ). η controls the step

size (shrinkage) applied to weights at each boosting

iteration. Smaller η values lead to more conservative

models and require more boosting rounds. λ applies

penalty to the leaf weights based on the sum of their

squares. Increasing λ makes the model more con-

servative. For Pruning, the Minimum split improve-

ment (γ) parameter is used. It acts as a regularization

parameter specifying the minimum loss reduction re-

quired to make a split, thereby controlling tree com-

plexity and preventing overﬁtting. To reduce variance

and improve generalization, Sampling is applied to

data instances or features for each tree or iteration.

In this study, Column sub-sampling and Row sam-

pling are employed. Column sub-sampling refers to

the fraction of features randomly sampled per tree or

per level when building trees, while Row sampling is

the fraction of data instances randomly sampled per

tree or per round.

2.3 Feature Importance

XGBoost’s built-in feature ranking, a key tool for

model interpretation and feature selection, is anal-

ogous to that of RF, as both techniques commonly

use the mean decrease in impurity (Gini Score) dur-

ing training. However, this method is known to

have limitations, such as bias towards correlated and

high-cardinality features, and relies solely on train-

ing data. To provide a more robust ranking, a sec-

ond feature ranking approach was implemented. This

approach involves decorrelating features using hier-

archical clustering and subsequently ranking them

based on permutation importance scores. Permutation

importance is often preferred over MDI as it directly

measures a feature’s impact on model performance on

unseen data and is less susceptible to training-phase

biases. This second approach follows the methodol-

ogy described by (Neupane and Griva, 2024).

2.4 Principal Component Analysis

The analysis in this study employs Principal Com-

ponent Analysis (PCA), a classic unsupervised tech-

nique for data decorrelation and compression. This

method has demonstrated effectiveness in various ap-

plications, notably in studies on UIT (Deng et al.,

2021), (Neupane and Griva, 2024), and the detailed

methodology followed is based on that described by

(Neupane and Griva, 2024).

2.5 Performance Measure

Model performance is evaluated using a 2 × 2 confu-

sion matrix organized by actual and predicted classes,

schematically represented by Table 1. Assuming

‘Lawful’ is the positive class (+) and ‘Unlawful’ is

the negative class (-), the matrix yields four outcomes:

True Positives (TP) for correct positive predictions,

True Negatives (TN) for correct negative predictions,

False Positives (FP) for negative instances incorrectly

predicted as positive, and False Negatives (FN) for

positive instances incorrectly predicted as negative.

From this matrix, metrics like overall accuracy (ACC)

and Precision (PRE) are calculated. ACC measures

the total proportion of correct classiﬁcations, and PRE

(for the positive class) is the proportion of predicted

positives that are truly positive.

3 EXPERIMENTAL SETUP

The experimental settings broadly replicate Neupane

et al. (2024). Data originates from SEC Form 4

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

174

Table 1: Organization of the 2 × 2 grid of confusion matrix

used to measure state of lawfulness of insider trading trans-

actions.

Predicted Label (PP+PN)

Actual

Labels

Total

Population

Positive Negative

Lawful -

Positive

True

Lawful

False

Unlawful

Unlawful -

Negative

False

Lawful

True

Unlawful

ﬁlings, linked with CRSP and Compustat-CapitalIQ

trade and ﬁnance data via personid, cik, and com-

panyid. Comprising 3984 fully labeled transactions

(1992 unlawful) with 110 dimensions per row, the

merged dataset was used alongside a 320-transaction

subset for comparison. Each dataset subset, balanced

(0.5:0.5 ratio) and sub-divided by feature sets (orig-

inal vs. PCA-integrated), was then split deterministi-

cally 80 percent (training): 20 percent (test) for analy-

sis. Numerical features X

(i = 1,...,n) were normal-

ized using the z-score method

, while categorical fea-

tures were one-hot-encoded. Hyperparameters such

as η, γ, max depth, and sample rate were initialized in

a random search space, with tuning conducted over

5 iterations within 5-fold cross-validation. Feature

rankings were derived from MDI (based on training

data) and permutation importance (applied to train-

ing and test data), with the latter’s ﬂexibility allowing

for the ranking of test data even after feature decor-

relation. Correlation was removed by performing hi-

erarchical clustering based on Spearman rank-order

correlation and selecting a representative feature from

each cluster. The experiment was performed with 100

repetitions using scikit-learn and xgboost libraries,

where each repetition involved randomly sampling

lawful transactions.

4 ANALYSIS AND RESULTS

This section reports and interprets the performance of

the implemented methods based on confusion matrix

metrics, drawing upon the dataset characteristics il-

lustrated in Table 2. Performance metrics, averaged

over 100 experiments (Table 4), are presented. Hyper-

parameter tuning was performed to optimize model

performance, involving 5-fold cross-validation and

100 repetitions, using AUC as the stopping criterion.

This process optimized parameters such as ntrees, η,

max depth, γ, and sample rate: for instance, ntrees

was typically optimized to values around 500 to 520,

The z-score transformation standardizes features to

have a mean of 0 and standard deviation of 1, placing pre-

dictors on a common scale (

−µ

) (Gelman, 2008).

Table 2: Distribution of balanced unlawful and randomly

selected lawful transactions. The right-hand side shows a

random subset of this data matching transaction counts from

Deng et al. (2019). Example referenced from Neupane et

al. (2024).

All Trans. Subset of Trans.

Label Sell Pur. Total Sell Pur. Total

Lawful 405 1587 1992 27 133 160

Unlawful 318 1674 1992 26 134 160

Table 3: Performance evaluation metrics for benchmark

methods applied to UIT detection referenced from Deng et

al. 2021, Deng et al. 2019.

Random Forest* XGBoost†

Label ANN SVM Adaboost No

PCA

With

PCA

Classic GA NSGA

ACC 69.57 75.33 74.75 79.01 77.15 77.88 81.77 84.99

FNR 19.21 21.42 26.62 21.97 20.14 22.70 16.43 13.47

FPR 34.07 27.75 24.42 19.57 25.48 21.56 20.10 16.31

TNR 65.93 72.75 75.58 80.43 74.52 78.44 83.69 83.69

TPR 80.79 78.58 73.38 78.03 79.86 77.30 83.57 86.53

PRE - - - - - 78.94 - -

Notes: * (Deng et al., 2019), † (Deng et al., 2021)

max depth often favored values around 16, and η was

right around the default value of 0.03. To compare

the reported metrics, benchmark results from (Deng

et al., 2019) are presented in Table 3.

4.1 Results of Classiﬁcation of Insider

Trading Transactions

Performance varies with transaction count, feature set

size, and PCA integration. The benchmark method

(XGBoost-NSGAII) achieves an accuracy of 84.99

percent (Table 3). In the implemented settings using

320 transactions, the average ACC is 83.105 (Table

4), closely approaching the benchmark. Performance

with 320 transactions improves signiﬁcantly to 89.24

percent ACC when PCA is not integrated. Further-

more, utilizing the full 3984 transactions consistently

leads to improved performance across all feature set

sizes and PCA conditions. For instance, using the full

dataset, ACC averages 90.61 percent, surpassing the

benchmark.

Based on the data illustrated in Table 2, the per-

formance of implemented methods is compiled and

Table 4: Average of the performance metrics of 100 exper-

iments in 5-fold cross-validation. The ﬁrst four columns

are based on 320 random selections from 3984 transactions

matching the count of the previous study.

Subset (n=320) 3984 Trans.

Metric 25 Features 110 Features 25 Features 110 Features

PCA

With

PCA

With

PCA

With

PCA

With

PCA

ACC 83.34 78.79 89.24 81.05 98.12 97.43 99.02 97.96

PRE 84.67 79.38 89.59 80.01 98.19 97.01 97.32 97.32

TPR 81.88 78.7 89.3 83.5 98.05 97.87 98.98 98.64

FNR 18.12 21.3 10.7 16.5 1.95 2.13 1.02 1.36

FPR 15.2 21.12 10.82 21.39 1.8 3.01 0.93 2.71

TNR 84.8 78.88 89.18 78.61 98.2 96.99 99.07 97.29

An Extreme Gradient Boosting (XGBoost) Trees Approach to Detect and Identify Unlawful Insider Trading (UIT) Transactions

175

presented in confusion matrix metrics, averaged over

100 experiments and 5-fold cross-validation (Table

4). To compare the results, those from (Deng et al.,

2021) and (Deng et al., 2019) are compiled in Table

3. Among the benchmarks, XGBoost-NSGAII (last

column of Table 3) achieves an accuracy of 84.99 per-

cent, the highest. Comparatively, in Table 4 that uses

320 transactions, the ACC with 25 features is 83.34

(ﬁrst column of Table 4), a very close result compared

to the benchmark. The performance declines to 78.79

percent when PCA is used in the same setting. But

with the addition of features (110 Features) within the

same settings (320 transactions), the results start ap-

proaching the benchmark’s highest performance. As

the number of transactions is added (3984 transac-

tions), with either limited set of features (25) or addi-

tional (110), the ACC starts improving substantially.

A notable performance increase, averaging 90.61 per-

cent ACC, is observed when using the full 3984 trans-

actions with either 25 or 110 features (with or without

PCA).

Beyond overall accuracy, other key metrics from

the confusion matrix provide further insights into

performance (Table 4). For metrics where higher

values indicate better performance – True Positive

Rate (TPR), True Negative Rate (TNR), and Precision

(PRE) – the implemented method generally demon-

strates competitive or superior results compared to

benchmark methods (Table 3). While the bench-

mark’s best reported TPR, TNR, and PRE are 86.53

percent, 83.69 percent, and 78.94 percent respec-

tively, the implemented method achieves signiﬁcantly

higher values in several scenarios (Table 4). For in-

stance, using all 3984 transactions, TPR averages ap-

proximately 98.38 percent (reaching a high of 98.98

percent), and TNR averages approximately 97.9 per-

cent (reaching a high of 99.07 percent). Consistent

with ACC, TPR and TNR improve with increased

data size.

Conversely, for metrics where lower values indi-

cate better performance – False Positive Rate (FPR)

and False Negative Rate (FNR) – the implemented

method also shows strong results, particularly with

increased data (Table 4). Compared to benchmark

FPRs which average 16.31 percent (Table 3), the im-

plemented method’s FPR averages 17.13 percent with

320 transactions but drops signiﬁcantly to approxi-

mately 2.11 percent with 3984 transactions. Simi-

larly, benchmark FNRs range from 13.47 percent to

26.62 percent (Table 3), whereas the implemented

method’s FNR sees a substantial reduction from

16.66 percent with 320 transactions to a remarkable

1.62 percent with 3984 transactions, highlighting few

missed unlawful transactions with more data. The im-

pact of PCA varies; on average, performance metrics

are better when PCA is not integrated.

A direct comparison was made between the

performance metrics of the implemented XGBoost

method (Table 4) and the Random Forest results

from Table 5 of (Neupane and Griva, 2024), who

used the same experimental conditions. Both mod-

els achieved exceptionally high performance when

trained and evaluated on the full set of 3984 trans-

actions, demonstrating strong accuracy and low error

rates across various conﬁgurations (25/110 features,

with/without PCA). A detailed comparison highlights

key strengths of the implemented XGBoost method.

XGBoost achieves accuracy exceeding 99 percent in

optimal conﬁgurations (Table 4) and demonstrates

remarkably strong control over false negative rates,

reaching a minimum FNR of 1.02 percent, which is

marginally lower than the best Random Forest FNR

(1.07 percent) reported in Table 5 of (Neupane and

Griva, 2024) . This strong performance in minimizing

missed unlawful transactions, alongside high overall

accuracy and robust control over other error rates, po-

sitions XGBoost as a highly effective and potentially

preferred classiﬁer for this task.

4.2 Variable Importance

The strong performance achieved by XGBoost (see

Table 4), which consistently outperformed bench-

mark studies, warrants an investigation into the con-

tributions of individual input features to UIT clas-

siﬁcation. Analyzing these contributions enhances

model explainability and interpretability. Therefore,

to address this common limitation of many ML meth-

ods, feature importance ranking was conducted using

XGBoost’s inbuilt Mean Decrease of Impurity (based

on Gini Scores), a training-data-based technique in-

ﬂuenced by correlation, and permutation importance,

a computationally expensive method that can be ap-

plied to training and test data after decorrelation us-

ing hierarchical clustering and representative feature

selection (see Section 2.3 for details).

Figures 1 and 2 are horizontal bar charts illustrat-

ing feature importance rankings, where the length of

each bar indicates the importance score of a speciﬁc

feature, with features ordered from most important at

the top to least important at the bottom. A longer bar

signiﬁes higher importance according to the speciﬁc

method used. Figure 1 presents features ranked by

MDI scores, while Figure 2 displays the ranking ob-

tained using Permutation Importance before applying

decorrelation. As discussed, MDI-based ranking is

based solely on training data and is known to be par-

ticularly sensitive to highly correlated features, which

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

176

Figure 1: Ranking of the importance of features based on

Mean Decrease in Impurity extracted during training phase

(see (Neupane and Griva, 2024) for details)

are common in ﬁnancial datasets, potentially not gen-

eralizing well to test samples ((Meinshausen, 2008)).

Permutation importance is employed to address these

shortcomings. This model-agnostic method evalu-

ates feature contribution by measuring the decrease in

model performance when a feature’s values are ran-

domly permuted (Nembrini et al., 2018), and impor-

tantly, can be applied to test data, unlike MDI.

Figure 2: Ranking of the importance of features based on

Permutation Importance (see (Neupane and Griva, 2024) for

details).

However, a visual comparison of Figure 1 and Fig-

ure 2 reveals notable differences in the top-ranked

features and their relative importance. While MDI

tends to rank proﬁtability and volatility-related fea-

tures highly (e.g., Return on Asset, Total Volatility),

Permutation Importance before decorrelation ranks

features such as Total Debt to Equity, Excess Re-

turns, and Price Operating Earnings (Basic) as most

important. This discrepancy, highlights that Permuta-

tion Importance is also signiﬁcantly affected by cor-

relation when applied to correlated data. In highly

correlated datasets, permuting one feature might not

signiﬁcantly decrease performance if a highly corre-

lated feature provides redundant information to the

model. Consequently, neither the MDI ranking nor

the Permutation Importance ranking before decorre-

lation provides a fully reliable measure of true feature

importance in this highly correlated ﬁnancial dataset.

This underscores the importance of applying permu-

tation importance after decorrelation for a more accu-

rate assessment.

Figure 3: Hierarchical clustering of features using Spear-

man rank-order correlations visualized by this dendrogram,

showing the relationships and grouping of features based on

similarity.

To mitigate the impact of correlation on feature

ranking, hierarchical clustering was performed based

on Spearman rank correlation, using Ward’s mini-

mum variance linkage and a distance matrix derived

from the correlation matrix. This process is visual-

ized in Figure 3, which shows the resulting dendro-

gram and Figure 4, which displays the correlation ma-

trix as a heatmap. In the heatmap (Figure 4), features

are arranged along both axes, and the color intensity

of each cell indicates the strength of the correlation

between the corresponding features, with darker col-

ors representing stronger positive or negative correla-

tions; the diagonal shows perfect correlation of each

feature with itself. The dendrogram (Figure 3) illus-

trates the hierarchical clustering results; the vertical

branches show how features are merged into clus-

ters based on their distance (indicated on the hori-

zontal axis), with shorter branches connecting more

similar features. Features grouped by branches form

clades. For instance, Price Earnings (basic) and Re-

turn on Equity form a clade, connected together with

An Extreme Gradient Boosting (XGBoost) Trees Approach to Detect and Identify Unlawful Insider Trading (UIT) Transactions

177

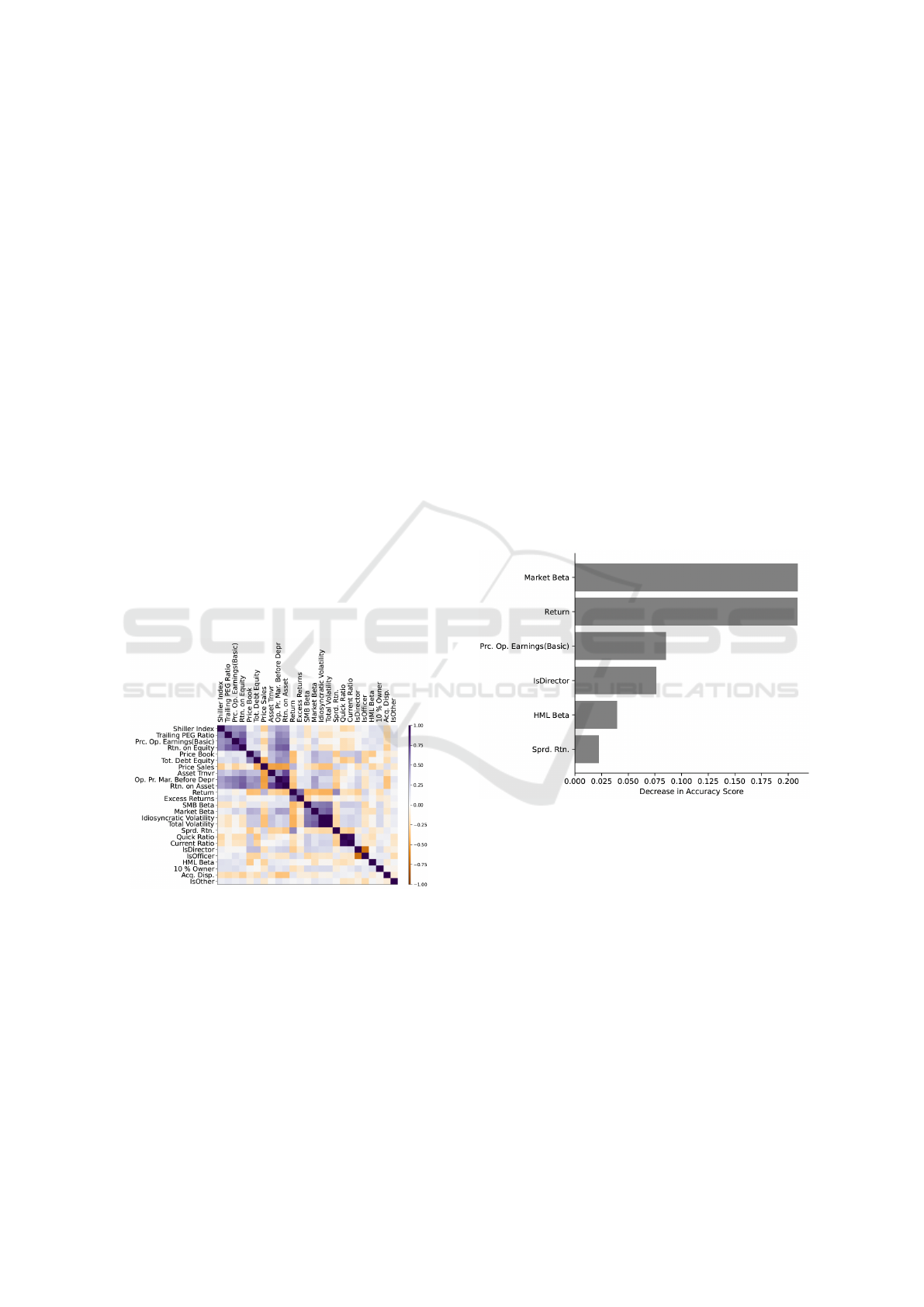
the Trailing PEG Ratio, forming the leftmost clade.

A representative feature was then selected from each

cluster based on these relationships.

Figure 5 illustrate the impact of correlation re-

moval on feature ranking. Figure 2 shows the ranking

obtained using Permutation Importance before decor-

relation, while Figure 5 displays the ranking after hi-

erarchical clustering and representative feature selec-

tion. The ranking in Figure 5 highlights the promi-

nence of features related to market risk, corporate

governance, and valuation. Prominent features in-

clude Market β, Return, Price Operating Earnings

(Basic), and IsDirector. Compared to the ranking be-

fore decorrelation (Figure 2), the analysis after decor-

relation emphasizes features such as Market β and Is-

Director, which hold higher ranks. Price Operating

Earnings (Basic) also appears more inﬂuential after

decorrelation, consistent with its role as an important

gauge for company valuation. The high ranking of

IsDirector indicates the importance of a role on the

company’s board in inﬂuencing UIT. The importance

of market β and value premium features (like HML

β) in this decorrelated context aligns with ﬁnancial

theories, particularly considering the potential insti-

tutional inﬂuence of executives on policies (e.g., divi-

dend policy, (Campbell and Shiller, 1988), (Grinblatt

et al., 1984)).

Figure 4: Spearman Rank-Order Correlation Matrix for Se-

lected Features (Illustrative), visualizing pairwise correla-

tions to aid in identifying groups. In the color gradient, dark

purple represents (perfect positive correlation), and dark or-

ange represents (perfect negative correlation).

A comparative assessment of feature importance

rankings from MDI (Figure 1), Permutation Impor-

tance before decorrelation (Figure 2), and Permuta-

tion Importance after decorrelation (Figure 5) reveals

signiﬁcant differences across the three approaches.

While MDI and Permutation Importance applied be-

fore decorrelation produce differing rankings across

the full feature set, both methods are substantially af-

fected by the presence of highly correlated features

common in ﬁnancial data, leading to potentially mis-

leading importance scores. In contrast, the Permu-

tation Importance ranking after hierarchical cluster-

ing and representative feature selection (Figure 5)

shows a distinct set of prominent features and gen-

erally higher importance scores for a subset of repre-

sentatives. Following decorrelation, features such as

Market β, Return, Price Operating Earnings (Basic),

and IsDirector emerge as highly inﬂuential in Figure

5. Results are consistent with previous studies; the top

features contributing most to the prediction of unlaw-

ful activities are related to ownership, inﬂuence, and

market risk, indicating that daily activities in the capi-

tal market play an important role in determining UIT.

The disparity among the three rankings underscores

the profound impact of correlation on feature impor-

tance measures and highlights why the ranking ob-

tained after decorrelation (Figure 5) provides a more

reliable understanding of true feature contributions by

mitigating the masking effects of correlation.

Figure 5: Ranking of feature importance based on permuta-

tion values after removal of correlation due to hierarchical

clustering. The horizontal axis is the scaled value of rela-

tive importance. The vertical axis represents the variables.

The bars are organized in descending order of the relative

importance.

In summary, the overall results of the supervised

classiﬁer, presented in Table 4, demonstrate strong

performance. To note, the classiﬁer demonstrated a

consistent performance with high true positive and

negatives as well as a low false positive rate (fall out

rate). This is crucial, as wrongfully classifying an un-

lawful transaction as lawful is anecdotally equivalent

to a courtroom acquittal. The obtained false positive

rates, as shown in Table 4, compare favorably against

benchmark methods presented in Table 3, showing the

model successfully minimizes false alarms. Further-

more, XGBoost demonstrates a thorough examina-

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

178

tion of information, leading to low false negative rates

(miss rate), as evident in Table 4. Just as an incorrect

incarceration has high stakes, misclassifying a lawful

transaction as unlawful is critical. The results indicate

XGBoost does not disregard or overlook hidden infor-

mation, resulting in low missing rates. In addition to

controlling false classiﬁcations, the proposed method

produces strong true positive results, correctly identi-

fying lawful transactions. The high ratio of true nega-

tive to negative further conﬁrms the model’s ability to

correctly identify unlawful transactions as unlawful.

XGBoost effectively handles both lawful and unlaw-

ful transactions across different scenarios, even when

the unlawful transactions are unchanged and lawful

ones are randomly sampled (50 percent). The sim-

ple parameter tuning method proved to be an effec-

tive strategy for achieving high accuracy. Finally, the

analysis indicates that decorrelation is impactful; by

decorrelating, corporate and institutional features like

IsDirector gained prominence in the ranking, appear-

ing alongside key trade and ﬁnance features (Sigrist,

2023), (Meinshausen, 2008).

5 CONCLUSIONS AND FUTURE

WORK

In a high-dimensional feature space approach shows

an excellent performance to detect the UIT with ac-

curacy over 97 percent. The reliability of the re-

sults is assured by averaging them from 5-fold cross-

validation. The experiments run 100 times with a new

set of lawful transactions randomly sampled from a

pool of 9.6 millions. Overall, comparing the imple-

mented XGBoost results (Table 4) with Random For-

est results (Table 5 of (Neupane and Griva, 2024)) and

the benchmark methods (Table 3), the implemented

XGBoost method demonstrates high performance for

UIT detection, comparing favorably against the other

methods, notably achieving higher overall accuracy

and remarkably lower false negative rates. Besides,

the results demonstrate that XGBoost provides the

ranking of the features that play the most important

role in identiﬁcation of the UIT. Those features re-

lated to governance, ﬁnancial and trading can be ma-

nipulated by the corporate insiders for personal un-

lawful ﬁnancial gains and naturally contribute to un-

covering fraudulent behaviors. Therefore, the appli-

cation of the advanced supervised machine learning

techniques may have signiﬁcant practical impact on

automated detection of the UIT.

For the future, the credibility of the detection of

UIT can be improved with the help of causality anal-

ysis. (Athey, 2019) emphasizes decision trees are

the most relevant machine learning techniques to ex-

tract underlying causality. As a domain agnostic, an

effective decision trees method designed to handle

large datasets, XGBoost is a promising candidate for

the future explorations. Exploring XGBoost-causality

nexus therefore may provide a high-stake end-to-end

utility and transparency to the SEC’s overall pro-

cess related to the detection of insider trading. Re-

searchers, further, can contribute by studying the re-

lationship between classiﬁcation-causality. Besides,

tying features to an economic, a ﬁnancial and/or an

institutional theory reduces the uncertainty and inex-

plainability of models (Harvey et al., 2016). There-

fore, implementing decision tree methods to explain

the tenets of UIT within the realm of the economic

and/or ﬁnancial theories that includes features ana-

lyzed in this research (25 or 110) or 447 as proposed

by (Hou et al., 2020) is a valuable future direction.

In addition, during the experiments the random grid-

search of the hyper-parameters with a preset of the

lower and upper-bound was implemented that which

may potentially warrant resource waste with grow-

ing features space. In the future, by exposing and

comparing results from the alternative parameter opti-

mization techniques, such as, Bayesian Optimization,

Grid Search, Evolutionary and so on is another av-

enue to follow. Further, apart from the one-hot en-

coding method applied to encode categorical features,

meaningful insights can be extracted by exploiting the

existing relationships with application of more ad-

vanced methods (e.g, target embedding) (Rodr

ıguez

et al., 2018) which remains unexplored in the context

of UIT to the best of current knowledge.

REFERENCES

Amihud, Y. and Mendelson, H. (1987). Trading mecha-

nisms and stock returns: An empirical investigation.

The Journal of Finance, 42.

Anderson, H. M. (2007). New introduction to multiple time

series analysis. Economic Record, 83(260):109–110.

Armstrong, C. S., Balakrishnan, K., and Cohen, D. (2012).

Corporate governance and the information environ-

ment: Evidence from state antitakeover laws. Journal

of Accounting and Economics, 53.

Athey, S. (2019). The Impact of Machine Learning on Eco-

nomics. In The Economics of Artiﬁcial Intelligence:

An Agenda. University of Chicago Press.

Bainbridge, S. M. (2022). Manne on insider trading.

Box, G. E. P., Jenkins, G. M., and MacGregor, J. F. (1972).

Some Recent Advances in Forecasting and Control.

Part II.

Camerer, C. F. (2019). Artiﬁcial Intelligence and Behav-

ioral Economics. In The Economics of Artiﬁcial Intel-

ligence: An Agenda. University of Chicago Press.

An Extreme Gradient Boosting (XGBoost) Trees Approach to Detect and Identify Unlawful Insider Trading (UIT) Transactions

179

Campbell, J. Y. and Shiller, R. J. (1988). The dividend-

price ratio and expectations of future dividends and

discount factors. The Review of ﬁnancial studies,

1(3):195–228.

Cao, C., Field, L. C., and Hanka, G. (2004). Does insider

trading impair market liquidity? evidence from ipo

lockup expirations. Journal of Financial and Quanti-

tative Analysis, 39(1):25–46.

Chen, T. and Guestrin, C. (2016). Xgboost: A scalable

tree boosting system. In Proceedings of the 22nd acm

sigkdd international conference on knowledge discov-

ery and data mining, pages 785–794.

Cohen, L., Malloy, C., and Pomorski, L. (2012). Decoding

inside information. Journal of Finance, 67.

Cumming, D., Johan, S., and Li, D. (2011). Exchange trad-

ing rules and stock market liquidity. Journal of ﬁnan-

cial economics, 99(3):651–671.

Deng, S., Wang, C., Fu, Z., et al. (2021). An intelligent

system for insider trading identiﬁcation in chinese se-

curity market. Computational economics, 57(2):593–

616.

Deng, S., Wang, C., Li, J., et al. (2019). Identiﬁcation of

insider trading using extreme gradient boosting and

multi-objective optimization. Information (Basel),

10(12):367–.

Easley, D., Kiefer, N. M., O’Hara, M., et al. (1996). Liquid-

ity, information, and infrequently traded stocks. The

Journal of Finance, 51.

Fishman, M. J. and Hagerty, K. M. (1995). The mandatory

disclosure of trades and market liquidity. The Review

of ﬁnancial studies, 8(3):637–676.

Fudenberg, D. and Liang, A. (2019). Predicting and under-

standing initial play. The American economic review,

109(12):4112–4141.

Gangopadhyay, P. and Yook, K. (2022). Proﬁts to oppor-

tunistic insider trading before and after the dodd-frank

act of 2010. Journal of Financial Regulation and

Compliance, 30.

Ge, X. and Smyth, P. (2000). Deformable markov model

templates for time-series pattern matching. In Pro-

ceedings of the sixth ACM SIGKDD international con-

ference on knowledge discovery and data mining, Kdd

’00, pages 81–90. Acm.

Gelman, A. (2008). Scaling regression inputs by dividing

by two standard deviations. Statistics in medicine,

27(15):2865–2873.

Goldberg, H. G., Kirkland, J. D., Lee, D., et al. (2003). The

nasd securities observation, new analysis and regula-

tion system (sonar). In Iaai, pages 11–18. Citeseer.

Grinblatt, M. S., Masulis, R. W., and Titman, S. (1984). The

valuation effects of stock splits and stock dividends.

Journal of ﬁnancial economics, 13(4):461–490.

Hamilton, J. D. (1989). A new approach to the economic

analysis of nonstationary time series and the business

cycle. Econometrica, 57(2):357–384.

Hand, D. J. (2009). Forecasting with exponential smooth-

ing: The state space approach by rob j. hyndman, anne

b. koehler, j. keith ord, ralph d. snyder. International

Statistical Review, 77(2):315–316.

Harvey, C. R., Liu, Y., and Zhu, H. (2016). . . . and the

cross-section of expected returns. The Review of Fi-

nancial Studies, 29(1):5–68.

Hou, K., Xue, C., and Zhang, L. (2020). Replicat-

ing anomalies. The Review of ﬁnancial studies,

33(5):2019–2133.

Huddart, S. J. and Ke, B. (2007). Information asymmetry

and cross-sectional variation in insider trading. Con-

temporary accounting research, 24(1):195–232.

Iskhakov, F., Rust, J., and Schjerning, B. (2020). Machine

learning and structural econometrics: contrasts and

synergies. The econometrics journal, 23(3):S81–s124.

Islam, S. R., Khaled Ghafoor, S., and Eberle, W. (2018).

Mining illegal insider trading of stocks: A proactive

approach. In 2018 IEEE International Conference on

Big Data (Big Data), pages 1397–1406, Ithaca. Ieee.

Jacobs, H. and Weber, M. (2015). On the determinants of

pairs trading proﬁtability. Journal of ﬁnancial mar-

kets, 23:75–97.

John, K. and Narayanan, R. (1997). Market manipulation

and the role of insider trading regulations. The Journal

of business (Chicago, Ill.), 70(2):217–247.

Kyle, A. S. (1985). Continuous auctions and insider trading.

Econometrica, 53.

Leamer, E. E. (1978). Speciﬁcation searches: Ad hoc infer-

ence with nonexperimental data. (No Title).

Li, G., Li, Z., Wang, Z., et al. (2022). Identiﬁcation of

insider trading in the securities market based on multi-

task deep neural network. Computational intelligence

and neuroscience, 2022:4874516–9.

Lin, J.-C. and Howe, J. S. (1990). Insider trading in the otc

market. Journal of Finance, 45(4):1273–84.

Louzada, F. and Ara, A. (2012). Bagging k-dependence

probabilistic networks: An alternative powerful fraud

detection tool. Expert Systems with Applications,

39(14):11583–11592.

Malhotra, A. (2021). A hybrid econometric–machine learn-

ing approach for relative importance analysis: pri-

oritizing food policy. Eurasian economic review,

11(3):549–581.

Manne, H. G. (1966). Insider trading and the stock market.

Free Press.

Mayo, D. G. and Hand, D. (2022). Statistical signiﬁcance

and its critics: practicing damaging science, or dam-

aging scientiﬁc practice? Synthese, 200(3):220.

Meinshausen, N. (2008). Hierarchical testing of variable

importance. Biometrika, 95(2):265–278.

Mushava, J. and Murray, M. (2022). A novel xgboost exten-

sion for credit scoring class-imbalanced data combin-

ing a generalized extreme value link and a modiﬁed

focal loss function. Expert Systems with Applications,

202:117233.

Nembrini, S., K

onig, I. R., and Wright, M. N. (2018).

The revival of the Gini importance? Bioinformatics,

34(21):3711–3718.

Neupane, K. and Griva, I. (2024). A random forest approach

to detect and identify unlawful insider trading. arXiv

preprint arXiv:2411.13564.

DATA 2025 - 14th International Conference on Data Science, Technology and Applications

180

Pagano, M. and R”oell, A. (1996). Transparency and liquid-

ity: a comparison of auction and dealer markets with

informed trading. The Journal of Finance, 51(2):579–

611.

Rabiner, L. and Juang, B. (1986). An introduction to hidden

markov models. IEEE ASSP magazine, 3(1):4–16.

Rizvi, B., Attew, D., and Farid, M. (2022). Unsupervised

manipulation detection scheme for insider trading. In

International Conference on Intelligent Systems De-

sign and Applications, pages 244–257. Springer.

Rodr

ıguez, P., Bautista, M. A., Gonzalez, J., and Escalera,

S. (2018). Beyond one-hot encoding: Lower dimen-

sional target embedding. Image and Vision Comput-

ing, 75:21–31.

Rozeff, M. S. and Zaman, M. A. (1988). Market efﬁciency

and insider trading: New evidence. Journal of Busi-

ness, pages 25–44.

Sang, X., Xiao, W., Zheng, H., Yang, Y., and Liu, T. (2020).

Hmmpred: Accurate prediction of dna-binding pro-

teins based on hmm proﬁles and xgboost feature se-

lection. Computational and mathematical methods in

medicine, 2020(1):1384749.

Seth, T. and Chaudhary, V. (2020). A predictive analyt-

ics framework for insider trading events. In 2020

IEEE international conference on big data (Big Data),

pages 218–225. Ieee.

Seyhun, H. (1986). Insiders’ proﬁts, costs of trading, and

market efﬁciency. Journal of ﬁnancial economics,

16(2):189–212.

Sigrist, F. (2023). A comparison of machine learning meth-

ods for data with high-cardinality categorical vari-

ables. arXiv preprint arXiv:2307.02071.

Sundarkumar, G. G. and Ravi, V. (2015). A novel hybrid un-

dersampling method for mining unbalanced datasets

in banking and insurance. Engineering Applications

of Artiﬁcial Intelligence, 37:368–377.

Varol, O., Ferrara, E., Davis, C. A., Menczer, F., and

Flammini, A. (2017). Online human-bot interactions:

Detection, estimation, and characterization. CoRR,

abs/1703.03107.

Wang, K., Li, M., Cheng, J., Zhou, X., and Li, G. (2022a).

Research on personal credit risk evaluation based on

xgboost. Procedia computer science, 199:1128–1135.

Wang, S., Peng, H., Hu, Q., and Jiang, M. (2022b). Anal-

ysis of runoff generation driving factors based on hy-

drological model and interpretable machine learning

method. Journal of Hydrology: Regional Studies,

42:101139.

Zhang, Y., Tong, J., Wang, Z., and Gao, F. (2020). Customer

transaction fraud detection using xgboost model. In

2020 International Conference on Computer Engi-

neering and Application (ICCEA), pages 554–558.

IEEE.

An Extreme Gradient Boosting (XGBoost) Trees Approach to Detect and Identify Unlawful Insider Trading (UIT) Transactions

181