SportPoseNet: Leveraging Pose Estimation and Deep Learning for

Sports Activity Classiﬁcation

Saakshi M V, Dhanya Rao, Nidhi M, Anurag Hurkadli and Sneha Varur

KLE Technological University, Hubballi, Karnataka, India

Keywords:

Pose Estimation, Sports Classiﬁcation, MediaPipe, ResNet, Keypoint Detection, Activity Recognition, Sports

Recognition, Pose-Based Classiﬁcation, Image Classiﬁcation, Sports Activity Detection.

Abstract:

SportPoseNet is designed to recognize and classify sports activities by combining advanced pose estimation

techniques with the powerful ResNet-200 architecture. To support this effort, we curated a custom sports

dataset tailored speciﬁcally for training and evaluation purposes. By utilizing MediaPipe, the system accu-

rately extracts keypoints to create pose landmarks that represent a wide range of sports activities.These pose

landmarks are then processed by a ﬁne-tuned ResNet-200 model, which achieves an impressive validation

accuracy of 92.67. The system is capable of classifying activities like cricket, badminton, hockey, and football

with remarkable precision. By blending the lightweight and efﬁcient pose estimation capabilities of Medi-

aPipe with the robust performance of ResNet-200, SportPoseNet provides a scalable and accurate solution

for real-time sports activity recognition. This approach not only demonstrates the power of custom datasets

and cutting-edge technologies in sports analysis but also paves the way for improved athlete monitoring and

performance insights.

1 INTRODUCTION

The rapid advancement of machine learning has

brought remarkable progress in human pose estima-

tion and activity recognition. Pose estimation, which

involves identifying and analyzing key points of the

human body, such as joints, plays a crucial role in ap-

plications across sports, healthcare, and ﬁtness. By

accurately capturing human movement, it provides

valuable insights that can help improve performance

and ensure safety during physical activities. However,

many existing systems struggle to meet the demands

of real-time applications, especially in dynamic en-

vironments like sports, where precision, speed, and

usability are essential. This highlights the need for

a more robust and practical solution. One of the

main challenges in current pose estimation systems

is the lack of accessible and user-friendly tools that

can provide real-time feedback on posture and move-

ment (Garg, Saxena et al. 2023). Many conventional

systems either fall short in delivering the accuracy

needed for precise activity classiﬁcation or are too

computationally intensive to function in real-time set-

tings. This gap underscores the need for a more efﬁ-

cient and reliable system that can address these lim-

itations while remaining practical for everyday use.

To tackle these challenges, this research introduces a

system that combines the power of the ResNet-200

(Khosla, Teterwak, et al. 2020) architecture with

advanced pose estimation techniques to deliver efﬁ-

cient pose classiﬁcation and correction. ResNet-200,

renowned for its strong feature extraction and classi-

ﬁcation capabilities, is ﬁne-tuned to meet the speciﬁc

demands of human activity recognition. Addition-

ally, the system utilizes MediaPipe for pose detection,

ensuring accurate and lightweight landmark extrac-

tion. By integrating these technologies with a custom

sports dataset, the proposed framework adapts seam-

lessly to a variety of sports activities, delivering high

precision and real-time performance while paving the

way for improved analysis and feedback in sports and

ﬁtness applications.

A key achievement of this work is the devel-

opment of a custom dataset speciﬁcally tailored for

sports activity recognition. Unlike generic datasets,

this collection includes a diverse range of sports ac-

tivities, allowing the system to accurately learn and

classify poses across various disciplines. To comple-

ment this, we have designed a specialized pipeline

that seamlessly integrates pose estimation and activity

M V, S., Rao, D., M, N., Hurkadli, A. and Varur, S.

SportPoseNet: Leveraging Pose Estimation and Deep Learning for Sports Activity Classiﬁcation.

DOI: 10.5220/0013632600004664

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 3rd International Conference on Futuristic Technology (INCOFT 2025) - Volume 3, pages 581-588

ISBN: 978-989-758-763-4

581

classiﬁcation for each sport. This not only enables the

detection of human poses (Lugaresi, Tang et al. 2019)

but also categorizes them into speciﬁc sport-related

activities, offering valuable insights for analyzing per-

formance and improving posture. The primary goal of

this research is to create a system that can accurately

estimate human poses, classify them into predeﬁned

categories, and provide real-time feedback for pos-

ture correction. By addressing the limitations of ex-

isting methods, this work introduces a scalable and

user-friendly solution that is both efﬁcient and practi-

cal. With a strong focus on sports applications, (Lu-

garesi, Tang et al. 2019) such as activity classiﬁca-

tion and posture monitoring, this system holds great

potential to enhance performance analysis and help

prevent injuries, paving the way for smarter and more

effective training tools. The paper is organized as

follows: Section II provides a detailed background on

the pose estimation techniques used in this research,

including MediaPipe and models. Section III explains

the methodology, discussing the dataset and approach

used to develop the system. Section IV presents the

results and analysis of the model’s performance. Sec-

tion V concludes the study, summarizing the key ﬁnd-

ings. Section VI outlines the future scope, suggesting

potential improvements and applications. Section VII

lists the references cited in this research. Finally, Sec-

tion VIII acknowledges the contributions and support

received during the study.

2 BACKGROUND STUDY

2.1 ResNet-200 Model

To delve deeper into the utility and effectiveness of

ResNet-200, it’s important to ﬁrst understand the

challenges associated with very deep networks. As

neural networks become deeper, the optimization pro-

cess becomes increasingly difﬁcult due to issues like

vanishing gradients, where gradients during back-

propagation diminish as they propagate through the

network. This makes it harder for earlier layers to ad-

just their weights properly, leading to slow or ineffec-

tive training. Additionally, as networks grow deeper,

they are more prone to overﬁtting and difﬁculty gen-

eralizing to unseen data. ResNet (Khosla, Teterwak,

et al. 2020) addresses these challenges by introducing

the concept of residual connections, which allows the

network to learn the residual mapping rather than the

direct mapping. Residual connections are essentially

shortcut paths that allow the input x of a layer to by-

pass certain transformations and be added directly to

the output. This mechanism ensures that the network

does not need to learn the identity function explicitly,

making it easier to train and enabling it to maintain

the ﬂow of gradients, which is especially crucial in

very deep networks like ResNet-200.

The mathematical formula that describes the

residual block is:

y = F(x) + x (1)

Here, F(x) is the function representing the trans-

formation applied by the convolutional layers, and x

is the original input to the block. The addition of x

to F(x) allows the network to learn the residual (the

difference between the output and the input), rather

than trying to learn the full transformation. This ap-

proach makes it easier for the network to learn, as

it only needs to focus on learning small corrections

or residuals, rather than the entire function. When

considering the deeper ResNet-200 model, this design

principle allows the network to stack a large number

of layers—up to 200—without suffering from (Wang,

Jiang et al. 2017) performance degradation. The

residual connections allow the gradients to ﬂow more

effectively during training, even through hundreds of

layers, because the skip connections ensure that the

gradients are propagated without becoming too small.

This is particularly important for training deep net-

works, where traditional architectures would struggle

to maintain gradient magnitudes across many layers.

The effectiveness of the residual connections can

be further understood by looking at the backpropaga-

tion process. When computing gradients for a resid-

ual block, the gradient of the loss with respect to the

input x is :

∂L

∂x

∂L

∂y

∂x

∂L

∂y



1 +

∂F(x)

∂x



(2)

This equation highlights that the gradient ﬂowing

through the shortcut connection (identity mapping) is

always 1, ensuring that the gradient is never com-

pletely diminished. This is in stark contrast to tra-

ditional deep networks, where gradients can become

very small as they are propagated back through many

layers, leading to what is called the vanishing gradient

problem.

In practice, the residual block structure enables

very deep networks, like ResNet-200, to be trained

more effectively and efﬁciently. The additional lay-

ers allow the network to learn increasingly complex

hierarchical features. For example, in image classi-

ﬁcation tasks, shallow layers might learn basic fea-

tures like edges, while deeper layers in the network

can learn more complex representations, such as tex-

tures or object parts. By utilizing residual connec-

tions, ResNet-200 (He, Zhang, et al. 2016) can ef-

INCOFT 2025 - International Conference on Futuristic Technology

582

fectively train these deeper representations without

facing the difﬁculties that typically arise with tradi-

tional deep networks. Another key beneﬁt of resid-

ual networks is that they are less prone to overﬁtting

compared to traditional deep networks. The residual

connections allow for a more direct and efﬁcient ﬂow

of information, which reduces the risk of overﬁtting

the data. This is particularly important in large-scale

tasks such as object recognition and classiﬁcation on

high-dimensional datasets like ImageNet.

Output = ResNet-200(x) = F(x) + x (3)

ResNet-200’s ability to train deep networks with

hundreds of layers is largely due to the introduction of

residual connections (Wang, Jiang et al. 2017). These

connections enable the network to focus on learning

residuals (corrections to the input), rather than learn-

ing the full transformation at each layer. As a result,

ResNet-200 avoids the vanishing gradient problem,

stabilizes the gradient ﬂow during backpropagation,

and allows for effective learning of complex features

even in very deep architectures. This makes ResNet-

200 (Khosla, Teterwak, et al. 2020) a powerful model

for tasks requiring large-scale feature extraction, such

as image classiﬁcation, object detection, and even in

other domains such as natural language processing.

2.2 MediaPipe

MediaPipe is a powerful, cross-platform machine

learning framework developed by Google. It facili-

tates the deployment of machine learning (ML) mod-

els across various devices and platforms with real-

time processing capabilities. By offering a set of pre-

built pipelines for tasks like human pose estimation,

object detection, and face tracking, MediaPipe (Lu-

garesi, Tang et al. 2019) simpliﬁes the integration

of ML solutions into applications. Initial Convolu-

tion and Pooling Layer The network begins with a

7×7 convolution layer with a stride of 2, followed

by batch normalization and a ReLU activation. This

layer extract low level features like edges and textures

from the input image. Itis immediately followed by

a 3×3 max-pooling layer, reducingthe spatial dimen-

sions while retaining critical features.

The pipeline Architecture. Directed Acyclic

Graph (DAG): MediaPipe (Lugaresi, Tang et al.

2019) pipelines are structured as directed acyclic

graphs, where each node (calculator) performs

a task.Input Nodes: Responsible for feeding

raw data (e.g., images, video streams) into the

pipeline.Processing Nodes: Handle tasks like pre-

processing, feature extraction, and inference.Output

Figure 1: Human Pose Keypoint Diagram with 33 annotated

points representing major body joints and features like the

nose, eyes, ears, and limbs.

Nodes: Render results such as overlays or numerical

outputs for further processing.The pipeline for Pose

Estimation:

Input Video → Preprocessing → Keypoint Detec-

tion → Postprocessing → Rendering

MediaPipe provides a robust pose estimation

pipeline capable of detecting 33 keypoints on the

human body.Methodology:Utilizes a two-stage pro-

cess involving a detector for rough localization

and a reﬁner for precise keypoint detection.Outputs

a 3D skeleton overlayed on the video/image in-

put.Applications: Fitness tracking, gaming, aug-

mented realityThe extracted pose (Lugaresi, Tang et

al. 2019) keypoints are split into two sets: one

for training and the other for validation.This divi-

sion ensures the model can learn effectively while be-

ing evaluated on unseen data to measure its perfor-

mance. The ResNet200 model processes the pose

(Wang, Tan et al. 2021) data through a hierarchi-

cal feature extraction pipeline:The stage 1 includes

convolutional layers, batch normalization, ReLU ac-

tivation, and max pooling to detect fundamental spa-

tial features.The stages 2–5 includes sequential con-

volutional and identity blocks progressively reﬁne

these features, identifying higher-order patterns rele-

vant to speciﬁc sports activities.The skip connections

in ResNet200 alleviate vanishing gradient issues, en-

suring efﬁcient learning in deeper networks.An aver-

age pooling layer compresses the spatial dimensions

of the feature maps, followed by a ﬂattening layer to

convert the data into a 1D vector.A fully connected

(FC) layer processes the vector for classiﬁcation.The

ResNet200 model learns to associate unique pose pat-

terns with speciﬁc sports activities based on the train-

ing data.

SportPoseNet: Leveraging Pose Estimation and Deep Learning for Sports Activity Classiﬁcation

583

3 METHODOLOGY

3.1 Data Design and Preparation

The dataset used in this project consists of 1,010 im-

ages, representing ﬁve different sports: Badminton,

Cricket, Football, Hockey, and Shooting. These im-

ages were carefully selected to capture a wide range

of poses and actions typical of each sport, ensuring

diversity and variety in the data. The images were

organized into individual folders for each sport, with

each folder containing images corresponding to one

speciﬁc category. The dataset was split (Garg, Sax-

ena et al. 2023) into training and validation sets, with

80percent of the images allocated for training and the

remaining 20percent for validation.

TABLE 1: Dataset Distribution.

sports Dataset Images

Badminton 200

Cricket 210

Football 200

Hockey 200

Shooting 200

To improve the model’s ability to generalize, data

augmentation techniques were applied to the training

set. These included resizing the images to 224x224

pixels, performing random horizontal ﬂips, rotating

images by up to 15 degrees, and adjusting the bright-

ness, contrast, and hue of images. These augmenta-

tion (Kim, Choi et al. 2023)s helped simulate real-

world variability, improving the model’s robustness to

different camera angles and lighting conditions. Fur-

thermore, the images were normalized using standard

mean and standard deviation values from the Ima-

geNet dataset, facilitating the transfer of learned fea-

tures from the pretrained ResNet-200 model to this

custom sports dataset.

In addition to data augmentation, class imbal-

ance was addressed by computing class weights using

the compute-class-weight function from scikit-learn.

This ensured that the model was more sensitive to un-

derrepresented classes, helping to mitigate the impact

of class imbalance on the training process.

Pose Estimation and Classiﬁcation:

One of the key contributions of this project is the

creation of our own dataset and the implementation

of pose estimation and classiﬁcation. The custom

dataset allowed us to focus on the speciﬁc poses and

actions relevant to the ﬁve sports categories (Gamra

and Akhlouﬁ, 2021), and it was designed to train a

model that could identify sports based on pose recog-

Figure 2: Sample dataset images for badminton, cricket,

football, hockey and shooting.

nition. Pose estimation was used to recognize the

human body’s key landmarks in the images, such as

limbs, joints, and body positions, which are critical

for classifying the speciﬁc sport being performed.

Through the application of pose estimation, the

model learned to identify unique sport-related pos-

tures, which were then used for accurate sport clas-

siﬁcation. By leveraging deep learning models like

ResNet-200, which were ﬁne-tuned on the custom

dataset, we were able to perform pose-based classi-

ﬁcation. This means that the model didn’t just iden-

tify the presence of a sport, but also correlated spe-

ciﬁc poses or actions with the respective sports. This

dual focus on pose estimation and classiﬁcation en-

hanced the model’s ability to generalize (Lin, Jiao et

al. 2023) across varied poses and visual contexts,

making it more adaptable to real-world applications

where poses can vary widely based on the athlete’s

position or the camera angle.

Model Architecture and Training:

Figure 3: Architecture of proposed approach for human

pose estimation.

The core of the model architecture is based on

ResNet-200, a deep convolutional neural network

(CNN) that is known for its ability to handle very

deep architectures without suffering from the van-

ishing gradient problem. ResNet-200 uses residual

connections or skip connections that allow the gradi-

ents to bypass certain layers during backpropagation,

ensuring that the network can learn effectively even

with hundreds of layers. This makes ResNet-200 par-

ticularly well-suited for complex image classiﬁcation

tasks such as sports pose recognition.

The ResNet-200 model was used without pre-

trained weights, allowing it to be ﬁne-tuned speciﬁ-

cally for the sports pose classiﬁcation task. To retain

INCOFT 2025 - International Conference on Futuristic Technology

584

the knowledge learned from the pretraining on Ima-

geNet, the early layers of the model were frozen, and

only the ﬁnal layers were unfrozen for ﬁne-tuning.

The model’s ﬁnal fully connected layer (Wang, Tan et

al. 2021) was modiﬁed to match the number of classes

in the dataset, which is 5 (corresponding to the ﬁve

sports categories). During training, the Cross-Entropy

Loss function was used to measure the difference be-

tween the predicted outputs and the true labels. Since

the dataset might exhibit class imbalance, the class

weights were incorporated into the loss function to

give higher penalties for misclassifying underrepre-

sented classes. The optimizer used was Adam, which

adapts the learning rate during training, and the learn-

ing rate was further adjusted using a scheduler that re-

duces it when the validation accuracy plateaus. This

helped to improve convergence and prevent overﬁt-

ting.

Key Concepts and Theories:

A key concept used in this project is transfer learn-

ing, which involves taking a model pretrained (Song,

Yu et al. 2021) on a large dataset (like ImageNet)

and ﬁne-tuning it for a more speciﬁc task, such as

sports pose classiﬁcation. Transfer learning allows

the model to leverage learned features like edges, tex-

tures, and basic shapes, which are useful for various

image classiﬁcation tasks. This reduces the amount of

training data needed and accelerates the training pro-

cess. The Residual Networks (ResNet)(He, Zhang, et

al. 2016) architecture is based on the idea of residual

learning, where the model learns to predict the dif-

ference between the output and the input, rather than

learning the output directly. Mathematically, this is

expressed as:

y = F(x, {W

}) + x

where x is the input, F(x, {W

}) is the transforma-

tion applied by the residual block, and y is the out-

put.These residual connections help solve the vanish-

ing gradient problem by ensuring that gradients can

ﬂow directly through the network, even in deep mod-

els.

Another critical concept is data augmentation,

which is used to artiﬁcially increase the size of the

training dataset (Li, Yang et al. 2022) by applying

random transformations to the original images. This

technique is particularly important when the dataset

is small, as it prevents overﬁtting by providing the

model with more diverse examples.

Finally, class weighting is used to adjust the loss

function in the case of class imbalance. The class

weights are computed based on the frequency of each

class in the dataset (Gamra and Akhlouﬁ, 2021) and

are incorporated into the loss function. This ensures

that the model places more emphasis on learning the

underrepresented classes, which helps mitigate the

bias that can occur if certain classes dominate the

training process.

3.2 Algorithm

Input: Images with 2D keypoints detected

using Mediapipe, Pre-trained ResNet-200

model.

Output: Predicted poses or actions for each

image.

Preprocess Input Images: Extract 2D

keypoints using Mediapipe and save

structured data for training/testing.

Setup Model: Load the pre-trained

ResNet-200 model and ﬁne-tune it for pose

classiﬁcation.

Prepare Dataset: Split the dataset into

training and validation sets, apply data

augmentation, and normalize images.

Train the Model: Use weighted

cross-entropy loss, optimize with Adam,

and monitor training loss and validation

accuracy.

Validate the Model: Compute validation

accuracy and save model weights if

accuracy improves.

Test the Model: Predict class of test images

using preprocessing steps and forward pass

through the ResNet model.

Visualize Results: Display test images with

predicted classes and highlight errors for

analysis.

Deploy the Model: Save the trained model

and implement a prediction function for new

images or videos.

Algorithm 1: :Pose Estimation and Classiﬁcation Sys-

tem

The ResNet With Mediapipe (Lugaresi, Tang et

al. 2019) to achieve accurate classiﬁcation of Sport

poses. The input layer consistes of differnt sport ac-

tivity images where each image consists of one human

subject. Then the mediapipe is employed to extract

2D keypoints from each input image.

The Algorithm provides a comprehensive

overview of the SportPoseNet framework, designed

to classify various sports activities by leveraging

human pose estimation and deep learning (Zheng,

Wu et al. 2023). This architecture is meticulously

structured to process images of athletes engaged in

diverse sports, effectively distinguishing activities

SportPoseNet: Leveraging Pose Estimation and Deep Learning for Sports Activity Classiﬁcation

585

based on body posture, movement patterns, and

visual cues.The system begins with input images

representing athletes in different sports, such as

badminton, cricket, football, hockey, and shooting.

These images are diverse in angles, lighting con-

ditions, and action postures to ensure generalizability.

The Mediapipe pose estimation module is applied to

the input images. It extracts keypoints corresponding

to various joints and skeletal landmarks, 1 - nose, 2

- left eye 3 - right eye, 4 - left ear, 5 - right ear, 6 -

mouth (left), 7 - mouth (right), 8 - left shoulder, 9 -

right shoulder, 10 - left elbow, 11 - right elbow, 12

- left wrist, 13 - right wrist, 14 - left hip, 15 - right

hip, 16 - left knee, 17 - right knee, 18 - left ankle, 19

- right ankle, 20 - left heel, 21 - right heel, 22 - left

foot and 23 - right foot.The resulting skeleton over-

lay maps each athlete’s body posture and movement,

creating a structured representation of their physical

activity. This simpliﬁes the complexity of raw im-

age data while preserving essential spatial and angu-

lar information.For interpretability, the system over-

lays keypoint detections on the input images, high-

lighting the athlete’s posture and the corresponding

skeletal structure. This visualization helps validate

the model’s predictions by showing the body poses

that inﬂuenced the decision.

4 RESULTS AND ANALYSIS

In this section, we present the performance of our

deep learning model for 2D human pose classiﬁca-

tion. The model was evaluated on a test set, and sev-

eral evaluation metrics were calculated, including ac-

curacy, precision, recall, and F1-score. (Lin, Jiao et

al. 2023) Additionally, we present the confusion ma-

trix and the training/validation accuracy over epochs.

The performance metrix of Resnet50 Model is as be-

low table:

TABLE 2:Performance Metrics.

Metric Value

Training accuracy 95.26%

Validation accuracy 92.67%

The model achieved an accuracy of 92.67% on the

test dataset. A detailed classiﬁcation report, including

precision, recall, and F1-score for each class, is shown

below:

TABLE 3: Classiﬁcation Performance Metrics.

Category Precision Recall F1-Score

Badminton-images 0.97 0.97 0.97

Football-images 0.93 0.78 0.85

Hockey-images 0.67 0.50 0.57

Cricket-images 0.89 1.00 0.94

Shooting-images 1.00 1.00 1.00

Accuracy 0.92

Macro avg 0.89 0.85 0.87

Weighted avg 0.91 0.92 0.91

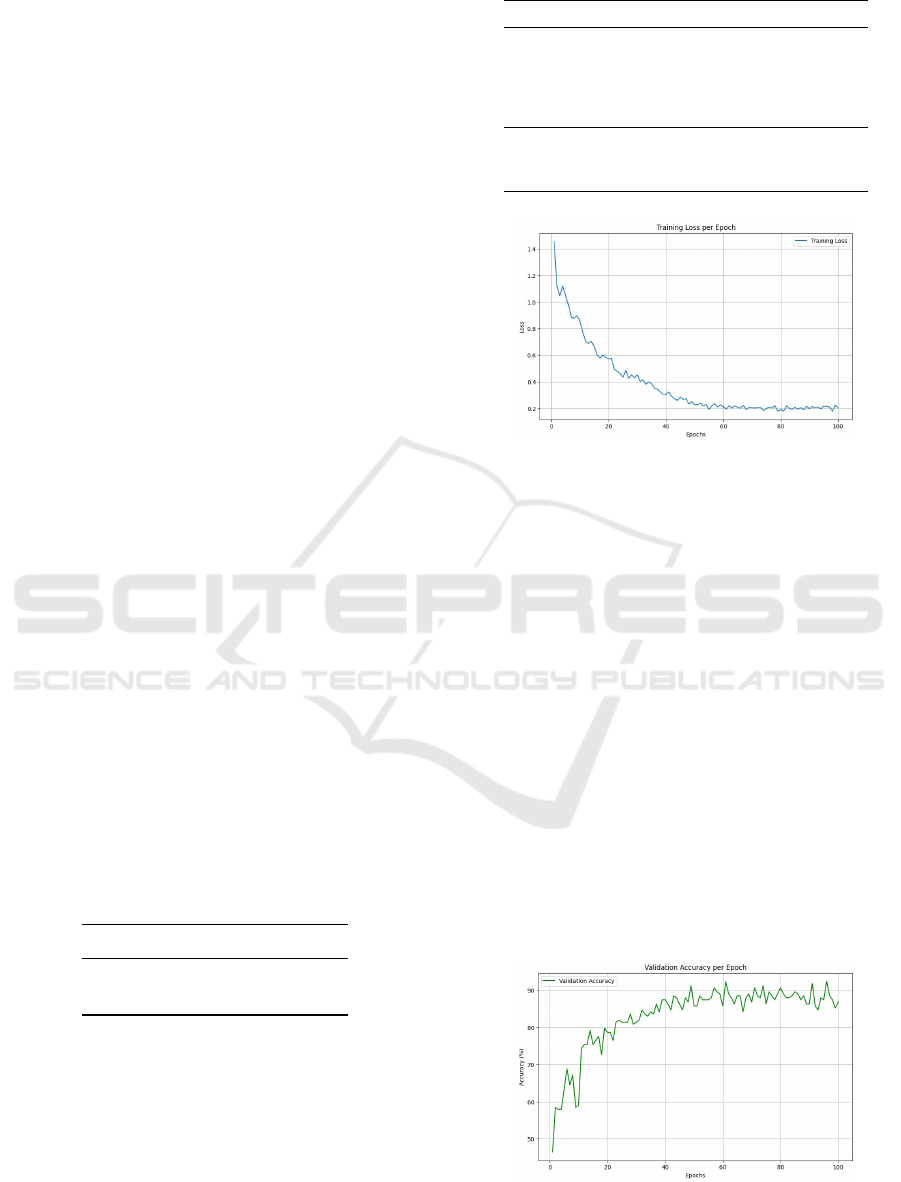
Figure 4: Training Loss per Epochs.

4.1 Training and Validation Accuracy

The ﬁrst graph illustrates the training loss per epoch,

providing insights into the model’s learning progress

over 100 epochs. At the start, the loss is signiﬁ-

cantly high, approximately 1.4, which is expected as

the model begins with random or unoptimized param-

eters. During the initial 20 epochs, the loss rapidly

declines, reﬂecting the model’s ability to capture fun-

damental patterns in the training data. Beyond this

point, the reduction in loss becomes more gradual,

with smaller improvements as the model ﬁne-tunes its

parameters. By the ﬁnal epochs, the loss stabilizes

around 0.2, signifying that the model has achieved

(Wang, Jiang et al. 2017) convergence and is no

longer making signiﬁcant errors. The smooth decline

without sudden spikes or oscillations suggests that the

training process is stable, the optimizer is functioning

effectively, and the model avoids overﬁtting or stag-

nation.

Figure 5: Validation Accuracy per Epochs.

INCOFT 2025 - International Conference on Futuristic Technology

586

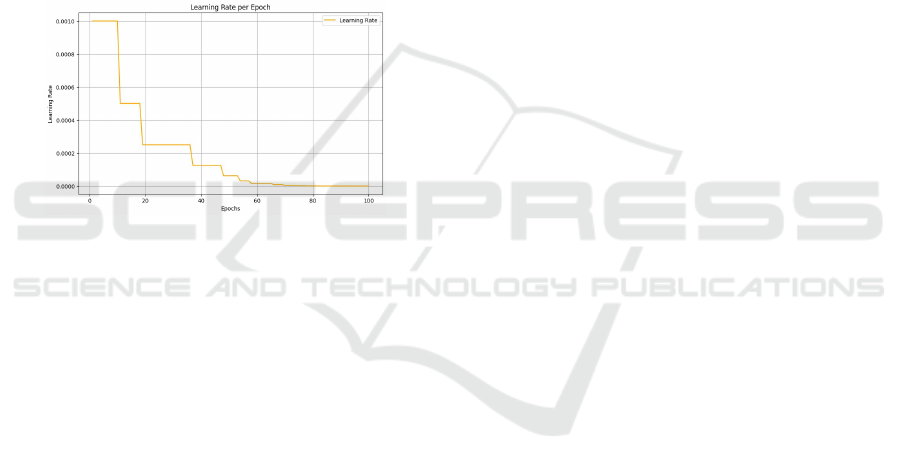
The second graph displays the learning rate per

epoch, showcasing how the learning rate dynamically

adjusts throughout the training process. It begins

with a relatively high value of 0.001, which allows

the model to make large updates to its parameters,

enabling a swift reduction in training loss. Around

epoch 10, the learning rate decreases signiﬁcantly,

marking the start of a more cautious phase of learn-

ing. Further reductions occur around epochs 30 and

50, leading to smaller and more precise updates to

the model’s weights. By the ﬁnal epochs, the learn-

ing rate approaches near-zero values, ensuring sta-

bility and preventing over-adjustment of the weights.

This schedule reﬂects a well-designed training strat-

egy, balancing rapid initial optimization with careful

reﬁnement in later stages, ultimately contributing to

the model’s successful convergence.

Figure 6: Learning Rate Per Epochs.

The graph illustrates the progression of valida-

tion accuracy over 100 training epochs, showcasing

how the model’s performance improves and stabilizes

as training progresses. Initially, the validation accu-

racy begins around 50percent, reﬂecting the model’s

limited ability to generalize to unseen data in its un-

trained state. In the ﬁrst 20 epochs, there is a steep and

rapid rise in accuracy, reaching approximately 80per-

cent. This indicates that the model is quickly learn-

ing meaningful patterns in the data during the early

stages of training.Beyond epoch 20, the improvement

becomes more gradual, with the accuracy continuing

to rise and ﬂuctuating around 90percent (Zheng, Wu

et al. 2023) for the remainder of the training. These

oscillations in validation accuracy are a natural out-

come of the training process, possibly inﬂuenced by

the inherent noise in the data or the stochastic nature

of the optimization algorithm. Despite these ﬂuctua-

tions, the trend remains consistently high, suggesting

that the model has achieved a strong ability to gener-

alize.

5 CONCLUSION AND FUTURE

SCOPE

To summarize, this study highlights the successful

application of ResNet-200 for accurate classiﬁcation

of sports activities, demonstrating its potential in ad-

vancing (Singh, Kumbhare et al. 2021) sports an-

alytics and training methodologies. The integration

of pose estimation and deep learning enables precise

recognition of actions, paving the way for enhanced

performance monitoring and personalized coaching.

Future advancements may focus on optimizing model

efﬁciency for real-time applications and expanding

its scope to diverse (Song, Yu et al. 2021) physical

activities, including rehabilitation and ﬁtness track-

ing. This work underscores the transformative role of

technology in sports, promoting innovation in train-

ing practices and fostering a data-driven approach to

athletic performance improvement.

Future work for this system involves optimiz-

ing the pose estimation model for real-time applica-

tions using lightweight architectures and deploying it

on mobile platforms for broader accessibility (Wang,

Jiang et al. 2017). Enhancing the model’s accuracy

with diverse datasets and advanced techniques like at-

tention mechanisms will improve its ability to gener-

alize across various sports activities. Integrating real-

time feedback systems, collaborating with sports ex-

perts for custom datasets, and extending the applica-

tion to rehabilitation and training assistance are key

next steps. Additionally, deploying the system on

cloud platforms can enable remote coaching and an-

alytics, promoting technology-driven sports training

and activity monitoring.

REFERENCES

K. He, X. Zhang, S. Ren, and J. Sun, ”Identity mappings in

deep residual networks,” in Computer Vision–ECCV

2016: 14th European Conference, Amsterdam, The

Netherlands, October 11–14, 2016, Proceedings, Part

IV 14, pp. 630–645, 2016.

P. Khosla, P. Teterwak, C. Wang, A. Sarna, Y. Tian, P. Isola,

A. Maschinot, C. Liu, and D. Krishnan, ”Supervised

contrastive learning,” in Advances in Neural Informa-

tion Processing Systems, vol. 33, pp. 18661–18673,

2020.

F. Wang, M. Jiang, C. Qian, S. Yang, C. Li, H. Zhang,

X. Wang, and X. Tang, ”Residual attention network

for image classiﬁcation,” in Proceedings of the IEEE

Conference on Computer Vision and Pattern Recogni-

tion, pp. 3156–3164, 2017.

J.-W. Kim, J.-Y. Choi, E.-J. Ha, and J.-H. Choi, ”Human

pose estimation using mediapipe pose and optimiza-

SportPoseNet: Leveraging Pose Estimation and Deep Learning for Sports Activity Classiﬁcation

587

tion method based on a humanoid model,” Applied

Sciences, vol. 13, no. 4, p. 2700, 2023.

C. Lugaresi, J. Tang, H. Nash, C. McClanahan, E. Uboweja,

M. Hays, F. Zhang, C.-L. Chang, M. G. Yong, J. Lee,

W.-T. Chang, W. Hua, M. Georg, and M. Grundmann,

”MediaPipe: A Framework for Building Perception

Pipelines,” arXiv preprint arXiv:1906.08172, 2019.

[Online]. Available: https://arxiv.org/abs/1906.08172

K.-Y. Chen, J. Shin, M. Md, M. M. Hasan, J.-J. Liaw, Y.

Okuyama, Y. Tomioka, ”Fitness Movement Types and

Completeness Detection Using a Transfer-Learning-

Based Deep Neural Network,” Sensors, vol. 22, no.

15, p. 5700, 2022.

C. Lugaresi, J. Tang, H. Nash, C. McClanahan, E. Uboweja,

M. Hays, F. Zhang, C.-L. Chang, M. G. Yong, J. Lee,

et al., ”Mediapipe: A framework for perceiving and

processing reality,” in Proceedings of the Third Work-

shop on Computer Vision for AR/VR at IEEE Com-

puter Vision and Pattern Recognition (CVPR), 2019.

Y. Lin, X. Jiao, and L. Zhao, ”Detection of 3d human pos-

ture based on improved mediapipe,” Journal of Com-

puter and Communications, vol. 11, no. 2, pp. 102–

121, 2023.

S. Garg, A. Saxena, and R. Gupta, ”Yoga pose classiﬁca-

tion: a CNN and MediaPipe inspired deep learning

approach for real-world application,” Journal of Am-

bient Intelligence and Humanized Computing, vol. 14,

no. 12, pp. 16551–16562, 2023.

A. K. Singh, V. A. Kumbhare, and K. Arthi, ”Real-time

human pose detection and recognition using medi-

apipe,” in Proceedings of the International Confer-

ence on Soft Computing and Signal Processing, pp.

145–154, 2021.

J. Wang, S. Tan, X. Zhen, S. Xu, F. Zheng, Z. He, and L.

Shao, ”Deep 3D human pose estimation: A review,”

Computer Vision and Image Understanding, vol. 210,

p. 103225, 2021.

C. Zheng, W. Wu, C. Chen, T. Yang, S. Zhu, J. Shen, N. Ke-

htarnavaz, and M. Shah, ”Deep learning-based human

pose estimation: A survey,” ACM Computing Surveys,

vol. 56, no. 1, pp. 1–37, 2023.

M. B. Gamra and M. A. Akhlouﬁ, ”A review of deep learn-

ing techniques for 2D and 3D human pose estimation,”

Image and Vision Computing, vol. 114, p. 104282,

2021.

L. Song, G. Yu, J. Yuan, and Z. Liu, ”Human pose esti-

mation and its application to action recognition: A

survey,” Journal of Visual Communication and Image

Representation, vol. 76, p. 103055, 2021.

Y. Li, S. Yang, P. Liu, S. Zhang, Y. Wang, Z. Wang, W.

Yang, and S.-T. Xia, ”Simcc: A simple coordinate

classiﬁcation perspective for human pose estimation,”

in Proceedings of the European Conference on Com-

puter Vision, pp. 89–106, 2022.

INCOFT 2025 - International Conference on Futuristic Technology

588