PRIV

E: Towards Privacy-Preserving Swarm Attestation

Nada El Kassem

1 a

, Wouter Hellemans

2 b

, Ioannis Siachos

3 c

, Edlira Dushku

4 d

Stefanos Vasileiadis

3 e

, Dimitrios S. Karas

3 f

, Liqun Chen

1 g

, Constantinos Patsakis

5 h

and Thanassis Giannetsos

3 i

University of Surrey, Guildford, U.K.

ES&S, COSIC, ESAT, KU Leuven, Leuven, Belgium

UBITECH Ltd., Athens, Greece

Aalborg University, Copenhagen, Denmark

University of Pireaus, Piraeus, Attiki, Greece

Keywords:

Swarm Attestation, Privacy, Direct Anonymous Attestation, Remote Attestation, In-Vehicle Networks.

Abstract:

In modern large-scale systems comprising multiple heterogeneous devices, the introduction of swarm attes-

tation schemes aims to alleviate the scalability and efﬁciency issues of traditional single-Prover and single-

Veriﬁer attestation. In this paper, we propose PRIV

E , a privacy-preserving, scalable, and accountable swarm

attestation scheme that addresses the limitations of existing solutions. Speciﬁcally, we eliminate the assump-

tion of a trusted Veriﬁer, which is not always applicable in real-world scenarios, as the need for the devices

to share identiﬁable information with the Veriﬁer may lead to the expansion of the attack landscape. To this

end, we have designed an enhanced variant of the Direct Anonymous Attestation (DAA) protocol, offering

traceability and linkability whenever needed. This enables PRIV

E to achieve anonymous, privacy-preserving

attestation while also providing the capability to trace a failed attestation back to the compromised device.

To the best of our knowledge, this paper presents the ﬁrst Universally Composable (UC) security model for

swarm attestation accompanied by mathematical UC security proofs, as well as experimental benchmarking

results that highlight the efﬁciency and scalability of the proposed scheme.

1 INTRODUCTION

In recent years, the exponential proliferation of low-

cost embedded devices and the Internet of Things

(IoT) has signiﬁcantly contributed to developing

innovative environments, particularly in advancing

Intelligent Transportation Systems. Unfortunately,

these devices represent natural and attractive malware

attack targets despite many beneﬁts. To ensure the

correctness of the operational state of a device, Re-

https://orcid.org/0000-0002-2827-6493

https://orcid.org/0000-0003-2344-044X

https://orcid.org/0009-0003-2310-921X

https://orcid.org/0000-0002-4974-9739

https://orcid.org/0009-0005-2193-4464

https://orcid.org/0000-0002-2680-6374

https://orcid.org/0000-0003-2680-4907

https://orcid.org/0000-0002-4460-9331

https://orcid.org/0000-0003-0663-2263

mote Attestation (RA) has been proposed to detect un-

expected modiﬁcations in the conﬁguration of loaded

binaries and check software integrity. However, typ-

ical RA schemes assume the existence of a single

Prover and a single Veriﬁer, introducing efﬁciency

and scalability issues for large-scale systems compris-

ing multiple Edge and IoT devices. In this context,

swarm attestation (Ambrosin et al., 2020) has been

proposed to enable the root Veriﬁer (V ) to check the

sanity of a set of swarm devices simultaneously.

Several swarm attestation schemes have been pro-

posed in the literature (Asokan et al., 2015; Am-

brosin et al., 2016; Dushku et al., 2023; Le-Papin

et al., 2023) to verify the integrity and establish trust

among devices in large-scale systems. In such envi-

ronments, trust is pivotal in the decision-making pro-

cesss as it helps the devices to select collaborators,

to assess the trustworthiness of incoming data, and to

mitigate threats from untrustworthy or hostile entities.

However, in state-of-the-art solutions, the trust is typ-

El Kassem, N., Hellemans, W., Siachos, I., Dushku, E., Vasileiadis, S., Karas, D. S., Chen, L., Patsakis, C. and Giannetsos, T.

PRIVÉ: Towards Privacy-Preserving Swarm Attestation.

DOI: 10.5220/0013629000003979

In Proceedings of the 22nd International Conference on Security and Cryptography (SECRYPT 2025), pages 247-262

ISBN: 978-989-758-760-3; ISSN: 2184-7711

247

ically conﬁned to system integrity and dependability

aspects, excluding other important dimensions such

as identity privacy (anonymity) and evidence privacy.

In such complex and dynamic systems, we of-

ten have to make trust decisions based on incom-

plete, conﬂicting, or uncertain information. Tradi-

tional probabilistic models assume that we have com-

plete knowledge of all possibilities and their respec-

tive probabilities, but in dynamic, distributed environ-

ments, this is rarely the case. For example, a sys-

tem might receive conﬂicting data from different data

sources or communication channels. Also, not all data

sources are equally reliable, and some may be com-

promised or faulty.

In such environments, the use of an evidence-

based theory for trust assessment becomes essential,

because it allows us to explicitly represent uncer-

tainty. Rather than forcing a decision based on in-

complete data, we can account for the fact that we

do not have enough information, thus reﬂecting un-

certainty in our trust assessments. A core enabler in

this direction is the use of robust (swarm) attestation

mechanisms for extracting evidence on the status of

the target device in a veriﬁable manner. Depending

on the property of the device to be assessed, differ-

ent types of evidence may be required. In the context

of security-related trust properties, trust sources in-

clude detection mechanisms, e.g., Intrusion Detection

Systems, Misbehaviour Detection Systems, or mecha-

nisms to evaluate the existence and/or enforcement of

security claims such as secure boot, conﬁguration in-

tegrity etc. In its simplest form, the received evidence

can be distinguished into one main category: Binary

evidence that allows the veriﬁer to compute whether a

security claim is valid or not. For instance, this is the

case of the secure boot certiﬁcate chain that allows a

veriﬁer to make an informed decision that the prover

has executed its secure boot process. On the other

side, there is evidence that results in claims expressed

in the form of a range. This is the case of some Misbe-

haviour Detection systems that provide a score- e.g.,

conﬁdence level- about abnormal behaviour of a de-

vice. This diversity of the evidence outcome intro-

duces the need for robust attestation mechanisms to

enable the quantiﬁcation of trustworthiness in an efﬁ-

cient and reliable manner.

Typical swarm attestation schemes rely on a span-

ning tree (Asokan et al., 2015; Carpent et al., 2017)

to aggregate the attestation results, where swarm de-

vices are attested by neighboring devices based on a

parent-child relationship in a tree format with a cen-

tralized Veriﬁer. To address this ﬁxed parent-child re-

lationship, other works leverage the broadcasting ag-

gregate pattern, in which every device broadcasts its

response to the attestation challenge to its neighbors

(Kohnh

auser et al., 2018). However, there has been

very limited focus on privacy issues of the swarm de-

vices (Abera et al., ). While some schemes do not

provide information about the individual devices or

devices causing a failed attestation, they do not ex-

plicitly focus on privacy (e.g., (Asokan et al., 2015),

(Ambrosin et al., 2016)). Conversely, other attestation

schemes only provide information about the devices

causing a failed attestation, such as (Ammar et al.,

2020). Moreover, two schemes are proposed in (Car-

pent et al., 2017), one of which keeps a list of the

failed devices, and the other does not.

Swarm attestation faces signiﬁcant challenges in

maintaining identity and evidence privacy, especially

in large-scale systems with numerous IoT and edge

devices. In this context, we have to be able to make

trust decisions based on fresh trustworthiness evi-

dence without impeding the privacy of the overall

system. Therefore, it is crucial to conceal each de-

vice’s identity and the nature of the evidence they

present. However, the dynamic nature of such (multi-

agent) systems requires that trust assessment is not

only based on reasoning under uncertainty (evidence

may be incomplete, conﬂicting, or contain uncertain

information on the integrity of the device), but it also

ensures that the evidence used to compute trust opin-

ions is veriﬁable. Trust cannot be randomly assigned

or assumed from previous interactions but must be

continuously veriﬁed and updated through collectable

evidence. This principle aligns with the Zero-Trust

paradigm, which dictates that no entity should be in-

herently trusted without validation. Veriﬁcation of ev-

idence is related to the use of Trust Anchors since they

are the starting point for verifying the chain of trust.

Consider, for instance, the case of Connected

and Cooperative Automated Mobility (CCAM) ser-

vices in the automotive domain, where it is critical

to assess trustworthiness in terms of integrity without

compromising the safety-critical proﬁle and privacy

of the running services (e.g., Collision Avoidance).

Especially when considering the need to share such

trusting opinions between different administrative do-

mains. Swarm attestation must effectively verify the

status of these devices within the in-vehicle network

to ensure that safety decisions are made based on reli-

able sensor inputs. On the other hand, Veriﬁers should

not ascertain which speciﬁc device attests to which

property or the exact expected measurement values.

Disclosing such information could lead to implemen-

tation disclosure attacks, vehicle ﬁngerprinting, or

driver behavior tracking. These concepts, while in-

terrelated, require clearer terminological distinctions

to facilitate practical trust assessment and manage-

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

248

ment within decentralized environments of mixed-

criticality.

One efﬁcient technique that allows for checking

the integrity of the devices while preserving their

anonymity is called Direct Anonymous Attestation

(DAA). In this work, we extend the DAA to offer two

security properties besides anonymity: evidence pri-

vacy and traceability. The evidence privacy means

that the signer doesn’t disclose the signed message,

such as the current device’s conﬁguration, to the Veri-

ﬁer while still allowing public veriﬁability. We obtain

this by binding the use of the DAA signing key to a re-

stricted policy that only allows the key to sign a mes-

sage if the policy is satisﬁed. This subsequently al-

lows the Veriﬁer to trust the attestation results without

accessing sensitive information. Traceability enables

the correct tracing of a device in case of any failed

attestation. The dual protection of device identity

and evidence ensures privacy and robust accountabil-

ity, making it essential for trustworthiness evidence

provision in today’s evidence-based trust assessment

frameworks.

To address the aforementioned challenges, this

paper introduces a secure and efﬁcient attestation

scheme that can correctly make valid statements

about the integrity of both single devices and a swarm

of devices in a privacy-preserving but accountable

manner. This means that the designed scheme should

be able to provide veriﬁable evidence on the correct-

ness of a swarm by concealing the identities of the de-

vices, and only in the case of a possible compromise

detection should it allow for tracing back a failed at-

testation to the swarm device that caused the failure,

instead of isolating the entire swarm.

Contributions. In this paper, we pro-

pose the PRIV

E swarm attestation scheme for

privacy-preserving swarm attestation. We lever-

age trusted computing technologies and strong

privacy-enhancing cryptographic protocols (e.g.,

DAA (Brickell et al., 2004; Chen et al., 2023)), which

provide decentralized privacy-preserving attestation

using blind group signatures. PRIV

E considers an in-

terconnected network of heterogeneous IoT and Edge

devices to convince a Veriﬁer (V ) of the integrity

of the attestation result based on signed attestation

evidence of the enrolled swarm devices. Addition-

ally, in its operation, PRIV

E safeguards the devices’

identity privacy but also provides traceability in case

the attested device is deemed compromised. Thus,

we do not assume the trustworthiness of the IoT/Edge

devices or the Veriﬁer. To the best of our knowledge,

we provide the ﬁrst detailed mathematical analysis

for swarm attestation schemes in the Universally

Composable (UC) model. This analysis provides

proof regarding all envisioned security and privacy

requirements in PRIV

E. Furthermore, we provide a

benchmarking analysis to demonstrate the protocol’s

performance and real-world applicability.

2 PRELIMINARIES

Notation.We present the notations that will be fol-

lowed throughout the paper in Table 1.

PRIV

E Building Blocks. To enable a privacy-

preserving and accountable swarm attestation ap-

proach, PRIV

E adopts DAA to compute the device

attestation with zero knowledge and relies on bilin-

ear aggregation signatures to efﬁciently aggregate the

devices’ signatures across the swarm.

Direct Anonymous Attestation (DAA). DAA

(Brickell et al., 2004; Brickell et al., 2008), is

a platform authentication mechanism that allows

privacy-preserving remote attestation of a device

associated with a Trusted Component (TC) but does

not support the property of traceability. In general,

DAA requires an Issuer and a set of Signers. , and

a set of Veriﬁers. It includes ﬁve algorithms: Setup,

Join, Sign, Verify, and Link. The issuer produces

a DAA membership credential for each signer,

corresponding to a signature of the signer’s identity.

A DAA signer consists of the Host and TC pair.

Bilinear Aggregation Signatures. The purpose of

designing aggregate signatures is to reduce the length

of digital signatures in applications that use multiple

signatures (Boneh et al., 2003b). In a general aggre-

gate signatures scheme, the aggregation can be done

by anyone without the signers’ cooperation. In par-

ticular, each given user i signs her message m

to ob-

tain a signature σ

. Consider a set of k signatures

,...,σ

on messages m

,...,m

under public keys

,...,PK

, respectively. In this case, anyone can

use a public aggregation algorithm to compress all k

signatures into a single signature σ, whose length is

the same as a signature on a single message. To ver-

ify it, all the original messages and public keys are

needed. In particular, given an aggregate signature σ,

public keys PK

,...,PK

and messages m

,...,m

, the

aggregate veriﬁcation algorithm veriﬁes whether the

aggregate signature σ is valid.

The bilinear aggregate signature scheme (Boneh

et al., 2003b) enables efﬁcient aggregation, allow-

ing an arbitrary aggregating party unrelated to, and

untrusted by, the original signers to combine k pre-

existing signatures into a single aggregated signature.

The scheme consists of the following algorithms:

Key Generation. For a particular user, pick random

x ← Z

and compute w ← g

. x ∈ Z

and w ∈ G

are

PRIVÉ: Towards Privacy-Preserving Swarm Attestation

249

Table 1: Notation Summary.

Symbol Description Symbol Description

TC Trusted Component (x,y) The Privacy CA private key

The j

edge device (X ,Y) The Privacy CA public key

TC that corresponds to the j

edge device (x

) The IoT device long-term key-pair

The host that corresponds to j

edge device (x

) The IoT device short-term key-pair (pseudonym)

V Veriﬁer σ

DAA

DAA signature on the long-term public key y

v Number of edge devices in the swarm σ

IoT device signature on its current state m

t TC’s private key SPK Signature based Proof of Knowledge

’s public key known by the Privacy CA ch, f Attestation challenges

(a,b, c, d) E

’s credential created by the Privacy CA ρ,r, s Random numbers in Z

’s public tracing key known by the Opener k Number of IoT devices in the swarm

T The Opener’s Tracing Key σ

[1−n]

An aggregated signature of n IoT devices

q A prime number deﬁning the order of cyclic groups bsn A random input in {0,1}

∗

Generators of the groups G

∗

IoT devices’ golden conﬁguration (legitimate state)

Function Description Proofs Description

H Hash function: H : {0,1}

∗

−→ G

ipk

Proof of CA public key construction

e Pairing function: e : G

× G

→ G

,π

Proofs of construction of Q

and T

e(g

) → g

Proof of E

’s credential construction

,π

Proofs of construction of y

and y

, respectively

the user’s private and public keys, respectively.

Signing. For a particular user, given the public key w,

the private key x, and a message m ∈ {0,1}

∗

, compute

h ← H(w,m), where h ∈ G

, and σ ← h

Veriﬁcation. Given a user’s public key w, a message

m, and a signature σ, compute h ← H(w, m). The sig-

nature is accepted as valid if e(σ,g

) = e(h,w).

Aggregation. Arbitrarily assign an index i to each

user whose signature will be aggregated, ranging

from 1 to k. Each user i provides a signature σ

∈ G

on a message m

∈ {0,1}

∗

of her choice. Compute

signature σ ←

∏

i=1

Aggregate Veriﬁcation. Given an aggregate signa-

ture σ ∈ G

for a set of users (indexed as before),

the original messages m

∈ {0,1}

∗

, and public keys

∈ G

. To verify the aggregate signature σ, com-

pute h

← H(w

) for 1 ≤ i ≤ k, and accept if

e(σ,g

) =

∏

i=1

e(h

) holds.

3 SYSTEM MODEL

We consider a static interconnected network of het-

erogeneous devices consisting of v edge devices and

k IoT devices, following a hierarchical fog computing

structure (ope, 2018), as depicted in Fig. 1.

IoT Devices (D): An untrusted and resource-

constrained device (e.g., a sensor), that is uniquely

identiﬁed as D

for i ∈ [1,k]. It is assumed that D has

a minimal Trusted Computing Base (TCB) and is con-

nected to only one edge device. The TCB includes (1)

a Read-Only Memory (ROM) containing the attesta-

tion protocol code, and (2) Secure Key Storage that is

read-accessed only by the attestation protocol.

Edge Devices (E): An untrusted, powerful device

with sizeable computational power and storage ca-

pacity. It is a combination of a Host H

(i.e., “nor-

Edge 2: σ

DAA

Edge 3: σ

DAA

Edge 1: σ

DAA

the secret key of the i

IoT device and σ

= H(m)

DAA

σ[1−3]

DAA

σ[4−6]

σ[1−3] = σ

× σ

σ[4−6] = σ

× σ

σ[1−3]× σ[4-6]

DAA

| σ

DAA

| σ

DAA

Figure 1: Overview of the Swarm Topology.

mal world”) and a Trusted Component (TC) (i.e., “se-

cure world”) such as Trusted Platform Module (TPM

2.0) (tpm, 2016). Each edge device is uniquely iden-

tiﬁed as E

for j ∈ [1,v]. Each E is a parent of a set of

heterogeneous IoT devices and knows its children’s

legitimate state (i.e., a hash of the binaries). Thus,

each edge device authenticates its children’s IoT de-

vices.

Veriﬁer (V ): Any third party that initiates the attes-

tation and validates the trustworthiness of the swarm.

The Veriﬁer knows the number of IoT devices in-

volved in the swarm. We assume an honest-but-

curious Veriﬁer that legitimately performs the veriﬁ-

cation but will attempt to learn all possible informa-

tion from the received attestation results.

Privacy Certiﬁcation Authority (Privacy CA): A

trusted third party that acts both as an Issuer and Net-

work Operator. It is responsible for conducting the

secure setup of the fog architecture, verifying the cor-

rect creation of all cryptographic primitives, and au-

thorizing the devices to join the network.

Opener (Opener or Tracer): A trusted entity that

traces the compromised device(s) when the swarm at-

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

250

testation fails to perform recovery actions.

Threat Model. In the context of the system de-

scribed above, we consider remote software adver-

saries (Adv

) that aim to compromise IoT and edge

devices in the swarm by exploiting software vulner-

abilities and injecting malicious code. Moreover, we

consider honest but curious adversaries Adv

HBC

who

are legitimate participants in the swarm but aim to

disclose the device’s privacy. Additionally, swarms

are susceptible to network adversaries (Adv

NET

) that

can forge, drop, delay, and eavesdrop on the messages

exchanged among two devices in the swarm. We con-

sider a classic Dolev-Yao (DY) (Dolev and Yao, 1983)

adversary with full control over the communication

channel between an IoT device and edge device in

the swarm, two edge devices, or one edge device and

the Veriﬁer. However, in line with other works (Ca-

menisch et al., 2017; Wesemeyer and all, 2020), we

assume a perfectly secure channel between the Host

and the TC in an edge device. Thus, the Adv

NET

can-

not intercept the interaction between the Host and the

TC or use the TC as an oracle. Physical Adversaries

(Adv

PHY

) are beyond our scope.

4 SECURITY REQUIREMENTS

To prove the security properties of PRIV

E , we em-

ploy the UC model introduced in (§ 6.1), for which

we deﬁne the following high-level security properties:

Anonymity (SP1): It should be possible to conceal

the identity of honest Edge and IoT devices from Ver-

iﬁer V by creating anonymous signatures that per-

fectly hide the identities of the devices in a swarm.

Traceability (SP2): It should be possible for the

Opener to trace the source of an attestation failure

back to its source so that a potentially compromised

edge device can be revoked. On the other hand, an

honest parent edge device can trace its children IoT

signatures back to their source IoT devices (SP3).

Correctness (SP4): Honestly generated signatures

should always be considered valid, and honest users

should not be revoked.

Non-frameability (SP5): It should not be possible

for an adversary to create signatures that successfully

impersonate an honest device or link to honest signa-

tures. This extends to Unforgeability (SP6), where it

should be computationally infeasible to forge a signa-

ture σ on a message µ that is accepted by the veriﬁca-

tion algorithm when no honest device signs µ.

Linkability (SP7): It should be possible for a Veriﬁer

to check if any two DAA signatures signed under the

same basename originate from the same edge device

without breaching its privacy.

5 THE PRIV

E PROTOCOL

We present an overview of the main phases of our pro-

posed protocol PRIV

E without ﬁrst including the de-

tails of internal cryptographic primitives, which will

be presented in § 5.1. The setup phase is a one-time

ofﬂine procedure performed by the Privacy Certiﬁ-

cation Authority (Privacy CA) to guarantee the se-

cure deployment and enrollment of the devices in the

swarm and the creation of the IoT device short-term

keys (pseudonyms). The attestation process is then

initiated by the Veriﬁer V that sends a challenge f

to one or more edge devices, which will then dis-

tribute it recursively to all its (children) swarm de-

vices. Then, each IoT Device D

produces and signs

its attestation evidence (attestation claim) using a pre-

certiﬁed pseudonym. All these claims are sent to the

parent Edge Device, E

, that aggregates them, ap-

pends its DAA signature, and sends the aggregated

claims together with its DAA signature to the root

edge (such as Edge 1 in Figure 1). When the root

edge receives all other edges’ contributions, it creates

its DAA signature, aggregates the received IoT ag-

gregated claims and appends all the DAA signatures,

including its own. This constitutes the swarm signa-

ture. The swarm signature is then forwarded to V .

After obtaining the swarm attestation report, V ver-

iﬁes DAA signatures and checks the total number of

IoT signatures to ensure that all IoT devices have been

included in the report. In the case of a non-valid DAA

signature or a missing IoT signature, V leverages the

novel traceability feature of PRIV

E to trace the result

back to the compromised device.

5.1 Detailed Description of PRIV

In this section, we provide a detailed description

of PRIV

E . The required notation is presented in

Tab. 1, The protocol consists of the Setup and Join

(§ 5.1.1), Attestation (§ 5.1.2), and Veriﬁcation

(§ 5.1.3) phases.

5.1.1 Setup and Join Phases

The setup phase starts with the Privacy CA being

equipped with the necessary key pairs x,y ← Z

where X = g

and Y = g

. The Privacy CA, if needed,

can prove the well-formed construction of the secret

key (x, y) through the creation of a proof of knowl-

edge π

ipk

(that can also be signed by the Root Certi-

ﬁcation Authority in such systems). (X,Y ) are public

parameters shared by the Privacy CA and other sys-

tem parameters.

Edge-Join. The edge device Enrollment process

starts from an edge device E

, where j ∈ [1,v], that

PRIVÉ: Towards Privacy-Preserving Swarm Attestation

251

sends an enrollment request to the Privacy CA for

joining the target service graph chain. The Privacy

CA chooses a fresh nonce ρ and sends it to E

, who

forwards it to its embedded TC denoted by M

. Then,

chooses a secret key t ← Z

, sets its public key

= g

. We use a policy that can be satisﬁed if

a selection of the Platform Conﬁguration Registers

(PCR)s matches a predetermined value, referencing

a trusted state. We use PolicyPCR commands (of the

underlying Root-of-Trust) to ensure that the edge de-

vice signing key is inoperable if the integrity of the

Edge device is compromised (cf. Section 8 for fur-

ther details on the implementation of such commands

in the case of a Trusted Platform Module (TPM) as

the host secure element). M

can also compute π

a proof of construction of Q

. This proof, Q

, can

be signed with the embedded TC’s endorsement key,

thus elevating it to a veriﬁable credential over the cor-

rect construction and binding of the secret key t. The

pair (Q

,π

) (alongside the public part of the TC’s

root certiﬁcate) is then sent to the Privacy CA who

veriﬁes π

and checks whether the edge device is el-

igible to join, i.e. the edge device DAA key has not

been registered before. Upon validation, the Privacy

CA picks a random r ← Z

and generates E

’s DAA

credential (a,b,c,d) by setting a = g

,b = a

,c =

rxy

and d = Q

. The Privacy CA also generates a

proof π

on the credential construction.

Generating the Tracing Keys by the Opener. Each

sets T

= g

and computes π

as a proof of con-

struction of T

. M

sends (T

,π

) via E

to the

Opener. The Opener veriﬁes π

and π

and makes

sure that T

and Q

link to the same TC by checking

if the following holds:

e(Q

) = e(g

) (1)

To convince the Opener that T

is a correct key, M

may also send to the Opener the DAA credential of

issued by the Privacy CA. After receiving all edge

devices T

, for all j ∈ [1, v], and their corresponding

public keys Q

, the Opener sets its tracing key T as

follows: T = {T

,...,T

} and keeps the (Q

)

pairs for all j ∈ [1, v].

IoT-Join. Each IoT device is equipped with a long-

term key pair (x

∈ Z

) whose public part y

represents the IoT device’s identity and is certi-

ﬁed by the Privacy CA. Let π

represent a proof of

construction of y

= g

. The enrollment of IoT de-

vices consists of the following steps:

1. Each edge device certiﬁes its children’s IoT long-

term key by creating a DAA signature σ

DAA

on y

2. Once the long-term key is certiﬁed, each IoT

device creates short-term random keys (x

∈

= g

,π

), for each integer p ∈ [1,...P]

where π

is a proof of construction of y

and P is

the total number of pseudonyms (short-term ran-

dom keys) that will be certiﬁed by the edge de-

vice. This is called pseudonymity, which is the

ability of an edge device to use a resource or

service without disclosing the IoT user’s identity

while still being accountable for that action.

3. The IoT device self-certiﬁes its public key y

creating a signature σ

on y

using its own long-

term secret key x

. This signature prevents any

other device (including edge devices and author-

ities) from signing on behalf of the IoT device

without knowing the IoT device’s long-term se-

cret signing key x

. Finally, the IoT device sends

,σ

,π

) for each p ∈ [1,...P] to its mother.

4. The edge device veriﬁes π

and σ

on y

for

each p ∈ [1, . . . P]. Upon successful veriﬁcation,

the edge device keeps (y

,σ

DAA

,σ

) in its

records to be able to link each set of certiﬁed IoT

pseudonyms to their long-term key for each child

IoT device. This is particularly useful in cases

where an edge device needs to trace the identity

of its children’s IoT signatures.

We remove the index p from the remaining protocol

description and use σ

and (x

) to denote the D

’s

signature and short-term key, respectively.

5.1.2 Attestation Phase

The swarm attestation is initiated by a Veriﬁer V that

sends a challenge f to an edge device, which will then

distribute it recursively to all devices in the swarm.

The IoT devices sign their attestation results and re-

port them to their parent edge devices.

IoT Device Signature. When an IoT device receives

an attestation challenge f , it concatenates its current

conﬁguration m

∗

with the challenge f . Then, signs

the attestation response m

= (m

∗

| f ) using one of its

short-term keys x

previously certiﬁed by its parent

edge device during the enrollment procedure. Each x

is only used once to achieve IoT identity privacy. The

IoT device computes a BLS signature as follows:

= H(m

)

(2)

The IoT device sends σ

and y

to its parent edge. The

parent edge device checks that every received y

is cer-

tiﬁed, relying on its records. The edge then aggregates

all the c received children signatures σ

,...σ

in one

signature σ

[1−c]

as follows σ

[1−c]

= σ

× ... × σ

H(m

)

× . . . × H(m

)

. When the attestation of a

given IoT device is missing, the edge device will not

include it in the aggregation.

Edge Device Signature & Traceability. The creation

of a traceable DAA signature starts with an edge de-

vice E

, with an embedded trusted component M

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

252

that gets a Veriﬁer basename bsn deﬁned as a random

string {0,1}

∗

to enable traceability and linkability of

DAA signatures. The signature generation follows the

following steps:

1. To sign a message µ with respect to the basename

bsn, the edge device randomizes its credential by

choosing a random s ← Z

, sets (a

′

) ←

), and then sends (µ,bsn,b

′

) to M

2. Next, M

calculates the link token nym = (bsn)

and M

calculate a a Signature based Proof of

Knowledge SPK of the secret key t and its creden-

tial as follows:

SPK{t : nym = H(bsn)

′

= b

′t

}(bsn,µ) (3)

samples ω ← Z

, sets K = H(bsn)

, J = b

′ω

and sends (nym,K, J) to E

that calculates the

challenge ch = H(a

′

,nym,K,J,µ) in Z

and sends it to M

. M

then creates a Shnorr sig-

nature δ = ω + ch t. Finally, the SPK has a form

of (δ,ch) and is included in the DAA signature.

3. The DAA signature is (a

′

,SPK,nym). To

this end, the swarm signature is



[1−k]

,σ

DAA



∀ i ∈ [1 − k] and j ∈ [1 − v], where k and v are

the total numbers of IoT and edge devices in the

swarm, respectively and σ

[1−k]

denotes the aggre-

gation of all the IoT signatures in the swarm. The

root edge performs this aggregation. If the attesta-

tion of some IoT devices is unsuccessful or miss-

ing, the mother edge device does not aggregate

such attestations. The ﬁnal swarm aggregated sig-

nature will be as follows:



[1−l]

,σ

DAA



, ∀ i ∈

[1 − l] with l < k.

5.1.3 Veriﬁcation Phase

Attestation Report Veriﬁcation. After receiv-

ing an attestation report, the Veriﬁer checks

the DAA signature of each edge device σ =



′

,nym, SPK = (δ, ch)



on a message µ

w.r.t. a basename bsn that is published with the sig-

nature. In particular, the Veriﬁer veriﬁes SPK w.r.t.

(µ,bsn) and nym, and checks that a

′

̸= 1, e(a

′

,Y ) =

e(b

′

), e(c

′

) = e(a

′

,X).

We assume that the veriﬁers have access to the i

IoT

devices’ golden conﬁguration, denoted by M

∗

, ∀ i ∈

[1,k]. The Veriﬁer calculates H(M

), with M

∗

| f ), and checks the following equation:

e(σ

[1−k]

)

= e



H(M

),y



× .. . × e



H(M

),y



(4)

that is only valid if the IoT device’s current conﬁgu-

ration m

, used in Equation 2, matches the golden one

without knowing the value of m

; this offers IoT

evidence privacy. The Veriﬁer claims that the swarm

attestation has failed if the aggregate result has less

than k aggregated signatures or if the veriﬁcation of

Equation 4 fails. The veriﬁer also checks that ch =

H(a

′

,nym,H(bsn)

nym

−ch

′

−ch

,µ).

Further, the Veriﬁer can interact with the Opener

to initiate the tracing of the device with a failed

attestation.

Link. When a Veriﬁer can access different

swarm attestation reports, she can check whether

any two DAA signatures originate from the same

edge device. Speciﬁcally, the Veriﬁer checks if

both signatures are signed under the same base-

name known by the Veriﬁer. More formally,

given σ

= (a

′

,nym

,SPK

) and σ

′

,nym

,SPK

) on a message µ w.r.t. a

basename bsn. In this setting, the output is 1 when

both signatures are valid and nym

= nym

; other-

wise, the output is 0.

The linkability of the IoT devices in a swarm attes-

tation relies on the static topology of the swarm; each

parent edge device has in its records the set of all cer-

tiﬁed pseudonyms associated with the corresponding

IoT device long-term key (used as the identity of the

IoT device) for each child IoT device. Thus, when-

ever an IoT device creates two signatures in two dif-

ferent SA instantiations, the edge device can identify

whether these two signatures originate from the same

IoT device (the edge device uses traceability to sup-

port linkability of IoT devices).

Tracing/Opening. In PRIV

E , traceability consists of

two levels: The ﬁrst level of swarm attestation trace-

ability relies on the traceability of the DAA signature,

which can be done by the Opener using its tracing

key. We achieve this by adding a traceability require-

ment for the existing DAA scheme (Camenisch et al.,

2016) to obtain a novel Traceable DAA protocol that

meets our security and privacy requirements. The sec-

ond level relies on the static swarm topology that links

each parent to their children. Tracing the IoT device

can be done by the edge device with the knowledge

of the IoT long-term key corresponding to the cer-

tiﬁed short-term pseudonyms. Speciﬁcally, starting

with a DAA signature σ

DAA

with a corresponding link

token nym = H(bsn)

, the Opener uses its tracing key

T = {T

,...,T

} to check the following equation:

e(nym,g

) = e(H(bsn), T

) ∀ j ∈ [1 − v] (5)

A successful veriﬁcation allows the Opener to recover

’s public key Q

corresponding to T

in its records,

as explained previously during the setup of the Trac-

ing Keys by the Opener. Once the edge device’s iden-

tity is recovered, it is easy for the edge device to re-

cover any of its children’s long-term public keys that

are certiﬁed by this edge device.

PRIVÉ: Towards Privacy-Preserving Swarm Attestation

253

Revocation. Any Revocation Authority (RA), which

may also be the Opener, can remove misbehaving

edge devices without revealing the edge device’s

identity. The intuition behind the revocation scheme

is to be able to deactivate any DAA credential of

an edge device created during its enrollment (Larsen

et al., 2021). We assume that a Revocation Authority

RA has access to a set of revoked DAA keys KRL.

The revocation authority checks that the DAA key

used to create the DAA signature is not in the revo-

cation list. This is done by checking that: ∀ t

∗

∈

KRL, nym ̸= H(bsn)

∗

. PRIV

E also supports revo-

cation of the IoT devices by their parent edge de-

vice. We assume the edge device has access to a set

of IoT revoked keys called the IoT-Key Revocation

List IoTKRL. It can then check that each of its chil-

dren’s IoT signatures were not produced by any key

in IoTKRL. Relying on the trust of the edge devices

and the accuracy of the updated IoTKRL, edge de-

vices would also be able to correctly revoke the IoT

devices that their keys are IoTKRL.

6 PRIV

E SECURITY ANALYSIS

In this section, we ﬁrst introduce the Universally

Composable (UC) framework(§ 6.1), then we model

PRIV

E in the Universally Composable (UC) frame-

work(§ 6.2), capturing all the security and privacy re-

quirements deﬁned in § 4.

6.1 Methodology

Due to the complexity of the PRIV

E scheme, it isn’t

easy to perform a complete security proof based on

traditional formal veriﬁcation and symbolic modeling

techniques as the speciﬁed models might prove chal-

lenging to analyze and verify even in computational

rich machines (Meier et al., 2013). Therefore, we em-

ploy the Universal Composability (UC) model, based

on which we aim to equate the real-world network

topology to an ideal-world model, both being indis-

tinguishable from each other from the perspective of

an adversary, in which it is possible to break down the

proposed scheme into simpler building blocks with

provable security. Speciﬁcally, the security deﬁni-

tion of our swarm attestation protocol is given with

respect to an ideal functionality F . This is depicted

in Figure 2 for a swarm of three edges and four IoT

devices. However, the UC model can be generalized

to any network topology and swarm size. In UC, an

environment E should not be able to distinguish, with

a non-negligible probability, between the two worlds:

The real world, where each of the PRIV

E parties:

j+1

Real World

j−1

i−1

i+1

i+2

j+1

Ideal World

j−1

i−1

i+2

i+1

Figure 2: UC security model: the Real and the Ideal world

executions are indistinguishable to the environment E.

an Issuer I , a parent edge E

, a child IoT device D

and a Veriﬁer V executes its assigned part of the real-

world protocol PRIV

E denoted by Π. The network is

controlled by an adversary A that communicates with

the environment E. The ideal world, in which all par-

ties forward their inputs to a trusted entity, called the

ideal functionality F , which internally performs (in a

trustworthy manner) all the required tasks and creates

the parties’ outputs in the presence of a simulator S.

The endmost goal is to ensure that PRIV

E se-

curely realizes all internal cryptographic tasks if for

any real-world adversary A that interacts with the

swarm, running Π, there exists an ideal world simu-

lator S that interacts with the ideal functionality F so

that no probabilistic polynomial time environment E

can distinguish whether it is interacting with the real

A or the ideal world adversary S . Another key point

of UC towards reducing the computational complex-

ity of the speciﬁed protocol is the composition theo-

rem that preserves the security of PRIV

E , even if it is

arbitrarily composed with other instances of the same

or different protocols.

6.2 PRIV

E UC Model

We now explain our security model in the UC

framework based on the ideal functionality F origi-

nally proposed in (Camenisch et al., 2016) and later

adopted in (Chen et al., 2019; El Kassem et al.,

2019). We assume that F internally runs the sub-

functionalities deﬁned in (Camenisch et al., 2016). In

protocol’s join phase, we adopt the key binding pro-

tocol introduced in (Chen et al., 2024), which ensures

an authenticated channel between the TC and the Is-

suer even in the presence of a corrupt Host; therefore,

in contrast to (Camenisch et al., 2016), we don’t need

to model the semi-authenticated channel.

The UC framework lets us focus the analysis on

a single protocol instance with a globally unique

session identiﬁer sid. F uses session identiﬁers of

the form sid = (I , sid

′

) for some Issuer I and a

unique string sid

′

. In the real world, these strings are

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

254

mapped to the Issuer’s public key, and all parties use

sid to link their stored key material to the particular

Issuer. We deﬁne the Edge-JOIN, the IoT-JOIN,

and the SIGN sub-session identiﬁers jsid

, jsid

i j

and ssid, respectively, to distinguish several join

and sign sessions that might run in parallel. We

deﬁne two “macros” to determine whether a secret

key key is consistent with the internal functionality

records. This is checked at several places in the ideal

functionality interfaces and depends on whether key

belongs to an honest or corrupt party. The ﬁrst macro

CheckkeyHonest is used when the functionality

stores a new key that belongs to an honest party and

checks that none of the existing valid signatures are

identiﬁed as belonging to this party. The second

macro CheckkeyCorrupt is used when storing a

new key that belongs to a corrupt party and checks

that the new key does not break the identiﬁability

of signatures, i.e., it checks that there is no other

known key

∗

, unequal to key, such that both keys are

identiﬁed as the owner of a signature. Both functions

output a bit b, where b = 1 indicates that the new key

is consistent with the stored information, whereas

b = 0 signals an invalid key. We assume that the

Host H

represents the same entity as E

. Thus,

and E

correspond to the TC and the Host in

an edge device E

. Finally, our model deﬁnes lists

that will be kept in the ideal functionality record

for the consistency of the joining devices, keys,

signatures, veriﬁcation results, and key revocation

lists namely: EdgeMembers, EdgeKeys, EdgeSigned,

EdgeVer, IoTMembers, IoTKeys, IoTSigned, IoTVer

KRL and IoTKRL. Next, we present the interfaces of

PRIV

E ideal functionality F .

SETUP: On input (SETUP, sid) from an Issuer I ,

output (SETUP, sid) to S . F then expects the adver-

sary S to provide the following algorithms, namely

(Kgen, Sign, Verify, Link, and Identify), that will be

used inside the functionality as follows:

Kgen: It consists of two probabilistic sub-algorithms:

Kgen that generates keys tsk and dsk for honest TCs

and IoT devices, respectively. Note that E

and D

are

uniquely identiﬁed by their keys tsk

and dsk

, respec-

tively. We remove the indices from the keys in our

security model description. PSEUDO-Kgen that takes

dsk as an input and generates a random short-term key

pair (s,o) for honest IoT devices.

Sign: A probabilistic algorithm used for honest TCs

and IoT devices to create the type of signature re-

quired by the corresponding operation. It consists of

the following sub-algorithms:

1. sig

DAA

(tsk,µ,bsn): On input of a secret key tsk, a

message µ and a basename bsn, it outputs a DAA

signature σ

DAA

on behalf of E

2. sig

IoT

(dsk, m): It creates signatures on behalf of

. It runs PSEUDO-Kgen to create a short-term

key pair (s,o), then creates a signature σ

on a

message m using the secret short-term key s.

Aggregate: A deterministic algorithm that aggregates

the IoT signatures using agg algorithm that takes as

inputs c IoT signatures σ

,σ

,...,σ

and outputs an

aggregated signature σ

[1−c]

Verify: A deterministic algorithm that outputs a

binary result on the correctness of a signature. It con-

sists of two sub-algorithms:

1. ver

DAA

(σ

DAA

,µ,bsn): On input of a signature

DAA

, a message µ and a basename bsn, it outputs

b = 1 if the signature is valid, 0 otherwise.

2. ver

IoT

(σ,m,o): On input of a signature σ, a mes-

sage m and a public short-term key o, it outputs

b = 1 if the signature is valid, 0 otherwise.

Link: (σ

,µ

,σ

,µ

): A deterministic algorithm

that checks if two signatures originate from the same

device. In the case of DAA signature linkability

checks, an extra parameter bsn is required as an in-

put. It outputs 1 if the same device generates σ

and

, and 0 otherwise.

Identify: A deterministic algorithm that ensures

consistency with the ideal functionality F ’s internal

records by connecting a signature to the key used to

generate it. It consists of two sub-algorithms:

1. identify

DAA

(tsk,σ

DAA

,µ,bsn): It outputs 1 if tsk

was used to produce σ

DAA

, 0 otherwise.

2. identify

IoT

(σ,m,dsk, s): It outputs 1 if σ was pro-

duced by an IoT device D, with an identity key

dsk, on a message m using the short term key s, 0

otherwise.

On input (ALGORITHMS, sid) from S, the ideal

functionality checks that Aggregate, Verify, Link, and

Identify are deterministic, store the algorithms and

output (SETUPDONE, sid) to I .

Edge-JOIN: On input (JOIN, sid, jsid

, M

) from

, create a join session record ⟨ jsid

⟩ and

output (JOINPROCEED, sid, jsid

, M

) to I . On

input (JOINCOMPLETE,sid, jsid

,tsk) from S :

• Abort if I or M

is honest and a record ⟨M

,∗,∗⟩ ∈

EdgeMembers already exists.

• If M

and E

are honest, set tsk ← ⊥.

• Else, verify that the provided tsk is eligible by:

• CheckkeyHonest(tsk) = 1 if M

is honest and E

is corrupt, or CheckkeyCorrupt(tsk) = 1 if M

corrupt and E

is honest.

Insert ⟨M

,tsk⟩ into EdgeMembers and output

(JOINED, sid, jsid

) to E

IoT-JOIN: On input (JOIN,sid, jsid

i j

) from

, create a join session record ⟨ jsid

i j

⟩ and

output (JOINPROCEED, sid, jsid

i j

, D

) to E

PRIVÉ: Towards Privacy-Preserving Swarm Attestation

255

On input (JOINCOMPLETE,sid, jsid

i j

,dsk) from S:

• Abort if I or D

is honest and a record ⟨D

,∗,∗⟩ ∈

IoTMembers already exists.

• If D

and E

are honest, set dsk ← ⊥.

• Else, verify that the provided dsk is eligible by

CheckkeyHonest(dsk) = 1 if D

is honest, or

CheckkeyCorrupt(dsk) = 1 if D

is corrupt.

Insert ⟨D

,dsk⟩ into IoTMembers and output

(JOINED, sid, jsid

i j

, D

) to E

IoT-SIGN: For all i ∈ [1,c

], where c

is the num-

ber of E

’s children IoT devices participating in

the swarm attestation. On input (SIGN, sid, ssid, m

)

from D

, with m

is the message to be signed

by a child D

, if I is honest and no entry

⟨D

,∗⟩ in IoTMembers, abort. Else, create

a sign session record ⟨ssid, D

⟩ and output

(SIGNPROCEED,sid,ssid) to D

• On input (SIGNCOMPLETE,sid, ssid, σ

) from S,

if D

and E

are honest, ignore the adversary’s sig-

nature σ

and internally generate the signature for a

fresh dsk or established dsk:

– Retrieve dsk from IoTKeys, if no key

exists, set dsk ← Kgen() and check

CheckkeyHonest(dsk) = 1.

– Compute signature σ

← sig

IoT

(dsk, m

) that in-

ternally runs PSEUDO-Kgen to create a short-

term key pair (s

) for D

, then check that

ver

IoT

(σ

) and identify

IoT

(σ

,dsk, s

)

are both equal to 1.

– Check that there is no D

′

̸= D

with key dsk

′

registered in IoTMembers or IoTKeys with

identify

IoT

(σ

,dsk

′

) = 1.

• Store ⟨D

,dsk, (s

)⟩ in IoTKeys.

• Compute σ

[1−c

]

← agg(σ

, σ

, ..., σ

• Output (sid, ssid, σ

[1−c

]

,{σ

}

i∈[1,c

]

) to E

AGGREGATION: Calculate the aggregation of the

v (total number of edges in a swarm) aggregated sig-

natures as follows: σ

[1−v]

← agg(σ

[1−c

]

,...σ

[1−c

]

and store ⟨σ

[1−v]

,σ

[1−c

]

,(σ

)

i∈[1,l]

⟩ in

IoTSigned, where l =

∑

j=1

Edge-SIGN: On input (SIGN, sid, ssid, M

, µ, bsn)

from E

, where j ∈ [1,v]. If I is honest and no en-

try ⟨M

,∗⟩ exists in EdgeMembers, abort. Else,

create a sign session record ⟨ssid, M

,µ,bsn⟩ and

output (SIGNPROCEED, sid, ssid, µ, bsn) to M

On input (SIGNCOMPLETE, ssid, σ

DAA

) from S:

• If M

and E

are honest, ignore the adversary’s sig-

nature and internally generate the signature for a

fresh or established tsk:

– If bsn ̸= ⊥, retrieve tsk from ⟨M

,bsn,tsk⟩ ∈

EdgeKeys. If no such tsk exists or bsn = ⊥, set

tsk ← Kgen(). Check CheckkeyHonest(tsk) = 1

and store ⟨M

, bsn, tsk⟩ in EdgeKeys.

– Compute σ

DAA

← sig

DAA

(tsk,µ,bsn) and check

ver

DAA

(σ

DAA

,µ,bsn) = 1.

– Check identify

DAA

(σ

DAA

,µ,bsn,tsk) = 1 and

check that there is no M

′

̸= M

with key tsk

′

registered in EdgeMembers or EdgeKeys with

identify

DAA

(σ

DAA

,µ,bsn,tsk

′

) = 1.

• If E

and M

are honest, store ⟨σ

DAA

, µ,

bsn, M

, E

⟩ in EdgeSigned and output

(SIGNATURE,sid,ssid,σ

DAA

) to E

Edge-VERIFY: On input (VERIFY, sid, µ, bsn,

DAA

, σ

[1−l]

, o

, KRL), i ∈ [1,l] and j ∈ [1,v] from

V .

• For each j, retrieve all pairs (tsk,M

) from

⟨M

,∗,tsk⟩ ∈ EdgeKeys where identify

DAA

(σ

DAA

µ, bsn, tsk) = 1. Set f

= 0 if at least one of the

following conditions holds:

CHECK 1. More than one key tsk was found.

CHECK 2. I is honest and no pair (tsk,M

) was found.

CHECK 3. There is an honest M

but no entry

⟨∗,µ,bsn,M

⟩ ∈ EdgeSigned exists.

CHECK 4. There is a tsk

∗

∈ KRL where

identify

DAA

(σ

DAA

, µ, bsn, tsk

∗

) = 1

and no pair (tsk, M

) for an honest M

was

found.

• If f

̸= 0, set f

= ver

DAA

(σ

DAA

, µ, bsn).

• Add ⟨σ

DAA

,µ,bsn,KRL, f

⟩ to EdgeVer, then pro-

ceed to verify the children IoT signatures.

IoT-VERIFY Output 0 if l ̸= k, else, retrieve

⟨σ

[1−v]

,σ

[1−c

]

,(σ

)

i∈[1,l]

⟩ from IoTSigned.

For each i retrieve all pairs (dsk,D

) from

IoTMembers and ⟨D

,dsk, (s

)⟩ ∈ IoTKeys

where identify

IoT

(σ

, m

, dsk, (s

)) = 1. Set f

= 0

if at least one of the following conditions holds:

CHECK1. More than one key dsk was found.

CHECK2. If the parent edge E

is honest, no (dsk,D

)

was found.

CHECK3. There is an honest D

but no entry

⟨∗,∗,(σ

,∗)⟩ ∈ IoTSigned exists.

CHECK4. There is a dsk

∗

∈ IoTKRL where

identify

IoT

(σ

,dsk

∗

,(s

)) = 1 and

no (dsk, D

,(s

)) for honest D

was found.

• If f

̸= 0, set f

= ver

IoT

(σ

) and add

⟨σ

,IoTKRL, f

⟩ to IoTVer.

• Output (VERIFIED, 0, sid, σ

DAA

,σ

[1−k]

), to V

if there exists at least one f

or f

equals to

0 for all j ∈ [1,v] and i ∈ [1,l]. Otherwise

(VERIFIED,1,sid,σ

DAA

,σ

[1−l]

Edge-LINK: On input (LINK, sid, σ, µ, σ

′

, µ

′

, bsn)

from some party V with bsn ̸= ⊥, else:

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

256

• Output ⊥ to V if at least one signature tuple (σ, µ,

bsn) or (σ

′

, µ

′

, bsn) is not valid.

• For each tsk in EdgeMembers and EdgeKeys com-

pute b = identify

DAA

(σ, µ, bsn, tsk) and b

′

identify

DAA

(σ

′

, µ

′

, bsn, tsk), set f = 0 if b ̸= b

′

and

f = 1 if b = b

′

= 1.

• If f is not deﬁned yet, set f = link(σ, µ, σ

′

, µ

′

, bsn).

Output (LINK, sid, f ) to V .

Edge-TRACE On input (TRACE,sid,σ

DAA

,µ,bsn)

from V , retrieve all pairs (tsk,M

) from

⟨M

,∗,tsk⟩ ∈ EdgeKeys where identify

DAA

(σ

DAA

, µ,

bsn, tsk) = 1. Output (TRACE,sid,E

) to V .

IoT-LINK: On input (LINK, sid, σ, m, σ

′

, m

′

) from

, output ⊥ to E

if at least one signature tuple (σ, m)

or (σ

′

) is not valid (veriﬁed via the verify inter-

face with IoTKRL =

0), else:

• For each (dsk,s

) in IoTMembers and IoTKeys

compute b = identify

IoT

(σ,m,dsk, s) and b

′

identify

IoT

(σ

′

,dsk

′

) and set f = 0 if b ̸= b

′

and f = 1 if b = b

′

= 1.

• If f is not deﬁned yet, set f = link(σ,m,σ

′

• Output (LINK,sid, f ) to E

IoT-TRACE On input (TRACE, sid, σ

) from E

retrieve all pairs (dsk,D

) from IoTMembers and

⟨D

,dsk, (s

)⟩ ∈ IoTKeys where identify

IoT

(σ

, m

dsk, (s

)) = 1. Output (TRACE,sid, D

) to E

6.3 Realizing Security Requirements

The complete security model of the intelligence part

of PRIV

E expressed in UC terms, including the ideal

functionality interfaces for all the internal phases and

some essential checks, is presented in § 6.2. Before

proceeding with the UC security proof in § 7, we ﬁrst

map the modeled interfaces to the security properties

outlined in § 4.

Anonymity (SP1): The anonymity of honest edge

devices, equipped with a valid TC, and their benign

(children) IoT devices is guaranteed by F due to

the random choice of tsk (E

’s private key) and dsk

’s private key) for the construction of every DAA

and IoT signature as part of the Edge/IoT-SIGN in-

terfaces. In case of corrupt devices (either Edge or

IoT), S provides the signature, which conveys the

signer’s identity, as the signing key is extracted from

the respective device key pair. This reﬂects that the

anonymity of the whole swarm is only guaranteed if

both the Edge and IoT devices are honest.

Traceability (SP2): CheckkeyHonest described in

§ 6 prevents registering an honest tsk/dsk in the

Edge/IoT-JOIN interfaces that match an existing sig-

nature, so that conﬂicts can be avoided and sig-

natures can always be traced back to the origin

devices. Moreover, in the context of Revocation

(SP3), CHECK4 guarantees that valid signatures in

the Edge/IoT-VERIFY interfaces are not revoked

due to the identify algorithm being deterministic.

Correctness (SP4): When an honest device success-

fully creates a signature, honest Veriﬁers will always

accept this signature. This is since honestly gener-

ated signatures in the Edge/IoT-SIGN interfaces pass

through ver

DAA

and ver

IoT

checks before being output

to the external environment.

Non-frameability (SP5): The non-frameability

property guarantees that this signature cannot be

linked to a legitimate one created by the target device.

In this context, CHECK3 in the Edge/IoT-VERIFY

interfaces ensures that if the edge (respectively IoT)

device is honest, then no adversary can create signa-

tures that are identiﬁed to be signed by the edge (re-

spectively IoT) device. This extends to the unforge-

ability (SP6) property, which dictates that it is com-

putationally infeasible to forge signatures.

Linkability (SP7): CheckkeyCorrupt deﬁned in § 6.2

prevents a corrupt tsk/dsk, matching with an exist-

ing signature, from being added to the lists of existing

members and keys, thus enabling the correct linkabil-

ity of signatures.

7 PRIV

E SECURITY PROOF

(SKETCH)

Since we have deﬁned the UC security model of

PRIV

E , we can now proceed with the security proof

of the proposed scheme, leveraging the Discrete Log-

arithm (DL) and Decisional Difﬁe-Hellman (DDH)

assumptions. This can be expressed as follows:

Deﬁnition 7.1. (The Discrete Logarithm (DL) as-

sumption (McCurley, 1990)) Given y ∈ G

, ﬁnd an

integer x such that g

= y .

Deﬁnition 7.2. (Decisional Difﬁe-Hellman (DDH)

assumption (Boneh, 1998)) Let G be a group gen-

erated by some g. Given g

and g

, for random

and independent integers a, b ∈ Z

, a computation-

ally bounded adversary cannot distinguish g

from

any random element g

in the group.

Theorem 7.1. The PRIV

E protocol securely realizes

F using random oracles and static corruptions when

DL and DDH assumptions hold if the CL signature

(Camenisch and Lysyanskaya, 2004) and the BLS sig-

nature (Boneh et al., 2003a) are unforgeable.

Proof of Theorem 7.1: We ﬁrst present a high-level

description of our proof that consists of a sequence

of games starting with the real-world protocol exe-

cution in Game 1. Moving on to the next game, we

PRIVÉ: Towards Privacy-Preserving Swarm Attestation

257

construct one entity, C, that runs the real-world pro-

tocol for all honest parties. Then, we split C into

two pieces: an ideal functionality F and a simula-

tor S that simulates the real-world parties. Initially,

we start with an “empty” functionality F . With each

game, we gradually change F and update S accord-

ingly, moving from the real world to the ideal world,

and culminating in the full PRIV

E F being realized

as part of the ideal world, thus proving our proposed

security model presented in § 6.2. The endmost goal

of our proof is to prove the indistinguishability be-

tween Game 1 and Game 14, i.e., between the com-

plete real world and the fully functional ideal world.

This is done by proving that each game is indistin-

guishable from the previous one, starting from Game

1 and reaching Game 14.

Our proof of Theorem 7.1 starts with setting up

the real-world games (Game 1 and Game 2), then in-

troducing the ideal functionality in Game 3. At this

stage, the ideal functionality F only forwards its in-

puts to the simulator and simulates the real world.

From Game 4 onward, F starts executing the setup

interface on behalf of the Issuer. Moving on to Game

5, F handles simple veriﬁcation and linking checks

without performing any detailed checks at this stage;

i.e., it only checks if the device belongs to a revoca-

tion list separately. In Games 6 − 7, F executes the

Join interface while performing checks to maintain

the registered keys’ consistency. It also adds checks

that allow only the devices that have successfully been

enrolled to create signatures. Game 8 proves the

anonymity of PRIV

E by letting F handle the sign

queries on behalf of honest devices by creating swarm

attestation using freshly generated random keys in-

stead of running the sign algorithm using the device’s

signing key. At the end of this game, we prove that by

relying on DDH and DL constructions, an external en-

vironment will notice no change from previous games

where the real-world sign algorithm was executed as

explained in our UC model (§ 6.2). The sequence of

games is explained in Figure 3. We use the “≈” sign

to express games’ indistinguishability. F

and S

Figure 3 represent the ideal functionality F and the

simulator S, respectively, as deﬁned in the i

game

for 3 ≤ i ≤ 14. Next, we present a sketch UC proof

for Theorem 7.1.

Proof. Game 1 (Real World): This is PRIV

E .

Game 2 (Transition to the Ideal World): An entity

C is introduced. C receives all inputs from the hon-

est parties and simulates the real-world protocol for

them. This is equivalent to Game 1, as this change is

invisible to E .

Game 3 (Transition to the Ideal World with Differ-

ent Structure): We now split C into two parts, F and

S, where F behaves as an ideal functionality. It re-

ceives all the inputs and forwards them to S, which

simulates the real-world protocol for honest parties

and sends the outputs to F . F then forwards these

outputs to E . This game is essentially equivalent to

Game 2 with a different structure.

Game 4 (F handles the Setup): F now behaves dif-

ferently in the setup interface, as it stores the algo-

rithms deﬁned in Section 6.2. F also performs checks

and ensures that the structure of sid, which represents

the issuer’s unique session identiﬁer for an honest I ,

aborts if not. When I is honest, S will start simulat-

ing it. Since S is now running I , it knows its secret

key. In case I is corrupt, S extracts I ’s secret key

from π

ipk

and proceeds to the setup interface on be-

half of I . By the simulation soundness of π

ipk

, this

game transition is indistinguishable for the adversary

(Game 4 ≈ Game 3).

Game 5 (F handles the veriﬁcation and Linking):

F now performs the veriﬁcation and linking checks

instead of forwarding them to S. There are no pro-

tocol messages; the outputs are exactly as in the

real-world protocol. However, the only difference is

that the veriﬁcation algorithms that F uses (namely

ver

DAA

and ver

IoT

) do not contain revocation checks,

so knowing KRL and IoTKRL for corrupt edge and

IoT, respectively, F performs these checks separately,

and the outcomes are equal (Game 5 ≈ Game 4).

Game 6 (F Handles the join): The join interface of

F is now changed. Speciﬁcally, F stores the mem-

bers that joined in its records. If I is honest, then

F stores the secret keys tsk and x

extracted from π

and π

by S for corrupt edge and IoT devices, respec-

tively. F sets the tracing key for each honest edge

device (as it already knows its key tsk) or calculates

it from the extracted tsk (for corrupt edge devices).

Only if the edge or the IoT device is already registered

in EdgeMembers or IoTMembers, F will abort the

protocol. However, I has already tested this case be-

fore continuing with the query JOINPROCEED; thus,

F will not abort. Knowing tsk and all children dsks,

F proceeds with adding the children IoT devices into

IoTMembers on behalf of edge devices. Therefore,

F and S can interact to simulate the real protocol in

all cases. Due to the simulation soundness of π

and

, Game 6 ≈ Game 5.

Game 7 (F Further Handles the join): If I is hon-

est, then F only allows the devices that joined to sign.

An honest edge device will always check whether it

joined with a TC in the real-world protocol, so there

is no difference for honest edge devices. In the case

that an honest M

performs a join protocol with a cor-

rupt edge device E

and an honest Issuer, S will make

a join query with F to ensure that M

and E

are in

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

258

Figure 3: Overview of the UC PRIV

E Proof.

EdgeMembers. Also, only joined IoT devices with

certiﬁed public keys can create signatures. The parent

edge device will check this before verifying its chil-

dren’s IoT signatures. Therefore Game 7 ≈ Game 6.

Game 8 (F Handles the Sign/ SP1: Anonymity):

(Simulating an edge device without knowing its se-

cret): In this game, we want to prove that an ex-

ternal environment cannot distinguish when F inter-

nally handles the signing queries instead of merely

forwarding them to S for M

. Suppose an environ-

ment can distinguish a signature (created by an honest

edge device with a secret signing key tsk) from a sig-

nature constructed by the same party but with a ran-

domly chosen fresh tsk. Then, we can use that envi-

ronment to break a Decisional Difﬁe–Hellman DDH

instance. M

uses tsk to set Q ← g

tsk

in the JOIN pro-

tocol, creates the proofs π

in joining and π in sign-

ing, and to compute link tokens nym. In the simula-

tion, we set Q ← α and simulate all proofs π

and

π. For nym, the power over the random oracle is

used: S chooses H

(bsn) = g

for r ← Z

, and sets

nym ← α

= H

(bsn)

tsk

without knowing tsk and out-

put a signature. Anonymity of the IoT devices is also

achieved against Veriﬁers through the use of entirely

random pseudonyms (s,o) that don’t reveal the iden-

tities of the IoT devices. Thus, starting with an IoT

pseudonym, V cannot tell the identity of the IoT de-

vice that generated this pseudonym unless it collabo-

rates with the edge device. An external environment

cannot distinguish between an honest IoT signature

and a signature by the same party but with a randomly

chosen fresh dsk. Therefore, Game 8 ≈ Game 7.

Game 9 (SP2: Traceability): When storing a new

tsk or dsk, F checks if CheckkeyHonest = 1 or

CheckkeyCorrupt = 1 for both keys. If the device

is corrupt, F checks that CheckkeyCorrupt = 1 for

the keys tsk or/and dsk that the simulator extracted.

This check prevents the adversary from choosing dif-

ferent keys. There exists only a single tsk for ev-

ery valid signature where identify

DAA

(σ

DAA

, µ, bsn,

tsk) = 1, and only a single dsk for every valid sig-

nature where identify

IoT

((σ, m, dsk, (s,o)) = 1 for

each edge and device, respectively, thus this check

will never fail. For keys of honest devices, F veri-

ﬁes that CheckkeyHonest = 1 whenever it receives or

creates a new key. With these checks, we avoid reg-

istering keys for which matching signatures already

exist. Since keys for honest devices are chosen uni-

formly from an exponentially large group and each

signature has exactly one matching key, the chance

that a signature under that key already exists is negli-

gible (Game 9 ≈ Game 8).

Game 10 (SP4: Correctness): In this game, F

checks that honestly generated signatures are always

valid. This is true since the sig

DAA

and sign

IoT

algo-

rithms always create signatures that pass through ver-

iﬁcation checks. Also, they satisfy identify

DAA

(tsk,

DAA

, µ, bsn)=1 and identify

IoT

((σ, m, dsk, (s, o)) =

1. F ensures, using its internal records MemberList

and DomainKeys, that honest users aren’t sharing the

same secret key tsk or dsk; this is reduced with a non-

negligible probability of solving the DL problem. As-

sume that F receives an instance h ∈ G

of the DL

problem and must answer log

(h). F chooses an

honest device and simulates its tasks using the un-

known DL of h as its secret key. When a tsk/dsk

matches one of this device’s signatures in the revo-

cation list, then this must be the discrete log of h, as

there is only one tsk/dsk matching a signature (Game

10 ≈ Game 9).

Game 11 (SP5: Non-Frameability): CHECK1 en-

sures that there are no multiple tsk or dsk values

matching one signature. F also checks, with the help

of its internal key records Members and DomainKeys,

that no other device already has a key that would

match this newly generated signature. If this fails, we

can solve the DL problem: We simulate a TC using

the unknown discrete logarithm of the DL instance as

tsk or dsk, as in the DDH reduction before. If a match-

ing tsk or dsk is found, then we have a solution to the

DL problem. Therefore, if solving the DL problem is

computationally infeasible, Game 11 ≈ Game 10.

Game 12 (SP6: Unforgeability): CHECK3 is added

to F to prevent anyone from forging signatures by

using honest tsk or dsk and their credentials. If the

Issuer is honest, CHECK2 prevents signing with in-

valid join credentials. This property is built on the un-

forgeability of the CL (Camenisch et al., 2016), com-

bined with the unforgeability of the aggregate signa-

tures (Boneh et al., 2003b).

Game 13 (SP3: Revocation): CHECK4 is added to

F . This ensures that honest devices are not being

PRIVÉ: Towards Privacy-Preserving Swarm Attestation

259

revoked. If an honest device is simulated, when a

matching key is identiﬁed in KRL or IoTKRL, it must

be the key of the target instance. Equivalent to solv-

ing the DL of the problem (Game 13 ≈ Game 12).

Game 14 (SP7: Linkability): All the remaining

checks of the ideal functionality F related to link

queries are now included. Since tsk, dsk only match

one signature and no other signature, Game 14 is in-

distinguishable from Game 13, and F now includes

all the functionalities. This concludes the proof.

8 EVALUATION

We analytically evaluate the computational complex-

ity and performance of our protocol by measuring

the execution time of the core phases described in

§ 5.1. These can be divided into (i) ofﬂine, i.e.,

the operations which can be pre-computed or do not

need to be executed in real-time (such as the Setup

and Join phases described in § 5.1.1) and (ii) on-

line operations. Since we are interested in the evalu-

ation of PRIV

E during runtime, the experiments pre-

sented here focus on the online operations (described

in § 5.1.2 and § 5.1.3).

Evaluation Environment Setup & Testing Meth-

ods: To better capture the resource-constrained nature

of real-world environments, each edge device was

emulated by a Raspberry Pi 4 (ARM v8), representing

a node with medium computational power and storage

capacity. Additionally, each edge device is equipped

with an Inﬁneon Optiga

SLB 9670 TPM 2.0, as the

underlying Root-of-Trust, leveraging the BN P256 el-

liptic curve for all ECC-oriented crypto operations.

The same platform was also used for evaluating the

veriﬁcation process of the attestation claims

. Each

IoT node was represented by the following platforms:

Raspberry Pi Pico (ARM Cortex M0+) and Arduino

Nano (ESP32-S3), demonstrating PRIV

E’s capability

to operate effectively on resource-constrained embed-

ded devices.

(IoT) Signature Construction: Running the proto-

col on IoT devices consists of two sequential steps:

(i) hash computation (for the construction of the at-

testation claims comrpising the necessary trustworthi-

ness evidence), and (ii) signature computation (hash-

to-point and point multiplication). Tab. 2 summarizes

the respctive computational costs. Our experiments

highlight the efﬁciency of the (conﬁguration) integrity

checks even for a rather large codebase (≈ 4 KB) (in

real-world IoT actuators the average code size is ≈

Please note that in practice, the Veriﬁer can be a more

powerful platform, resulting in improved veriﬁcation tim-

ings

Table 2: Overhead of PRIV

E on the IoT devices during

signing.

Raspberry Pi Pico Arduino Nano

Codebase (bytes) Mean (ms) ± (95% CI) Mean (ms) ± (95% CI)

SHA-256

2048 2.644 0.009 1.056 0.003

4096 5.158 0.008 2.007 0.002

SHA3

2048 5.210 0.017 2.037 0.003

4096 10.019 0.018 3.864 0.003

Hash to point 70.846 0.042 14.474 0.006

Point multiplication 140.719 0.529 32.011 0.109

Table 3: Aggregation and veriﬁcation of IoT signatures.

No. Aggregation Veriﬁcation

IoT (ms) (ms)

1 - 10.455

2 0.104 12.017

4 0.291 16.885

8 0.630 26.065

16 1.333 47.494

32 2.933 82.484

64 5.663 161.994

128 11.081 307.348

256 21.885 606.069

2 KB). As it will be described later on, the online

operations performed by the IoT device incur signif-

icantly lower overhead on the overall protocol lifecy-

cle compared to the tasks of the attestation process

executed on the more resource-rich edge device.

Aggregation (Edge) and Veriﬁcation (V ): The time

required for the aggregation of IoT signed attestation

claims (by the edge device), and their subsequent ver-

iﬁcation by V , is summarized in Tab. 3, for a varying

space of IoT signatures. What we can observe is that

the complexity of the aggregated signature construc-

tion is nearly linear to the number of signatures. This

Table 4: DAA SIGN Operation Timing (HW-TPM).

Activity Mean (ms) ± (95% CI)

Total Application Stack 609.05 0.57/0.55

TPM2 StartAuthSession 23.93 2.67

TPM2 PolicyCommandCode 14.99 0.03

TPM2 PolicyOR 21.64 0.09

TPM2 LoadExternal 71.34 0.24/0.44

TPM2 VerifySignature 55.97 2.64

TPM2 PolicyAuthorize 34.36 7.74

TPM2 Commit 95.11 0.03/0.05

TPM2 Hash 34.04 0.04/0.009

TPM2 StartAuthSession 23.19 2.67

TPM2 PolicyNV 20.99 0.03

TPM2 PolicyOR 40.62 0.09

TPM2 VerifySignature 53.92 2.64

TPM2 PolicyAuthorize 34.36 7.41

TPM2 Sign 39.77 0.04/0.01

TPM2 FlushContext 13.27 0.02/0.01

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

260

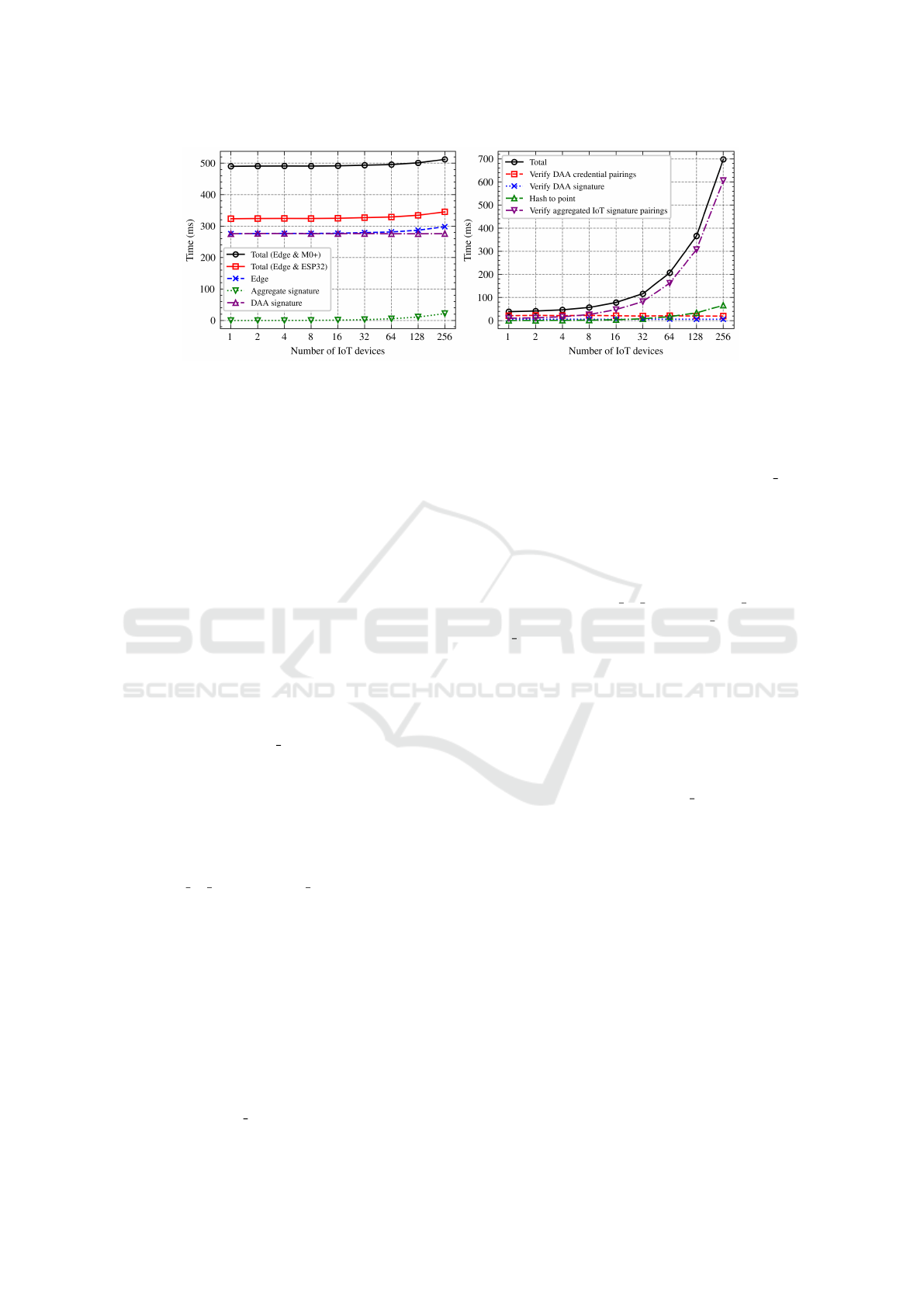
(a) Signing (b) Veriﬁcation

Figure 4: Scalability of PRIV

E under trusted Edge devices.

is crucial to the overall protocol serving as evidence

to its low complexity; i.e., does not increase (e.g.,

by growing exponentially) with the number of signa-

tures, making the aggregation operation efﬁcient even

for a large size of IoT devices. In Figs. 4a and 4b, we

also capture the device-level overhead during the at-

testation and veriﬁcation phases under a trusted edge

setting; i.e., without key restriction policies, which

necessitates the execution of additional commands for

asserting the correctness of the attestation key bind-

ing.

In this context, the most performance-intensive

operation is the veriﬁcation of the validity of each

edge device DAA signature on the aggregate re-

sult w.r.t, to the basename leveraged (dictating the

anonymity level). This is also then followed by the

validation of the overall aggregated IoT result (§ 4).

For the former, the DAA VERIFY is split into two

operational blocks: veriﬁcation of the (randomized)

DAA credential that takes up ≈ 155ms (irrespective

of whether (bsn) changes for every signature or not)

and veriﬁcation of the ECDSA signature that takes up

≈ 20ms. The DAA Credential veriﬁcation, while efﬁ-

cient, sums up to a higher required time than a simple

veriﬁcation, as it also includes the execution of addi-

tional TPM2 NV Read and TPM2 PolicyNV commands

for asserting that the credential’s associated private

DAA Key is binded to the correct key restriction us-

age policy holding the policy hash of the expected

(correct) device conﬁguration integrity. For the latter,

the veriﬁcation of the aggregated IoT signature can be

split into a ”hash-to-point” step to compute H(m

and the computations of the pairings to perform the

actual IoT signature veriﬁcation. This slow veriﬁca-

tion time is mainly due to the complexity of the pair-

ing operation, which is very expensive w.r.t. elliptic

curve point additions used for the aggregation.

DAA Signature (Edge): In Tab. 4, we present the

timings of the DAA SIGN operation (performed by

edge devices) in a zero-trust setting. Although the

overall signing takes ≈ 600 ms, it should be high-

lighted that the actual signing operation (TPM2 Sign

command) is quite fast, requiring ≈ 40 ms. How-

ever, recall that in the zero-trust setting, the DAA

key is protected by key restriction usage policies,

so it can only be used if the device is in a correct

state (and, thus, providing implicit attestation of the

edge device). As aforementioned, this is captured by

the execution of TPM2 NV Read and TPM2 PolicyNV

commands, followed by the TPM2 PolicyOR and

TPM2 PolicyAuthorize commands, which not only

verify the correct key binding (otherwise, the sig-

nature will not have been constructed correctly if

the current device state does not match with the

trusted state been stored on the Platform Conﬁgura-

tion Registers) but also enable the ratiﬁcation of the

pseudonyms’ validity used by the IoT devices; i.e.,

not have been revoked prior to be used for signing.

This process takes ≈ 100ms. Also, note that the du-

ration of 95.11 ms for the TPM2 Commit command

refers to the case where linkability is not needed,

therefore a basename is not used. In case linkabil-

ity capabilities are needed, a basename needs to be

used, which increases the execution time of this com-

mand to 224 ms, thus introducing a trade-off in terms

of efﬁciency versus linkability. However, even in this

case, the time needed for tracing back to the source of

a failed attestation signature, irrespectively of the size

and depth of the swarm topology, is rather efﬁcient

- serving as evidence on the applicability of PRIV

in safety-critical applications where pinpointing pos-

sible indications of risk is crucial; i.e., enabling the

fast deployment of reaction strategies.

PRIVÉ: Towards Privacy-Preserving Swarm Attestation

261

9 CONCLUSIONS

In this paper, we provided a novel design for a swarm

attestation protocol, with the innovative feature of

identity privacy preservation and accountable attesta-

tion, by creating an enhanced version of a DAA vari-

ant with traceability. Our solution avoids the limi-

tations of existing schemes by providing the ability

to conceal the identity of the devices (unless they are

compromised) and the ability to trace a failed attesta-

tion to the source swarm device that caused the fail-

ure. Additionally, to the best of our knowledge, we

provide the ﬁrst security analysis for swarm attesta-

tion with enhanced privacy features in the UC model.

Future work will explore how PRIV

E can be lever-

aged to achieve attestation evidence privacy, leading

us to complete Zero Trust architectures.

ACKNOWLEDGMENT

This research has received funding from the Euro-

pean Union’s Horizon Europe EU Research & In-

novation programs ENTRUST and REWIRE under

Grant Agreement No. 101095634 and 101070627, re-

spectively.

Additionally, Wouter Hellemans is an SB Ph.D.

fellow at FWO (Research Foundation Flanders) under

grant agreement 1SH3824N.

REFERENCES

(2016). Trusted Platform Module Library Part 1: Architec-

ture. Standard, Trusted Computing Group (TCG).

(2018). IEEE standard for adoption of OpenFog reference

architecture for fog computing. IEEE Std 1934-2018.

Abera, T., Brasser, F., Jauernig, P., Koisser, D., and Sadeghi,

A.-R. Granddetauto: Detecting malicious nodes in

large-scale autonomous networks. RAID ’21.

Ambrosin, M., Conti, M., Ibrahim, A., Neven, G., Sadeghi,

A.-R., and Schunter, M. (2016). SANA: Secure and

Scalable Aggregate Network Attestation. In CCS ’16.

Ambrosin, M., Conti, M., Lazzeretti, R., Rabbani, M. M.,

and Ranise, S. (2020). Collective remote attestation at

the internet of things scale: State-of-the-art and future

challenges. IEEE Comm. Survey, 22(4).

Ammar, M., Crispo, B., and Tsudik, G. (2020). Simple: A

remote attestation approach for resource-constrained

iot devices. In ACM/IEEE on Cyber-Physical Systems.

Asokan, N., Brasser, F., Ibrahim, A., Sadeghi, A.-R.,

Schunter, M., Tsudik, G., and Wachsmann, C. (2015).

Seda: Scalable embedded device attestation. CCS ’15.

Boneh, D. (1998). The decision difﬁe-hellman problem. In

International algorithmic number theory symposium,

pages 48–63. Springer.

Boneh, D., Gentry, C., Lynn, B., and Shacham, H. (2003a).

A Survey of Two Signature Aggregation Techniques.

CryptoBytes, 6.

Boneh, D., Gentry, C., Lynn, B., and Shacham, H. (2003b).

Aggregate and Veriﬁably Encrypted Signatures from

Bilinear Maps. EUROCRYPT 2003, pages 416–432.

Brickell, E., Camenisch, J., and Chen, L. (2004). Direct

Anonymous Attestation. CCS ’04, pages 132–145.

Brickell, E., Chen, L., and Li, J. (2008). A New Direct

Anonymous Attestation Scheme from Bilinear Maps.

In Trust 2008, page 166–178.

Camenisch, J., Chen, L., Drijvers, M., Lehmann, A.,

Novick, D., and Urian, R. (2017). One tpm to bind

them all: Fixing tpm 2.0 for provably secure anony-

mous attestation. In 2017 IEEE Symposium on Secu-

rity and Privacy (SP), pages 901–920.

Camenisch, J., Drijvers, M., and Lehmann, A. (2016). Uni-

versally Composable Direct Anonymous Attestation.

In PKC, volume 9615 of LNCS, pages 234–264.

Camenisch, J. and Lysyanskaya, A. (2004). Signature

schemes and anonymous credentials from bilinear

maps. In International cryptology Conf. Springer.

Carpent, X., ElDefrawy, K., Rattanavipanon, N., and

Tsudik, G. (2017). Lightweight swarm attestation: A

tale of two lisa-s. ASIA CCS ’17.

Chen, L., Dong, C., El Kassem, N., Newton, C. J., and

Wang, Y. (2023). Hash-based direct anonymous attes-

tation. In International Conference on Post-Quantum

Cryptography, pages 565–600. Springer.

Chen, L., El Kassem, N., Lehmann, A., and Lyubashevsky,

V. (2019). A framework for efﬁcient lattice-based daa.

In CYSARM, pages 23–34.

Chen, L., El Kassem, N., and Newton, C. J. (2024). How

to bind a tpm’s attestation keys with its endorsement

key. The Computer Journal, 67(3):988–1004.

Dolev, D. and Yao, A. (1983). On the security of public key

protocols. IEEE Trans. on Inf. Theory, 29(2).

Dushku, E., Rabbani, M. M., Vliegen, J., Braeken, A., and

Mentens, N. (2023). Prove: Provable remote attes-

tation for public veriﬁability. Journal of Information

Security and Applications, 75:103448.

El Kassem, N., Chen, L., El Bansarkhani, R., El Kaa-

farani, A., Camenisch, J., Hough, P., Martins, P., and

Sousa, L. (2019). More efﬁcient, provably-secure di-

rect anonymous attestation from lattices. Future Gen-

eration Computer Systems, 99:425–458.

Kohnh

auser, F., B

uscher, N., and Katzenbeisser, S. (2018).

Salad: Secure and lightweight attestation of highly dy-

namic and disruptive networks. ASIACCS ’18.

Larsen, B., Giannetsos, T., Krontiris, I., and Goldman, K.

(2021). Direct anonymous attestation on the road:

Efﬁcient and privacy-preserving revocation in c-its.

WiSec ’21, page 48–59.

Le-Papin, J., Dongol, B., Treharne, H., and Wesemeyer, S.

(2023). Verifying list swarm attestation protocols. In

Proceedings of the 16th ACM Conference on Security

and Privacy in Wireless and Mobile Networks.

McCurley, K. S. (1990). The discrete logarithm problem.

In Proc. of Symp. in Applied Math, volume 42. USA.

Meier, S., Schmidt, B., Cremers, C., and Basin, D. (2013).

The tamarin prover for the symbolic analysis of secu-

rity protocols. In Conf. on Comp. Aided Veriﬁcation.

Wesemeyer, S. and all (2020). Formal analysis and imple-

mentation of a tpm 2.0-based direct anonymous attes-

tation scheme. ASIA CCS ’20.

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

262