A Safety-Centric Analysis and Benchmarks of Modern Open-Source

Homomorphic Encryption Libraries

Nges Brian Njungle

1 a

, Milan Stojkov

2 b

and Michel A. Kinsy

1 c

STAM Center, Ira A. Fulton Schools of Engineering, Arizona State University, 85281, U.S.A.

Faculty of Technical Sciences, University of Novi Sad, Serbia

Keywords:

Open-Source Software, Advanced Cryptography, Homomorphic Encryption, Security and Performance

Analysis.

Abstract:

Homomorphic Encryption (HE) is a rapidly evolving ﬁeld in secure computation, offering very strong secu-

rity guarantees in privacy-preserving data processing. A large number of commercial systems that prioritize

privacy depend on open-source HE libraries to ensure secure and conﬁdential computation. However, the

security of these open-source libraries remains questionable, as they do not demonstrate strong security as-

surances, such as formal veriﬁcation, in their development process. In this work, we investigate security

vulnerabilities and the efﬁciency of the implementations of the four main HE schemes in the most commonly

used open-source HE libraries. To analyze security, we employ the SafeRewrite open-source dynamic analysis

tool, which uses symbolic execution techniques to validate code correctness. The study reveals several secu-

rity vulnerabilities, errors, and warnings in all of the libraries. In terms of performance, we assess the latency

and scalability of the fundamental HE operations in these libraries. The results indicate that the Cheon-Kim-

Kim-Song (CKKS) scheme is the fastest HE scheme, whereas OpenFHE is, on average, the best-performing

HE library. Overall, this research underscores the signiﬁcance of using secure development approaches and

frameworks in implementing HE algorithms to ensure stronger security guarantees and correctness while min-

imizing performance impacts.

1 INTRODUCTION

Modern and advanced security and privacy proto-

cols such as multi-party computation (Lindell, 2020),

zero-knowledge proofs (Aad et al., 2023), blockchain

technology (Adam Hayes, 2023), differential privacy

(Hilton and Cal, 2012), and homomorphic encryp-

tion (Ogburn et al., 2013) represent an opportunity

to reevaluate trust, enhance privacy, and improve the

security of critical systems. Homomorphic encryp-

tion (HE) is a compelling area of study due to its po-

tential applications in privacy-preserving outsourced

cloud computation, machine learning, and edge tech-

nologies. It provides ﬁrm security guarantees based

on complex mathematical problems during compu-

tations. Many privacy-preserving initiatives utiliz-

ing other protocols, such as multi-party computation,

still often employ it to minimize communication over-

https://orcid.org/0009-0006-3393-6851

https://orcid.org/0000-0002-0602-0606

https://orcid.org/0000-0002-1432-6939

head and enhance security guarantees (Pulido-Gaytan

et al., 2021). While the open-source community

offers numerous implementations of HE protocols,

the sophistication and complexity of their algorithms

pose challenges in understanding their implementa-

tion integrity (Alenezi and Zarour, 2020).

Open Source Software (OSS) provides a platform

for sharing code openly, allowing global develop-

ers to collaborate by accessing, reviewing, editing,

and modifying codebases. For good reasons, OSS

is highly valued due to its ﬂexibility, reduced devel-

opment time, cost-efﬁciency, and strong community

backing. However, OSS also presents security chal-

lenges as it allows hackers to exploit vulnerabilities

by scrutinizing code through code reviews, examin-

ing public bug trackers, and even injecting malicious

code into public repositories. The Log4Shell bug and

exploits illustrates the problem with trusting OSS for

critical systems, as it creates a potential for critical

security exposure (Doll et al., 2025). While enter-

prise software also contains bugs, it holds an edge

over OSS because its source code is not publicly ac-

Njungle, N. B., Stojkov, M. and Kinsy, M. A.

A Safety-Centric Analysis and Benchmarks of Modern Open-Source Homomorphic Encryption Libraries.

DOI: 10.5220/0013626400003979

In Proceedings of the 22nd International Conference on Security and Cryptography (SECRYPT 2025), pages 483-494

ISBN: 978-989-758-760-3; ISSN: 2184-7711

483

cessible. As a result, attackers need to employ more

advanced techniques like decompilation to derive any

valuable insights (Bernstein, 2019).

With the widespread adoption of open-source

HE libraries in critical applications and systems like

in privacy preserving machine learning applications

(Njungle et al., 2025) and biometric systems (Yang

et al., 2023), there have been no efforts to prove that

these open-source HE libraries are devoid of all types

of software vulnerabilities. Between the complex-

ity of HE, the entangled development process, the

open-source nature of these libraries, and the absence

of implemented security assurances in any of the li-

braries make it highly challenging to guarantee users

that they are entirely free from human errors, design

ﬂaws, and other factors that could lead to future secu-

rity breaches. A single security exploit in any of these

libraries could have catastrophic consequences for the

applications built on them, primarily because they are

used in developing highly sensitive privacy-centric

applications. This study evaluates the security and

performance implications of leading open-source HE

libraries — Microsoft SEAL, TFHE/TFHE-rs, HElib,

and OpenFHE. Our main contributions are as follows:

• Security analysis of open-source HE libraries by

examining key modules extensively utilized in

different components of the libraries using a dy-

namic analysis tool called SafeRewrite. We show

some potential security ﬂaws detected in SEAL,

HElib, and OpenFHE and their exploitability.

• Performance benchmarking of the basic opera-

tions required for HE applications built on the

libraries across the HE schemes of BGV, BFV,

CKKS, and TFHE. Additionally, we analyze how

these operations scale with different security pa-

rameters using micro-benchmarks.

In this work, we evaluate the two most critical

aspects of HE implementation in leading libraries.

Given the high computational complexity of HE algo-

rithms, this evaluation is essential for providing users

with insights to compare libraries and schemes under

speciﬁc security parameters. These benchmarks help

guide users in selecting the most suitable library and

scheme for different application scenarios.

2 BACKGROUND

2.1 Homomorphic Encryption

Homomorphic encryption is an advanced crypto-

graphic concept that allows users to perform com-

putations on encrypted data without having to de-

crypt it. The concept of Fully Homomorphic Encryp-

tion (FHE) was ﬁrst introduced by in (Gentry, 2009),

which proposed the use of bootstrapping to overcome

noise growth—an idea that marked a turning point

in the development of HE. Today’s prominent HE

schemes are built around a core set of at least ﬁve fun-

damental cryptographic operations, as detailed below.

Key Generation: It is used to generate the public key

(pk) and secret key (sk) from the scheme (Gupta et al.,

2023). It takes a security parameter λ, which dictates

the level of security, such as key length or complexity,

and randomly selects secret elements $ that belong to

some distribution χ deﬁned by the encryption scheme.

The public key is generated by applying some crypto-

graphic function φ to sk.

Encryption: It is the process of converting a plain-

text message into ciphertext to prevent unauthorized

access (Bharti Kaushik, 2023). It uses a public key

pk to generate the ciphertext, ensuring that only au-

thorized users with the corresponding secret key sk

can decrypt the ciphertext back into its original mes-

sage. Given an encryption function Encrypt deﬁned

for a cryptographic scheme, this function takes as in-

put a plaintext message m and a public key pk and

outputs the corresponding ciphertext ctxt.

Addition: In HE, addition is deﬁned as a function

that takes two or more ciphertexts and outputs a new

ciphertext corresponding to the sum of plaintext mes-

sages within those ciphertexts (Gupta et al., 2023).

The result is an encrypted value that, when decrypted,

matches the sum of the original plaintexts. This prop-

erty is a crucial feature of HE schemes as it allows

computations to be performed directly on ciphertexts.

Multiplication: It takes two or more ciphertexts and

produces a new ciphertext containing multiplicative

results of the messages in the ciphertext (Gupta et al.,

2023). Multiplication and addition allow ciphertext

to be manipulated in a way that preserves the original

mathematical operations on plaintexts, creating a ﬁeld

structure essential for all computations.

Decryption: It is the process of converting encrypted

information back to plaintext (Bharti Kaushik, 2023).

It takes a secret key sk and an encrypted message in

the form of a ciphertext ctxt and returns the hidden

message in the ciphertext. It is usually the mathemat-

ical inverse of the encryption function.

2.2 Most Adopted FHE Schemes

FHE schemes are classiﬁed into four generations,

each marked by advancements in efﬁciency, perfor-

mance, and practical usability (Zhang, 2021). The

ﬁrst generation of schemes were theoretically ground-

breaking but computationally demanding, as seen in

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

484

the one proposed in (Gentry, 2009). These schemes

laid the foundation for FHE, proving that it is pos-

sible to perform arbitrary computations on encrypted

data. The second generation focused on optimizing

HE’s efﬁciency, which led to the ﬁrst set of practical

schemes for a limited number of applications. Ex-

amples of schemes here include: the Brakerski, Gen-

try, Vaikuntanathan (BGV) (Aggarwal et al., 2014)

scheme and the Brakerski/Fan-Vercauteren (BFV)

scheme (Fan and Vercauteren, 2012). The third gener-

ation further enhanced performance by reﬁning math-

ematical techniques. An example of a scheme here

is the Fast Homomorphic Encryption Over the Torus

(TFHE) scheme (Chillotti et al., 2018). The fourth

generation focused on efﬁciency and practicality. In-

novations here included more sophisticated mathe-

matical structures and optimizations for speciﬁc use

cases. An example here is the Cheon, Kim, Kim, and

Song (CKKS) Scheme (Cheon et al., 2016a).

CKKS, TFHE, BFV, and BGV are four distinct

schemes that form the foundation for most contempo-

rary work in HE-based privacy and security.

2.3 Open-Source Homomorphic

Encryption Libraries

A wide range of applications that utilize HE depend

on open-source libraries for implementation. Given

the mathematical complexity and technical challenges

involved in developing HE systems, these libraries are

essential in making the technology more accessible

and fostering its broader adoption.

Homomorphic Encryption library (HElib): The

HElib library supports the BGV and CKKS schemes

(Halevi and Shoup, 2020). It incorporates bootstrap-

ping for the BGV scheme and enables HE evaluation

of ciphertexts at the bit level. It adopts optimiza-

tions such as the Single Instruction, Multiple Data

(SIMD) ciphertext packing technique, assembly lan-

guage implementation for HE, automatic noise man-

agement, multi-threading capabilities, and the intro-

duction of plaintext objects that mirror the functional-

ity of ciphertext. HElib lacks a good documentation,

but learning from examples provided on GitHub is

straightforward for people with a background in cryp-

tography (Halevi and Shoup, 2020).

Fast Fully Homomorphic Encryption Library over

Torus (TFHE)/TFHE-rs: TFHE was proposed in

2016 by Ilaria et al. and saw its original C++ im-

plementation released in 2017 (Chillotti et al., 2016).

It relies on Fast Fourier Transform (FFT) proces-

sors for enhanced computational speed and perfor-

mance. TFHE has seen recent enhancements and the

introduction of new features through a more recent

Rust implementation. Both the original C++ imple-

mentation and the Rust implementations support the

homomorphic evaluation of twelve gates ( NAND,

OR, AND, XNOR, NOT, COPY, CONSTANT, NOR,

ANDNY, ANDYN, ORNY, ORYN) as well as the

MUX gate, which plays a crucial role in it’s pro-

grammable bootstrapping. While the C++ library of-

fers only a native interface, the Rust library provides

a C interface, client-side WebAssembly, and Rust in-

terface, making it easy to use in applications across

multiple programming languages (Zama, 2022b).

OpenFHE (Formerly PALISADE): It encompasses

various schemes such as BGV, BFV, CKKS, FHEW,

TFHE, along with the LMKCDEY schemes (Badawi

et al., 2022). It draws from efﬁcient implemen-

tations of prior HE projects, such as PALISADE,

HEAAN, and HElib. Also, it introduced novel con-

cepts to enhance the design, scalability, and perfor-

mance of HE implementations. The core modules

of the implementation include the Primitive Math

layer for low-level arithmetic and number-theoretic

transforms, the Cryptographic Layers for various HE

scheme implementations, the Encoding Layer for

scheme-speciﬁc encoding, and the Polynomial Op-

erations Layer that supports lattice and ring algebra

operations (Al Badawi et al., 2022). OpenFHE also

extends BFV, BGV, and CKKS to implement Thresh-

old HE for multi-party computing and Proxy Re-

Encryption for Cloud Computing. Notably, OpenFHE

provides functionality to switch between CKKS and

FHEW/TFHE, aiding in more precise evaluation of

non-linear functions in CKKS applications.

Microsoft Simple Encrypted Arithmetic Library

(SEAL): It is currently the most adopted HE li-

brary, offering support for the BFV, BGV, and CKKS

schemes (SEAL, 2023). The library is enhanced with

support for the Intel HEXL accelerator, Microsoft

GSL for array memory bound checking access, and

ZLIB and Zstandard for ciphertext compression. With

SEAL, only the polynomial degree is required for

setup, thus widely considered the easiest to use among

all HE libraries. It supports Python, JavaScript, and

TypeScript interfaces for the development of HE ap-

plications.

The Other HE libraries not included in this

study are Lattigo, a multi-party HE library devel-

oped in the Go programming language, thus not

supported by SafeRewrite (Mouchet et al., 2023).

Palisade (Polyakov et al., 2018), HEAAN (Cheon

et al., 2016b), and FV-NFLlib (Aguilar-Melchor et al.,

2021) are all deprecated HE libraries. Concrete is a

Python extension of TFHE-rs for prototyping privacy-

preserving machine learning (Zama, 2022a).

A Safety-Centric Analysis and Benchmarks of Modern Open-Source Homomorphic Encryption Libraries

485

3 EXPERIMENT

In this work, we used TFHE-rs 0.7.1, Microsoft

SEAL 4.1, HElib 2.3.0, and OpenFHE 1.1.2, the latest

stable versions of these libraries at the time this work

was completed. We performed these experiments on

an Intel Core i7-11700 processor, 16 GB of RAM, an

8-core CPU with 16 threads, and Ubuntu 22.04.

3.1 SafeRewrite

SafeRewrite is an open-source dynamic analysis soft-

ware tool designed to enhance code veriﬁcation

through dynamic testing of various inputs (Bernstein,

2021). The tool was created for software veriﬁcation

in the ﬁeld of Post-Quantum Cryptography (PQC),

where there is limited experience in developing its

cryptographic primitives. It has broader applications

in the development of all advanced cryptography. The

tool employs symbolic execution techniques, system-

atically reasoning about the program’s paths using

mathematical formulas to verify the code’s correct-

ness. This veriﬁcation level is important in HE, where

the security stakes are very high, and experience in

developing its principles is also limited. It dynami-

cally analyzes inputs for each section of the program,

tracking symbolic values rather than relying on ac-

tual inputs as in normal execution. It utilizes Valgrind

(Nethercote and Seward, 2007) and Angr.io (Shoshi-

taishvili et al., 2016) for bug detection as they further

enhance its capabilities to ensure the integrity and cor-

rectness of code. It compiles code snippets into bina-

ries, which are unrolled to check different input cases

automatically. It ensures that optimized software is

precisely the same as the reference software for all

unrolled cases. The tool speciﬁes two compilers used

to compile the code, and results from these compilers

are compared. For C code, it uses GCC and Clang,

and to handle C++ code, it was modiﬁed to support

G++ and Clang++ compilers as well. Each function

has an API ﬁle specifying the parameters required for

veriﬁcation. The code is passed through the analyzer,

which compiles and generates binaries for Valgrind

and Angr.io. The main limitations of SafeRewrite are

that it works only with ﬁxed-length inputs and is efﬁ-

cient only with very small code modules.

3.2 Threat Model

The security analysis conducted in this work aims to

identify potential vulnerabilities in open-source HE

libraries. The use of these libraries in critical ap-

plications necessitates proving that their code is not

vulnerable to any type of exploit, as any future ex-

ploit would have devastating consequences in the real

world. In this work, we analyzed a subset of func-

tions in these libraries. For each library, we present

and discuss one implementation ﬂaw detected. We

consider an attacker to be any software analyst who

can study the code of these open-source libraries,

determine issues, and carefully mount equivalent at-

tacks on the different deployment instances of these

libraries. Such attacks include: data corruption at-

tacks and side-channel attacks. We do not mount any

active attacks on these libraries using any of the issues

detected in this work. However, we provide simple

code snippets that can exploit some of the identiﬁed

vulnerabilities in isolation. For any code snippet dis-

cussed in this paper, we ensured that we identiﬁed at

least one usage instance in the equivalent library that

creates a system state with the issue.

3.3 Security Analysis

3.3.1 Issues Criteria

This experiment utilizes SafeRewrite to test for na

ıve

but critical bugs in state-of-the-art open-sourced HE

libraries. SafeRewrite was chosen because it is openly

available, already used to safeguard PQC primitives,

and has a higher probability of violation detection for

generic function constructs (Bernstein, 2021). The

tool was modiﬁed to support C++ code through G++

and Clang++. This work focused on memory safety

issues, which account for approximately 70% of vul-

nerability assignments in the Common Vulnerabili-

ties and Exposures database (Lord, 2023). We exam-

ine these issues through non-constant-time code, mis-

matched results from different compilers, and unsafe

unrollsplit and unsafe unrollment errors and warn-

ings. These issues are selected because they offer con-

cise insights into the behavior of every input set.

Non-constant-time code is identiﬁed by variations

in runtime across different compilers. If the refer-

enced code is equivalent to the optimized code for

every case, both compilers will yield the same re-

sults; otherwise, further optimization is needed. This

is marked as unsafe because it is generally the basis

for timing side-channel attacks, for example, the PQC

Frodo Software key-recovery timing attack of 2020

(Guo et al., 2020). A compiler mismatch warning oc-

curs if the same input set produces different results

from the two compilers. This occurs when memory

allocations are not handled properly and is often ac-

companied by an unsafe unrollment or unsafe unroll-

split error pinpointing the speciﬁc cases that caused

this behavior. An exploit of this type of issue is the

CCA FrodoKem bug detected by Saarinen (Saarinen,

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

486

2020). Unsafe unrollment shows the different cases

encountered during the software’s unrollment process

where inputs were unsafe. On the other hand, unsafe

unrollsplit shows out-of-range unsafe inputs detected

during the unrollment process since SafeRewrite test

how the code handles out of range inputs.

3.3.2 Analyzed Functions

Ideally, we would want to check the entire codebase

of every library for correctness, but this would be

time-consuming and cumbersome. Also, SafeRewrite

is not sophisticated enough to support large and com-

plex codebases like those found in these libraries,

thus, analyzing libraries as a whole is not tractable.

To still gain insight into the prevalence of errors in

some of the simplest yet essential functions of these

libraries, we conducted a manual study to understand

the workings of various modules. We then classi-

ﬁed the functions from each library into three classes:

common, somewhat common, and high-level based on

their similarities across the different libraries.

Common functions are general cryptographic

primitives used as basic building blocks to implement

HE schemes. Most of the code in these functions is

the same across multiple cryptography libraries, such

as random number generator and Blake2b hash func-

tion implementations in SEAL and OpenFHE. Ran-

dom number generators are used to generate seed

numbers, while hash functions are often used for data

integrity. Both modules are required for sampling and

integrity during key generation and data encryption.

Somewhat common functions have the same func-

tionality but different implementations in different li-

braries. Examples include the Shake256, SHA3-256,

and factorization functions in OpenFHE, SEAL, and

HElib libraries. Functions in this class sometimes use

functions from the common functions class.

High-level functions are the library’s implementa-

tion of different high-level operations, some of which

are exposed to the library users through API calls. Ex-

amples of functions here include addition, multipli-

cation, re-linearization, and key generation functions

found in all libraries. high-level functions are often

implemented as part of C++ classes, and they use very

sophisticated structures while inheriting from some-

what common and common function classes. Func-

tion implementation at this level differs signiﬁcantly

across libraries, as system design plays a vital role in

the organization of these functions.

In this work, we extracted a total of forty functions

from all classes and analyzed them with SafeRewrite.

This was no trivial task, as it required a deep under-

standing of the codebases of each library and making

the necessary modiﬁcations for SafeRewrite.

For TFHE security analysis, we utilized the orig-

inal TFHE library and TFHE-rs. The TFHE library

was developed in C and C++ and is no longer actively

maintained, although some applications still use it.

We extracted functions from it and ran them through

SafeRewrite. For completeness, since TFHE-rs is

the most actively maintained and widely used TFHE

implementation, and SafeRewrite does not support

Rust, we ran the code through the Cargo audit static

analyzer for Rust. The analyzer returned thirty

warnings related to design issues. Subsequently,

we executed the TFHE-rs code through the Cargo

test, and surprisingly, four (4) unit tests failed. The

failed test cases came from the conversion of 64-bit

ﬂoating point numbers to 64-bit integer numbers in

the function convert f64 i64, a buffer overﬂow

when dealing with bit blocks used in the construction

of the circuits in the block decomposition

function, and poor validation of integers in

test invalid generic compact integer and

test invalid generic compact integer list

functions. Scanning TFHE-rs through the online code

analyzer Snyk (Aman Anupam, 2020) does not give

any errors. However, it indicates eight medium-level

errors in packages used in development.

3.3.3 load64 Function from SEAL

The load64 function in Listing 1 is used to load 8

bytes into an unsigned 64-bit integer in little-endian

order. This function is used in the keccak absorb

function, which is used in the absorbing step of Kec-

cak in constructing various hash functions. The hash-

ing functions are used to construct the underlying

operations, such as key generation and encryption,

for all schemes implemented in SEAL. Results from

SafeRewrite indicate that, during the unrolling pro-

cess for some inputs, there is a mismatch in the output

between different compilers. This happens because of

an invalid pointer, which leads to a buffer over-read if

the size of the x array differs from 8 bytes.

1 stati c u i n t 64_t load6 4 ( c onst

uint8_ t x [ 8]) {

2 unsigne d int i;

3 uint64_ t r = 0;

4 for (i =0; i <8; i ++)

5 r |= ( u i n t64_t ) x [ i ] << 8* i ;

6 retu r n r ; }

Listing 1: Load64 function extracted from SEAL.

If the x array passed to load64 is smaller than

8 bytes, the function may also read data adjacent in

memory into r. Also, if the input array to load64

points to out-of-bound memory, the function also

reads 8 bytes of it into r; thus, an attacker can leak

A Safety-Centric Analysis and Benchmarks of Modern Open-Source Homomorphic Encryption Libraries

487

or corrupt information in an application by exploring

this issue and forcing a smaller or larger size array

into the application using this load64 function.

For illustrative purposes, Listing 2 initialize a seed

array of type uint8 t and size 8 and a uint32 t in-

teger value of 136. If we loop through the seed array

using the load64 function, we will load more data

into the application than we would by accessing up to

17 bytes of memory.

1 int main ( int argc , char

* arg v [] ) {

2 uint8_ t m [8] =

{0 ,0 ,0 ,0 ,0 ,0 ,0 ,0};

3 int r = 1 36;

4 for ( int j = 0; j < r /8; j ++) {

5 uint64_ t c = load 6 4 ( m +

8* j ) ;

6 prin t f ( " loa d 64 result :

% ll u \ n " , c );

7 }

8 retu r n 0; }

Listing 2: Reading out-of-bounds using load64 function.

This code snippet demonstrates how load64 is

being used in the keccak absorb function, which

is used in shake256 absorb. shake256 is the

default hash function used in SEAL. It is initial-

ized in refill buffer with an 8-byte seed array.

shake256 absorb initializes keccak absorb with a

macro called SHAKE256 RATE whose value is 136 and

the seed array of size 8 bytes. The keccak absorb

calls the load64 function through an iteration of rate

bytes, which is equal to SHAKE256 RATE divided by

8. Calling load64 as shown in Listing 2 with these

parameters can load data into the application beyond

the 8 bytes of the seed input array.

3.3.4 store64 Function in OpenFHE

The store64 function in Listing 3 is used to store

a 64-bit unsigned integer in memory at a loca-

tion pointed to by dst. This function is used in

blake2b final, which is used in the blake2b func-

tion, and further used in the construction of the hash

function used in encryption and key generation func-

tions implemented in the OpenFHE library. memcpy is

used to copy the integer into the destination memory

on little-endian systems. The data is extracted byte af-

ter byte and stored at the memory destination on non-

little-endian systems. There is an assumption that the

memory pointed to by the destination has at least 8

bytes available to store the 8 bytes of the uint64 t

variable. However, there is no check to ensure the

destination actually has a valid memory location with

sufﬁcient space. Suppose the destination points to

an invalid memory location. In that case, the pro-

gram will lead to unexpected behavior. If the destina-

tion memory is smaller than 8 bytes, the function will

override adjacent memory blocks if it receives data

larger than the available memory.

1 stati c B L A K E 2 _ I N L I N E void

store6 4 ( vo id * dst , u i n t64_t w ) {

2 # if

define d ( NATI V E _ L I T T L E_ENDI A N )

3 memc p y ( dst , &w , siz e of

w) ;

4 # els e

5 uint8 _ t *p = ( u int8_t

*) ds t ;

6 p [0 ] = ( uint8_ t ) (w >>

0) ;

7 p [1 ] = ( uint8_ t ) (w >>

8) ;

8 p [2 ] = ( uint8_ t ) (w >>

16) ;

9 p [3 ] = ( uint8_ t ) (w >>

24) ;

10 p [4 ] = ( uint8_ t ) (w >>

32) ;

11 p [5 ] = ( uint8_ t ) (w >>

40) ;

12 p [6 ] = ( uint8_ t ) (w >>

48) ;

13 p [7 ] = ( uint8_ t ) (w >>

56) ; }

Listing 3: Store64 function found in OpenFHE.

To show how this function can be exploited,

Listing 4 initializes a uint8 t array and stores a

uint64 t value larger than the maximum value of

uint8 t. In this case, the value at desti[1] is over-

written by the value of a since desti[0] cannot hold

the value of a. It is also worth noting that the value

of desti[0] is not equal to the value of a as it is a

wrap-around the size of uint8 t.

1 int main ( int argc , char

* arg v [] ) {

2 uint64_ t a = 40 0; uint8_t

dest i [64];

3 store 6 4 (& dest i [0] , a);

4 prin t f ( " The v alue of a: % ld

\n " , a ) ;

5 prin t f ( " Sto r ed values : % u % u

\n " , des t i [0] , desti [1]) ;

6 retu r n 0; }

Listing 4: Memory overide exploit with store64.

In OpenFHE, this same issue appears in the

blake2b final function. Data is stored dynami-

cally into a buffer of type uint8 t from S->h[i] of

type uint64 t. S->h[i] receives its data from the

blake2b compress function where three uint64 t

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

488

values are XORed with each other. This indicates that

S->h[i] can hold values larger than 256, which is

the maximum value of uint8 t, thus inputting unin-

tended data into the buffer.

3.3.5 RevInc Function in HElib

The RevInc function in the code snippet shown in

Listing 5 is used to reverse the increments of a long

integer up to a speciﬁc bit position k. The function

is used in the BRC init function, which is part of the

BasicBitReverseCopy function in NTL, used in the

construction of all mathematical operations, such as

addition and multiplication, for both schemes in HE-

lib. The function takes two long input arguments a

and k. The code will lead to an integer overﬂow when

shifting one bit to the left by (k-1) bits if k-1 ex-

ceeds the number of bits in long, which is the size

of m. The maximum value of k for this operation is

sizeof(long) * 8, but the function can receive val-

ues of k much larger.

1 stati c long R e vInc ( lon g a , lo ng

k) {

2 long j = k ; lo ng m = 1 L << (k

- 1) ;

3 whi l e ( j && (m & a ) ) {

4 a ˆ= m ;

5 m > >= 1;

6 j - -; }

7 if (j )

8 a ˆ= m ;

9 retu r n a ; }

Listing 5: RevInc function found in HElib.

For an illustrative exploit of this function, if the

value of k = 64, regardless of the value of a, RevInc

will return a large negative number due to the integer

overﬂow error present in its implementation. Looking

at an instance where k = 64 and a = 0, the return

value of RevInc is the largest negative long integer

−9223372036854775808 as shown in Listing 6.

1 int main ( int argc , char

* arg v [] ) {

2 l ong a = 0; long b = 64;

lon g c ;

3 c = Rev I nc (a , b ) ;

4 prin t f ( " lo ng a : % ld \ n " , a ) ;

5 prin t f ( " th is is the r evInc

% ld \ n " , c);

6 retu r n 0; }

Listing 6: RevInc function Exploit demonstration in HElib.

In the context of HElib, the function BRC init

calls RevInc and stores the value into an array rev.

In the function BasicBitReverseCopy, the values of

rev are used as indices of another array B. Trying to

access the value of B at an index for this case of k will

result in an out-of-bounds read, since it is not possible

to have an array with negative indices.

As shown in Table 1, forty functions were ex-

tracted from all libraries and all function classes.

Modiﬁcations were made in some cases, such as

changing complex return types, removing complex

sections of functions that depend on other extremely

large modules, and setting an upper bound for loops

to ease veriﬁcation. All changes were carefully an-

alyzed to ensure that the holistic nature of the func-

tions is maintained with no new states introduced by

the changes. Primarily, we did not introduce any new

code or remove security checks from the modiﬁed

functions. From the extracted functions, thirty-ﬁve

errors and warnings were detected in these libraries.

Though we did not exploit any of the identiﬁed is-

sues, the mere presence of these vulnerable states is a

cause for concern—especially given their use in appli-

cations that demand extremely high levels of security.

Table 1: Summary of Security Analysis results from open-

source FHE Libraries with SafeRewrite. F: Function, SC:

Somewhat Common HL: High Level.

Criterion SEAL OpenFHE HElib TFHE

Extracted F 13 11 9 7

Common F 6 5 2 1

SC F 5 2 2 2

HL F 2 4 5 4

C F 8 3 0 5

C++ F 5 8 9 2

Unrollment 0 1 1 0

Unrollsplit 2 4 0 0

Unrollment 6 5 2 1

Unrollmismatch 6 4 2 1

GCC == Clang 1 2 - 1

G++ == Clang++ 2 2 3 0

3.4 Performance Analysis

This part of the experiment evaluates the performance

of the major HE schemes: BGV, BFV, CKKS, and

TFHE across the major open-source HE libraries:

SEAL, OpenFHE, HElib, and TFHE-rs. The exper-

iment was designed to evaluate the performance of

various HE schemes across different libraries by com-

paring their latency under a range of security param-

eters. Variations in performance are largely attributed

to the distinct implementation choices and optimiza-

tions made by each library’s developers. For instance,

OpenFHE uses a custom implementation of the Num-

ber Theoretic Transform (NTT) for polynomial mul-

tiplication, while HElib depends on the NTL library

for its fundamental mathematical operations. These

design differences also inﬂuence how the libraries

A Safety-Centric Analysis and Benchmarks of Modern Open-Source Homomorphic Encryption Libraries

489

are used in practice while also affecting their perfor-

mance and scalability during computations.

Our investigation involved a detailed analysis of

each library’s functionality, accompanied by the de-

velopment of micro-benchmarks for all supported

schemes. We measured the latency of key gener-

ation, encryption, and decryption for a single vari-

able. For homomorphic addition and multiplica-

tion, performance was evaluated through two consec-

utive operations involving three variables. This ap-

proach accounted for internal operations such as re-

linearization and rescaling, which are integral to these

operations. These experiments were conducted on a

dataset of 200 randomly generated 64-bit integer val-

ues, as no standardized dataset exists for this type of

work. For each operation, we computed the aver-

age execution time. Then, we repeated the evaluation

across multiple HE security parameters to measure

the scalability of these different implementations.

This work also provides valuable insights into

how homomorphic operations scale with varying se-

curity parameters across different libraries. A clear

trend emerges: as the polynomial degree increases, so

does the latency of each operation. Table 2 outlines

the polynomial degrees and plaintext moduli used in

this work. These parameters were selected to ensure

a minimum security level of 128 bits across all imple-

mentations—commonly regarded as the baseline for

secure asymmetric encryption. Furthermore, the cho-

sen values represent common, uniformly supported

parameter pairs across the HE libraries and schemes.

Due to structural constraints speciﬁc to TFHE, we

adopted the preset parameters provided by the TFHE-

rs library for 128-bit security, which includes a poly-

nomial degree of 2048 and an LWE dimension of 742.

For BGV, BFV, and CKKS, polynomial degree and

plaintext modulus were standardized to enable fair

and equitable performance comparisons. This con-

sistency allows for meaningful, direct comparisons of

these schemes across different applications.

Table 2: Polynomial Degrees and Plaintext Moduli used for

Performance Analysis.

Polynomial Degree Plaintext Modulus

16384 1032193

32768 798433

65536 798433

In this experiment, we used C++ APIs for SEAL,

OpenFHE, and HElib while resorting to the C API

for TFHE-rs since there is no C++ interface for the

latter. Graphical representations are employed to vi-

sualize the performance metrics of each HE scheme

and library combination, providing valuable insights

into the efﬁciency of operations. The operation tim-

ings are measured in milliseconds, affording a gran-

ular level of detail necessary for informed decision-

making. Time for Multiplication and Addition is

shown for two operations between a trio of variables

(x1, x2, x3). We measured timing for a single vari-

able (x1) for encryption, decryption, and key gener-

ation. Figures 1 to 15 present a comparative analy-

sis of different operations across various libraries for

each scheme, using the parameter sets listed in Ta-

ble 2. Every row has three graphs of the same scale,

showing a single basic HE operation and its scaling

across the different libraries and security parameters.

We do not have results from SEAL for a polyno-

mial degree of 65536 since it does not support this

security parameters for this it. Also, the BFV scheme

does not yield any results in HElib because the library

does not have an implementation of it. The values

of encryption and decryption are often very close to

0 ms, making it challenging to differentiate between

schemes and libraries based on these operations.

The latency of TFHE scheme arithmetic opera-

tions, as implemented in the TFHE-rs library, is pre-

sented separately in Figure 16. These results are not

directly compared to those of the other libraries, as

TFHE-rs uses a different set of parameters. Nonethe-

less, the graph offers valuable insights into the per-

formance of TFHE operations in practical scenarios.

Among the measured operations, multiplication is the

most computationally intensive, whereas encryption

and decryption exhibit the lowest latency. It is worth

highlighting that TFHE-rs remains the sole library

offering support for ciphertext arithmetic operations

within the TFHE scheme, even though these opera-

tions tend to be computationally expensive in practi-

cal scenarios. TFHE distinguishes itself through its

support for programmable bootstrapping, which en-

ables the efﬁcient evaluation of non-linear functions a

major limitation of the other schemes. Furthermore,

the performance of TFHE is highly dependent on par-

allelization, with execution efﬁciency improving sig-

niﬁcantly on multi-threading systems.

TFHE is a computationally expensive scheme,

particularly in terms of multiplication and addition,

which is not comparable to the performance of other

HE schemes, as illustrated in Figure 16. Addition-

ally, TFHE’s basic operations are based on Boolean

gates, which are used to construct circuits for com-

putation. As a result, our comparative analysis was

conducted at this circuit level. While TFHE-rs is a

dedicated library for the TFHE scheme, OpenFHE

implements TFHE and FHEW functionalities within

its binary gate context as well as provide support for

converting CKKS ciphertexts to TFHE and vice versa

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

490

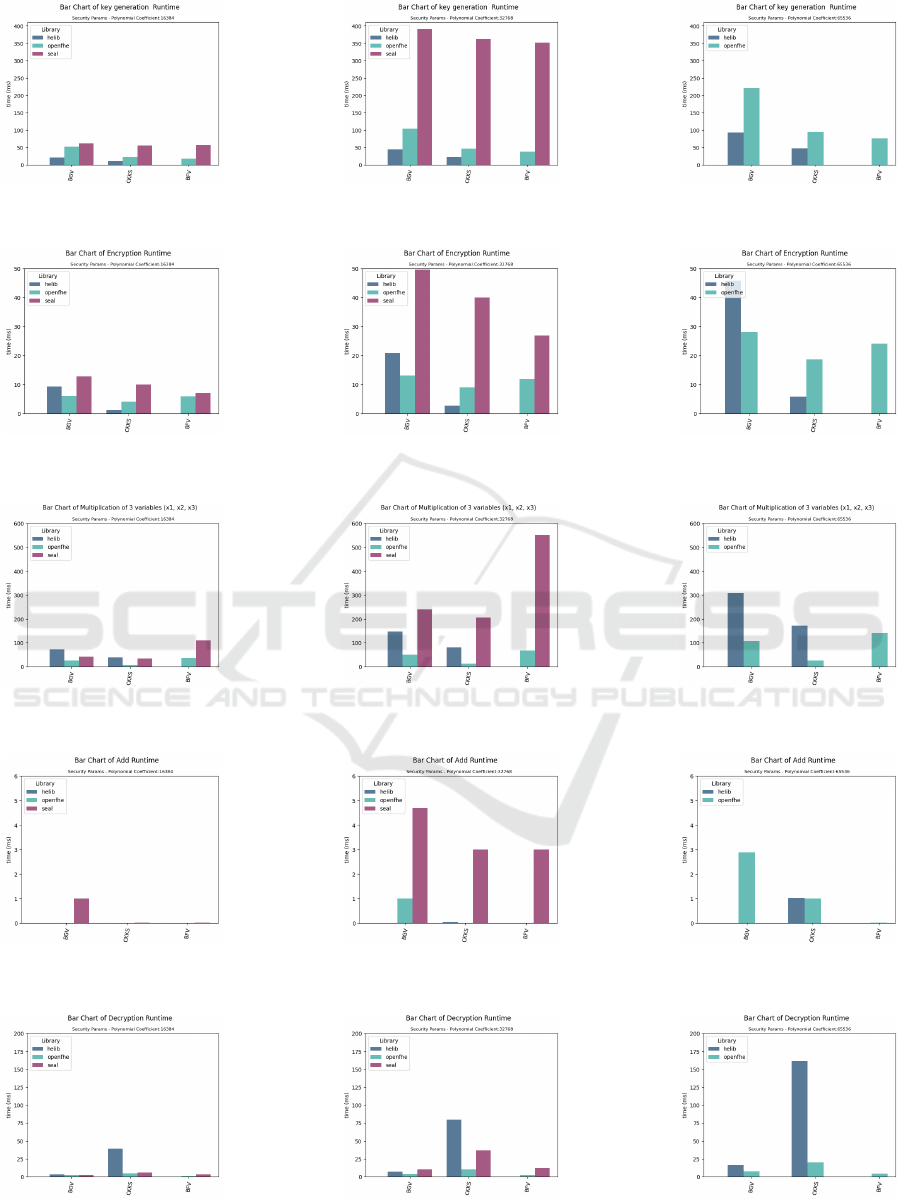
Figure 1: Key Generation with

Polynomial degree 16384.

Figure 2: Key Generation with

Polynomial degree 32768.

Figure 3: Key Generation with

Polynomial degree 65536.

Figure 4: Encryption with

Polynomial degree 16384.

Figure 5: Encryption with

Polynomial degree 32768.

Figure 6: Encryption with

Polynomial degree 65536.

Figure 7: Multiplication with

Polynomial degree 16384.

Figure 8: Multiplication with

Polynomial degree 32768.

Figure 9: Multiplication with

Polynomial degree 65536.

Figure 10: Addition with

Polynomial degree 16384.

Figure 11: Addition with

Polynomial degree 32768.

Figure 12: Addition with

Polynomial degree 65536.

Figure 13: Decryption with

Polynomial degree 16384.

Figure 14: Decryption with

Polynomial degree 3276.

Figure 15: Decryption with

Polynomial degree 65536.

A Safety-Centric Analysis and Benchmarks of Modern Open-Source Homomorphic Encryption Libraries

491

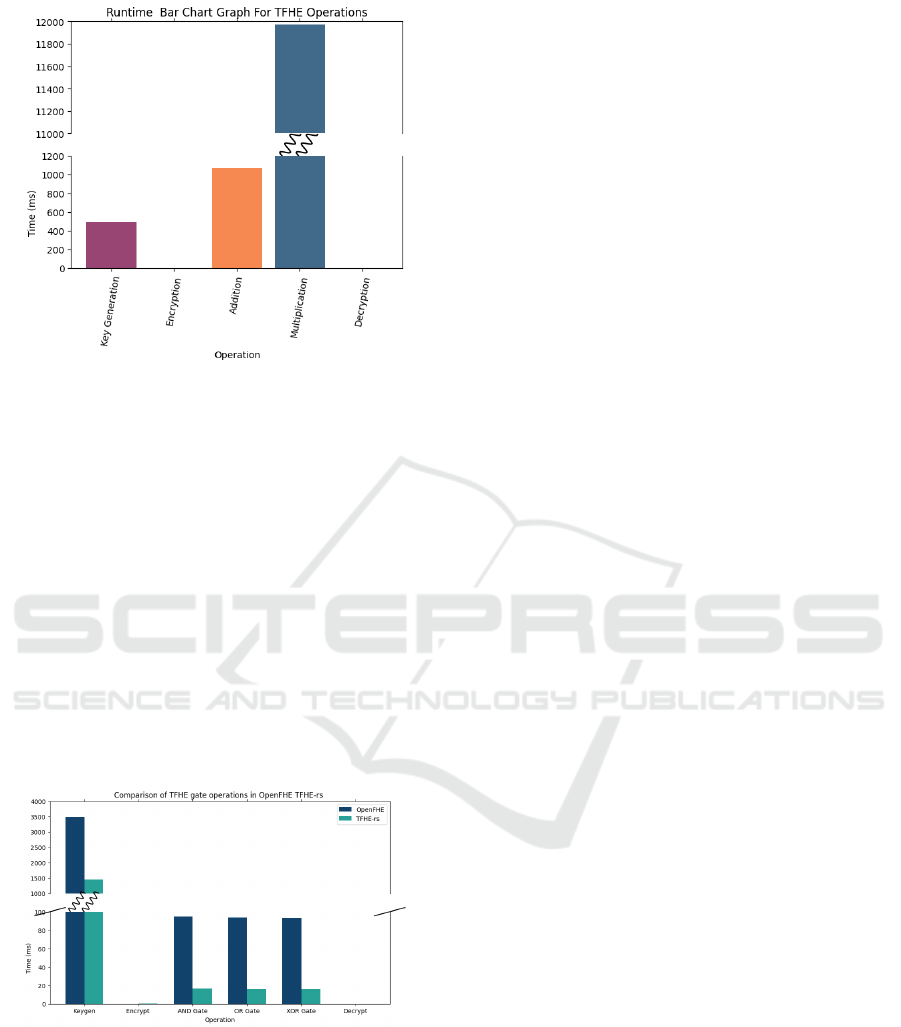
Figure 16: TFHE Runtime Barchart for all FHE operations

in the TFHE-rs library.

using (Boura et al., 2018). We carried out the perfor-

mance comparison of the three primary gates, namely

AND, OR, and XOR, as well as the basic HE func-

tions of Key generation, encryption, and decryption.

We used a polynomial degree of 1024 and an LWE di-

mension of 595, which are the preset parameters for

a security level of 128 bits in OpenFHE. Figure 17

shows a comparative analysis between OpenFHE and

TFHE-rs. This result indicates that key generation

is an expensive operation in TFHE compared to gate

evaluation. It also show a six times higher latency

in OpenFHE gates compared to TFHE-rs. While the

cost of gate evaluation is about 15 ms in TFHE-rs, it

is about 90 ms in OpenFHE. Lastly, encryption and

decryption are also very cheap operations in TFHE.

Figure 17: TFHE Runtime for OpenFHE and TFHE-rs.

All the code associated with this work is avail-

able at https://github.com/stamcenter/heevaluation.

The security analysis conducted will help the commu-

nity better understand the prevalence of errors in HE

code. Although the functions reviewed represent only

a small portion of the overall codebases, the number

of warnings and failures identiﬁed is signiﬁcant. Con-

currently, performance analysis is equally important,

as it establishes a benchmark for future improvements

to the libraries and provides a solid foundation for

comparing new HE implementations.

4 RELATED WORKS

(Mouris et al., 2018) released a performance analy-

sis on HElib, Lattigo, Palisade, SEAL, and TFHE us-

ing a compiler called T2 Compiler. The paper pro-

vided a series of benchmark suites called Terminator

2 Benchmark suites, which offer insights gained from

running various FHE backends. Their evaluation in-

cludes encryption, decryption, addition, subtraction,

multiplication, and division in HE, approximating la-

tency through the number of operations available in

a feedforward neural network’s image inference, and

a private information retrieval task. While the anal-

ysis did not detail how the parameters were set for

each library or how the schemes were selected, the

approach is generic, as it does not provide informa-

tion about individual operations. (Jiang and Ju, 2022)

also released FHEBench, which compares major FHE

schemes, showing how they perform under differ-

ent multiplication depths in SEAL, HElib, HEAAN,

TFHE, and Palisade. A major limitation of this work

is that it did not give implementation details or discuss

the data used. Furthermore, HEAAN, Palisade, and

TFHE are deprecated. (Tsuji and Oguchi, 2024) con-

ducted a comparative analysis of the implementation

of FHE schemes in OpenFHE, Lattigo, and TFHE-

rs. While the paper covers the most recent libraries,

its comparisons are geared toward TFHE-rs on dif-

ferent DRAMs compared to other libraries. (Melchor

et al., 2018) compared HElib, SEAL, and FV-NFLlib

libraries. They evaluated large plaintext moduli with

three different FHE libraries to show their respec-

tive capabilities and performance. The paper covers

multiplication across the libraries but does not handle

other basic HE operations such as addition, encryp-

tion, key generation, and decryption. Thus, it is only

helpful for HE multiplicative-intensive applications.

Our research ﬁlls these voids by covering the most

signiﬁcant and modern HE schemes and libraries. We

perform direct benchmarks of all fundamental opera-

tions required for a full-featured HE suite, with de-

tailed explanations of our design choices provided

through targeted HE micro-benchmarks. Besides

CKKS, BFV, and BGV, which are analyzed by most

related works, we also provide TFHE-rs benchmarks.

However, we were unable to directly compare the

arithmetic operations in TFHE with those of other

schemes due to structural differences. We then evalu-

ate and compare the three basic gates: AND, OR, and

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

492

XOR, in OpenFHE and TFHE-rs. In this work, we fo-

cused on state-of-the-art HE libraries, thus, outdated

libraries such as HEAAN, FV-NFLib, and TFHE

were not covered. Additionally, this work covers the

security analysis of HE libraries, which, to the best

of our knowledge, has not been covered by any prior

work. Assessing the security of these libraries is cru-

cial, given their use in very sensitive applications.

5 CONCLUSION AND FUTURE

WORK

In this work, we conducted two sets of experiments on

open-source HE libraries to evaluate their implemen-

tation security and performance. We employed a dy-

namic analysis tool called SafeRewrite to identify se-

curity vulnerabilities in four major open-source HE li-

braries: OpenFHE, HELib, SEAL, and TFHE/TFHE-

rs. A total of 40 functions were extracted from these

libraries and analyzed using the tool, which revealed

35 implementation errors and warnings. To illustrate

the implications, 3 representative functions were se-

lected and examined in detail, demonstrating their

roles within the libraries and highlighting potential

exploitation scenarios when used in isolation. These

ﬁndings show the importance of a carefully planned

transition from research to practical implementation

of HE as well as the other advance security and pri-

vacy protocols such as zero-knowledge proofs.

On the other hand, the performance experiment

showed the latency of the fundamental HE operations

and how they scale across different security param-

eters within these libraries. Our results indicate that

CKKS is the fastest HE scheme for all security pa-

rameter sets used. OpenFHE is the best-performing

library under examination, with HElib also showing

signiﬁcant beneﬁts in some cases. TFHE-rs outper-

forms OpenFHE by a factor of six in TFHE gates eval-

uation thus the ideal library for TFHE applications.

While this work reveals potential vulnerabilities in

some functions present in HE libraries, the inherent

limitations of SafeRewrite prevent an in-depth analy-

sis. Using more complex security analysis tools, com-

bined with powerful system software such as compil-

ers, is a promising direction that can provide more

insights as well as a holistic security understanding

of these libraries. Another interesting research di-

rection from this work is developing tools that can

be integrated into the open-source development pro-

cess of advanced security and privacy software. For-

mal veriﬁcation techniques such as symbolic execu-

tion and model checking, are essential in this pro-

cess. Finally, although HE is already applied in vari-

ous domains, its implementations across the different

libraries remain signiﬁcantly slower than native com-

putations. Advancements in performance through al-

gorithmic improvements, hardware acceleration, and

implementation-level optimizations also represent an-

other direction for valuable contributions.

REFERENCES

Aad, Imad Mulder, V., Mermoud, A., Lenders, V., and Tel-

lenbach, B. (2023). Zero-Knowledge Proof, pages 25–

30. Springer Nature Switzerland, Cham.

Adam Hayes, JeFreda R. Brown, S. K. (2023). Blockchain

facts, what it is, how it works and how it can be used.

investopedia. Accessed: 2024-03-06.

Aggarwal, N., Gupta, C., and Sharma, I. (2014). Fully ho-

momorphic symmetric scheme without bootstrapping.

In Proceedings of 2014 International Conference on

Cloud Computing and Internet of Things, pages 14–

17.

Aguilar-Melchor, C., Barrier, J., Guelton, S., Guinet, A.,

Killijian, M.-O., and Lepoint, T. (2021). NFLlib:

NTT-based Fast Lattice Library. CORE.

Al Badawi, A., Bates, J., Bergamaschi, F., Cousins, D. B.,

Erabelli, S., Genise, N., Halevi, S., Hunt, H., Kim, A.,

Lee, Y., Liu, Z., Micciancio, D., Quah, I., Polyakov,

Y., R.V., S., Rohloff, K., Saylor, J., Suponitsky, D.,

Triplett, M., Vaikuntanathan, V., and Zucca, V. (2022).

Openfhe: Open-source fully homomorphic encryption

library. In Proceedings of the 10th Workshop on En-

crypted Computing & Applied Homomorphic Cryp-

tography, WAHC’22, pages 53–63, New York, NY,

USA. Association for Computing Machinery.

Alenezi, M. and Zarour, M. (2020). On the relationship

between software complexity and security. Interna-

tional Journal of Software Engineering & Applica-

tions (IJSEA), Vol.11, No.1,.

Aman Anupam, Prathika Gonchigar, S. S. (2020). ”analysis

of open source node.js vulnerability scanners”. Inter-

national Research Journal of Engineering and Tech-

nology.

Badawi, A. A., Bates, J., Bergamaschi, F., Cousins, D. B.,

Erabelli, S., Genise, N., Halevi, S., Hunt, H., Kim, A.,

Lee, Y., Liu, Z., Micciancio, D., Quah, I., Polyakov,

Y., R.V., S., Rohloff, K., Saylor, J., Suponitsky, D.,

Triplett, M., Vaikuntanathan, V., and Zucca, V. (2022).

Openfhe: Open-source fully homomorphic encryption

library. Cryptology ePrint Archive, Paper 2022/915.

https://eprint.iacr.org/2022/915.

Bernstein, D. J. (2019). Does open-source cryptographic

software work correctly? ”https://cr.yp.to/talks/201

9.05.16/slides- djb-20190516- correctly- 4x3.pdf”.

Accessed: 2024-03-06.

Bernstein, D. J. (2021). Fast veriﬁed post-quantum soft-

ware. https://cr.yp.to/talks/2021.11.26/slides-djb-202

11126-saferewrite-4x3.pdf. Accessed: 2024-08-19.

Bharti Kaushik, Vikas Malik, V. S. (2023). A review paper

on data encryption and decryption. International

Journel for Research in Applied Science and Engi-

neering Technology. https://www.ijraset.com/best-

A Safety-Centric Analysis and Benchmarks of Modern Open-Source Homomorphic Encryption Libraries

493

journal/a-review-paper-on-data-encryption-and-

decryption.

Boura, C., Gama, N., Georgieva, M., and Jetchev, D.

(2018). CHIMERA: Combining ring-LWE-based

fully homomorphic encryption schemes. Cryptology

ePrint Archive, Paper 2018/758. https://eprint.iacr.or

g/2018/758.

Cheon, J. H., Kim, A., Kim, M., and Song, Y. (2016a). Ho-

momorphic encryption for arithmetic of approximate

numbers. Cryptology ePrint Archive, Paper 2016/421.

https://eprint.iacr.org/2016/421.

Cheon, J. H., Kim, A., Kim, M., and Song, Y. (2016b). Ho-

momorphic encryption for arithmetic of approximate

numbers. Cryptology ePrint Archive, Paper 2016/421.

https://eprint.iacr.org/2016/421.

Chillotti, I., Gama, N., Georgieva, M., and Izabach

ene, M.

(August 2016). TFHE: Fast fully homomorphic en-

cryption library. https://tfhe.github.io/tfhe/.

Chillotti, I., Gama, N., Georgieva, M., and Izabach

ene,

M. (2018). Tfhe: Fast fully homomorphic encryp-

tion over the torus. Cryptology ePrint Archive, Paper

2018/421. https://eprint.iacr.org/2018/421.

Doll, J., McCarthy, C., McDougall, H., and Bhunia, S.

(2025). Unraveling log4shell: Analyzing the impact

and response to the log4j vulnerabil. arXiv preprint

arXiv:2501.17760.

Fan, J. and Vercauteren, F. (2012). Somewhat practical

fully homomorphic encryption. IACR Cryptol. ePrint

Arch., 2012:144.

Gentry, C. (2009). A fully homomorphic encryption scheme.

PhD thesis, Stanford University. crypto.stanford.edu/

craig.

Guo, Q., Johansson, T., and Nilsson, A. (2020). A key-

recovery timing attack on post-quantum primitives us-

ing the fujisaki-okamoto transformation and its appli-

cation on FrodoKEM. Cryptology ePrint Archive, Pa-

per 2020/743. https://eprint.iacr.org/2020/743.

Gupta, H., Kabra, M., G

omez-Luna, J., Kanellopoulos, K.,

and Mutlu, O. (2023). Evaluating homomorphic oper-

ations on a real-world processing-in-memory system.

In 2023 IEEE International Symposium on Workload

Characterization (IISWC), pages 211–215.

Halevi, S. and Shoup, V. (2020). Design and implemen-

tation of helib: a homomorphic encryption library.

Cryptology ePrint Archive, Paper 2020/1481. https:

//eprint.iacr.org/2020/1481.

Hilton, M. and Cal (2012). Differential privacy : A histori-

cal survey.

Jiang, L. and Ju, L. (2022). Fhebench: Benchmarking fully

homomorphic encryption schemes.

Lindell, Y. (2020). Secure multiparty computation. Com-

mun. ACM, 64(1):86–96.

Lord, B. (August 2023). The urgent need for memory safety

in software products. https://www.cisa.gov/news-eve

nts/news/urgent-need-memory-safety-software-pro

ducts. Accessed: 2024-02-27.

Melchor, C. A., Killijian, M.-O., Lefebvre, C., and Ricosset,

T. (2018). A comparison of the homomorphic encryp-

tion libraries helib, seal and fv-nﬂlib. In International

Conference on Security for Information Technology

and Communications (SECITC 2018), volume 11359

of Lecture Notes in Computer Science, pages 425–

442, Bucharest, Romania. Springer. Rapport LAAS

n° 18688.

Mouchet, C., Bossuat, J.-P., Troncoso-Pastoriza, J., and

Hubaux, J.-P. (2023). Lattigo: a multiparty homomor-

phic encryption library in go. https://github.com/tun

einsight/lattigo. EPFL-LDS, Tune Insight SA, Ac-

cessed: 2024-03-06.

Mouris, D., Tsoutsos, N. G., and Maniatakos, M.

(2018). TERMinator Suite: Benchmarking Privacy-

Preserving Architectures. IEEE Computer Architec-

ture Letters, 17(2):122–125.

Nethercote, N. and Seward, J. (2007). Valgrind: a frame-

work for heavyweight dynamic binary instrumenta-

tion. SIGPLAN Not., 42(6):89–100.

Njungle, N. B., Jahns, E., Wu, Z., Mastromauro, L., Sto-

jkov, M., and Kinsy, M. A. (2025). Guardianml:

Anatomy of privacy-preserving machine learning

techniques and frameworks. IEEE Access, 13:61483–

61510.

Ogburn, M., Turner, C., and Dahal, P. (2013). Homomor-

phic encryption. Procedia Computer Science, 20:502–

509. Complex Adaptive Systems.

Polyakov, Y., Rohloff, K., and Ryan, G. W. (2018). Pal-

isade lattice cryptography library. Cybersecur. Res.

Center, New Jersey Inst. Technol., Newark, NJ, USA,

Tech. Rep.

Pulido-Gaytan, B., Tchernykh, A., Cort

es-Mendoza, J. M.,

Babenko, M., Radchenko, G., Avetisyan, A., and

Drozdov, A. Y. (2021). Privacy-preserving neural net-

works with homomorphic encryption: Challenges and

opportunities. Peer-to-Peer Networking and Applica-

tions, 14:1748–1765.

Saarinen, M.-J. O. (2020). Round 3 ofﬁ-

cial comment: Frodokem – cca bug.

https://groups.google.com/a/list.nist.gov/g/pqc-

forum/c/kSUKzDNc5ME/m/EMFYz9RNCAAJ?pli=1.

SEAL (2023). Microsoft SEAL (release 4.1). https:

//github.com/Microsoft/SEAL. Microsoft Research,

Redmond, WA., Accessed: 2024-02-27.

Shoshitaishvili, Y., Wang, R., Salls, C., Stephens, N.,

Polino, M., Dutcher, A., Grosen, J., Feng, S., Hauser,

C., Kruegel, C., and Vigna, G. (2016). SoK: (State

of) The Art of War: Offensive Techniques in Binary

Analysis. In IEEE Symposium on Security and Pri-

vacy.

Tsuji, A. and Oguchi, M. (2024). Comparison of fhe

schemes and libraries for efﬁcient cryptographic pro-

cessing. 2024 International Conference on Comput-

ing, Networking and Communications (ICNC): Edge

Computing, Cloud Computing and Big Data.

Yang, W., Wang, S., Cui, H., Tang, Z., and Li, Y. (2023).

A review of homomorphic encryption for privacy-

preserving biometrics. Sensors, 23(7):3566.

Zama (2022a). Concrete: TFHE Compiler that converts

python programs into FHE equivalent. Accessed:

2024-03-06.

Zama (2022b). TFHE-rs: A Pure Rust Implementation

of the TFHE Scheme for Boolean and Integer Arith-

metics Over Encrypted Data. https://github.com/zam

a-ai/tfhe-rs.

Zhang, W. (2021). Fully homomorphic encryption (fhe)

frameworks. openminded. Accessed: 2024-02-27.

SECRYPT 2025 - 22nd International Conference on Security and Cryptography

494