Dynamic E-Commerce Pricing: Optimizing Routes and Forecasting

Demand with Machine Learning

Sri Ramya Divakarla, Prabina Subedi, Kamatchi S and Giriraja C. V.

Electronics and Communication Engineering, Amrita Vishwa Vidyapeetham, Bengaluru, India

Keywords:

Dynamic Pricing, E-Commerce,Geographic Network Analysis, Dijkstra’s Algorithm, Machine Learning,

Demand Prediction, Price Optimization.

Abstract:

Dynamic pricing is a vital strategy in e-commerce, enabling retailers to adapt to ﬂuctuating demand and ge-

ographic constraints. This paper introduces a novel framework that integrates geographic network analysis,

Dijkstra’s algorithm, and machine learning (ML) for dynamic pricing optimization. A geographic network

is constructed with cities as nodes and edges representing the shortest paths calculated using Dijkstra’s algo-

rithm, which facilitates location-based price adjustments. ML techniques are used to predict demand across

cities using historical retail data, enabling real-time adjustments based on geographic proximity and demand

variability. Computational efﬁciency is achieved through KD-Trees for spatial searches and multiprocessing

for large datasets. The proposed approach demonstrates the ability to optimize pricing strategies by account-

ing for both geographic and demand variability, resulting in enhanced customer satisfaction and increased

revenue. This work offers a robust methodology for e-Commerce platforms to personalize pricing and lever-

age predictive analytics, providing a competitive edge in dynamic and diverse markets.

1 INTRODUCTION

In the highly competitive landscape of e-Commerce,

dynamic pricing has emerged as a vital strategy that

allows retailers to adjust prices in real-time based on

ﬂuctuating market conditions, demand patterns, and

geographic factors. Unlike traditional static pricing,

dynamic pricing provides a more ﬂexible approach

that can signiﬁcantly enhance customer satisfaction

and increase revenue by offering prices that reﬂect the

true value of products in different contexts.(Deksnyte

and Lydeka, 2012)

This project explores a novel approach to dynamic

pricing by integrating geographic network analysis

with Dijkstra’s algorithm and machine learning (ML)

techniques. Using physical distances between cities,

our methodology enables location-based price adjust-

ments, where customers closer to distribution hubs

might experience reduced shipping costs, and those

farther away see adjusted prices. Dijkstra’s algorithm

is applied to efﬁciently calculate the shortest routes

across a network of cities, creating a foundation for

calculating distance-based price modiﬁcations.(gee, )

Beyond geographic adjustments, demand predic-

tion is crucial to optimizing pricing. Therefore, ma-

chine learning models are used to predict demand

for different cities and product categories, allow-

ing dynamic pricing that adapts not only to geo-

graphic distance but also to anticipated customer de-

mand.(Enache, 2021) This combination of distance-

based pricing and ML-driven demand prediction cre-

ates a robust and scalable pricing system that aligns

with both spatial and temporal variations in consumer

behavior.(Saci, )

The contributions of this project include an efﬁ-

cient computational framework using KD-Trees for

fast spatial searches, parallel processing to handle

large datasets, and a comprehensive demand fore-

casting model that enhances pricing decisions.(

Aguila

et al., 2015) By integrating geographic insights with

predictive analytics, this project demonstrates a pow-

erful approach to dynamic pricing in e-commerce, of-

fering a competitive edge for retailers seeking to per-

sonalize pricing and maximize revenue.

2 LITERATURE SURVEY

Dynamic pricing has emerged as a critical tool in rev-

enue management, allowing businesses to optimize

444

Divakarla, S. R., Subedi, P., S, K. and C. V., G.

Dynamic E-Commerce Pricing: Optimizing Routes and Forecasting Demand with Machine Learning.

DOI: 10.5220/0013621300004664

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 3rd International Conference on Futuristic Technology (INCOFT 2025) - Volume 3, pages 444-454

ISBN: 978-989-758-763-4

pricing strategies based on real-time factors such as

demand, competition, and supply. Traditional ap-

proaches rely on static pricing models, which often

fail to adapt to market ﬂuctuations. Advanced tech-

niques, such as machine learning and algorithmic

methods, have proven effective in addressing these

limitations. Dijkstra’s algorithm, a well-known graph

traversal method, has been successfully applied in cal-

culating shortest paths for distance-based optimiza-

tion, particularly in logistics and supply chain con-

texts. Using datasets like the world cities dataset, dy-

namic pricing models can integrate spatial and logis-

tical factors, enhancing decision-making for location-

sensitive pricing strategies.

The paper by Samuel B. Hwang and Sungho Kim

(Hwang and Kim, 2006) introduces a model that auto-

mates price adjustments to optimize proﬁt and reduce

sales time by gathering competitor prices through

web crawlers and employing a three-phase process

of data collection, strategic analysis, and formula-

tion. While this approach focuses on competitor-

based pricing and frequent updates to enhance com-

petitiveness, the proposed work focuses on logistics-

driven pricing strategy. By leveraging the World

Cities dataset and Dijkstra’s algorithm, it dynamically

adjusts prices based on delivery costs and customer

location, prioritizing the balance between logistical

expenses and accessibility over competitor undercut-

ting.

El Youbi et al. (2023)(El Youbi et al., 2023) dy-

namic pricing using machine learning, focusing on

developing an accurate pricing model. Their study

compared Gradient Boosting Machines (GBM), Ran-

dom Forest, and Neural Networks, with GBM out-

performing the others, achieving a low Mean Squared

Error (MSE) of 0.012 and an R-squared score of 0.92.

By incorporating features like customer segmentation

and product categories, their approach aligns pricing

with customer behavior and market trends. The study

underscores the potential of machine learning in cap-

turing complex pricing dynamics and highlights the

importance of feature engineering and hyperparame-

ter optimization for effective implementation.

The study by Chunli Yin and Jinglong Han (Yin

and Han, 2020)explores dynamic pricing strategies

for e-commerce platforms using deep reinforcement

learning (DRL), emphasizing the technology’s ability

to optimize pricing decisions by adapting to consumer

behaviors and market ﬂuctuations. The research inte-

grates game-theoretic models with DRL algorithms,

such as Q-learning, SARSA, and Monte Carlo meth-

ods, to address pricing challenges under diverse mar-

ket and consumer conditions. The authors propose a

multi-layered dynamic pricing framework, consisting

of a data layer for collecting and preprocessing trans-

action data, an analysis layer utilizing machine learn-

ing techniques like clustering and association rules

to uncover pricing patterns, and a decision layer im-

plementing strategies like market segmentation and

auction-based pricing. Their experimental results val-

idate the model’s efﬁciency in achieving equilibrium

in both single and multi-commodity auctions, show-

ing signiﬁcant potential to enhance proﬁt maximiza-

tion and competitiveness. While the study bridges the

gap between AI technologies and economic theories

in pricing, it identiﬁes future research opportunities

in integrating production planning with pricing strate-

gies to fully capture supply chain dynamics.

W.Feijen et al.(Feijen and Sch

afer, 2021) explore

the fusion of Machine Learning with Dijkstra’s Short-

est Path Algorithm. Their method uses machine learn-

ing predictions to preemptively estimate likely short-

est paths, enhancing Dijkstra’s computational efﬁ-

ciency. This hybrid approach is particularly effective

in large, complex networks, reducing computation

time while retaining accuracy in pathﬁnding. This re-

search demonstrates the utility of machine learning as

a complementary tool in traditional algorithms, em-

phasizing applications in large-scale networks where

computational savings are essential

A.Abudureheman et al.(Abudureheman and Nilu-

paer, 2023) introduce an Optimization Model for

Cross-border E-commerce during the COVID-19 pan-

demic, integrating Dijkstra’s algorithm to optimize

transportation routes under pandemic restrictions.

This model factors in cross-border logistics chal-

lenges, including limited transportation options and

ﬂuctuating demand, using a modiﬁed shortest-path al-

gorithm to reduce delivery times. The study by Zhang

et al. contributes to logistics optimization in con-

strained environments, illustrating how traditional al-

gorithms can be adapted to meet the challenges of the

modern supply chain during global crises.

Dynamic pricing in e-commerce has evolved with

the integration of AI and machine learning, enabling

more efﬁcient and adaptive pricing strategies. Chen

and Chen (2015) (Chen and Chen, 2015)laid the

groundwork with models addressing the challenges of

competition and limited demand information, empha-

sizing the need for real-time adjustments. Schlosser

and Boissier (2018)(Schlosser and Boissier, 2018)

contributed reactive AI-based pricing strategies using

historical data to simulate price adjustments and their

effects on customer behavior. Proactive approaches,

such as those by Mohamed et al. (2022)(Mohamed

et al., 2022), employed regression models and neural

networks to forecast prices, particularly for seasonal

products, highlighting the predictive power of AI in

Dynamic E-Commerce Pricing: Optimizing Routes and Forecasting Demand with Machine Learning

445

dynamic pricing. Tseng et al. (2018)(Tseng et al.,

2018) extended this with auto regressive models and

neural networks for pricing in electronics, showcas-

ing the versatility of these methods. Reinforcement

learning-based strategies, as explored by Yin and Han

(2021)(Yin and Han, 2020), demonstrated the efﬁcacy

of algorithms like Q-learning and SARSA in auction-

based pricing scenarios. Beser et al. (2019)(Beser

et al., 2019) emphasized simulation-based individ-

ualized pricing, advocating for its integration into

decision-making frameworks for greater automation.

Despite these advancements, challenges persist, in-

cluding data privacy concerns, algorithmic bias, and

the need for standardized datasets for benchmarking.

Future research should focus on developing uniﬁed

frameworks that seamlessly integrate AI into existing

IT systems, enabling fully automated and ethical dy-

namic pricing.

The paper by Shukla et al.(Shukla et al., 2023)

proposes an innovative framework for dynamic pric-

ing optimization in e-commerce platforms, integrat-

ing fuzzy logic systems with demand-side manage-

ment to address the uncertainty inherent in customer

demand. By utilizing fuzzy logic, the system incorpo-

rates linguistic variables to represent imprecise fac-

tors like demand levels, time of day, and competi-

tor pricing. It generates dynamic, customer-speciﬁc

pricing strategies through fuzziﬁcation, fuzzy infer-

ence, and defuzziﬁcation processes. This adaptive

pricing system enhances both customer satisfaction

and platform revenue by balancing real-time demand

changes and consumer preferences. The study high-

lights fuzzy logic’s advantages over traditional ma-

chine learning techniques, including interpretability,

reduced data requirements, and effective handling of

the cold start problem.

Using information from Bangalore’s ”Dunzo” op-

erations, Hrithik T. H. et al.’s paper (Hrithik et al.,

2024)suggests a machine learningbased architecture

for online shopping platform warehouse site opti-

mization. In order to forecast the demand for new

warehouse locations, the study focuses on important

variables such order volume, delivery distance, and

the availability of alternative facilities. KNN, Support

Vector Regression (SVR), Random Forest, Decision

Trees, Gradient Boost, Artiﬁcial Neural Networks

(ANN), and Long Short-Term Memory (LSTM) were

among the machine learning techniques that were as-

sessed. Among these models, the Random Forest

and Gradient Boost regressors outperformed others,

achieving the highest R-squared values and minimal

error rates, thereby proving to be the best ﬁt for the ap-

plication. In contrast, SVR and Decision Trees were

found to be less effective due to high errors and over-

ﬁtting issues. The paper underscores the effectiveness

of machine learning in reducing delivery costs and

improving customer satisfaction by accurately pre-

dicting optimal warehouse locations. It also high-

lights the potential for further advancements through

the integration of deep learning models, which could

provide higher accuracy and efﬁciency in addressing

the growing demands of e-commerce logistics.

Prakash D. et al. (D et al., 2023)use Dijkstra’s

approach in conjunction with Genetic approach (GA)

and Particle Swarm Optimization (PSO) to optimize

EV charging routes and waiting times. One notable

feature of Dijkstra’s algorithm is its capacity to de-

termine the shortest routes in trafﬁc networks while

taking charging station lines, trafﬁc situations, and

battery levels into consideration. Although it high-

lights speed and adaptability limitations in compari-

son to ﬂexible approaches like PSO, which demon-

strated greater performance in the majority of cases,

the study shows its efﬁcacy in identifying the best

routes for EVs. However, because of its determin-

istic nature and accurate pathﬁnding, Dijkstra’s al-

gorithm continues to be a fundamental technique for

routing. This makes it especially pertinent in situa-

tions that demand certain and dependable outcomes,

such static trafﬁc networks or established routes.The

ﬁndings highlight how important it is to combine Di-

jkstra’s algorithm with other optimization techniques

for increased effectiveness in real-time EV routing ap-

plications.

Madhura Srinivasan and Sireesha K. (Srinivasan

and Sireesha, 2022)combine K-Means++ clustering

with Ant Colony Optimization (ACO) to provide

an optimum solution to the Logistic Routing Prob-

lem (LRP), a subset of the Vehicle Routing Prob-

lem (VRP). Using K-Means++ initially to group geo-

graphical areas and then using ACO for route creation

and optimization, the method reduces travel costs and

distances. In order to improve routing performance,

the methodology uses the elbow method to ﬁnd the

ideal number of clusters and emphasizes the impor-

tance of hyperparameter tweaking in ACO, such as

pheromone evaporation and attractiveness. Accord-

ing to the results, this hybrid approach outperforms

conventional methods in terms of computing efﬁ-

ciency and solution quality, greatly increasing route

efﬁciency and lowering trip distances across datasets.

As a result, it is a scalable and useful framework for

real-world logistics challenges.

In order to ﬁnd the best pricing that maximizes

revenue and corresponds with customer willingness

to pay, Mandava Jaswanth et al.’s (Jaswanth et al.,

2022)research offers a framework for product price

optimization that uses the Least Squares Regression

INCOFT 2025 - International Conference on Futuristic Technology

446

approach. To determine important pricing character-

istics, the study uses regression and demand curve

analysis methodologies, backed by information gath-

ered from e-commerce platform web scraping. The

model demonstrates the efﬁciency of Least Squares

in determining the best regression lines based on vari-

ables like cost, demand, and consumer behavior by

training and testing product pricing predictions using

Python’s sklearn package. The results of the experi-

ments show that the pricing projections for a range of

products are correct, highlighting the importance of

dynamic pricing techniques in increasing proﬁtabil-

ity. The study ends with recommendations for the use

of cutting-edge machine learning models to improve

real-time pricing decisions.

Akshay A. S. et al.’s(A S et al., 2023) research

investigates last-mile delivery optimization with so-

phisticated algorithms including the Distance Matrix

API, Optical Character Recognition (OCR) and the

Traveling Salesman Problem (TSP). It presents a soft-

ware program for e-commerce logistics that optimizes

routes, greatly cutting delivery times and distances

while improving customer happiness and operational

effectiveness. The system adjusts to changing cir-

cumstances, such as trafﬁc, by using Google APIs for

precise distance computations and OCR for precise

location data extraction from invoices. Comparative

studies show signiﬁcant efﬁciency improvements over

conventional techniques, underscoring the revolution-

ary potential of algorithm-driven logistics. Sangwan’s

insights into heuristic and exact TSP-solving strate-

gies and Ripon et al.’s work on genetic algorithms for

TSP optimization are only two examples of the contri-

butions that the study draws upon, incorporating these

developments into a robust framework for real-world

applications.

In order to improve customer engagement on

e-commerce platforms, the recommendation algo-

rithms are examined in the article by Ranjith Ku-

mar et al.(Kumar et al., 2024) It shows a number

of strategies, such as collaborative ﬁltering for tai-

lored recommendations based on user-item interac-

tions, popularity-based systems for attracting new

users, and sophisticated techniques such as utility ma-

trix factorization and latent component models for

more granular customization. Clustering techniques

such as K-Means are used to analyze product char-

acteristics and provide contextually relevant recom-

mendations to solve the cold start problem. In order

to increase recommendation accuracy, recent devel-

opments are examined, including sentiment analysis,

the integration of demographic features, and graph-

based neural models. System efﬁcacy and ﬂexibility

are guaranteed by evaluation metrics such as CTR,

MAE, RMSE, and clustering-speciﬁc measurements.

In order to satisfy the various demands of users and

enterprises, the proposed hybrid solution effectively

combines cooperative ﬁltering and clustering.

3 METHODOLOGY

The proposed work employs a multi-step method-

ology designed to optimize dynamic pricing in e-

commerce using a combination of geographic net-

work analysis, Dijkstra’s algorithm, and machine

learning-based demand prediction. The process can

be divided into the following key phases:

3.1 Data Collection and Preprocessing

3.1.1 City Data

The geographic dataset contains city information, in-

cluding latitude, longitude, and city names. This data

is crucial for building a geographic network.

3.1.2 Retail Data

E-commerce transaction data includes ﬁelds such as

product information, quantity, price, and customer lo-

cation (city). This dataset is used for both dynamic

pricing and demand prediction.

3.1.3 Data Cleaning and Column Detection

The preprocessing stage automatically detects column

names for essential ﬁelds such as latitude, longitude,

and city, making the method adaptable to datasets

with different structures.

3.2 Geographic Network Construction

Using KD-Trees

3.2.1 KD-Tree Implementation

To efﬁciently handle geographic data, we construct

a KD-Tree using latitude and longitude coordinates.

KD-Trees enable fast spatial searching, allowing for

an efﬁcient calculation of neighboring cities within

a speciﬁed maximum distance (e.g., 500 km). The

distance between two geographic points is calculated

using the Haversine formula, which accounts for the

Dynamic E-Commerce Pricing: Optimizing Routes and Forecasting Demand with Machine Learning

447

curvature of the Earth:

d = 2r · arcsin

sin



− φ



cos(φ

) · cos(φ

) · sin



− λ



(1)

Where:

• d: Great-circle distance between two points (in

kilometers)

• r: Radius of the Earth (r ≈ 6371 km)

• φ

, φ

: Latitudes of the two points (in radians)

• λ

, λ

: Longitudes of the two points (in radians)

This formula is used to determine whether two cities

are within the speciﬁed radius when constructing the

graph.

3.2.2 Graph Creation with Dijkstra’s Algorithm

Once the KD-Tree identiﬁes nearby cities, a graph is

constructed where:

• Nodes represent cities.

• Edges represent connections between cities that

are within the speciﬁed radius, weighted by the

great-circle distance between them.

To calculate the shortest paths between all city

pairs, Dijkstra’s algorithm is applied. The algorithm

iteratively minimizes the path cost for each node by

updating the shortest known distance. The formula

used is:

d[v] = min (d[v], d[u] + w(u, v)) (2)

Where:

• d[v]: Current shortest distance to node v

• d[u]: Current shortest distance to node u (a neigh-

boring node)

• w(u, v): Weight of the edge between nodes u and

v (distance between the cities)

The algorithm initializes all distances as inﬁnity

(∞) except for the source node, which starts at zero. It

then iteratively updates the distances until the shortest

paths to all nodes are found.

3.2.3 Edge Optimization and Deduplication

To reduce computational complexity, edges are ﬁl-

tered and deduplicated by only adding one-way con-

nections for each city pair, ensuring efﬁcient process-

ing of geographic data.

3.3 Dynamic Pricing Calculation Using

Distance-Based Adjustments and

Demand

Dynamic pricing in the code is calculated by incorpo-

rating transportation costs based on the distance from

London and demand adjustments through the quan-

tity sold. The transportation cost is determined using

the great-circle distance, precomputed with Dijkstra’s

algorithm, and calculated as the product of the dis-

tance (in kilometres), fuel consumption per kilometre

(0.025 litres/km), and petrol price per litre ($1.72).

Dynamic Price = (Distance (km)

× Fuel Consumption per km

× Petrol Price per litre)

+ Unit Price

+ (Quantity × 0.05) (3)

This ensures that cities farther from London in-

cur higher transportation costs, which are reﬂected

in the ﬁnal price. Additionally, demand is factored

in through a 5% adjustment based on the quantity

sold, accounting for the increased logistical and sup-

ply challenges associated with higher demand. The

ﬁnal dynamic price is obtained by summing the orig-

inal unit price, the distance-based transportation cost,

and the demand adjustment. This approach dynami-

cally adjusts prices to reﬂect real-world logistics and

demand, offering a sustainable and region-speciﬁc

pricing strategy for e-commerce operations.

3.4 Demand Prediction Using Machine

Learning

3.4.1 Feature Engineering

Transactional data is enhanced with new features such

as month and year derived from the transaction date,

which helps in identifying seasonal trends.

3.4.2 Model Selection and Training

To predict demand, machine learning models (e.g.,

Random Forest Regressor) are trained on historical

sales data. The model input includes product and lo-

cation features, along with temporal data, allowing it

to capture variations in demand across cities and sea-

sons.

3.4.3 Model Evaluation

Models are evaluated using metrics such as Mean

Squared Error (MSE) to ensure accurate demand fore-

INCOFT 2025 - International Conference on Futuristic Technology

448

casts. Hyperparameter tuning and cross-validation are

performed to optimize model performance.

3.5 Parallel Computation for Efﬁciency

3.5.1 Batch Processing with Multiprocessing

To handle the large number of city pairs and retail

transactions, the project leverages the Python multi-

processing library. Distance calculations are divided

into batches and processed in parallel, signiﬁcantly

reducing computation time.

3.5.2 Efﬁcient Memory Management

By batching data and using memory-efﬁcient struc-

tures, the project minimizes memory overhead, which

is particularly important for large datasets commonly

seen in e-commerce applications.

3.6 System Integration and Output

Generation

3.6.1 Integration of Dynamic Pricing and

Demand Prediction

The ﬁnal dynamic prices, adjusted for distance and

demand, are computed and added to the retail dataset.

This integration allows for real-time or periodic pric-

ing updates in e-commerce systems.

3.6.2 Output Storage

The processed dataset, with columns for dynamic

prices and demand forecasts, is saved in a structured

format (e.g. CSV).

3.7 Visualisation and Analysis

Graph and Demand Visualisations , including geo-

graphic scatter plots of city connections, shortest path

histograms, and monthly demand trends, are used to

analyze and validate the methodology’s effectiveness.

In addition, feature importance plots for the machine

learning model and pricing impact distributions are

generated to provide insights into the factors inﬂuenc-

ing pricing and demand.

3.8 Workﬂow

The workﬂow diagram presented in Figure 1 outlines

the main steps of the proposed method.

Figure 1: Dynamic pricing using Dijikstra’s and ML work-

ﬂow

4 RESULTS AND OUTPUT

The outcomes of the dynamic pricing methodology

and the demand prediction model, as well as the key

metrics, graphs, and outputs are analyzed to demon-

strate the effectiveness of the approach.

Dynamic E-Commerce Pricing: Optimizing Routes and Forecasting Demand with Machine Learning

449

4.1 City Graph Construction and

Connectivity Analysis

The city graph represents a dense logistics network

with 258 nodes (cities) and 30,916 edges, where

nodes denote cities, and edges represent connections

between cities within a maximum distance of 500 km.

Each edge’s weight corresponds to the great-circle

distance, reﬂecting real-world logistics feasibility.

Figure 2: KD-tree graph based on distance

Figure 3: City Graph Construction using KD Trees, Dijik-

stra’s implementation and dynamic pricing calculation

The graph was constructed efﬁciently in just

2.72 seconds using a KD-tree for nearest-neighbour

searches, signiﬁcantly reducing computational com-

plexity by identifying city pairs within the speciﬁed

distance threshold. This approach highlights a scal-

able method for building large geographical networks

for e-commerce logistics and route optimization.

4.2 Insights from Dynamic Pricing

Adjustments in Retail Dataset

The updated dataset incorporates a dynamic pricing

model that adjusts product prices based on transporta-

tion costs and demand sensitivity. The Dynamic Price

column reﬂects the impact of distance from London,

with cities farther away incurring higher prices due to

increased logistical expenses. Additionally, demand-

based adjustments are evident, as a 5% price incre-

ment is applied based on the Quantity sold, account-

ing for supply chain and market dynamics. This

model highlights a strategic approach to pricing, en-

suring proﬁtability while adapting to regional market

conditions. The diverse range of products and cus-

tomer locations underscores the ﬂexibility and appli-

cability of this pricing strategy across varying regions

and consumer demands. These insights emphasize

how businesses can optimize pricing for proﬁtability

while addressing logistical and market-speciﬁc chal-

lenges effectively.

Figure 4: Updated retail dataset with calculated dynamic

price

4.3 Comparing Original and Dynamic

Pricing: Impact of Distance and

Demand Adjustments

The box plot titled ”Original vs Dynamic Prices”

compares the distribution of the Unit Price (original

price) and Dynamic Price (adjusted price based on

distance and demand). The plot shows how the dy-

namic pricing model inﬂuences the prices of products

in comparison to their original prices.

4.3.1 UnitPrice

The original prices appear to have a tight range with a

few outliers, indicating that most products are priced

within a similar range but there are some high-priced

outliers.

4.3.2 DynamicPrice

The dynamic prices show a wider spread, including

lower and higher outliers. This is expected, as the dy-

namic pricing model accounts for transportation costs

(distance from London) and additional demand-based

increments, causing a more varied price range. The

larger spread in DynamicPrice compared to UnitPrice

suggests that the model effectively adjusts for geo-

graphical and demand factors, which could result in

higher prices for customers located farther from the

central point (London) or with higher demand. The

presence of outliers indicates that certain locations

INCOFT 2025 - International Conference on Futuristic Technology

450

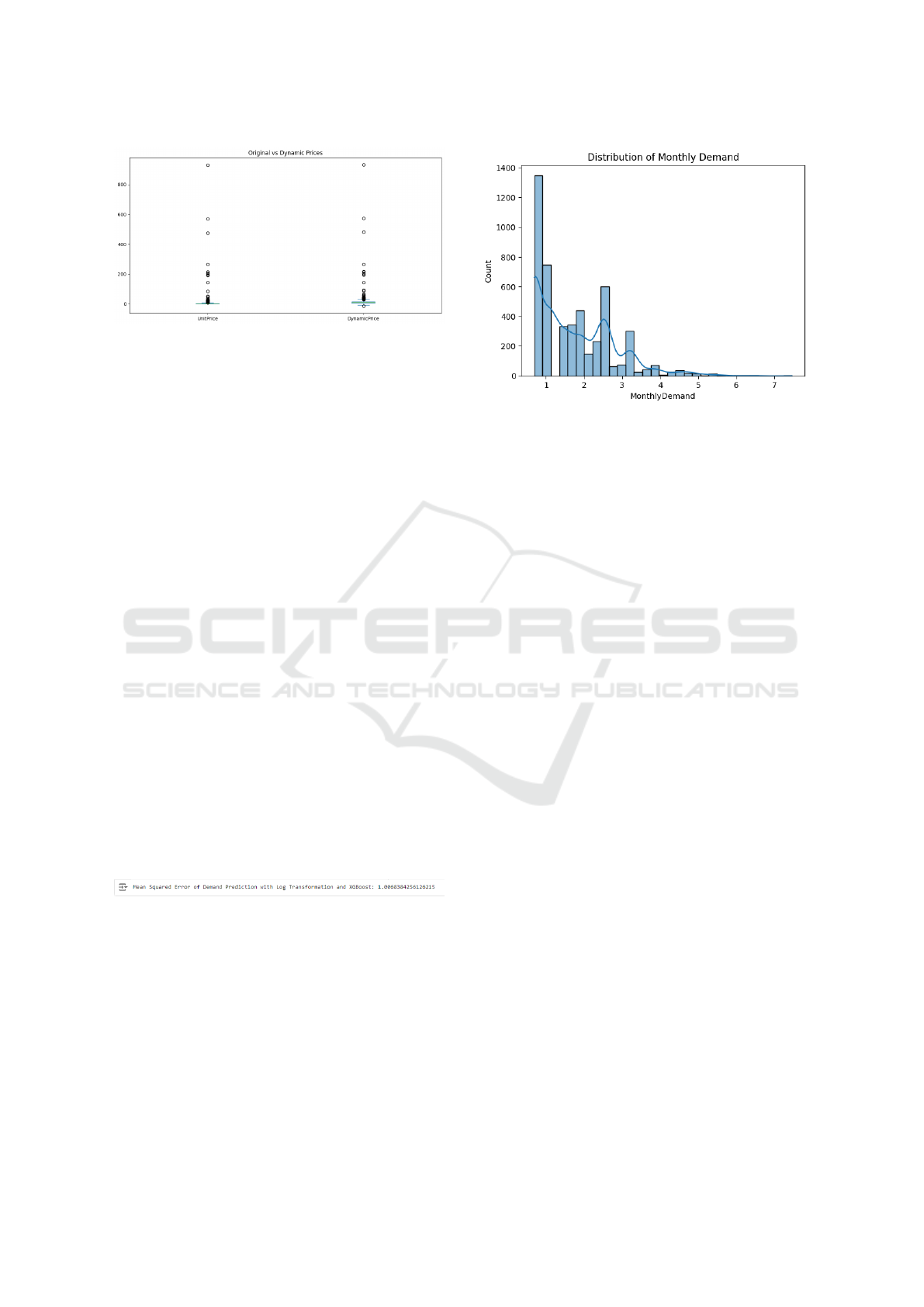
Figure 5: Original Price vs Dynamic Price

or products might be disproportionately affected by

these adjustments.

4.4 Predicting Monthly Demand Using

Machine Learning Models

In this analysis, we predict the monthly demand for

retail products based on various features such as City,

StockCode, and Month. The dataset was ﬁrst aggre-

gated to calculate monthly demand for each product

in each city. Categorical variables (City, StockCode,

Month) were one-hot encoded to make them suitable

for machine learning models. Two machine learn-

ing models were trained: Random Forest Regressor

and XGBoost Regressor, to predict the demand. The

Mean Squared Error (MSE) was calculated to evalu-

ate the models’ performance, with the Random For-

est model yielding a baseline MSE and the XGBoost

model providing a more accurate prediction with a

lower MSE of 1.0068384256126215. Low MSE val-

ues indicate that the model performs well in predict-

ing demand across cities and products. This is es-

sential for the pricing model, as accurate demand

forecasts enable more responsive price adjustments.

A well-tuned model ensures that pricing reﬂects not

only logistical costs but also anticipated customer de-

mand, balancing supply-side and demand-side fac-

tors.

Figure 6: Accuracy of the XGBoost model

The monthly demand distribution was also visu-

alized, revealing the skewed nature of the demand

data. This analysis demonstrates how machine learn-

ing techniques can be applied to predict demand,

which is crucial for inventory management and pric-

ing strategies.

The histogram illustrates the monthly demand dis-

tribution for a speciﬁc product or service. The x-

axis represents the demand values, while the y-axis

shows the frequency of occurrences within each de-

Figure 7: Monthly Demand Prediction

mand range. The data indicates that the majority of

demand falls between 1 and 2 units per month, with

the frequency decreasing as demand rises. The super-

imposed curve suggests a right-skewed distribution,

implying that while most months experience low to

moderate demand, there are a few months with ex-

ceptionally high demand.

4.5 Customer Segmentation Based on

Spending Behaviour

The box plot visualizes customer segmentation based

on their total spending habits. Segment 0 displays a

wide box and long whiskers, which indicates that cus-

tomers in this segment have a large range of spending,

from low to high. This suggests a diverse group with

varying spending behaviours. In contrast, Segment 1

has a narrow box and shorter whiskers, indicating that

most customers in this segment have similar, concen-

trated spending patterns, with less variation. Finally,

Segment 2, like Segment 0, shows a wider box and

longer whiskers, meaning customers in this segment

exhibit a broader range of spending, but with more

moderate to high spending habits. These insights help

businesses tailor their strategies, such as targeted mar-

keting or personalized offers, to better meet the needs

of each group of customers.

4.6 Feature Importance in Demand

Prediction

A bar chart of feature importance (Fig.9) of the ML

model describes which factors (e.g., city, product cat-

egory) most inﬂuence demand predictions. Features

of high importance are the primary drivers of demand

variability. For example, if geographic location (city)

and seasonal trends (month) show high importance,

Dynamic E-Commerce Pricing: Optimizing Routes and Forecasting Demand with Machine Learning

451

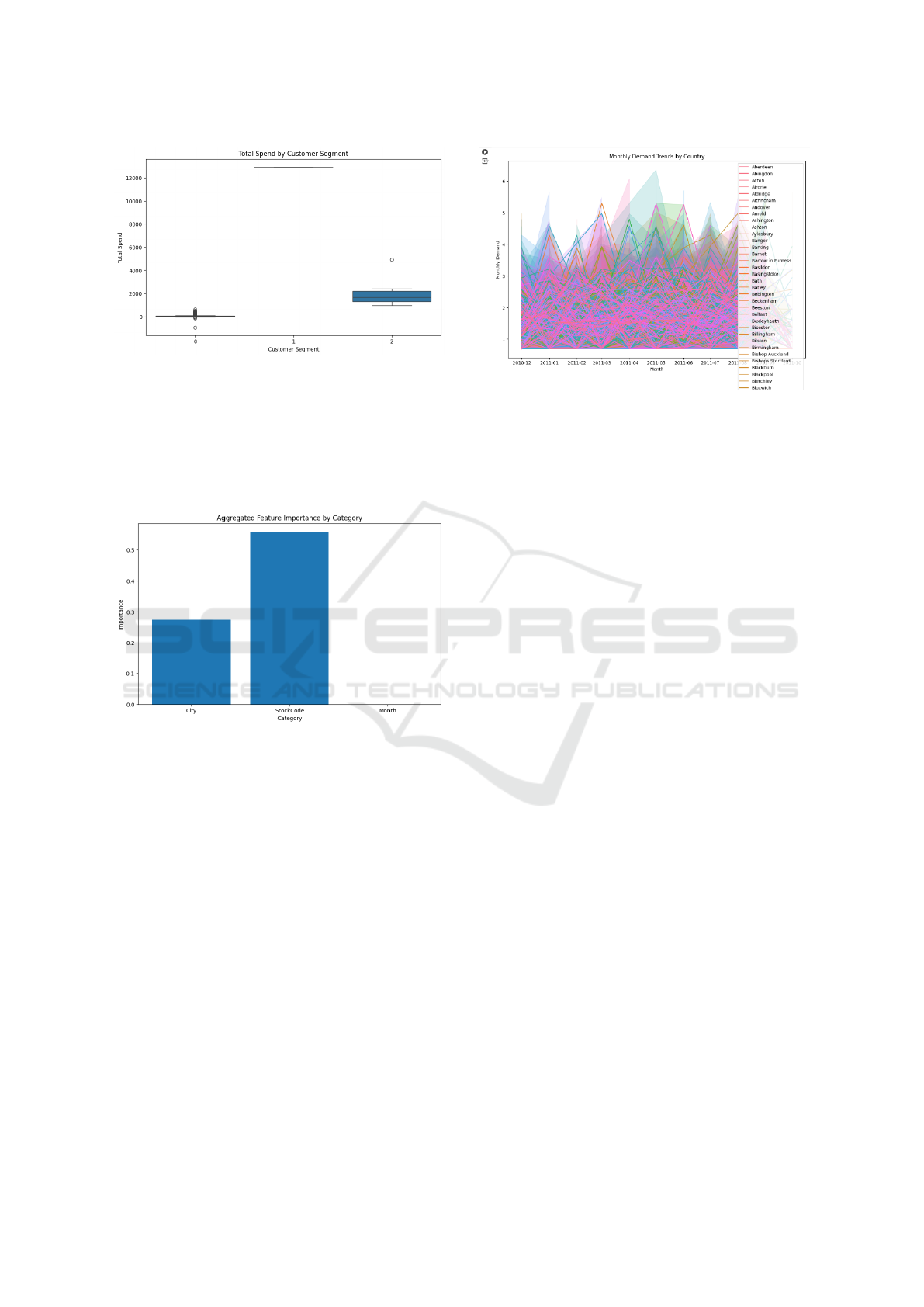
Figure 8: Customer Segmentation Based on Spending Be-

haviour

this implies that location-based and temporal adjust-

ments are critical for accurate pricing. Insights from

feature importance can inform further reﬁnement of

the pricing and demand models, enhancing the over-

all robustness of the system.

Figure 9: Feature Importance in Demand Prediction

4.7 Demand Trends Over Time

A time series plot (Fig.10) showing monthly demand

across various cities or products provides a visual of

demand trends and seasonal patterns.

Seasonal spikes or dips in demand help in ad-

justing pricing strategies accordingly. For instance,

higher demand during certain months might prompt a

slight increase in prices, while lower demand periods

could result in discounts. Visualizing demand trends

allows for a nuanced approach to pricing that aligns

with customer purchasing behaviors.

4.8 Summary

The results show that the proposed approach suc-

cessfully integrates geographic distance with ma-

chine learning predictions to enable a dynamic, opti-

mized pricing system. The graph-based city network

Figure 10: Demand trends of different cities over time

and ML-driven demand forecasts enhance responsive-

ness, while efﬁcient data structures ensure scalabil-

ity. Overall, this system demonstrates a robust solu-

tion for personalized, demand-responsive pricing in

e-commerce, aligning logistical costs with customer

demand to maximize revenue potential.

5 Gaps And Novelty

In existing e-commerce pricing systems, dynamic

pricing often relies heavily on historical sales and de-

mand without adequately accounting for geographic

factors and real-time demand variations. Traditional

pricing algorithms may lack adaptability to distance-

based cost structures, which are especially relevant in

large-scale, geographically distributed markets. This

gap in spatial awareness leads to uniform pricing

strategies that overlook potential cost optimizations

and competitive advantages for nearby customers.

Additionally, while demand prediction is widely im-

plemented, integrating it with dynamic pricing in a

way that also accounts for geographic distances re-

mains underexplored.

This project introduces a novel integration of

geographic network analysis, Dijkstra’s algorithm,

and machine learning for a comprehensive, location-

aware dynamic pricing system. By constructing a

city-based graph using KD-Trees and applying Di-

jkstra’s shortest path calculations, this approach en-

ables distance-based price adjustments efﬁciently, en-

hancing the pricing model’s responsiveness to geo-

graphic proximity. Coupled with machine learning

for demand prediction, the project provides a dual-

layered approach that adjusts prices based not only

on geographic logistics but also on forecasted demand

patterns. This combined framework addresses previ-

ously identiﬁed gaps, creating a scalable and adapt-

able pricing system that is bettee-Commercewith real-

INCOFT 2025 - International Conference on Futuristic Technology

452

world e-commerce dynamics.

6 CONCLUSION AND FUTURE

SCOPE

The proposed project demonstrates an approach to

dynamic pricing in e-commerce by integrating geo-

graphic network analysis, Dijkstra’s algorithm, and

machine learning for demand prediction. By con-

structing a geographic network of cities and calculat-

ing shortest paths, the system effectively incorporates

distance as a factor in price determination, allowing

for a more cost-efﬁcient and competitive pricing strat-

egy. The use of machine learning to predict demand

across different regions and product categories fur-

ther strengthens the model, enabling prices that adapt

not only to logistical costs but also to anticipated

consumer demand. This dual approach to pricing

optimization provides a scalable and responsive so-

lution, particularly valuable in e-commerce environ-

ments that demand both personalization and agility.

The results show that this integrated method not only

improves pricing precision but also enhances the cus-

tomer experience by offering context-aware prices

that reﬂect both proximity and demand insights.

Future work can explore the integration of real-

time data sources, such as live trafﬁc patterns, weather

conditions, and regional events, to reﬁne demand

prediction and pricing strategies. Incorporating ad-

vanced machine learning models, such as deep learn-

ing architectures, could enhance the accuracy of de-

mand forecasting by capturing complex, non-linear

patterns in customer behavior. Expanding the geo-

graphic network to include international logistics and

cross-border trade scenarios would make the model

applicable to global e-commerce platforms. Addi-

tionally, integrating blockchain technology for trans-

parency in pricing calculations and logistics data shar-

ing could improve trust among consumers and stake-

holders. These advancements would broaden the ap-

plicability of the proposed approach, paving the way

for smarter, more inclusive, and globally adaptable

dynamic pricing systems.

REFERENCES

Minimum Cost using Dijkstra by Modifying Cost of an

Edge - GeeksforGeeks — geeksforgeeks.org. https:

//www.geeksforgeeks.org/minimum-cost-using-dijks

tra-by-reducing-cost-of-an-edge/. [Accessed 19-11-

2024].

A S, A., Yesudas, G., Yoonus, M. A., Abhishek, S., and T,

A. (2023). Revolutionizing last-mile delivery: Un-

leashing unprecedented efﬁciency in package logis-

tics. In 2023 Innovations in Power and Advanced

Computing Technologies (i-PACT), pages 1–5.

Abudureheman, A. and Nilupaer, A. (2023). Retraction

note: Optimization model design of cross-border e-

commerce transportation path under the background

of prevention and control of COVID-19 pneumonia.

Soft Comput., 27(3):1843.

Beser, A., Lackes, R., and Siepermann, M. (2019). Differ-

ent prices for different customers - optimising individ-

ualised prices in online stores by artiﬁcial intelligence.

In International Conference on Interaction Sciences.

Chen, M. and Chen, Z.-L. (2015). Recent developments in

dynamic pricing research: Multiple products, compe-

tition, and limited demand information. Production

and Operations Management, 24(5):704–731.

D, P., G, L., and G, J. (2023). Analysis of shortest routing

and waiting time of electric vehicle charging stations.

In 2023 14th International Conference on Computing

Communication and Networking Technologies (ICC-

CNT), pages 1–6.

Deksnyte, I. and Lydeka, P. (2012). Dynamic pricing and

its forming factors. International Journal of Business

and Social Science, 3.

El Youbi, R., Messaoudi, F., and Loukili, M. (2023). Ma-

chine learning-driven dynamic pricing strategies in e-

commerce. pages 1–5.

Enache, M. (2021). Machine learning for dynamic pricing

in e-commerce. Annals of Dunarea de Jos University

of Galati. Fascicle I. Economics and Applied Infor-

matics, 27:114–119.

Feijen, W. and Sch

afer, G. (2021). Using machine learning

predictions to speed-up dijkstra’s shortest path algo-

rithm.

Hrithik, T. H., Deepa, K., and Sangeetha, S. T. (2024). Pre-

dicting warehouse location of online shopping plat-

forms with machine learning algorithm – a case study.

In 2024 International Conference on E-mobility,

Power Control and Smart Systems (ICEMPS), pages

1–5.

Hwang, S. B. and Kim, S. (2006). Dynamic pricing al-

gorithm for e-commerce. In Sobh, T. and Ellei-

thy, K., editors, Advances in Systems, Computing

Sciences and Software Engineering, pages 149–155,

Dordrecht. Springer Netherlands.

Jaswanth, M., Narayana, N. K. L., Rahul, S., Subramani.,

R., and Murali., K. (2022). Product price optimization

using least square method. In 2022 IEEE 2nd Interna-

tional Conference on Mobile Networks and Wireless

Communications (ICMNWC), pages 1–5.

Kumar, M. R., Vishnu, S., Roshen, G., Kumar, D. N., Re-

vathi, P., and Baster, D. R. L. (2024). Product recom-

mendation using collaborative ﬁltering and k-means

clustering. In 2024 IEEE International Conference on

Computing, Power and Communication Technologies

(IC2PCT), volume 5, pages 1722–1728.

Mohamed, M., El-henawy, I., and Salah, A. (2022). Price

prediction of seasonal items using machine learning

Dynamic E-Commerce Pricing: Optimizing Routes and Forecasting Demand with Machine Learning

453

and statistical methods. Computers, Materials and

Continua, 70:3473–3489.

Saci, S. Machine Learning for Retail Demand Forecasting

— towardsdatascience.com. https://towardsdatascien

ce.com/machine-learning-for-store-demand-forecasti

ng-and-inventory-optimization-part-1-xgboost-vs-9

952d8303b48. [Accessed 19-11-2024].

Schlosser, R. and Boissier, M. (2018). Dynamic pricing

under competition on online marketplaces: A data-

driven approach. pages 705–714.

Shukla, S., Kharde, Y., Mandala, G. N., Bhikaji Jadhav, S.,

and Doguparthy, G. S. (2023). Optimization of dy-

namic pricing in e-commerce platform with demand

side management using fuzzy logic system. In 2023

Second International Conference on Augmented Intel-

ligence and Sustainable Systems (ICAISS), pages 848–

853.

Srinivasan, M. and Sireesha, K. (2022). Optimal path ﬁnd-

ing algorithm for logistic routing problem. In 2022

International Conference on Intelligent Innovations

in Engineering and Technology (ICIIET), pages 203–

209.

Tseng, K.-K., Lin, R., Zhou, H., Kurniajaya, K., and Li,

Q. (2018). Price prediction of e-commerce products

through internet sentiment analysis. Electronic Com-

merce Research, 18.

Yin, C. and Han, J. (2020). Dynamic pricing model of

e-commerce platforms based on deep reinforcement

learning. Computer Modeling in Engineering & Sci-

ences, 127:291–307.

Aguila, J. J., Arias, E., Artigao, M. M., and Miralles, J. J.

(2015). Parallel kd-tree based approach for computing

the prediction horizon using wolf’s method. Mathe-

matical Problems in Engineering, 2015(1):687313.

INCOFT 2025 - International Conference on Futuristic Technology

454