Parameter Estimation of PID Controller Using Machine Learning

Tanuja R Pathare, Masud Akatar, Abdul Mateen Abdul Hai Momin, Rajeev Ranjan Pathak,

Leah S Joshi and Pooja Chandaragi

KLE Technological University, Electrical and Electronics Engineering, Huballi, Karnataka, India

Keywords:

Machine Learning, Deep Learning, PID Controller.

Abstract:

DL (Deep Learning) method of approach towards PID (Proportional-Integral-Derivative) parameter tuning is

inspired by the improvisation of Ziegler-Nichols method and linear regression. For any varying values of

characteristics of a PID controller i.e, Ess (Steady State Error), peak overshoot, settling time, and rise time; a

unique solution is obtained for k

, k

, and k

. This is demonstrated by the means of a more efﬁcient method

which is DL. Research is proposed to acknowledge which of the three mentioned methods provides the best

ﬁt for a model.Using the older methods for PID parameter tuning can be proven to slower the rate of process

or cause human error. Hence, to avoid this an advanced tuning method is proposed via machine learning

1 INTRODUCTION

A PID controller is widely used in control systems

and industrial applications due to its ﬂexibility and

versatility. The history began since 1911 when the

ﬁrst evolution of PID controller was developed by

Elmer Sperry. Popularity grew when Ziegler and

Nichols tuning rules were brought into the limelight.

However, it came with back-leashes such as time

consumption, and the method does not guarantee

reaching a robust and stable solution; hence, to over-

come the cons, a much efﬁcient and advanced method

is proposed using machine learning. In this paper,

three methods of PID controller parameter tuning are

collated, namely Ziegler-Nichols, linear regression

and DL.

2 LITERATURE SURVEY

2.1 Survey on PID Controller Tuning

Using Machine Learning

PID controllers are a staple in industrial control sys-

tems due to their simplicity and effectiveness. How-

ever, manual tuning of PID parameters can be time-

consuming and inefﬁcient, especially in complex sys-

tems. ML (Machine Learning) techniques, such as

DL and reinforcement learning, are increasingly be-

ing employed to automate and enhance PID tuning.

These approaches promise adaptive, efﬁcient, and ro-

bust performance across various applications(Rahmat

et al., 2023) .

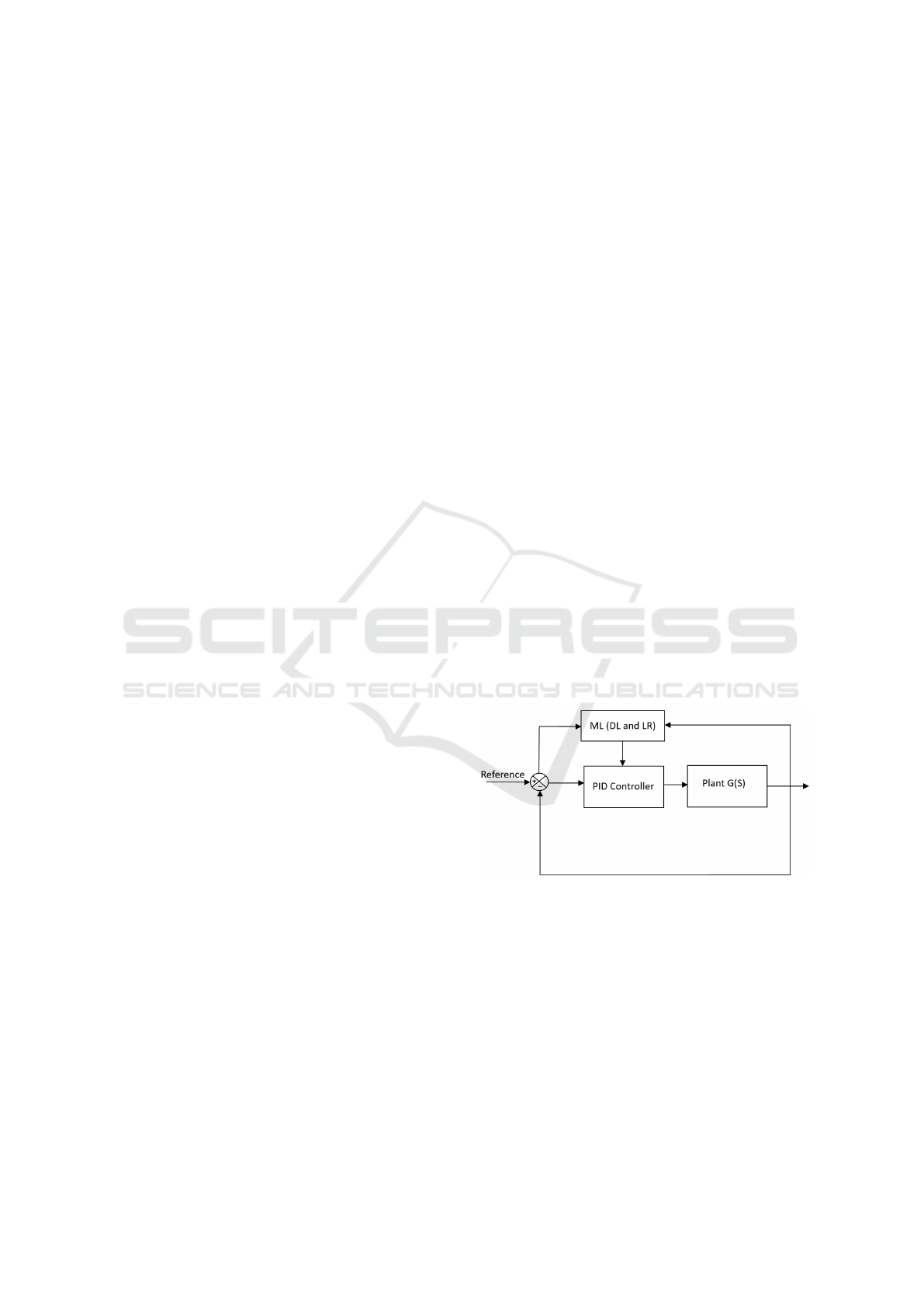
Figure 1: Block diagram for PID parameter estimation us-

ing ML

A PID controller can be used on its own or as

a combination of its three modes. Fig.1 shows the

block diagram of the PID controller. It consists of a

controller that makes decisions and ML block for au-

tonomous tuning via two methods.

2.2 DL for PID Tuning

Use of DL in tuning PID controllers for electrome-

chanical systems is presented in a paper. The model

utilized a neural network trained on system response

Pathare, T. R., Akatar, M., Momin, A. M. A. H., Pathak, R. R., Joshi, L. S. and Chandaragi, P.

Parameter Estimation of PID Controller Using Machine Learning.

DOI: 10.5220/0013617700004664

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 3rd International Conference on Futuristic Technology (INCOFT 2025) - Volume 3, pages 387-392

ISBN: 978-989-758-763-4

387

data, enabling real-time parameter optimization and

superior performance in terms of stability and speed

compared to traditional methods. This approach sig-

niﬁcantly reduced overshoot and settling time, mak-

ing it ideal for complex control environments (Saini

et al., 2023).

2.3 Reinforcement Learning for

Autonomous PID Tuning

RL (Reinforcement Learning) has emerged as a dom-

inant tool for adaptive PID tuning. Recent research

explored RL-based approaches where agents learn op-

timal control strategies by interacting with the en-

vironment. For instance, one study utilized model-

based RL to achieve robust PID tuning. The method

effectively handled non-linearity and uncertainties,

demonstrating robust performance under varying con-

ditions (Trujillo et al., 2022).

2.4 Hybrid Approaches Combining ML

and Classical Methods

Several papers propose hybrid approaches that inte-

grate ML with traditional PID tuning techniques. For

example, researchers employed RLS (Recursive Least

Squares) for system identiﬁcation and ANN (Artiﬁ-

cial Neural Networks) for parameter estimation. This

combination ensured precise tuning and reduced com-

putational overheads (Dogru et al., 2022).

2.5 Application-Speciﬁc

Implementations

Industrial Systems: Studies on electromechanical ac-

tuators showed how ML-based tuning could improve

operational efﬁciency. One example involved tuning

a 3-stage cascaded PID for BLDC (Brush Less Di-

rect Current) motors, which yielded a 90 percent, im-

provement in overshoot and reduced energy consump-

tion.

Process Control: In chemical and thermal process

industries, ML-based PID tuning has been applied to

optimize control loops, resulting in improved energy

efﬁciency and product quality (Jesawada et al., 2022).

Neural networks are seen to outperform some

other intelligent methods in terms of PID adaptive and

tuning (Lazar et al., 2004), (Iplikci, 2010).

Collection of the accurate data labels can be de-

manding in actual engineering problems (Guan and

Yamamoto, 2020).

ML methods have gained widespread attention

since they are data driven and real-time capable and

the literature has focused on diagnosing PID con-

troller performance issues. Machine Learning clas-

siﬁers such as SVM (Suport Vector Machine), deci-

sion trees, and neural networks have been used to de-

tect performance degradation in the absence of de-

tailed system models. Other studies delve into hy-

brid conﬁgurations that integrate conventional con-

trol alongside ML to enhance reliability in several

ﬁelds, notably in manufacturing, power plants, and

aerospace. Future work entails handling more com-

plex datasets for higher accuracy, developing explain-

able models, and evolving to predictive maintenance

to apply maintenance actions before the problem and

prevent the faults. (Ya

gcı et al., 2024).

This study utilizes the use of neural networks

and reinforcement learning to develop an adaptive

PID controller to control pressure drops in non-linear

ﬂuid systems. The method integrates Hammerstein

identiﬁcation for system identiﬁcation and actor-critic

learning to enable real-time PID tuning. This hy-

brid approach improves adaptability and robustness,

achieving better performance than traditional PID

controllers in simulation. This study reveals that a

combination of neural networks and ML can lead

to modern nonlinear environment control solutions,

which is a scalable and is advanced solution for com-

plex industrial ﬂuid systems (Bawazir et al., 2024).

The authors present a generalized and readily tun-

able method to discriminate between acceptable and

poor closed-loop performance. Their approach de-

ﬁnes optimal but feasible closed-loop performance

based on intuitive quality factors. A diversiﬁed set of

CPI (Control Performance Indices) serve as discrim-

inative features for the ofﬂine generated training set.

Thus, the proposed system is intended to be used im-

mediately without further learning (i.e, during regular

operation) (Grelewicz et al., 2023).

The paper explores usage of neural networks for

PID tuning. The challenge discussed is selection of

training sample and suggests replacement of PID con-

trollers with the stated PID tuning method, for better

control (Zhilov, 2022)

DRL (Deep Reinforcement Learning) based PI

gain tuning in robot driver system is proposed, which

utilizes simulation training. D3QN is implemented to

reduce errors and optimize gains. A signiﬁcant im-

provement is seen in the performance as compared

to older fuzzy logic controllers in testing of vehicles

(Park et al., 2022)

A PID controller is compared to gradient descent

tuning and CNN-based cloning. The study concludes

that PID control displays more accurate and stable re-

sults when tested (Abed et al., 2020)

INCOFT 2025 - International Conference on Futuristic Technology

388

2.6 Challenges and Opportunities

Challenges: ML-based PID tuning requires large

datasets for training, which may not always be fea-

sible. Additionally, deploying ML models in real-

time systems involves computational constraints and

the risk of over-ﬁtting.

Opportunities: Advances in lightweight ML mod-

els and cloud-based computation open avenues for

broader application of these techniques. Future work

could focus on integrating ML-based tuning with IoT-

enabled devices for real-time adaptability.

Conclusion and Future Directions: Machine

learning offers trans-formative potential for PID con-

troller tuning, addressing limitations of manual and

heuristic approaches. As ML models are more robust

and computationally efﬁcient, their integration into

industrial control systems will likely become main-

stream. Future research should explore scalable so-

lutions, ensuring compatibility with diverse industrial

applications and hardware constraints.

3 PROPOSED METHODOLOGY

Methodology for the problem statement proposed in

this research, ﬁrst, consists generating a dataset of a

total of seven parameters, including both inputs and

outputs; and ﬁltering it. Second, it incorporates train-

ing the model to evaluate the values of k

, k

, and

by all the three mentioned tuning techniques, that

is, Ziegler-Nichols, linear regression, and DL; when

steady-stare error, overshoot, rise time and settling

time are given. Then, a comparison is made to ﬁnd

best of the three mentioned tuning methods.

3.1 Data collection

• To perform parameter tuning, MATLAB gener-

ates a dataset comprising 15,000 values using a

Python code. It consists of two sets of variable

parameters. The input parameters comprise rise

time, steady-state error, maximum overshoot, and

settling-time; while the response parameters for

the PID system are k

(derivative component), k

(integral gain) and k

(proportional gain).

3.2 Data Processing

• It consists of normalizing the input and output

data to train model efﬁciently. The system re-

sponse characteristics (overshoot, Ess, settling

and rise time) are drawn out by the code as input

characteristics that are stored in variable X. PID

gains (k

, k

and k

) are stored as output targets in

variable Y. Input and output data are normalized

using ”StandardScaler”.

• The obtained normalized data is split into testing

and training sets. 80% of the data is utilized in

training set while the rest 20% in test set.

3.3 Model training

• A Linear Regression model is deﬁned and trained

with ”ﬁt() method”, this minimizes error.

• For DL, a neural network architecture is deﬁned

that will be used for the prediction of PID con-

troller gains. Model compilation is done by an

optimizer, MSE (Mean Squared Error) and MAE

(Mean Absolute Error). The deﬁned DL model is

trained on the training data. The ”ﬁt() method” is

used for training. Model undergoes 100 epochs,

with a batch size of 16.

• Model is composed using MSE. It measures the

average squared difference between the predicted

values and the actual values of a dataset; which is

calculated by the formula given below in equation

(1).

MSE =

∑

i=1

− ˆx

)

(1)

MSE = Mean Squared Error

N = Number of data points

= observed values

ˆx

= predicted values

• MAE is evaluated by equation (2), which gives the

average of absolute value of difference between

the actual and predicted values.

MAE =

∑

i=1

− y

(2)

MAE = mean absolute error

= prediction

= true value

N = total number of data points

3.4 Model Evaluation

• Once trained, model predicts the PID values in

the test set. Model performance is evaluated us-

ing two error metrics namely MSE and MAE. Ac-

curacy calculation is done by the equation given

below (3):

Parameter Estimation of PID Controller Using Machine Learning

389

Accuracy (%) = 100−



MAE

Mean of true values

× 100



(3)

3.5 Visualization

• After obtaining the predicted outcomes, visu-

als are provided for the pre-requisite parameters,

which allows easy elucidation of data. This way

comparison can be made between the three meth-

ods for tuning of PID controller.

4 RESULTS AND ANALYSIS

The model is run by entering values for system pa-

rameters, according to the user requirement to obtain

values of k

, k

and k

. The predicted output is ob-

tained and visual representation of the same is pro-

vided. This way an easy contrast can be made.

The below equation is a closed loop transfer func-

tion (4) :

1 + G

(S) ∗ G

(S) ∗ H(S) = 0 (4)

The transfer function considered for validation of re-

sults in the proposed research is given below in (5).

1 + (K

+ K

S) ∗

(1 + 0.1S)(0.2S + 1)

∗ 1 = 0

(5)

Hence, the characteristic equation obtained is as

given in equation (6):

0.02s

+ (0.3 + K

+ (K

+ 1)s + K

= 0 (6)

Step input is given as ”1” in Simulink (MATLAB),

for both the samples considered in Table 1.

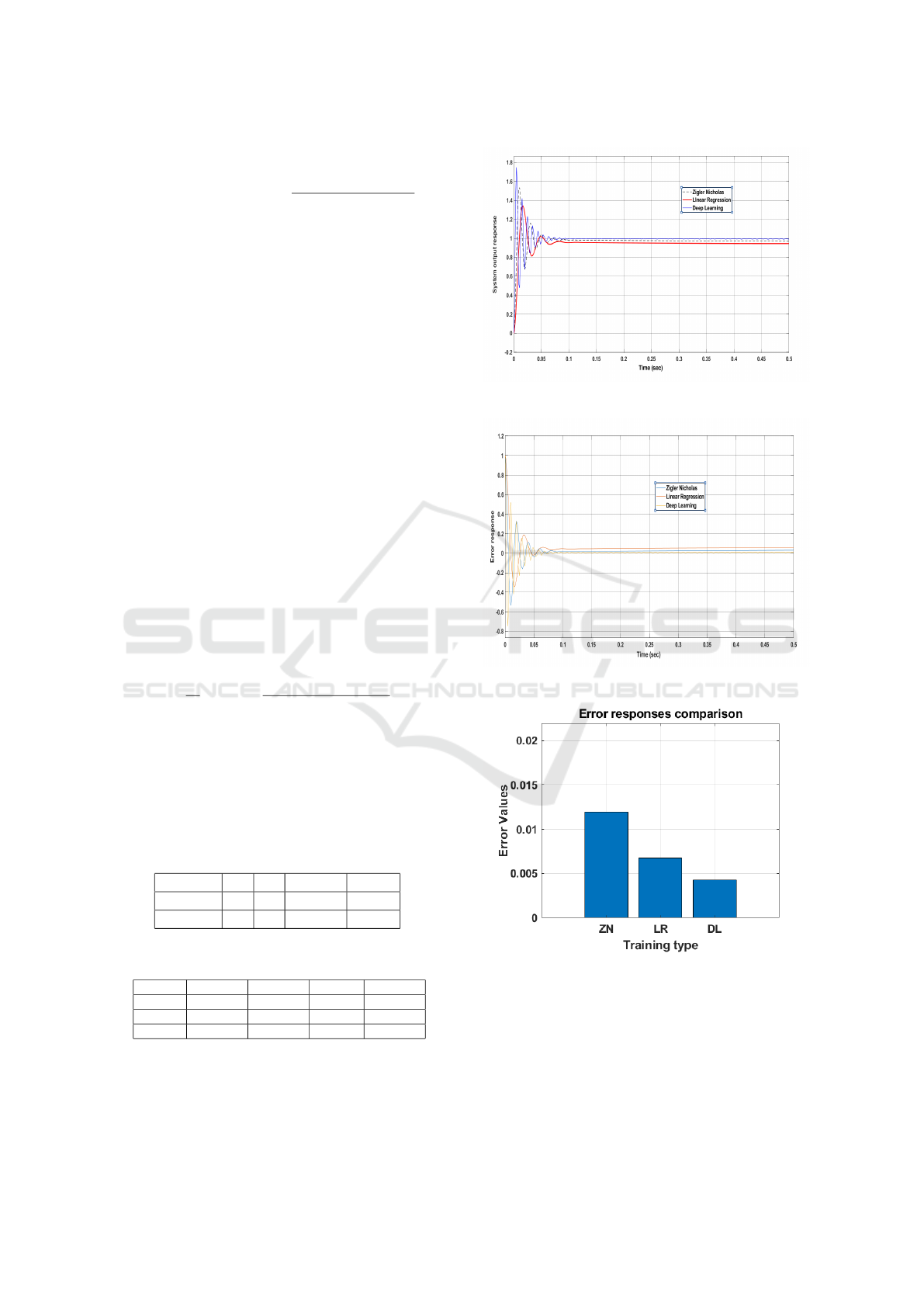
Table 1: Data for Sample 1 and Sample 2

Sample T

MP % Ess

1 3 5 10 0.05

2 7 5 12 0.052

Table 2: Response for Sample 1

Method K

ISE

ZN 5.5 0.495 10 0.1195

LR 9.9607 30.9843 11.6628 0.006748

DL 142.2267 318.0241 38.5982 0.004228

Figure 2: Output Response for Sample 1

Figure 3: Error Response for Sample 1

Figure 4: Error comparison for Sample 1

Considering values of Sample 1 (Table 1), the pre-

dicted output is stated in Table 2. From Fig.2 it can be

observed that out of all the three mentioned methods,

DL method displays the most accurate results. Since

the step input is given as 1, expected output for an ef-

ﬁcient model should be same as the input; this is ob-

served along the output line representing DL (which

INCOFT 2025 - International Conference on Futuristic Technology

390

is closest to 1). The error response of all the three

methods is displayed in Fig 3 which is the least in

DL method. ISE of DL for Sample 1, can be visu-

alized from Fig.4, which is the least when compared

to the other two methods i.e, 0.004228 < 0.1195 and

0.004228 < 0.006748. This results in better perfor-

mance of the system, and an enhanced performance

in terms of precision and stability.

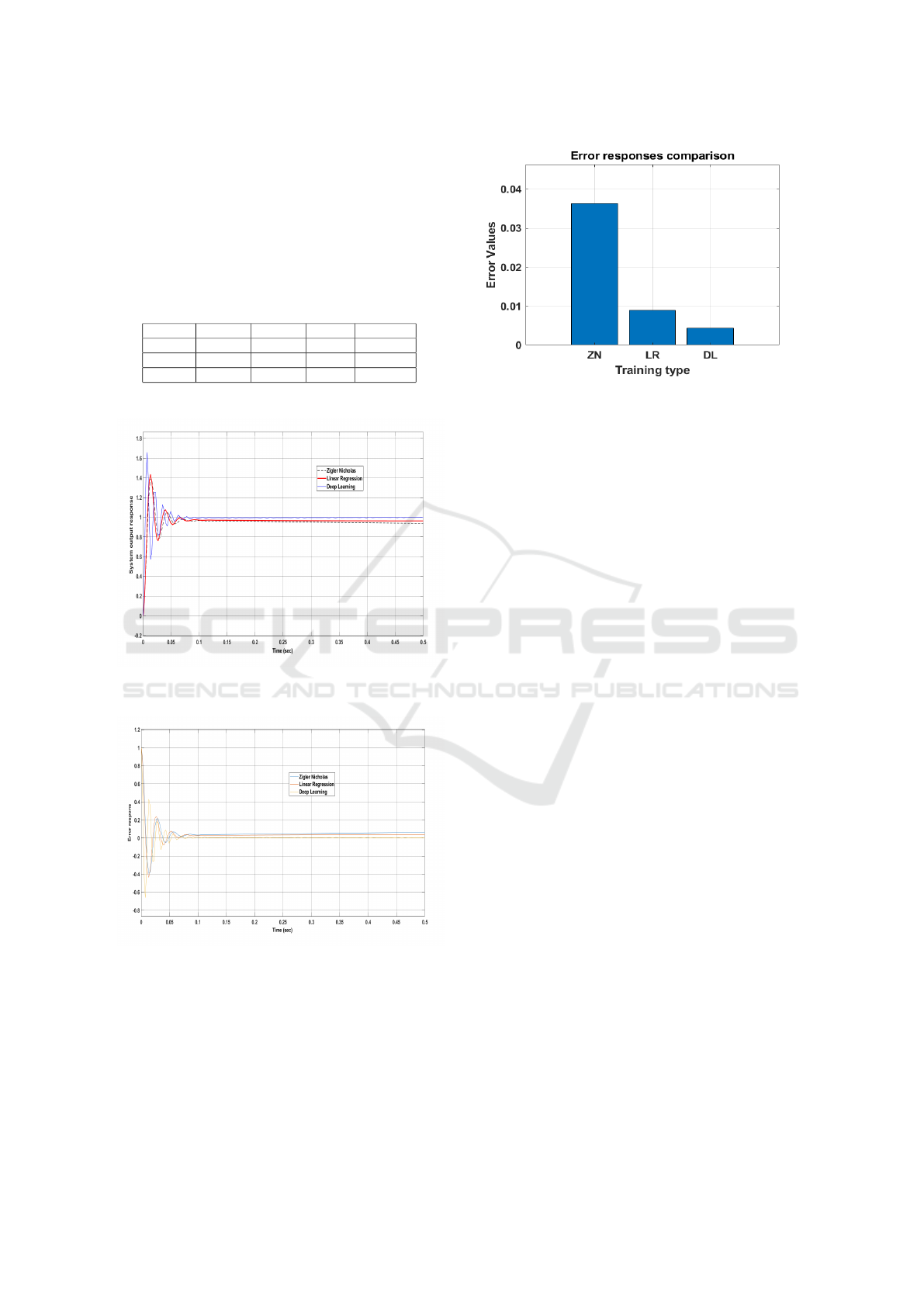
Table 3: Response for Sample 2

Method K

ISE

ZN 11.4874 0.90581 20 0.03635

LR 6.6725 20.6890 7.6736 0.008989

DL 42.61 67.31 82.45 0.004251

Figure 5: Output Response for Sample 2

Figure 6: Error Response for Sample 2

The above stated conclusions can be supported by

considering Sample 2 (refer Table1). The output re-

sponse is stated in Table 3, visuals of which can be

observed in Fig.5 which depicts that line represent-

ing DL is nearly equal to 1, when compared to the

other two. Error of DL is the least i.e, nearly equal

to 0; which can be visualized from Fig.6 pointing

to the fact that DL is more efﬁcient. The visuals of

Figure 7: Error comparison for Sample 2

ISE are provided in the form of a bar graph in Fig.7,

which depicts that ISE is the least in DL method i.e,

0.004251 < 0.008989 and 0.004251 < 0.03635.

5 CONCLUSION

In this paper we propose an advanced PID parameter

tuning method which minimizes error, and provides

accurate and stable output response for a system.

It can hence be concluded that DL is seen as a

better approach for PID parameter tuning; for the rea-

son that it can be used for modeling complex mod-

els while linear regression and Ziegler-Nichols can

only be used for the training of simpler models. This

clearly shows that this method is more efﬁcient, faster

and convenient than Ziegler-Nichols and linear re-

gression method.

ACKNOWLEDGEMENTS

We would like to acknowledge the Department of

Electrical and Electronics Engineering of KLE Tech-

nological University for all the resources.

REFERENCES

Abed, M. E., Aly, M., Ammar, H. H., and Shalaby,

R. (2020). Steering control for autonomous vehi-

cles using pid control with gradient descent tuning

and behavioral cloning. 2020 2nd Novel Intelligent

and Leading Emerging Sciences Conference (NILES),

pages 583–587.

Bawazir, A. F., AL-Yazidi, N. M., Al-Dogail, A. S., Bin Ga-

ufan, K. S., and Saif, A.-W. A. (2024). Adap-

tive pid controller using neural network for pressure

drop in nonlinear ﬂuid systems. 2024 21st Interna-

Parameter Estimation of PID Controller Using Machine Learning

391

tional Multi-Conference on Systems, Signals & De-

vices (SSD), pages 272–277.

Dogru, O., Velswamy, K., Ibrahim, F., Wu, Y., Sun-

daramoorthy, A. S., Huang, B., Xu, S., Nixon, M., and

Bell, N. (2022). Reinforcement learning approach to

autonomous pid tuning. 2022 American Control Con-

ference (ACC), pages 2691–2696.

Grelewicz, P., Khuat, T. T., Czeczot, J., Nowak, P., Klopot,

T., and Gabrys, B. (2023). Application of machine

learning to performance assessment for a class of pid-

based control systems. IEEE Transactions on Systems,

Man, and Cybernetics: Systems, 53(7):4226–4238.

Guan, Z. and Yamamoto, T. (2020). Design of a reinforce-

ment learning pid controller. 2020 International Joint

Conference on Neural Networks (IJCNN), pages 1–6.

Iplikci, S. (2010). A comparative study on a novel model-

based pid tuning and control mechanism for nonlinear

systems. International Journal of Robust and Nonlin-

ear Control, 20(13):1483–1501.

Jesawada, H., Yerudkar, A., Del Vecchio, C., and Singh,

N. (2022). A model-based reinforcement learning ap-

proach for robust pid tuning. 2022 IEEE 61st Con-

ference on Decision and Control (CDC), pages 1466–

1471.

Lazar, C., Carari, S., Vrabie, D. L., and Kloetzer, M. (2004).

Neuro-predictive control based self-tuning of pid con-

trollers. ESANN, pages 391–395.

Park, J., Kim, H., Hwang, K., and Lim, S. (2022). Deep

reinforcement learning based dynamic proportional-

integral (pi) gain auto-tuning method for a robot driver

system. IEEE Access, 10:31043–31057.

Rahmat, B., Waluyo, M., Rachmanto, T. A., Agussalim,

Pratama, A. R., Muljono, M., Diyasa, I. G. S. M.,

Swari, M. H. P., and Hendrasarie, N. (2023). itclab

pid control tuning using deep learning. 2023 IEEE 9th

Information Technology International Seminar (ITIS),

pages 1–4.

Saini, S., Hernandez, J., and Nayak, S. (2023). Auto-tuning

pid controller on electromechanical actuators using

machine learning. –, pages 1–8.

Trujillo, K. B.,

Alvarez, J. G., and Cort

es, E. (2022). Pi and

pid controller tuning with deep reinforcement learn-

ing. 2022 IEEE International Conference on Automa-

tion/XXV Congress of the Chilean Association of Au-

tomatic Control (ICA-ACCA), pages 1–6.

gcı, M., Forsman, K., and B

oling, J. M. (2024). A ma-

chine learning classiﬁer for detection of performance

issues in industrial closed-loop pid controllers. 2024

10th International Conference on Control, Decision

and Information Technologies (CoDIT), pages 1231–

1236.

Zhilov, R. (2022). Application of the neural network ap-

proach when tuning the pid controller. 2022 Interna-

tional Russian Automation Conference (RusAutoCon),

pages 228–233.

INCOFT 2025 - International Conference on Futuristic Technology

392