Multi-Objective Evolutionary Computation for the Portfolio

Optimization Problem with Respect to Environmental, Social, and

Governance Criteria

Riley Herman and Malek Mouhoub

Department of Computer Science, University of Regina, Regina, Canada

Keywords:

Multi-Objective Evolutionary Computation (MOEA), Metaheuristics, Portfolio Optimization.

Abstract:

A common problem facing many is the tension between doing what aligns with our values and doing what

is ﬁscally best. We propose a system leveraging Multi-Objective Evolutionary Computation, speciﬁcally

MOEA/D, to produce highly performant portfolios tailored to an individual’s Environmental, Social, and

Governance (ESG) preferences given a custom survey that we have designed. The survey is conducted to

construct a weighting to normalize a given investor’s own responses and allow a single portfolio from the

collection of the best portfolios to be matched to that investor. We have adopted two potential architectures

to build our proposed system: Architecture 1, where the optimization is run for each investor that takes the

survey, and Architecture 2 where a multi-objective optimization is run less frequently and the investor is given

a portfolio from the Pareto front. This subset consists of all the non-dominated portfolios. The user may have

different experiences, including quality or response time, depending on the architecture chosen. The results

of the experiments we conducted demonstrate that both architectures performed comparably and produced

high-quality portfolios. However, the best portfolio from Architecture 2 was better in most respects than any

portfolio from Architecture 1. All Architecture 1 portfolios were more signiﬁcantly tailored to each of the in-

dividuals’ preferences. For Architecture 2, a limited number of high performing portfolios was generated: as a

result, more investors would potentially be recommended to the same few portfolios, especially in comparison

to Architecture 1.

1 INTRODUCTION

A common problem facing many is the tension be-

tween doing what aligns with our values and doing

what is ﬁscally best. In our age of mass information,

the availability of a publicly traded company’s ESG

(Environment, Social, Governance) data has resulted

in a demand for ﬁnancial portfolios that reﬂect the

values of consumers. With the gluttony of choices

in stocks and other investment vehicles as well as

the gluttony of data on publicly listed companies, it

is an overwhelming task to compute portfolios that

are performant as well as personally ethical. The ma-

jority of researchers exploring the portfolio optimiza-

tion problem as an example of a multi-objective op-

timization problem are using two objective optimiza-

tions, as Markowitz ﬁrst proposed: risk and return.

Here, the problem is extended to better reﬂect the real

world and to produce a practical and useful applica-

https://orcid.org/0000-0001-7381-1064

tion. Independent objectives of environmental, social,

and governance scores are added to further address

the needs of data-savvy investors. In addition, risk is

split to capture two types of risk measurement to bet-

ter encapsulate different types of risk.

In addition, this paper presents a survey. This sur-

vey gathers and synthesizes data on the prospective

investor’s preferences towards ESG, as well as their

risk tolerance. The survey was necessary to answer

a question: What score deﬁnes a stock that performs

“well” with respect to an ESG criteria? The same sur-

vey can be reused as input for the potential investor

to be categorized and given a ﬁnal singular portfolio

from the collection of all the best performing portfo-

lios.

In order for this research to be as practical as pos-

sible, two potential architectures of a recommenda-

tion system are presented. In much of the literature,

the step from theory to practical application in the real

world is not considered. Given the possible types of

data one may attempt to use, the hardware available

Herman, R. and Mouhoub, M.

Multi-Objective Evolutionary Computation for the Portfolio Optimization Problem with Respect to Environmental, Social, and Governance Criteria.

DOI: 10.5220/0013604500003970

In Proceedings of the 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2025), pages 357-365

ISBN: 978-989-758-759-7; ISSN: 2184-2841

357

to a potential implementer, or even the market seg-

ment one may try to target, these two architectures

could both be successful in different situations. This

choice requires a modiﬁcation to the model, and as

such, both modiﬁcations are presented. In sum, the

following contributions are presented.

• Two architectures for a portfolio recommender

system

• A survey for the gathering of risk and ESG pref-

erences

• A problem deﬁnition grounded in the literature

2 PORTFOLIO OPTIMIZATION

The portfolio optimization problem is as follows:

Given a set of investment vehicles and some cor-

responding information about each investment vehi-

cle (here, the potential risk, return, and ESG scores),

compute a portfolio of investment vehicles such that

the total return is maximized, risk is minimized, and

the portfolio does not cost more than a given budget.

This is also extended to maximize positive environ-

mental, social and governance criteria.

This problem ﬁnds its roots in Markowitz. Many

different routes have been traversed on this problem:

This is not a comprehensive history of attempts at

solving this problem, but should give ample justiﬁca-

tion for the techniques explored here. Mathematically

speaking, of course, this is a solved problem. The is-

sue is no longer whether an optimal portfolio can be

found, but rather how quickly a sufﬁciently optimal

portfolio can be found.

Several metaheuristics (Lynn and Suganthan, 0

01; Darmstadt and Approximity, 2003; Korani and

Mouhoub, 2021; Korani and Mouhoub, 2022; Sadred-

din et al., 2022) have been applied to solve portfolio

optimization problems. The ﬁrst of which was PSO

in the mid-1990s (Darmstadt and Approximity, 2003).

Interestingly, in 2015 some improvements to the orig-

inal PSO were published that apply much closer to

the recommender system described here, namely Het-

erogeneous Multiple Population Particle Swarm Op-

timization. The idea is to break the initial population

into smaller sub-variants of the larger PSO problem.

(Lynn and Suganthan, 0 01)

Ant Colony Optimization underwent similar treat-

ment on the same cycle; improvements to expand an

early 1990s algorithm (Nayar et al., 2021) to bet-

ter incorporate multiple objectives in the early 2010s.

(Samantha Bastiani et al., 2015). Unique to the ge-

netic algorithm approach is the production of multiple

portfolios as a non-comparable Pareto front - other

algorithms discussed above focus on giving a single

portfolio as a solution. This makes these approaches

universal and more efﬁcient if the objective is to cre-

ate portfolios for any kind of investor. The multi-

objective focused algorithms SPEA-2, NSGA-II, and

MOEA/D described above have all been applied to

this problem. The ﬁrst papers for all of these appli-

cations use two objectives - some measure of risk and

some measure of return, later to be expanded. (Mil-

homem and Dantas, 1 01)

3 PROPOSED METHODOLOGY

3.1 Problem Deﬁnition

Given a set of investment vehicles and a budget, one

must use risk and return to ﬁnd an amount of each

stock to purchase such that risk is minimal and re-

turn is maximal. Risk and return are not comparable.

Thus, the solution is a set of options, each one best

in its own way. Once the problem is formulated in

terms of variables (the investment vehicles and how

much to buy of each one, v

...v

), constraints (given

in Equation 1

B ≥

∑

(1)

where B is the budget and p

is the price of one in-

stance of that investment vehicle), and objective func-

tions (risk and return), the problem is ready to be

modelled as a constraint optimization problem.

This is the standard deﬁnition of the problem: two

objectives and one constraint, which is the minimum

required for a problem to be a multi-objective con-

straint optimization problem. In order to capture the

different types of risk, risk here is split into two non-

comparable objectives: VaR and CVaR. Expanding on

this, environmental, social and governance scores are

each added as individual objectives, giving a total of

six objectives in this formulation.

∑

VaR

(2)

∑

CVaR

(3)

Equation 2 and Equation 3 form the risk objectives,

which should be minimized. Each investment vehicle

also has a known environmental (e

), social (s

) and

governance (g

) score which should be maximized:

∑

(4)

∑

(5)

∑

(6)

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

358

Figure 1: Flow chart for Architecture 1.

3.2 System Architecture

3.2.1 Architecture 1

Architecture 1 (depicted in Figure 1) runs the opti-

mization each time an investor wishes to ﬁnd a portfo-

lio using their preferences as weights. This would be

a weighted constraint optimization problem in which

one optimal portfolio is produced for that investor -

in other words, a single objective constraint optimiza-

tion problem. The investor may sit at their desk, an-

swer the survey, and then wait for the algorithm to

ﬁnish computing their portfolio. Once the survey is

answered, the following steps are executed.

1. Takes a snapshot of the TSX market data.

2. Computes the single optimized portfolio using a

simpliﬁcation of MOEA/D

• Firstly, random solutions are generated using

the snapshotted data.

• The optimization is run per the conﬁgurations

from section 4.2.1, however, this is a single ob-

jective optimization because the six objectives

are able to be combined into one via the weights

already provided by the user.

3. Presents this portfolio to the end user.

The biggest advantage of this is also connected to its

biggest problem: if live pricing is used, then the port-

folio may be out-of-date by the time it has ﬁnished

computing. This is slightly mitigated by the speed

of a single optimization when compared to a multi-

optimization. If it uses the closing price data for the

previous day, there are two scenarios depending on

the time the investor chooses to create their portfolio:

1. Use the service when the markets are closed and

act once the markets are open, or

2. Accept the risk that the prices are inaccurate by

the day’s market activity.

3.2.2 Architecture 2

The second architecture (Figure 2) runs a multi-

objective optimization with all investors in mind.

Figure 2: Flow chart for Architecture 2.

Once the individual investor sits down and requests

a portfolio, that portfolio is computed as the high-

est scoring member of the Pareto front with respect

to that investor’s weighting. This would have linear

growth based on the number of portfolios in the Pareto

front, making it extremely quick. A day in the life of

this architecture would look like this:

1. Any time after the market closes for the day, a

snapshot of TSX data is taken

2. Using MOEA/D, a Pareto front of Pareto optimal

portfolios is computed and saved

• Firstly, random solutions are generated using

the snapshotted data.

• The optimization is run per the conﬁgurations

from section 4.2.1. This is a six objective opti-

mization, but it is only run one time per day.

• The ﬁnal Pareto front produced by MOEA/D is

saved, the former day’s discarded.

3. Every time an investor completes the survey, their

results are converted to weights (per section 3.3.4)

4. Take each portfolio from today’s Pareto front,

multiply each objective value by its corresponding

weight from the investor, and pick the maximal.

The biggest speed constraint for this method is, of

course, that the optimization must run for a shorter

amount of time than the time between the market clos-

ing and the market’s next-day opening. Thus, the ac-

curacy of the Pareto front solutions could be greater

than the accuracy of the signiﬁcantly more speed-

conscious Architecture 1 because of the realignment

of priorities when considering the parameters.

3.3 Survey

The survey in its entirety can be viewed in Appendix

5. It is divided into four parts: risk proﬁling, short,

medium, and long.

3.3.1 Risk Proﬁling

Several publicly available risk assessment question-

naires were consulted before writing the risk section

Multi-Objective Evolutionary Computation for the Portfolio Optimization Problem with Respect to Environmental, Social, and Governance

Criteria

359

of the survey. These are commonplace and often fol-

low similar patterns: many multiple choice questions

where the answers ascend from low to high risk toler-

ance (an example one from a well known investment

ﬁrm can be found in (Morningstar, )). Intentionally,

there are a mix of even number (four) answer ques-

tions and odd number (ﬁve) answer questions. The

even number of answers forces an indecisive investor

to choose which side they lean on even if they want to

remain relatively balanced.

3.3.2 ESG Survey

The short survey consists of one question: in essence,

does the investor care about ESG metrics. If the in-

vestor does not, the survey endeavours to respect your

time. More information is provided if the participant

requires it to make this choice. If the participant is

willing to give their preferences, the medium survey

is presented.

The medium survey is intended to give a brief

overview of the participants’ preferences. This con-

sists of an open text box that is currently unused in

analysis (see Future Work for further information on

why this is included), a ranking question, and three

questions each of the following form: environmen-

tally (or socially or governance) conscious companies

should represent what percent of the portfolio. Then

another checkpoint is presented, and if the participant

wishes to continue, they can do the long survey.

The long survey is based on the Sustainable De-

velopment Goals of the United Nations. There are

three ranking questions, each referencing one of envi-

ronment, social, and governance, and ﬁnally another

open text box that is unused for the same reason as ex-

pressed in the Future Work section. In the European

Union (EU), by regulation, ESG must be incorporated

into the investment advisory process. Thus, the devel-

opment of surveys that conform to MiFID II sets the

benchmark for surveys on the topic. A representative

sample questionnaire that conforms to MiFID II that

was consulted for the development of the survey pre-

sented here can be found here (Initiative, 2022).

3.3.3 Converting a Survey Result into Weights

Each survey question carries the same weight in the

ﬁnal weighting. The risk scoring is as follows for each

question in the Risk Survey, starting from a score of

• Each answer of A subtracts 2 from the overall

score

• Each answer of B subtracts 1 from the overall

score

• Each answer of C on a question with 5 possible

answers adds 0. If there are 4 possible answers, a

C adds 1

• Each answer of D on a question with 5 possible

answers adds 1. If there are 4 possible answers, a

D adds 2

• Each answer of E adds 2 to the overall score.

As is evident from the multiple choice answers and

the scoring matrix, a higher score indicates a higher

risk tolerance and vice versa.

For any ﬁnal answer C to the short survey,

the investor’s environmental, social, and governance

weights are all taken as 0, since the investor has indi-

cated that they do not have any ESG preferences.

The scoring for each environmental, social, or

governance questions from the medium and long sur-

veys that take the form of a ranking is derived using

the number of criteria that are ranked over the total

number of criteria. For example, if an investor ranks

8/16 as the environmentally focused question (the

ﬁrst question of the long survey), that will add 0.5 to

their environmental score. The medium survey rank-

ing question (the second question in the medium sur-

vey) contributes to all three scores in order to account

for an investor that has a general preference in ESG

but no distinguishing difference between environmen-

tal, social, or governance. The three medium survey

questions asking for numbers are directly added as

percentages to the score given that they are provided

as valid percentages (between 0 and 100, then divided

by 100).

3.3.4 Converting a Collection of Survey Results

into Weights

Because no two survey results are alike and because

deﬁning whether a certain score in a certain metric is

high or low begs the question “compared to what?”,

it is necessary to deﬁne how a survey score relates to

a weight. Given a collection of survey results, each

weight (corresponding to an objective) is normalized

to its peers using a simple formula.

− min

max

− min

(7)

where s

is the ith investor’s score for objective o,

max

and min

are the global maximum (minimum)

of the scores for objective o. Note that the risk weight

is evenly split between the VaR and CVaR objectives.

In addition, as there is no return objective deduced

from the survey, the return takes up the rest of the

weighting.

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

360

4 EXPERIMENTATION

4.1 Inputs and Conﬁgurations

4.1.1 Price

For consistency and comparability, the closing price

for the previous day is used. One of the advantages of

doing the optimization as it is done in Architecture 1

is that live pricing data or snapshots taken close to the

time of optimization (and therefore close to the time

of investing). While this is preferable for this archi-

tecture, it is not a possibility for Architecture 2 and

so in order to preserve the comparability of the two

architectures, the same pricing data are used for both.

This can be considered a snapshot taken closest to the

optimization when the optimization is run between a

market’s close and open.

In addition, all investment vehicles with a price

of less that $1.00 per share have been excluded from

the data. This is to mitigate the problem-speciﬁc over

weighting of penny stocks, which are known to have

extremely high volatility. The whole list of TSX list-

ings as well as the data for the included stocks are

available in Appendix 5

4.1.2 Risk

VaR is calculated using the parametric method (also

known as the variance-covariance method) of com-

puting daily VaR. Although this carries the normal

distribution assumption, it is extremely computation-

ally efﬁcient and is used widely when historical data

is either difﬁcult to come by or is not available at all

(for example, for newly listed companies). Here, it is

conﬁgured to use conﬁdence 95%. VaR is also used in

the computation of CVaR, so this normal distribution

assumption is also present there.

CVaR (also called expected shortfall) is calculated

according to the standardized formula

CVaR =

1 − c

VaR

−1

x (8)

where c refers to the conﬁdence mentioned above

(again, 95%) and x is the normally distributed returns

over the period.

4.1.3 Return and CAPM

The expected return is calculated according to the

capital asset pricing model (CAPM). The standard

formula for CAPM is

CAPM = R

+ β

(ER

− R

) (9)

where R

is the risk-free rate of the market, β

is the

beta value of the stock, and ER

is the expected return

of the market as a whole. The expression ER

− R

can be considered the amount that one potentially

gains given that they invest in the market as opposed

to a risk-free asset and is often called the market risk

premium.

For a risk-free asset, the Bank of Canada CORRA

(Canadian Overnight Repo Rate Average) rate is used.

This is Canada’s free rate and is sourced from the

Bank of Canada (Bank of Canada, ). For the expected

return of the market, the S&P TSX index is used. The

important thing to choose this rate is that it mirrors

the benchmark used to compare the performance of an

investment vehicle with the market as a whole. S&P

TSX is a broad-reaching index also used elsewhere in

the literature when it comes to Canadian markets.

4.1.4 Benchmark

S&P TSX is a commonly used benchmark for the

Canadian stock market, so to preserve future compa-

rability, it is used here. It is also useful to use the

same benchmark as is used for the calculation of the

expected return (CAPM), as this allows for a more

accurate comparison between the benchmark and the

performance of a portfolio whose returns are already

calculated compared to that benchmark.

4.1.5 Morningstar and ESG Data

The TSX and ESG data used in this implementation

are sourced from Yahoo Finance. Yahoo Finance ag-

gregates data from several sources: sustainability data

is provided by Sustainalytics and Morningstar and

corporate governance scoring is provided by Institu-

tional Shareholder Services. Morningstar also pro-

vides historical chart data and ﬁnancial statements.

Company proﬁle data comes from S&P Global Mar-

ket Intelligence. The TSX pricing data are sourced in

real time from ICE Data Services. (Finance, )

4.2 Algorithm Conﬁgurations

4.2.1 MOEA/D Conﬁguration

For the experiment, conﬁgurations that allow this rec-

ommender system to be compared to other implemen-

tations of MOEA/D. The conﬁgurations given in Ta-

ble 1 are also consistent between the two architec-

tures.

4.2.2 Problem Speciﬁc Mutation Mechanism

An undersold inﬂuence on the performance of the so-

lutions is the mutation operation in the genetic algo-

rithm. There is a problem non-speciﬁc method of

Multi-Objective Evolutionary Computation for the Portfolio Optimization Problem with Respect to Environmental, Social, and Governance

Criteria

361

Table 1: MOEA/D Conﬁgurations.

No. runs 10

No. individuals 500

No. generations 10

No. nearest neighbours 50

Percentage of genes mutating 20%

Budget $100,000

combining two parents into a child: simply swap a

random collection of half the genes from each par-

ent. This is common in the literature; however, when

this was attempted, often the swap would be reversed

because the combination violated the budgetary con-

straint. Thus, the swap has been swapped for this

problem speciﬁc mutation. It takes half the value of

each of the investment vehicles from each parent (and

therefore half the used budget) rounded down. For

example, given a mother that has options 30 of in-

vestment vehicle A, 20 of B, and 10 of C and a father

with 10 of A, 21 of B, and 10 of D, the child will have

A = ⌊

30+10

⌋ = 20, B = ⌊

20+21

⌋ = 20, C = ⌊

10+0

⌋ =

5, and D = ⌊

0+10

⌋ = 5.

Notice that the sum of units from before the mu-

tation is less than the exact average number of units

between both parents. Because the child will tend to

have a lower budget utilization than its parents (the

constraint is kept by the fact that the ﬂoor of the aver-

age of two numbers is less than or equal to the exact

average, so this difference would in effect turn to un-

used “cash”), there is then a reﬁll phase. Each option

is checked in a random order to see whether the addi-

tional budget space can be used: if so, one additional

unit is added. In this way, the mutation tends towards

higher budget utilization over time.

4.3 Results

4.3.1 Example Investors - Sam, Jars, and Alice

Sam is very socially aware and has deep rooted prefer-

ences. They want their portfolio to reﬂect their values

as much as it can. Sam is also gearing up for retire-

ment - given that they don’t have a long time hori-

zon for this investment, preserving the initial capital

is high on their priorities as well.

Sam took the survey and their weights are given in

Table 2.

Table 2: Sam’s weights.

Risk 0.1

Environmental 0.3

Social 0.3

Governance 0.2

Jars is just starting their career - they have ﬁ-

nally paid back their student debt and now want their

money to work as hard as they are. Jars does not par-

ticularly trust the ESG rating system and so would

rather take their chances with casting a wider net. Jars

took the survey and their weights are given in Table 3.

Table 3: Jars’ weights.

Risk 0.9

Environmental 0.0

Social 0.0

Governance 0.0

Alice has been acutely aware of all things Corpo-

rate Governance for as long as they can remember.

They feel their best impact can stay in their expertise.

Alice has a little money for investing, but is also plan-

ning a down payment on a house so would like to keep

a balanced portfolio in order to be able to jump on any

housing opportunity they see. Alice took the survey

and their weights are given in Table 4.

Table 4: Alice’s weights.

Risk 0.3

Environmental 0.0

Social 0.0

Governance 0.6

4.3.2 Architecture 1 Results

The three portfolio examples of investors are given in

the Appendix 5.

Given Architecture 1 as deﬁned, these would be

their results. The results are the best taken from the

10 runs. Sam’s portfolio metrics are in Table 5, Jars’

portfolio metrics are in Table 6, and Alice’s portfolio

metrics are in Table 7

Table 5: Sam’s Architecture 1 portfolio.

Portfolio Benchmark (S&P TSX)

Return 0.8750 0.0112

VaR 0.9901 0.9999

CVaR 0.9894 1.000

Environmental 0.8681 N/A

Social 1.6878 N/A

Governance 2.9182 N/A

4.3.3 Architecture 2 Results

Architecture 2 gives a Pareto front of potential portfo-

lios. All of these portfolios are available in Appendix

5. The metrics for the best of the 10 runs are pre-

sented here. Sam’s portfolio metrics are in Table 8,

Jars’ portfolio metrics are in Table 9, and Alice’s port-

folio metrics are in Table 10.

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

362

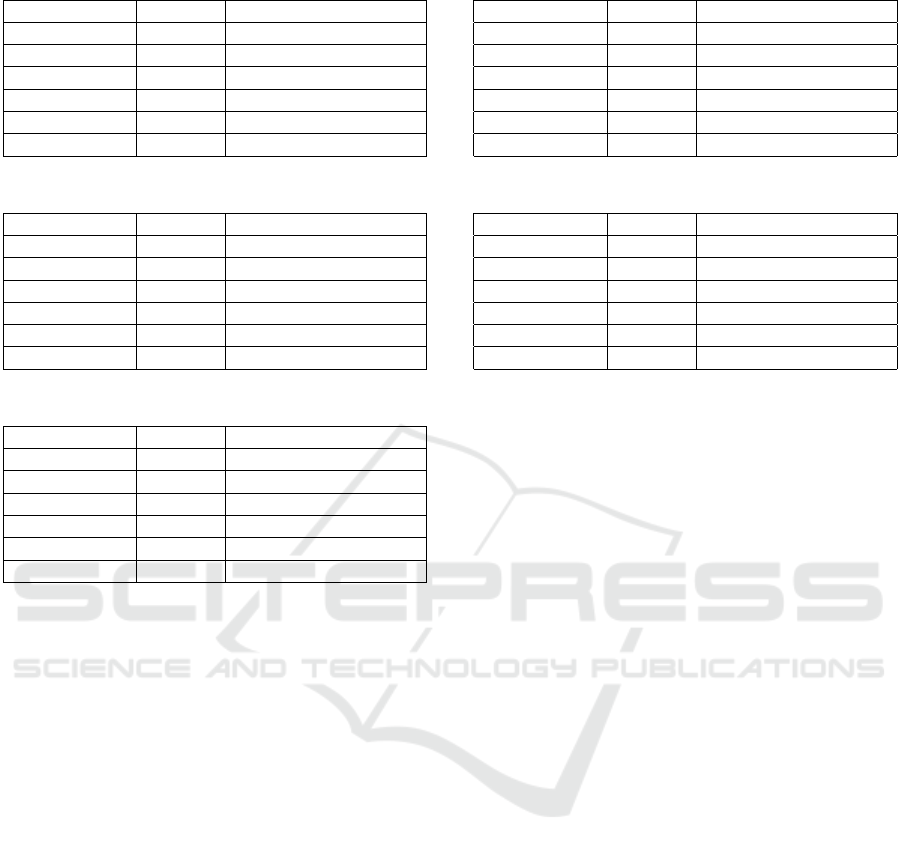
Table 6: Jars’ Architecture 1 portfolio.

Portfolio Benchmark (S&P TSX)

Return 0.7760 0.0112

VaR 0.7868 0.9999

CVaR 0.7818 1.000

Environmental 0.0000 N/A

Social 0.0000 N/A

Governance 0.0000 N/A

Table 7: Alice’s Architecture 1 portfolio.

Portfolio Benchmark (S&P TSX)

Return 0.6980 0.0112

VaR 0.9566 0.9999

CVaR 0.9531 1.000

Environmental 0.0000 N/A

Social 0.0000 N/A

Governance 4.9238 N/A

Table 8: Sam’s Architecture 2 portfolio.

Portfolio Benchmark (S&P TSX)

Return 0.4679 0.0112

VaR 0.9934 0.9999

CVaR 0.9948 1.000

Environmental 0.1350 N/A

Social 0.4011 N/A

Governance 0.1546 N/A

4.3.4 General Portfolio Observations

There appears to be a strong correlation between the

three ESG criteria. This provides a reason for these

to be combined into one weight for ESG, which is

frequently assumed but not explored in the literature.

VaR and CVaR are also strongly correlated across

the board. This is unsurprising as CVaR is based on

VaR and while the values are not precisely equal, a

company that is risky is very likely to be risky based

on both metrics.

As assumed in the mean variance model, higher

risk appears to be correlated to higher returns. This

can be attributed in part to the metric used for the

return. CAPM takes risk into account when it at-

tempts to predict the return using the beta of the in-

vestment vehicle, so risk can be considered to be dou-

bly counted here. However, the risk measure used is

neither VaR nor CVaR, it is the value β, so it is pos-

sible that the outliers perform differently. Both risk

metrics and return, in these graphs, appear to be in-

versely related to ESG criteria. That is, with higher

ESG ratings come lower risk and lower returns. As

mentioned in the review of the literature, the litera-

ture differs substantially on this topic.

With all that being said, this does corroborate

some conclusions found in the literature. Although

Table 9: Jars’ Architecture 2 portfolio.

Portfolio Benchmark (S&P TSX)

Return 0.4679 0.0112

VaR 0.9934 0.9999

CVaR 0.9948 1.000

Environmental 0.1350 N/A

Social 0.2310 N/A

Governance 0.1546 N/A

Table 10: Alice’s Architecture 2 portfolio.

Portfolio Benchmark (S&P TSX)

Return 0.4679 0.0112

VaR 0.9934 0.9999

CVaR 0.9948 1.000

Environmental 0.1350 N/A

Social 0.2310 N/A

Governance 0.1546 N/A

the Architecture 2 portfolios for each of our investors

are similar, they do fulﬁll the needs of that investor

remarkably well. This aligns with the result of (Utz

et al., 4 16), (De Spiegeleer et al., 0 16) and (Naffa and

Fain, 1 01) who concluded that there is no substantial

difference in performance whether given ESG con-

straints/objectives or not. The best portfolio from Ar-

chitecture 2 was better in most regards than any port-

folio from Architecture 1. All Architecture 1 port-

folios were more signiﬁcantly tailored to each of the

individuals’ preferences.

5 CONCLUSION

Ultimately, if the goal of the system is to tailor and

adhere to the preferences of the individuals, the bet-

ter performer is clearly Architecture 1; if the goal is

to produce quality portfolios, the better architecture

is Architecture 2. For Architecture 2, a limited num-

ber of high performing portfolios was generated: as

a result, more investors would potentially be recom-

mended to the same few portfolios as in Architec-

ture 1. It was demonstrated that a system leverag-

ing multi-objective evolutionary computation, specif-

ically MOEA/D, was able to produce highly perfor-

mant portfolios tailored to an individual given a cus-

tom survey. This survey, written using the greater

context of other risk and ESG relevant surveys, was

conducted and used to construct a weighting to nor-

malize a given investor’s own survey responses and

allow a single portfolio from the collection of the best

portfolios to be matched to that investor.

Two potential architectures were considered. For

Architecture 1, the optimization is run for each in-

vestor that takes the survey. This allows real-time

Multi-Objective Evolutionary Computation for the Portfolio Optimization Problem with Respect to Environmental, Social, and Governance

Criteria

363

pricing as well as a more dynamic resource alloca-

tion (because for n investors, when n is small, the

expensive optimization task is n times, which is also

small). However, this has the cost of the inverse: at

high volumes, the expensive optimization task is run

many times (for the same reason). For Architecture 2,

a multi-objective optimization is run less frequently

(thereby taking a snapshot of pricing data and losing

the advantage of live pricing data) and the investor is

given a portfolio from the Pareto front. This subset

are all the best dominant portfolios and the match-

ing process is extremely fast. The result of the ex-

periment was that both architectures produced highly

performant portfolios that performed comparablely.

Each portfolio produced by both architectures signif-

icantly outperformed the benchmark portfolio (S&P

TSX) signiﬁcantly. For Architecture 2, the number of

portfolios generated was not high for large numbers

of generations: as a result, more investors would po-

tentially be recommended to the same few portfolios

compared to Architecture 1.

The following directions could be pursued in this

research:

• exploring more under-served markets, the point

at which too many objectives becomes problem-

atic for the portfolios generated by adding more

objectives such as transaction cost, liquidity, and

media sentiment, and how different ESG ven-

dors/metrics change the portfolios generated, and

how different algorithms change the portfolios

generated,

• using the survey as an input to a different problem,

such as using the open text answers to perform

sentiment analysis or any other NLP application,

• and realizing the implementation as a robo-

advisor and address the following questions:

– how well does the robo-advisor perform when

compared to a human advisor?

– do people trust the robo-advisor as much as the

human advisor?

– does the robo-advisor properly take the needs

of the individual into account (ie does the sur-

vey satisfy this need fully)?

REFERENCES

Bank of Canada. Canadian overnight repo rate average.

Darmstadt, T. F. and Approximity, A. R. (2003). Risk and

performance optimization for portfolios of bonds and

stocks. In Proceedings of the International AFIR Col-

loquium.

De Spiegeleer, J., H

ocht, S., Jakubowski, D., Reyners, S.,

and Schoutens, W. (2020-10-16). ESG: A new dimen-

sion in portfolio allocation.

Finance, Y. Exchanges and data providers on yahoo ﬁnance

| ﬁnance for web help - SLN2310.

Initiative, T. . I. (2022). Draft questionnaire & guidance for

client sustainability preferences - 2dii.

Korani, W. and Mouhoub, M. (2021). Review on nature-

inspired algorithms. In Operations research forum,

volume 2, page 36. Springer.

Korani, W. and Mouhoub, M. (2022). Discrete mother tree

optimization and swarm intelligence for constraint

satisfaction problems. In Proceedings of the 14th In-

ternational Conference on Agents and Artiﬁcial Intel-

ligence, ICAART 2022, Volume 3, Online Streaming,

February 3-5, 2022, pages 234–241. SCITEPRESS.

Lynn, N. and Suganthan, P. N. (2015-10-01). Heteroge-

neous comprehensive learning particle swarm opti-

mization with enhanced exploration and exploitation.

Swarm and Evolutionary Computation, 24:11–24.

Milhomem, D. and Dantas, M. (2022-01-01). Analysis

of new approaches used in portfolio optimization:

A systematic literature review. In Evolutionary and

Memetic Computing for Project Portfolio Selection

and Scheduling, pages 125–157. Springer.

Morningstar, I. Risk proﬁling and risk scoring tools.

Naffa, H. and Fain, M. (2022-01-01). A factor approach

to the performance of ESG leaders and laggards. Fi-

nance Research Letters, 44:102073.

Nayar, N., Gautam, S., Singh, P., and Mehta, G. (2021). Ant

colony optimization: A review of literature and appli-

cation in feature selection. In Smys, S., Balas, V. E.,

Kamel, K. A., and Lafata, P., editors, Inventive Com-

putation and Information Technologies, pages 285–

297. Springer Nature.

Sadreddin, A., Mouhoub, M., and Sadaoui, S. (2022). Port-

folio selection for SAT instances. In IEEE Interna-

tional Conference on Systems, Man, and Cybernetics,

SMC 2022, Prague, Czech Republic, October 9-12,

2022, pages 2962–2967. IEEE.

Samantha Bastiani, S., Cruz-Reyes, L., Fernandez, E.,

omez, C., and Rivera, G. (2015). An ant colony al-

gorithm for solving the selection portfolio problem,

using a quality-assessment model for portfolios of

projects expressed by a priority ranking. In Melin,

P., Castillo, O., and Kacprzyk, J., editors, Design of

Intelligent Systems Based on Fuzzy Logic, Neural Net-

works and Nature-Inspired Optimization, pages 357–

373. Springer International Publishing.

Utz, S., Wimmer, M., Hirschberger, M., and Steuer, R. E.

(2014-04-16). Tri-criterion inverse portfolio optimiza-

tion with application to socially responsible mutual

funds. European Journal of Operational Research,

234(2):491–498.

SIMULTECH 2025 - 15th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

364

APPENDIX

Recommender System Code

The following repositories were written in the mak-

ing of this recommender system, hosted at https://

rileyherman.ca/survey:

• Main implementation of algorithms

• Import data from yahoo ﬁnance and massage into

input

• Match portfolios from outputs to survey results

(Architecture 2)

• Website backend, including po, pomatch, and

poimport

• Website frontend, including survey and portfolio

presentation

Survey

Available as a public link here.

Portfolios

Please note that these portfolios are not intended as

investment advice and have absolutely no guarantee

of performance: they are provided as an addendum to

the recommender system. The author does not hold

any responsibility should an individual see these re-

sults and decide to invest.

• Graphs, including generational progressions as

well as pairwise comparisons between objectives

• All Architecture 2 portfolios across all runs

• All architecture 1 portfolios across all runs

• The beta values for each of the portfolios above

• The snapshot of all the data from TSX used to

generate the portfolios above

• A snapshot of companies listed on the TSX. Each

company listed here that does not exist in the in-

cluded data set either had insufﬁcient data to be

included or was priced at less than $1.00 per share

• The comparison between the portfolios generated

and the benchmark

Multi-Objective Evolutionary Computation for the Portfolio Optimization Problem with Respect to Environmental, Social, and Governance

Criteria

365