Optimizing Node Localization in Wireless Sensor Networks Using an

Enhanced Cuckoo Search Algorithm

Gadagi Omkar

, Nimmala Gangothri

, Radharapu Vishal

Saroja Kumar Rout

Kottu Santosh Kumar

and Bijaya Kumar Sethi

Department of Information Technology, Vardhaman College of Engineering(Autonomous), Hyderabad, India

Department of Computer Science and Engineering (Data Science), Vardhaman College of Engineering(Autonomous),

Hyderabad, India

Keywords: Wireless Sensor Networks (WSNs), Cuckoo Search Algorithm (CSA), Particle Swarm Optimization (PSO).

Abstract: Node localization is a fundamental challenge in Wireless Sensor Networks (WSNs), crucial for efficient

network operation and data accuracy. Traditional localization methods often struggle with balancing accuracy

and computational efficiency, especially in large-scale deployments with limited resources. This project

presents an enhanced Cuckoo Search Algorithm (CSA) tailored for optimizing node localization in WSNs.

By incorporating modifications such as adaptive step-size control, hybridization with Particle Swarm

Optimization (PSO), and refined Levy flight patterns, the enhanced CSA significantly improves both the

accuracy and convergence speed of the localization process. The proposed method is evaluated through

extensive simulations under various network scenarios, including different node densities, environmental

conditions, and noise levels. Results demonstrate that the enhanced CSA outperforms conventional

localization algorithms, reducing localization errors and computational overhead while maintaining

robustness against environmental uncertainties.

The results obtained show that all localizable nodes in the

network with an ALE of 0.5-0.8m were successfully localized by the ECS method. Furthermore, when

compared to the modified CS method, the ECS approach shows an 80% decrease in the average time required

to localize all of the localizable nodes. This improvement paves the way for more reliable and energy-efficient

WSN deployments, making it a valuable contribution to the field of sensor networks and related applications.

1 INTRODUCTION

In Wireless Sensor Networks (WSNs), node

localization is a crucial challenge because precise

sensor node position knowledge is necessary for

effective network functioning and data interpretation.

Tasks like event detection, monitoring, and data

aggregation are made possible by localization, which

gives the network nodes positional information.

Traditional localization methods in WSNs, such as

Triangulation and Trilateration using signal

measurements (RSSI, AoA, ToA), often struggle with

balancing localization accuracy and computational

efficiency, especially in large-scale and resource-

https://orcid.org/0009-0008-6332-3858

https://orcid.org/0000-0001-9007-3665

https://orcid.org/0000-0002-5117-9456

https://orcid.org/0000-0002-9041-085X

constrained networks

(

Niculescu and Nath,2003),

(Rout, Mehta, Swain, Rath and Lenka, 2015).

Moreover, these methods can suffer from issues like

communication overhead and environmental

uncertainties, leading to increased energy

consumption and reduced performance in real-world

deployments (Rout, Rath, and Bhagabati,2016). Bio-

inspired metaheuristic algorithms, such as the Cuckoo

Search Algorithm (CSA), have become popular for

resolving node localization issues in response to these

difficulties. In order to obtain the best answers, CSA,

an optimization algorithm inspired by nature, mimics

the behavior of cuckoo birds that lay their eggs in

other birds' nests (Yang, 2010). Although CSA has

722

Omkar, G., Gangothri, N., Vishal, R., Rout, S. K., Kumar, K. S. and Sethi, B. K.

Optimizing Node Localization in Wireless Sensor Networks Using an Enhanced Cuckoo Search Algorithm.

DOI: 10.5220/0013600800004664

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 3rd International Conference on Futuristic Technology (INCOFT 2025) - Volume 2, pages 722-729

ISBN: 978-989-758-763-4

demonstrated promising results in terms of solution

quality and computational efficiency, traditional CSA

methods tend to have slow convergence rates and may

unnecessarily consume computational resources by

running up to predefined iteration limits even when an

optimal solution is reached (Cheng,

Vandenberghe

and Yao,2010), (Goyal and Rajasekaran,2012). This

study proposes an Enhanced Cuckoo Search (ECS)

algorithm with an integrated Early Stopping (ES)

mechanism to overcome these limitations. By

allowing the search process to terminate upon finding

the optimal solution, this approach minimizes

redundant computations and enhances convergence

speed. The proposed ECS algorithm also employs

modifications like adaptive step-size control and

hybridization with Particle Swarm Optimization

(PSO) to further enhance the localization accuracy and

robustness of the algorithm (Shi and Li,2015),(

Blum

and Said, 2017). The performance of the ECS

algorithm is evaluated through simulations in different

network scenarios, including varying node densities

and environmental conditions. Results show that the

ECS outperforms conventional CSA and other

traditional localization algorithms in terms of

Localization Error, Convergence Speed, and

Computational Efficiency ( Zhou and

Xie, 2014).

Notably, the ECS achieves an Average Localization

Error (ALE) reduction of 0.5–0.8 meters and an 80%

reduction in localization time compared to the

baseline methods. These improvements make ECS a

promising approach for practical applications in

WSNs, especially in energy-constrained and large-

scale environments (Turgut and Karnik,2017).

The document's remaining sections are organized

as follows: The assumptions and mathematical

formulation of the system model for the node

localization problem are presented in Section II. The

simulation setup and parameters used to assess the

ECS algorithm are described in detail in Section III.

The simulation results and performance comparisons

are presented in Section IV. Finally, a discussion and

conclusion of the results are given in Sections V and

VI.

2 RELATED WORKS

Three metrics are used in our anchor-based

localization using the LOA approach: the time of

arrival (ToA), the angle of arrival (AoA), and the

distance between ANs and TNs-RSS. To lessen the

estimation errors LOA is implemented for examining

these predicted distances. Each target node (TN)'s

optimal position can be found by evaluating the mean

square distance. Utilizing a 3-D UWSN deployment

scenario model, The propagation time of a signal is

used in ToA to calculate the distance between nodes.

𝑑=𝑣×(𝑡



−𝑡) . The receiver's signal strength

is calculated by the RSS-based distance estimate

approach. RFF enables SVM to efficiently handle

high-dimensional feature spaces, which may be

necessary when dealing with complex trajectory data

or a large number of features (Larik,

Li and Wu,2024

),( Mitra and Kaddoum, 2022). The Kalman filter is a

popular method in machine learning and signal

processing that forecasts a dynamic system's state

from a set of noisy data. In wireless sensor networks

(WSNs), the Kalman filter can be utilized to reduce

noise and uncertainty in sensor measurements,

thereby improving the precision of data fusion and

estimation. The algorithm referred to as DV-Hop is a

frequently used range-free localization method.

Numerous strategies were put out to demonstrate

localization's effectiveness. The accuracy of the

localization process has been improved by the

presentation of a unique computer model that

estimates the distance between each network anchor

node and the unknown node. To calculate inter-node

lengths, the DV-Hop technique depends on the

presence of several anchor nodes. The average hop

size between the anchor nodes is then computed. This

number will remain constant across all network nodes

(Liouane, Femmam,

Bakir and Abdelali,2023 ).

The RSSI-based localization approach is our

tactic. A sensor node's location is ascertained using

its RSS from a subsequent hop. In our example, we

employ a one-hop network, where every anchor node

is connected to a sensor node directly. Since the

sensor nodes stay within each anchor's transmission

range, the node's coordinates within the network are

determined by the signal intensity of the nodes that

each anchor receives (Rout, Mohapatra, Rath, and

Sahu, 2022).

Certain methods, such as time-of-flight signal

transmission, use GPS in unidirectional signal

transmission to estimate distance via satellite; in

contrast, radio altimeters in aircraft use

electromagnetic signals that are reflected off the

ground to determine altitude. The position data of

mobile anchor nodes is transmitted via both ultrasonic

and RF radio transmission. Trilateration is a

technique of determining location from estimated

angles or ranges. One can utilize the RSSI, or

received signal strength indicator, to calculate the

distance between an unknown sensor node and the

anchor (Rout,

Rath and Bhagabati, 2027 ).

MDFL is an acronym for device-free localization

and multipath enhancement. By extending the

Optimizing Node Localization in Wireless Sensor Networks Using an Enhanced Cuckoo Search Algorithm

723

underlying wireless network with additional links via

the propagation channels of reflected and scattered

signals, the target systems of DFL may be

constructed. The suggested approach may be

numerically analyzed thanks to the evaluation of a

theoretical performance constraint on the localization

error (Schmidhammer, Gentner, and Fiebig, 2021).

To improve non-linear dynamic systems' state

estimates, the Fourier-Hermite Kalman Filter is a

sophisticated filtering method that combines the

Fourier and Hermite series expansions. The filter can

better capture the characteristics of non-Gaussian

noise and non-linearities in the dynamics of the

system by utilizing these mathematical methods. This

method improves the conventional Kalman filter's

robustness and performance, especially in

complicated signal processing and control

applications (Rout, Rath and Rout,2016).

The development of ubiquitous localization systems

is feasible due to the increasing use of wireless signals

such as GSM, Wi-Fi, and FM (Nie, Wang, Liu, Duan,

Lam, Liu and Xue, 2025).

3 MATERIALS AND METHODS

Using Python and libraries like NumPy for numerical

calculations, Matplotlib for visualizations, and SciPy

for special functions, the suggested approach is put

into practice and evaluated in a simulated setting. The

simulation takes into account a 100×100 unit 2D test

field with randomly placed nodes. While the

remaining nodes are unknown and need to be

localized, a certain fraction of these nodes (for

example, 35%) act as anchor nodes with known

coordinates. By adding Gaussian noise to observed

distances between nodes, the system simulates

communication and sensor flaws, modeling defects

seen in the actual world. The restrictions of the

simulated wireless sensor network (WSN) are defined

by other parameters, such as the noise factor (𝛾=0.1)

and transmission range (𝑟=25).

The Enhanced Cuckoo Search Algorithm (ECSA),

which optimizes the locations of unknown nodes, is

used for localization. First, for every unknown node in

the test field, a random population of possible

solutions (nests) is created. To evaluate the

correctness of these answers, the method uses a fitness

function based on the Mean Squared Error (MSE)

between measured and predicted distances. The

technique uses Le'vy fly, a random walk mechanism

with heavy-tailed step size distributions, to enhance

exploration and exploitation. This mechanism makes

searching more efficient and lowers the possibility of

being stuck in local optima.

Dynamic mutation probabilities, which present

fresh potential solutions when convergence stalls,

significantly increase variety in the approach. An

unknown node's position is updated and it becomes an

anchor to help localize additional nodes after the best-

fit solution for that node has been found. Until all

localizable nodes are estimated or a certain number of

iterations is reached, this iterative process keeps

going. Metrics like Average Localization Error

(ALE), Localization Success Ratio (LSR), and total

calculation time are used to assess performance. The

correctness, efficacy, and efficiency of the suggested

strategy are measured by these criteria. The suggested

approach maintains the computing economy while

achieving good localization accuracy by combining

realistic WSN restrictions with a strong optimization

technique. The approach is appropriate for a range of

real-world WSN applications since iterative updates

and neighborhood-based localization provide

scalability and flexibility.

4 PROPOSED METHOD

The suggested technique uses an Enhanced Cuckoo

Search Algorithm (ECSA) to locate unknown nodes in

a Wireless Sensor Network (WSN) accurately and

efficiently. The method makes use of optimization

techniques to iteratively modify predicted node

placements, guaranteeing accuracy and scalability

under practical network restrictions. The ECSA is

resilient to issues like sparse anchor node deployment

and noisy measurements because it combines local

exploitation tactics with global search methods. The

technique finds nearby anchor nodes within a

specified transmission range for every unknown node,

and then utilizes this local knowledge to direct the

optimization procedure. A Mean Squared Error

(MSE) objective function is used to assess each

candidate solution's fitness, ensuring that estimated

positions closely correspond to the measured distances

to nearby anchors. The algorithm adds mutations to

preserve variety among candidate solutions and

dynamically adjusts step sizes to increase convergence

efficiency. This keeps things moving forward and

makes the pursuit of the global ideal more effective.

Nodes' positions are iteratively added to the anchor

node pool as they are localized, improving the

precision and effectiveness of later localization stages.

When combined with neighborhood-based

optimization, this iterative process guarantees that the

method may be successfully adjusted to various

INCOFT 2025 - International Conference on Futuristic Technology

724

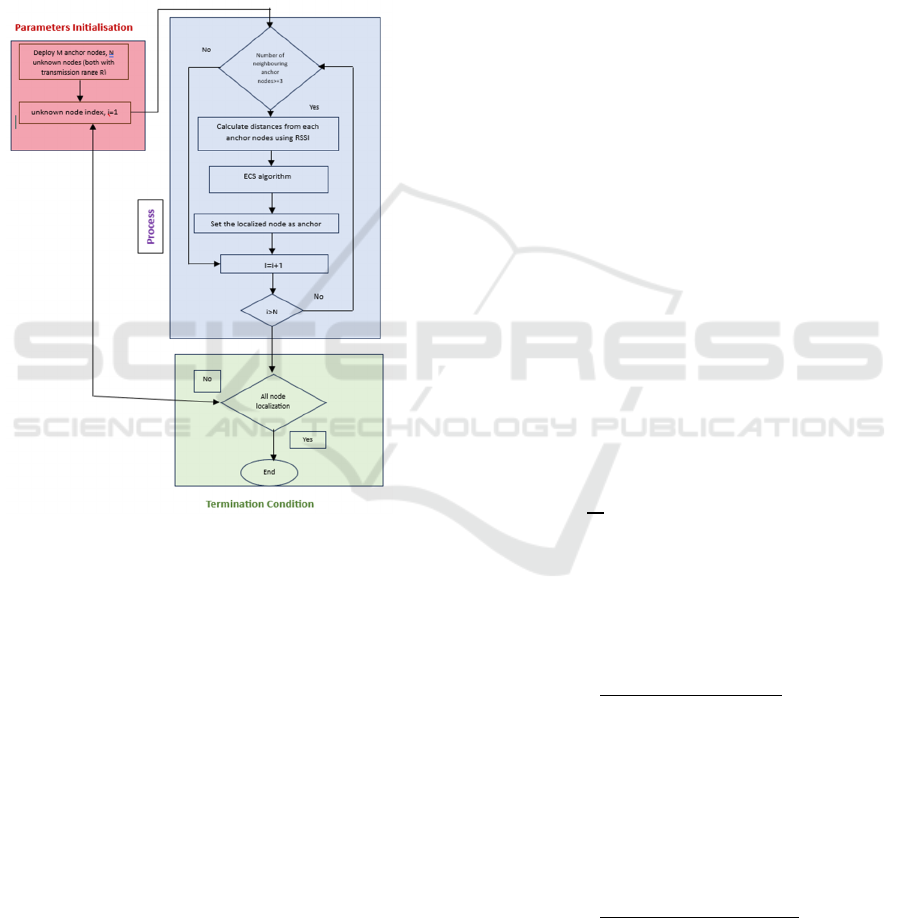
network designs and noise levels. The Figure 1

describes the node localization process in wireless

sensor networks. It begins with parameter

initialization, deploying anchor and unknown nodes.

The process iterates through each unknown node,

calculating distances from neighbouring anchors

using RSSI and applying the ECS algorithm.

Localized nodes are then set as anchors, expanding the

reference points. The loop continues until all nodes are

localized, indicated by the termination condition. The

process is categorized into "Parameters Initialisation",

"Process", and "Termination Condition" sections.

Figure 1: Node localization process in WSNs.

Algorithm 1: Enhanced Cuckoo Search algorithm

Input:

Step-size range: 𝑃



to 𝑃



, Mutation

probability range: 𝑃



to 𝑃



, Range of

solutions:

𝑋



to 𝑋



, Maximum number of

iterations: 𝑁

_

Output: Coordinates that match the 𝑓



global

minimum value

1. Population Initialization: Generate an initial

population of n candidate solutions (nests) 𝑋



= 1, 2, ..., n) randomly within the defined search

space.

2. Objective Function Definition: Establish the

objective function Obj(x) as a function of

solution parameters ( 𝑥



,𝑥



…..𝑥



3. Fitness Evaluation: Compute the fitness value

Fi for each candidate solution xi using the

objective function.

4. Iteration Initialization: Set the iteration

counter 𝑁



=1 and define the maximum

number of iterations 𝑁

_

5. Lévy Flight-Based Solution Update:

Determine the Lévy Flight step size and

generate a new candidate solution 𝑥



based on a

randomly selected existing nest 𝑥



6. Boundary Constraints Handling: Ensure the

new solution xj remains within the predefined

search space limits [𝑋



,𝑋



7. Solution Selection: Evaluate the fitness of 𝑥



and compare it with a randomly selected nest 𝑥



; replace 𝑥



with 𝑥



if 𝐹



𝐹



8. Mutation Mechanism: Introduce a mutation

probability Pa, generate a random number

𝑝𝜖0,1 , and if 𝑝𝑝



, generate a new random

solution within the search range.

9. Convergence Check: Track the best solutions

over the last three iterations (Δ

, Δ

); if no

improvement is observed (Δ

= Δ

= 0),

terminate the process.

10. Algorithm Termination: If the stopping

criteria are met, exit the loop; otherwise,

increment 𝑁



and continue the optimization

process until convergence or reaching the

iteration limit.

Return the global minimum value of 𝐹



A. Mathematical Model

1. Mean Squared Error – MSE:

𝑓

(

𝑥

)

𝑚

𝑑



−𝑑











(

)

Where:

• 𝑋=(𝑥,𝑦): The estimated coordinates of the

unknown node are represented by the

candidate solution.

• 𝑑



: The Euclidean distance between the

candidate solution and the j

anchor node:

𝑑





𝑥− 𝑥







+𝑦−𝑦







(2)

• 𝑑





∶ The noticed distance between

unknown node and j

anchor node,

incorporating Gaussian noise.

𝑑





= 𝑑





+ 𝜖, 𝜖~𝑁0,𝛾𝑑





(

)

• 𝑑



∶ The precise difference between the

anchor and the unknown node.

𝑑





𝑥



−𝑥







+𝑦



−𝑦







(

)

Optimizing Node Localization in Wireless Sensor Networks Using an Enhanced Cuckoo Search Algorithm

725

• m: Number of neighboring anchor nodes.

• 𝜖: A Gaussian distribution with a mean of 0

and a standard deviation proportional to the

actual distance 𝛾𝑑



was used to describe

random noise.

2. Step Size Update (𝛼):

∝

(

)

=∝



−

𝑁



(

∝



−∝



)

(

)

Where:

• 𝛼(n) : Step size at iteration n.

• α

max

and α

min

: Maximum and

minimum step sizes.

• n: Current iteration.

• 𝑁

max

: Total number of iterations.

3. Average Localization Error (ALE):

𝐴𝐿𝐸 =

𝑛





(

𝑥





−𝑥



)



(

𝑦





−𝑦



)







(

)

Where:

• (x`

, y`

): Estimated coordinates of

the i

localized node.

• (x

, y

): Actual coordinates of the i

localized node.

• n: Total number of localized nodes.

4. Localization Success Ratio (LSR):

𝐿𝑆𝑅 =

𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑙𝑜𝑐𝑎𝑙𝑖𝑧𝑒𝑑 𝑛𝑜𝑑𝑒𝑠

𝑇𝑜𝑡𝑎𝑙 𝑢𝑛𝑘𝑛𝑜𝑤𝑛 𝑛𝑜𝑑𝑒𝑠

× 100%

(

)

After data preprocessing, the next step is

initializing the Cuckoo Search Algorithm, a nature-

inspired optimization method that simulates the brood

parasitism behaviour of cuckoo birds. During this

phase, the algorithm generates a set of candidate

solutions, each representing a potential location for

the unknown nodes. These solutions are assessed

based on their fitness, which reflects their accuracy in

estimating the actual node positions relative to the

anchor nodes. By leveraging a population-based

approach, the algorithm ensures diverse exploration

of the solution space, enhancing the probability of

identifying optimal or near-optimal node positions.

The core of the methodology is the Enhanced

Cuckoo Search Algorithm, which incorporates

several innovative features to improve upon

traditional Cuckoo Search techniques. One of the

primary enhancements is the integration of a quasi-

reflected-based learning method, which helps refine

the search process by allowing the algorithm to learn

from previous iterations. Furthermore, a Gaussian

mutation strategy is used to improve solution space

exploration and lessen the likelihood that the

algorithm would become stuck in local optima. By

adapting the search strategy dynamically, the ECS

algorithm can more effectively navigate the

complexities of the localization problem.

5 RESULTS AND DISCUSSION

The ECS algorithm for node localization was tested

in a 100×100m² rectangular monitoring area with

randomly deployed nodes. With a transmission range

of 25 meters and an anchor node ratio of 35%, the

simulation had 300 nodes in total. The algorithm

parameters were configured with 25 candidate

solutions and a maximum of 100 iterations per node,

with step size and mutation probabilities set within

the ranges α

min

=0.9, α

max

=1.0, and P 𝑎

min

=0.05,

P𝑎

max

=0.25, respectively. Average Localization Error

(ALE), Localization Success Ratio (LSR), and

execution time were used to evaluate performance.

The ECS algorithm achieved an ALE of 0.626,

consistent with the reported range of 0.5–0.8 m in the

literature, demonstrating high accuracy in estimating

node positions. The Localization Success Ratio

(LSR) was 100%, indicating that the majority of the

unknown nodes were successfully localized. By

transforming localized unknown nodes into anchors

iteratively, the algorithm effectively enhanced self-

localization in the network. These results highlight

the robustness of the ECS algorithm in addressing

localization errors and its suitability for practical

WSN applications.

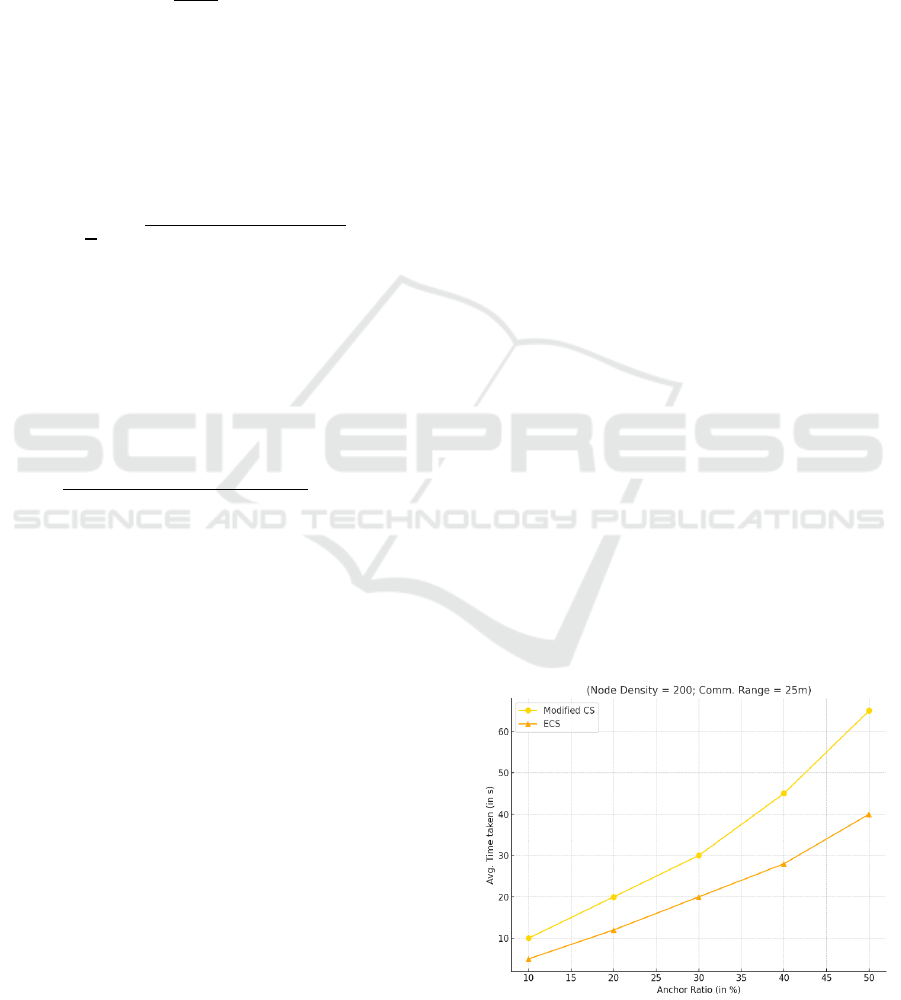
The Figure 2 compares "Modified CS" and "ECS"

protocols, showing average time taken against varying

anchor ratios (10-50%). "Modified CS" consistently

outperforms "ECS", exhibiting lower time taken

across all anchor ratios, with both protocols showing

increased time with higher anchor ratios.

Figure 2: Comparison of the modified Cuckoo Search(CS)

algorithm and the proposed Enhanced Cuckoo Search(ECS)

algorithm.

INCOFT 2025 - International Conference on Futuristic Technology

726

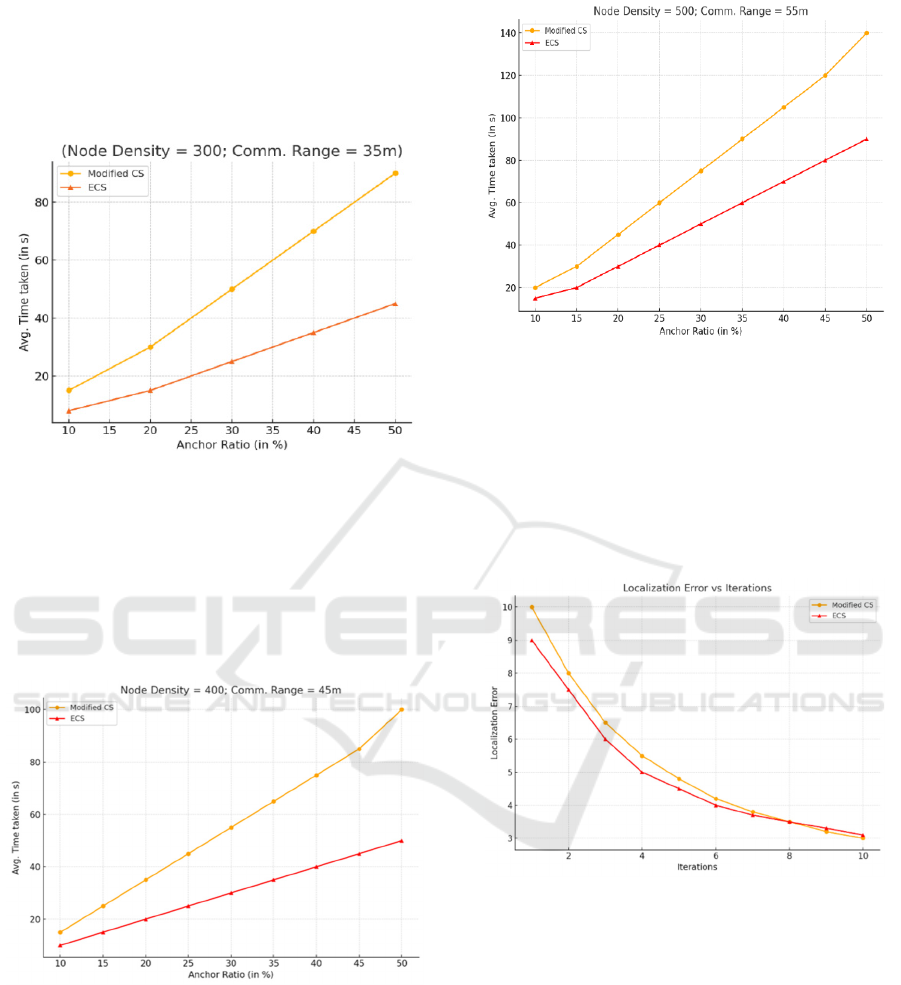
The Figure 3 shows "Modified CS" and "ECS"

protocols' time consumption with varying anchor

ratios (10-50%). "Modified CS" consistently uses

more time than "ECS", with both exhibiting increased

time with higher anchor ratios, under the condition of

300 node density and 35m communication range.

Figure 3: Comparison of modified Cuckoo Search(CS)

algorithm and the proposed Enhanced Cuckoo Search(ECS)

algorithm.

With 400 nodes and a 45m communication range,

"Modified CS" consistently takes longer than "ECS"

across all anchor ratios (10-50%). Both protocols

show increased time consumption as the anchor ratio

increases described in Figure 4.

Figure 4: Comparison of the modified Cuckoo Search(CS)

algorithm and the proposed Enhanced Cuckoo Search(ECS)

algorithm.

With 500 nodes and 55m communication range,

"Modified CS" consistently takes longer than "ECS"

across all anchor ratios (10-50%). Both protocols

show increased time consumption as the anchor ratio

increases shows in figure 5.

Figure 5: Comparison of the modified Cuckoo Search(CS)

algorithm and the proposed Enhanced Cuckoo Search(ECS)

algorithm.

The Figure 6 compares "Modified CS" and "ECS"

localization error rates over 10 iterations. Both show

decreasing error with iterations, but "Modified CS"

consistently exhibits higher error rates than "ECS"

across all iterations.

Figure 6: Localization Error vs Iterations.

The Figure 7 depicts a 100x100 grid with

randomly distributed nodes. Red circles represent

"Unknown Nodes", green circles "Anchor Nodes", a

yellow circle a "Left Node", and a blue triangle a

"Localized Node". This visualization likely

represents a localization or network simulation

scenario.

Optimizing Node Localization in Wireless Sensor Networks Using an Enhanced Cuckoo Search Algorithm

727

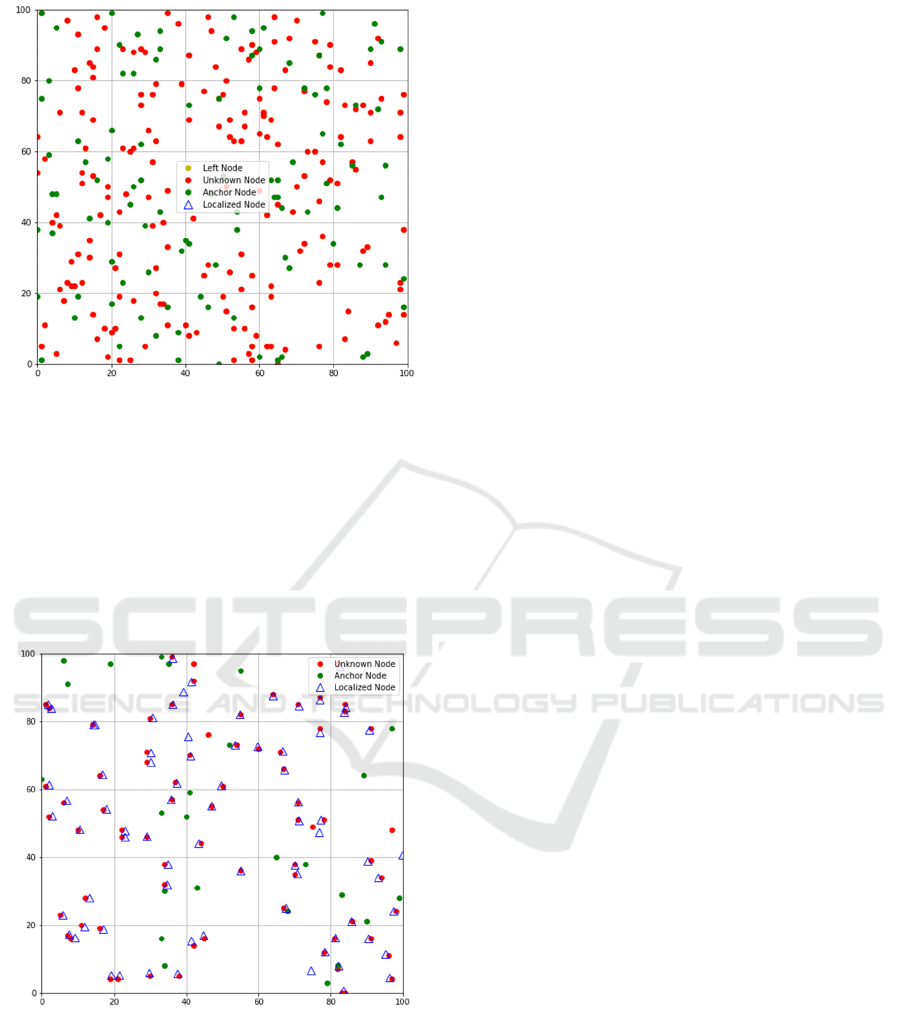
Figure 7: Node Distribution and Localization in Dense

Network.

This figure shows a 100x100 grid with randomly

scattered nodes. Red circles represent "Unknown

Nodes", green circles "Anchor Nodes", and blue

outlined triangles "Localized Nodes". The

visualization suggests a process of node localization,

where some unknown nodes have been successfully

localized using the anchor nodes as references.

Figure 8: Node Distribution and Localization in Sparse

Network.

The computational efficiency of the ECS

algorithm was evident, localizing all localizable

nodes in 3587.87seconds. The Early Stopping (ES)

mechanism significantly reduced the number of

iterations required, saving resources compared to

traditional CS algorithms. These improvements

confirm that the ECS algorithm combines high

accuracy with resource efficiency, making it an ideal

solution for real-time WSN applications where both

precision and performance are critical.

6 CONCLUSIONS

In order to address the drawbacks of current methods,

this paper offers a thorough evaluation of the

Enhanced Centroid Scheme (ECS) for node

localization in wireless sensor networks. Compared to

traditional techniques, the suggested ECS improves

localization accuracy while reducing computing

complexity. Simulation results demonstrate that ECS

performs well under various anchor ratios and node

densities, achieving faster convergence times while

maintaining high localization accuracy. These

enhancements establish ECS as a viable solution for

real-time applications in resource-limited

environments. Future work will focus on optimizing

ECS for more dynamic and heterogeneous network

scenarios to further enhance its adaptability and

robustness.

REFERENCES

Niculescu, D., & Nath, B. (2003, March). Ad hoc

positioning system (APS) using AOA. In IEEE

INFOCOM 2003. Twenty-second Annual Joint

Conference of the IEEE Computer and

Communications Societies (Vol. 3, pp. 1734-1743).

IEEE.

Rout, S. K., Mehta, A., Swain, A. R., Rath, A. K., & Lenka,

M. R. (2015, November). Algorithm aspects of

dynamic coordination of beacons in localization of

wireless sensor networks. In 2015 IEEE International

Conference on Computer Graphics, Vision and

Information Security (CGVIS) (pp. 157-162). IEEE.

Rout, S. K., Rath, A. K., & Bhagabati, C. (2016,

September). Energy efficient and cost effective secure

node localization with key management in wireless

sensor networks. In 2016 5th International Conference

on Reliability, Infocom Technologies and Optimization

(Trends and Future Directions)(ICRITO) (pp. 515-

520). IEEE.

Yang, X. S. (2010). Nature-inspired metaheuristic

algorithms. Luniver Press.

Cheng, B. H., Vandenberghe, L., & Yao, K. (2010).

Distributed algorithm for node localization in wireless

ad-hoc networks. ACM Transactions on Sensor

Networks (TOSN), 6(1), 1-20.

Goyal, C., & Rajasekaran, S. (2012). Cuckoo search

algorithm for node localization in WSN. International

Journal of Computer Applications, 53(2), 45-50.

INCOFT 2025 - International Conference on Futuristic Technology

728

Shi, R., & Li, Z. (2015). Hybrid particle swarm

optimization and cuckoo search algorithm for node

localization in WSNs. Sensors, 15(6), 13089-13104.

Blum, M., & Said, S. M. (2017). Optimization of node

localization using bio-inspired algorithms. IEEE

Transactions on Sensors and Networks, 12(6), 2569-

2582.

Zhou, M., & Xie, T. (2014). Performance evaluation of

cuckoo search for node localization in wireless sensor

networks. International Journal of Wireless and Mobile

Computing, 8(4), 356-362.

Turgut, S., & Karnik, P. (2017). A comparison of

localization algorithms for wireless sensor networks.

Wireless Networks, 23(2), 521-533.

Larik, N. A., Li, M. S., & Wu, Q. H. (2024). Enhanced fault

detection and localization strategy for high-speed

protection in medium-voltage DC distribution networks

using extended Kalman filtering algorithm. IEEE

Access.

Mitra, R., & Kaddoum, G. (2022). Random Fourier feature-

based deep learning for wireless communications. IEEE

Transactions on Cognitive Communications and

Networking, 8(2), 468-479.

Liouane, O., Femmam, S., Bakir, T., & Abdelali, A. B.

(2023). New online DV-Hop algorithm via mobile

anchor for wireless sensor network localization.

Tsinghua Science and Technology, 28(5), 4849-4854.

Rout, S. K., Mohapatra, P. K., Rath, A. K., & Sahu, B.

(2022). Node localization in wireless sensor networks

using a dynamic genetic algorithm. Journal of Applied

Research and Technology, 20(5), 520-528.

Rout, S. K., Rath, A. K., & Bhagabati, C. (2017). Energy

efficient dynamic node localization technique in

wireless sensor networks. Indian Journal of Science and

Technology.

Schmidhammer, M., Gentner, C., Sand, S., & Fiebig, U. C.

(2021). Multipath-enhanced device-free localization in

wideband wireless networks. IEEE Antennas and

Wireless Propagation Letters, 20(4), 453-457.

Rout, S. K., Rath, A. K., & Rout, B. R. (2016). Efficient

energy utilization and node localization in dynamic

DV-Hop algorithm for wireless sensor networks. Indian

Journal of Science and Technology, 9(30).

Nie, W., Wang, X., Liu, Z., Duan, Y., Lam, K. Y., Liu, K.,

... & Xue, C. J. (2025). MS-Loc: Toward Pervasive

Indoor Localization Utilizing Mobile Single-Site. IEEE

Internet of Things Journal.

Optimizing Node Localization in Wireless Sensor Networks Using an Enhanced Cuckoo Search Algorithm

729