Hybridized Approach for Prepossessing Stage Design for Lungs CT

Images

Sheenam Middha

and Bobbinpreet Kaur

Department of Computer Science and Engineering, Chandigarh University, Mohali, Punjab, India

Keywords: Image Processing, Filters, Noise Reduction.

Abstract: This paper presents a hybrid denoising technique that utilizes the combination of top-hat and bottom-hat

morphological transformations. The scheme effectively solves the problems of uneven illumination and

background noise while preserving the quality of the content in the document. By combining the top-hat

transformation (which enhances the bright features in the background) and the bottom-hat transformation

(which emphasizes the dark features against the lighter ones in the background), the model complements the

noise level and improves the contrast. Experimental validation of [specific data, e.g. medical images, satellite

data] shows significant improvements in denoising, optimization, and performance compared to traditional

methods. Hybrid top and bottom hat models are a promising solution for applications requiring efficient and

noise-resistant preprocessing.

1 INTRODUCTION

Noise in an image is characterized as any degradation

in the visual signal induced by an external

disturbance. In general, the goal of digital image

processing is to improve the quality of information so

that it can be easily interpreted and understood by

humans. Additionally, it tries to analyze picture data

for storage, transmission, and reproduction for

machine perception. In many circumstances, the

image's sharpness is distorted due to noise pollution.

Impulse noise, Rayleigh noise, and Gaussian noise

degrade the image at all stages of acquisition, capture,

transmission, reception, storage, and retrieval. To get

a very clear visual display in applications such as

image authentication, broadcasting, medicine,

automatic control equipment, and military

surveillance, the processed picture signal must be free

of noise contamination and blur.

Digital images are frequently distorted and noise

seeps in during the collecting process. This is the

result of several picture-processing flaws. In a similar

vein, errors resulting from imprecise energy level

estimation and poor communication can also cause

noise to be added during transmission. Photometric or

electronic sources are also to blame for this. Any

component in the imaging chain, such as a lens, etc.,

may lead to the deterioration of image quality. Both

linear and nonlinear filters can be used to eliminate

noise that results from this kind of degradation.

1.1 Types of Noise

Various noise exists in the Images shown in Figure 1

1.1.1 Gaussian Noise

Gaussian noise is a refined version of white noise.

The signal strength fluctuates randomly, which is the

source of this. It frequently appears in the collected

data. The addition of value from the Gaussian

distribution to every pixel in an image is the

characteristic of Gaussian noise.

https://orcid.org/0000-0002-0639-5539

https://orcid.org/0000-0001-8946-2444

472

Middha, S. and Kaur, B.

Hybridized Approach for Prepossessing Stage Design for Lungs CT Images.

DOI: 10.5220/0013594800004664

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 3rd International Conference on Futuristic Technology (INCOFT 2025) - Volume 2, pages 472-477

ISBN: 978-989-758-763-4

Figure 1: Type of Nnoise

The probability distribution function for this kind

of noise is bell-shaped and has a Gaussian

distribution. Additive White Gaussian Noise

(AWGN) dominates the noise during the acquisition

process, and its variation is quite low. Satellite image

acquisition is the primary cause of this noise; other

factors are essentially insignificant. Thus, the

primary. Eliminating this noise, which has an impact

on the digital image during transmission, is the focus

of research efforts. Normally, the transmission noise

is linear (Boyat and Kumar, 2015).

The edges of the images get blurry and AWGN

enters as a contamination when the image data is

transmitted across a linear dispersive channel.

The PDF of Gaussian Noise is represented by

Equation

𝐺𝑁

(

𝑍

)



√





𝑒





()



……………………(1)

Where, x → Gray_level

m → Mean/average value

d → Standard_deviation

d2 → Variance

1.1.2 Speckle Noise (SN)

Speckle Noise (SN) is a further kind of noise that

tampers with the visual signal. Synthetic

Augmentation Radiation (SAR) imaging and

ultrasonic imaging both frequently generate this kind

of noise. There is multiplicative speckle noise. The

device sends a signal to the item to take a picture of

it, and then records the signal that is reflected. As the

signal is transmitted both forward and backward,

noise builds up. Because of the fluctuating reflecting

quality of the, the reflected signal changes in strength

(Mudhafar, Rusul, et al. , 2023).

The object's surface. As a result, noise varies

according to an object's reflecting quality. As a result,

the noise turns into a multiplicative noise.

AWGN, SPN, and RVIN noises are present in the

majority of applications. As was already said, speckle

noise only appears in a small number of applications,

such as SAR and ultrasonic imaging. "Mixed Noise"

refers to a combination of these noise kinds.

1.1.3 Rayleigh Noise

The Rayleigh distribution is a continuous distribution

of probabilities that applies to positive random

variables as well. It is common when a vector's

amplitude and direction components are related.

The pdf of Rayleigh noise is defined as

𝑅𝑁

(

𝑌

)





(

𝑌−𝑎

)

𝑒



()

for Y>=a…………(2)

1.1.4 Erlang Noise

With the support of π ∈ (0, ∞), the Erlang probability

distribution has two parameters. One of the two

parameters is a positive integer denoted by shape z.

A positive real denotes the "rate" π; occasionally,

the is utilized to symbolize the rate's inverse. The

exponential distribution and the Erlang distribution

with shape z tending to 1 have the same appearance.

It belongs to the Gamma distribution as a particular

case. With a mean of 1 each, it is the distribution of

the sum of z independent exponential variables.

The PDF of the Erlang noise is given by

Hybridized Approach for Prepossessing Stage Design for Lungs CT Images

473

𝑁

(

𝑍

)







(



)

(



)

𝑒



𝑓𝑜𝑟 𝑍 ≥ 0………..………(3)

1.1.5 Exponential Noise

The exponential distribution is the probability

distribution that describes the time relation between

events in a Poisson process. It is a particular case of

the gamma distribution.

The PDF of the exponential noise is given by

𝐸𝑁

(

𝑍

)

=𝑎𝑒



𝑓𝑜𝑟 𝑍 ≥ 0……………(4)

1.1.6 Uniform Noise:

Quantization noise is the noise that results from

quantizing an image's pixels to a variety of different

levels. Its distribution is fairly close to a uniform

distribution. The noise is evenly dispersed throughout

the homogeneous noise (Senthil and Sukumar, 2019).

The PDF of the uniform noise is given by:

𝑈𝑁

(

𝑍

)

(

𝑏−𝑎

)



𝑓𝑜𝑟 𝑎 ≤ 𝑍 ≤ 𝑏… ..(5)

2 IMPULSE NOISE

Another name for impulse noise is salt and pepper

noise. Sharp and unexpected fluctuations in the

grayscale values of the image are the source of this. It

appears as sporadic black or white pixels dispersed

throughout the image.

NI(Z)=Pa for Z=a…………………………….(6)

NI(Z)= Pb for Z=b……………………………(7)

PI(Z)=0 otherwise…………………………….(8)

2.1 Types of Filters

Image restoration is done using filtering algorithms.

Image restoration filters can be applied in either the

spatial or frequency domains. There are two sorts of

filters: linear and non-linear. Both approaches are

detailed below.

2.1.1 Linear contrast stretching Filter

(LCH)

Linear contrast stretching is a fundamental image

processing technique that aims to improve an image's

visual quality by altering the contrast. It works by

extending the range of intensity values for pixels to

include the complete spectrum, which is typically 0 to

255 for an 8-bit grayscale image. Initially, the

minimum and maximum intensity values in the image

are determined by scanning its pixels. With these

values, a linear transformation function is created.

This function uses a linear relationship to remap the

original intensity values to stretched counterparts.

Each pixel's intensity value, z, is converted using the

formula:

T(x)=(max−minx/min) × 255………..(9)

The terms "min" and "max" refer to the least and

maximum intensity values. Finally, this

transformation is done to each pixel in the image,

essentially spreading intensities across the 0-255

scale. As a result, darker areas become darker, and

brighter sections become brighter, resulting in a more

contrasty and clearer image. Despite its simplicity,

linear contrast stretching is commonly utilized in

picture improvement and preprocessing applications.

2.1.2 Tophat Gaussian filter (TGF)

The top-hat transform, when paired with a Gaussian

filter, is a useful image-processing method for

detecting and enhancing small-scale structures or

details. The top-hat transform highlights localized

differences in intensity or texture that are smaller than

the filter kernel size. This approach is especially good

for spotting little items or fine details in an image.

The Gaussian filter is a smoothing filter that uses

a Gaussian kernel to reduce noise and blur the image.

It is widely used as a preprocessing step to improve

image quality before performing additional analysis.

The Gaussian filter, when used with the top-hat

transform, enhances the contrast between small-scale

structures and the background by smoothing the

image and minimizing noise. The top-hat transform

retrieves these tiny elements by subtracting the

smoothed image from the original, resulting in an

image with emphasis on small-scale details.

2.1.3 Proposed - Tophat bottom hat

The combination of top-hat and bottom-hat

transforms is a versatile image processing approach

used mostly for image enhancement and feature

extraction. The top-hat transform accentuates brilliant

structures or regions smaller than the structuring

element, whereas the bottom-hat transform, also

known as the black-hat transform, emphasizes dark

structures or regions.

In the context of the top-hat transform, the

technique starts with a morphological opening

INCOFT 2025 - International Conference on Futuristic Technology

474

operation on the image. This procedure efficiently

soothes the image while removing small features and

noise. The opening operation's outcome is then

subtracted from the original image. The final image

emphasizes bright structures or regions that were

smaller than the structuring element utilized in the

opening process. This method is very useful when

recognizing little bright objects or details against a

somewhat homogeneous background.

In contrast, the bottom-hat transform begins the

pre-processing of non-local images with a

morphological closing operation on the image, which

aids in the filling of dark gaps or indentations and the

smoothing of the background. The original picture is

then subtracted from the closing result. This produces

an image in which dark structures or regions that are

smaller than the structuring element are highlighted.

The bottom hat transform is widely employed to

detect dark items or features against a relatively light

background.

3 RELATED WORK

Nandhini and Saraswathy (Senthil and Sukumar,

2019), (Nandhini and Saraswathy, 2013) discovered

that de-speckling focuses on removing speckle noise

while retaining structural features and edges during

the MAP estimator approach employing wavelet and

curvelet transforms. The quality measure is evaluated

and studied for the use of wavelet and curvelet

transforms to de-speckle the noise.

Images. Liu et al (Liu, Scott, et al. , 2015)

employed a dynamic feature from a Marginal Ice Zone

(MIZ) to investigate a curvelet-based feature

extraction method. This was done as a first step in

using SAR images and identifying the MIZ so that the

SAR image could be classified as open water,

dynamic ice, or consolidated ice. An experiment

involving tenfold cross-validation was carried out.

Finally, to assess the effectiveness of the curvelet-

based feature, the SVM classifier was applied. The

curvelet-based feature resulted in a precise

classification of the dynamic ice. Because of its

directional sensitivity, multidirectional image analysis

is critical in SAR imaging. Thus, multidirectional

transforms receive the attention they deserve. Peifeng

and Shiqi (Peifeng and Shiqi, 2015) examined the

study of feature coefficients in SAR images for

decomposition utilizing curvelet transforms by proper

selection, reorganization, and fusing of feature

coefficients at various scales. Laghrib et al. (Laghrib,

Ghazdali, et al. , 2016) proposed a system for

increasing the resilience of super-determination

strategies. They proposed a new, enhanced SR

reproduction approach for slightly twisted low-

determination images to minimize misregistration

issues and vexing vintage rarities like ringing relics

and hidden, sharp edges

4 RESULTS AND DISCUSSIONS

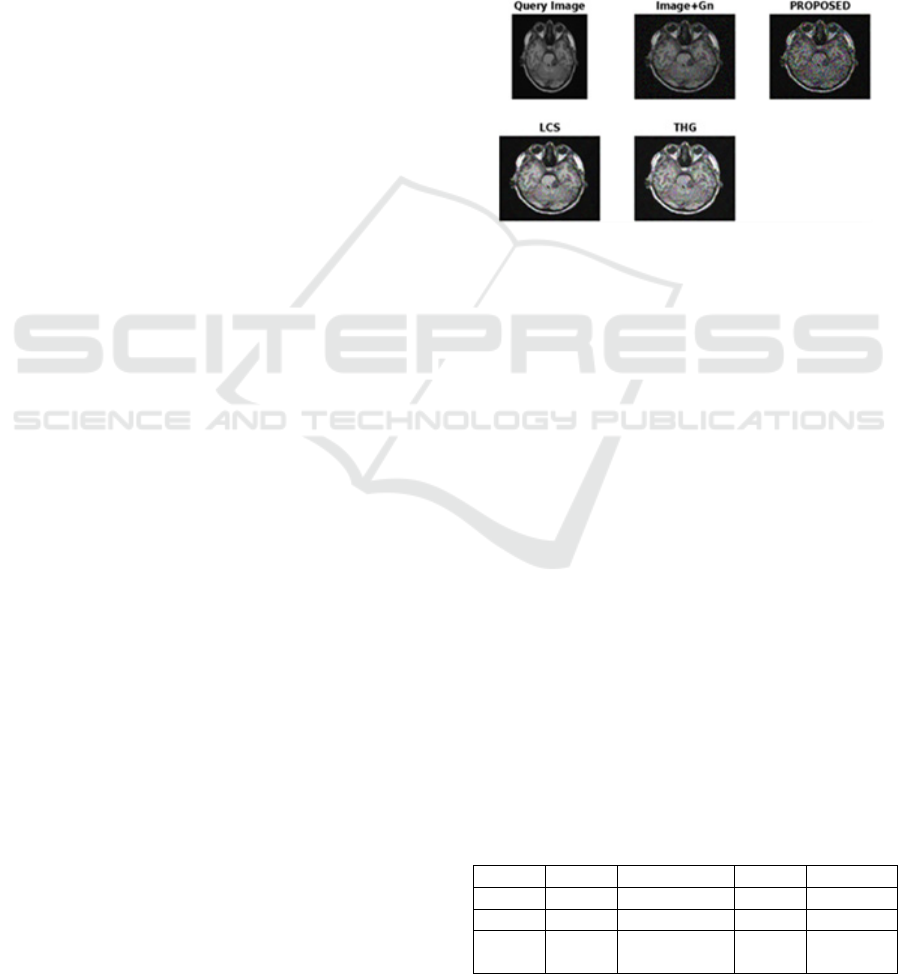
The Proposed filter's ability to remove Gaussian noise

from images. Visual comparisons indicate a

significant reduction in noise while maintaining

image detail.

Figure 2: Gaussian Noise

Quantitative measures validate the improvement,

showing a 5% increase in noise reduction over the

original photos. These findings show the filter's

useful in improving image quality for applications

that need reliable analysis and Figure 2 shows that the

proposed image is gaussian noise free and which

helps to sharpen the edge of the images.

Table 1 compares image quality metrics obtained

from several filtering algorithms designed to remove

Gaussian noise. Linear Contrast Stretching (LCS)

performs moderately, with a PSNR of 16.15 dB and a

reasonably high MSE of 1.5764e+03, indicating a

significant departure from the original image.

However, both Top-Hat Gaussian (THG) and the

Proposed Filter demonstrate benefits. THG achieves

a PSNR of 18.02 dB and a lower MSE, indicating

higher image fidelity than LCS. Nonetheless, the

proposed filter outperforms both LCS and THG, with

a PSNR of 19.72 dB and a much lower MSE,

indicating improved noise reduction and image

integrity. Furthermore, it achieves higher SSIM and

NIQE scores, indicating improved image detail

preservation and overall quality.

Table 1: GAUSSIAN NOISE

PSNR MSE SSIM NIQE

LCS 16.15 1.5764e+03 0.7355 8.9369

THG 18.02 1.0256e+03 0.8882 11.9330

PROP

OSED

19.72 692.5313 0.8440 15.1100

Hybridized Approach for Prepossessing Stage Design for Lungs CT Images

475

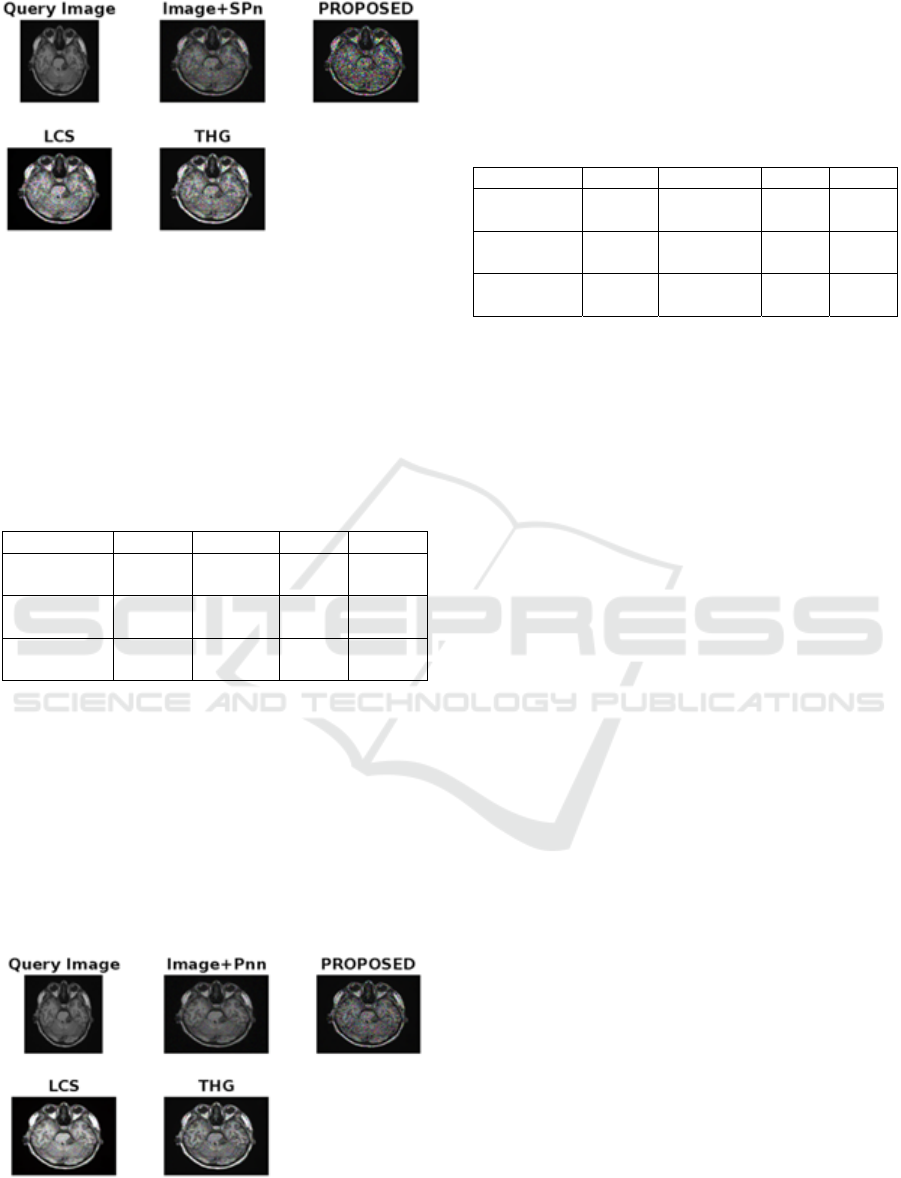
Figure 3: Speckle Noise

In Figure 3 the proposed images are speckle-free

noise which helps to analyze further disease detection

by removing the unnecessary noises from the images.

Table 2 compares the image quality metrics

produced by several Spackle noise-removal filtering

algorithms which further conclude that the proposed

hybrid filter is having better results than the existing

filters.

Table 2: Speckle Noise

PSNR MSE SSIM NIQE

LCS

18.407

938.325

0.915

8.9099

THG

19.396

747.189

0.616

7.7101

PROPOSE

20.809

539.703

0.847

10.216

In Figure 4 shows that reducing Poisson noise

from the photos leads to considerable increases in

image quality. We used the proposed filter to reduce

the noise, modifying the parameters as needed. Visual

comparisons show a significant reduction in noise

levels while preserving critical image features.

Poisson noise elimination improves image clarity and

sharpness, allowing subtle characteristics to be seen

more clearly. Quantitative analysis confirms these

findings, demonstrating a significant boost in image

fidelity.

Figure 4: Poisson Noise

Table 3 compares the image quality metrics

produced by several Poisson noise-removal filtering

algorithms which further conclude that the proposed

Tophat-Bottomhat filter is having better results than

the existing filters.

Table 3: POISSON NOISE

PSNR MSE SSIM NIQE

LCS

17.204

1.2379e+0

0.656

7.645

THG

20.848

534.8309 0.916

6.400

PROPOSE

26.125

158.6748

0.867

9.183

5 CONCLUSIONS

This paper concludes that the hybrid filter

successfully removes Gaussian, Poisson, and speckle

noise from images. The hybrid filter reduces noise

comprehensively by combining multiple filtering

techniques, including Gaussian filtering for

smoothing and noise reduction, Poisson noise

elimination, and speckle noise suppression. This

leads to significant improvements in image quality,

including better clarity, sharpness, and detail

preservation. The hybrid filter's adaptability makes it

a useful tool for a variety of image processing

applications, allowing for reliable image analysis and

interpretation across domains.

REFERENCES

Boyat, Ajay Kumar and Brijendra Kumar Joshi. “A Review

Paper: Noise Models in Digital Image

Processing.” ArXiv abs/1505.03489 (2015):

Mudhafar, Rusul & El abbadi, Nidhal. (2023). Image Noise

Detection and Classification Based on Combination of

Deep Wavelet and Machine Learning: non. Al-Salam

Journal for Engineering and Technology. 3. 23-36.

10.55145/ajest.2024.03.01.003.

Senthil Selvi A, Sukumar R. Removal of salt and pepper

noise from images using hybrid filter (HF) and fuzzy

logic noise detector (FLND). Concurrency Computat

Pract

Exper. 2019; 31:e4501. https://doi.org/10.1002/cpe.45

Nandhini, G., &Saraswathy, C. (2013, February). Speckle

suppression of SAR image based on curvelet and dual-

tree complex wavelet transform. In Information

Communication and Embedded Systems (ICICES),

2013 International Conference on (pp. 650-654). IEEE

Liu, J., Scott, K. A., &Fieguth, P. (2015, July). Curvelet

based feature extraction of dynamic ice from SAR

INCOFT 2025 - International Conference on Futuristic Technology

476

imagery. In Geoscience and Remote Sensing

Symposium (IGARSS), 2015 IEEE International (pp.

3462-3465). IEEE

Peifeng, S., &Shiqi, H. (2015, December). Analysis and

selection of coefficient feature by curvelet transform for

SAR images. In Advanced Information Technology,

Electronic and Automation Control Conference

(IAEAC), 2015 IEEE (pp. 1069-1072). IEEE.

Amine Laghrib, 2016. Abdelghani Ghazdali, Abdelilah

Hakim, Said Raghay, “A multi-frame super-resolution

using diffusion registration and a nonlocal variational

image restoration,” Computers & Mathematics with

Applications, Volume 72, Issue 9, November, Pages

2535-2548.

Senthil Selvi A, Sukumar R. Removal of salt and pepper

noise from images using hybrid filter (HF) and fuzzy

logic noise detector (FLND). Concurrency Computat

Pract

Exper. 2019; 31:e4501. https://doi.org/10.1002/cpe.45

Sakthidasan Sankaran, K., Velmurugan Nagappan, N.

2016. Noise free image restoration using hybrid filter

with adaptive genetic algorithm, Computers &

Electrical Engineering, Volume 54, August, Pages 382-

392, ISSN 0045-7906.

Shen, X., Yan, Q., Xu, L., Ma, L. and Jia, J. 2015.

"Multispectral Joint Image Restoration via Optimizing

a Scale Map," in IEEE Transactions on Pattern Analysis

and Machine Intelligence, vol. 37, no. 12, pp. 2518-

2530, Dec.

Hybridized Approach for Prepossessing Stage Design for Lungs CT Images

477