Leveraging Nash Equilibrium and Integer Linear Programming for

Real-Time Fraud Detection and Optimization in Blockchain Networks

Munna Prasad Gupta, Penmatcha Ganga Puneeth, Aryan Kumar Sah,

Sreebha Bhaskaran and Gayathri Ramasamy

Dept. of Computer Science and Engineering, Amrita School of Computing, Bengaluru, Amrita Vishwa Vidyapeetham, India

Keywords:

Blockchain Network, Nash Equilibrium, Integer Linear Programming, Scalability, Optimization, Scenarios in

Blockchain Applications

Abstract:

A blockchain network is a distributed, decentralized, digital ledger that records transactions in more than one

computer within a network. Blockchain organizes data in a uniquely secure, transparent and distributed man-

ner that enhances the reliability of the completed transaction providing it with applications such as cryptocur-

rency, supply chain, voting, decentralized ﬁnance and many more. The mobile applications of the blockchain

network have several issues which include scalability effects in large transactions, computation resources,

longer veriﬁcation times, security threats, compatibility issues with the platforms, and problems of distributed

decision-making issues. Solving these problems calls for rationality in the use of resources, mitigation of

transaction inconsistencies, and better deﬁned rules. In this work, we combine Nash Equilibrium with Integer

Linear Programming to solve different scenarios in applications of the blockchain network. We contrast the

stated Algorithms in various settings to identify which strategy offers the best solution to all of the afore-

mentioned issues, such as low scalability, high energy utilization, substantial latency, and communication

discordance among different blockchain networks. The combination of both of these techniques provides a

proactive solution to improve the reliability, optimization, and communications capability of blockchain sys-

tems, thus paving the way for blockchain technology to fully revolutionize industries around the world.

1 INTRODUCTION

Blockchain is an actualization of a distributed

database across nodes, relevant in applications of

cryptocurrencies, smart IoT devices, and supply

chain. Regarding the problems of blockchain net-

work such as scalability, low throughput, high energy

consumption, and lack of communication, this paper

proposes to use Nash Equilibrium with Integer Lin-

ear Programming (ILP). During high congestion and

transaction imbalances, the Nash Equilibrium is fair

and reliable in resource allocation (Tang et al., 2023).

However, ILP improves this by bringing the efﬁciency

of complex decision making, while also directing re-

sources and handling transactions (Song et al., 2023).

Given a shift in perception towards the partici-

pants, Nash Equilibrium is used to study blockchain

systems by considering individuals as selﬁsh players

whose actions shape system performance. This ap-

proach demonstrates how resources can be utilized

in decentralized conditions where traditional control

measures fail because there is no central power (Wang

et al., 2023a). In total, utilizing Nash Equilibrium, be-

havior expectations of participants in many-developer

and multi-researcher systems can be predicted, peak

usage performance can be optimized, transaction

crowd can be minimized, and fairness,system in-

tegrity can be maintained (Bappy et al., 2024).

ILP offers a mathematically rich formalism that

proves to be suitable for tasks in blockchain networks,

such as power supply distribution, storage organiza-

tion, or fraud detection (Wu et al., 2024). It makes

sound decisions because aspects related to things such

as capacity and resources are factored in to arrive at

the best solution within the limits of certain param-

eters (Ebrahimi et al., 2024). This optimization is

important especially where timely decision making

is important in countering network threats. In addi-

tion to enhancing organizational efﬁciency, ILP ad-

dresses emerging risks to ensure greater security of

blockchains.

The key contributions of this work are:

Gupta, M. P., Puneeth, P. G., Sah, A. K., Bhaskaran, S. and Ramasamy, G.

Leveraging Nash Equilibrium and Integer Linear Programming for Real-Time Fraud Detection and Optimization in Blockchain Networks.

DOI: 10.5220/0013585900004664

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 3rd International Conference on Futuristic Technology (INCOFT 2025) - Volume 2, pages 12-21

ISBN: 978-989-758-763-4

• Comparison of ILP and Nash-like approach for

optimization in blockchain networks

• Fraudulent transaction detection based on multi-

ple thresholds

• Determining cost-minimization strategies consid-

ering multiple factors

• Performance improvisation in blockchain net-

works integrating both algorithms for different

scenarios

• Adaptive decision-making framework for

blockchain efﬁciency.

Concisely, this paper proposes a framework using

Nash equilibrium and ILP to improve the reliability

and efﬁciency of a blockchain system (Liu et al.,

2023). This integration solves many operational

problems and contributes to innovations in areas such

as supply chain and decentralized ﬁnance (Zhang

and Wang, 2024). The approach is meant to improve

efﬁciency in managing transactions and resources

and to guarantee the longevity and robustness of

decentralized applications around the world (Mssassi

and Abou El Kalam, 2024).

The remainder of the paper is structured as fol-

lows. The surveyed literature is presented in Sec-

tion 2. Section 3 details the methodology used in

this study. The implementation process is described

in Section 4. Section 5 presents the results and the

discussion, analyzing the ﬁndings in detail. Finally,

conclusions carried with future scope are drawn in

Section 6.

2 LITERATURE SURVEY

Tang et al. suggested a blockchain framework to im-

prove trust with the speciﬁed tourism service level

agreements (Tang et al., 2023). Song et al. used

blockchain in the management of construction funds

(Song et al., 2023), and Wang et al. elucidated on the

use of blockchain in data control (Wang et al., 2023a).

Similarly, Bappy et al. applied parallelism as a way

to deal with a simultaneous transaction request to op-

timize (Bappy et al., 2024). Some authors presented

ShardingSim, a CB SB simulator to enhance scalabil-

ity and performance (Wu et al., 2024).

Using blockchain technology, Ebrahimi et al. in-

troduced a framework for the privacy and security of

Federated Learning (Ebrahimi et al., 2024). To illus-

trate this cause, Liu et al. proposed an anonymous au-

thentication system for secure crowd-sourcing of mo-

bile devices (Liu et al., 2023). Speciﬁcally, based on

game theory, Zhang et al. proposed a Proof of Sam-

pling (PoSP) system to prevent dishonesty (Zhang

and Wang, 2024). Mssassi and Abou El Kalam in

their research used game theory to improve cooper-

ation in the blockchain network (Mssassi and Abou

El Kalam, 2024), and Stodt and Reich used taxation

and game theory to control imperfect behavior (Stodt

and Reich, 2023). Li et al. analyzed the evolution-

ary game to enhance compliance in blockchain-based

ﬁnancial contracts (Li et al., 2023).

Blockchain has improved reliability and effective-

ness in different areas. Shukla et al. presented an elec-

tronic voting using blockchain (Punith et al., 2022),

while Wang et al. provided techniques for anonymity

in payment in ﬁnancial operations (Jie et al., 2023).

Shashank et al. integrated IoT with blockchain for

secure health monitoring by researchers (Shashank

et al., 2023). Li et al. examined the application

of blockchain technology to improve government ef-

ﬁciency (Li et al., 2024). Notara is a blockchain-

based asset notarization system (Toyos-Marfurt et al.,

2024) for the credibility of the public sector by Toyo-

Marfurt et al. Finally, Yin et al. introduced a decen-

tralized resource management system for multi-agent

systems using blockchain (Yin et al., 2024).

To improve the believability and protect smart

contracts of PEVM-based PoA private blockchains,

Wang et al. introduced a proxy layer (Wang et al.,

2023b). Narang & Verma have addressed the aspect

of how blockchain can enhance the chances of food

safety and accurate supply chain data (Krishna and

Rekha, 2022). In 2020, Shi et al. formulated a

range of mathematical models that can be applied to

incorporate blockchain into research of operations in

plywood supply chains (Shi et al., 2022). Dhanala

and Radha proposed a recruitment management ar-

chitecture based on a blockchain layer for candidate

data and to improve the quality of credential data

(Dhanala and Radha, 2020).

3 METHODOLOGY

3.1 System Architecture

Fig.1 illustrates the process ﬂow of Real-Time Frauds

and Optimization in blockchain networks and consists

of the fraud detection process, task distribution pro-

cess, and optimization process. The system takes in-

put data, which are most probably transaction or sys-

tem data from a blockchain network. The fraud detec-

tion module employs the identiﬁcation of fraudulent

and non-fraudulent patterns in these data. As for the

Leveraging Nash Equilibrium and Integer Linear Programming for Real-Time Fraud Detection and Optimization in Blockchain Networks

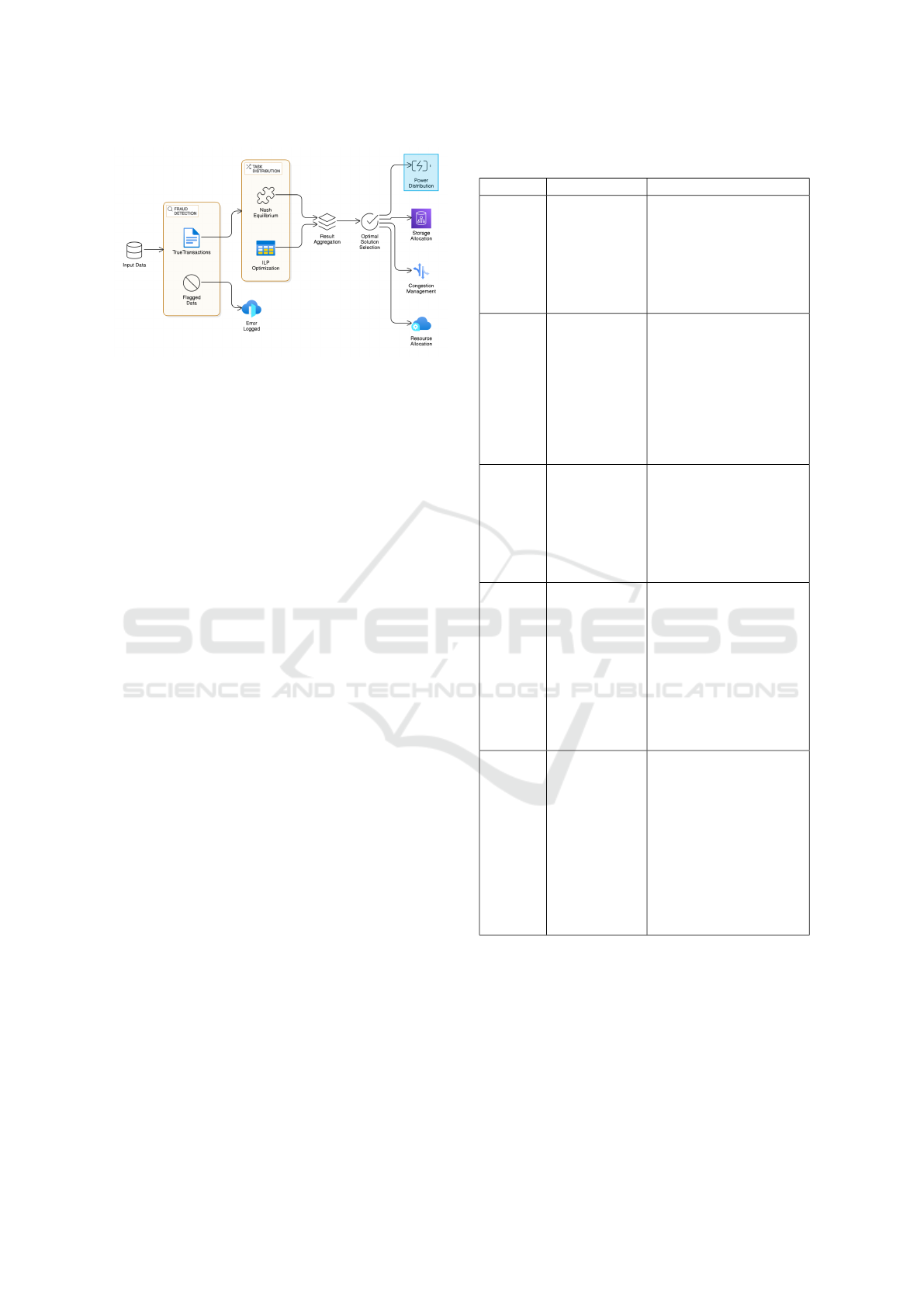
Figure 1: Architecture Diagram

reliable transactions, the true transactions are passed

to the Task Distribution component. This particular

module guarantees that tasks associated with different

scenarios are directed to the right optimization pro-

cesses. Used here is Nash Equilibrium logic which,

given a game theory, the system is able to ration and

strategically allocate tasks and resources.

Further, ILP Optimization is a technique, em-

ployed to apply mathematical modeling and integer

linear programming to determine the most optimal so-

lution with regard to transaction processing within the

constraints of the system. The outcomes of these opti-

mization processes shall be collected in the Final Ac-

tion Outcome step to have the best action to take orig-

inating from the Nash equilibrium and the ILP Opti-

mization. Compiling the results from all the assess-

ments, the system identiﬁes the Optimal Solution that

best addresses the current requirements in fraud de-

tection and tasking distribution, such as Power Distri-

bution, Storage Allocation, Congestion Control, and

Resource Distribution. These individual elements are

described fairly effectively below.

3.2 Related Work and Contribution

Based on the works described above, our research

extends the studies of (Wang et al., 2023a), (Bappy

et al., 2024),(Zhang and Wang, 2024),(Mssassi and

Abou El Kalam, 2024) and (Yin et al., 2024) to opti-

mize the deployment of the blockchain resources pre-

sented in Table 1. Wang et al. pay attention to data

storage management and offer the ﬁndings that we

generalize to apply to the aspects of computational

power, network capacity, and safeguard. Bappy et al.

increase the correlation between parallelism and the

relation between activities that are dependent on each

other, which in turn can be applied to our Nash equi-

librium and ILP models that allocate the resources

better.

(Zhang and Wang, 2024) use the Nash equi-

librium for decentralized systems, the knowledge of

Table 1: Key Methods from Literature and Their Relation

to the Current Study

Paper Methods Inference

(Wang

et al.,

2023a)

Data storage

management

in blockchain

systems,

focusing on

optimizing

storage usage.

It can be expanded to

cover data storage man-

agement in this study to

improve the model’s ver-

satility by adding storage

resources to blockchain.

(Bappy

et al.,

2024)

Performance

optimization

in blockchain,

focusing

on paral-

lelism and

dependency

management.

The paper recommend

for parallelism and

computational optimiza-

tion to be employed to

minimize the time taken

in computation the Nash

Equilibrium and ILP

models of optimization

of resources.

(Zhang

and

Wang,

2024)

Nash

Equilibrium-

based pro-

tocol for

decentralized

systems using

veriﬁcation.

Nash Equilibrium is then

adopted in this study to

allocate scarce resources

in blockchain networks,

so that competing nodes

can get the best distribu-

tion.

(Mssassi

and

Abou

El Kalam,

2024)

Game theory

to design

incentives for

mitigating

malicious

behavior in

blockchain

networks.

This work employs Nash

Equilibrium concerning

resource distribution in

blockchain; in the same

manner that game the-

ory proclaims motiva-

tions for proper conduct

which guarantees opti-

mum ripple without ri-

valry.

(Yin

et al.,

2024)

Resource

optimization

in distributed

systems com-

bined with

blockchain

technology.

This paper addresses the

problem of how to better

coordinate the resource

partition and distribution

in a blockchain system

when it is deployed over

multiple nodes so that

the extents of process-

ing, bandwidth, and se-

curity offered by the sys-

tem can be enhanced.

which helps us to ﬂow resources by avoiding com-

plicated clashes.(Mssassi and Abou El Kalam, 2024)

discussed game theory and opportunistic fair schedul-

ing of resources, while we utilized Nash Equilibrium

to model node interactions or allocate resources.(Yin

et al., 2024) aim at the distributed node resources, and

propose the basic theory for the Nash: Equilibrium,

ILP we employed for fair and efﬁcient resource allo-

cation.

INCOFT 2025 - International Conference on Futuristic Technology

Taken together, these papers provide a solid

ground for our further investigation of improvements

in blockchain systems. We apply their extension to

state their methodology into broader areas such as

game theory and optimization techniques to design

better solutions that can be used for coordinated sys-

tem resource allocation, security analysis, and perfor-

mance in decentralized blockchains.

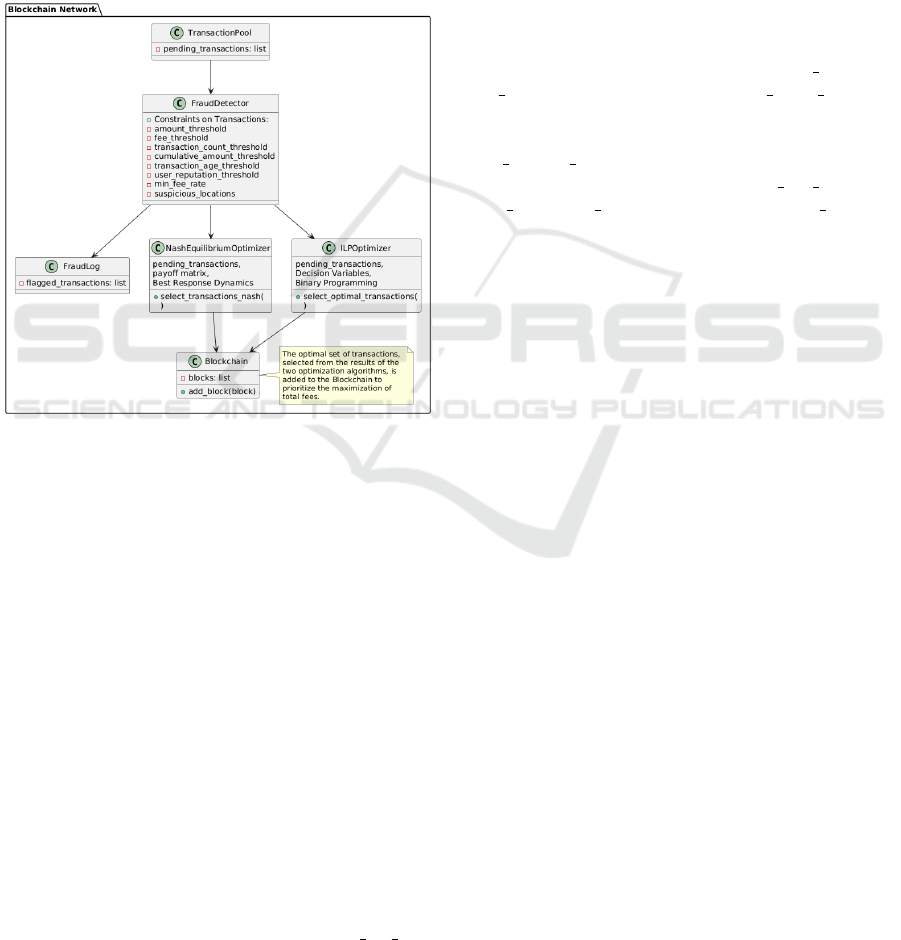
3.3 Fraud Detection

Figure 2: WorkFlow of Fraud Detection Process

In Fraud Detection, thresholds are determined by

the transactional properties of the behavior, the user’s

history, and the requirements of the necessary sector.

For the ﬁnancial area, the amount threshold warns of

large payments and therefore of potentially fraudulent

operations. In e-commerce, a fee threshold means

that when the fee is small, it is recognized that it may

be part of an effort to evade detection. The frequency

threshold concerns user transaction behavior and will

trigger some kind of alert of anomalous activities

such as money laundering. In the banking sector,

the number of total amount triggers pits the users

with total transaction volume above the ﬁxed amount

regarding fraudulent transfers. The transaction age

threshold validates the age of the transactions, with

the ability to hold old transactions that may be related

to fraud, especially in insurance fraud. The user

reputation threshold determines the trustworthiness,

identifying unreliable users and is essential for such

internet-based services as peer-to-peer lending, where

user credibility is essential. The minimum fee rate

is compared with amounts where transaction fees

are compared with amounts and in this case, it will

highlight transactions below a speciﬁed value as

possibly fraudulent. The new thresholds feature of

suspicious locations raises red ﬂags to such transac-

tions originating from areas considered risky; ideal

for industries like bitcoin trading or global remittance

services where some regions are more vulnerable to

fraud. These thresholds vary in consideration of the

tendency of the past, the recent user activities and the

risks of the sector to allow only genuine transactions

while blocking the fraudsters.

The payment acceptance and conﬁrmation of a

blockchain network have been described in Fig.2;

Different types of limitations related to the trans-

actions for detecting any abnormality have been

described. They include the amount threshold,

fee threshold, and transaction count threshold

that restricts the size and fees of the transac-

tions. Also, there are limitations like cumula-

tive amount threshold to measure the user activity

and transaction history, transaction age threshold,

user reputation threshold, and suspicious locations

to map transactions from potentially bad regions.

The following fraud detection, two optimization

algorithms are applied: Nash Equilibrium with Best

Response Dynamics and Integer Linear Programming

SBA Magnet in Delhi. These are used to identify the

set of transactions that is best suited to the objectives

of the network. The transactions are then selected for

integration into the blockchain to enhance the overall

fee given the capability to occupy more available

space when the transactions are associated with

higher fees than the current blockchain capacity. This

guarantees that the blockchain is both safe and costly

in the effectiveness of the blocks with the processed

transactions being passed over to the next module.

The singularity approach that combines the incorpo-

ration of sophisticated fraud detection systems and

optimization software enables blockchain networks

to achieve enhanced security, service efﬁciency, and

ﬁnancial sustainability under conditions character-

ized by complexity, decentralization, and dynamism.

3.4 Optimization Algorithms: Nash

Equilibrium and Integer Linear

Programming (ILP)

Out of the different methods available like linear pro-

gramming or the greedy algorithm, the Nash equilib-

rium optimization technique is selected for perform-

ing the optimization task as shown in Fig. 3 because

the Nash equilibrium strategy works well with scenar-

ios that entail interconnection and interactions among

Leveraging Nash Equilibrium and Integer Linear Programming for Real-Time Fraud Detection and Optimization in Blockchain Networks

Figure 3: WorkFlow of Nash Equilibrium

Figure 4: WorkFlow of Integer Linear Programming

the numerous decision players, including nodes or

plants. In this model, each player (node or plant)

best responds locally to the current state and antici-

pates the response of others to arrive at a Nash equi-

librium in which no player can make himself better off

by changing his strategy while others remain passive.

The Nash Optimization Algorithm presented in Fig.

3 elaborated the capacities, demands, and cost matri-

ces of the nodes as well as penalties for demands un-

met or capacities over-utilized to derive the best plan

and total cost. This considerably decentralizes the

system because it ensures that everyone can move in

harmony with everyone else, maintaining an organic

harmony from top to bottom, which minimizes con-

ﬂict and maximizes the smooth running of the whole

system.

As illustrated in Fig. 4, the choice of the opti-

mization technique is ILP since it presents the best

solution decisions when problems are formulated us-

ing linear equations with integer variables. The tech-

nique focuses on trying to improve an explicit mea-

sure of performance, possibly by increasing or de-

creasing it, under certain conditions of capacity, de-

mand, or resources, among others. Since decision

variables can only take certain predeﬁned values in

ILP, the method performs best on problems that in-

volve the assignment of transactions to agents or the

allocation groups of power supplies. Through the so-

lution of such linear models, ILP provides an assured

solution that meets the problem constraints without

the waste of resources. The approach is widely ap-

plied to blockchain-based applications for tasks re-

lated to the organization of the work of numerous

transactions, as well as managing the cache and stor-

age, for which certain and efﬁcient resource allocation

is vital for the functioning and stability of the systems.

4 IMPLEMENTATION

4.1 Overview

For decentralized decision-making among agents in

strategic interaction, we suggest Blockchain and the

Nash equilibrium, which are then amalgamated with

integer linear programming to solve resource alloca-

tion. As for the ILP formulation, we employ PuLP

which allows us to deﬁne and solve ILP models for

the transaction fees, distribution of power, and storage

optimization; meanwhile, the NumPy package is used

for providing numerical values to model interaction

and constraints. Visualization of identiﬁed resource

usage, congestion levels, and optimization outcomes

is done using Matplotlib and Seaborn. The resource-

sharing networks can be modeled by the NetworkX

tool while logging, time, and datetime enables moni-

toring as well as timestamp. Hashlib is used to ensure

cryptographic security and json for transactions. This

framework also focuses on congestion control, cost

minimization as well as proﬁt maximization and math

optimization and game theory functions in a strong

Blockchain framework.

4.2 Power Distribution Scenario

In a blockchain system for power distribution, trans-

actions are mailed as digital entries in transac-

tions,checked to ensure compliance with capacity re-

quirements by the nodes. Detection of fraud results in

situations being ﬂagged and, thereby, stopping fraud-

ulent transactions. Once validated, the transactions

are recorded in a secure and immutable block, which

is then passed to an optimization model to distribute

power from multiple plants to various regions using

two approaches: An ILP and a Nash-like approach,

which incorporates penalties. Special types of ILP-

integrated models help minimize the entire cost of

distribution while meeting demand and capacity con-

straints in each region and plant. The Nash-like ap-

proach targets the allocation of power by the ratio of

plant costs and discourages the awarding of overca-

pacity. Use of a heat map and bar graphs to present

the power distribution for both approaches, the total

power supplied to each region, and the total power

distributed by the plant. The latter helps to compare

the efﬁciency and cost effectiveness of the two meth-

ods with a focus on the power distribution rates.

INCOFT 2025 - International Conference on Futuristic Technology

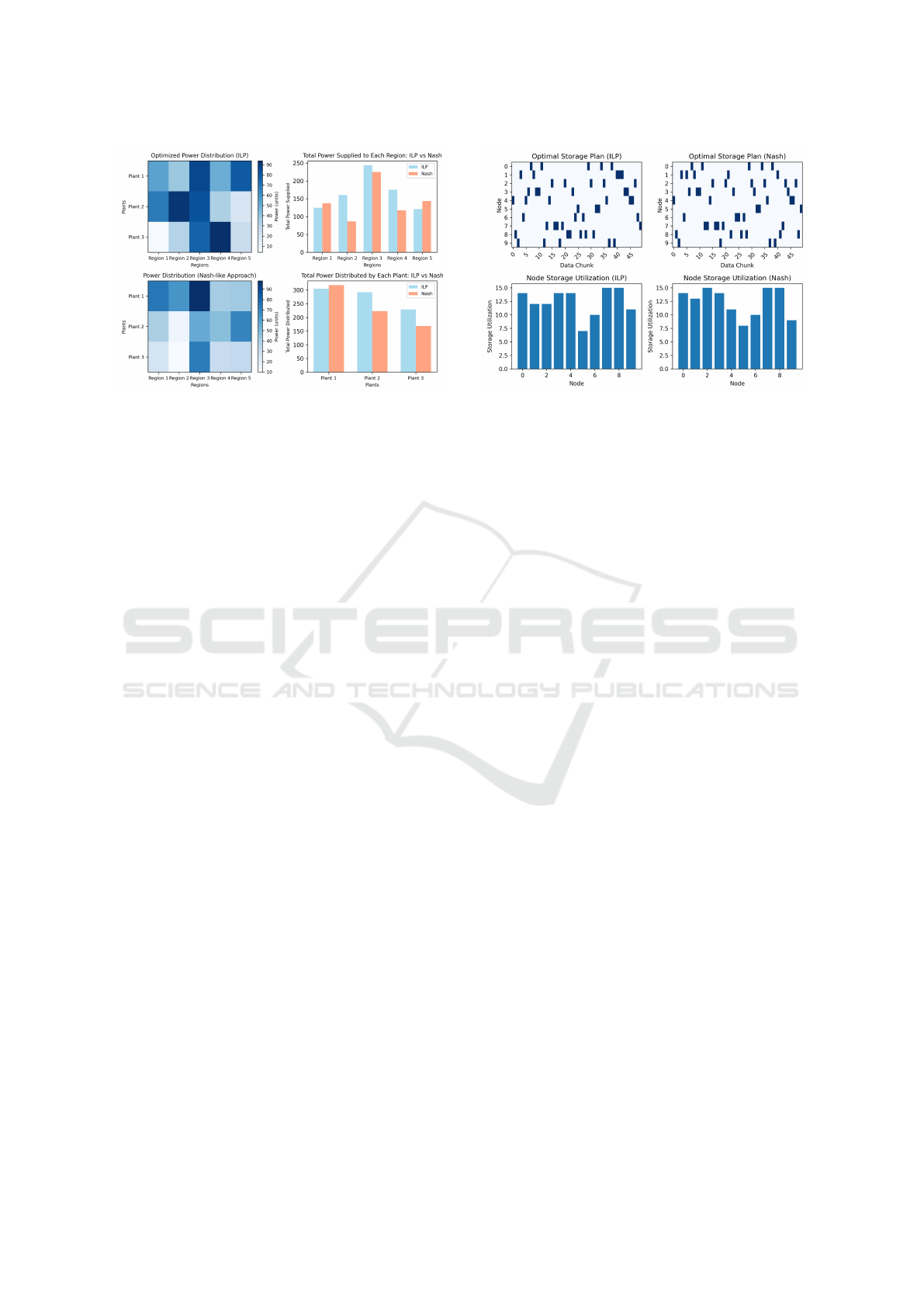
Figure 5: Power Distribution ILP VS NASH

From Fig. 5. it is clear that the ILP approach de-

centralized more power among all plants and regions

compared to the Nash approach except for Region 5

where Nash provides more power. Power ﬂow under

Nash is only tilted upwards from plants to regions;

some regions consume more power than others like

Region 3 for Plant 1 and Region 2 for Plant 2. How-

ever, for ILP, the materials are more evenly divided

and more rationally allocated than for FRP, particu-

larly for Plants 2 and 3. In general, ILP has a better

distribution of power to plants and regions than that

provided by the Nash.

4.3 Storage Optimization Scenario

The sale of storage to be performed on the blockchain

goes ﬁrst through a fraud ﬁlter mechanism and then

through a proﬁtability-based scheduler, such as trans-

action fees and efﬁciency, and then stored in blocks.

These transactions in a block are then optimized us-

ing two approaches: Combinatorial demand-creation

models include ILP and a Nash-like greedy strategy.

ILP sets an optimization model to ﬁnd globally op-

timal solutions due to balanced resource allocation,

minimal storage, and lower latency cost. The Nash-

like approach, on the other hand, enables nodes to

self-organize the storage by letting nodes decide what

they want to store for the faster locally optimal so-

lution. Combined, ILP guarantees the optimal allo-

cation of resources for the future to optimize expen-

diture throughout the while the Nash-like method is

key when facing scenarios that are constantly unpre-

dictable in the present.

From Fig. 6. the simulation results reveal that the

proposed ILP approach attains a higher node utiliza-

tion of 14.5% compared to the Nash approach with a

maximum node utilization of 12.5 %. This means that

the ILP strategy results in a relatively higher level of

hospital utilization compared to Nash. As evidenced

Figure 6: Storage Optimization ILP VS NASH

by the two plans, the node usage experiences some

level of ﬂuctuation, while in ILP, the data chunks are

spread evenly across the nodes. However, decentral-

ization of decision making in the Nash approach re-

duces total utility and indicates a lower efﬁciency of

resource allocation and, in particular, a 2% decrease

in overall utilization, with respect to the maximum

values obtained using the two methods. This differ-

ence suggests the potential of the ILP to create an ide-

ally efﬁcient and balanced storage plan.

4.4 Dynamic High Congestion

Management Scenario

Dynamic high congestion in the blockchain net-

works happens when transaction volume is above the

Replace-by-Fee, resulting in a slow rate, higher fees,

and network problems. This is sometimes attributed

to things such as low block size, overall transactions,

and Initial Coin Offering events. Congestion might

cause users to pay more fees, which in turn aggra-

vates the problem. Congestion is addressed by some

solutions like Nash Equilibrium and Integer Linear

Programming Optimization. Frequency line duplica-

tion works with the intent of locating many converg-

ing nodes that are easily recognizable, since their de-

gree of connection can differentiate them from either

one or a few neighbors. The execution time of both

the ILPO strategy: The variance is compared with the

partner selection approach as a function of variance,

execution time, and global performance at different

congestion levels.

Examining the four subgraphs in Fig.7. provides

valuable information for understanding the relative

performance of the Nash equilibrium and the ILP for

congestion control. The result derived from the Nash

Equilibrium approach reveals a mere, steady rise of

variance compared to that depicted by ILP which fea-

Leveraging Nash Equilibrium and Integer Linear Programming for Real-Time Fraud Detection and Optimization in Blockchain Networks

Figure 7: Dynamic Congestion Management NASH VS

ILP

tures a steep rise and therefore is more sensitive to

congestion. For execution time, Nash Equilibrium has

much less ﬂuctuation and keeps a very low moving

average while ILP has a much higher moving aver-

age at higher congestion levels showing inefﬁciency

at high congestion levels. The heatmap again vali-

dates the conclusion that the Nash equilibrium outper-

forms by achieving fewer variances and shorter exe-

cution times. In addition, the average variance for JE

and NE is much closer, but the latter is much lower,

which explains its efﬁciency in controlling conges-

tion. In general, therefore, the Nash equilibrium ap-

proach is more effective and less sensitive to dynamic

high congestion conditions.

4.5 Resource Allocation Scenario

Transactions for resource allocation come into a

blockchain network as a request or transfer, typically

handled by a smart contract. Since these transactions

are done online, they are ﬁrst ﬁltered by a fraud detec-

tion system to ﬁlter out fraudulent ones. On veriﬁca-

tion, they are passed through an optimization model

to determine the most appropriate transactions that

would yield the highest proﬁts with security and con-

cerning transparency. The validated transactions are

then routed to a task distribution module where the

authors provide a solution that offers a comparison

between two solutions for the management of multi-

resource transactions; namely the Nash Equilibrium

and the Integer Linear Programming. This module is

capable of producing useful performance measures,

including computation time and utility, and is efﬁcient

in portraying the ﬁndings. This is particularly helpful

in observing how Nash equilibrium and ILP optimiza-

tion function in various state circumstances.

In Fig. 8, the runs created for the Nash equilib-

rium have less computation time than those for ILP,

Figure 8: Resource Allocation NASH VS ILP

and there are runs where Nash equilibrium needs sig-

niﬁcantly less computation time than ILP. Nash equi-

librium has a lower median computation time and is

more centralized, showing that it delivered faster yet

more uniform results. However, as we have seen from

the results tables, ILP is less predictable with average

computation time for some runs being much higher,

which makes it less consistent. Although both meth-

ods offer the same amount of utility, Nash Equilib-

rium has slightly better average utility, and this utility

varies less from the average, suggesting lower volatil-

ity. The utility distribution plots for both methods

are relatively symmetric and close together, and while

the means are nearly identical, the Nash equilibrium

is slightly higher than coordination, but it is much

faster to compute, so it is the better strategy in this

case. However, the results show that the Nash equi-

librium has better computational performance and is

more useful compared to ILP.

5 RESULTS AND DISCUSSIONS

The use of ILP over Nash equilibrium helps to

illustrate the important trade-off between efﬁciency

and decentralization in block chain networks. ILP

gives optimal decisions worldwide and promotes the

redemption of constraints, yet it troubles with greater

time consumption and limited extensibility. However,

Nash equilibrium is real-time, expandable and less

rigid in the dynamic setting, but it is known to pro-

duce inefﬁcient results and poor costs. Both are el-

egant for different reasons as shown in Table 2, ILP

more suited to the smaller scale, cost-optimize prob-

lem, while Nash equilibrium being far better placed

to deal with the more complex real-time problems at

scale.

The performance measures employed in the eval-

uation of Nash and ILP are utilization, capturing re-

INCOFT 2025 - International Conference on Futuristic Technology

Table 2: Comparison of ILP and Nash Equilibrium in

Blockchain Network

Metric ILP (Integer Linear

Programming)

Nash Equilibrium

Solution Quality Globally optimal solution Suboptimal solution due to

decentralized approach

Cost Efﬁciency Minimizes total cost, strictly

satisﬁes constraints

Higher cost due to subopti-

mal allocation

Adherence to Con-

straints

Strict adherence to all re-

gional demands and plant

capacities

May fail to strictly satisfy

constraints (e.g., capacity

breaches)

Computational Time Higher execution time due

to complex optimization

Faster execution time, better

for real-time needs

Scalability Less scalable for large net-

works due to computational

overhead

Highly scalable due to de-

centralized nature

Resource Utilization Balanced and optimal across

resources

Uneven utilization, potential

under/over utilization

Performance at High

Congestion

Higher variance, less effec-

tive at handling congestion

Balanced congestion distri-

bution, lower variance

Flexibility in Dy-

namic Conditions

Less ﬂexible with changes in

dynamic conditions due to

optimization complexity

More ﬂexible due to decen-

tralized decision-making

Optimization Target Focus on global optimiza-

tion (minimizing overall

costs)

Focus on local optimization

per agent or node

Application Suitabil-

ity

Best for smaller-scale prob-

lems with global optimiza-

tion requirements

Suitable for larger-scale

problems or where execu-

tion time is critical

Penalty for

Suboptimal Alloca-

tion

None, since it provides an

optimal solution

Penalties for suboptimal al-

locations and breaches

Use Case Example Power Distribution and

Storage Optimization in

blockchain networks

Blockchain Congestion

Management and Dynamic

Resource Allocation in

blockchain networks

Table 3: Results Based on Power Distribution Scenario

Metrics Utilization Fairness Demand

Satisfac-

tion

Load Im-

balance

Nash 0.4257 0.6157 0.5162 0.092

ILP 0.6294 0.6682 0.7529 0.0694

source usage; fairness, which ensures equality in re-

source allocation; demand satisfaction, which por-

trays user demand satisfaction by the particular sys-

tem; load balance showing the workload distribution

and the throughput which represents system process-

ing capacity; and scalability which displays the sys-

tem capability in handling intricate demands. These

metrics are of pre-importance in evaluating perfor-

mance, costs, equity, and ﬂexibility, and useful in

comparing the efﬁciency of various systems.

From the results provided in Tables 3 and 4, it

can be concluded that ILP outperforms Nash in all

observed measures depending on the optimization

strategies for power distribution and storage. In the

power distribution scenario, this algorithm exhibits

superior resource usage, fairness, and demand sat-

isfaction compared to Nash, with a better distribu-

tion of client transaction loads on sender nodes. Yet

Table 4: Results Based on Storage Optimization Scenario

Metrics Utilization Fairness Demand

Satisfac-

tion

Load Im-

balance

Nash 0.10 0.9216 1.0 0.2917

ILP 0.52 0.9833 1.0 0.1304

Table 5: Results Based on Dynamic High Congestion Man-

agement Scenario

Metrics Throughput Fairness Scalability Load Im-

balance

Nash 0.914375 0.6296 1.0 0.14026

ILP 0.54 0.2192 0.28 0.162

Table 6: Results Based on Resource Allocation Scenario

Metrics Throughput Fairness Scalability Load Im-

balance

Nash 0.92 0.9833 0.9020 0.1304

ILP 0.472 0.8243 0.4608 0.4618

there is one important criticism disregarding the oc-

currence of the Nash equilibrium, ﬁrstly, it cannot en-

sure proper distribution of resources as well as fair

play among all the players involved. For instance,

in a situation where many nodes have to draw power

from a single power source, Nash can result in cer-

tain nodes being favorably allocated a use a lot of

power while others are starved of power. Likewise

in the storage optimization scenario, ILP provides a

more fair solution in which nodes at every point re-

ceive more resources and have better resource use ef-

ﬁciency than the centers, and a higher net-utility ratio.

ILP also meets demand effectively and handles load

differentiation better, making it the preferred method

in models where the precision and efﬁcient use of sys-

tem resources are important. However, Nash equilib-

rium may be useful, especially when the decisions are

needed more frequently and when the pay-offs are es-

pecially high for each individual. Speciﬁcally, there-

fore, the ILP is the most suitable for system environ-

ments where accuracy and societal improvement are

paramount and where the precision of powering dif-

ferent units is important such as smart grid and cloud

computing, especially in billing and management of

resource data centers and other computing units.

The dynamic high-congestion management and

resource allocation that are presented in Tables 5 and

6 show that the proposed Nash equilibrium is supe-

rior to the conventional implementation of the ILP

approach in terms of total throughput, fairness, and

scalability. Hence, the superior performance of Nash,

especially in dynamic high-congestion management,

makes it suitable for a large decentralized system. In

addition, in the resource allocation situation, Nash

performs favorably well in the throughput, fairness,

and scalability values to support the applicability of

the theory to systems where demand and availability

vary greatly, scaling utilization better than ILP. In the

case of dynamic optimal allocation of resources and

especially in cases of quick changes in demand, Nash

outperforms ILP in load balancing when the changes

in demand are minimal. Since ILP is highly central-

Leveraging Nash Equilibrium and Integer Linear Programming for Real-Time Fraud Detection and Optimization in Blockchain Networks

ized in the computational process and involves high

complexity, it is not an optimum solution for dynamic

and large-scale applications with frequent changes in

the environment, such as a high-congestion resource

distribution. However, the Nash equilibrium serves

the best purpose in dealing with decentralized prob-

lem solving, which is more scalable and effective in

complex systems with a number of agents. This has

made it the most suitable for use in large systems, de-

centralized systems, and dynamic systems, especially

where congestion is a complication.

6 CONCLUSION

The analysis of the ILP and Nash equilibrium re-

ﬂects that the selection of the appropriate method-

ology depends on the system requirements and the

characteristics of the scenario. The proposed frame-

work uses ILP in static, optimization-focused stages,

such as power distribution and storage, where the

strength of the approach, global optimum, and min-

imum resource wastage come in handy in conditions

with little variation and maximum requirement for ef-

ﬁciency. On the other hand, when demand is unpre-

dictable, roads over-saturated, and real-time response

crucial, scalability, throughput, and fair resource shar-

ing of Nash Equilibrium are valued, which is ben-

eﬁcial in complex environment with many agents

and high demand for timely responses and adaptive

behavior. Thus, the framework optimizes resource

use by combining trends in the methodology of ef-

ﬁcient large-scale organizations with decentralized

structures, thus achieving some of the features of both

methods needed for dynamic blockchain networks.

Future research may look at how usage of en-

hanced consensus algorithms or even studying the ef-

fect of integration with smart contracts in decision

making more deeply. Further expansion of the frame-

work for highly heterogeneous nets and the incorpo-

ration of efﬁcient protection against destructive ele-

ments in decentralized structures might also improve

its relevance. Last but not least, using empirical eval-

uations over various blockchain applications and the

changing environment to identify areas for improve-

ment for additional ﬁne-tuning.

REFERENCES

Bappy, F. H., Zaman, T. S., Islam Sajid, M. S., Ah-

san Pritom, M. M., and Islam, T. (2024). Maximizing

blockchain performance: Mitigating conﬂicting trans-

actions through parallelism and dependency manage-

ment. In 2024 IEEE International Conference on

Blockchain (Blockchain), pages 140–147.

Dhanala, N. S. and Radha, D. (2020). Implementation and

testing of a blockchain based recruitment management

system. In 2020 5th International conference on com-

munication and electronics systems (ICCES), pages

583–588. IEEE.

Ebrahimi, E., Sober, M., Hoang, A.-T., Ileri, C. U., Sanders,

W., and Schulte, S. (2024). Blockchain-based feder-

ated learning utilizing zero-knowledge proofs for veri-

ﬁable training and aggregation. In 2024 IEEE Interna-

tional Conference on Blockchain (Blockchain), pages

54–63.

Jie, W., Qiu, W., Koe, A. S. V., Li, J., Wang, Y., Wu, Y.,

Li, J., and Zheng, Z. (2023). A secure and ﬂexi-

ble blockchain-based ofﬂine payment protocol. IEEE

Transactions on Computers, 73(2):408–421.

Krishna, G. S. R. and Rekha, P. (2022). Food supply

chain traceability system using blockchain technol-

ogy. In 2022 8th International Conference on Signal

Processing and Communication (ICSC), pages 370–

375. IEEE.

Li, J., Li, S., Zhang, Y., and Tang, X. (2023). Evolutionary

game analysis of rent seeking in inventory ﬁnancing

based on blockchain technology. Managerial and De-

cision Economics, 44(8):4278–4294.

Li, J., Zhang, M., Jia, X., and Lin, D. (2024). A blockchain-

based service for public sector governance. In

2024 IEEE International Conference on Web Services

(ICWS), pages 1406–1408. IEEE.

Liu, G., Han, H., Ding, W., Fei, S., and Yan, Z. (2023).

Demo paper: Anonymous authentication on trust in

blockchain-based mobile crowdsourcing system. In

2023 IEEE International Conference on Blockchain

(Blockchain), pages 140–144.

Mssassi, S. and Abou El Kalam, A. (2024). Game theory-

based incentive design for mitigating malicious be-

havior in blockchain networks. Journal of Sensor and

Actuator Networks, 13(1):7.

Punith, M., Shukla, R., and Yadav, S. (2022). Blockchain

based electronic voting machine. In 2022 Interna-

tional Conference on Edge Computing and Applica-

tions (ICECAA), pages 479–483. IEEE.

Shashank, S. A., Prajapati, V. K., Manitha, P., and Nithya,

M. (2023). Iot-driven health monitoring system cou-

pled with blockchain. In 2023 Fourth International

Conference on Smart Technologies in Computing,

Electrical and Electronics (ICSTCEE), pages 1–5.

IEEE.

Shi, C. J. L., Bugtai, N. T., and Billones, R. K. C. (2022).

Multi-period inventory management optimization us-

ing integer linear programming: A case study on ply-

wood distribution. In 2022 IEEE 14th International

Conference on Humanoid, Nanotechnology, Informa-

tion Technology, Communication and Control, Envi-

ronment, and Management (HNICEM), pages 1–5.

IEEE.

Song, W., Wu, H., Meng, H., Bian, Y., Tang, C., Xi, J., and

Zhu, H. (2023). A blockchain based fund manage-

ment system for construction projects - a comprehen-

sive case study in xiong’an new area china. In 2023

INCOFT 2025 - International Conference on Futuristic Technology

Tenth International Conference on Software Deﬁned

Systems (SDS), pages 28–33.

Stodt, F. and Reich, C. (2023). Introducing a fair tax method

to harden industrial blockchain applications against

network attacks: A game theory approach. Comput-

ers, 12(3).

Tang, W., Zhang, J., and Guo, R. (2023). A blockchain-

based for trustworthy tourism service level agreement.

In 2023 3rd International Conference on Computer

Science and Blockchain (CCSB), pages 195–199.

Toyos-Marfurt, G., Abdallah, R., and Garc

ıa-P

erez,

(2024). Notara: Efﬁcient blockchain asset notariza-

tion service. In 2024 6th Conference on Blockchain

Research & Applications for Innovative Networks and

Services (BRAINS), pages 1–3. IEEE.

Wang, X., Jia, J., Cao, Y., Du, J., Hu, A., Liu, Y., and Wang,

Z. (2023a). Application of data storage management

system in blockchain-based technology. In 2023 IEEE

2nd International Conference on Electrical Engineer-

ing, Big Data and Algorithms (EEBDA), pages 1437–

1440.

Wang, Y., Ali, J., Arshad, J., and Liu, Y. (2023b). A proxy-

layer approach to secure smart contract deployment

on private evm-based poa blockchains. In 2023 IEEE

International Conference on Blockchain (Blockchain),

pages 109–112. IEEE.

Wu, Y., Wang, Y., Yan, F., and Chen, W. (2024).

Shardingsim: A modular committee-based shard-

ing blockchain simulator. In 2024 IEEE Interna-

tional Conference on Blockchain and Cryptocurrency

(ICBC), pages 273–278.

Yin, Z., Bai, B., Liu, Y., and Cheng, T. (2024). Research on

distributed node resource optimization mechanism for

multi-agent systems combined with blockchain tech-

nology. In 2024 IEEE International Conference on

Blockchain (Blockchain), pages 536–541. IEEE.

Zhang, Y. and Wang, S. (2024). Proof of sampling: A

nash equilibrium-secured veriﬁcation protocol for de-

centralized systems.

Leveraging Nash Equilibrium and Integer Linear Programming for Real-Time Fraud Detection and Optimization in Blockchain Networks